Mutual Information in Molecular and Macromolecular Systems
Abstract
:1. Introduction
2. Dynamical Heterogeneity and Mutual Information between Particle Displacements
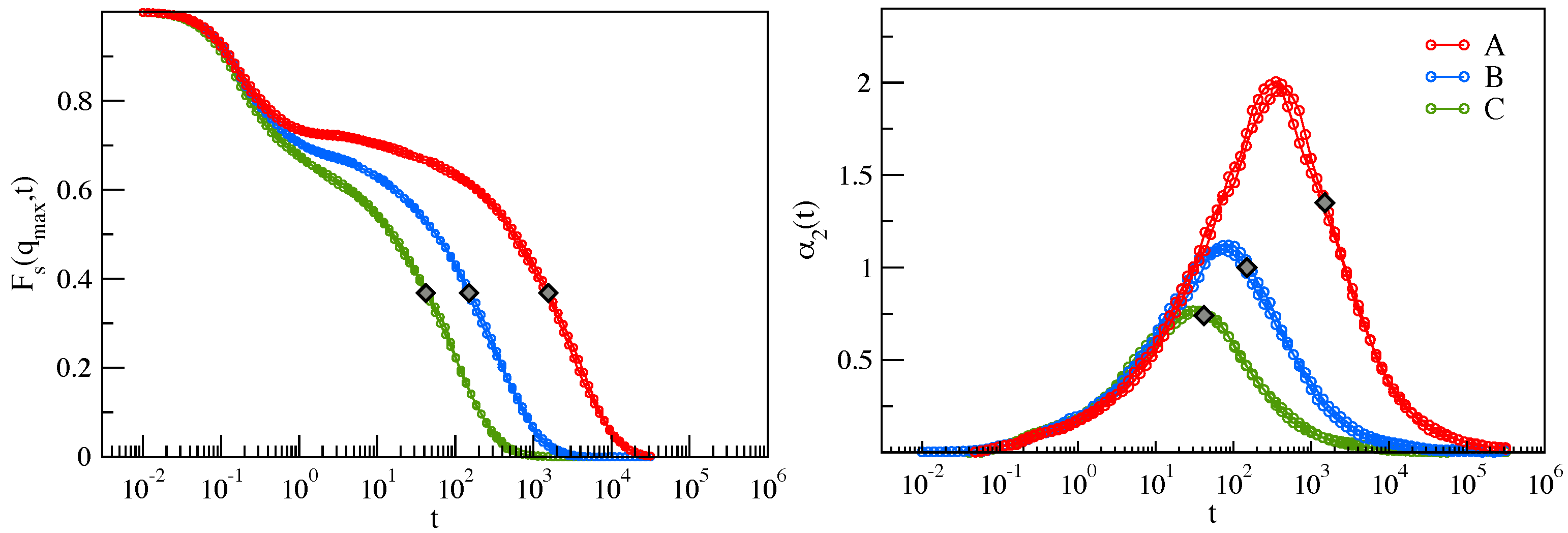
2.1. Mutual Information Reveals DH in a Molecular Liquid
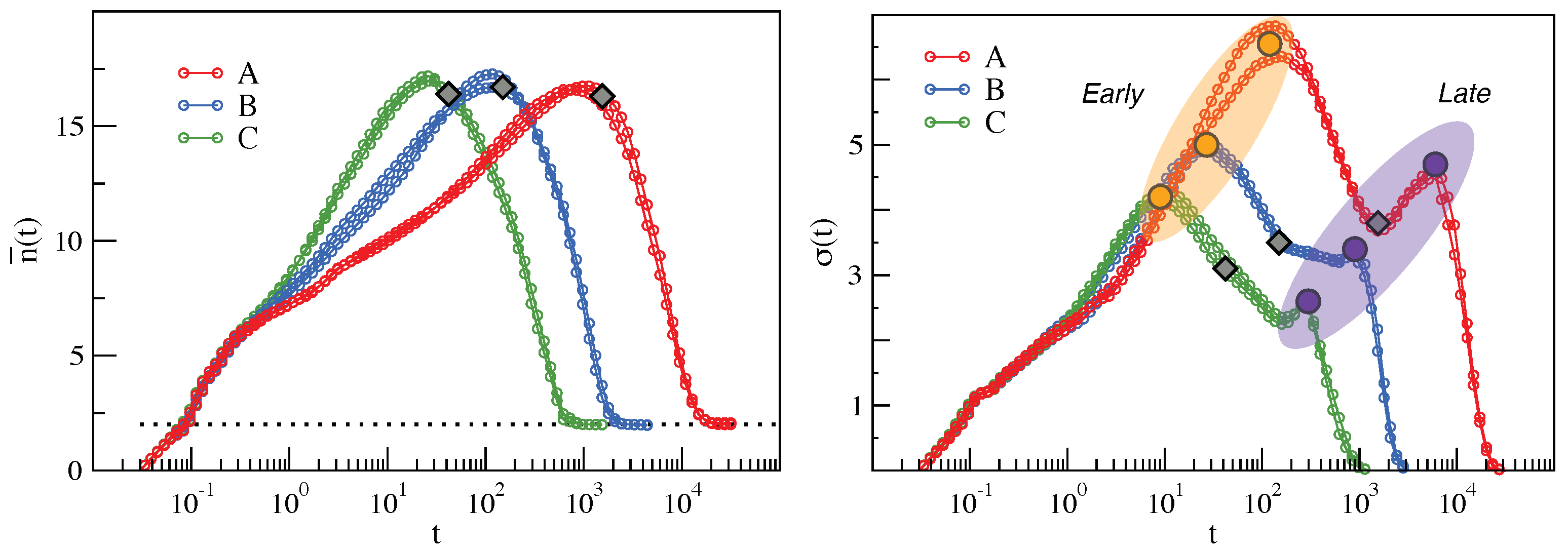
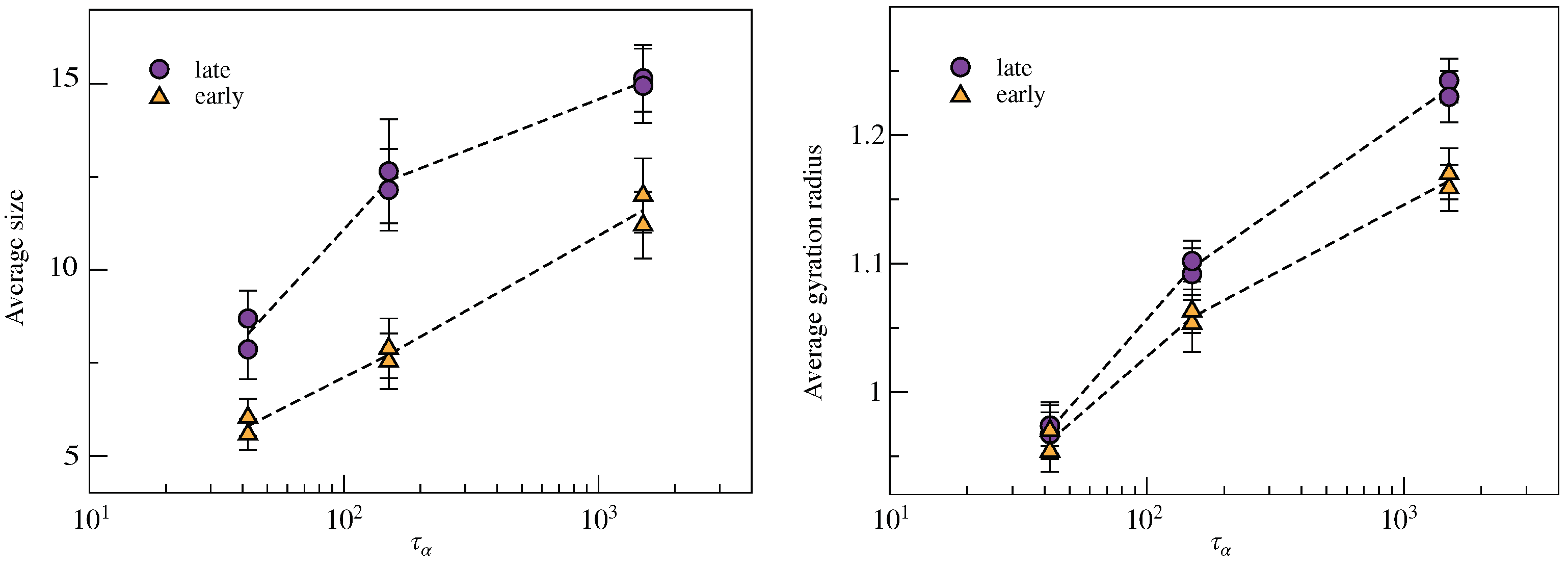
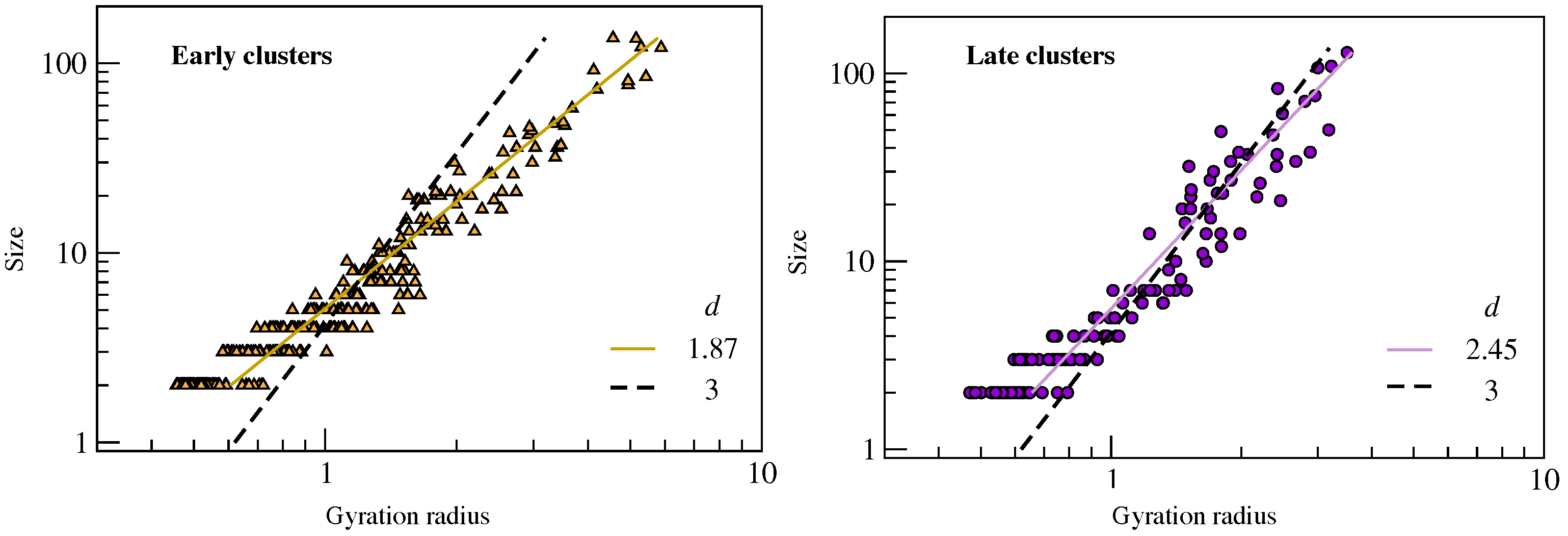
2.2. Clustering of Early and Late Fractions
- 1
- A particle of a given population is chosen and included as first member of a possible cluster;
- 2
- Particles of the same population within distance ℓ from the first member are searched and, in the positive case, added to the cluster;
- 3
- Step 2 is repeated for all new members of the cluster;
- 4
- If no new members are found and , the cluster is completed and its size M is defined;
- 5
- All of the particles involved in the already identified clusters are removed, and the procedure is restarted from step 1 by considering one left particle.
3. Mutual Information and Johari–Goldstein -Relaxation in a Model Polymer Melt
3.1. Mutual Information and Bond Reorientation
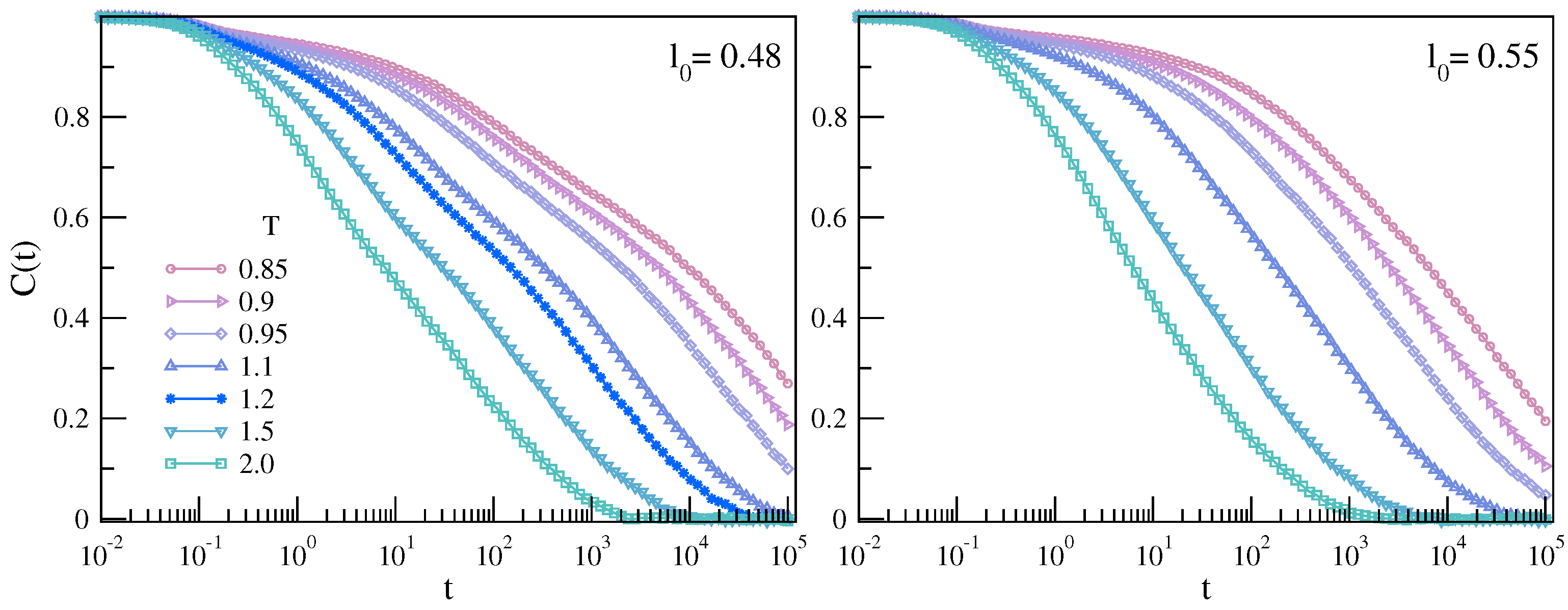
3.1.1. MI Correlation in Time Domain
3.1.2. MI Correlation in the Frequency Domain
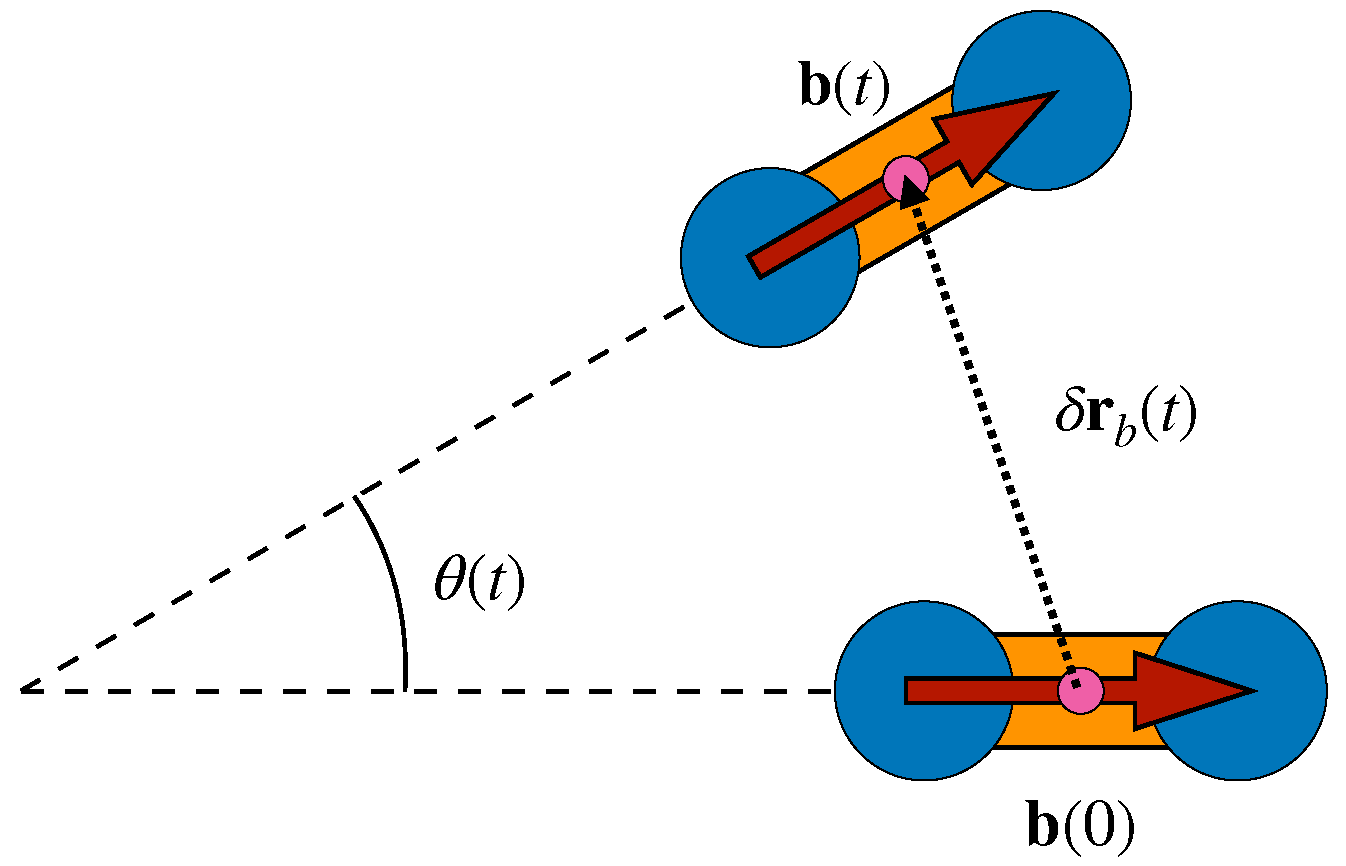
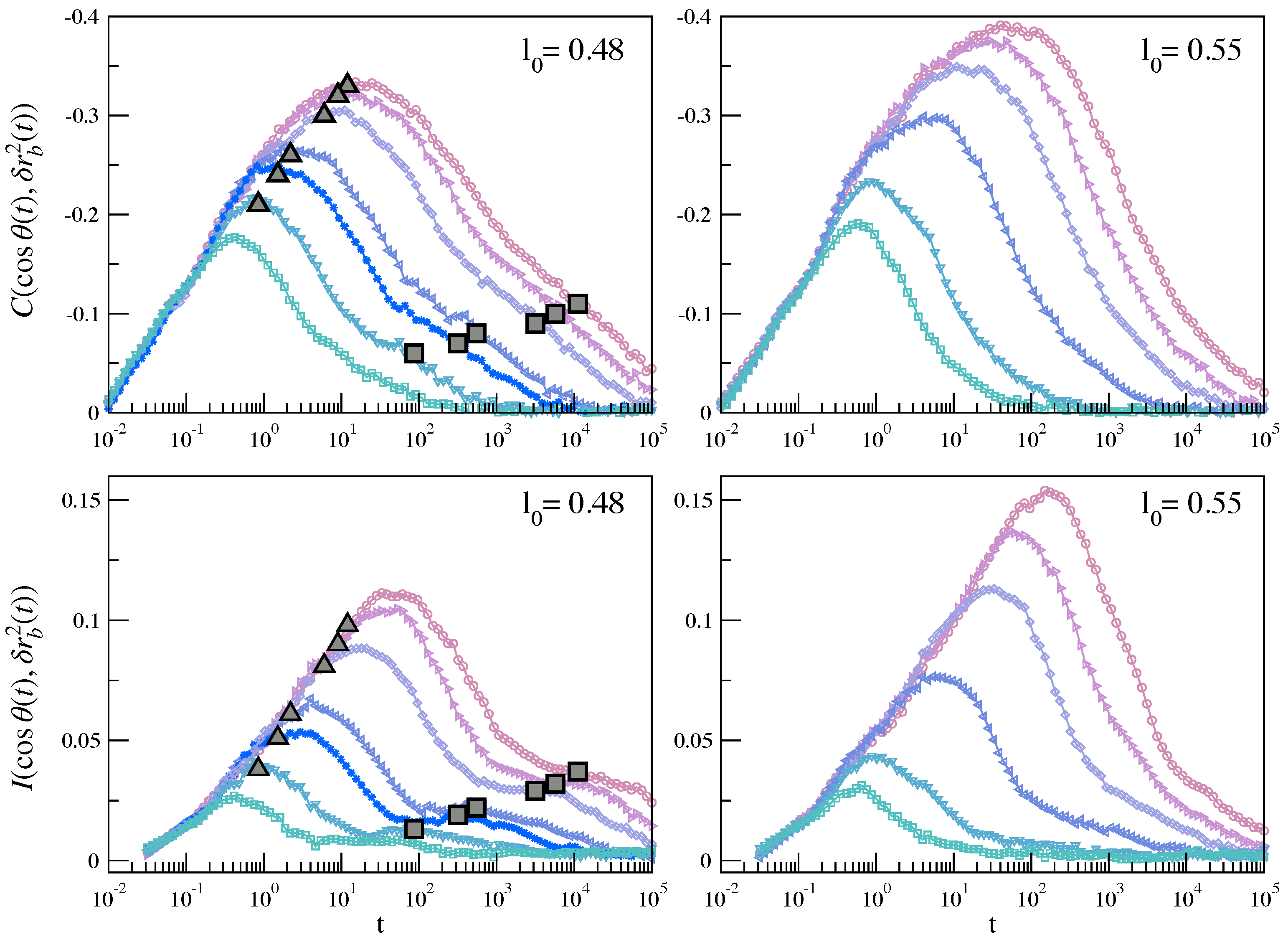
3.2. Dynamic Heterogeneity and Mutual Information between Displacement and Rotation of the Bond
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCF | Bond correlation function |
| DH | Dynamical heterogeneity |
| GT | Glass transition |
| ICE | Iso-configurational ensemble |
| ISF | Intermediate scattering function |
| JG | Johari–Goldstein |
| MD | Molecular Dynamics |
| MI | Mutual information |
| NGP | Non-Gaussian parameter |
References
- Debenedetti, P.G. Metastable Liquids; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef]
- Schmidt-Rohr, K.; Spiess, H.W. Nature of nonexponential loss of correlation above the glass transition investigated by multidimensional NMR. Phys. Rev. Lett. 1991, 66, 3020–3023. [Google Scholar] [CrossRef]
- Schiener, B.; Böhmer, R.; Loidl, A.; Chamberlin, R.V. Nonresonant Spectral Hole Burning in the Slow Dielectric Response of Supercooled Liquids. Science 1996, 274, 752–754. [Google Scholar] [CrossRef]
- Böhmer, R.; Hinze, G.; Diezemann, G.; Geil, B.; Sillescu, H. Dynamic heterogeneity in supercooled ortho-terphenyl studied by multidimensional deuteron NMR. Europhys. Lett. (EPL) 1996, 36, 55–60. [Google Scholar] [CrossRef]
- Lačević, N.; Starr, F.W.; Schrøder, T.B.; Glotzer, S.C. Spatially heterogeneous dynamics investigated via a time-dependent four-point density correlation function. J. Chem. Phys. 2003, 119, 7372–7387. [Google Scholar] [CrossRef] [Green Version]
- Charbonneau, P.; Reichman, D.R. Dynamical Heterogeneity and Nonlinear Susceptibility in Supercooled Liquids with Short-Range Attraction. Phys. Rev. Lett. 2007, 99, 135701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sethna, J.P. Statistical Mechanics: Entropy, Order Parameters, and Complexity, 2nd ed.; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Evans, D.J.; Morriss, G. Statistical Mechanics of Nonequilibrium Liquids, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Smith, R. A mutual information approach to calculating nonlinearity. Stat 2015, 4, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Mézard, M.; Montanari, A. Information, Physics, and Computation; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Latham, P.E.; Roudi, Y. Mutual information. Scholarpedia 2009, 4, 1658, revision #186917. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Li, W. Mutual information functions versus correlation functions. J. Stat. Phys. 1990, 60, 823–837. [Google Scholar] [CrossRef]
- Dunleavy, A.J.; Wiesner, K.; Royall, C.P. Using mutual information to measure order in model glass-formers. Phys. Rev. E 2012, 86, 041505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunleavy, A.J.; Wiesner, K.; Yamamoto, R.; Royall, C.P. Mutual information reveals multiple structural relaxation mechanisms in a model glass former. Nat. Commun. 2015, 6, 6089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, H.; Tanaka, H. Role of Attractive Interactions in Structure Ordering and Dynamics of Glass-Forming Liquids. Phys. Rev. Lett. 2020, 124, 225501. [Google Scholar] [CrossRef]
- Iaconis, J.; Inglis, S.; Kallin, A.B.; Melko, R.G. Detecting classical phase transitions with Renyi mutual information. Phys. Rev. B 2013, 87, 195134. [Google Scholar] [CrossRef] [Green Version]
- Sriluckshmy, P.V.; Mandal, I. Critical scaling of the mutual information in two-dimensional disordered Ising models. J. Stat. Mech. Theory Exp. 2018, 2018, 043301. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.C.; Widom, M. Information Entropy of Liquid Metals. J. Phys. Chem. B 2018, 122, 3550–3555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tripodo, A.; Giuntoli, A.; Malvaldi, M.; Leporini, D. Mutual information does not detect growing correlations in the propensity of a model molecular liquid. Soft Matter 2019, 15, 6784–6790. [Google Scholar] [CrossRef]
- Tripodo, A.; Puosi, F.; Malvaldi, M.; Leporini, D. Vibrational scaling of the heterogeneous dynamics detected by mutual information. Eur. Phys. J. E 2019, 42, 1–10. [Google Scholar] [CrossRef]
- Tripodo, A.; Puosi, F.; Malvaldi, M.; Capaccioli, S.; Leporini, D. Coincident Correlation between Vibrational Dynamics and Primary Relaxation of Polymers with Strong or Weak Johari-Goldstein Relaxation. Polymers 2020, 12, 761. [Google Scholar] [CrossRef] [Green Version]
- Puosi, F.; Tripodo, A.; Malvaldi, M.; Leporini, D. Johari–Goldstein Heterogeneous Dynamics in a Model Polymer. Macromolecules 2021, 54, 2053–2058. [Google Scholar] [CrossRef]
- Sillescu, H. Heterogeneity at the glass transition: A review. J. Non-Cryst. Solids 1999, 243, 81–108. [Google Scholar] [CrossRef]
- Ediger, M.D. Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 2000, 51, 99–128. [Google Scholar] [CrossRef] [Green Version]
- Richert, R. Heterogeneous dynamics in liquids: Fluctuations in space and time. J. Phys. Condens. Matter 2002, 14, R703–R738. [Google Scholar] [CrossRef]
- Tracht, U.; Wilhelm, M.; Heuer, A.; Feng, H.; Schmidt-Rohr, K.; Spiess, H.W. Length Scale of Dynamic Heterogeneities at the Glass Transition Determined by Multidimensional Nuclear Magnetic Resonance. Phys. Rev. Lett. 1998, 81, 2727–2730. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the Temperature Dependence of Cooperative Relaxation Properties in Glass-Forming Liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef] [Green Version]
- Albert, S.; Bauer, T.; Michl, M.; Biroli, G.; Bouchaud, J.P.; Loidl, A.; Lunkenheimer, P.; Tourbot, R.; Wiertel-Gasquet, C.; Ladieu, F. Fifth-order susceptibility unveils growth of thermodynamic amorphous order in glass-formers. Science 2016, 352, 1308–1311. [Google Scholar] [CrossRef] [Green Version]
- Biroli, G.; Karmakar, S.; Procaccia, I. Comparison of Static Length Scales Characterizing the Glass Transition. Phys. Rev. Lett. 2013, 111, 165701. [Google Scholar] [CrossRef] [Green Version]
- Wyart, M.; Cates, M.E. Does a Growing Static Length Scale Control the Glass Transition? Phys. Rev. Lett. 2017, 119, 195501. [Google Scholar] [CrossRef] [Green Version]
- Karmakar, S.; Dasgupta, C.; Sastry, S. Length scales in glass-forming liquids and related systems: A review. Rep. Prog. Phys. 2015, 79, 016601. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 3rd ed.; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Puosi, F.; Tripodo, A.; Leporini, D. Fast Vibrational Modes and Slow Heterogeneous Dynamics in Polymers and Viscous Liquids. Int. J. Mol. Sci. 2019, 20, 5708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Larini, L.; Ottochian, A.; De Michele, C.; Leporini, D. Universal scaling between structural relaxation and vibrational dynamics in glass-forming liquids and polymers. Nat. Phys. 2008, 4, 42–45. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Clustering Methods. In Data Mining and Knowledge Discovery Handbook, 2nd ed.; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2010; pp. 321–352. [Google Scholar] [CrossRef]
- Donati, C.; Douglas, J.F.; Kob, W.; Plimpton, S.J.; Poole, P.H.; Glotzer, S.C. Stringlike Cooperative Motion in a Supercooled Liquid. Phys. Rev. Lett. 1998, 80, 2338–2341. [Google Scholar] [CrossRef] [Green Version]
- Donati, C.; Glotzer, S.C.; Poole, P.H. Growing Spatial Correlations of Particle Displacements in a Simulated Liquid on Cooling toward the Glass Transition. Phys. Rev. Lett. 1999, 82, 5064–5067. [Google Scholar] [CrossRef] [Green Version]
- Starr, F.W.; Douglas, J.F.; Sastry, S. The relationship of dynamical heterogeneity to the Adam-Gibbs and random first-order transition theories of glass formation. J. Chem. Phys. 2013, 138, 12A541. [Google Scholar] [CrossRef] [Green Version]
- McCrum, N.G.; Read, B.E.; Williams, G. Anelastic and Dielectric Effects in Polymeric Solids; Dover Publications: New York, NY, USA, 1991. [Google Scholar]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef] [Green Version]
- Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: Berlin, Germany, 2011. [Google Scholar]
- Johari, G.P.; Goldstein, M. Viscous Liquids and the Glass Transition. II. Secondary Relaxations in Glasses of Rigid Molecules. J. Chem. Phys. 1970, 53, 2372. [Google Scholar] [CrossRef]
- Ngai, K. Relation between some secondary relaxations and the a relaxations in glass-forming materials according to the coupling model. J. Chem. Phys. 1998, 109, 6982–6994. [Google Scholar] [CrossRef]
- Ngai, K.L.; Paluch, M. Classification of secondary relaxation in glass-formers based on dynamic properties. J. Chem. Phys. 2004, 120, 857–873. [Google Scholar] [CrossRef] [PubMed]
- Capaccioli, S.; Paluch, M.; Prevosto, D.; Wang, L.M.; Ngai, K.L. Many-Body Nature of Relaxation Processes in Glass-Forming Systems. J. Phys. Chem. Lett. 2012, 3, 735–743. [Google Scholar] [CrossRef]
- Cicerone, M.T.; Zhong, Q.; Tyagi, M. Picosecond Dynamic Heterogeneity, Hopping, and Johari-Goldstein Relaxation in Glass-Forming Liquids. Phys. Rev. Lett. 2014, 113, 117801. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.B.; Richert, R.; Samwer, K. Structural rearrangements governing Johari-Goldstein relaxations in metallic glasses. Sci. Adv. 2017, 3, 1701577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedrov, D.; Smith, G.D. Molecular dynamics simulation study of the α and β-relaxation processes in a realistic model polymer. Phys. Rev. E 2005, 71, 050801. [Google Scholar] [CrossRef] [PubMed]
- Bedrov, D.; Smith, G.D. Secondary Johari–Goldstein relaxation in linear polymer melts represented by a simple bead-necklace model. J. Non-Cryst. Solids 2011, 357, 258–263. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Roland, C.M. Participation in the Johari–Goldstein Process: Molecular Liquids versus Polymers. Macromolecules 2017, 50, 4039–4042. [Google Scholar] [CrossRef] [Green Version]
- Fragiadakis, D.; Roland, C.M. Molecular dynamics simulation of the Johari-Goldstein relaxation in a molecular liquid. Phys. Rev. E 2012, 86, 020501. [Google Scholar] [CrossRef] [Green Version]
- Barbieri, A.; Campani, E.; Capaccioli, S.; Leporini, D. Molecular dynamics study of the thermal and the density effects on the local and the large-scale motion of polymer melts: Scaling properties and dielectric relaxation. J. Chem. Phys. 2004, 120, 437–453. [Google Scholar] [CrossRef] [Green Version]
- Ngai, K.L. Dynamic and thermodynamic properties of glass-forming substances. J. Non-Cryst. Solids 2000, 275, 7–51. [Google Scholar] [CrossRef]
- Bordat, P.; Affouard, F.; Descamps, M.; Ngai, K.L. Does the interaction potential determine both the fragility of a liquid and the vibrational properties of its glassy state? Phys. Rev. Lett. 2004, 93, 105502. [Google Scholar] [CrossRef] [Green Version]
- Caporaletti, F.; Capaccioli, S.; Valenti, S.; Mikolasek, M.; Chumakov, A.I.; Monaco, G. A microscopic look at the Johari-Goldstein relaxation in a hydrogen-bonded glass-former. Sci. Rep. 2019, 9, 14319. [Google Scholar] [CrossRef] [PubMed] [Green Version]



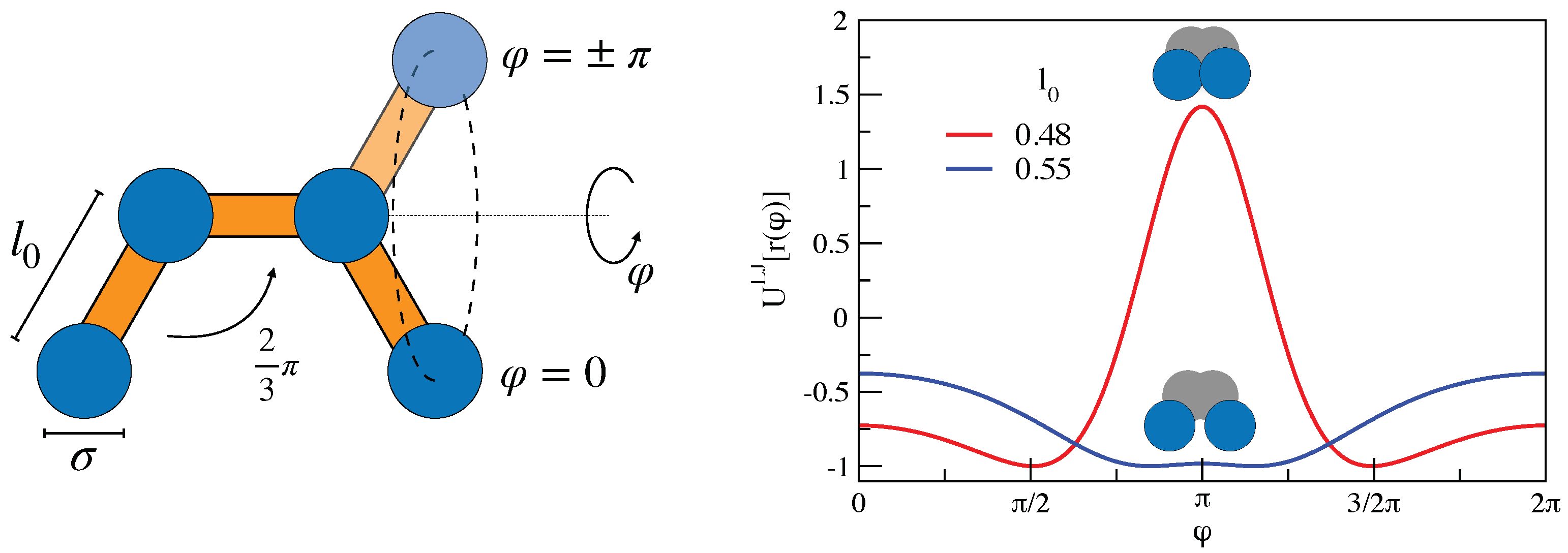



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tripodo, A.; Puosi, F.; Malvaldi, M.; Leporini, D. Mutual Information in Molecular and Macromolecular Systems. Int. J. Mol. Sci. 2021, 22, 9577. https://doi.org/10.3390/ijms22179577
Tripodo A, Puosi F, Malvaldi M, Leporini D. Mutual Information in Molecular and Macromolecular Systems. International Journal of Molecular Sciences. 2021; 22(17):9577. https://doi.org/10.3390/ijms22179577
Chicago/Turabian StyleTripodo, Antonio, Francesco Puosi, Marco Malvaldi, and Dino Leporini. 2021. "Mutual Information in Molecular and Macromolecular Systems" International Journal of Molecular Sciences 22, no. 17: 9577. https://doi.org/10.3390/ijms22179577
APA StyleTripodo, A., Puosi, F., Malvaldi, M., & Leporini, D. (2021). Mutual Information in Molecular and Macromolecular Systems. International Journal of Molecular Sciences, 22(17), 9577. https://doi.org/10.3390/ijms22179577






