Catalytic Asymmetry in Homodimeric H+-Pumping Membrane Pyrophosphatase Demonstrated by Non-Hydrolyzable Pyrophosphate Analogs
Abstract
:1. Introduction
2. Results
2.1. Kinetics of Dh-mPPase Inhibition by Substrate Analogs Demonstrates Nonequivalent Active Sites
2.2. Metal Cofactors Modulate Catalytic Asymmetry in mPPase
2.3. Membrane Role in Catalytic Asymmetry
3. Discussion
3.1. Catalytic Asymmetry in mPPase
3.2. The Roles of the Metal Cofactors in the Catalytic Asymmetry
4. Materials and Methods
4.1. Materials
4.2. PPi Hydrolysis Assay
4.3. Calculations and Data Treatment
5. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baltscheffsky, H. Energy conversion leading to the origin and early evolution of life: Did inorganic pyrophosphate precede adenosine triphosphate? In Origin and Evolution of Biological Energy Conversion; Baltscheffsky, H., Ed.; VCH: New York, NY, USA, 1996; pp. 1–9. [Google Scholar]
- Heinonen, J.K. Biological Role of Inorganic Pyrophosphate; Kluwer Academic Publishers: London, UK, 2001. [Google Scholar]
- Baltscheffsky, H.; Von Stedingk, L.V.; Heldt, H.W.; Klingenberg, M. Inorganic pyrophosphatase: Formation in bacterial photophosphorylation. Science 1966, 153, 1120–1122. [Google Scholar] [CrossRef]
- Baykov, A.A.; Malinen, A.M.; Luoto, H.H.; Lahti, R. Pyrophosphate-fueled Na+ and H+ transport in prokaryotes. Microbiol. Mol. Biol. Rev. 2013, 77, 267–276. [Google Scholar] [CrossRef] [Green Version]
- Tsai, J.Y.; Kellosalo, J.; Sun, Y.J.; Goldman, A. Proton/sodium pumping pyrophosphatases: The last of the primary ion pumps. Curr. Opin. Struct. Biol. 2014, 27, 38–47. [Google Scholar] [CrossRef]
- Serrano, A.; Pérez-Castiñeira, J.; Baltscheffsky, M.; Baltscheffsky, H. H+-PPases: Yesterday, today and tomorrow. IUBMB Life 2007, 59, 76–83. [Google Scholar] [CrossRef]
- Drozdowicz, Y.M.; Rea, P.A. Vacuolar H+ pyrophosphatases: From the evolutionary backwaters into the mainstream. Trends Plant Sci. 2001, 6, 206–211. [Google Scholar] [CrossRef]
- Maeshima, M. Vacuolar H+-pyrophosphatase. Biochim. Biophys. Acta 2000, 1465, 37–51. [Google Scholar] [CrossRef] [Green Version]
- Gaxiola, R.A.; Palmgren, M.G.; Schumacher, K. Plant proton pumps. FEBS Lett. 2007, 581, 2204–2221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gutiérrez-Luna, F.M.; Hernandez-Dominguez, E.E.; Valencia-Turcotte, L.G.; Rodríguez-Sotres, R. Pyrophosphate and pyrophosphatases in plants, their involvement in stress responses and their possible relationship to secondary metabolism. Plant Sci. 2018, 267, 11–19. [Google Scholar] [CrossRef]
- Pérez-Castiñeira, J.R.; Serrano, A. The H+-translocating inorganic pyrophosphatase from Arabidopsis thaliana is more sensitive to sodium than its Na+-translocating counterpart from Methanosarcina mazei. Front. Plant Sci. 2020, 11, 1240. [Google Scholar] [CrossRef] [PubMed]
- Igamberdiev, A.U.; Kleczkowski, L.A. Pyrophosphate as an alternative energy currency in plants. Biochem. J. 2021, 478, 1515–1524. [Google Scholar] [CrossRef]
- Boyer, P.D. The binding change mechanism for ATP synthase–some probabilities and possibilities. Biochim. Biophys. Acta Bioenerg. 1993, 1140, 215–250. [Google Scholar] [CrossRef]
- Boyer, P.D. Energy, life, and ATP (Nobel Lecture). Angew. Chem. Int. Ed. 1998, 37, 2297–2307. [Google Scholar] [CrossRef]
- Walker, J.E. ATP synthesis by rotary catalysis (Nobel Lecture). Angew. Chem. Int. Ed. 1998, 37, 2309–2319. [Google Scholar] [CrossRef]
- Noji, H.; Yasuda, R.; Yoshida, M.K.K., Jr. Direct observation of the rotation of F1-ATPase. Nat. Cell Biol. 1997, 386, 299–302. [Google Scholar] [CrossRef]
- Lin, S.M.; Tsai, J.Y.; Hsiao, C.D.; Huang, Y.T.; Chiu, C.L.; Liu, M.H.; Tung, J.Y.; Liu, T.H.; Pan, R.L.; Sun, Y.J. Crystal structure of a membrane-embedded H+-translocating pyrophosphatase. Nature 2012, 484, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Baykov, A.A. Energy coupling in cation-pumping pyrophosphatase—Back to Mitchell. Front. Plant Sci. 2020, 11. [Google Scholar] [CrossRef] [Green Version]
- Artukka, E.; Luoto, H.H.; Baykov, A.A.; Lahti, R.; Malinen, A.M. Role of the potassium/lysine cationic center in catalysis and functional asymmetry in membrane-bound pyrophosphatases. Biochem. J. 2018, 475, 1141–1158. [Google Scholar] [CrossRef]
- Leigh, R.A.; Pope, A.J.; Jennings, I.R.; Sanders, D. Kinetics of the vacuolar H+-pyrophosphatase. The roles of magnesium, pyrophosphate, and their complexes as substrates, activators, and inhibitors. Plant Physiol. 1992, 100, 1698–1705. [Google Scholar] [CrossRef] [Green Version]
- Luoto, H.H.; Nordbo, E.; Malinen, A.M.; Baykov, A.A.; Lahti, R. Evolutionarily divergent, Na+-regulated H+-transporting membrane-bound pyrophosphatases. Biochem. J. 2015, 467, 281–291. [Google Scholar] [CrossRef]
- Wu, J.J.; Ma, J.T.; Pan, R.L. Functional size analysis of pyrophosphatase from Rhodospirillum rubrum determined by radiation inactivation. FEBS Lett. 1991, 283, 57–60. [Google Scholar] [CrossRef]
- Sarafian, V.; Potier, M.; Poole, R.J. Radiation-inactivation analysis of vacuolar H+-ATPase and H+-pyrophosphatase from Beta vulgaris L. Functional sizes for substrate hydrolysis and for H+ transport. Biochem. J. 1992, 283, 493–497. [Google Scholar] [CrossRef] [Green Version]
- Tzeng, C.M.; Yang, C.Y.; Yang, S.J.; Jiang, S.S.; Kuo, S.Y.; Hung, S.-H.; Ma, J.T.; Pan, R.L. Subunit structure of vacuolar proton-pyrophosphatase as determined by radiation inactivation. Biochem. J. 1996, 316, 143–147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vidilaseris, K.; Kiriazis, A.; Turku, A.; Khattab, A.; Johansson, N.G.; Leino, T.O.; Kiuru, P.S.; Boije af Gennäs, G.; Meri, S.; Yli-Kauhaluoma, J.; et al. Asymmetry in catalysis by Thermotoga maritima membrane bound pyro-phosphatase demonstrated by a nonphosphorus allosteric inhibitor. Sci. Adv. 2019, 5, eaav7574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boduszek, B.; Dyba, M.; Jezowska-Bojczuk, M.; Kiss, T.; Kozłowski, H. Biologically active pyridine mono- and bis-phosphonates: Efficient ligands for co-ordination of Cu2+ ions. J. Chem. Soc. Dalton Trans. 1997, 973–976. [Google Scholar] [CrossRef]
- Reynolds, M.A.; Gerlt, J.A.; Demou, P.C.; Opperheimer, N.J.; Kenyon, G.L. 15N and 17O NMR studies of the proton binding sites in imidodiphosphate, tetraethyl imidodiphosphate, and adenylyl imidodiphosphate. J. Am. Chem. Soc. 1983, 105, 6475–6481. [Google Scholar] [CrossRef]
- Baykov, A.A.; Anashkin, V.A.; Malinen, A.M. Good-practice non-radioactive assays of inorganic pyrophosphatase activities. Molecules 2021, 26, 2356. [Google Scholar] [CrossRef]
- Baykov, A.A.; Dubnova, E.B.; Bakuleva, N.P.; Evtushenko, O.A.; Zhen, R.-G.; Rea, P.A. Differential sensitivity of membrane-associated pyrophosphatases to inhibition by diphosphonates and fluoride deliniates two classes of enzyme. FEBS Lett. 1993, 2, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Gordon-Weeks, R.; Parmar, S.; Davies, T.G.E.; Leigh, R.A. Structural aspects of the effectiveness of bisphosphonates as competitive inhibitors of the plant vacuolar proton-pumping pyrophosphatase. Biochem. J. 1999, 337, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Bisswanger, H. Enzyme Kinetics. Principles and Methods, 2nd ed.; Wiley-VCH Verlag: Weinheim, Germany, 2008. [Google Scholar] [CrossRef]
- Kellosalo, J.; Kajander, T.; Kogan, K.; Pokharel, K.; Goldman, A. The structure and catalytic cycle of a sodium-pumping pyrophosphatase. Science 2012, 337, 473–476. [Google Scholar] [CrossRef]
- Li, K.M.; Wilkinson, C.; Kellosalo, J.; Tsai, J.Y.; Kajander, T.; Jeuken, L.J.C.; Sun, Y.J.; Goldman, A. Membrane pyrophosphatases from Thermotoga maritima and Vigna radiata suggest a conserved coupling mechanism. Nat. Commun. 2016, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Jodaitis, L.; van Oene, T.; Martens, C. Assessing the role of lipids in the molecular mechanism of membrane proteins. Int. J. Mol. Sci. 2021, 22, 7267. [Google Scholar] [CrossRef]
- Baykov, A.A.; Bakuleva, N.P.; Rea, P.A. Steady-state kinetics of substrate hydrolysis by vacuolar H+-pyrophosphatase. A simple three-state model. Eur. J. Biochem. 1993, 217, 755–762. [Google Scholar] [CrossRef]
- Baykov, A.A.; Sergina, N.V.; Evtushenko, O.A.; Dubnova, E.B. Kinetic characterization of Rhodospirillum rubrum H+ pyrophosphatase in membrane-bound and isolated states. Eur. J. Biochem. 1996, 236, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Malinen, A.M.; Baykov, A.A.; Lahti, R. Mutual effects of cationic ligands and substrate on activity of the Na+-transporting pyrophosphatase of Methanosarcina mazei. Biochemistry 2008, 47, 13447–13454. [Google Scholar] [CrossRef]
- Bradford, M.M. A rapid and sensitive method for the quantitation of microgram quantities of protein utilizing the principle of protein-dye binding. Anal. Biochem. 1976, 72, 248–254. [Google Scholar] [CrossRef]
- Nielsen, M.L.; Ferguson, R.R.; Coackley, W.S. Sodium imidodiphosphate. Synthesis, identification and hydrolytic degradation. J. Am. Chem. Soc. 1961, 83, 99–104. [Google Scholar] [CrossRef]
- Himeno, S.; Ueda, T.; Shiomi, M.; Hori, T. Raman studies on the formation of 12-molybdopyrophosphate. Inorg. Chim. Acta 1997, 262, 219–223. [Google Scholar] [CrossRef]
- Gridney, G.B.; Nichol, C.A. Micro procedure for determination of pyrophosphate and orthophosphate. Anal. Biochem. 1970, 33, 114–119. [Google Scholar]
- Gordon-Weeks, R.; Steele, S.H.; Leigh, R.A. The role of magnesium, pyrophosphate, and their complexes as substrates and activators of the vacuolar H+-pumping inorganic pyrophosphatase. Studies using ligand protection from covalent inhibitors. Plant Physiol. 1996, 111, 195–202. [Google Scholar] [CrossRef] [Green Version]
- Wada, H.; Fernando, Q. Interaction of methanehydroxyphosphonic acid and ethane-1-hydroxy-1,1-diphosphonic acid with alkali and alkaline earth metal ions. Anal. Chem. 1972, 44, 1640–1643. [Google Scholar] [CrossRef]
- Shah, N.R.; Wilkinson, C.; Harborne, S.; Turku, A.; Li, K.-M.; Sun, Y.-J.; Harris, S.; Goldman, A. Insights into the mechanism of membrane pyrophosphatases by combining experiment and computer simulation. Struct. Dyn. 2017, 4, 032105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calisto, F.; Sousa, F.M.; Sena, F.V.; Refojo, P.N.; Pereira, M.M. Mechanisms of energy transduction by charge translocating membrane proteins. Chem. Rev. 2021, 121, 1804–1844. [Google Scholar] [CrossRef] [PubMed]

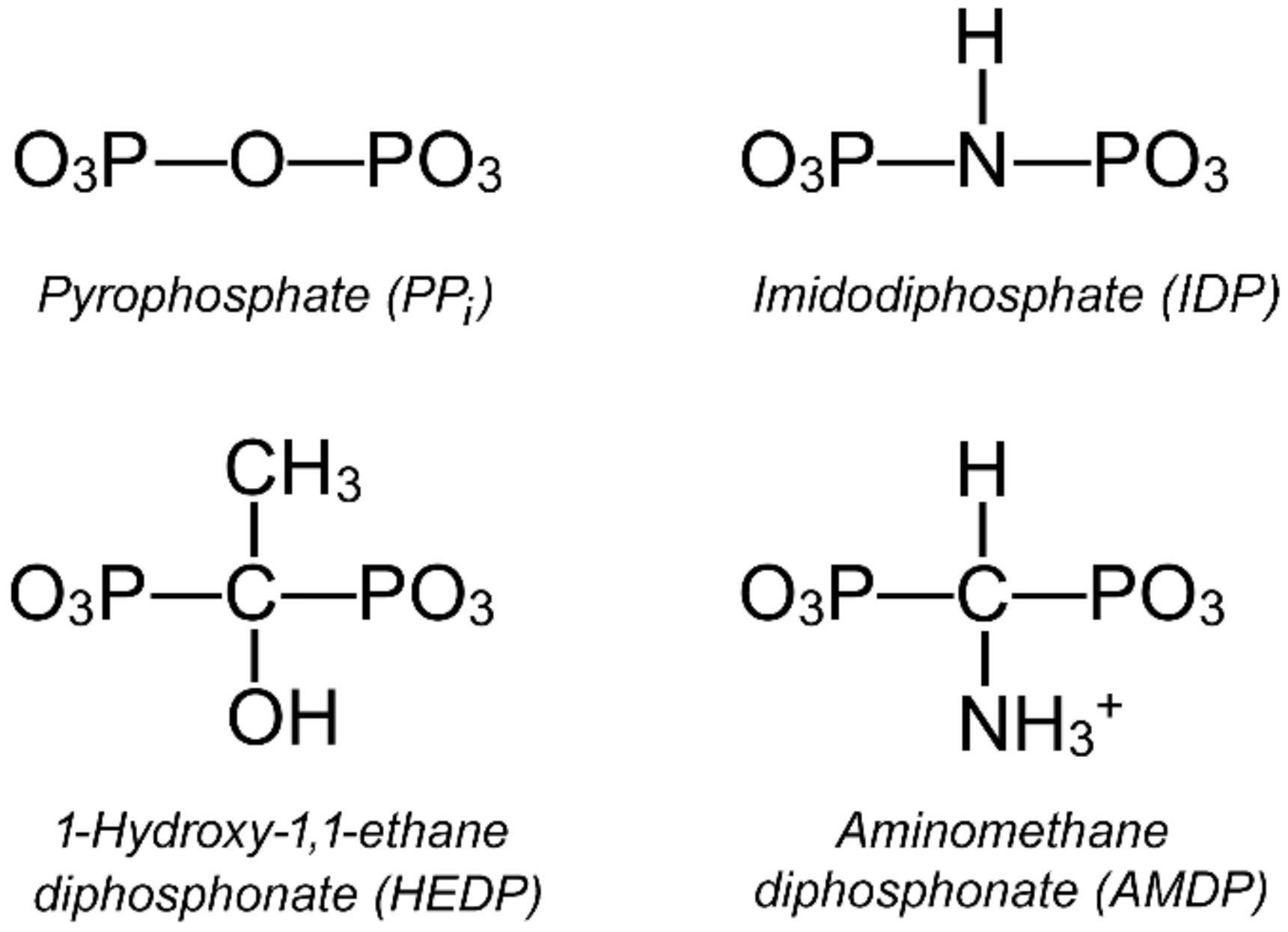
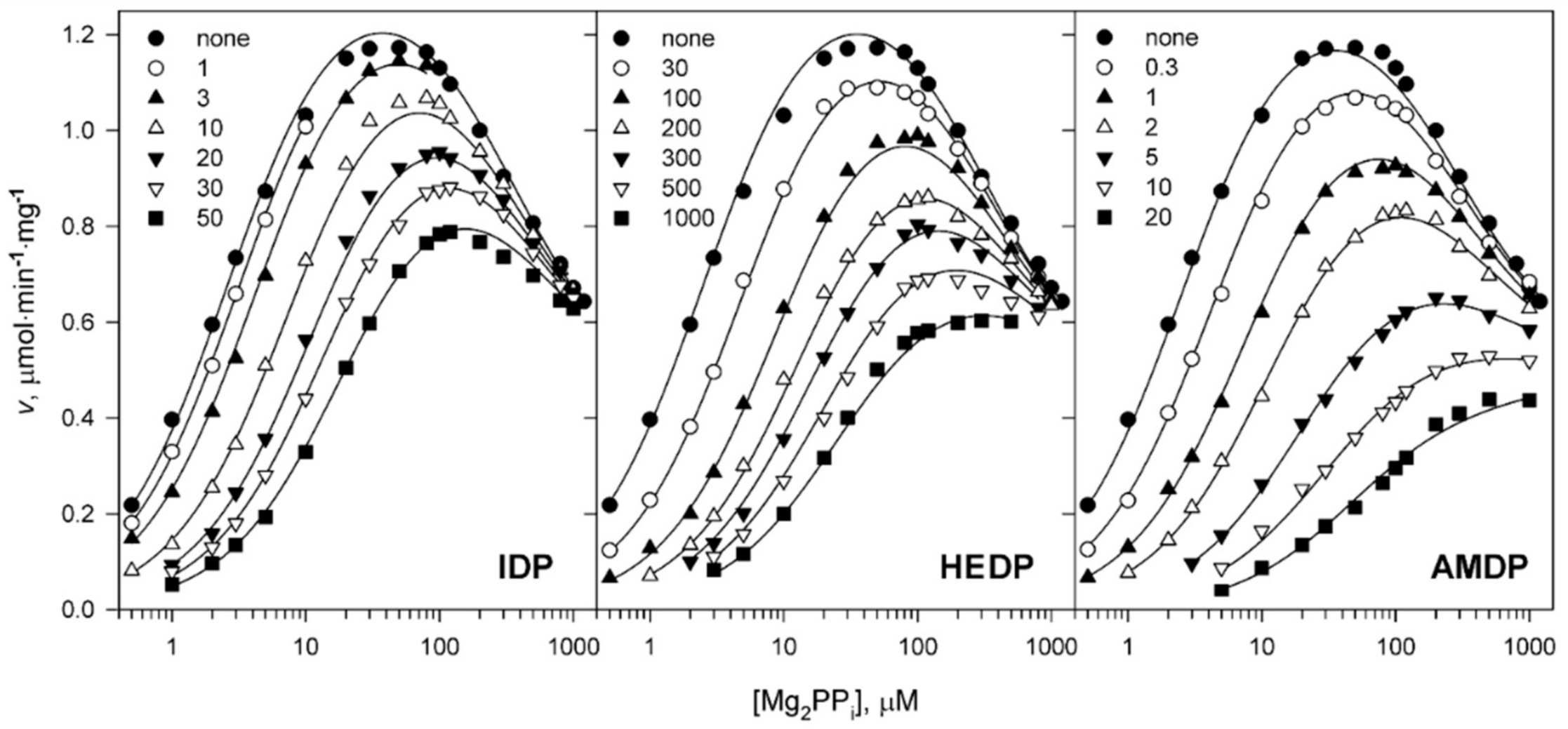



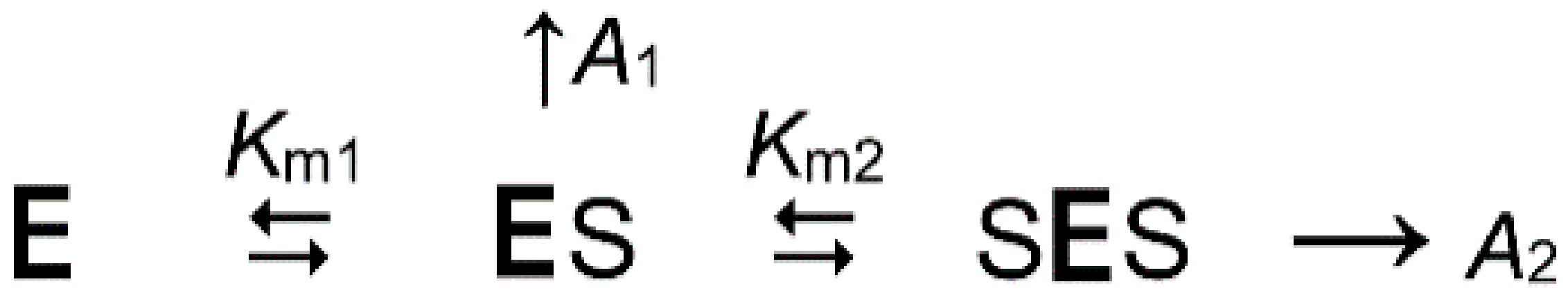

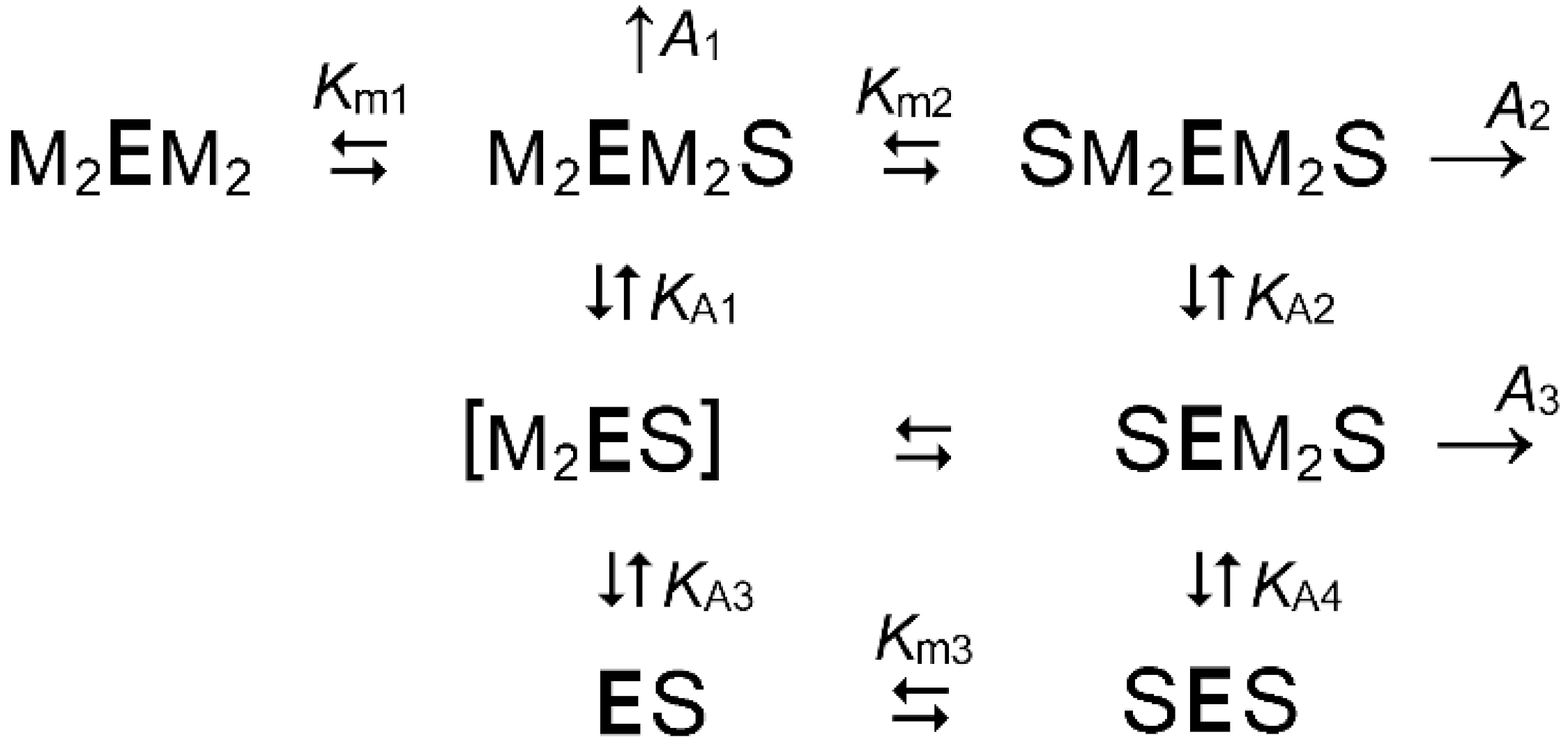

| Parameter | Value | |||
|---|---|---|---|---|
| IDP | HEDP | AMDP | IDP (Na) | |
| A1 (µmol·min−1·mg−1) | 1.32 ± 0.01 | 1.31 ± 0.02 | 1.34 ± 0.02 | 0.27 ± 0.01 |
| A2 (µmol·min−1·mg−1) | 0.40 ± 0.04 | 0.37 ± 0.04 | 0.49 ± 0.02 | <0.20 |
| A3 (µmol·min−1·mg−1) | 0.53 ± 0.05 | 0.51 ± 0.02 | 0.23 ± 0.03 | 0.07 ± 0.04 |
| Ki1 (µM) | 4.2 ± 0.2 | 27 ± 1 | 0.40 ± 0.02 | 2.2 ± 0.2 |
| Ki2 (µM) | >500 | >10,000 | 12.5 ± 2.5 | >500 |
| Ki(s) (µM) | 90 ± 10 | 470 ± 30 | 4.4 ± 0.4 | 110 ± 30 |
| Km1 (µM) | 2.5 ± 0.1 | 2.3 ± 0.1 | 2.6 ± 0.1 | 1.4 ± 0.1 |
| Km2 (µM) | 460 ± 60 | 490 ± 50 | 280 ± 30 | >1000 |
| Km(i) * (µM) | 53 ± 6 | 40 ± 3 | 27 ± 3 | 70 ± 20 |
| RMSD (%) | 3.46 | 3.62 | 3.39 | 7.08 |
| Parameter | Value | |
|---|---|---|
| Scheme 3 | Scheme 3 without M2ES | |
| A1 (µmol·min−1·mg−1) | 1.27 ± 0.02 | 1.27 ± 0.02 |
| A2 (µmol·min−1·mg−1) | 0.40 ± 0.06 | 0.40 ± 0.05 |
| A3 (µmol·min−1·mg−1) | 0.60 ± 0.05 | 0.62 ± 0.05 |
| KA1 (µM2) | 0.004 ± 0.002 | - |
| KA2 (µM2) | 0.47 ± 0.09 | 0.53 ± 0.09 |
| KA3 (µM2) | 0.17 ± 0.12 | - |
| KA4 (µM2) | 0.10 ± 0.01 | 0.10 ± 0.01 |
| KA1KA3 (µM4) | 0.00057 ± 0.00002 | 0.00060 ± 0.00002 |
| KA2KA4 (µM4) | 0.05 ± 0.01 | 0.05 ± 0.01 |
| Km1 (µM) | 2.2 ± 0.1 | 2.17 ± 0.05 |
| Km2 (µM) | 420 ± 70 | 430 ± 80 |
| Km3 * (µM) | 5 ± 1 | |
| RMSD (%) | 3.80 | 3.82 |
| Ligand | Alkali Metal Ion (50 mM) | Dissociation Constant, mM | |
|---|---|---|---|
| KML | KM2L | ||
| PPi | K+ | 0.112 | 2.84 |
| PPi | Na+ | 0.122 | 2.84 |
| HEDP | K+ | 0.200 | 1.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkin, V.A.; Malinen, A.M.; Bogachev, A.V.; Baykov, A.A. Catalytic Asymmetry in Homodimeric H+-Pumping Membrane Pyrophosphatase Demonstrated by Non-Hydrolyzable Pyrophosphate Analogs. Int. J. Mol. Sci. 2021, 22, 9820. https://doi.org/10.3390/ijms22189820
Anashkin VA, Malinen AM, Bogachev AV, Baykov AA. Catalytic Asymmetry in Homodimeric H+-Pumping Membrane Pyrophosphatase Demonstrated by Non-Hydrolyzable Pyrophosphate Analogs. International Journal of Molecular Sciences. 2021; 22(18):9820. https://doi.org/10.3390/ijms22189820
Chicago/Turabian StyleAnashkin, Viktor A., Anssi M. Malinen, Alexander V. Bogachev, and Alexander A. Baykov. 2021. "Catalytic Asymmetry in Homodimeric H+-Pumping Membrane Pyrophosphatase Demonstrated by Non-Hydrolyzable Pyrophosphate Analogs" International Journal of Molecular Sciences 22, no. 18: 9820. https://doi.org/10.3390/ijms22189820
APA StyleAnashkin, V. A., Malinen, A. M., Bogachev, A. V., & Baykov, A. A. (2021). Catalytic Asymmetry in Homodimeric H+-Pumping Membrane Pyrophosphatase Demonstrated by Non-Hydrolyzable Pyrophosphate Analogs. International Journal of Molecular Sciences, 22(18), 9820. https://doi.org/10.3390/ijms22189820







