Charge Mobility in Discotic Liquid Crystals
Abstract
1. Introduction
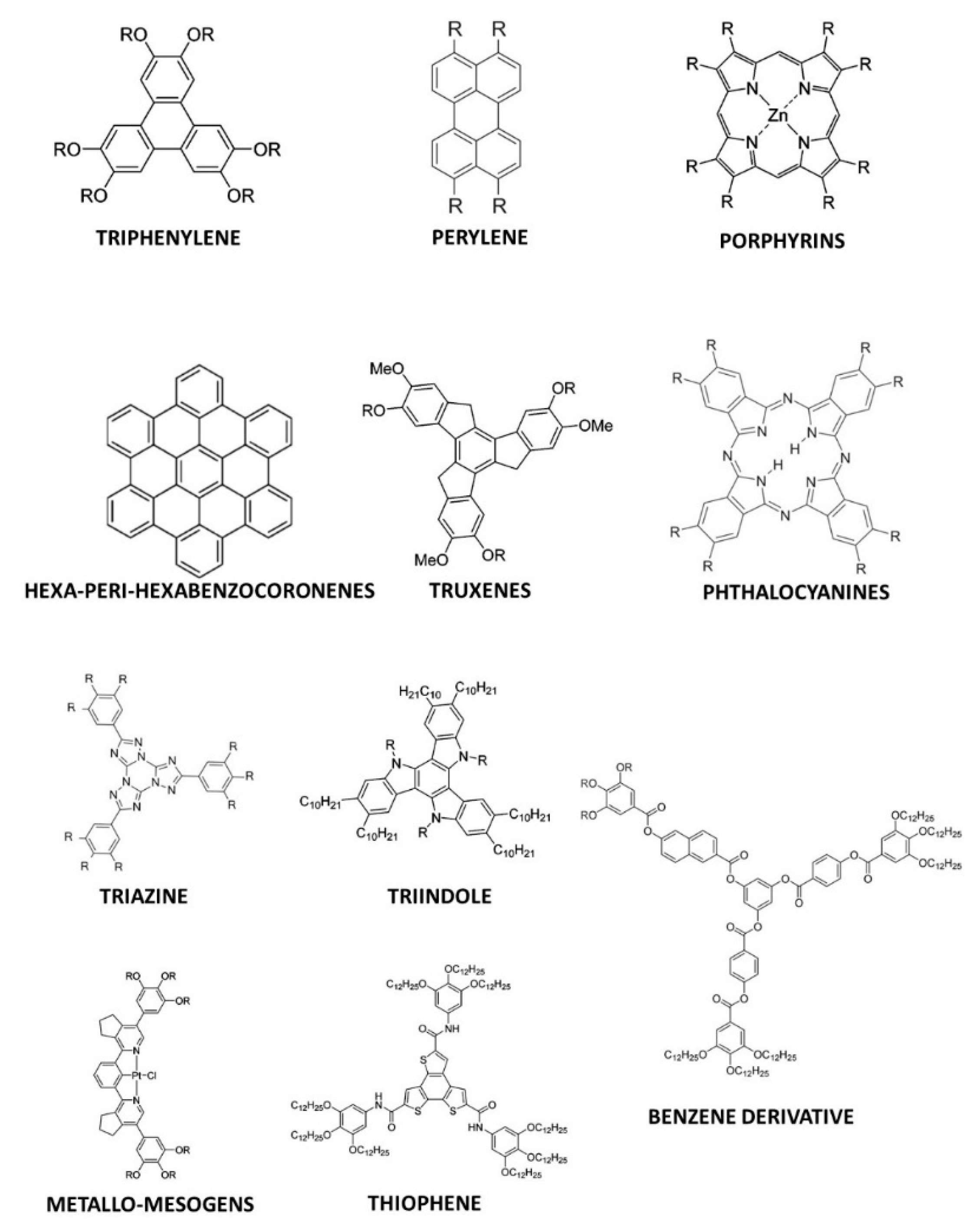
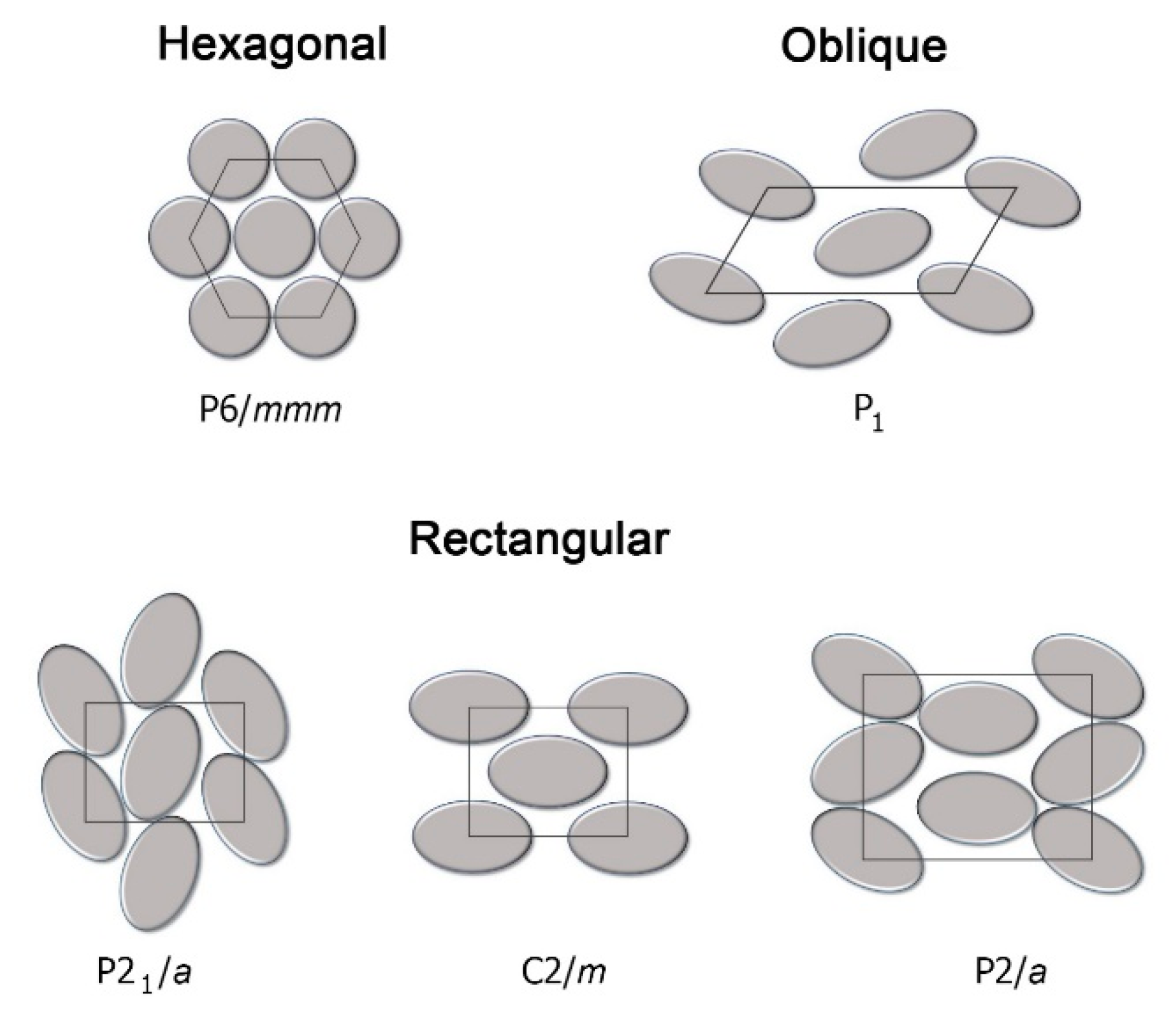
2. Discotic Mesophases
3. Charge Transport in Molecular Materials
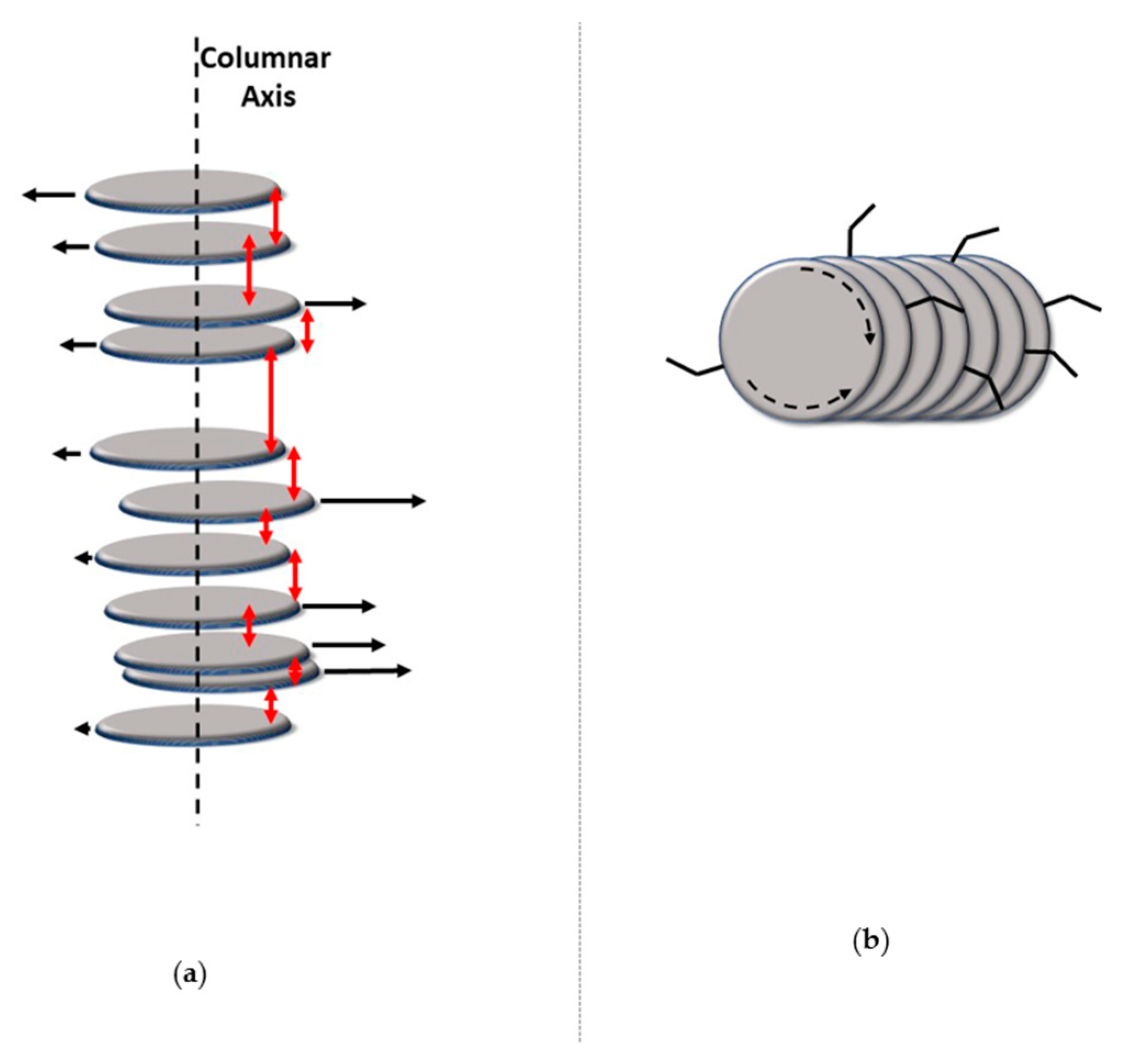
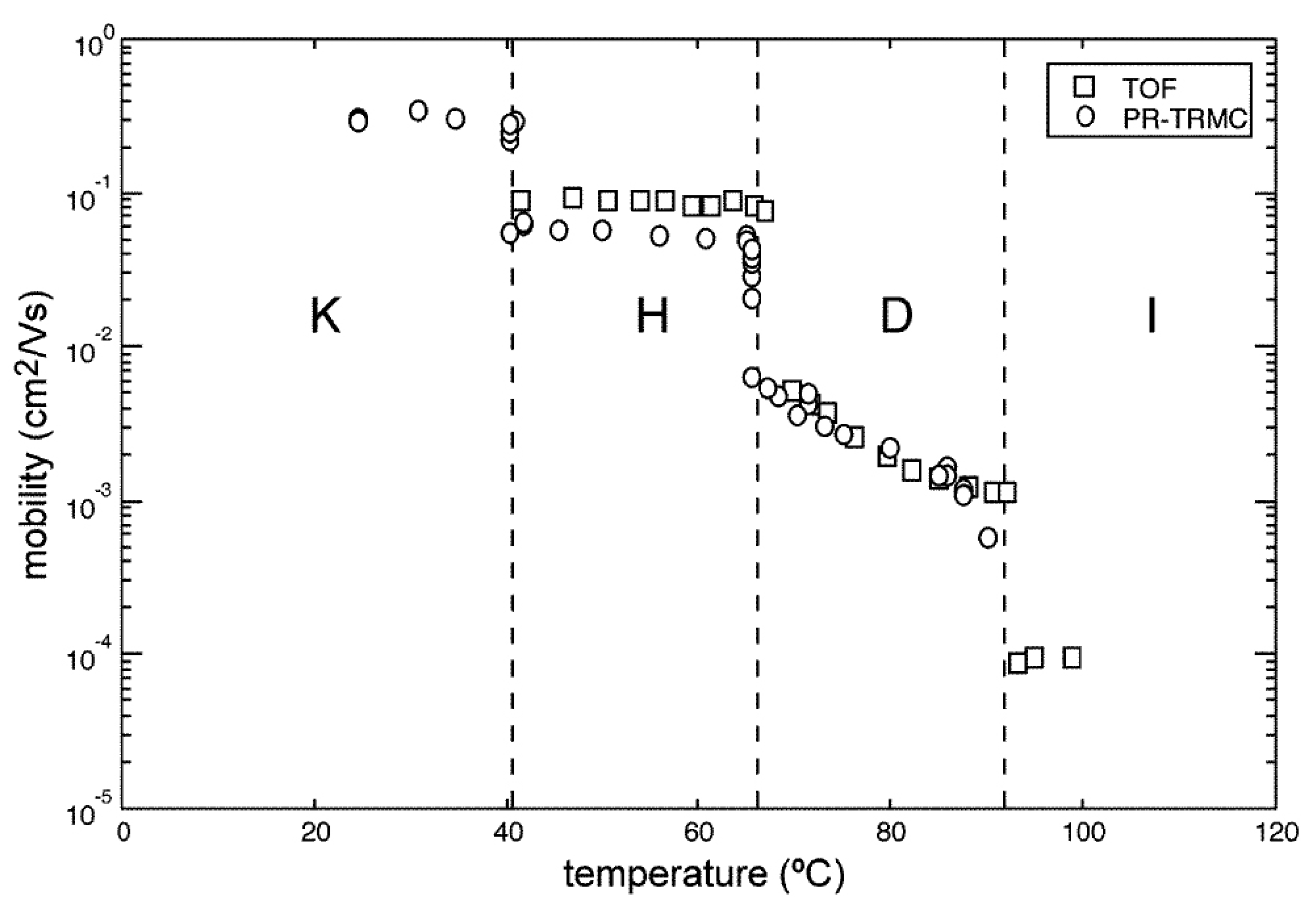
Charge Transport in Columnar Phases
4. Measurement of Charge Mobility
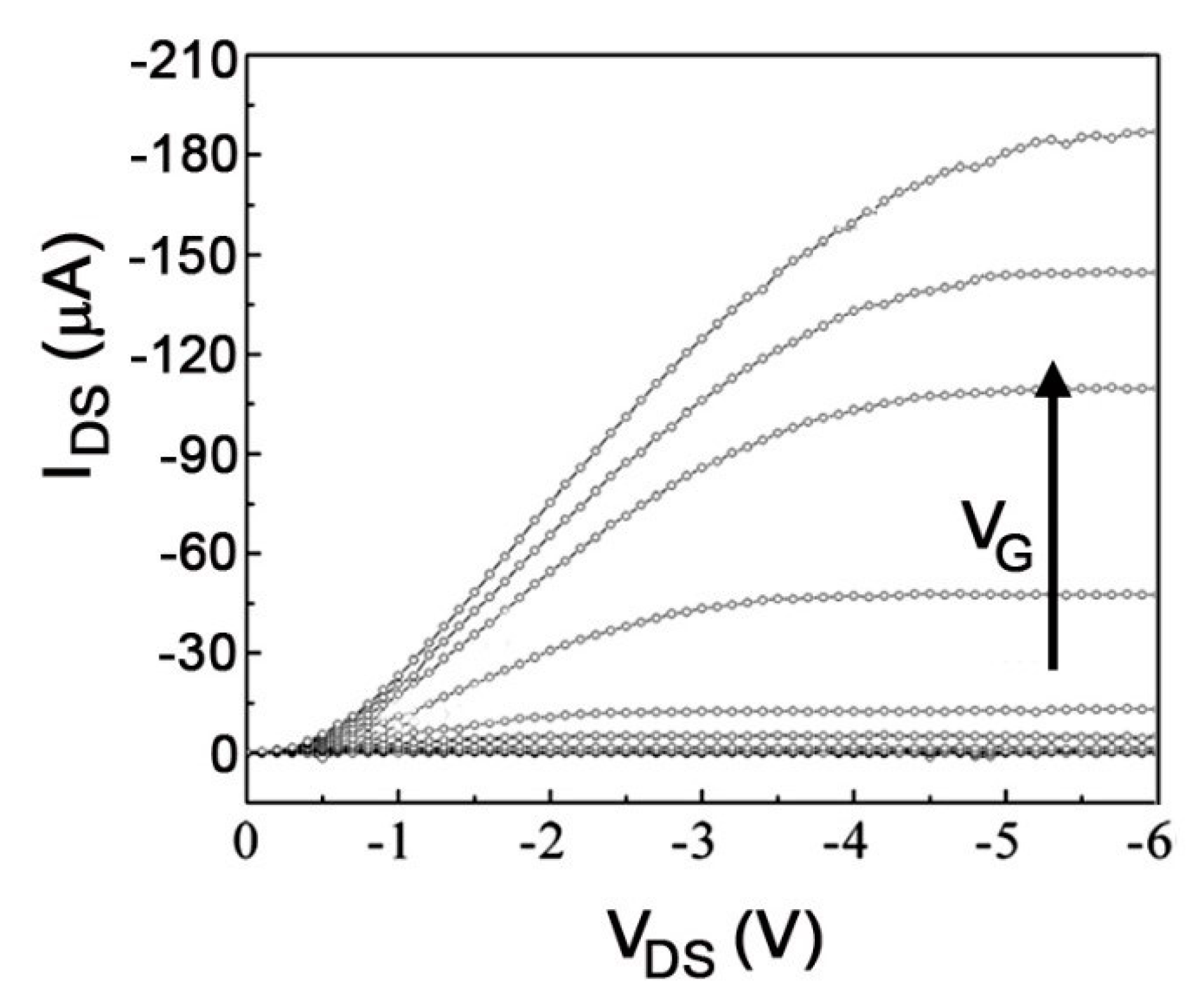
4.1. Field-Effect Transistors
4.2. Time of Flight

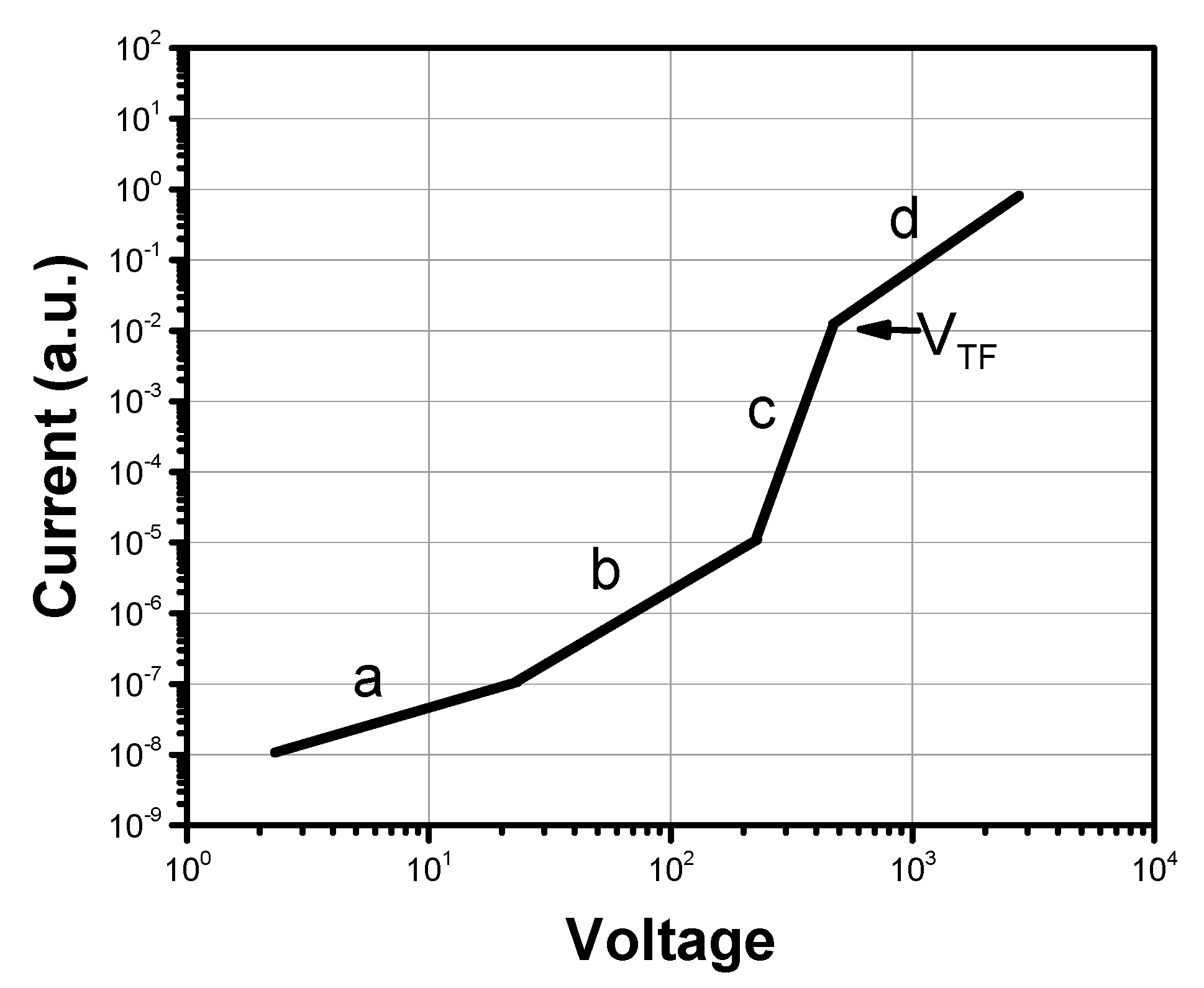
4.3. Space Charge Limited Current (SCLC)
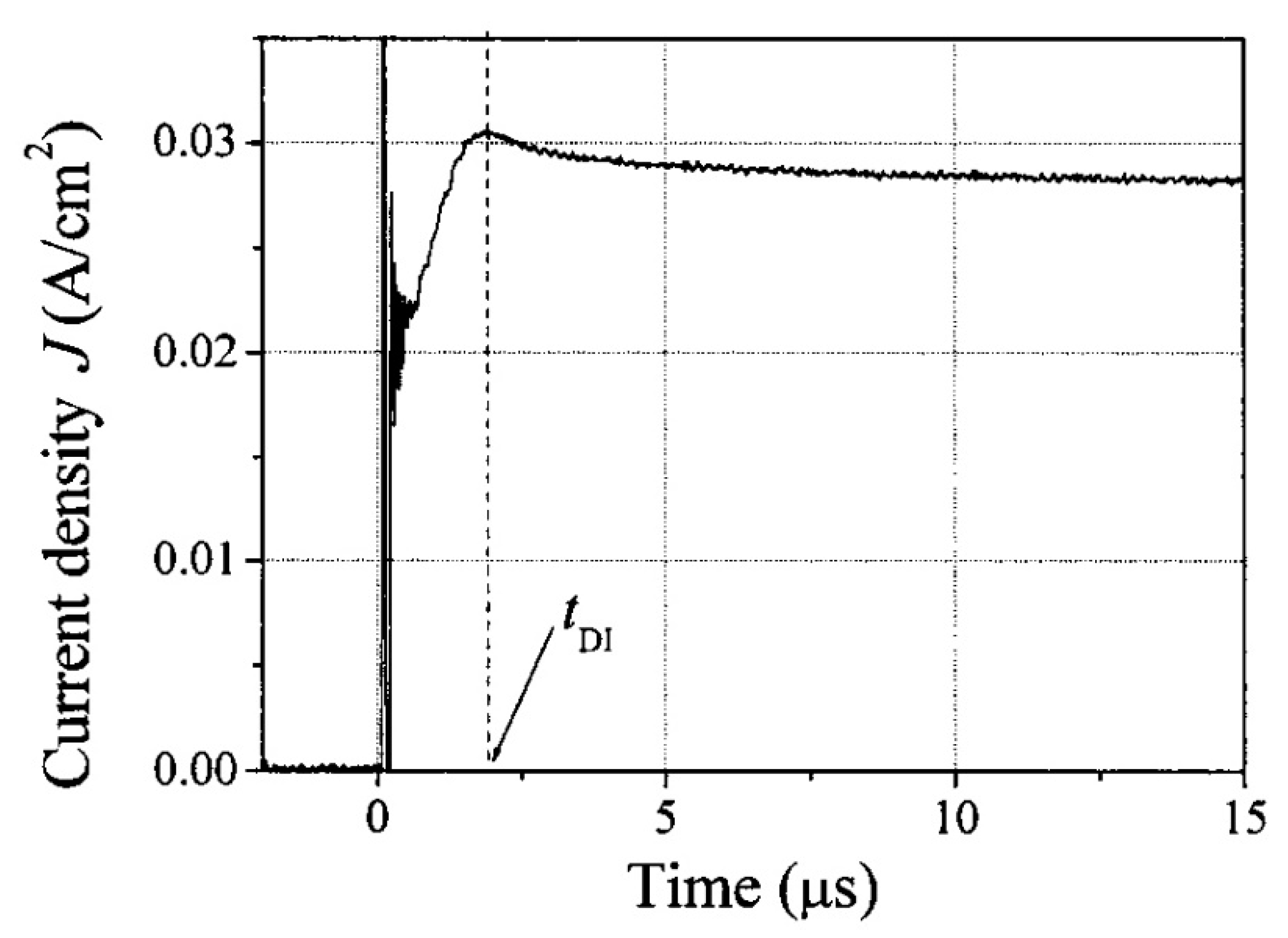
4.4. Charge Extraction by Linearly Increasing Voltage
4.5. Time-Resolved Microwave Conductivity
4.6. Admittance Spectroscopy
5. Recent Advances in the Study of Discotic Liquid Crystals
5.1. Mesophase Order
5.2. Computational Approaches
5.3. Mesophase Alignment
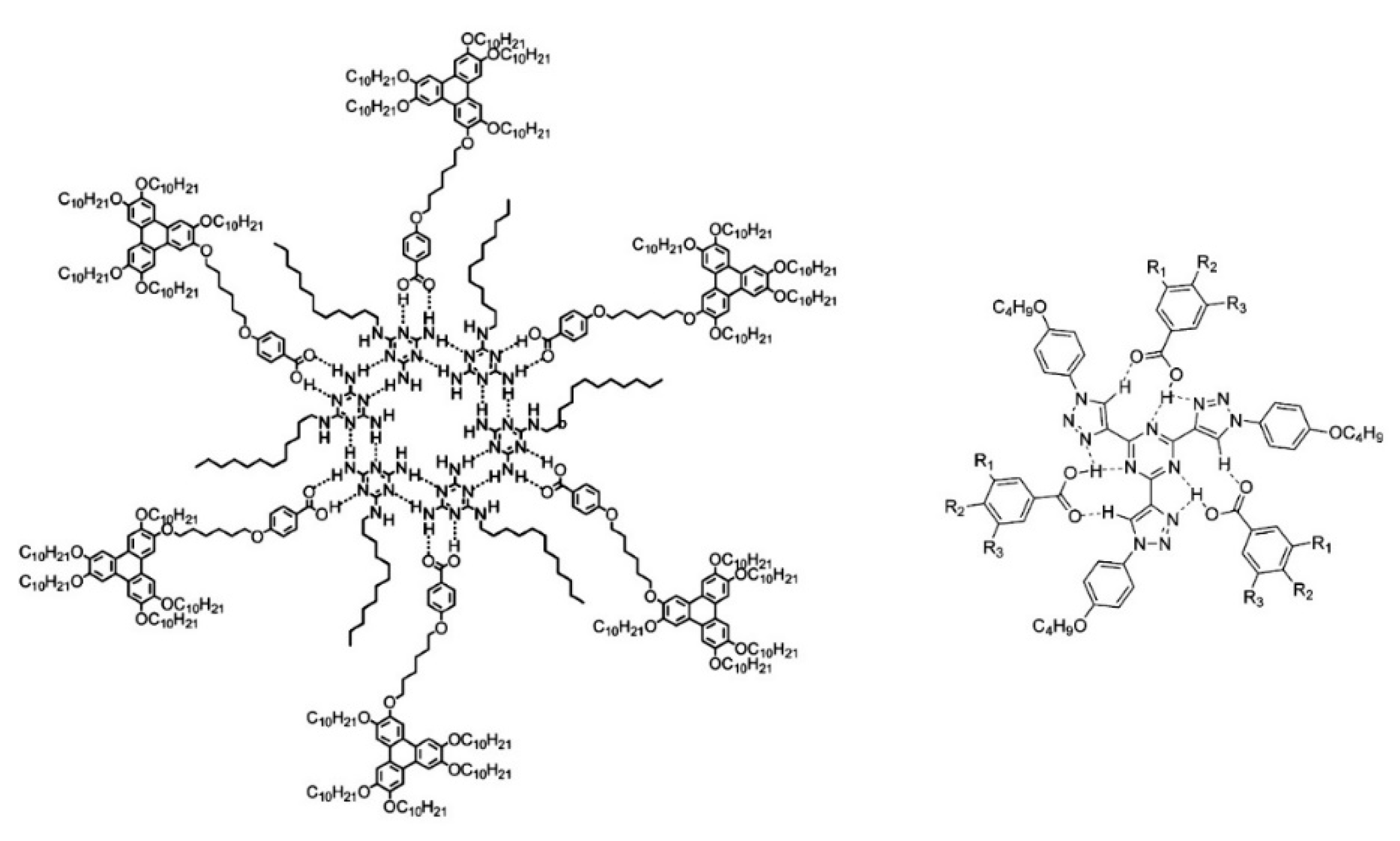
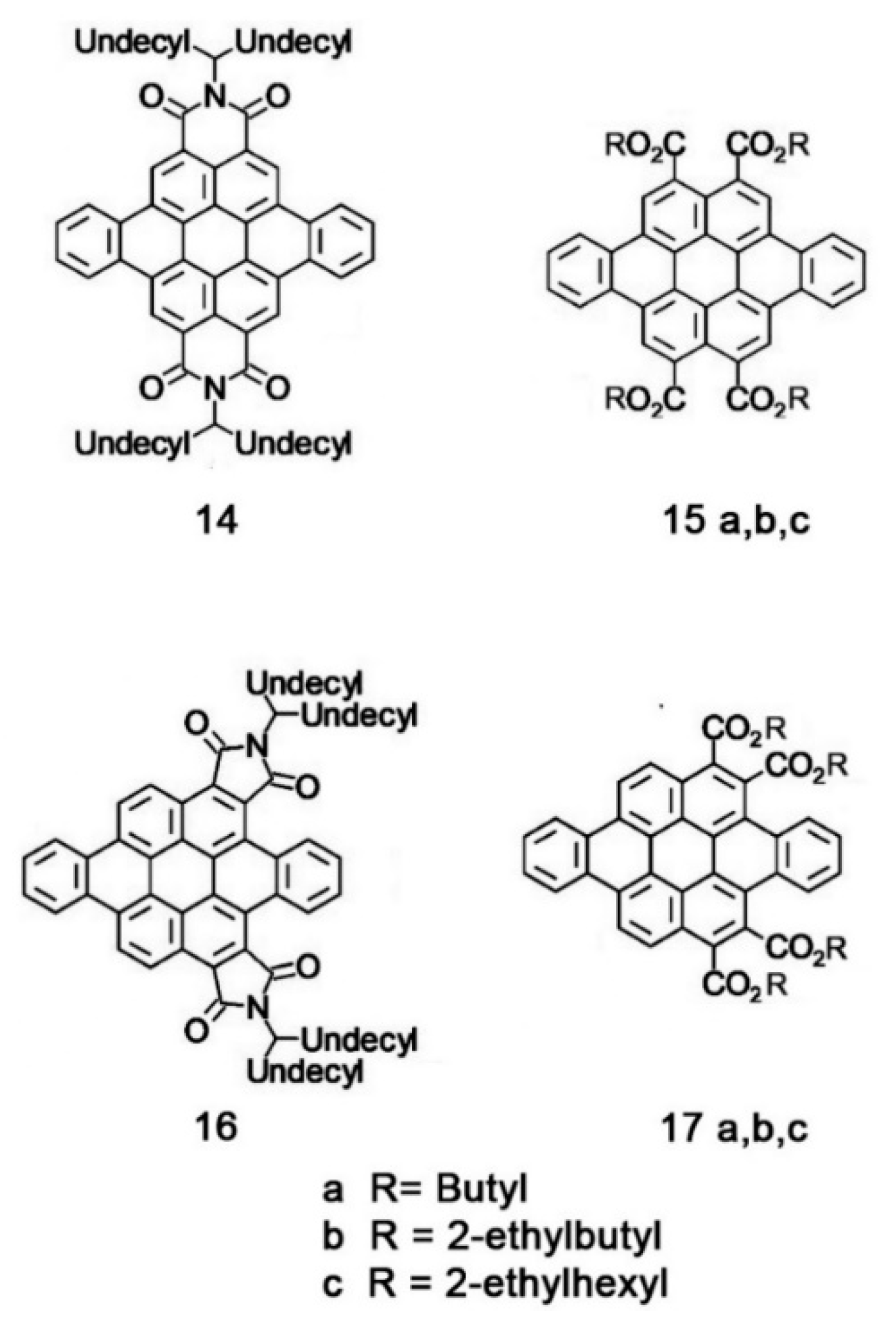
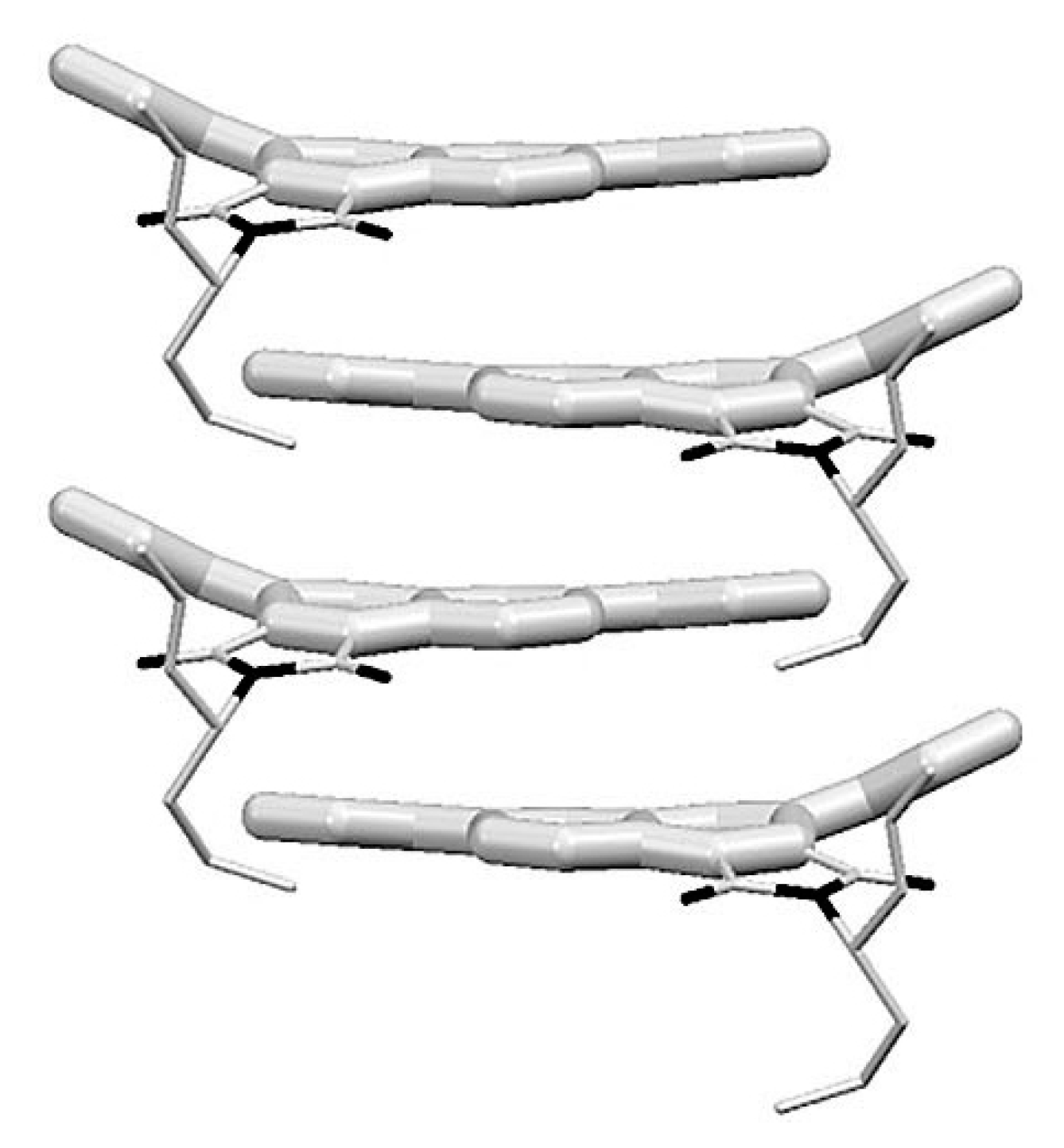
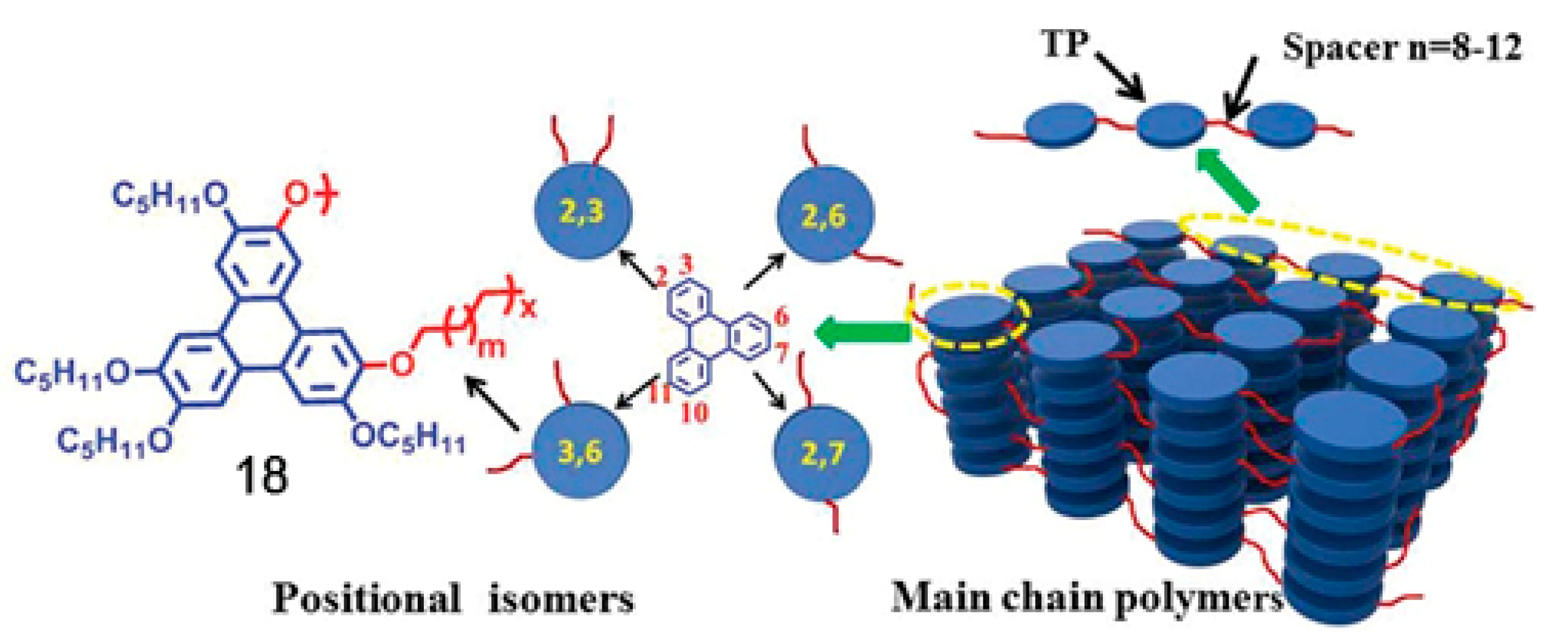
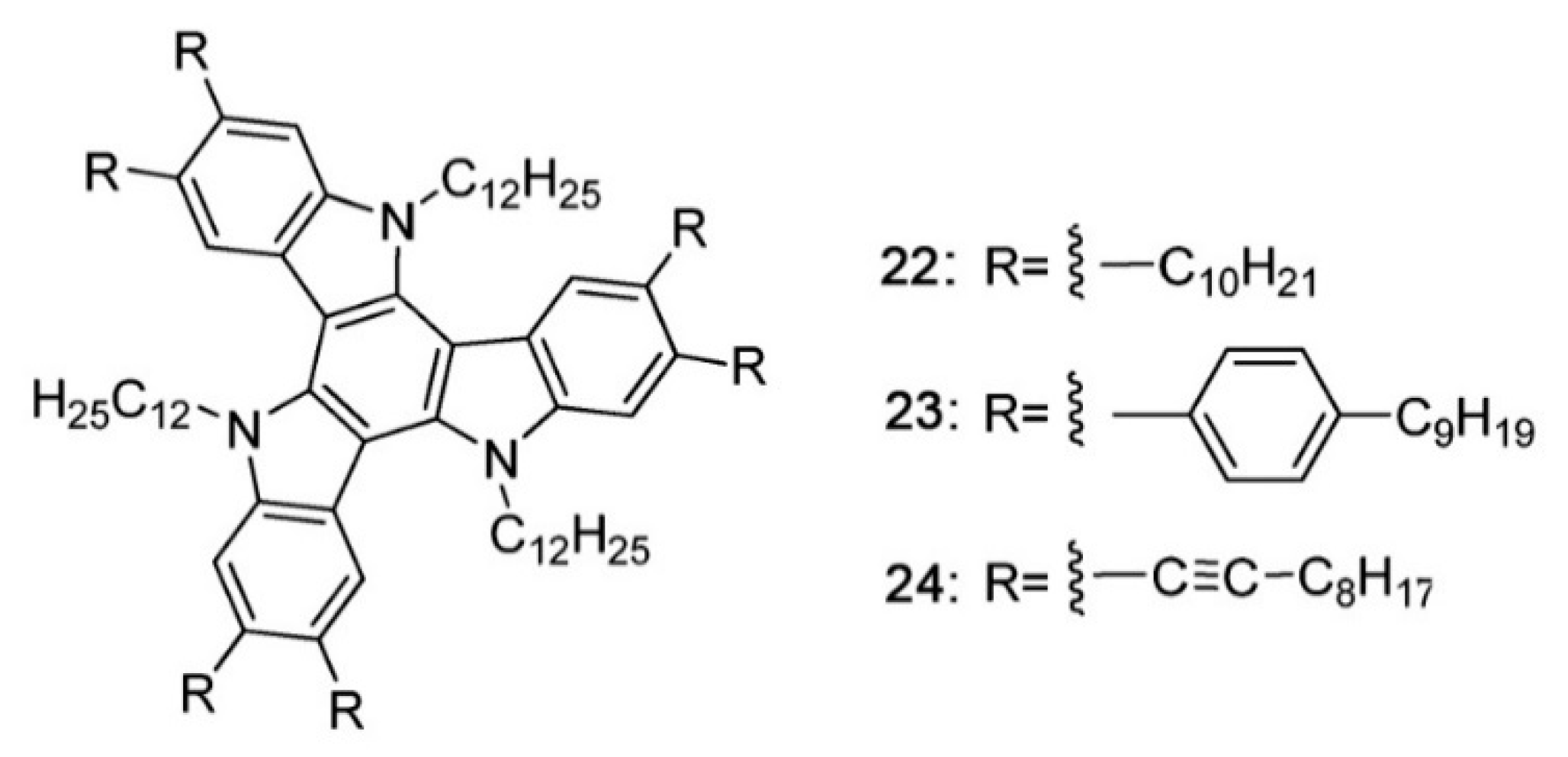
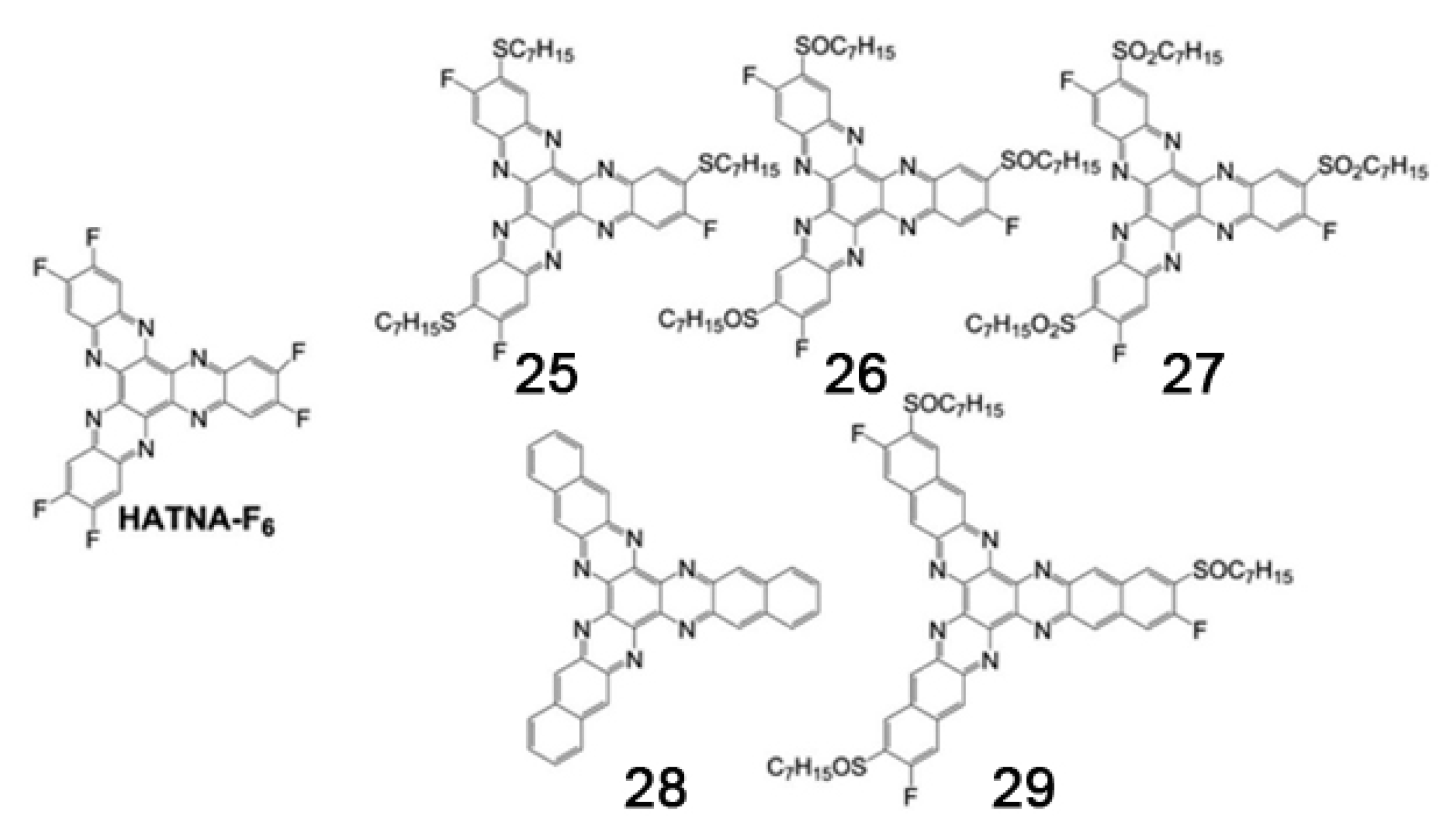
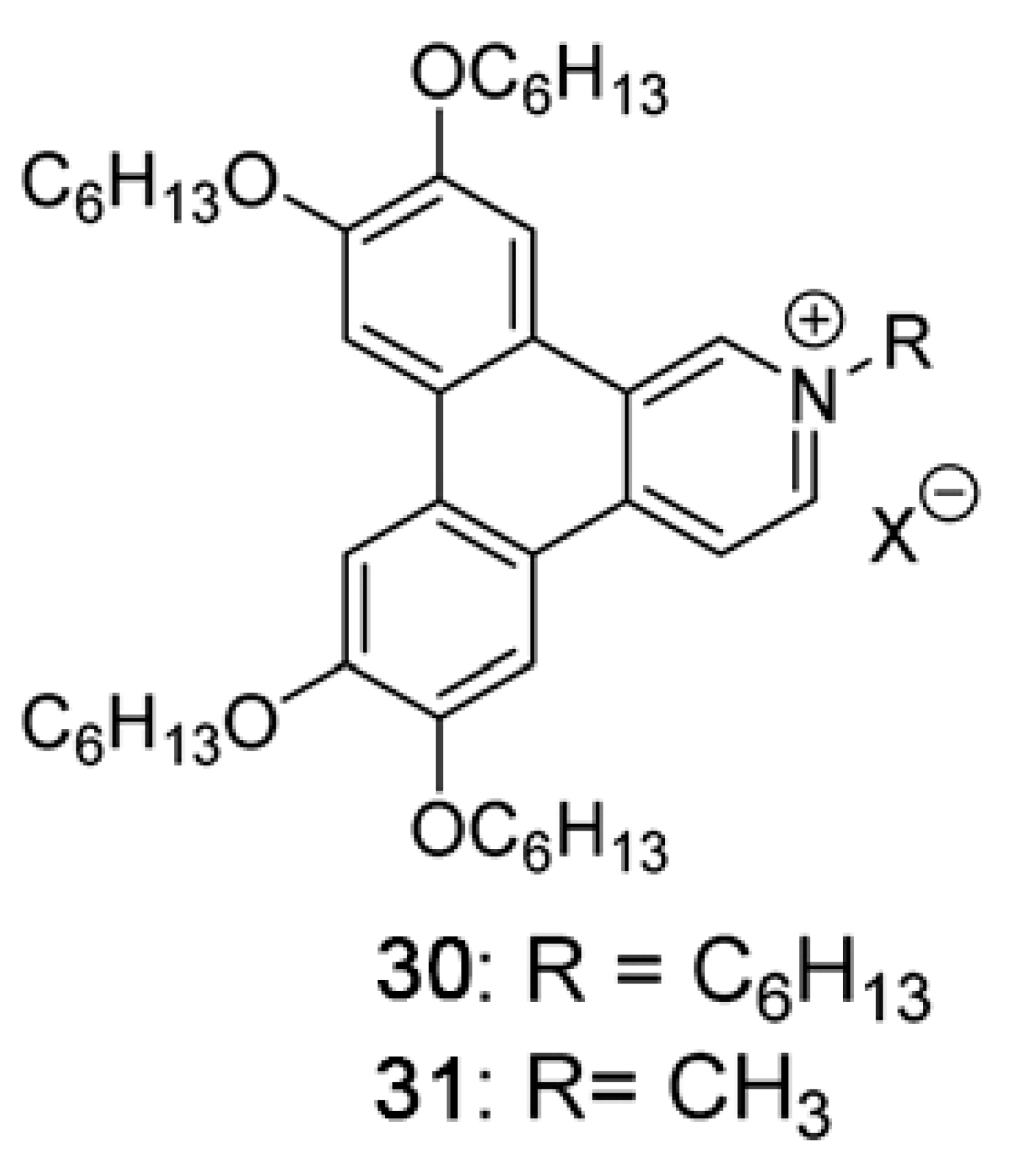
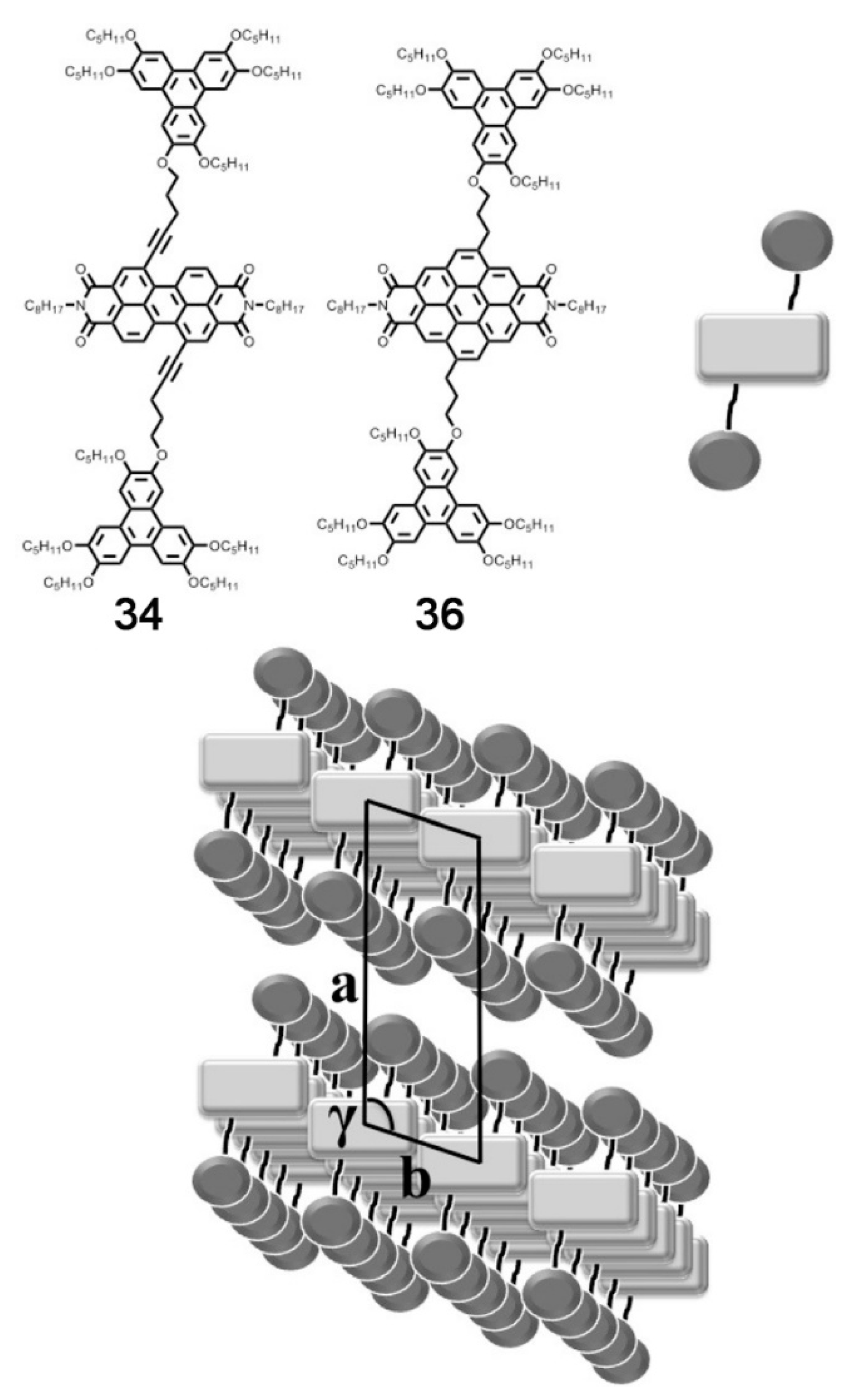
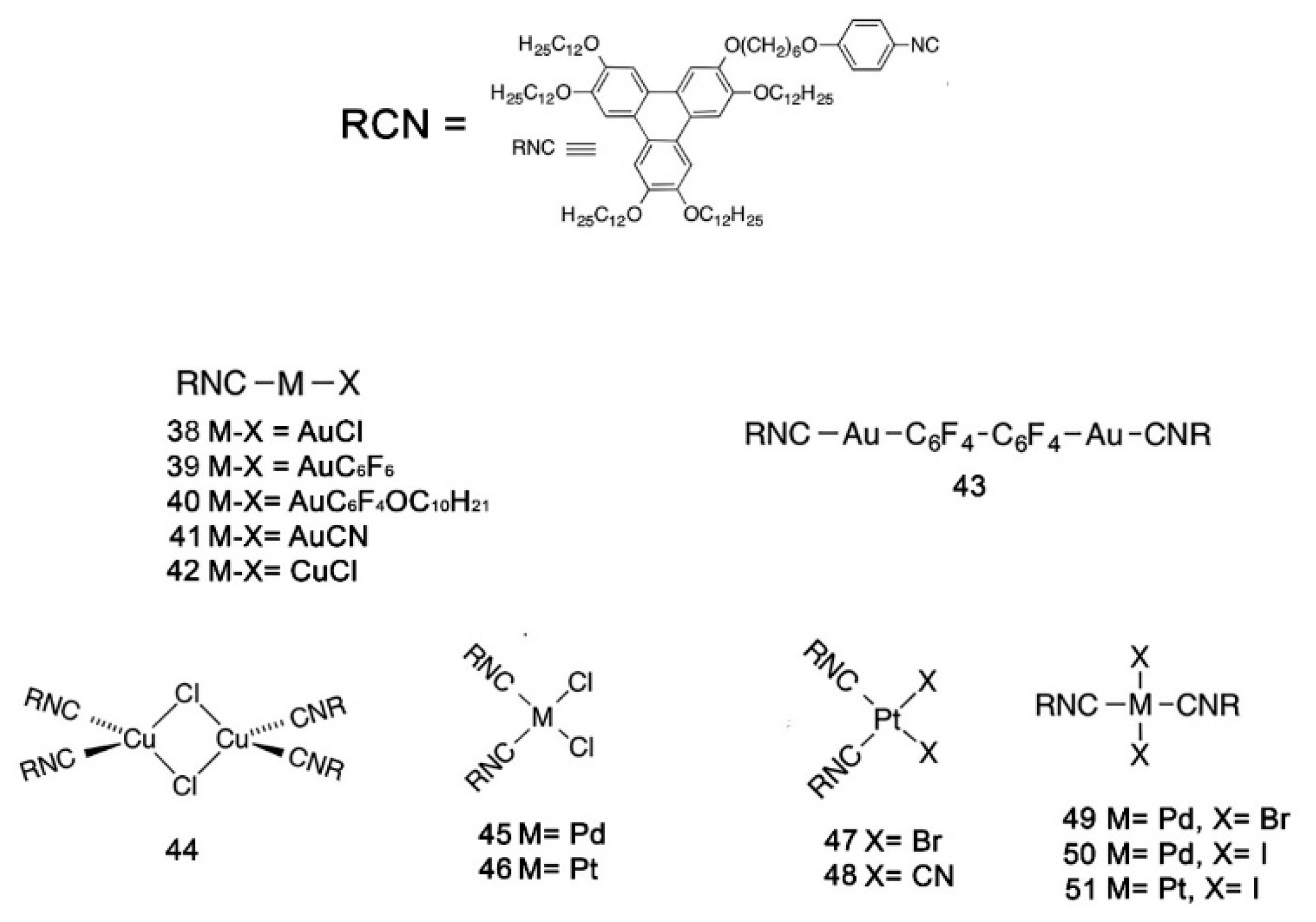
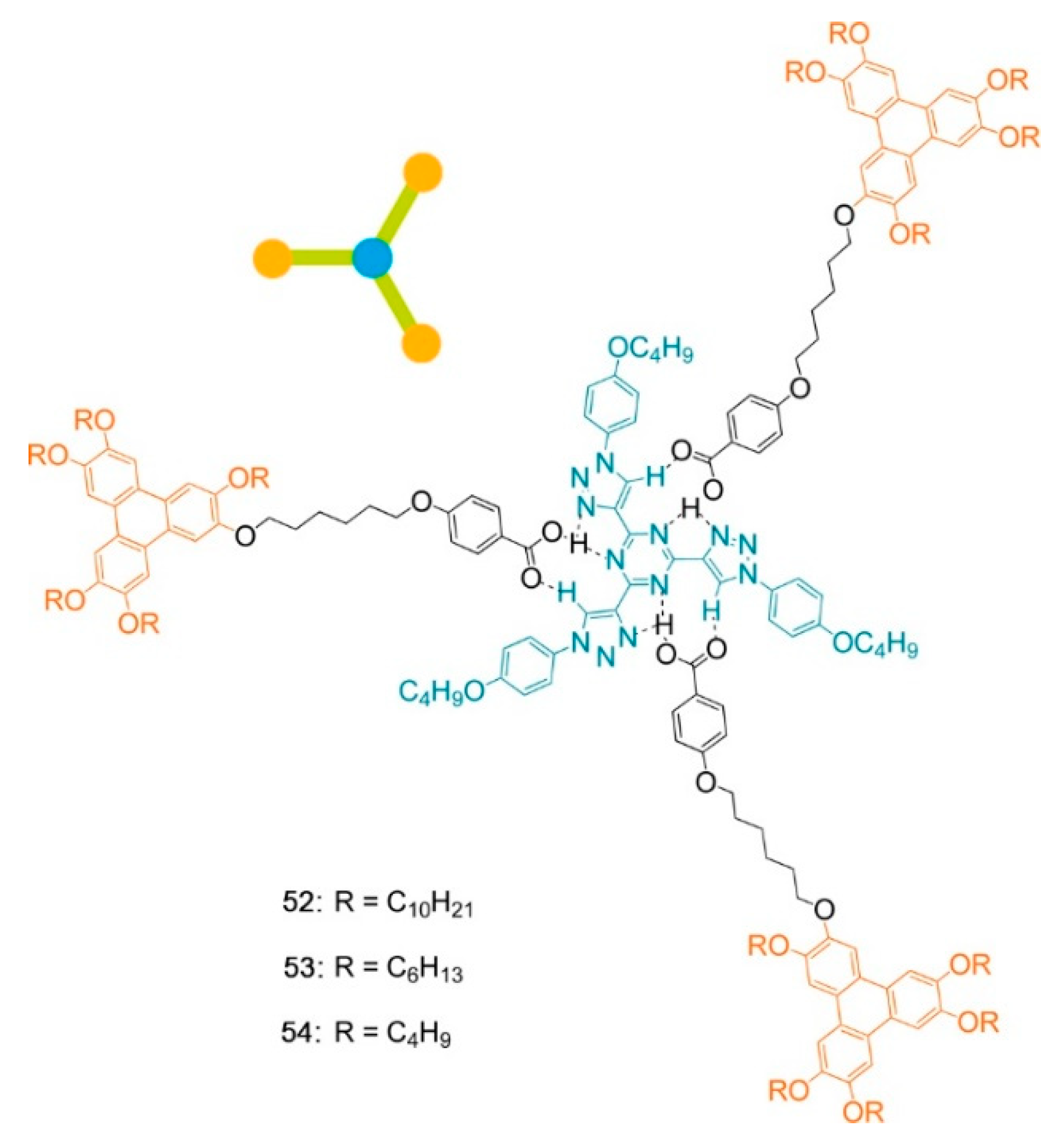
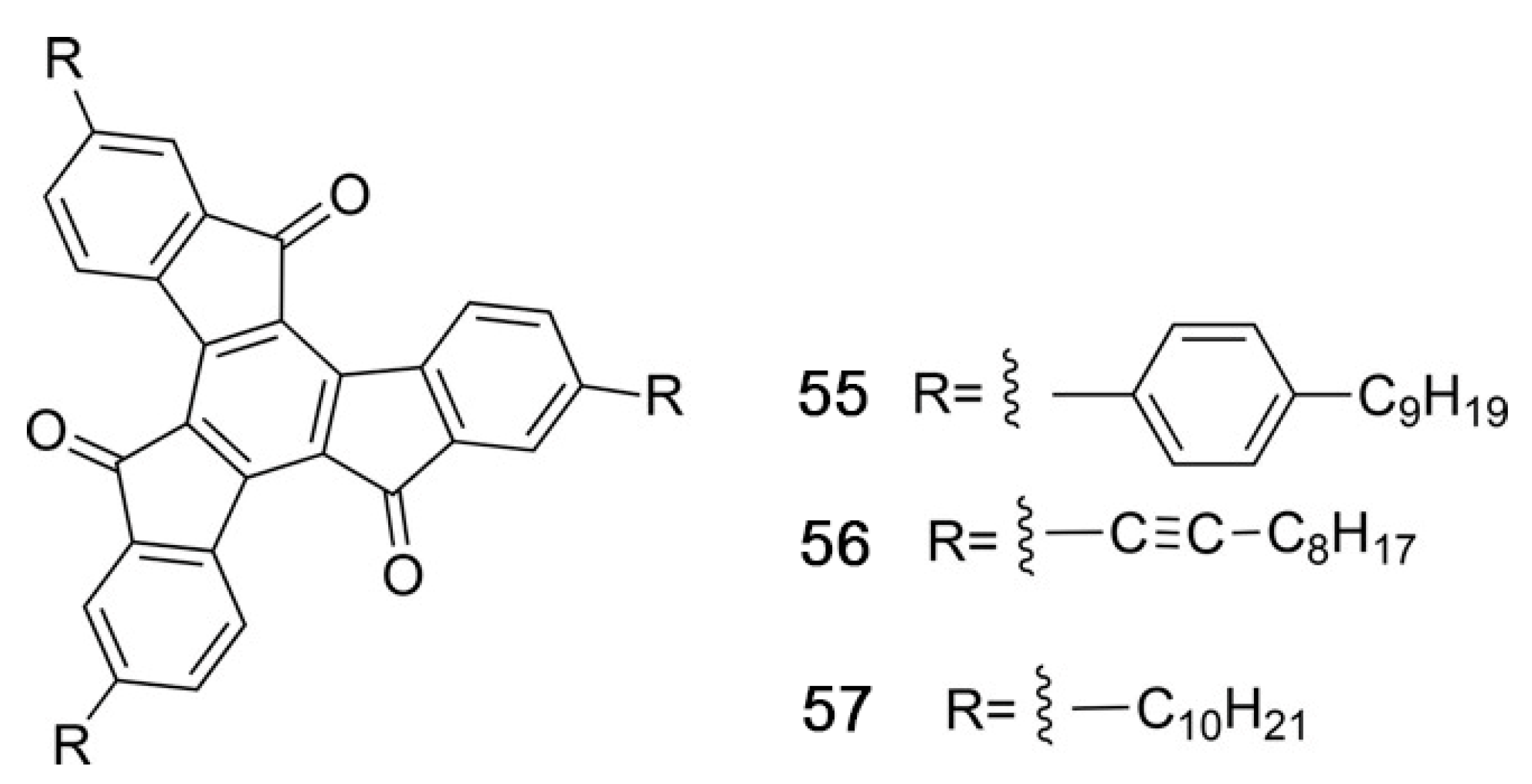
5.4. Synthetic Developments
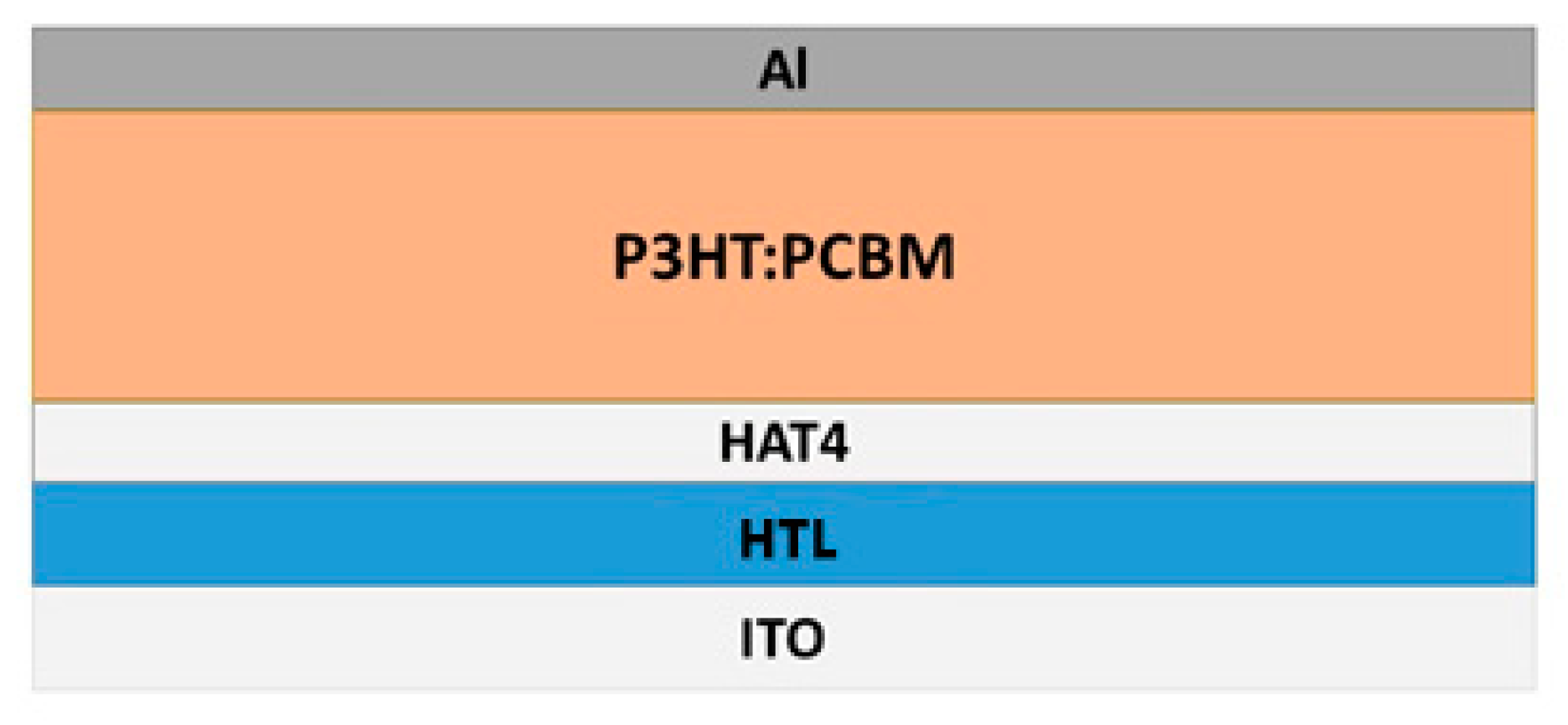
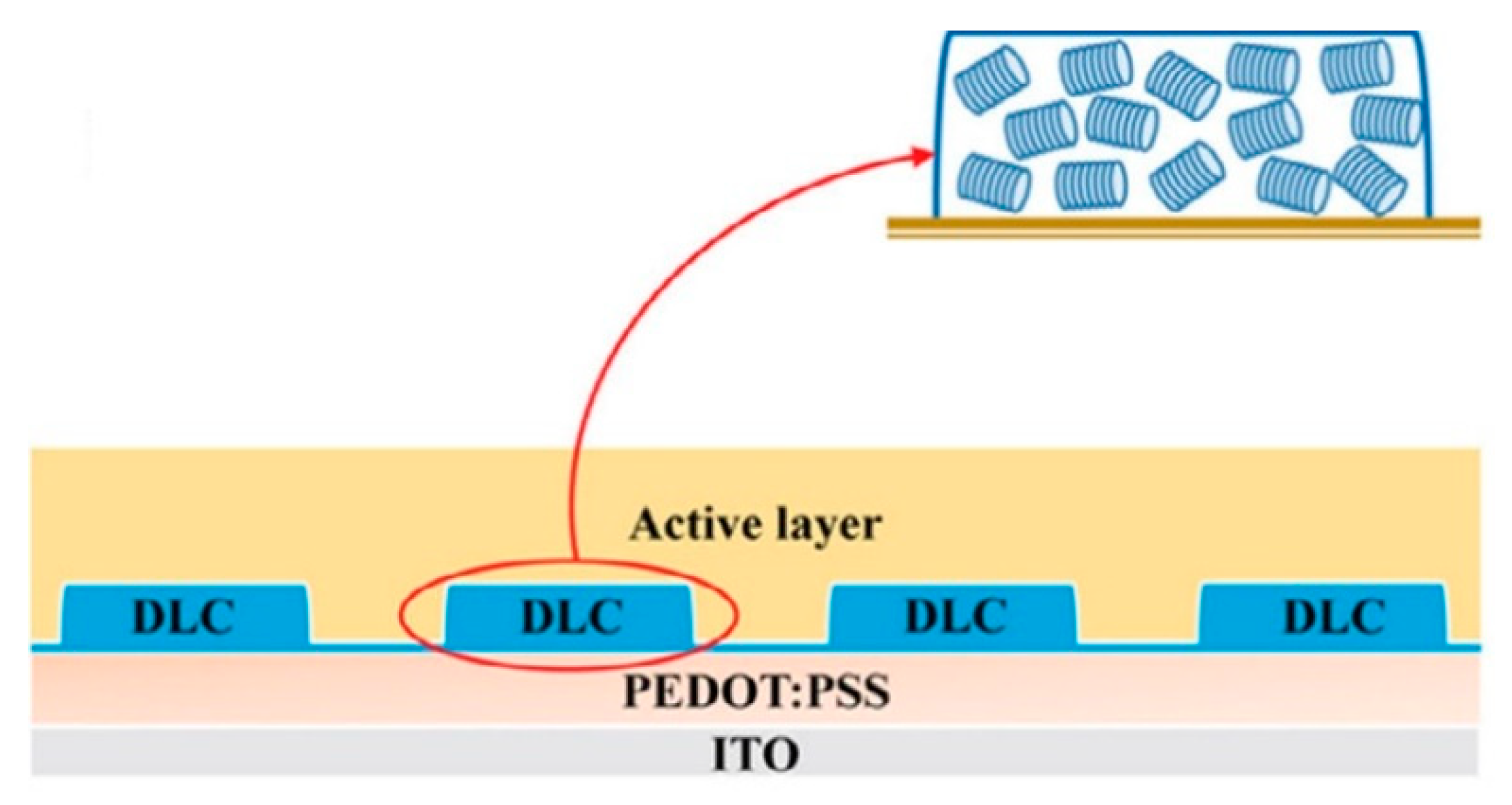
5.5. Applications of Discotic Liquid Crystals (DLC)
Funding
Conflicts of Interest
Abbreviations
| AAO | Anodic Aluminum Oxide |
| C6PcH2 | 1,4,8,11,15,18,22,25-octahexylphthalocyanine |
| C6TBTAPH2 | 1,4,8,11,15,18,22,25-octahexyltetrabenzotriazaporphyrin |
| CELIV | Charge Extraction by Linearly Increasing Voltage |
| Colh | Columnar Hexagonal |
| Colobl | Columnar Oblique |
| Colr | Columnar Rectangular |
| DFT | Density Functional Theory |
| DI-SCLC | Dark Injection Space Charge Limited Current |
| DLC | Discotic Liquid Crystals |
| DSC | Differential Scanning Calorimetry |
| ETM | Electron-Transporting Materials |
| F4TCNQ | 2,3,5,6-Tetrafluoro-7,7,8,8-tetracyanoquinodimethane |
| GIWAXS | Grazing Incidence Wide-angle X-ray scattering |
| HAT3 | 2,3,6,7,10,11-hexapropoxytriphenylene |
| HAT4 | 2,3,6,7,10,11-hexabutyloxytriphenylene |
| HAT5 | 2,3,6,7,10,11-hexapentyloxytriphenylene |
| HAT6 | 2,3,6,7,10,11-hexakis(n-hexyloxy)triphenylene |
| HATN-TEG- | hexaazatrinaphthylene-polyether |
| HATP | 2,3,6,7,10,11-hexaacetoxytriphenylene |
| HOMO | Highest Occupied Molecular Orbital |
| SAXS | Small-Angle X-ray Scattering |
| IUPAC | International Union of Pure and Applied Chemistry |
| CELIV | Charge Extraction by Linearly Increasing Voltage |
| ITO | Indium tin oxide |
| LUMO | Lowest Occupied Molecular Orbital |
| MC | Monte-Carlo |
| MD | Molecular Dynamics |
| MM | Molecular Mechanics |
| NC | Nematic Columnar |
| ND | Nematic Discotic |
| NL | Lateral Nematic |
| OFET | Organic Field-Effect Transistor |
| OLED | Organic Light Emitting Diode |
| OSC | Organic Solar Cell |
| P3HT | poly (3-hexylthiophene) |
| PC71BM | [6,6]-phenyl C71-butyric acid methyl ester |
| PCBM | [6,6]-phenyl-C61-butyric acid methyl ester |
| PEDOT: PSS | poly(3,4-ethylenedioxythiophene) polystyrene sulfonate |
| PEO | polyethylene oxide |
| POM | Polarized Optical Microscopy |
| PR-TRMC | Pulse-Radiolysis Time-Resolved Microwave Conductivity |
| PVK | poly (9-vinylcarbazole) |
| QM | Quantum Mechanics |
| RM | 2-methyl-1,4-phenylene bis(4-((6-(acryloyloxy)hexyl) oxy) benzoate) |
| SAXS | Small Angle X-ray Scattering |
| SCLC | Space Charge Limited Current |
| TEG | Triethyleneglycol |
| TOF | Time of Flight |
| TPBi | 2,2′,2″-(1,3,5-Benzinetriyl)-tris(1-phenyl-1-H-benzimidazole) |
References
- Klauk, H. Organic Electronics: Materials, Manufacturing and Applications; John Wiley & Sons: Weinheim, Germany, 2006. [Google Scholar]
- Klauk, H. (Ed.) Organic Electronics 2: More Materials and Applications; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Ostroverkhova, O. Organic optoelectronic materials: Mechanisms and applications. Chem. Rev. 2016, 116, 13279–13412. [Google Scholar] [CrossRef]
- Coropceanu, V.; Cornil, J.; da Silva Filho, D.A.; Olivier, Y.; Silbey, R.; Brédas, J.L. Charge transport in organic semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef] [PubMed]
- Ortmann, F.; Bechstedt, F.; Hannewald, K. Charge transport in organic crystals: Theory and modelling. Phys. Status Solidi Basic Res. 2011, 248, 511–525. [Google Scholar] [CrossRef]
- Liu, C.; Huang, K.; Park, W.T.; Li, M.; Yang, T.; Liu, X.; Liang, L.; Minari, T.; Noh, Y.Y. A unified understanding of charge transport in organic semiconductors: The importance of attenuated delocalization for the carriers. Mater. Horiz. 2017, 4, 608–618. [Google Scholar] [CrossRef]
- Yavuz, I. Dichotomy between the band and hopping transport in organic crystals: Insights from experiments. Phys. Chem. Chem. Phys. 2017, 19, 25819–25828. [Google Scholar] [CrossRef]
- Fratini, S.; Ciuchi, S.; Mayou, D.; de Laissardière, G.T.; Troisi, A. A map of high-mobility molecular semiconductors. Nat. Mater. 2017, 16, 998–1002. [Google Scholar] [CrossRef]
- Schweicher, G.; Garbay, G.; Jouclas, R.; Vibert, F.; Devaux, F.; Geerts, Y.H. Molecular semiconductors for logic operations: Dead-end or bright future? Adv. Mater. 2020, 32, 1905909. [Google Scholar] [CrossRef]
- Troisi, A. Charge transport in high mobility molecular semiconductors: Classical models and new theories. Chem. Soc. Rev. 2011, 40, 2347–2358. [Google Scholar] [CrossRef]
- Cornil, J.; Verlaak, S.; Martinelli, N.; Mityashin, A.; Olivier, Y.; van Regemorter, T.; D’Avino, G.; Muccioli, L.; Zannoni, C.; Castet, F.; et al. Exploring the energy landscape of the charge transport levels in organic semiconductors at the molecular scale. Acc. Chem. Res. 2013, 46, 434–443. [Google Scholar] [CrossRef]
- Schweicher, G.; Olivier, Y.; Lemaur, V.; Geerts, Y.H. What currently limits charge carrier mobility in crystals of molecular semiconductors? Isr. J. Chem. 2014, 54, 595–620. [Google Scholar] [CrossRef]
- Shuai, Z.; Geng, H.; Xu, W.; Liao, Y.; André, J.M. From charge transport parameters to charge mobility in organic semiconductors through multiscale simulation. Chem. Soc. Rev. 2014, 43, 2662–2679. [Google Scholar] [CrossRef] [PubMed]
- Fratini, S.; Mayou, D.; Ciuchi, S. The transient localization scenario for charge transport in crystalline organic materials. Adv. Funct. Mater. 2016, 26, 2292–2315. [Google Scholar] [CrossRef]
- Illig, S.; Eggeman, A.S.; Troisi, A.; Jiang, L.; Warwick, C.; Nikolka, M.; Schweicher, G.; Yeates, S.G.; Henri Geerts, Y.; Anthony, J.E.; et al. Reducing dynamic disorder in small-molecule organic semiconductors by suppressing large-Amplitude thermal motions. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Oberhofer, H.; Reuter, K.; Blumberger, J. Charge transport in molecular materials: An assessment of computational methods. Chem. Rev. 2017, 117, 10319–10357. [Google Scholar] [CrossRef]
- Groves, C. Simulating charge transport in organic semiconductors and devices: A review. Rep. Prog. Phys. 2017, 80. [Google Scholar] [CrossRef]
- Dieckmann, A.; Bassler, H.; Borsenberger, P.M. An assessment of the role of dipoles on the density-of-states function of disordered molecular solids. J. Chem. Phys. 1993, 99, 8136–8141. [Google Scholar] [CrossRef]
- Vladimirov, I.; Kühn, M.; Geßner, T.; May, F.; Weitz, R.T. Energy barriers at grain boundaries dominate charge carrier transport in an electron-conductive organic semiconductor. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, H.; Hu, W. Organic semiconductor single crystals for electronics and photonics. Adv. Mater. 2018, 30, 1–34. [Google Scholar] [CrossRef]
- Van de Craats, A.M.; Warman, J.M.; Fechtenkötter, A.; Brand, J.D.; Harbison, M.A.; Müllen, K. Record charge carrier mobility in a room-temperature discotic liquid-crystalline derivative of hexabenzocoronene. Adv. Mater. 1999, 11, 1469–1472. [Google Scholar] [CrossRef]
- Iino, H.; Takayashiki, Y.; Hanna, J.I.; Bushby, R.J.; Haarer, D. High electron mobility of 0.1 cm2V-1s-1 in the highly ordered columnar phase of hexahexylthiotriphenylene. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Iino, H.; Hanna, J.I.; Bushby, R.J.; Movaghar, B.; Whitaker, B.J.; Cook, M.J. Very high time-of-flight mobility in the columnar phases of a discotic liquid crystal. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Pisula, W.; Kastler, M.; Wasserfallen, D.; Mondeshki, M.; Piris, J.; Schnell, I.; Müllen, K. Relation between supramolecular order and charge carrier mobility of branched alkyl hexa-peri-hexabenzocoronenes. Chem. Mater. 2006, 18, 3634–3640. [Google Scholar] [CrossRef]
- Hanna, J.I.; Ohno, A.; Iino, H. Charge carrier transport in liquid crystals. Thin Solid Films 2014, 554, 58–63. [Google Scholar] [CrossRef]
- Funahashi, M. Integration of electro-active π-conjugated units in nanosegregated liquid-crystalline phases. Polym. J. 2017, 49, 75–83. [Google Scholar] [CrossRef]
- Iino, H.; Usui, T.; Hanna, J.I. Liquid crystals for organic thin-film transistors. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Piris, J.; Debije, M.G.; Stutzmann, N.; van de Craats, A.M.; Watson, M.D.; Müllen, K.; Warmam, J.M. Anisotropy in the mobility and photogeneration of charge carriers in thin films of discotic hexabenzocoronenes, columnarly self-assembled on friction-deposited poly(tetrafluoroethylene). Adv. Mater. 2003, 15, 1736–1740. [Google Scholar] [CrossRef]
- Pisula, W.; Menon, A.; Stepputat, M.; Lieberwirth, I.; Kolb, U.; Tracz, A.; Sirringhaus, H.; Pakula, T.; Müllen, K. A zone-casting technique for device fabrication of field-effect transistors based on discotic hexa-perihexabenzocoronene. Adv. Mater. 2005, 17, 684–689. [Google Scholar] [CrossRef]
- Monobe, H.; Awazu, K.; Shimizu, Y. Alignment control of a columnar liquid crystal for a uniformly homeotropic domain using circularly polarized infrared irradiation. Adv. Mater. 2006, 18, 607–610. [Google Scholar] [CrossRef]
- Gujral, A.; Gómez, J.; Ruan, S.; Toney, M.F.; Bock, H.; Yu, L.; Ediger, M.D. Vapor-deposited glasses with long-range columnar liquid crystalline order. Chem. Mater. 2017, 29, 9110–9119. [Google Scholar] [CrossRef]
- Lin, F.J.; Chen, H.H.; Tao, Y.T. Molecularly aligned hexa-peri-hexabenzocoronene films by brush-coating and their application in thin-film transistors. ACS Appl. Mater. Interfaces 2019, 11, 10801–10809. [Google Scholar] [CrossRef]
- Bisoyi, H.K.; Li, Q. Stimuli directed alignment of self-organized one-dimensional semiconducting columnar liquid crystal nanostructures for organic electronics. Prog. Mater. Sci. 2019, 104, 1–52. [Google Scholar] [CrossRef]
- Pisula, W.; Tomović, Ž.; El Hamaoui, B.; Watson, M.D.; Pakula, T.; Müllen, K. Control of the homeotropic order of discotic hexa-peri-hexabenzocoronenes. Adv. Funct. Mater. 2005, 15, 893–904. [Google Scholar] [CrossRef]
- Bushby, R.J.; Lozman, O.R. Discotic liquid crystals 25 years on. Curr. Opin. Colloid Interface Sci. 2002, 7, 343–354. [Google Scholar] [CrossRef]
- Sergeyev, S.; Pisula, W.; Geerts, Y.H. Discotic liquid crystals: A new generation of organic semiconductors. Chem. Soc. Rev. 2007, 36, 1902–1929. [Google Scholar] [CrossRef]
- Bisoyi, H.K.; Kumar, S. Discotic nematic liquid crystals: Science and technology. Chem. Soc. Rev. 2010, 39, 264–285. [Google Scholar] [CrossRef] [PubMed]
- Kaafarani, B.R. Discotic liquid crystals for opto-electronic applications. Chem. Mater. 2011, 23, 378–396. [Google Scholar] [CrossRef]
- Wöhrle, T.; Wurzbach, I.; Kirres, J.; Kostidou, A.; Kapernaum, N.; Litterscheidt, J.; Haenle, J.C.; Staffeld, P.; Baro, A.; Giesselmann, F.; et al. Discotic liquid crystals. Chem. Rev. 2016, 116, 1139–1241. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of phase transitions. In Collected Papers of L. D. Landau; Ter Haar, D., Ed.; Gordon & Breach: New York, NY, USA, 1965; p. 210. [Google Scholar]
- Chandrasekhar, S. Liquid Crystals, 2nd ed.; Cambridge UP: Cambridge, UK, 1992. [Google Scholar]
- Chandrasekhar, S. Discotic liquid crystals: Their structures and physical properties. In Handbook of Liquid Crystals; Demus, D., Goodby, J., Gray, G.W., Spiess, H.-W., Vill, V., Eds.; Wiley-VCH: Weinheim, Germany, 1998; Volume 2B. [Google Scholar]
- Goldfarb, D.; Luz, Z.; Zimmermann, H. A deuterium NMR study of the discotic mesophase of hexa-hexyloxytriphenylene. J. Phys. 1981, 42, 1303–1311. [Google Scholar] [CrossRef]
- Fischbach, I.; Ebert, F.; Spiess, H.W.; Schnell, I. Rotor modulations and recoupling strategies in 13C solid-state magic-angle-spinning NMR spectroscopy: Probing molecular orientation and dynamics. ChemPhysChem 2004, 5, 895–908. [Google Scholar] [CrossRef]
- Fischbach, I.; Pakula, T.; Minkin, P.; Fechtenkötter, A.; Müllen, K.; Spiess, H.W.; Saalwächter, K. Structure and dynamics in columnar discotic materials: A combined X-ray and solid-state NMR study of hexabenzocoronene derivatives. J. Phys. Chem. B 2002, 106, 6408–6418. [Google Scholar] [CrossRef]
- Levelut, A.M. Structures des phases mésomorphes formées de molécules discoïdes. J. Chim. Phys. 1983, 80, 149–161. [Google Scholar] [CrossRef]
- Destrade, C.; Foucher, P.; Gasparoux, H.; Tinh, N.H.; Levelut, A.M.; Malthete, J. Disc-like mesogen polymorphism. Mol. Cryst. Liq. Cryst. 1984, 106, 121–146. [Google Scholar] [CrossRef]
- Tschierske, C. Development of structural complexity by liquid-crystal self-assembly. Angew. Chem. Int. Ed. 2013, 52, 8828–8878. [Google Scholar] [CrossRef] [PubMed]
- Barón, M. Definitions of basic terms relating to low-molar-mass and polymer liquid crystals (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 845–895. [Google Scholar] [CrossRef]
- Safinya, C.R.; Liang, K.S.; Varady, W.A.; Clark, N.A.; Andersson, G. Synchrotron X-ray study of the orientational ordering D 2−D 1 structural phase transition of freely suspended discotic strands in triphenylene hexa-n-dodecanoate. Phys. Rev. Lett. 1984, 53, 1172–1175. [Google Scholar] [CrossRef]
- Fontes, E.; Heiney, P.A.; de Jeu, W.H. Liquid-crystalline and helical order in a discotic mesophase. Phys. Rev. Lett. 1988, 61, 1202–1205. [Google Scholar] [CrossRef]
- Vera, F.; Serrano, J.L.; Sierra, T. Twists in mesomorphic columnar supramolecular assemblies. Chem. Soc. Rev. 2009, 38, 781–796. [Google Scholar] [CrossRef]
- Morale, F.; Date, R.W.; Guillon, D.; Bruce, D.W.; Finn, R.L.; Wilson, C.; Blake, A.J.; Schröder, M.; Donnio, B. Columnar mesomorphism from hemi-disklike metallomesogens derived from 2,6-Bis[3′,4′,5′-tri(alkoxy)phenyliminomethyl]pyridines (L): Crystal and Molecular Structures of [M(L)Cl2] (M = Mn, Ni, Zn). Chem. Eur. J. 2003, 9, 2484–2501. [Google Scholar] [CrossRef]
- Lehmann, M.; Dechant, M.; Lambov, M.; Ghosh, T. Free space in liquid crystals—Molecular design, generation, and usage. Acc. Chem. Res. 2019, 52, 1653–1664. [Google Scholar] [CrossRef]
- Poupko, R.; Luz, Z.; Spielberg, N.; Zimmermann, H. Structure and dynamics of pyramidic liquid crystals by deuterium NMR and X-ray diffraction. J. Am. Chem. Soc. 1989, 111, 6094–6105. [Google Scholar] [CrossRef]
- Swager, T.M.; Xu, B. Liquid crystal calixarenes. J. Incl. Phenom. Mol. Recognit. Chem. 1994, 19, 389–398. [Google Scholar] [CrossRef]
- Fischer, M.; Lieser, G.; Rapp, A.; Schnell, I.; Mamdouh, W.; de Feyter, S.; de Schryver, F.C.; Höger, S. Shape-persistent macrocycles with intraannular polar groups: Synthesis, liquid crystallinity, and 2d Organization. J. Am. Chem. Soc. 2004, 126, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Fritzsche, M.; Bohle, A.; Dudenko, D.; Baumeister, U.; Sebastiani, D.; Richardt, G.; Spiess, H.W.; Hansen, M.R.; Höger, S. Empty helical nanochannels with adjustable order from low symmetry macrocycles. Angew. Chem. Int. Ed. 2011, 50, 3030–3033. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Yue, K.; Yan, Q.; Huang, H.; Wu, H.; Zhu, N.; Zhao, D. Triangular arylene ethynylene macrocycles: Syntheses, optical, and thermotropic liquid crystalline properties. Soft Matter 2012, 8, 2405–2415. [Google Scholar] [CrossRef]
- Lelj, F.; Morelli, G.; Ricciardi, G.; Roviello, A.; Sirigu, A. Discotic mesomorphism of 2,3,7,8,12,13,17,18-Octakis(alkyl-Thio) 5,10,15,20 tetraaza porphyrin and its complexes with some divalent transition metal ions synthesis and characterization. Liq. Cryst. 1992, 12, 941–960. [Google Scholar] [CrossRef]
- Serrano, J.L. (Ed.) Metallomesogens: Synthesis, Properties, and Applications; Wiley-VCH: Weinheim, Germany, 2008; ISBN 978-3-527-61508-7. [Google Scholar]
- Percec, V.; Glodde, M.; Bera, T.K.; Miura, Y.; Shiyanovskaya, I.; Singer, K.D.; Balagurusamy, V.S.K.; Heiney, P.A.; Schnell, I.; Rapp, A.; et al. Self-organization of supramolecular helical dendrimers into complex electronic materials. Nature 2002, 419, 384–387. [Google Scholar] [CrossRef]
- Davis, E.J.; Goodby, J.W. Amphitropic hydrogen-bonded liquid crystals. In Handbook of Liquid Crystals; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH: Weinheim, Germany, 2014; Volume 6, pp. 281–316. [Google Scholar]
- Feringán, B.; Folcia, C.L.; Termine, R.; Golemme, A.; Granadino-Roldán, J.M.; Navarro, A.; Serrano, J.L.; Giménez, R.; Sierra, T. Inspecting the electronic architecture and semiconducting properties of a rosette-like supramolecular columnar liquid crystal. Chem. Eur. J. 2018, 24, 17459–17463. [Google Scholar] [CrossRef]
- Kouwer, P.H.J.; Jager, W.F.; Mijs, W.J.; Picken, S.J. Synthesis and characterization of a novel liquid crystalline polymer showing a nematic columnar to nematic discotic phase transition. Macromolecules 2000, 33, 4336–4342. [Google Scholar] [CrossRef]
- Grafe, A.; Janietz, D.; Frese, T.; Wendorff, J.H. Star-shaped discotic oligomesogens based on radial pentakisphenylethynylbenzene moieties. Chem. Mater. 2005, 17, 4979–4984. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Wang, H.F.; Liu, C.X.; Zhao, K.Q.; Wang, B.Q.; Hu, P.; Monobe, H.; Heinrich, B.; Donnio, B. Molecular engineering of mesomorphic fluorene-bridged triphenylene triads: Thermotropic nematic/columnar mesophases, and p-type semiconducting behavior. Cryst. Growth Des. 2018, 18, 4296–4305. [Google Scholar] [CrossRef]
- Kouwer, P.H.J.; Jager, W.F.; Mijs, W.J.; Picken, S.J. The nematic lateral phase: A novel phase in discotic supramolecular assemblies. Macromolecules 2001, 34, 7582–7584. [Google Scholar] [CrossRef]
- Rivnay, J.; Jimison, L.H.; Northrup, J.E.; Toney, M.F.; Noriega, R.; Lu, S.; Marks, T.J.; Facchetti, A.; Salleo, A. Large modulation of carrier transport by grain-boundary molecular packing and microstructure in organic thin films. Nat. Mater. 2009, 8, 952–958. [Google Scholar] [CrossRef] [PubMed]
- Ortmann, F.; Bechstedt, F.; Hannewald, K. Charge transport in organic crystals: Interplay of band transport, hopping and electron-phonon scattering. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Fratini, S.; Nikolka, M.; Salleo, A.; Schweicher, G.; Sirringhaus, H. Charge transport in high-mobility conjugated polymers and molecular semiconductors. Nat. Mater. 2020, 19, 491–502. [Google Scholar] [CrossRef] [PubMed]
- Cornil, J.; Lemaur, V.; Calbert, J.P.; Brédas, J.L. Charge transport in discotic liquid crystals: A molecular scale description. Adv. Mater. 2002, 14, 726–729. [Google Scholar] [CrossRef]
- Skabara, P.J.; Arlin, J.B.; Geerts, Y.H. Close encounters of the 3D kind—Exploiting high dimensionality in molecular semiconductors. Adv. Mater. 2013, 25, 1948–1954. [Google Scholar] [CrossRef]
- Kohler, A.; Bassler, H. Electronic Processes in Organic Semiconductors, an Introduction; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Giannini, S.; Carof, A.; Blumberger, J. Crossover from hopping to band-like charge transport in an organic semiconductor model: Atomistic nonadiabatic molecular dynamics simulation. J. Phys. Chem. Lett. 2018, 9, 3116–3123. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry: Theory and experiment. Angew. Chem. Int. Ed. Eng. 1993, 32, 1111–1121. [Google Scholar] [CrossRef]
- Barbara, P.F.; Meyer, T.J.; Ratner, M.A. Contemporary issues in electron transfer research. J. Phys. Chem. 1996, 100, 13148–13168. [Google Scholar] [CrossRef]
- Brédas, J.L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge-transfer and energy-transfer processes in π-conjugated oligomers and polymers: A molecular picture. Chem. Rev. 2004, 104, 4971–5003. [Google Scholar] [CrossRef]
- Dimitrakopoulos, C.D.; Purushothaman, S.; Kymissis, J.; Callegari, A.; Shaw, J.M. Low-voltage organic transistors on plastic comprising high-dielectric constant gate insulators. Science 1999, 283, 822–824. [Google Scholar] [CrossRef] [PubMed]
- Warman, J.M.; de Haas, M.P.; Dicker, G.; Grozema, F.C.; Piris, J.; Debije, M.G. Charge mobilities in organic semiconducting materials determined by pulse-radiolysis time-resolved microwave conductivity: π-Bond-conjugated polymers versus π-π-stacked discotics. Chem. Mater. 2004, 16, 4600–4609. [Google Scholar] [CrossRef]
- Van de Craats, A.M.; Warman, J.M.; de Haas, M.P.; Adam, D.; Simmerer, J.; Haarer, D.; Schuhmacher, P. The mobility of carriers in all four phases of the columnar discotic material hexakis(hexylthio)triphenylene: Combined tof and PR-TRMC results. Adv. Mater. 1996, 8, 823–826. [Google Scholar] [CrossRef]
- Kazmaier, P.M.; Hoffmann, R. A Theoretical study of crystallochromy. quantum interference effects in the spectra of perylene pigments. J. Am. Chem. Soc. 1994, 116, 9684–9691. [Google Scholar] [CrossRef]
- Munn, R.W.; Silbey, R. Theory of electronic transport in molecular crystals. II. Zeroth order states incorporating nonlocal linear electron-phonon coupling. J. Chem. Phys. 1985, 83, 1843–1853. [Google Scholar] [CrossRef]
- Hannewald, K.; Stojanović, V.M.; Schellekens, J.M.T.; Bobbert, P.A.; Kresse, G.; Hafner, J. Theory of polaron bandwidth narrowing in organic molecular crystals. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 1–7. [Google Scholar] [CrossRef]
- Troisi, A. Prediction of the absolute charge mobility of molecular semiconductors: The case of rubrene. Adv. Mater. 2007, 19, 2000–2004. [Google Scholar] [CrossRef]
- Troisi, A.; Orlandi, G. Dynamics of the intermolecular transfer integral in crystalline organic semiconductors. J. Phys. Chem. A 2006, 110, 4065–4070. [Google Scholar] [CrossRef]
- Giannini, S.; Carof, A.; Ellis, M.; Yang, H.; Ziogos, O.G.; Ghosh, S.; Blumberger, J. Quantum localization and delocalization of charge carriers in organic semiconducting crystals. Nat. Commun. 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Schweicher, G.; D’Avino, G.; Ruggiero, M.T.; Harkin, D.J.; Broch, K.; Venkateshvaran, D.; Liu, G.; Richard, A.; Ruzié, C.; Armstrong, J.; et al. Chasing the “killer” phonon mode for the rational design of low-disorder, high-mobility molecular semiconductors. Adv. Mater. 2019, 31. [Google Scholar] [CrossRef]
- Nematiaram, T.; Ciuchi, S.; Xie, X.; Fratini, S.; Troisi, A. Practical computation of the charge mobility in molecular semiconductors using transient localization theory. J. Phys. Chem. C 2019, 123, 6989–6997. [Google Scholar] [CrossRef]
- Troisi, A. The speed limit for sequential charge hopping in molecular materials. Org. Electron. 2011, 12, 1988–1991. [Google Scholar] [CrossRef]
- Kaake, L.G.; Barbara, P.F.; Zhu, X.Y. Intrinsic charge trapping in organic and polymeric semiconductors: A physical chemistry perspective. J. Phys. Chem. Lett. 2010, 1, 628–635. [Google Scholar] [CrossRef]
- Haneef, H.F.; Zeidell, A.M.; Jurchescu, O.D. Charge carrier traps in organic semiconductors: A review on the underlying physics and impact on electronic devices. J. Mater. Chem. C 2020, 8, 759–787. [Google Scholar] [CrossRef]
- Boden, N.; Bushby, R.J.; Clements, J. Mechanism of quasi-one-dimensional electronic conductivity in discotic liquid crystals. J. Chem. Phys. 1993, 98, 5920–5931. [Google Scholar] [CrossRef]
- Arikainen, E.O.; Boden, N.; Bushby, R.J.; Clements, J.; Movaghar, B.; Wood, A. Effects of side-chain length on the charge transport properties of discotic liquid crystals and their implications for the transport mechanism. J. Mater. Chem. 1995, 5, 2161–2165. [Google Scholar] [CrossRef]
- Iino, H.; Hanna, J. Ambipolar charge carrier transport in liquid crystals. Opto-Electron. Rev. 2005, 13, 295–302. [Google Scholar]
- Gearba, R.I.; Bondar, A.I.; Goderis, B.; Bras, W.; Ivanov, D.A. Tailoring the thermotropic behavior of tetra-substituted phthalocyanines via the lateral chains architecture. Chem. Mater. 2005, 17, 2825–2832. [Google Scholar] [CrossRef]
- Iino, H.; Hanna, J.I.; Haarer, D.; Bushby, R.J. Fast electron transport in discotic columnar phases of triphenylene derivatives. Jpn. J. Appl. Physics Part 1 Regul. Pap. Short Notes Rev. Pap. 2006, 45, 430–433. [Google Scholar] [CrossRef]
- Deibel, C.; Janssen, D.; Heremans, P.; de Cupere, V.; Geerts, Y.; Benkhedir, M.L.; Adriaenssens, G.J. Charge transport properties of a metal-free phthalocyanine discotic liquid crystal. Org. Electron. 2006, 7, 495–499. [Google Scholar] [CrossRef][Green Version]
- Van de Craats, A.M.; Warman, J.M. Core-size effect on the mobility of charge in discotic liquid crystalline materials. Adv. Mater. 2001, 13, 130–133. [Google Scholar] [CrossRef]
- Brédas, J.L.; Calbert, J.P.; da Silva Filho, D.A.; Cornil, J. Organic semiconductors: A theoretical characterization of the basic parameters governing charge transport. Proc. Natl. Acad. Sci. USA 2002, 99, 5804–5809. [Google Scholar] [CrossRef] [PubMed]
- Haverkate, L.A.; Zbiri, M.; Johnson, M.R.; Deme, B.; Mulder, F.M.; Kearley, G.J. Conformation, defects, and dynamics of a discotic liquid crystal and their influence on charge transport. J. Phys. Chem. B 2011, 115, 13809–13816. [Google Scholar] [CrossRef]
- Feng, X.; Marcon, V.; Pisula, W.; Hansen, M.R.; Kirkpatrick, J.; Grozema, F.; Andrienko, D.; Kremer, K.; Müllen, K. Towards high charge-carrier mobilities by rational design of the shape and periphery of discotics. Nat. Mater. 2009, 8, 421–426. [Google Scholar] [CrossRef] [PubMed]
- Demenev, A.; Eichhorn, S.H.; Taerum, T.; Perepichka, D.F.; Patwardhan, S.; Grozema, F.C.; Siebbeles, L.D.A.; Klenkler, R. Quasi temperature independent electron mobility in hexagonal columnar mesophases of an H-bonded benzotristhiophene derivative. Chem. Mater. 2010, 22, 1420–1428. [Google Scholar] [CrossRef]
- Osawa, T.; Kajitani, T.; Hashizume, D.; Ohsumi, H.; Sasaki, S.; Takata, M.; Koizumi, Y.; Saeki, A.; Seki, S.; Fukushima, T.; et al. Wide-range 2D lattice correlation unveiled for columnarly assembled triphenylene hexacarboxylic esters. Angew. Chem. Int. Ed. 2012, 51, 7990–7993. [Google Scholar] [CrossRef] [PubMed]
- Adam, D.; Schuhmacher, P.; Simmerer, J.; Häussling, L.; Siemensmeyer, K.; Etzbachi, K.H.; Ringsdorf, H.; Haarer, D. Fast photoconduction in the highly ordered columnar phase of a discotic liquid crystal. Nature 1994, 371, 141–143. [Google Scholar] [CrossRef]
- Krishna Prasad, S.; Shankar Rao, D.S.; Chandrasekhar, S.; Kumar, S. X-ray studies on the columnar structures of discotic liquid crystals. Mol. Cryst. Liq. Cryst. 2003, 396, 121–139. [Google Scholar] [CrossRef]
- García-Frutos, E.M.; Pandey, U.K.; Termine, R.; Omenat, A.; Barberá, J.; Serrano, J.L.; Golemme, A.; Gõmez-Lor, B. High charge mobility in discotic liquid-crystalline triindoles: Just a core business? Angew. Chem. Int. Ed. 2011, 50, 7399–7402. [Google Scholar] [CrossRef]
- Grozema, F.C.; Siebbeles, L.D.A. Mechanism of charge transport in self-organizing organic materials. Int. Rev. Phys. Chem. 2008, 27, 87–138. [Google Scholar] [CrossRef]
- Kirkpatrick, J.; Marcon, V.; Nelson, J.; Kremer, K.; Andrienko, D. Charge mobility of discotic mesophases: A multiscale quantum and classical study. Phys. Rev. Lett. 2007, 98, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, J.; Marcon, V.; Kremer, K.; Nelson, J.; Andrienko, D. Columnar mesophases of hexabenzocoronene derivatives. II. Charge carrier mobility. J. Chem. Phys. 2008, 129, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Olivier, Y.; Muccioli, L.; Lemaur, V.; Geerts, Y.H.; Zannoni, C.; Cornil, J. Theoretical characterization of the structural and hole transport dynamics in liquid-crystalline phthalocyanine stacks. J. Phys. Chem. B 2009, 113, 14102–14111. [Google Scholar] [CrossRef] [PubMed]
- Cheung, D.L.; Troisi, A. Modelling charge transport in organic semiconductors: From quantum dynamics to soft matter. Phys. Chem. Chem. Phys. 2008, 10, 5941–5952. [Google Scholar] [CrossRef] [PubMed]
- Troisi, A.; Cheung, D.L.; Andrienko, D. Charge transport in semiconductors with multiscale conformational dynamics. Phys. Rev. Lett. 2009, 102, 18–21. [Google Scholar] [CrossRef]
- Mas-Torrent, M.; Rovira, C. Role of molecular order and solid-state structure in organic field-effect transistors. Chem. Rev. 2011, 111, 4833–4856. [Google Scholar] [CrossRef]
- Sirringhaus, H. 25th anniversary article: Organic field-effect transistors: The path beyond amorphous silicon. Adv. Mater. 2014, 26, 1319–1335. [Google Scholar] [CrossRef]
- Lüssem, B.; Keum, C.M.; Kasemann, D.; Naab, B.; Bao, Z.; Leo, K. Doped organic transistors. Chem. Rev. 2016, 116, 13714–13751. [Google Scholar] [CrossRef]
- Jacobs, I.E.; Moulé, A.J. Controlling molecular doping in organic semiconductors. Adv. Mater. 2017, 29, 1–39. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H.; Liu, A.; Zhu, H.H.; Li, W.; Lin, Y.F.; Noh, Y.Y. Doping: A key enabler for organic transistors. Adv. Mater. 2018, 30, 13–19. [Google Scholar] [CrossRef]
- Choi, H.H.; Cho, K.; Frisbie, C.D.; Sirringhaus, H.; Podzorov, V. Critical assessment of charge mobility extraction in FETs. Nat. Mater. 2017, 17, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Bittle, E.G.; Basham, J.I.; Jackson, T.N.; Jurchescu, O.D.; Gundlach, D.J. Mobility overestimation due to gated contacts in organic field-effect transistors. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, I.; Salleo, A.; Chabinyc, M. Avoid the kinks when measuring mobility. Science 2016, 352, 1521–1522. [Google Scholar] [CrossRef] [PubMed]
- Paterson, A.F.; Singh, S.; Fallon, K.J.; Hodsden, T.; Han, Y.; Schroeder, B.C.; Bronstein, H.; Heeney, M.; McCulloch, I.; Anthopoulos, T.D. Recent progress in high-mobility organic transistors: A reality check. Adv. Mater. 2018, 30, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455–2477. [Google Scholar] [CrossRef]
- Shakya, N.M. Studies of Electronic Transport in Novel Smectic and Discotic Liquid Cryalline Organic Semiconductors. Ph.D. Thesis, Kent State University, Kent, OH, USA, 2010. [Google Scholar]
- Nakagawa, D.; Nakano, C.; Ohmori, M.; Itani, H.; Shimizu, Y.; Fujii, A.; Ozaki, M. Miscibility and carrier transport properties in binary blend system of non-peripherally octa-hexyl-substituted phthalocyanine analogues. Org. Electron. 2017, 44, 67–73. [Google Scholar] [CrossRef]
- Kashima, K.; Sato, H.; Musha, K.; Kanno, K.I.; Takahashi, T. Carrier mobility for organic semiconductors: Reduction of noise of the short part drift time in the time of flight mobility method. Anal. Sci. 2007, 23, 1249–1251. [Google Scholar] [CrossRef]
- Paul, S. Charge Transport in Liquid Crystalline Smectic and Discotic Organic Semiconductors: New Results and Experimental Methodologies. Ph.D. Thesis, Kent State University, Kent, OH, USA, 2016. [Google Scholar]
- Dawson, N.J.; Patrick, M.S.; Paul, S.; Ellman, B.; Semyonov, A.; Twieg, R.J.; Matthews, R.; Pentzer, E.; Singer, K.D. Interfacial trapping in an aged discotic liquid crystal semiconductor. J. Appl. Phys. 2015, 118. [Google Scholar] [CrossRef]
- Duzhko, V.; Semyonov, A.; Twieg, R.J.; Singer, K.D. Correlated polaron transport in a quasi-one-dimensional liquid crystal. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 1–5. [Google Scholar] [CrossRef]
- Mott, N.F.; Gurney, R.W. Electronic Processes in Ionic Crystals, 2nd ed.; Clarendon Press: Oxford, UK, 1948. [Google Scholar]
- Murgatroyd, P.N. Theory of space-charge-limited current enhanced by Frenkel effect. J. Phys. D Appl. Phys. 1970, 3, 151–156. [Google Scholar] [CrossRef]
- Mark, P.; Helfrich, W. Space-charge-limited currents in organic crystals. J. Appl. Phys. 1962, 33, 205–215. [Google Scholar] [CrossRef]
- Bässler, H. Charge transport in disordered organic photoconductors a monte carlo simulation study. Phys. Status Solidi 1993, 175, 15–56. [Google Scholar] [CrossRef]
- Blakesley, J.C.; Clubb, H.S.; Greenham, N.C. Temperature-dependent electron and hole transport in disordered semiconducting polymers: Analysis of energetic disorder. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 1–9. [Google Scholar] [CrossRef]
- Van Mensfoort, S.L.M.; Vulto, S.I.E.; Janssen, R.A.J.; Coehoorn, R. Hole transport in polyfluorene-based sandwich-type devices: Quantitative analysis of the role of energetic disorder. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 78, 1–10. [Google Scholar] [CrossRef]
- Nicolai, H.T.; Wetzelaer, G.A.H.; Kuik, M.; Kronemeijer, A.J.; de Boer, B.; Blom, P.W.M. Space-charge-limited hole current in poly(9,9-dioctylfluorene) diodes. Appl. Phys. Lett. 2010, 96, 1–4. [Google Scholar] [CrossRef]
- De Boer, R.W.I.; Gershenson, M.E.; Morpurgo, A.F.; Podzorov, V. Organic single-crystal field-effect transistors. Phys. Status Solidi Appl. Res. 2004, 201, 1302–1331. [Google Scholar] [CrossRef]
- Nikolka, M.; Broch, K.; Armitage, J.; Hanifi, D.; Nowack, P.J.; Venkateshvaran, D.; Sadhanala, A.; Saska, J.; Mascal, M.; Jung, S.H.; et al. High-mobility, trap-free charge transport in conjugated polymer diodes. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Zubair, M.; Ang, Y.S.; Ang, L.K. Thickness dependence of space-charge-limited current in spatially disordered organic semiconductors. IEEE Trans. Electron. Devices 2018, 65, 3421–3429. [Google Scholar] [CrossRef]
- Blakesley, J.C.; Castro, F.A.; Kylberg, W.; Dibb, G.F.A.; Arantes, C.; Valaski, R.; Cremona, M.; Kim, J.S.; Kim, J.S. Towards reliable charge-mobility benchmark measurements for organic semiconductors. Org. Electron. 2014, 15, 1263–1272. [Google Scholar] [CrossRef]
- Many, A.; Rakavi, G. Theory of transient space-charge-limited currents in solids in the presence of trapping. Phys. Rev. 1962, 126, 1980–1988. [Google Scholar] [CrossRef]
- Campbell, A.J.; Bradley, D.D.C.; Antoniadis, H. Quantifying the efficiency of electrodes for positive carrier injection into poly(9,9-dioctylfluorene) and representative copolymers. J. Appl. Phys. 2001, 89, 3343–3351. [Google Scholar] [CrossRef]
- Poplavskyy, D.; Nelson, J. Nondispersive hole transport in amorphous films of methoxy-spirofluorene-arylamine organic compound. J. Appl. Phys. 2003, 93, 341–346. [Google Scholar] [CrossRef]
- Tse, S.C.; Tsang, S.W.; So, S.K. Polymeric conducting anode for small organic transporting molecules in dark injection experiments. J. Appl. Phys. 2006, 100, 1–5. [Google Scholar] [CrossRef]
- Juska, G.; Arlauskas, K.; Viliunas, M.; Kocka, J. Extraction current transients: New method of study of charge transport in microcrystalline silicon. Phys. Rev. Lett. 2000, 84, 4946–4949. [Google Scholar] [CrossRef] [PubMed]
- Ohmori, M.; Nishikawa, Y.; Fujii, A.; Ozaki, M. Homeotropic alignment of non-peripheral octahexyl phthalocyanine in thin film and its photovoltaic properties. Jpn. J. Appl. Phys. 2018, 57. [Google Scholar] [CrossRef]
- Juska, G.; Arlauskas, K.; Viliunas, M.; Genevicius, K.; Osterbaka, R.; Stubb, H. Charge transport in p-conjugated polymers from extraction current transients. Phys. Rev. B 2000, 62, R16235–R16238. [Google Scholar] [CrossRef]
- Bange, S.; Schubert, M.; Neher, D. Charge mobility determination by current extraction under linear increasing voltages: Case of nonequilibrium charges and field-dependent mobilities. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 1–7. [Google Scholar] [CrossRef]
- Mozer, A.J.; Sariciftci, N.S.; Pivrikas, A.; Österbacka, R.; Juška, G.; Brassat, L.; Bässler, H. Charge carrier mobility in regioregular poly(3-hexylthiophene) probed by transient conductivity techniques: A comparative study. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 71, 1–9. [Google Scholar] [CrossRef]
- Warman, J.M.; de Haas, M.P.; Hummel, A. The detection of electrons in pulse irradiated liquid hydrocarbons by microwave absorption. Chem. Phys. Lett. 1973, 22, 480–483. [Google Scholar] [CrossRef]
- Infelta, P.P.; de Haas, M.P.; Warman, J.M. The study of the transient conductivity of pulse irradiated dielectric liquids on a nanosecond timescale using microwaves. Radiat. Phys. Chem. 1977, 10, 353–365. [Google Scholar] [CrossRef]
- Warman, J.M.; de Haas, M.P.; Wentinck, H.M. THE study of radiation induced conductivity changes in microheterogeneous materials using microwaves. Radiat. Phys. Chem. 1989, 34, 581–586. [Google Scholar] [CrossRef]
- Warman, J.M.; van de Craats, A.M. Charge mobility in discotic materials studied by PR-TRMC. Mol. Cryst. Liq. Cryst. 2003, 396, 41–72. [Google Scholar] [CrossRef]
- Saeki, A.; Seki, S.; Koizumi, Y.; Sunagawa, T.; Ushida, K.; Tagawa, S. Increase in the mobility of photogenerated positive charge carriers in polythiophene. J. Phys. Chem. B 2005, 109, 10015–10019. [Google Scholar] [CrossRef] [PubMed]
- Seki, S.; Saeki, A.; Sakurai, T.; Sakamaki, D. Charge carrier mobility in organic molecular materials probed by electromagnetic waves. Phys. Chem. Chem. Phys. 2014, 16, 11093–11113. [Google Scholar] [CrossRef] [PubMed]
- Impedance Spectroscopy Theory, Experiment, and Applications, 3rd ed.; Barsoukov, E., Macdonald, J.R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2018; ISBN 9781119074083. [Google Scholar]
- Martens, H.C.F.; Brom, H.B.; Blom, P.W.M. Frequency-dependent electrical response of holes in poly(p-phenylene vinylene). Phys. Rev. B 1999, 60, R8489–R8492. [Google Scholar] [CrossRef]
- Tsang, S.W.; So, S.K.; Xu, J.B. Application of admittance spectroscopy to evaluate carrier mobility in organic charge transport materials. J. Appl. Phys. 2006, 99. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Schmeits, M.; Loebl, H.P. Determination of charge-carrier transport in organic devices by admittance spectroscopy: Application to hole mobility in α-NPD. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 75, 1–13. [Google Scholar] [CrossRef]
- Montero, J.M.; Bisquert, J. Features of capacitance and mobility of injected carriers in organic layers measured by impedance spectroscopy. Isr. J. Chem. 2012, 52, 519–528. [Google Scholar] [CrossRef]
- Zhang, Y.; Hanifi, D.; Alvarez, S.; Antonio, F.; Pun, A.; Klivansky, L.M.; Hexemer, A.; Ma, B.; Liu, Y. Charge transport anisotropy in n-type disk-shaped triphenylene-tris (aroyleneimidazole)s. Org. Lett. 2011, 13, 6528–6531. [Google Scholar] [CrossRef]
- Zhang, Y.; Hanifi, D.A.; Fernández-Liencres, M.P.; Klivansky, L.M.; Ma, B.; Navarro, A.; Liu, Y. Understanding Electron transport in disk-shaped triphenylene-tris (naphthaleneimidazole)s through structural modification and theoretical investigation. ACS Appl. Mater. Interfaces 2017, 9, 20010–20019. [Google Scholar] [CrossRef]
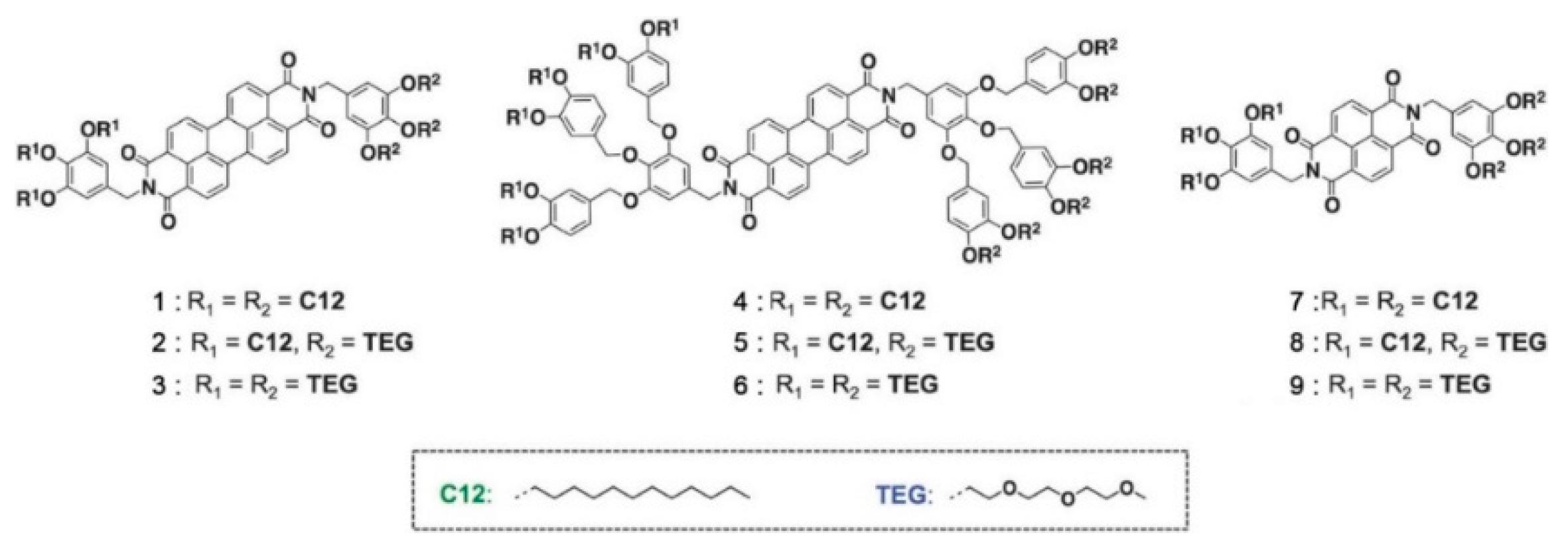
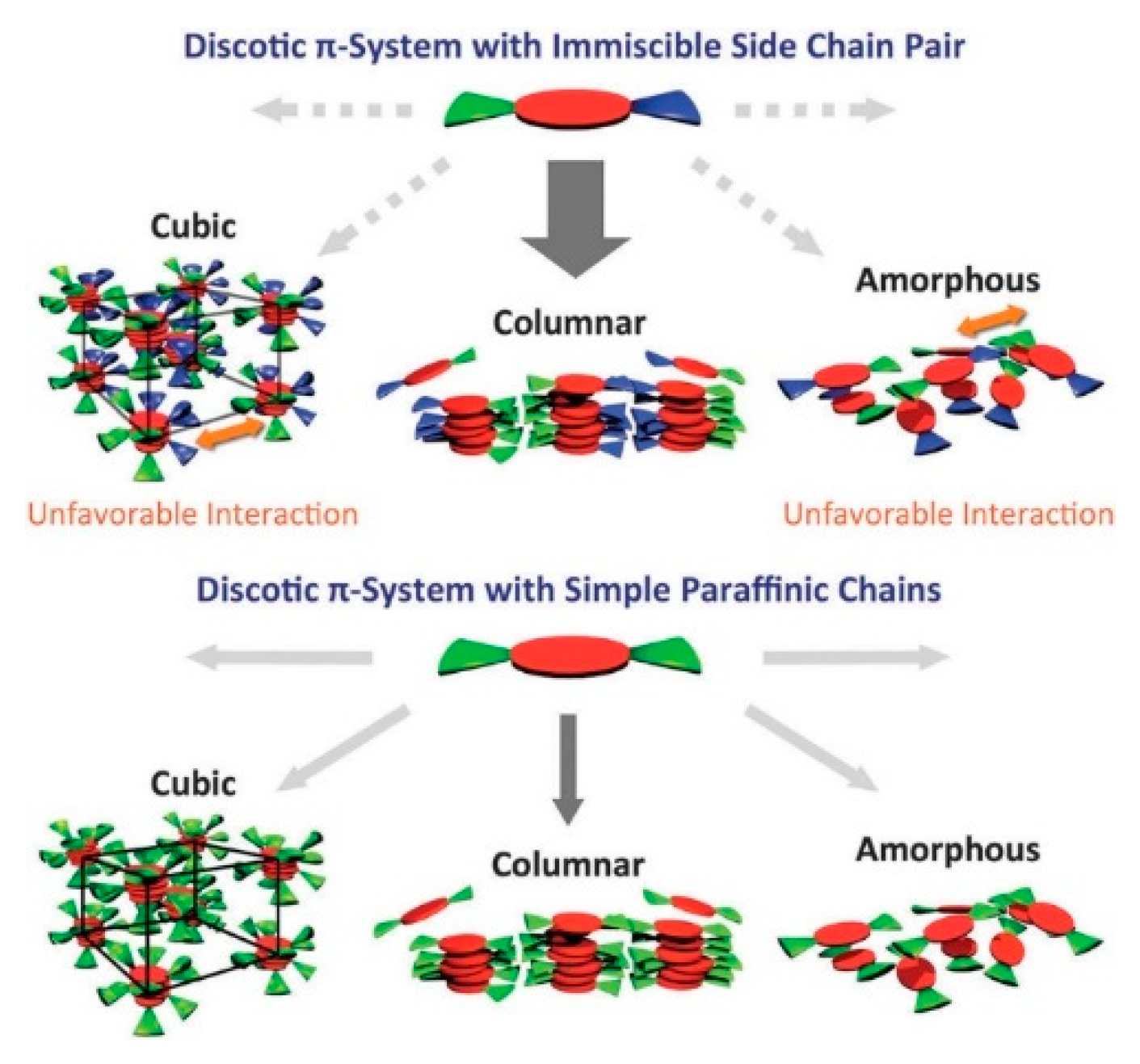
- Sakurai, T.; Tsutsui, Y.; Kato, K.; Takata, M.; Seki, S. Preferential formation of columnar mesophases via peripheral modification of discotic π-systems with immiscible side chain pairs. J. Mater. Chem. C 2016, 4, 1490–1496. [Google Scholar] [CrossRef]
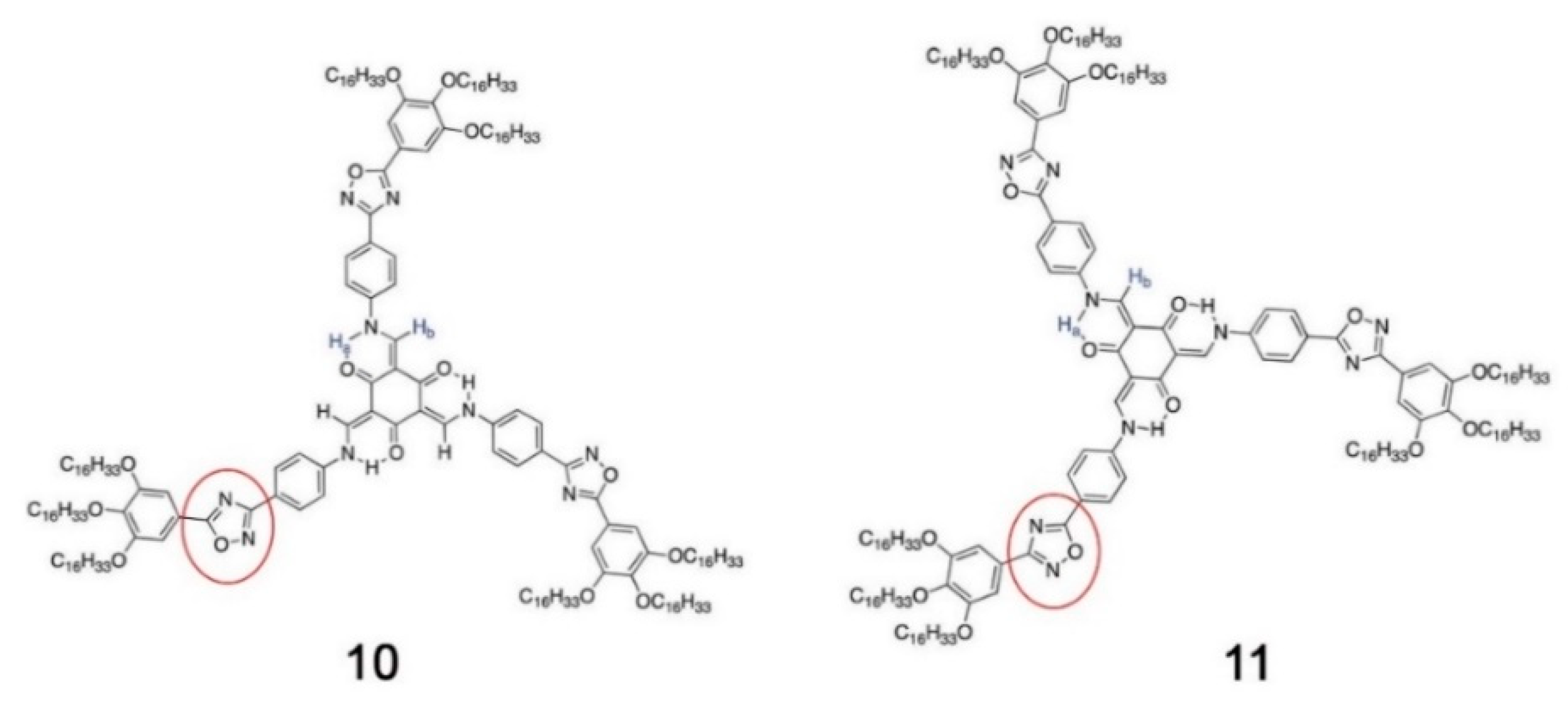
- Pathak, S.K.; Nath, S.; De, J.; Pal, S.K.; Achalkumar, A.S. The effect of regioisomerism on the mesomorphic and photophysical behavior of oxadiazole-based tris(N-salicylideneaniline)s: Synthesis and characterization. New J. Chem. 2017, 41, 9908–9917. [Google Scholar] [CrossRef]
- Ferreira, M.; Moreira, T.S.; Cristiano, R.; Gallardo, H.; Bentaleb, A.; Dechambenoit, P.; Hillard, E.A.; Durola, F.; Bock, H. Isomeric column-forming esters and imides with varying curvatures of the aromatic plane. Chem. Eur. J. 2018, 24, 2214–2223. [Google Scholar] [CrossRef] [PubMed]
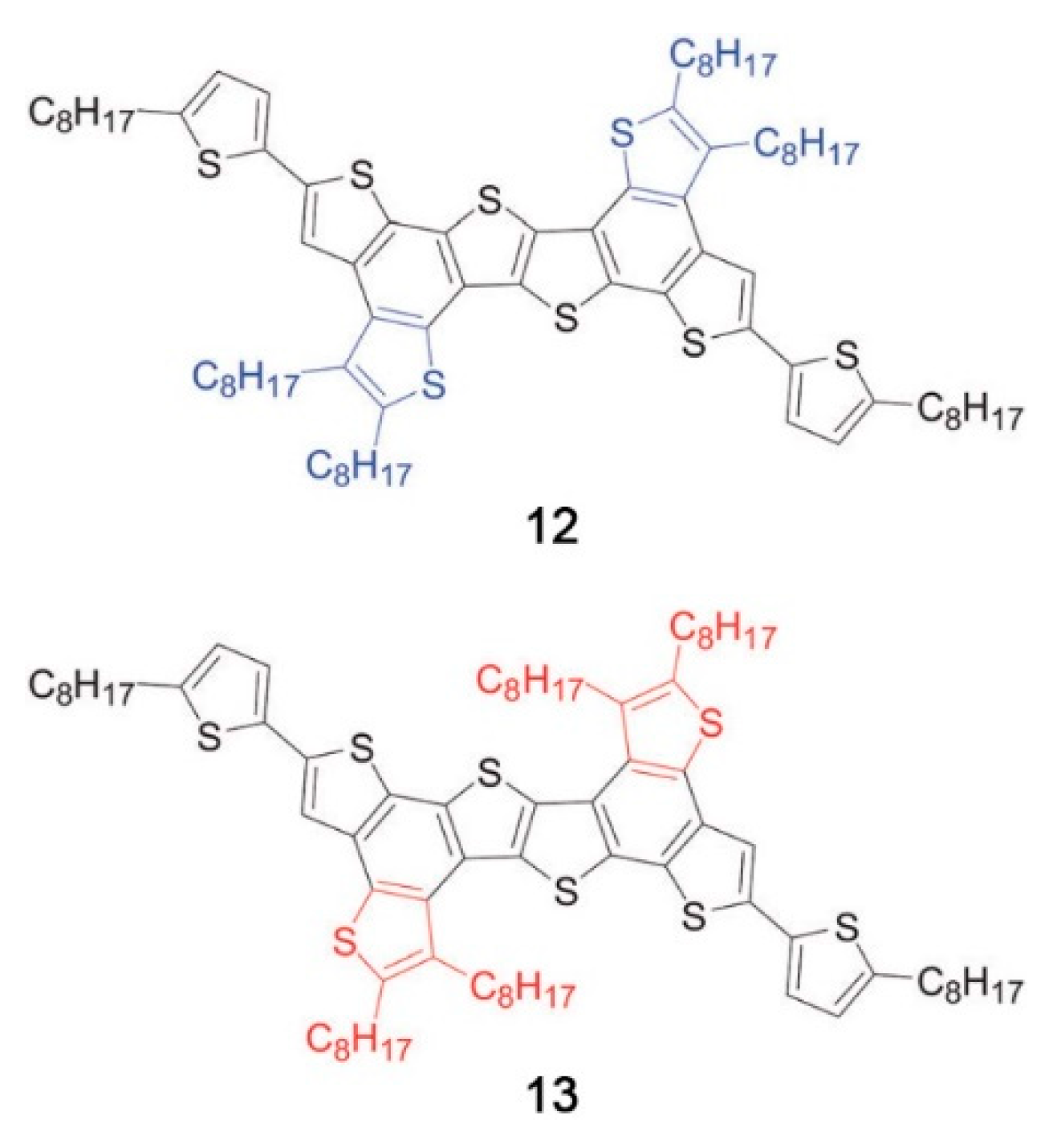
- Dang, D.; Zhou, P.; Wu, Y.; Xu, Y.; Zhi, Y.; Zhu, W. Isomeric organic semiconductors containing fused-thiophene cores: Molecular packing and charge transport. Phys. Chem. Chem. Phys. 2018, 20, 13171–13177. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Wang, J.; Hong, F.; Hao, X.; Zhang, A.; Wang, Y.; Wu, H.; Zhang, W.; Pu, J. Systematic studies on structure-properties relationship of main chain discotic liquid crystalline polyethers: Effects of the spacer lengths and substitution positions. Polym. Chem. 2016, 7, 3013–3025. [Google Scholar] [CrossRef]
- Hao, X.; Zhang, C.; Wang, J.; Zhang, W.; Hong, F.; Zhang, S.; Zhang, A.; Yang, H.; Zhang, Z.; Wang, Y.; et al. Competition and promotion of different mesophases in a series of novel unsymmetrical discotic dimers via subtle modification of spacers and peripheral side chains. J. Mater. Chem. C 2017, 5, 589–600. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Zhang, S.; Hao, X.; Hong, F.; Zhang, A.; Wang, Y.F.; Wu, H.; Zhang, W.; Pu, J.L. A systematic study on the influences of linkage length on phase behaviours and charge carrier mobilities of discotic dimers. Liq. Cryst. 2017, 44, 394–404. [Google Scholar] [CrossRef]
- Zhao, K.Q.; Jing, M.; An, L.L.; Du, J.Q.; Wang, Y.H.; Hu, P.; Wang, B.Q.; Monobe, H.; Heinrich, B.; Donnio, B. Facile transformation of 1-aryltriphenylenes into dibenzo[fg,op]tetracenes by intramolecular Scholl cyclodehydrogenation: Synthesis, self-assembly, and charge carrier mobility of large π-extended discogens. J. Mater. Chem. C 2017, 5, 669–682. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Zhang, Z.; Yang, H.; Zhang, A.; Hao, X.; Wang, J.; Zhang, C.; Pu, J. 2D organic superlattice promoted via combined action of π-π stacking and dipole-dipole interaction in discotic liquid crystals. J. Phys. Chem. B 2017, 121, 7519–7525. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Bi, J.; Zhang, A.; Fang, Y.; Feng, Y.; An, L.; Liang, L.; Zhang, C.; Pu, J. The leading role of the steric hindrance effect and dipole-dipole interaction in superlattice nanostructures formed via the assembly of discotic liquid crystals. New J. Chem. 2018, 42, 20087–20094. [Google Scholar] [CrossRef]
- Mu, B.; Hao, X.; Chen, J.; Li, Q.; Zhang, C.; Chen, D. Discotic columnar liquid-crystalline polymer semiconducting materials with high charge-carrier mobility via rational macromolecular engineering. Polym. Chem. 2017, 8, 3286–3293. [Google Scholar] [CrossRef]
- Concellón, A.; Marcos, M.; Romero, P.; Serrano, J.L.; Termine, R.; Golemme, A. Not only columns: High hole mobility in a discotic nematic mesophase formed by metal-containing porphyrin-core dendrimers. Angew. Chem. Int. Ed. 2017, 56, 1259–1263. [Google Scholar] [CrossRef] [PubMed]
- Concellón, A.; Termine, R.; Golemme, A.; Romero, P.; Marcos, M.; Serrano, J.L. Semiconducting and electropolymerizable liquid crystalline carbazole-containing porphyrin-core dendrimers. Org. Chem. Front. 2020, 7, 2008–2015. [Google Scholar] [CrossRef]
- Concellón, A.; Termine, R.; Golemme, A.; Romero, P.; Marcos, M.; Serrano, J.L. High hole mobility and light-harvesting in discotic nematic dendrimers prepared: Via “click” chemistry. J. Mater. Chem. C 2019, 7, 2911–2918. [Google Scholar] [CrossRef]
- Said, S.M.; Mahmood, M.S.; Daud, M.N.; Mohd Sabri, M.F.; Sairi, N.A. Structure-electronics relations of discotic liquid crystals from a molecular modelling perspective. Liq. Cryst. 2016, 43, 2092–2113. [Google Scholar] [CrossRef]
- Volpi, R.; Camilo, A.C.S.; Filho, D.A.D.S.; Navarrete, J.T.L.; Gómez-Lor, B.; Delgado, M.C.R.; Linares, M. Modelling charge transport of discotic liquid-crystalline triindoles: The role of peripheral substitution. Phys. Chem. Chem. Phys. 2017, 19, 24202–24208. [Google Scholar] [CrossRef]
- Zhao, D.; Zhu, Z.; Kuo, M.Y.; Chueh, C.C.; Jen, A.K.Y. Hexaazatrinaphthylene derivatives: Efficient electron-transporting materials with tunable energy levels for inverted perovskite solar cells. Angew. Chem. Int. Ed. 2016, 55, 8999–9003. [Google Scholar] [CrossRef]
- An, B.; Wen, K.; Feng, S.; Pan, X.; Wu, W.; Guo, X.; Zhang, J. Theoretical insights into the 1D-charge transport properties in a series of hexaazatrinaphthylene-based discotic molecules. J. Comput. Chem. 2018, 39, 773–779. [Google Scholar] [CrossRef]
- Mahmood, M.S.; Mohd Said, S.; Chatterjee, A.; Sabri, M.F.M.; Mainal, A.; Daud, M.N.; Sairi, N.A. DFT studies of structural-electronic correlation for the HAT6 discotic liquid crystal columnar stacking. Mater. Res. Express 2018, 5. [Google Scholar] [CrossRef]
- Thompson, I.R.; Coe, M.K.; Walker, A.B.; Ricci, M.; Roscioni, O.M.; Zannoni, C. Microscopic origins of charge transport in triphenylene systems. Phys. Rev. Mater. 2018, 2, 25–29. [Google Scholar] [CrossRef]
- Cagardová, D.; Matúška, J.; Poliak, P.; Lukeš, V. Design of novel generations of planar sunflower molecules: Theoretical comparative study of electronic structure and charge transport characteristics. J. Phys. Chem. C 2019, 123, 22752–22766. [Google Scholar] [CrossRef]
- Cagardová, D.; Michalík, M.; Poliak, P.; Lukeš, V. Electronic structure and charge-transport properties of symmetric linear condensed bis-benzothiadiazole derivatives. J. Mol. Struct. 2019, 1175, 297–306. [Google Scholar] [CrossRef]
- Benito-Hernández, A.; Pandey, U.K.; Cavero, E.; Termine, R.; García-Frutos, E.M.; Serrano, J.L.; Golemme, A.; Gómez-Lor, B. High hole mobility in triindole-based columnar phases: Removing the bottleneck of homogeneous macroscopic orientation. Chem. Mater. 2013, 25, 117–121. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, J.; Shi, J.; Qi, H.; Baranoff, E.; Xie, G.; Li, Q.; Tan, H.; Liu, Y.; Zhu, W. Influence of integrated alkyl-chain length on the mesogenic and photophysical properties of platinum-based metallomesogens and their application for polarized white OLEDs. Dyes Pigments 2016, 133, 238–247. [Google Scholar] [CrossRef]
- Zhao, H.; He, Z.; Xu, M.; Liang, C.; Kumar, S. Electron transporting organic materials with an exceptional large scale homeotropic molecular orientation. Phys. Chem. Chem. Phys. 2016, 18, 8554–8560. [Google Scholar] [CrossRef]
- Kondratenko, K.; Singh, D.P.; Boussoualem, Y.; Douali, R.; Legrand, C.; Daoudi, A. Hole transporting properties of discotic liquid-crystalline semiconductor confined in calamitic UV-crosslinked gel. J. Mol. Liq. 2019, 276, 27–31. [Google Scholar] [CrossRef]
- Park, W.; Feringán, B.; Yang, M.; Ryu, S.H.; Ahn, H.; Shin, T.J.; Sierra, T.; Giménez, R.; Yoon, D.K. Manipulation of supramolecular columnar structures of H-bonded donor-acceptor units through geometrical nanoconfinement. ChemPhysChem 2019, 20, 890–897. [Google Scholar] [CrossRef]
- Sentker, K.; Zantop, A.W.; Lippmann, M.; Hofmann, T.; Seeck, O.H.; Kityk, A.V.; Yildirim, A.; Schönhals, A.; Mazza, M.G.; Huber, P. Quantized self-assembly of discotic rings in a liquid crystal confined in nanopores. Phys. Rev. Lett. 2018, 120, 67801. [Google Scholar] [CrossRef]
- Gowda, A.; Jacob, L.; Joy, N.; Philip, R.; Kumar, S. Novel phenazine fused triphenylene discotic liquid crystals: Synthesis, characterisation, thermal, optical and nonlinear optical properties. New J. Chem. 2018, 42, 19034–19042. [Google Scholar] [CrossRef]
- Gowda, A.; Jacob, L.; Patra, A.; George, A.; Philip, R.; Kumar, S. Synthesis, mesomorphic properties and nonlinear optical studies of alkyl and alkoxy phenylacetylene containing phenazine fused extended triphenylene discotic liquid crystalline dyes. Dyes Pigments 2019, 160, 128–135. [Google Scholar] [CrossRef]
- Gowda, A.; Jacob, L.; Singh, D.P.; Douali, R.; Kumar, S. Charge transport in novel phenazine fused triphenylene supramolecular systems. ChemistrySelect 2018, 3, 6551–6560. [Google Scholar] [CrossRef]
- Zhao, K.Q.; Du, J.Q.; Long, X.H.; Jing, M.; Wang, B.Q.; Hu, P.; Monobe, H.; Henrich, B.; Donnio, B. Design of Janus triphenylene mesogens: Facile synthesis, mesomorphism, photoluminescence, and semiconductivity. Dyes Pigments 2017, 143, 252–260. [Google Scholar] [CrossRef]
- Dai, J.; Zhao, K.Q.; Wang, B.Q.; Hu, P.; Heinrich, B.; Donnio, B. Liquid crystal ionic self-assembly and anion-selective photoluminescence in discotic azatriphenylenes. J. Mater. Chem. C 2020, 8, 4215–4225. [Google Scholar] [CrossRef]
- Vadivel, M.; Kumar, I.S.; Swamynathan, K.; Raghunathan, V.A.; Kumar, S. Novel annulated triphenylene discotic liquid crystals generated by pictet-spengler cyclization. ChemistrySelect 2018, 3, 8763–8769. [Google Scholar] [CrossRef]
- Kong, X.; Xia, L.; Zhang, H.; Dai, S.; Yu, C.; Liu, Z.; Mu, L.; Wang, G.; He, Z. Synthesis and investigation on liquid crystal and optical properties of dyads based on triphenylene and perylene. RSC Adv. 2017, 7, 17030–17037. [Google Scholar] [CrossRef]
- Kong, X.; Dai, S.; Wang, G.; Zhang, Z.; Zhang, L.; Liao, P.; Liu, W. Synthesis and characterization of mesogenic triphenylene-perylene dyads with phenoxy-alkoxy linkers. Mol. Cryst. Liq. Cryst. 2017, 650, 56–64. [Google Scholar] [CrossRef]
- Feringán, B.; Romero, P.; Serrano, J.L.; Folcia, C.L.; Etxebarria, J.; Ortega, J.; Termine, R.; Golemme, A.; Giménez, R.; Sierra, T. H-bonded donor-acceptor units segregated in coaxial columnar assemblies: Toward high mobility ambipolar organic semiconductors. J. Am. Chem. Soc. 2016, 138, 12511–12518. [Google Scholar] [CrossRef]
- Guo, H.; Zhu, M.; Wang, Z.; Yang, F. Triphenylene–perylene–triphenylene triads with bay-substituents: Synthesis, mesomorphism, and electron transfer properties. Tetrahedron Lett. 2016, 57, 4191–4195. [Google Scholar] [CrossRef]
- Chico, R.; de Domingo, E.; Domínguez, C.; Donnio, B.; Heinrich, B.; Termine, R.; Golemme, A.; Coco, S.; Espinet, P. High one-dimensional charge mobility in semiconducting columnar mesophases of isocyano-triphenylene metal complexes. Chem. Mater. 2017, 29, 7587–7595. [Google Scholar] [CrossRef]
- Miguel-Coello, A.B.; Bardají, M.; Coco, S.; Donnio, B.; Heinrich, B.; Espinet, P. Triphenylene-imidazolium salts and their NHC metal complexes, materials with segregated multicolumnar mesophases. Inorg. Chem. 2018, 57, 4359–4369. [Google Scholar] [CrossRef]
- Mahesh, P.; Shah, A.; Swamynathan, K.; Singh, D.P.; Douali, R.; Kumar, S. Carbon dot-dispersed hexabutyloxytriphenylene discotic mesogens: Structural, morphological and charge transport behavior. J. Mater. Chem. C 2020, 8, 9252–9261. [Google Scholar] [CrossRef]
- Shah, A.; Duponchel, B.; Gowda, A.; Kumar, S.; Becuwe, M.; Davoisne, C.; Legrand, C.; Douali, R.; Singh, D.P. Charge transport in phenazine-fused triphenylene discotic mesogens doped with CdS nanowires. New J. Chem. 2020, 44, 14872–14878. [Google Scholar] [CrossRef]
- Khan, A.A.; Rughoobur, G.; Kamarudin, M.A.; Sepe, A.; Dolan, J.A.; Flewitt, A.J.; Qasim, M.M.; Wilkinson, T.D. Homologous binary mixtures and improved hole conduction of self-assembled discotic liquid crystals. Org. Electron. 2016, 36, 35–44. [Google Scholar] [CrossRef]
- Zhao, K.Q.; An, L.L.; Zhang, X.B.; Yu, W.H.; Hu, P.; Wang, B.Q.; Xu, J.; Zeng, Q.D.; Monobe, H.; Shimizu, Y.; et al. Highly segregated lamello-columnar mesophase organizations and fast charge carrier mobility in new discotic donor-acceptor triads. Chem. Eur. J. 2015, 21, 10379–10390. [Google Scholar] [CrossRef]
- Lee, K.J.; Woo, J.H.; Kim, E.; Xiao, Y.; Su, X.; Mazur, L.M.; Attias, A.J.; Fages, F.; Cregut, O.; Barsella, A.; et al. Electronic energy and electron transfer processes in photoexcited donor-acceptor dyad and triad molecular systems based on triphenylene and perylene diimide units. Phys. Chem. Chem. Phys. 2016, 18, 7875–7887. [Google Scholar] [CrossRef]
- Li, X.C.; Wang, C.Y.; Lai, W.Y.; Huang, W. Triazatruxene-based materials for organic electronics and optoelectronics. J. Mater. Chem. C 2016, 4, 10574–10587. [Google Scholar] [CrossRef]
- Ruiz, C.; Pandey, U.K.; Termine, R.; García-Frutos, E.M.; López-Espejo, G.; Ortiz, R.P.; Huang, W.; Marks, T.J.; Facchetti, A.; Ruiz Delgado, M.C.; et al. Mobility versus alignment of a semiconducting π-extended discotic liquid-crystalline triindole. ACS Appl. Mater. Interfaces 2016, 8, 26964–26971. [Google Scholar] [CrossRef]
- Barard, S.; Kreouzis, T.; Cammidge, A.N.; Cook, M.J.; Ray, A.K. Newly synthesised gadolinium bis-phthalocyanine sandwich complex: Ambipolar organic semiconductor. Semicond. Sci. Technol. 2018, 33. [Google Scholar] [CrossRef]
- Liu, C.X.; Wang, H.; Du, J.Q.; Zhao, K.Q.; Hu, P.; Wang, B.Q.; Monobe, H.; Heinrich, B.; Donnio, B. Molecular design of benzothienobenzothiophene-cored columnar mesogens: Facile synthesis, mesomorphism, and charge carrier mobility. J. Mater. Chem. C 2018, 6, 4471–4478. [Google Scholar] [CrossRef]
- Zhao, K.C.; Du, J.Q.; Wang, H.F.; Zhao, K.Q.; Hu, P.; Wang, B.Q.; Monobe, H.; Heinrich, B.; Donnio, B. Board-like fused-thiophene liquid crystals and their benzene analogs: Facile Synthesis, self-assembly, p-type semiconductivity, and photoluminescence. Chem. Asian J. 2019, 14, 462–470. [Google Scholar] [CrossRef]
- Gómez-Esteban, S.; Benito-Hernandez, A.; Termine, R.; Hennrich, G.; Navarrete, J.T.L.; Ruiz Delgado, M.C.; Golemme, A.; Gómez-Lor, B. High-mobility self-assembling truxenone-based n-type organic semiconductors. Chem. Eur. J. 2018, 24, 3576–3583. [Google Scholar] [CrossRef] [PubMed]
- Benito-Hernández, A.; El-Sayed, M.T.; López Navarrete, J.T.; Ruiz Delgado, M.C.; Gómez-Lor, B. Fused donor-acceptor π-conjugated diazatruxenones: Synthesis and electronic properties. Org. Chem. Front. 2018, 5, 1748–1755. [Google Scholar] [CrossRef]
- Gupta, R.K.; Shankar Rao, D.S.; Prasad, S.K.; Achalkumar, A.S. Columnar self-assembly of electron-deficient dendronized bay-annulated perylene bisimides. Chem. Eur. J. 2018, 24, 3566–3575. [Google Scholar] [CrossRef] [PubMed]
- Iguarbe, V.; Concellón, A.; Termine, R.; Golemme, A.; Barberá, J.; Serrano, J.L. Making coaxial wires out of janus dendrimers for efficient charge transport. ACS Macro Lett. 2018, 7, 1138–1143. [Google Scholar] [CrossRef]
- Fukui, H.; Nakano, S.; Uno, T.; Dao, Q.D.; Saito, T.; Fujii, A.; Shimizu, Y.; Ozaki, M. Miscibility in binary blends of non-peripheral alkylphthalocyanines and their application for bulk-heterojunction solar cells. Org. Electron. 2014, 15, 1189–1196. [Google Scholar] [CrossRef]
- Gregg, B.A.; Fox, M.A.; Bard, A.J. Photovoltaic effect in symmetrical cells of a liquid crystal porphyrin. J. Phys. Chem. 1990, 94, 1586–1598. [Google Scholar] [CrossRef]
- Bisoyi, H.K.; Li, Q. Discotic Liquid Crystals for Self-Organizing Photovoltaics; Springer: Cham, Switzerland, 2016; ISBN 9783319320236. [Google Scholar]
- Bajpai, M.; Yadav, N.; Kumar, S.; Srivastava, R.; Dhar, R. Bulk heterojunction solar cells based on self-assembling disc-shaped liquid crystalline material. Liq. Cryst. 2016, 43, 305–313. [Google Scholar] [CrossRef]
- Bajpai, M.; Yadav, N.; Kumar, S.; Srivastava, R.; Dhar, R. Incorporation of liquid crystalline triphenylene derivative in bulk heterojunction solar cell with molybdenum oxide as buffer layer for improved efficiency. Liq. Cryst. 2016, 43, 928–936. [Google Scholar] [CrossRef]
- Bajpai, M.; Yadav, N.; Kumar, S.; Srivastava, R.; Dhar, R. Bulk heterojunction solar cells made from carbazole copolymer and fullerene derivative with an inserted layer of discotic material with improved efficiency. Liq. Cryst. 2017, 44, 379–386. [Google Scholar] [CrossRef]
- Nakata, Y.; Usui, T.; Nishikawa, Y.; Nekelson, F.; Shimizu, Y.; Fujii, A.; Ozaki, M. Sandwich-cell-type bulk-heterojunction organic solar cells utilizing liquid crystalline phthalocyanine. Jpn. J. Appl. Phys. 2018, 57. [Google Scholar] [CrossRef]
- Dao, Q.D.; Fujii, A.; Ozaki, M. Fabrication of tandem solar cells with all-solution processed multilayer structure using non-peripherally substituted octahexyl tetrabenzotriazaporphyrins. Jpn. J. Appl. Phys. 2016, 55. [Google Scholar] [CrossRef]
- Ozaki, M.; Yoneya, M.; Shimizu, Y.; Fujii, A. Carrier transport and device applications of the organic semiconductor based on liquid crystalline non-peripheral octaalkyl phthalocyanine. Liq. Cryst. 2018, 45, 2376–2389. [Google Scholar] [CrossRef]
- Wang, T.; Niu, M.S.; Guo, J.J.; Zhang, K.N.; Wen, Z.C.; Liu, J.Q.; Qin, C.C.; Hao, X.T. 3D charge transport pathway in organic solar cells via incorporation of discotic liquid crystal columns. Sol. RRL 2020, 4, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, J.; Chen, J.; Zhu, W.; Baranoff, E. Recent progress in luminescent liquid crystal materials: Design, properties and application for linearly polarised emission. J. Mater. Chem. C 2015, 3, 7993–8005. [Google Scholar] [CrossRef]
- Sivadas, A.P.; Rao, D.S.S.; Kumar, N.S.S.; Prabhu, D.D.; Varghese, S.; Ramachandran, C.N.; Ongungal, R.M.; Krishna Prasad, S.; Das, S. Self-assembling and luminescent properties of chiral bisoxadiazole derivatives in solution and liquid-crystalline phases. J. Phys. Chem. B 2017, 121, 1922–1929. [Google Scholar] [CrossRef]
- De, J.; Gupta, S.P.; Sudheendran Swayamprabha, S.; Dubey, D.K.; Bala, I.; Sarkar, I.; Dey, G.; Jou, J.H.; Ghosh, S.; Pal, S.K. Blue luminescent organic light emitting diode devices of a new class of star-shaped columnar mesogens exhibiting π-π driven supergelation. J. Phys. Chem. C 2018, 122, 23659–23674. [Google Scholar] [CrossRef]
- Bala, I.; Ming, L.; Yadav, R.A.K.; De, J.; Dubey, D.K.; Kumar, S.; Singh, H.; Jou, J.H.; Kailasam, K.; Pal, S.K. Deep-blue OLED fabrication from heptazine columnar liquid crystal based AIE-active sky-blue emitter. ChemistrySelect 2018, 3, 7771–7777. [Google Scholar] [CrossRef]
- Bala, I.; Singh, N.; Yadav, R.A.K.; De, J.; Gupta, S.P.; Singh, D.P.; Dubey, D.K.; Jou, J.H.; Douali, R.; Pal, S.K. Room temperature perylene based columnar liquid crystals as solid-state fluorescent emitters in solution-processable organic light-emitting diodes. J. Mater. Chem. C 2020, 8, 12485–12494. [Google Scholar] [CrossRef]
- Vinayakumara, D.R.; Ulla, H.; Kumar, S.; Pandith, A.; Satyanarayan, M.N.; Rao, D.S.S.; Prasad, S.K.; Adhikari, A.V. Hydrogen bond-driven columnar self-assembly of electroluminescent D-A-D configured cyanopyridones. J. Mater. Chem. C 2018, 6, 7385–7399. [Google Scholar] [CrossRef]
- Vinayakumara, D.R.; Ulla, H.; Kumar, S.; Satyanarayan, M.N.; Adhikari, A.V. New fluorescent columnar mesogens derived from phenanthrene-cyanopyridone hybrids for OLED applications. Mater. Chem. Front. 2018, 2, 2297–2306. [Google Scholar] [CrossRef]
- Canimkurbey, B.; Canimkurbey, B.; Taşkan, M.C.; Demir, S.; Duygulu, E.; Atilla, D.; Yuksel, F. Synthesis and investigation of the electrical properties of novel liquid-crystal phthalocyanines bearing triple branched alkylthia chains. New J. Chem. 2020, 44, 7424–7435. [Google Scholar] [CrossRef]
- Hwang, J.D.; Chen, P.Y.; Ding, S.W.; Ong, C.W. Effect of noncovalent dispersion of poly (Ethylene oxide) in columnar polyether-based discotic liquid crystal on the ionic conductivity and dynamics of lithium ions. Crystals 2019, 9, 627. [Google Scholar] [CrossRef]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Termine, R.; Golemme, A. Charge Mobility in Discotic Liquid Crystals. Int. J. Mol. Sci. 2021, 22, 877. https://doi.org/10.3390/ijms22020877
Termine R, Golemme A. Charge Mobility in Discotic Liquid Crystals. International Journal of Molecular Sciences. 2021; 22(2):877. https://doi.org/10.3390/ijms22020877
Chicago/Turabian StyleTermine, Roberto, and Attilio Golemme. 2021. "Charge Mobility in Discotic Liquid Crystals" International Journal of Molecular Sciences 22, no. 2: 877. https://doi.org/10.3390/ijms22020877
APA StyleTermine, R., & Golemme, A. (2021). Charge Mobility in Discotic Liquid Crystals. International Journal of Molecular Sciences, 22(2), 877. https://doi.org/10.3390/ijms22020877





