Relationships between Molecular Structure of Carbohydrates and Their Dynamic Hydration Shells Revealed by Terahertz Time-Domain Spectroscopy
Abstract
:1. Introduction
2. Results
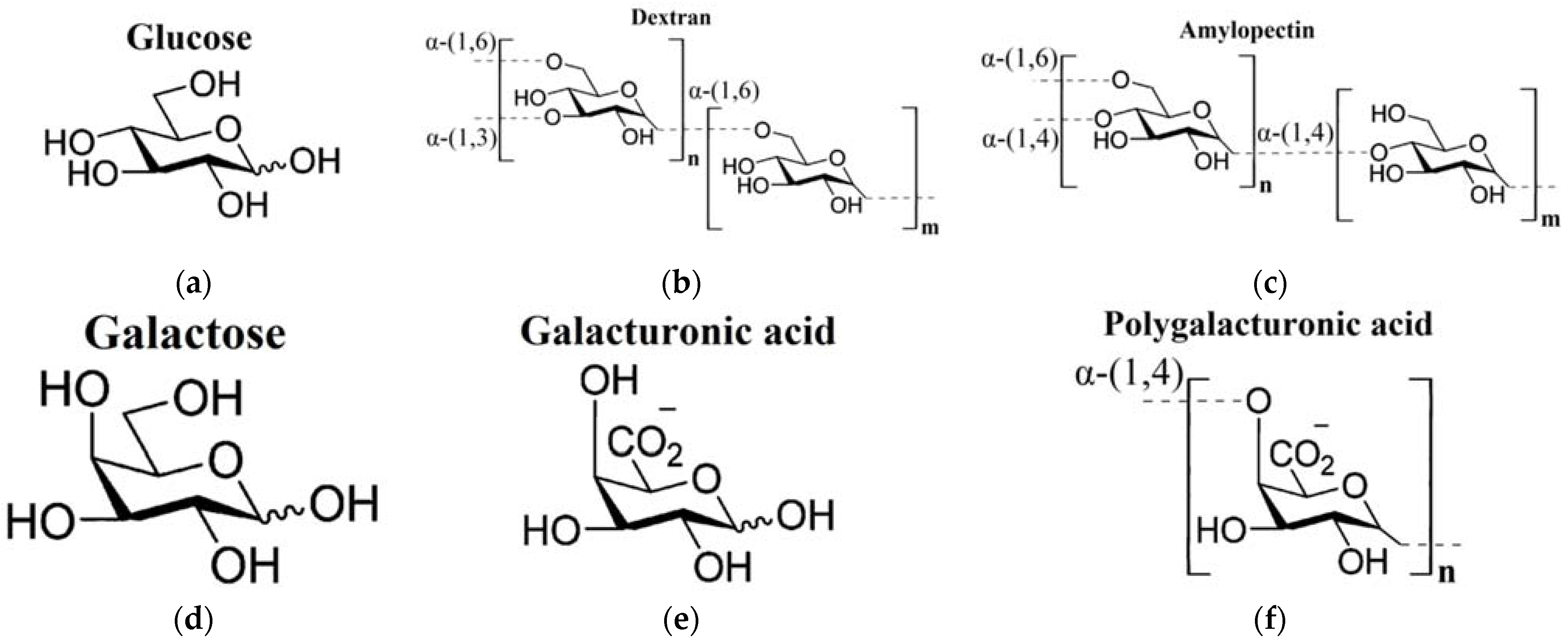
2.1. Characteristics of the Analyzed Carbohydrates in Dry Form
2.2. Solutions Conductivity
2.3. DPs of Water Phase of Carbohydrate Solutions
2.4. Parameters of the Model DPs of the Water Phase of Carbohydrate Solutions
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Solution Preparation
4.3. Preparation of Dry Samples for Spectral Analysis
4.4. THz-TDS
4.5. Calculation of DP of Water Phase of Carbohydrate Solution
4.6. Analysis of Water Phase DP in Carbohydrate Solutions
4.7. Measurement of Solution Conductivity
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- George, P.; Witonsky, R.J.; Trachtman, M.; Wu, C.; Dorwart, W.; Richman, L.; Richman, W.; Shurayh, F.; Lentz, B. “Squiggle-H2O”. An enquiry into the importance of solvation effects in phosphate ester and anhydride reactions. Biochim. Biophys. Acta Bioenerg. 1970, 223, 1–15. [Google Scholar] [CrossRef]
- Saenger, W.; Hunter, W.N.; Kennard, O. DNA conformation is determined by economics in the hydration of phosphate groups. Nature 1986, 324, 385–388. [Google Scholar] [CrossRef]
- Sokolov, A.P.; Roh, J.H.; Mamontov, E.; Sakai, V.G. Role of hydration water in dynamics of biological macromolecules. Chem. Phys. 2008, 345, 212–218. [Google Scholar] [CrossRef]
- Rupley, J.A.; Careri, G. Protein hydration and function. Adv. Protein Chem. 1991, 41, 37–172. [Google Scholar]
- Rademacher, T.W.; Parekh, R.B.; Dwek, R.A. Glycobiology. Ann. Rev. Biochem. 1988, 57, 785–838. [Google Scholar] [CrossRef]
- Birch, G.G. The chemical basis of sweetness perception in beverages. Food Chem. 1994, 51, 359–364. [Google Scholar] [CrossRef]
- Aroulmoji, V.; Mathlouthi, M.; Birch, G.G. Hydration properties of Na, K, Mg gluconates and gluconate/sucrose mixtures and their possible taste effect. Food Chem. 2000, 70, 471–482. [Google Scholar] [CrossRef]
- Magazu, S.; Migliardo, F.; Telling, M.T.F. Structural and dynamical properties of water in sugar mixtures. Food Chem. 2008, 106, 1460–1466. [Google Scholar] [CrossRef]
- Lerbret, A.; Bordat, P.; Affouard, F.; Descamps, M.; Migliardo, F. How homogeneous are the trehalose, maltose, and sucrose water solutions? An insight from molecular dynamics simulations. J. Phys. Chem. B 2005, 109, 11046–11057. [Google Scholar] [CrossRef] [Green Version]
- Kosmala, M.; Ko1odziejczyk, K.; Markowski, J.; Mieszczakowska, M.; Ginies, C.; Renard, C.M.G.C. Co-products of black-currant and apple juice production: Hydration properties and polysaccharide composition. LWT Food Sci. Technol. 2010, 43, 173–180. [Google Scholar] [CrossRef]
- Scatchard, G. The hydration of sucrose in water solution as calculated from vapor-pressure measurements. J. Am. Chem. Soc. 1921, 43, 2406–2418. [Google Scholar] [CrossRef] [Green Version]
- Cooke, S.A.; Jónsdóttir, S.Ó.; Westh, P. The vapour pressure of water as a function of solute concentration above aqueous solutions of fructose, sucrose, raffinose, erythritol, xylitol, and sorbitol. J. Chem. Thermodyn. 2002, 34, 1545–1555. [Google Scholar] [CrossRef]
- Gharsallaoui, A.; Roge, B.; Genotelle, J.; Mathlouthi, M. Relationships between hydration number, water activity and density of aqueous sugar solutions. Food Chem. 2008, 106, 1443–1453. [Google Scholar] [CrossRef]
- Branca, C.; Magazu, S.; Maisano, G.; Migliardo, F.; Migliardo, P.; Romeo, G. α,α -Trehalose/water solutions. 5. Hydration and viscosity in dilute and semidilute disaccharide solutions. J. Phys. Chem. B 2001, 105, 10140–10145. [Google Scholar] [CrossRef]
- Despond, S.; Espuche, E.; Cartier, N.; Domard, A. Hydration mechanism of polysaccharides: A comparative study. J. Polym. Sci. Part B 2005, 43, 48–58. [Google Scholar] [CrossRef]
- Singh, A.K.; Morales, J.A.; Estrada, N.A.; Rodriguebz, S.J.V.; Castro-Camus, E. Terahertz hydration dynamics in aqueous polysaccharides. In Proceedings of the 2018 43rd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Nagoya, Japan, 9–14 September 2018; pp. 1–2. [Google Scholar]
- Mlčoch, T.; Kučerík, J. Hydration and drying of various polysaccharides studied using DSC. J. Therm. Anal. Calorim. 2013, 113, 1177–1185. [Google Scholar] [CrossRef]
- Furuki, T. Effect of molecular structure on thermodynamic properties of carbohydrates. A calorimetric study of aqueous di- and oligosaccharides at subzero temperatures. Carbohydr. Res. 2002, 337, 441–450. [Google Scholar] [CrossRef]
- Mathlouthi, M. X-ray diffraction study of the molecular association in aqueous solutions of d-fructose, d-glucose, and sucrose. Carbohydr. Res. 1981, 91, 113–123. [Google Scholar] [CrossRef]
- Gekko, K. Hydration—structure—function relationships of polysaccharides and proteins. Food Hydrocoll. 1989, 3, 289–299. [Google Scholar] [CrossRef]
- Aeberhardt, K.; Laumer, J.-Y.S.; Bouquerand, P.-E.; Normand, V. Ultrasonic wave spectroscopy study of sugar oligomers and polysaccharides in aqueous solutions: The hydration length concept. Int. J. Biol. Macromol. 2005, 36, 275–282. [Google Scholar] [CrossRef]
- Magazu, S.; Migliardo, P.; Musolino, A.M.; Sciortino, M.T. α,α-Trehalose-water solutions. 1. Hydration phenomena and anomalies in the acoustic properties. J. Phys. Chem. B 1997, 101, 2348–2351. [Google Scholar] [CrossRef]
- Sato, Y.; Miyawaki, O. Relationship between proton NMR relaxation time and viscosity of saccharide solutions. Food Sci. Technol. Res. 2000, 6, 136–139. [Google Scholar] [CrossRef] [Green Version]
- Miyuki, I.; Hisashi, U. Natural-abundance oxygen-17 magnetic relaxation in aqueous solutions of apolar amino acids and glycine peptides. Bull. Chem. Soc. Jpn. 1989, 62, 1–4. [Google Scholar]
- Bari, M.D.; Deriu, A.; Albanese, G.; Cavatorta, F. Dynamics of hydrated starch saccharides. Chem. Phys. 2003, 292, 333–339. [Google Scholar] [CrossRef]
- Bari, M.D.; Cavatorta, F.; Deriu, A.; Albanese, G. Mean square fluctuations of hydrogen atoms and water-biopolymer interactions in hydrated saccharides. Biophys. J. 2001, 81, 1190–1194. [Google Scholar] [CrossRef] [Green Version]
- Branca, C.; Magazu, S.; Migliardo, F.; Migliardo, P. Destructuring effect of trehalose on the tetrahedral network of water: A Raman and neutron diffraction comparison. Phys. A 2002, 304, 314–318. [Google Scholar] [CrossRef]
- Pagnotta, S.E.; McLain, S.E.; Soper, A.K.; Bruni, F.; Ricci, M.A. Water and trehalose: How much do they interact with each other? J. Phys. Chem. B 2010, 114, 4904–4908. [Google Scholar] [CrossRef]
- Perticaroli, S.; Nakanishi, M.; Pashkovski, E.; Sokolov, A.P. Dynamics of hydration water in sugars and peptides solutions. J. Phys. Chem. B. 2013, 117, 7729–7736. [Google Scholar] [CrossRef]
- Lupi, L.; Comez, L.; Paolantoni, M.; Perticaroli, S.; Sassi, P.; Morresi, A.; Ladanyi, B.M.; Fioretto, D. Hydration and Aggregation in Mono- and Disaccharide Aqueous Solutions by Gigahertz-to-Terahertz Light Scattering and Molecular Dynamics Simulations. J. Phys. Chem. B 2012, 116, 14760–14767. [Google Scholar] [CrossRef]
- Magazu, S.; Maisano, G.; Middendorf, H.D.; Migliardo, P.; Musolino, A.M.; Villari, V. α,α -Trehalose-Water Solutions. II. Influence of Hydrogen Bond Connectivity on Transport Properties. J. Phys. Chem. B 1998, 102, 2060–2063. [Google Scholar] [CrossRef]
- Sidebottom, D.L.; Tran, T.D. Universal patterns of equilibrium cluster growth in aqueous sugars observed by dynamic light scattering. Phys. Rev. E 2010, 82, 051904. [Google Scholar] [CrossRef] [Green Version]
- Grossutti, M.; Dutcher, J.R. Correlation between chain architecture and hydration water structure in polysaccharides. Biomacromolecules 2016, 17, 1198–1204. [Google Scholar] [CrossRef]
- Grossutti, M.; Dutcher, J.R. Hydration Water Structure, Hydration Forces, and Mechanical Properties of Polysaccharide Films. Biomacromolecules 2020, 21, 4871–4877. [Google Scholar] [CrossRef]
- Haxaire, K.; Marechal, Y.; Milas, M.; Rinaudo, M. Hydration of hyaluronan polysaccharide observed by ir spectrometry. II. Definition and quantitative analysis of elementary hydration spectra and water uptake. Biopolymers 2003, 72, 149–161. [Google Scholar] [CrossRef]
- Branca, C.; Magazu, S.; Maisano, G.; Migliardo, P. α,α-trehalose-water solutions. 3. Vibrational Dynamics studies by inelastic light scattering. J. Phys. Chem. B 1999, 103, 1347–1353. [Google Scholar] [CrossRef]
- Hunger, J.; Bernecker, A.; Bakker, H.J.; Bonn, M.; Richter, R.P. Hydration dynamics of hyaluronan and dextran. Biophys. J. 2012, 103, L10–L12. [Google Scholar] [CrossRef] [Green Version]
- Suggett, A.; Clark, A.H. Molecular motion and interactions in aqueous carbohydrate solutions. I. Dielectric-relaxation studies. J. Solut. Chem. 1976, 5, 1–15. [Google Scholar] [CrossRef]
- Shiraga, K.; Adachi, A.; Nakamura, M.; Tajima, T.; Ajito, K.; Ogawa, Y. Characterization of the hydrogen-bond network of water around sucrose and trehalose: Microwave and terahertz spectroscopic study. J. Chem. Phys. 2017, 146, 105102. [Google Scholar] [CrossRef]
- Behrends, R.; Kaatze, U. Molecular dynamics and conformational kinetics of mono- and disaccharides in aqueous solution. Chem. Phys. Chem. 2005, 6, 1133–1145. [Google Scholar] [CrossRef]
- Shiraga, K.; Ogawa, Y.; Kondo, N.; Irisawa, A.; Imamura, M. Evaluation of the hydration state of saccharides using terahertz time-domain attenuated total reflection spectroscopy. Food Chem. 2013, 140, 315–320. [Google Scholar] [CrossRef]
- Heyden, M.; Ebbinghaus, S.; Havenith, M. Terahertz spectroscopy as a tool to study hydration dynamics. In Encyclopedia of Analytical Chemistry; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Shiraga, K.; Suzuki, T.; Kondo, N.; De Baerdemaeker, J.; Ogawa, Y. Quantitative characterization of hydration state and destructuring effect of monosaccharides and disaccharides on water hydrogen bond network. Carbohydr. Res. 2015, 406, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Heugen, U.; Schwaab, G.; Bründermann, E.; Heyden, M.; Yu, X.; Leitner, D.M.; Havenith, M. Solute-induced retardation of water dynamics probed directly by terahertz spectroscopy. Proc. Natl. Acad. Sci. USA 2006, 103, 12301–12306. [Google Scholar] [CrossRef] [Green Version]
- Heyden, M.; Bründermann, E.; Heugen, U.; Niehues, G.; Leitner, D.M.; Havenith, M. Long-range influence of carbohydrates on the solvation dynamics of water--answers from terahertz absorption measurements and molecular modeling simulations. J. Am. Chem. Soc. 2008, 130, 5773–5779. [Google Scholar] [CrossRef]
- Cherkasova, O.P.; Nazarov, M.M.; Konnikova, M.; Shkurinov, A.P. THz spectroscopy of bound water in glucose: Direct measurements from crystalline to dissolved state. J. Infrared Millim. Terahertz Waves 2020, 41, 1057–1068. [Google Scholar] [CrossRef]
- Nagai, M.; Yada, H.; Arikawa, T.; Tanaka, K. Terahertz time-domain attenuated total reflection spectroscopy in water and biological solution. Int. J. Infrared Millim. Waves 2006, 27, 505–515. [Google Scholar] [CrossRef]
- Engelsen, S.B.; Prrez, S. The hydration of sucrose. Carbohydr. Res. 1996, 292, 21–38. [Google Scholar] [CrossRef]
- Suzuki, T. The hydration of glucose: The local configurations in sugar-water hydrogen bonds. Phys. Chem. Chem. Phys. 2008, 10, 96–105. [Google Scholar] [CrossRef]
- Chen, C.; Li, W.Z.; Song, Y.C.; Weng, L.D.; Zhang, N. Formation of water and glucose clusters by hydrogen bonds in glucose aqueous solutions. Comput. Theor. Chem. 2012, 984, 85–92. [Google Scholar] [CrossRef]
- Lee, S.L.; Debenedetti, P.G.; Errington, J.R. A computational study of hydration, solution structure, and dynamics in dilute carbohydrate solutions. J. Chem. Phys. 2005, 122, 204511. [Google Scholar] [CrossRef]
- Sonoda, M.T.; Skaf, M.S. Carbohydrate clustering in aqueous solutions and the dynamics of confined water. J. Phys. Chem. B 2007, 111, 11948–11956. [Google Scholar] [CrossRef]
- Sato, Y.; Miyawaki, O. Analysis of hydration parameter for sugars determined from viscosity and its relationship with solution parameters. Food Chem. 2016, 190, 594–598. [Google Scholar] [CrossRef]
- Kawai, H.; Sakurai, M.; Inoue, Y.; Chûjô, R.; Kobayashi, S. Hydration of oligosaccharides: Anomalous hydration ability of trehalose. Cryobiology 1992, 29, 599–606. [Google Scholar] [CrossRef]
- Arikawa, T.; Nagai, M.; Tanaka, K. Characterizing hydration state in solution using terahertz time-domain attenuated total reflection spectroscopy. Chem. Phys. Lett. 2008, 457, 12–17. [Google Scholar] [CrossRef]
- Ebbinghaus, S.; Kim, S.J.; Heyden, M.; Xu, Y.; Heugen, U.; Gruebele, M.; Leitner, D.M.; Havenith, M. An Extended dynamical hydration shell around proteins. Proc. Nat. Acad. Sci. USA 2007, 104, 20749–20752. [Google Scholar] [CrossRef] [Green Version]
- Penkov, N.V.; Yashin, V.; Belosludtsev, K.N. Hydration shells of DPPC Liposomes from the point of view of terahertz time-domain spectroscopy. Appl. Spectrosc. 2021, 75, 189–198. [Google Scholar] [CrossRef]
- Penkov, N.V.; Penkova, N. Key differences of the hydrate shell structures of ATP and Mg·ATP Revealed by terahertz time-domain spectroscopy and dynamic light scattering. J. Phys. Chem. B 2021, 125, 4375–4382. [Google Scholar] [CrossRef]
- Aspnes, D.E. Local-field effects and effective-medium theory: A microscopic perspective. Am. J. Phys. 1982, 50, 704. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium Theory: Principle and Applications; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Sihvola, A. Mixing rules with complex dielectric coefficients. Subsurf. Sens. Technol. Appl. 2000, 1, 393–415. [Google Scholar] [CrossRef]
- Nazarov, M.M.; Cherkasova, O.P.; Shkurinov, A.P. Study of the dielectric function of aqueous solutions of glucose and albumin by THz time-domain spectroscopy. Quantum Electron. 2016, 46, 488–495. [Google Scholar] [CrossRef]
- Looyenga, H. Dielectric constants of heterogeneous mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Penkova, N.A.; Sharapov, M.G.; Penkov, N.V. Hydration Shells of DNA from the point of view of terahertz time-domain spectroscopy. Int. J. Mol. Sci. 2021, 22, 11089. [Google Scholar] [CrossRef]
- Penkov, N.V.; Penkova, N.A. Effective medium model applied to biopolymer solutions. Appl. Spectrosc. 2021, in press. [Google Scholar] [CrossRef]
- McNaught, A.D. Nomenclature of carbohydrates. Pure Appl. Chem. 1996, 68, 1919–2008. [Google Scholar] [CrossRef]
- Walther, M.; Fischer, B.M.; Jepsen, P.U. Noncovalent intermolecular forces in polycrystalline and amorphous saccharides in the far infrared. Chem. Phys. 2003, 288, 261–268. [Google Scholar] [CrossRef]
- Du, C.; Zhang, X.; Zhang, Z. Quantitative analysis of ternary isomer mixtures of saccharide by terahertz time domain spectroscopy combined with chemometrics. Vib. Spectrosc. 2019, 100, 64–70. [Google Scholar] [CrossRef]
- Antal, M.J., Jr.; Mok, W.S.; Richards, G.N. Mechanism of formation of 5-(hydroxymethyl)-2-furaldehyde from D-fructose and sucrose. Carbohydr. Res. 1990, 199, 91–109. [Google Scholar] [CrossRef]
- Nandi, N.; Bhattacharyya, K.; Bagchi, B. Dielectric relaxation and solvation dynamics of water in complex chemical and biological systems. Chem. Rev. 2000, 100, 2013–2046. [Google Scholar] [CrossRef] [PubMed]
- Levy, E.; Puzenko, A.; Kaatze, U.; Ishai, P.B.; Feldman, Y. Dielectric spectra broadening as the signature of dipole-matrix interaction. I. Water in nonionic solutions. J. Chem. Phys. 2012, 136, 114502. [Google Scholar] [CrossRef]
- Scheiner, S. Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Djikaev, Y.S.; Ruckenstein, E. Dependence of the number of hydrogen bonds per water molecule on its distance to a hydrophobic surface and a thereupon-based model for hydrophobic attraction. J. Chem. Phys. 2010, 133, 194105. [Google Scholar] [CrossRef]
- Yada, H.; Nagai, M.; Tanaka, K. Origin of the fast relaxation component of water and heavy water revealed by terahertz time domain attenuated total reflection spectroscopy. Chem. Phys. Lett. 2008, 464, 166–170. [Google Scholar] [CrossRef]
- Penkov, N.V.; Shvirst, N.E.; Yashin, V.A.; Fesenko, E.E. On singularities of molecular relaxation in water solutions. Biophysics 2013, 58, 731–738. [Google Scholar] [CrossRef]
- Penkov, N.; Yashin, V.; Fesenko, E., Jr.; Manokhin, A.; Fesenko, E. A study of the effect of a protein on the structure of water in solution using terahertz time-domain spectroscopy. Appl. Spectrosc. 2018, 72, 257–267. [Google Scholar] [CrossRef]
- Suzuki, M. What is “hypermobile” water?: Detected in alkali halide, adenosine phosphate, and F-actin solutions by highresolution microwave dielectric spectroscopy. Pure Appl. Chem. 2014, 86, 181–189. [Google Scholar] [CrossRef]
- Penkov, N.V.; Yashin, V.A.; Fesenko, E.E., Jr.; Fesenko, E.E. Calculation of the amount of free water molecules in aqueous solutions by means of spectral parameters from the terahertz frequency domain taking into account processes of screening. Biophysics 2014, 59, 347–350. [Google Scholar] [CrossRef]
- Galema, S.A.; Hoeiland, H. Stereochemical aspects of hydration of carbohydrates in aqueous solutions. 3. Density and ultrasound measurements. J. Phys. Chem. 1991, 95, 5321–5326. [Google Scholar] [CrossRef]
- Kerins, L.; Byrne, S.; Gabba, A.; Murphy, P.V. Anomer preferences for glucuronic and galacturonic acid and derivatives and influence of electron-withdrawing substituents. J. Org. Chem. 2018, 83, 7714–7729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galema, S.A.; Blandamer, M.J.; Engberts, J.B.F.N. Stereochemical aspects of the hydration of carbohydrates. Kinetic medium effects of monosaccharides on a water-catalyzed hydrolysis reaction. J. Am. Chem. Soc. 1990, 112, 9665–9666. [Google Scholar] [CrossRef]
- Hoiland, H.; Holvik, H. Partial molal volumes and compressibilities of carbohydrates in water. J. Solut. Chem. 1978, 7, 587–596. [Google Scholar] [CrossRef]
- Galema, S.A.; Blandamer, M.J.; Engberts, J.B.F.N. Stereochemical aspects of hydration of carbohydrates in aqueous solutions. 2. Kinetic medium effects. J. Org. Chem. 1992, 57, 1995–2001. [Google Scholar] [CrossRef]
- Keitaro, K. The volumes of hydrated glucose, sucrose and raffinose molecules, and the osmotic pressures of these aqueous saccharide solutions as measured by the freezing-point-depression method. Bull. Chem. Soc. Jpn. 1988, 61, 633–642. [Google Scholar]
- Vettori, M.H.P.B.; Franchetti, S.M.M.; Contiero, J. Structural characterization of a new dextran with a low degree of branching produced by Leuconostoc mesenteroides FT045B dextransucrase. Carbohydr. Polym. 2012, 88, 1440–1444. [Google Scholar] [CrossRef] [Green Version]
- Sandford, P.A.; Baird, J. Industrial utilization of polysaccharides. In The Polysaccharides; Aspinall, G.O., Ed.; Academic Press: Cambridge, MA, USA, 1983; Volume 2, p. 474. [Google Scholar]
- O’Sullivan, A.C.; Perez, S. The relationship between internal chain length of amylopectin and crystallinity in starch. Biopolymers 1999, 50, 381–390. [Google Scholar] [CrossRef]
- Upadhya, P.C.; Shen, Y.C.; Davies, A.G.; Linfield, E.H. Far-infrared vibrational modes of polycrystalline saccharides. Vib. Spectrosc. 2004, 35, 139–143. [Google Scholar] [CrossRef]
- Wang, H.; Tsuchikawa, S.; Inagaki, T. Terahertz time-domain spectroscopy as a novel tool for crystallographic analysis in cellulose: The potentiality of being a new standard for evaluating crystallinity. Cellulose 2021, 28, 5293–5304. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, H.W.; Tominaga, K.; Hayashi, M.; Hasunuma, T.; Kondo, A. Application of THz vibrational spectroscopy to molecular characterization and the theoretical fundamentals: An illustration using saccharide molecules. Chem. Asian J. 2017, 12, 324–331. [Google Scholar] [CrossRef]
- Zhong, J.; Mori, T.; Fujii, Y.; Kashiwagi, T.; Terao, W.; Yamashiro, M.; Minami, H.; Tsujimoto, M.; Tanaka, T.; Kawashima, H.; et al. Molecular vibration and Boson peak analysis of glucose polymers and ester via terahertz spectroscopy. Carbohydr. Polym. 2020, 232, 115789. [Google Scholar] [CrossRef]
- Kaminski, K.; Kaminska, E.; Ngai, K.L.; Paluch, M.; Wlodarczyk, P.; Kasprzycka, A.; Szeja, W. Identifying the origins of two secondary relaxations in polysaccharides. J. Phys. Chem. B 2009, 113, 10088–10096. [Google Scholar] [CrossRef]
- Lee, Y.-S. Principles of Terahertz Science and Technology; Springer: New York, NY, USA, 2009. [Google Scholar]
- Kindt, J.T.; Schmuttenmaer, C.A. Far-infrared dielectric properties of polar liquids probed by femtosecond terahertz pulse spectroscopy. Phys. Chem. 1996, 100, 10373–10379. [Google Scholar] [CrossRef]
- Sushko, M.Y.; Kris’kiv, S.K. Compact group method in the theory of permittivity of heterogeneous systems. Tech. Phys. 2009, 54, 423–427. [Google Scholar] [CrossRef]
- Durchschlag, H.; Zipper, P. Comparative investigations of biopolymer hydration by physicochemical and modeling techniques. Biophys. Chem. 2001, 93, 141–157. [Google Scholar] [CrossRef]
- Durchschlag, H. Specific volumes of biological macromolecules and some other molecules of biological interest. In Thermodynamic Data for Biochemistry and Biotechnology; Hinz, H.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Von Hippel, A.R. The dielectric relaxation spectra of water, ice, and aqueous solutions, and their interpretation. 2. Tentative interpretation of the relaxation spectrum of water in the time and frequency domain. IEEE Trans. Electr. Insul. 1988, 23, 817–823. [Google Scholar] [CrossRef]
- Laage, D.; Hynes, J.T. A molecular jump mechanism of water reorientation. Science 2006, 311, 832–835. [Google Scholar] [CrossRef]
- Zasetsky, A.Y. Dielectric relaxation in liquid water: Two fractions or two dynamics? Phys. Rev. Lett. 2011, 107, 117601. [Google Scholar] [CrossRef]
- Nielsen, O.F. Low-frequency spectroscopic studies of interactions in liquids. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 1993, 90, 3–44. [Google Scholar] [CrossRef]
- Nielsen, O.F. Low-frequency spectroscopic studies and intermolecular vibrational energy transfer in liquids. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 1996, 93, 57–99. [Google Scholar] [CrossRef]
- Ellison, W.J. Permittivity of pure water, at standard atmospheric pressure, over the frequency range 0–25 THz and the temperature range 0–100 °C. J. Phys. Chem. Ref. Data 2007, 36, 1–18. [Google Scholar] [CrossRef]
- Clough, S.A.; Beers, Y.; Klein, G.P.; Rothman, L.S. Dipole moment of water from Stark measurements of H2O, HDO, and D2O. J. Chem. Phys. 1973, 59, 2254–2259. [Google Scholar] [CrossRef]


| Carbohydrate | Δε1 | Δε2 | τ2, ps | ω0, cm−1 | γ, cm−1 | A/ω02 | n, % |
|---|---|---|---|---|---|---|---|
| Pure water | 68.86 ± 0.81 | 2.691 ± 0.042 | 0.316 ± 0.006 | 207.2 ± 4.3 | 196.5 ± 11.1 | 1.702 ± 0.019 | 3.78 ± 0.04 |
| Glucose | 62.45 ± 0.48 | 2.939 ± 0.039 | 0.326 ± 0.005 | 215.9 ± 3.9 | 202.6 ± 5.6 | 1.807 ± 0.038 | 3.91 ± 0.03 |
| Galactose | 62.23 ± 0.83 | 2.931 ± 0.046 | 0.327 ± 0.004 | 221.3 ± 4.9 | 217.3 ± 9.0 | 1.844 ± 0.029 | 3.86 ± 0.04 |
| Galacturonic acid | 63.20 ± 0.46 | 3.006 ± 0.024 | 0.334 ± 0.003 | 221.7 ± 4.7 | 223.1 ± 9.6 | 1.867 ± 0.022 | 3.91 ± 0.03 |
| Dextran | 63.81 ± 0.88 | 2.728 ± 0.052 | 0.321 ± 0.005 | 210.6 ± 4.2 | 200.0 ± 10.0 | 1.719 ± 0.018 | 3.80 ± 0.05 |
| Amylopectin | 65.97 ± 0.84 | 2.688 ± 0.045 | 0.319 ± 0.005 | 209.7 ± 4.5 | 197.4 ± 9.6 | 1.737 ± 0.016 | 3.74 ± 0.04 |
| Polygalacturonic acid | 63.75 ± 0.84 | 2.729 ± 0.051 | 0.312 ± 0.004 | 219.1 ± 7.0 | 208.2 ± 13.0 | 1.801 ± 0.025 | 3.72 ± 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penkov, N.V. Relationships between Molecular Structure of Carbohydrates and Their Dynamic Hydration Shells Revealed by Terahertz Time-Domain Spectroscopy. Int. J. Mol. Sci. 2021, 22, 11969. https://doi.org/10.3390/ijms222111969
Penkov NV. Relationships between Molecular Structure of Carbohydrates and Their Dynamic Hydration Shells Revealed by Terahertz Time-Domain Spectroscopy. International Journal of Molecular Sciences. 2021; 22(21):11969. https://doi.org/10.3390/ijms222111969
Chicago/Turabian StylePenkov, Nikita V. 2021. "Relationships between Molecular Structure of Carbohydrates and Their Dynamic Hydration Shells Revealed by Terahertz Time-Domain Spectroscopy" International Journal of Molecular Sciences 22, no. 21: 11969. https://doi.org/10.3390/ijms222111969
APA StylePenkov, N. V. (2021). Relationships between Molecular Structure of Carbohydrates and Their Dynamic Hydration Shells Revealed by Terahertz Time-Domain Spectroscopy. International Journal of Molecular Sciences, 22(21), 11969. https://doi.org/10.3390/ijms222111969






