Influence of Injection Application on the Sol–Gel Phase Transition Conditions of Polysaccharide-Based Hydrogels
Abstract
1. Introduction
2. Results
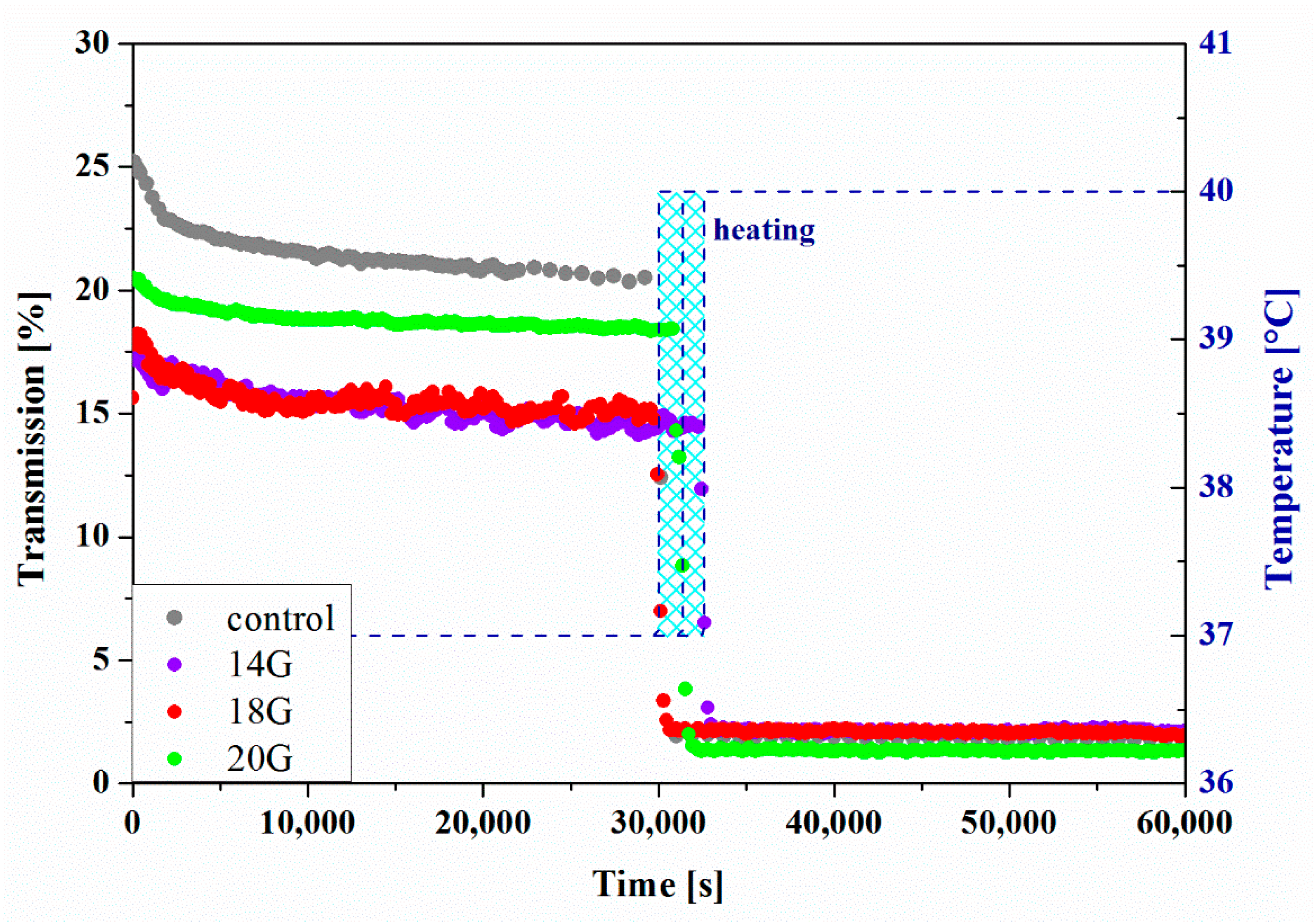
2.1. Preliminary Studies of Hydroxypropyl Cellulose Colloidal Suspension
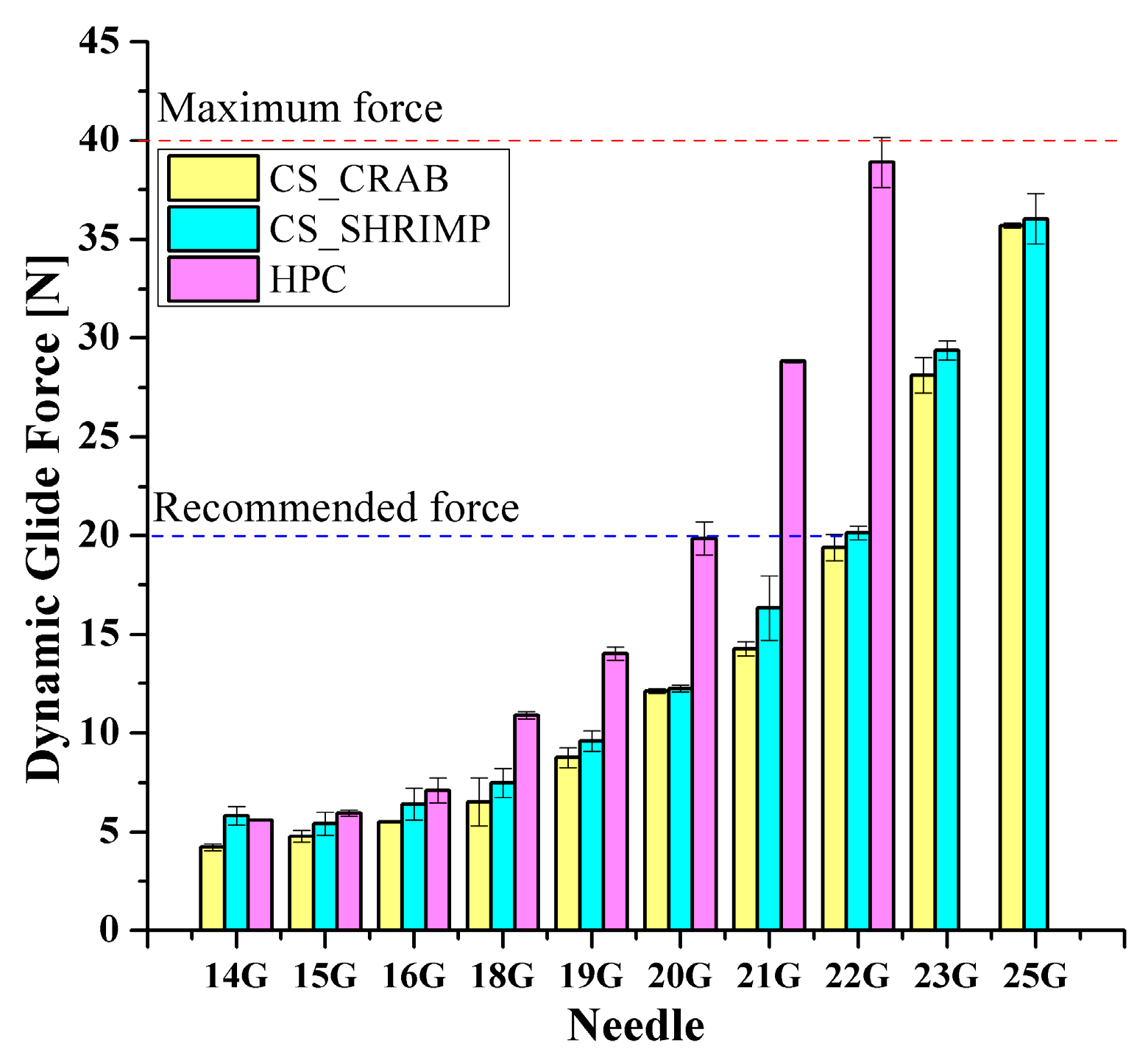
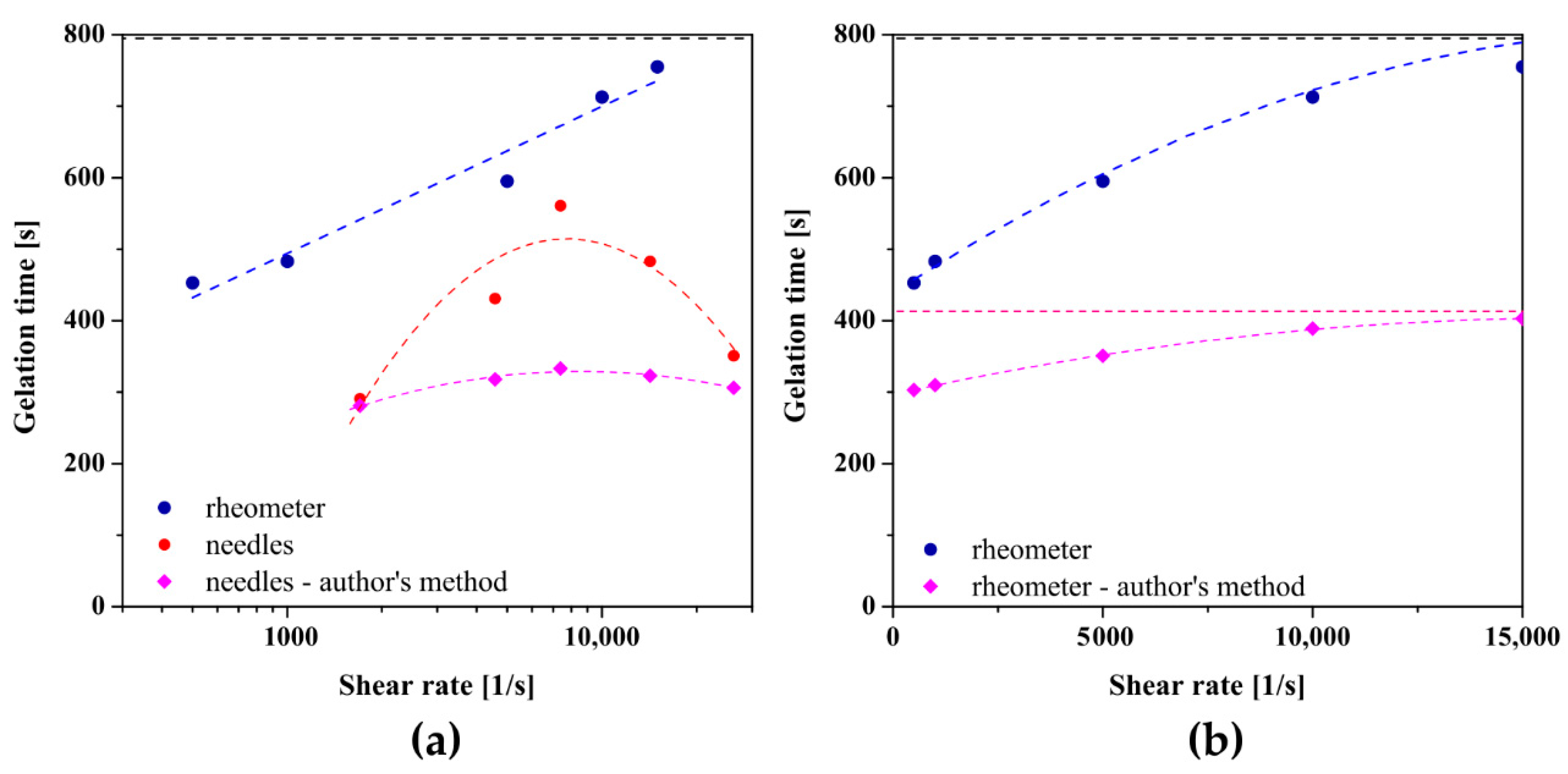
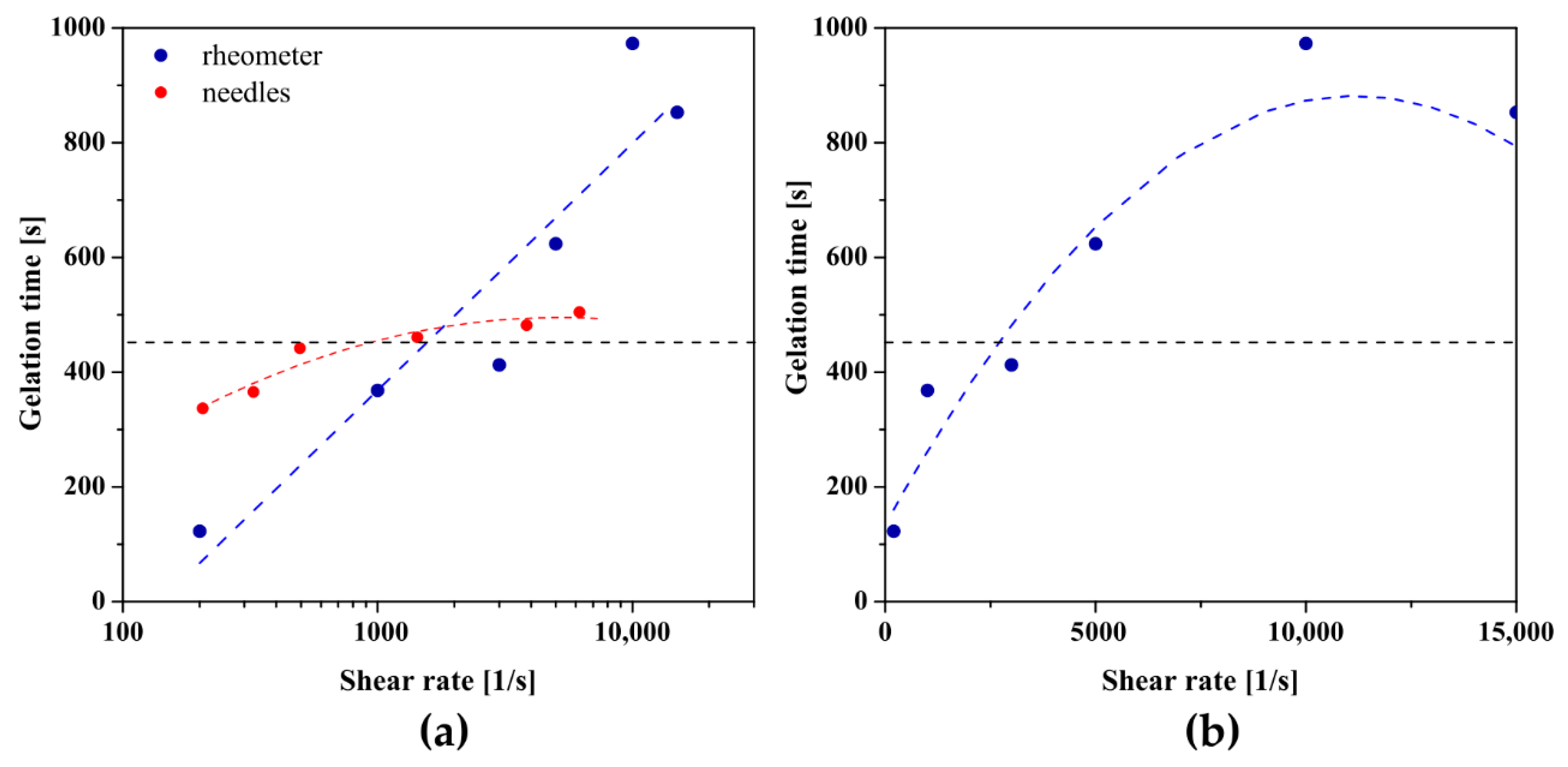
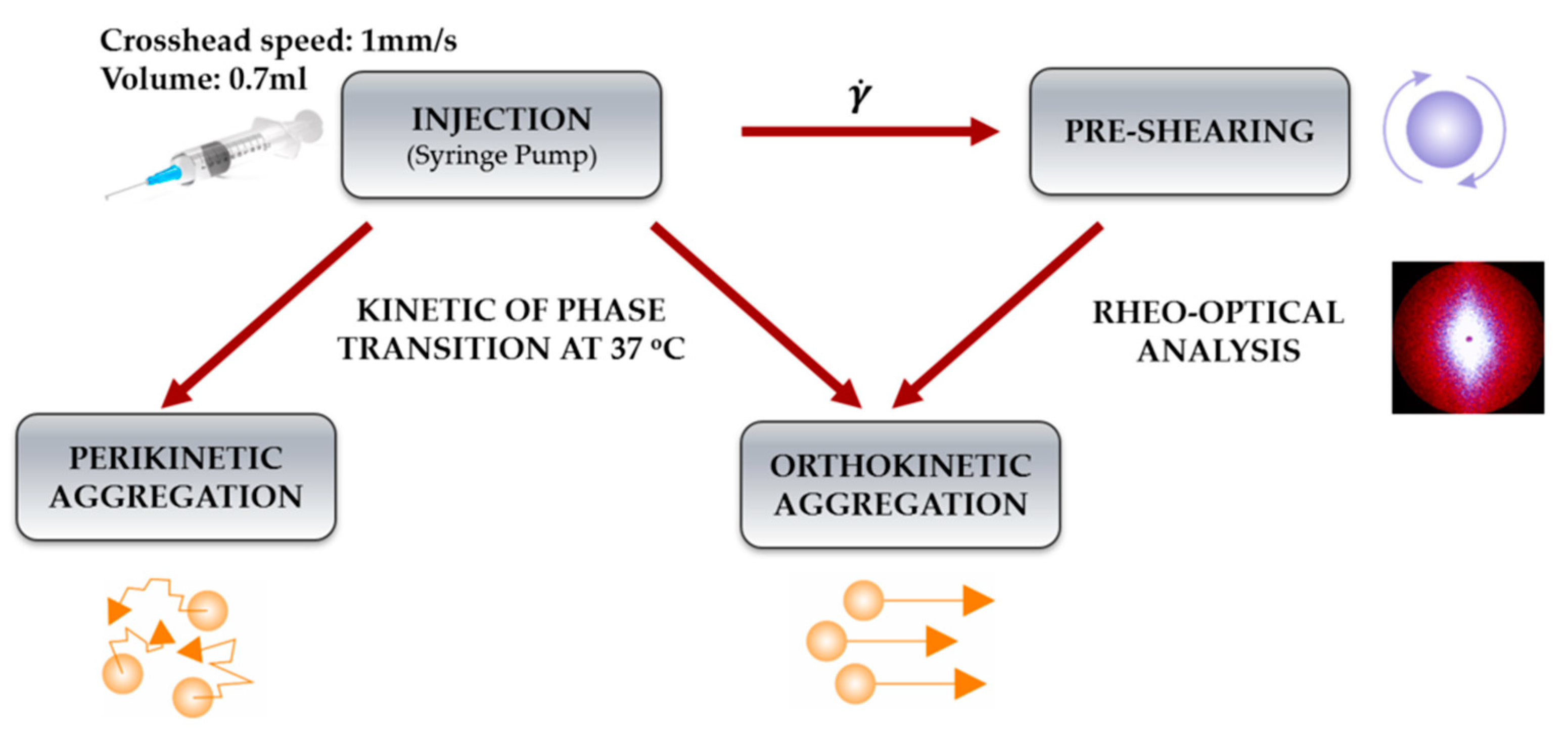
2.2. Instrumental Injectability Tests
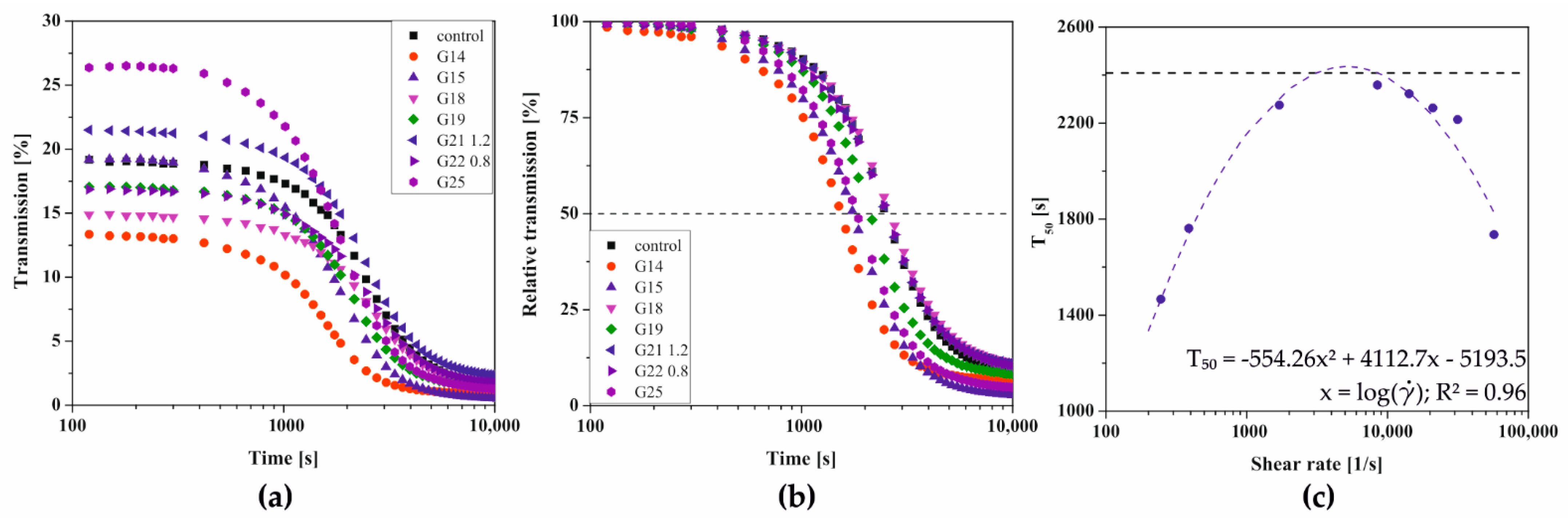
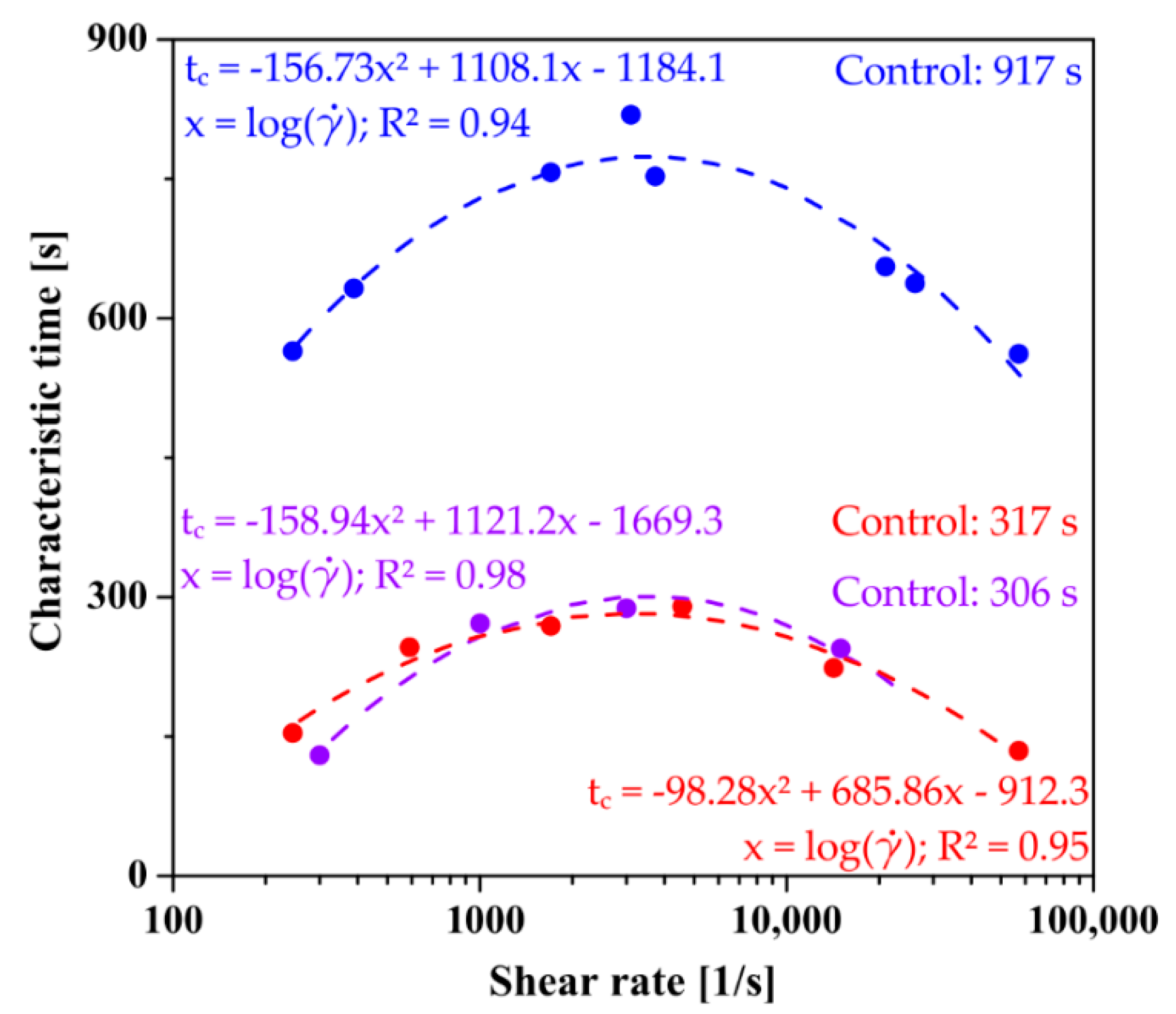
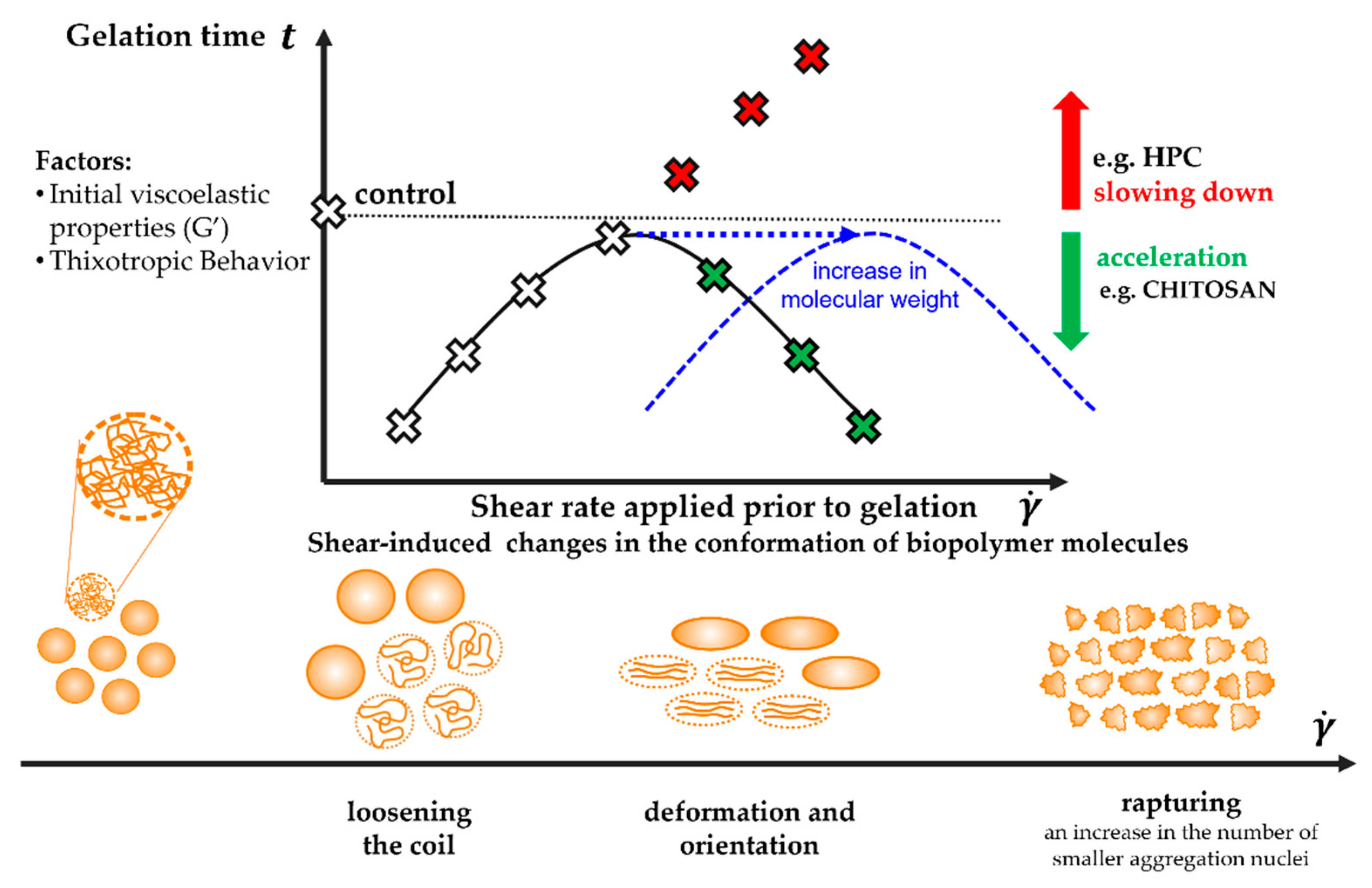
2.3. Kinetics of the Sol–Gel Phase Transition after Shear
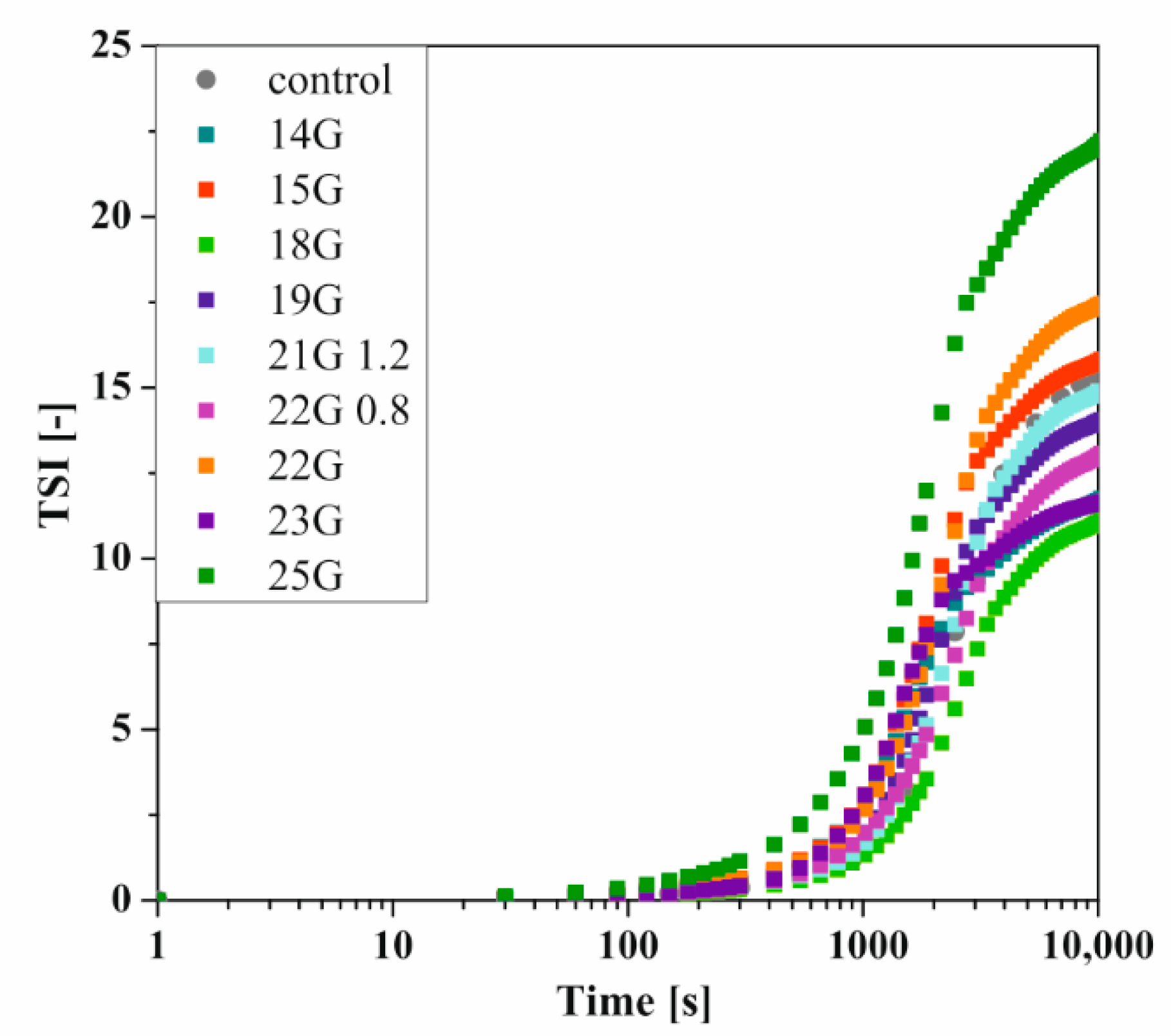
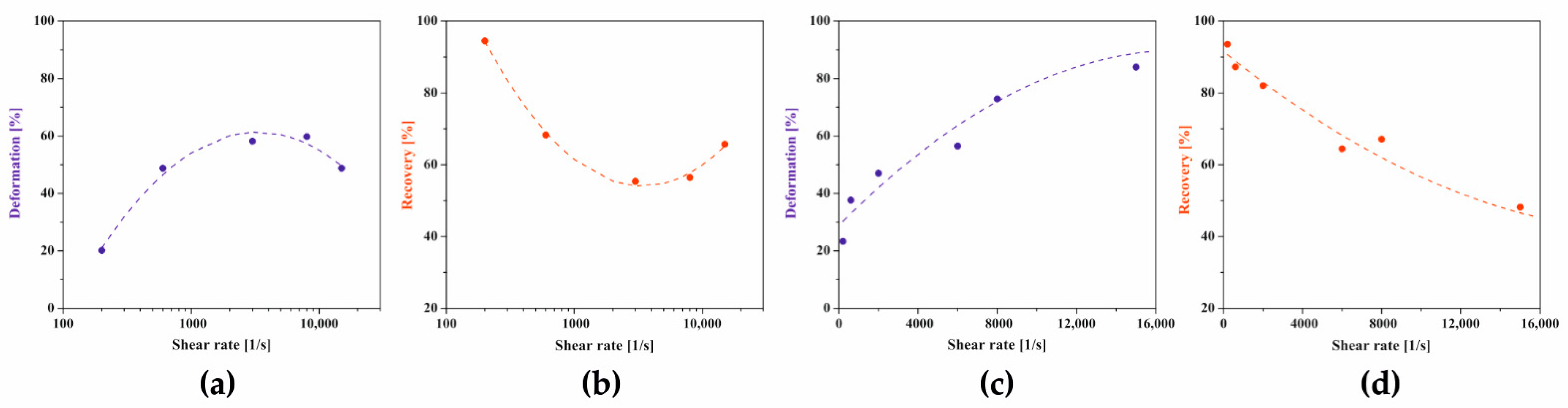
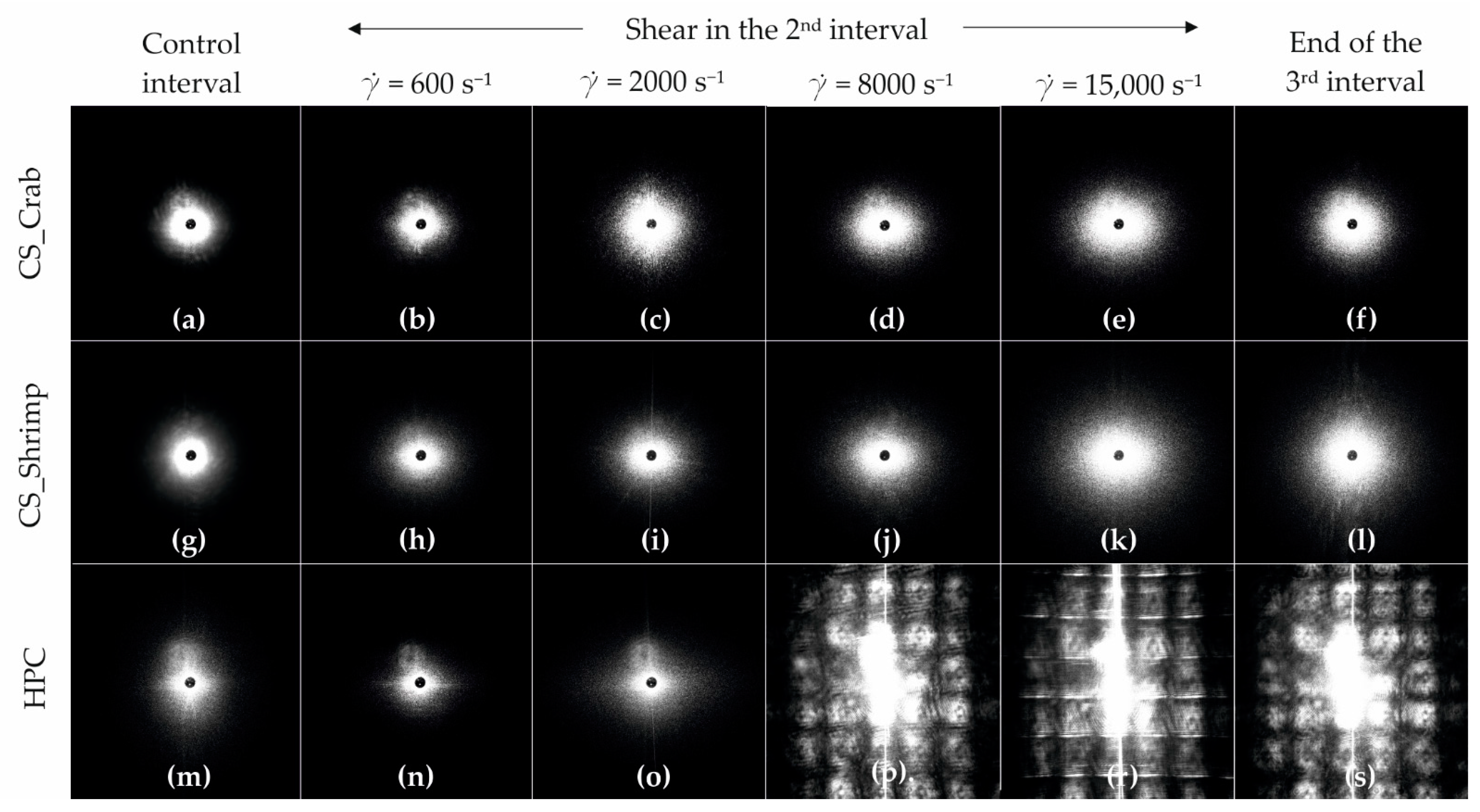
2.4. Comparison of Aggregation Conditions in the Regimes of Perikinetic and Orthokinetic after Short-Term Shear
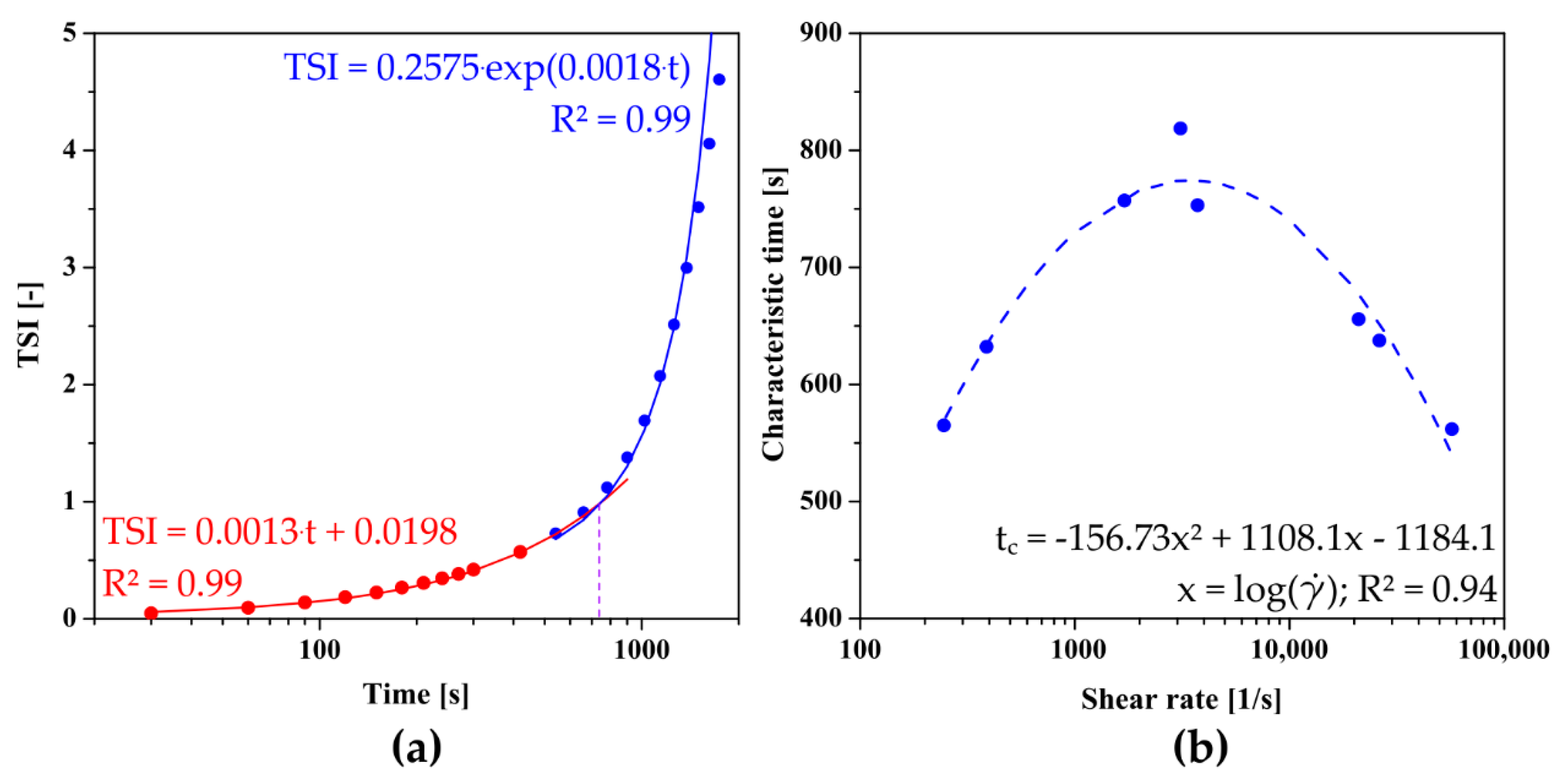
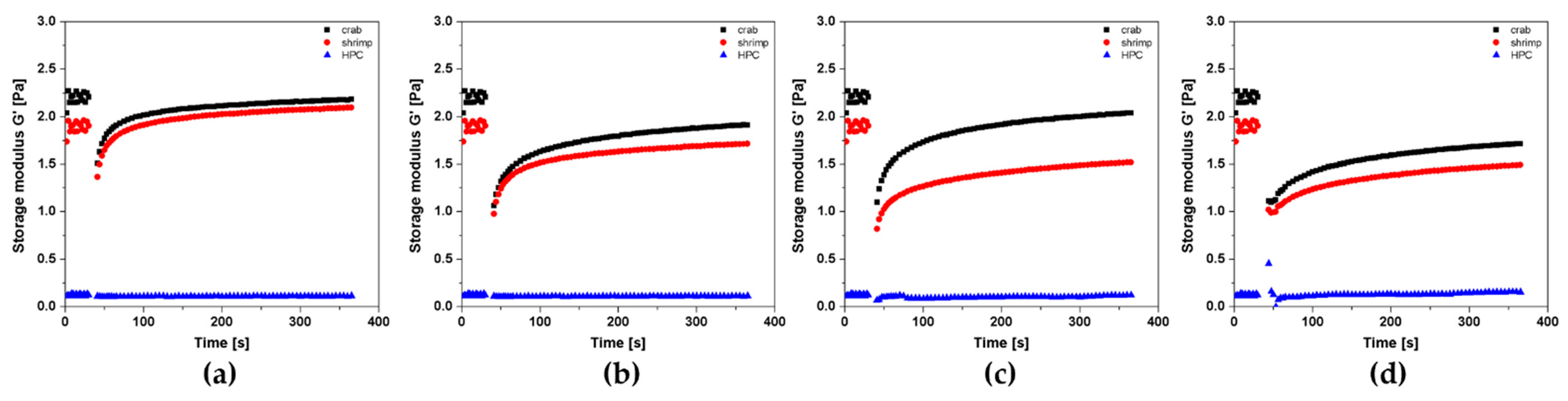
2.5. Aggregation Conditions of Shrimp Chitosan in the Peri- and Orthokinetic Regimes after Short-Term Shear
2.6. Aggregation Conditions of Hydroxypropyl Cellulose in the Peri- and Orthokinetic Regimes after Short-Term Shear
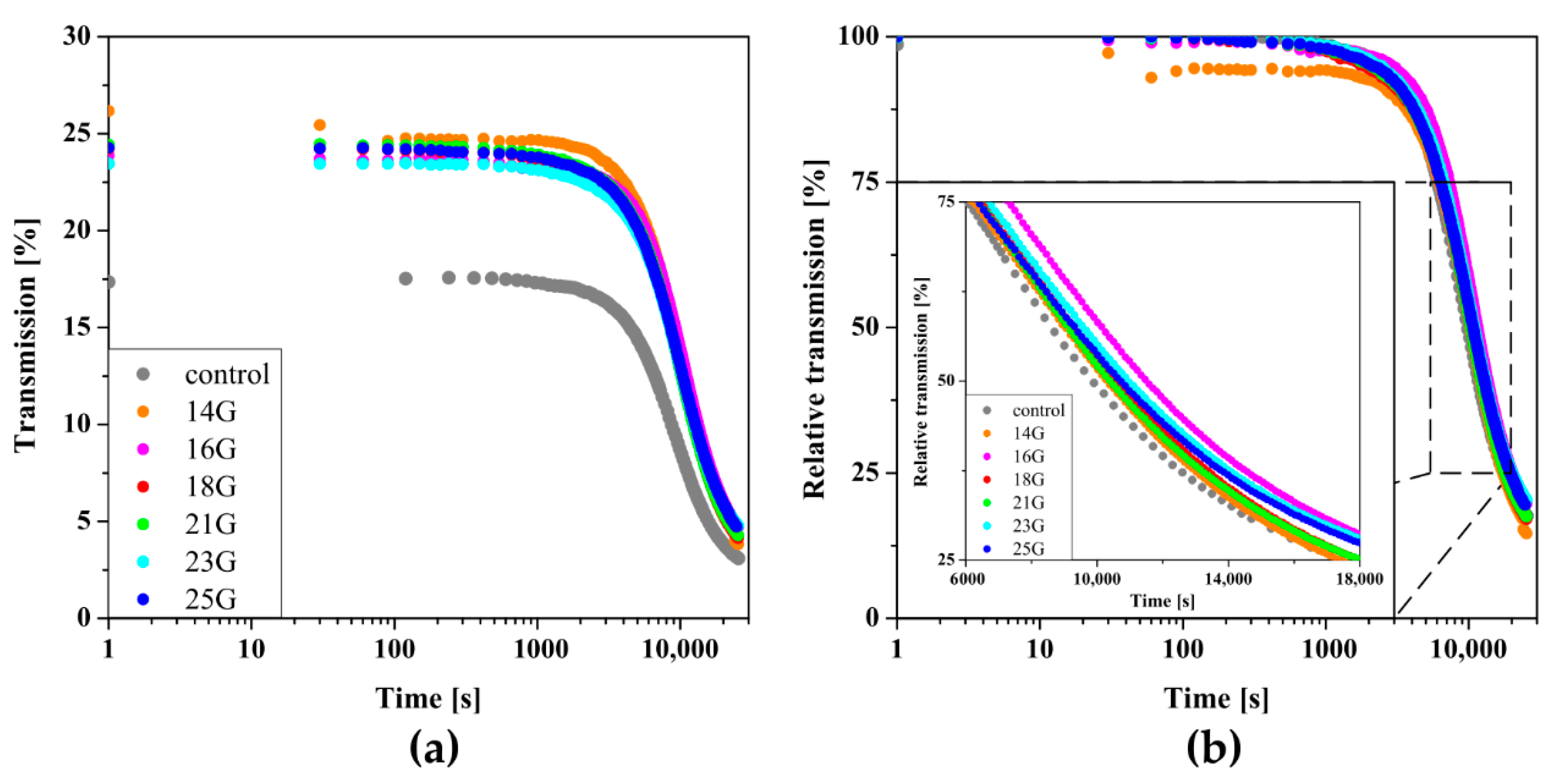
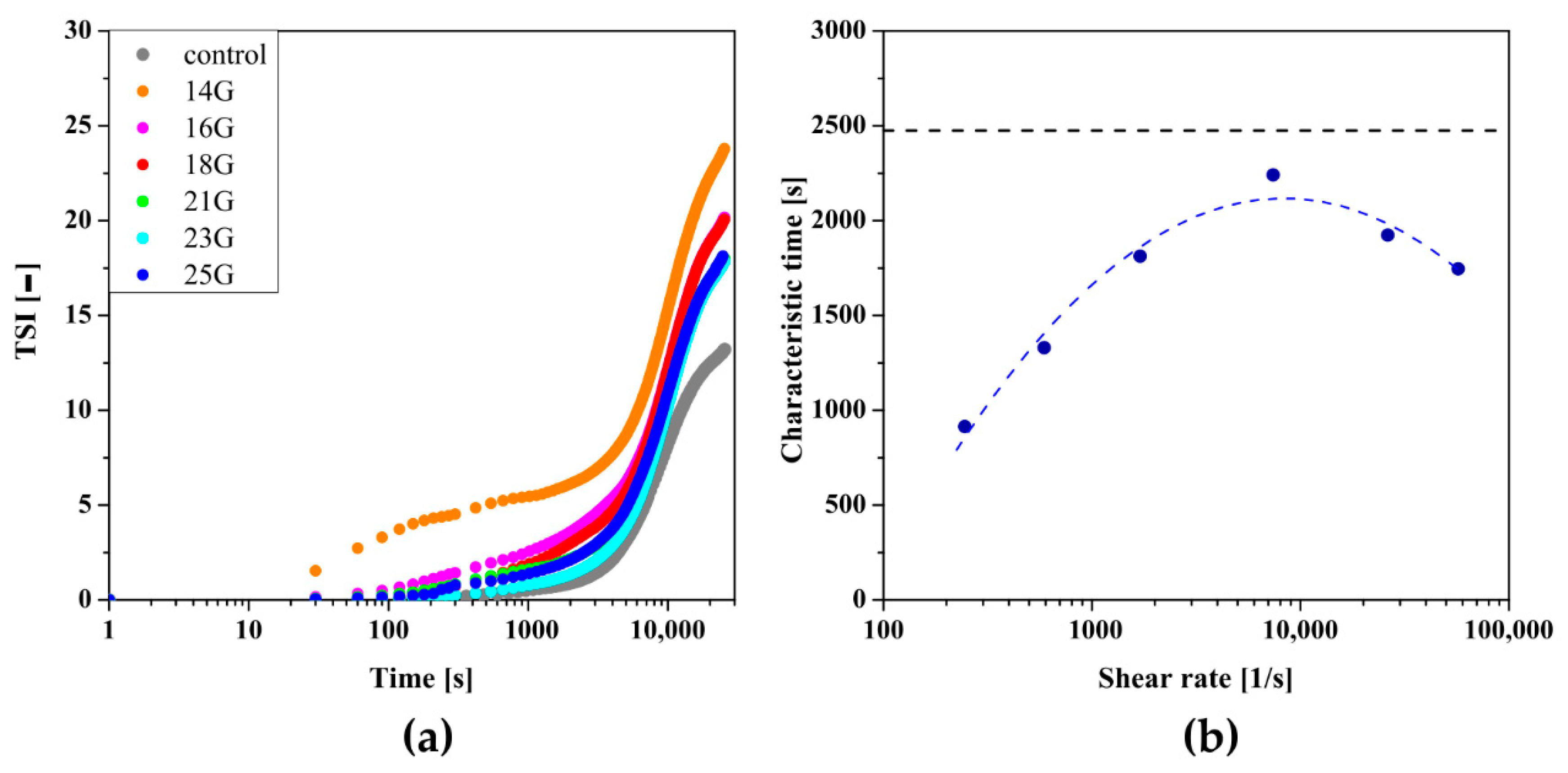
2.7. Reo-Optical Analysis of Thixotropic Properties
3. Discussion
4. Materials and Methods
4.1. Preparation of Thermosensitive Hydrogels
4.2. Rheological Analysis-Research Apparatus
4.3. Preliminary Rheological Characterization of Hydroxypropyl Cellulose Sol
4.4. Kinetics of the Phase Transition after Shearing
4.5. Rheo-Optical Analysis of Conformational Changes Caused by the Injection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Camponeschi, F.; Atrei, A.; Rocchigiani, G.; Mencuccini, L.; Uva, M.; Barbucci, R. New formulations of polysaccharide-based hydrogels for drug release and tissue engineering. Gels 2015, 1, 3–23. [Google Scholar] [CrossRef]
- Sivashanmugam, A.; Arun Kumar, R.; Vishnu Priya, M.; Nair, S.V.; Jayakumar, R. An overview of injectable polymeric hydrogels for tissue engineering. Eur. Polym. J. 2015, 72, 543–565. [Google Scholar] [CrossRef]
- Lee, J.H. Injectable hydrogels delivering therapeutic agents for disease treatment and tissue engineering. Biomater. Res. 2018, 22, 27. [Google Scholar] [CrossRef]
- Yu, L.; Ding, J. Injectable hydrogels as unique biomedical materials. Chem. Soc. Rev. 2008, 37, 1473–1481. [Google Scholar] [CrossRef] [PubMed]
- Overstreet, D.J.; Dutta, D.; Stabenfeldt, S.E.; Vernon, B.L. Injectable hydrogels. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 881–903. [Google Scholar] [CrossRef]
- González-Díaz, E.C.; Varghese, S. Hydrogels as extracellular matrix analogs. Gels 2016, 2, 20. [Google Scholar] [CrossRef] [PubMed]
- Tibbitt, M.W.; Anseth, K.S. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol. Bioeng. 2009, 103, 655–663. [Google Scholar] [CrossRef] [PubMed]
- Mellati, A.; Akhtari, J. Injectable hydrogels: A review of injectability mechanisms and biomedical applications. Res. Mol. Med. (RMM) 2019, 6, 1–14. [Google Scholar] [CrossRef]
- Qiu, Y.; Park, K. Environment-sensitive hydrogels for drug delivery. Adv. Drug Deliv. Rev. 2012, 64, 49–60. [Google Scholar] [CrossRef]
- Kouchak, M. In situ gelling systems for drug delivery. Jundishapur J. Nat. Pharm. Prod. 2014, 9, e20126. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Hui, P.C.; Kan, C. Thermoresponsive hydrogels and their biomedical applications: Special insight into their applications in textile based transdermal therapy. Polymers 2018, 10, 480. [Google Scholar] [CrossRef]
- Huang, H.; Qi, X.; Chen, Y.; Wu, Z. Thermo-sensitive hydrogels for delivering biotherapeutic molecules: A review. Saudi Pharm. J. 2019, 27, 990–999. [Google Scholar] [CrossRef]
- Zarrintaj, P.; Jouyandeh, M.; Ganjali, M.R.; Hadavand, B.S.; Mozafari, M.; Sheiko, S.S.; Vatankhah-Varnoosfaderani, M.; Gutiérrez, T.J.; Saeb, M.R. Thermo-sensitive polymers in medicine: A review. Eur. Polym. J. 2019, 117, 402–423. [Google Scholar] [CrossRef]
- Crespy, D.; Rossi, R.M. Temperature-responsive polymers with LCST in the physiological range and their applications in textiles. Polym. Int. 2007, 56, 1461–1468. [Google Scholar] [CrossRef]
- Taylor, M.J.; Tomlins, P.; Sahota, T.S. Thermoresponsive gels. Gels 2017, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Chenite, A.; Buschmann, M.; Wang, D.; Chaput, C.; Kandani, N. Rheological characterisation of thermogelling chitosan/glycerol-phosphate solutions. Carbohydr. Polym. 2001, 46, 39–47. [Google Scholar] [CrossRef]
- Owczarz, P.; Rył, A.; Modrzejewska, Z.; Dziubiński, M. The influence of the addition of collagen on the rheological properties of chitosan chloride solutions. Prog. Chem. Appl. Chitin Its Deriv. 2017, 22, 176–189. [Google Scholar] [CrossRef][Green Version]
- Owczarz, P.; Rył, A.; Dziubiński, M.; Sielski, J. Injectable chitosan scaffolds with calcium β-glycerophosphate as the only neutralizing agent. Processes 2019, 7, 297. [Google Scholar] [CrossRef]
- Carotenuto, C.; Grizzuti, N. Thermoreversible gelation of hydroxypropylcellulose aqueous solutions. Rheol. Acta 2006, 45, 468–473. [Google Scholar] [CrossRef]
- Rwei, S.-P.; Nguyen, T.-A. Formation of liquid crystals and behavior of LCST upon addition of xanthan gum (XG) to hydroxypropyl cellulose (HPC) solutions. Cellulose 2015, 22, 53–61. [Google Scholar] [CrossRef]
- Gosecki, M.; Setälä, H.; Virtanen, T.; Ryan, A.J. A facile method to control the phase behavior of hydroxypropyl cellulose. Carbohydr. Polym. 2021, 251, 117015. [Google Scholar] [CrossRef]
- Huichao, W.; Shouying, D.; Yang, L.; Ying, L.L.; Di, W. The application of biomedical polymer material hydroxy propyl methyl cellulose (HPMC) in pharmaceutical preparations. J. Chem. Pharm. Res. 2014, 6, 155–160. [Google Scholar]
- Fairclough, J.P.A.; Yu, H.; Kelly, O.; Ryan, A.J.; Sammler, R.L.; Radler, M. Interplay between Gelation and Phase Separation in Aqueous Solutions of Methylcellulose and Hydroxypropylmethylcellulose. Langmuir 2012, 28, 10551–10557. [Google Scholar] [CrossRef] [PubMed]
- Nagase, K.; Yamato, M.; Kanazawa, H.; Okano, T. Poly(N-Isopropylacrylamide)-based thermoresponsive surfaces provide new types of biomedical applications. Biomaterials 2018, 153, 27–48. [Google Scholar] [CrossRef]
- Kurakula, M.; Ahmed, T.A. Co-delivery of atorvastatin nanocrystals in PLGA based in situ gel for anti-hyperlipidemic efficacy. Curr. Drug Deliv. 2016, 13, 211–220. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, L.; Zhao, C.; Wang, Q.; Zheng, J. A robust, one-pot synthesis of highly mechanical and recoverable double network hydrogels using thermoreversible sol-gel polysaccharide. Adv. Mater. 2013, 25, 4171–4176. [Google Scholar] [CrossRef]
- Mirahmadi, F.; Tafazzoli-Shadpour, M.; Shokrgozar, M.A.; Bonakdar, S. Enhanced mechanical properties of thermosensitive chitosan hydrogel by silk fibers for cartilage tissue engineering. Mater. Sci. Eng. C 2013, 33, 4786–4794. [Google Scholar] [CrossRef] [PubMed]
- Rył, A.; Owczarz, P. Injectability of thermosensitive, low-concentrated chitosan colloids as flow phenomenon through the capillary under high shear rate conditions. Polymers 2020, 12, 2260. [Google Scholar] [CrossRef] [PubMed]
- Allahham, A.; Mainwaring, D.; Stewart, P.; Marriott, J. Development and application of a micro-capillary rheometer for in-vitro evaluation of parenteral injectability. J. Pharm. Pharmacol. 2004, 56, 709–716. [Google Scholar] [CrossRef]
- Zhang, Q.; Fassihi, M.A.; Fassihi, R. Delivery considerations of highly viscous polymeric fluids mimicking concentrated biopharmaceuticals: Assessment of injectability via measurement of total work done “WT” . AAPS PharmSciTech 2018, 19, 1520–1528. [Google Scholar] [CrossRef]
- Shavandi, A.; Bekhit, A.E.-D.A.; Sun, Z.; Ali, M.A. Injectable gel from squid pen chitosan for bone tissue engineering applications. J. Sol-Gel Sci. Technol. 2016, 77, 675–687. [Google Scholar] [CrossRef]
- Rył, A.; Owczarz, P. Thermoinduced aggegation of chitosan systems in perikinetic and orthokinetic regimes. Carbohydr. Polym. 2021, 255, 117377. [Google Scholar] [CrossRef]
- Snijkers, F.; Pasquino, R.; Olmsted, P.D.; Vlassopoulos, D. Perspectives on the viscoelasticity and flow behavior of entangled linear and branched polymers. J. Phys. Condens. Matter 2015, 27, 473002. [Google Scholar] [CrossRef] [PubMed]
- Colby, R.H.; Boris, D.C.; Krause, W.E.; Dou, S. Shear thinning of unentangled flexible polymer liquids. Rheol. Acta 2007, 46, 569–575. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; An, L. Shear Thinning behavior of linear polymer melts under shear flow via nonequilibrium molecular dynamics. J. Chem. Phys. 2014, 140, 174902. [Google Scholar] [CrossRef] [PubMed]
- Mykhaylyk, O.O.; Chambon, P.; Graham, R.S.; Fairclough, J.P.A.; Olmsted, P.D.; Ryan, A.J. The specific work of flow as a criterion for orientation in polymer crystallization. Macromolecules 2008, 41, 1901–1904. [Google Scholar] [CrossRef]
- Dunderdale, G.J.; Davidson, S.J.; Ryan, A.J.; Mykhaylyk, O.O. Flow-induced crystallisation of polymers from aqueous solution. Nat. Commun. 2020, 11, 3372. [Google Scholar] [CrossRef]
- Gregory, J. Monitoring particle aggregation processes. Adv. Colloid Interface Sci. 2009, 147–148, 109–123. [Google Scholar] [CrossRef] [PubMed]
- Kovalchuk, N.M.; Starov, V.M. Aggregation in colloidal suspensions: Effect of colloidal forces and hydrodynamic interactions. Adv. Colloid Interface Sci. 2012, 179–182, 99–106. [Google Scholar] [CrossRef]
- Ghernaout, D.; Al-Ghonamy, A.I.; Boucherit, A.; Ghernaout, B.; Naceur, M.W.; Messaoudene, N.A.; Aichouni, M.; Mahjoubi, A.A.; Elboughdiri, N.A. Brownian motion and coagulation process. Am. J. Environ. Prot. 2015, 4, 1. [Google Scholar] [CrossRef]
- Mokhtari, T.; Chakrabarti, A.; Sorensen, C.M.; Cheng, C.; Vigil, D. The effect of shear on colloidal aggregation and gelation studied using small-angle light scattering. J. Colloid Interface Sci. 2008, 327, 216–223. [Google Scholar] [CrossRef][Green Version]
- Berre, F.L.; Chauveteau, G.; Pefferkorn, E. Perikinetic and orthokinetic aggregation of hydrated colloids. J. Colloid Interface Sci. 1998, 199, 1–12. [Google Scholar] [CrossRef]
- Bekard, I.B.; Asimakis, P.; Bertolini, J.; Dunstan, D.E. The effects of shear flow on protein structure and function. Biopolymers 2011, 95, 733–745. [Google Scholar] [CrossRef] [PubMed]
- Siedlecki, C.A.; Lestini, B.J.; Kottke-Marchant, K.; Eppell, S.J.; Wilson, D.L.; Marchant, R.E. Shear-dependent changes in the three-dimensional structure of human von willebrand factor. Blood 1996, 88, 2939–2950. [Google Scholar] [CrossRef]
- Hamilton-Brown, P.; Bekard, I.; Ducker, W.A.; Dunstan, D.E. How does shear affect aβ fibrillogenesis? J. Phys. Chem. B 2008, 112, 16249–16252. [Google Scholar] [CrossRef] [PubMed]
- Gomme, P.T.; Prakash, M.; Hunt, B.; Stokes, N.; Cleary, P.; Tatford, O.C.; Bertolini, J. Effect of lobe pumping on human albumin: Development of a lobe pump simulator using smoothed particle hydrodynamics1. Biotechnol. Appl. Biochem. 2006, 43, 113–120. [Google Scholar] [CrossRef]
- Tirrell, M.; Middleman, S. Shear Modification of enzyme kinetics. Biotechnol. Bioeng. 1975, 17, 299–303. [Google Scholar] [CrossRef]
- Cilurzo, F.; Selmin, F.; Minghetti, P.; Adami, M.; Bertoni, E.; Lauria, S.; Montanari, L. Injectability Evaluation: An open issue. AAPS PharmSciTech 2011, 12, 604–609. [Google Scholar] [CrossRef]
- Watt, R.P.; Khatri, H.; Dibble, A.R.G. Injectability as a Function of viscosity and dosing materials for subcutaneous administration. Int. J. Pharm. 2019, 554, 376–386. [Google Scholar] [CrossRef]
- Owczarz, P.; Rył, A.; Sowiński, J. Influence of Glycerophosphate salt solubility on the gelation mechanism of colloidal chitosan systems. Int. J. Mol. Sci. 2021, 22, 4043. [Google Scholar] [CrossRef] [PubMed]
- Owczarz, P.; Ziółkowski, P.; Dziubiński, M. The application of small-angle light scattering for rheo-optical characterization of chitosan colloidal solutions. Polymers 2018, 10, 431. [Google Scholar] [CrossRef] [PubMed]
- Rangel Euzcateguy, G.; Parajua-Sejil, C.; Marchal, P.; Chapron, D.; Averlant-Petit, M.-C.; Stefan, L.; Pickaert, G.; Durand, A. Rheological investigation of supramolecular physical gels in water/dimethylsulfoxide mixtures by lysine derivatives. Polym. Int. 2021, 70, 256–268. [Google Scholar] [CrossRef]
- Läuger, J.; Heyer, P.; Pfeifer, G. A new integrated rheo small angle light scattering (Rheo-Sals) device. Annu. Trans. Nord. Rheol. Soc. 2004, 12, 137–140. [Google Scholar]
- Toker, O.S.; Karasu, S.; Yilmaz, M.T.; Karaman, S. Three interval thixotropy test (3ITT) in food applications: A novel technique to determine structural regeneration of mayonnaise under different shear conditions. Food Res. Int. 2015, 70, 125–133. [Google Scholar] [CrossRef]
- Secker, D.R.; Kaye, P.H.; Greenaway, R.S.; Hirst, E.; Bartley, D.L.; Videen, G. Light scattering from deformed droplets and droplets with inclusions. I. Experimental results. Appl. Opt. AO 2000, 39, 5023–5030. [Google Scholar] [CrossRef] [PubMed]
- Primavera, R.; Barbacane, R.; Congia, M.; Locatelli, M.; Celia, C. Laser diffraction and light scattering techniques for the analysis of food matrices. Biomed Int.–Adv. Food Saf. Health 2014, 6, 40–60. [Google Scholar]
- Singh, I.; Themistou, E.; Porcar, L.; Neelamegham, S. Fluid shear induces conformation change in human blood protein von willebrand factor in solution. Biophys. J. 2009, 96, 2313–2320. [Google Scholar] [CrossRef]
- Martin-Pastor, M.; Stoyanov, E. Mechanism of interaction between hydroxypropyl cellulose and water in aqueous solutions: Importance of polymer chain length. J. Polym. Sci. 2020, 58, 1632–1641. [Google Scholar] [CrossRef]
- Supper, S.; Anton, N.; Seidel, N.; Riemenschnitter, M.; Schoch, C.; Vandamme, T. Rheological study of chitosan/polyol-phosphate systems: Influence of the polyol part on the thermo-induced gelation mechanism. Langmuir 2013, 29, 10229–10237. [Google Scholar] [CrossRef]
- Filion, D.; Lavertu, M.; Buschmann, M.D. Ionization and solubility of chitosan solutions related to thermosensitive chitosan/glycerol-phosphate systems. Biomacromolecules 2007, 8, 3224–3234. [Google Scholar] [CrossRef]
- Lavertu, M.; Filion, D.; Buschmann, M.D. Heat-induced transfer of protons from chitosan to glycerol phosphate produces chitosan precipitation and gelation. Biomacromolecules 2008, 9, 640–650. [Google Scholar] [CrossRef] [PubMed]
- Maerker, J.M. Shear Degradation of partially hydrolyzed polyacrylamide solutions. Soc. Pet. Eng. J. 1975, 15, 311–322. [Google Scholar] [CrossRef]
- Culter, J.D.; Mayhan, K.G.; Patterson, G.K.; Sarmasti, A.A.; Zakin, J.L. Entrance effects on capillary degradation of dilute polystyrene solutions. J. Appl. Polym. Sci. 1972, 16, 3381–3385. [Google Scholar] [CrossRef]
- Niaounakis, M. Chapter 2-Properties. In Biopolymers: Processing and Products; Niaounakis, M., Ed.; William Andrew Publishing: Oxford, UK, 2015; pp. 79–116. ISBN 978-0-323-26698-7. [Google Scholar]
- Tsai, H.; Sussman, I.; Nagel, R. Shear stress enhances the proteolysis of von willebrand factor in normal plasma. Blood 1994, 83, 2171–2179. [Google Scholar] [CrossRef]
- Akkermans, C.; Venema, P.; Rogers, S.S.; van der Goot, A.J.; Boom, R.M.; van der Linden, E. Shear pulses nucleate fibril aggregation. Food Biophys. 2006, 1, 144–150. [Google Scholar] [CrossRef]
- Alexander-Katz, A.; Netz, R.R. Dynamics and instabilities of collapsed polymers in shear flow. Macromolecules 2008, 41, 3363–3374. [Google Scholar] [CrossRef]
- Owczarz, P.; Ziółkowski, P.; Modrzejewska, Z.; Kuberski, S.; Dziubiński, M. Rheo-kinetic study of sol-gel phase transition of chitosan colloidal systems. Polymers 2018, 10, 47. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Heuzey, M.-C.; Bégin, A.; Carreau, P.J. Physical gelation of chitosan in the presence of beta-glycerophosphate: The effect of temperature. Biomacromolecules 2005, 6, 3267–3275. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rył, A.; Owczarz, P. Influence of Injection Application on the Sol–Gel Phase Transition Conditions of Polysaccharide-Based Hydrogels. Int. J. Mol. Sci. 2021, 22, 13208. https://doi.org/10.3390/ijms222413208
Rył A, Owczarz P. Influence of Injection Application on the Sol–Gel Phase Transition Conditions of Polysaccharide-Based Hydrogels. International Journal of Molecular Sciences. 2021; 22(24):13208. https://doi.org/10.3390/ijms222413208
Chicago/Turabian StyleRył, Anna, and Piotr Owczarz. 2021. "Influence of Injection Application on the Sol–Gel Phase Transition Conditions of Polysaccharide-Based Hydrogels" International Journal of Molecular Sciences 22, no. 24: 13208. https://doi.org/10.3390/ijms222413208
APA StyleRył, A., & Owczarz, P. (2021). Influence of Injection Application on the Sol–Gel Phase Transition Conditions of Polysaccharide-Based Hydrogels. International Journal of Molecular Sciences, 22(24), 13208. https://doi.org/10.3390/ijms222413208





