Optimizing Chain Topology of Bottle Brush Copolymer for Promoting the Disorder-to-Order Transition
Abstract
:1. Introduction
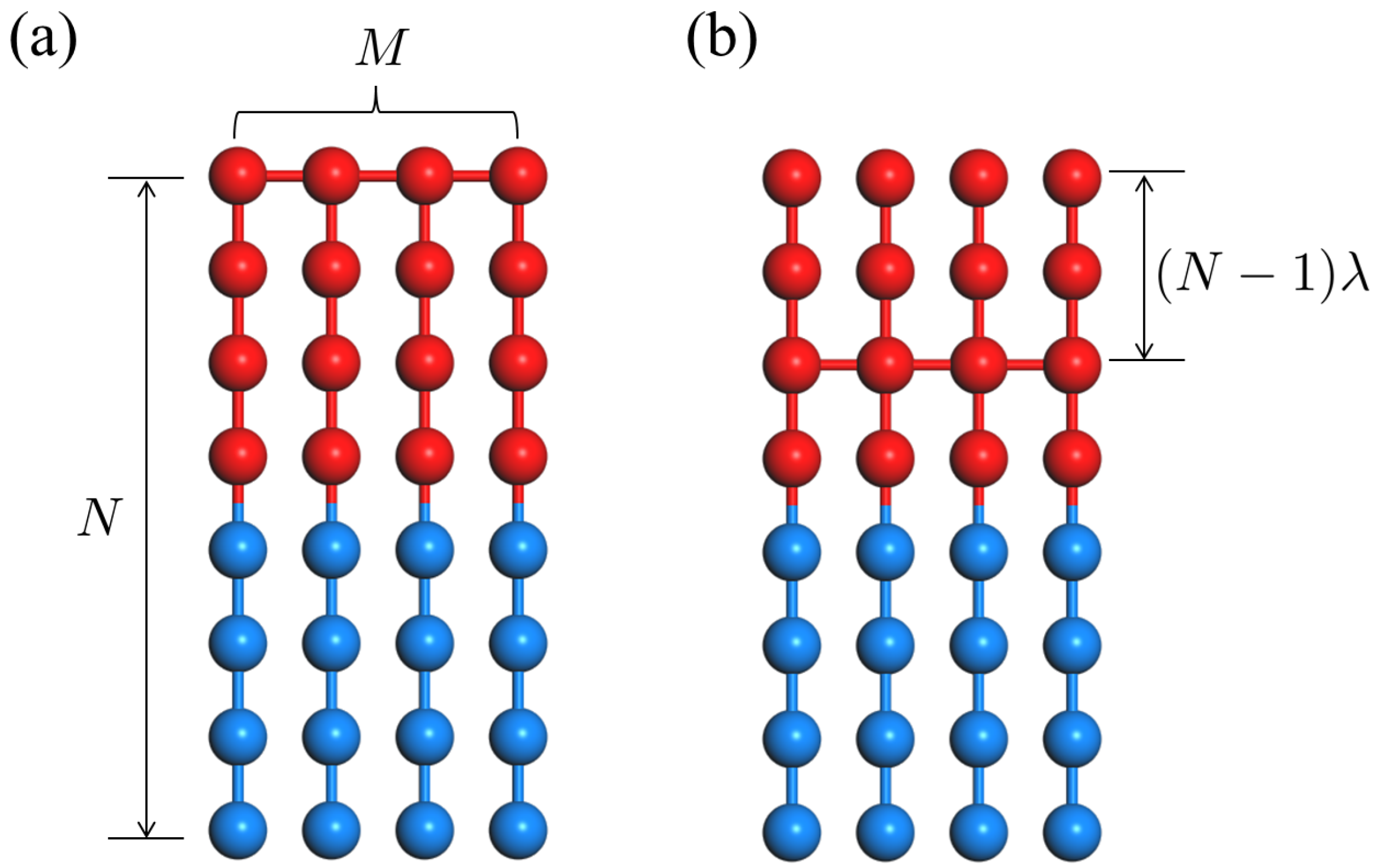
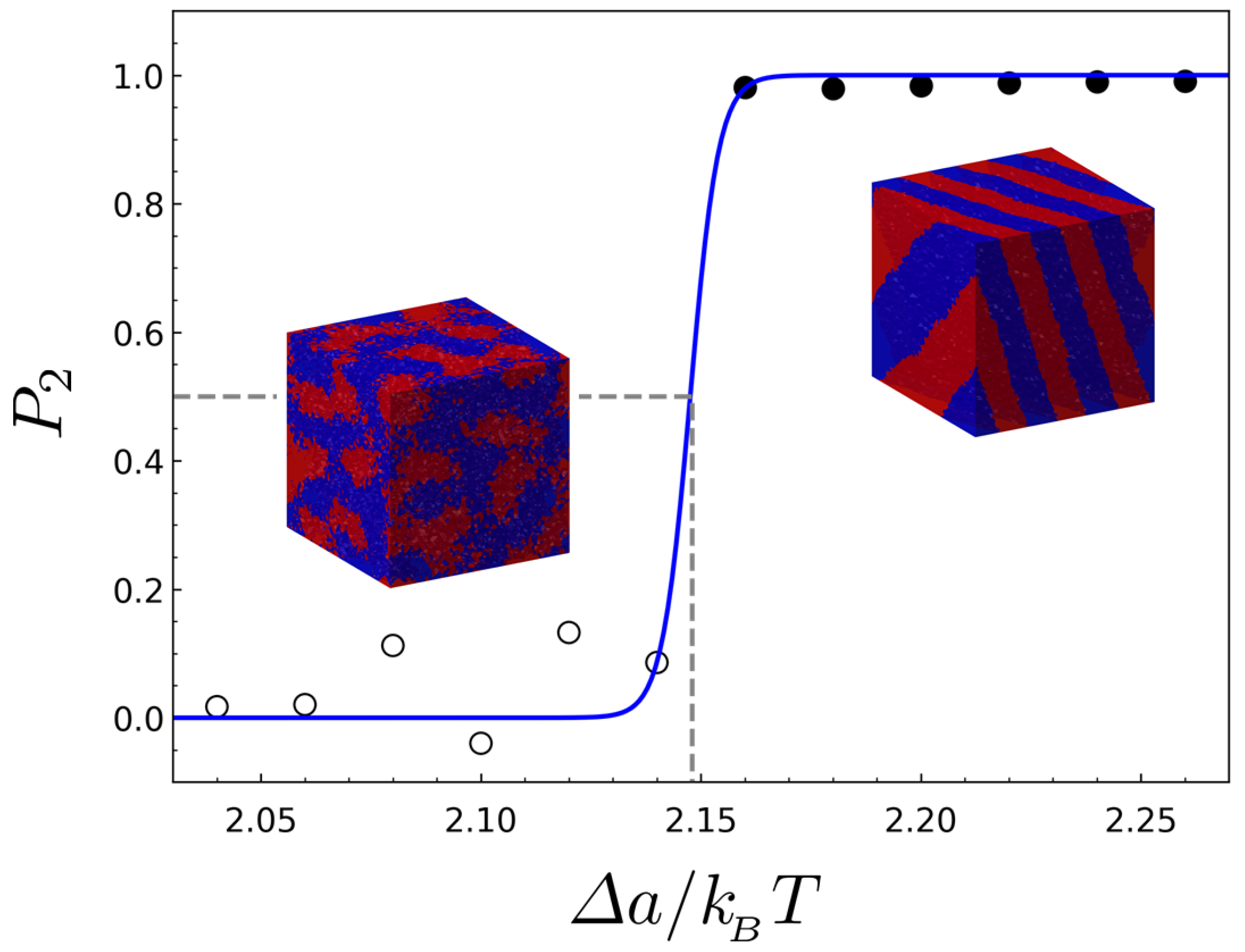
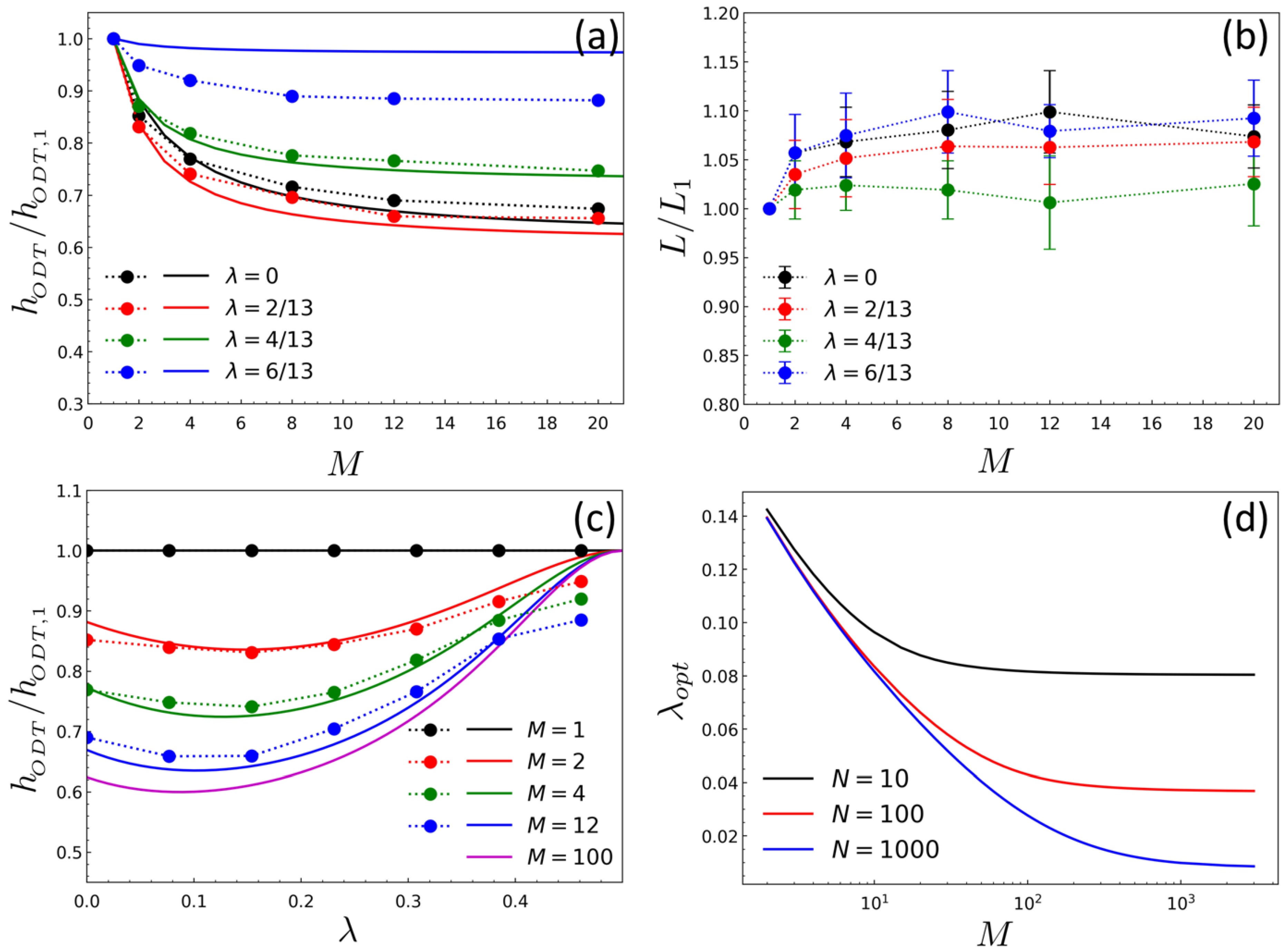
2. Results and Discussion
3. Simulation Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Runge, M.B.; Dutta, S.; Bowden, N.B. Synthesis of Comb Block Copolymers by ROMP, ATRP, and ROP and Their Assembly in the Solid State. Macromolecules 2006, 39, 498–508. [Google Scholar] [CrossRef]
- Runge, M.B.; Bowden, N.B. Synthesis of High Molecular Weight Comb Block Copolymers and Their Assembly into Ordered Morphologies in the Solid State. J. Am. Chem. Soc. 2007, 129, 10551–10560. [Google Scholar] [CrossRef] [PubMed]
- Runge, M.B.; Lipscomb, C.E.; Ditzer, L.R.; Mahanthappa, M.K.; Tivanski, A.V.; Bowden, N.B. Investigation of the Assembly of Comb Block Copolymers in the Solid State. Macromolecules 2008, 41, 7687–7694. [Google Scholar] [CrossRef]
- Xia, Y.; Olsen, B.D.; Kornfield, J.A.; Grubbs, R.H. Efficient Synthesis of Narrowly Dispersed Brush Copolymers and Study of Their Assemblies: The Importance of Side Chain Arrangement. J. Am. Chem. Soc. 2009, 131, 18525–18532. [Google Scholar] [CrossRef] [Green Version]
- Rzayev, J. Molecular Bottlebrushes: New Opportunities in Nanomaterials Fabrication. ACS Macro Lett. 2012, 1, 1146–1149. [Google Scholar] [CrossRef]
- Gu, W.; Huh, J.; Hong, S.W.; Sveinbjornsson, B.R.; Park, C.; Grubbs, R.H.; Russell, T.P. Self-Assembly of Symmetric Brush Diblock Copolymers. ACS Nano 2013, 7, 2551–2558. [Google Scholar] [CrossRef] [Green Version]
- Dalsin, S.J.; Rions-Maehren, T.G.; Beam, M.D.; Bates, F.S.; Hillmyer, M.A.; Matsen, M.W. Bottlebrush Block Polymers: Quantitative Theory and Experiments. ACS Nano 2015, 9, 12233–12245. [Google Scholar] [CrossRef]
- Lin, T.-P.; Chang, A.B.; Luo, S.-X.; Chen, H.-Y.; Lee, B.; Grubbs, R.H. Effects of Grafting Density on Block Polymer Self-Assembly: From Linear to Bottlebrush. ACS Nano 2017, 11, 11632–11641. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.-H.; Le, A.N.; Feng, X.; Choo, Y.; Liu, B.; Wang, D.; Wan, Z.; Gu, Y.; Zhao, J.; Li, V.; et al. Janus Graft Block Copolymers: Design of a Polymer Architecture for Independently Tuned Nanostructures and Polymer Properties. Angew. Chem. Int. Ed. 2018, 57, 8493–8497. [Google Scholar] [CrossRef]
- Spencer, R.K.W.; Matsen, M.W. Field-Theoretic Simulations of Bottlebrush Copolymers. J. Chem. Phys. 2018, 149, 184901. [Google Scholar] [CrossRef]
- Karavolias, M.G.; Elder, J.B.; Ness, E.M.; Mahanthappa, M.K. Order-to-Disorder Transitions in Lamellar Melt Self-Assembled Core-Shell Bottlebrush Polymers. ACS Macro Lett. 2019, 8, 1617–1622. [Google Scholar] [CrossRef]
- Miyake, G.M.; Piunova, V.A.; Weitekamp, R.A.; Grubbs, R.H. Precisely Tunable Photonic Crystals From Rapidly Self-Assembling Brush Block Copolymer Blends. Angew. Chem. Int. Ed. 2012, 51, 11246–11248. [Google Scholar] [CrossRef] [PubMed]
- Sveinbjörnsson, B.R.; Weitekamp, R.A.; Miyake, G.M.; Xia, Y.; Atwater, H.A.; Grubbs, R.H. Rapid Self-Assembly of Brush Block Copolymers to Photonic Crystals. Proc. Natl. Acad. Sci. USA 2012, 109, 14332–14336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liberman-Martin, A.L.; Chu, C.K.; Grubbs, R.H. Application of Bottlebrush Block Copolymers as Photonic Crystals. Macromol. Rapid Commun. 2017, 38, 1700058. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.; Cho, S.; Clark, C.; Verkhoturov, S.V.; Eller, M.J.; Li, A.; Pavıá-Jimeńez, A.; Schweikert, E.A.; Thackeray, J.W.; Trefonas, P.; et al. Nanoscopic Cylindrical Dual Concentric and Lengthwise Block Brush Terpolymers as Covalent Preassembled High-Resolution and High Sensitivity Negative-Tone Photoresist Materials. J. Am. Chem. Soc. 2013, 135, 4203–4206. [Google Scholar] [CrossRef]
- Hong, S.W.; Gu, W.; Huh, J.; Sveinbjörnsson, B.R.; Jeong, G.; Grubbs, R.H.; Russell, T.P. On the Self-Assembly of Brush Block Copolymers in Thin Films. ACS Nano 2013, 7, 9684–9692. [Google Scholar] [CrossRef] [Green Version]
- Leibler, L. Theory of Microphase Separation in Block Copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Matsen, M.W.; Bates, F.S. Unifying Weak- and Strong-Segregation Block Copolymer Theories. Macromolecules 1996, 29, 1091–1098. [Google Scholar] [CrossRef]
- Mayes, A.M.; Olvera de la Cruz, M. Microphase Separation in Multiblock Copolymer Melts. J. Chem. Phys. 1989, 91, 7228–7235. [Google Scholar] [CrossRef]
- Matsen, M.W.; Thompson, R.B. Equilibrium Behavior of Symmetric ABA Triblock Copolymer Melts. J. Chem. Phys. 1999, 111, 7139–7146. [Google Scholar] [CrossRef]
- Jeong, J.W.; Park, W.I.; Kim, M.-J.; Ross, C.A.; Jung, Y.S. Highly Tunable Self-Assembled Nanostructures from a Poly(2-vinylpyridine-b-dimethylsiloxane) Block Copolymer. Nano Lett. 2011, 11, 4095–4101. [Google Scholar] [CrossRef] [PubMed]
- Son, J.G.; Hannon, A.F.; Gotrik, K.W.; Alexander-Katz, A.; Ross, C.A. Hierarchical Nanostructures by Sequential Self-Assembly of Styrene-Dimethylsiloxane Block Copolymers of Different Periods. Adv. Mater. 2011, 23, 634–639. [Google Scholar] [CrossRef] [PubMed]
- Cushen, J.D.; Otsuka, I.; Bates, C.M.; Halila, S.; Fort, S.; Rochas, C.; Easley, J.A.; Rausch, E.L.; Thio, A.; Borsali, R.; et al. Oligosaccharide/Silicon-Containing Block Copolymers with 5 nm Features for Lithographic Applications. ACS Nano 2012, 6, 3424–3433. [Google Scholar] [CrossRef] [PubMed]
- Kennemur, J.G.; Yao, L.; Bates, F.S.; Hillmyer, M.A. Sub-5 nm Domains in Ordered Poly(cyclohexylethylene)-blockpoly(methyl methacrylate) Block Polymers for Lithography. Macromolecules 2014, 47, 1411–1418. [Google Scholar] [CrossRef]
- Wan, L.; Ruiz, R.; Gao, H.; Patel, K.C.; Albrecht, T.R. The Limits of Lamellae-Forming PS-b-PMMA Block Copolymers for Lithography. ACS Nano 2015, 9, 7506–7514. [Google Scholar] [CrossRef]
- Vora, A.; Wojtecki, R.J.; Schmidt, K.; Chunder, A.; Cheng, J.Y.; Nelson, A.; Sanders, D.P. Development of Polycarbonate-Containing Block Copolymers for Thin Film Self-Assembly Applications. Polym. Chem. 2016, 7, 940–950. [Google Scholar] [CrossRef]
- Woo, S.; Jo, S.; Ryu, D.Y.; Choi, S.-H.; Choe, Y.; Khan, A.; Huh, J.; Bang, J. Molecular Tailoring of Poly(styrene-b-methyl methacrylate) Block Copolymer Toward Perpendicularly Oriented Nanodomains with Sub-10 nm Features. ACS Macro Lett. 2017, 6, 1386–1391. [Google Scholar] [CrossRef]
- Kwak, J.; Mishra, A.K.; Lee, J.; Lee, K.S.; Choi, C.; Maiti, S.; Kim, M.; Kim, J.K. Fabrication of Sub-3 nm Feature Size Based on Block Copolymer Self-Assembly for Next-Generation Nanolithography. Macromolecules 2017, 50, 6813–6818. [Google Scholar] [CrossRef]
- Lane, A.P.; Yang, X.; Maher, M.J.; Blachut, G.; Asano, Y.; Someya, Y.; Mallavarapu, A.; Sirard, S.M.; Ellison, C.J.; Willson, C.G. Directed Self-Assembly and Pattern Transfer of Five Nanometer Block Copolymer Lamellae. ACS Nano 2017, 11, 7656–7665. [Google Scholar] [CrossRef]
- Zhang, X.; He, Q.; Chen, Q.; Nealey, P.F.; Ji, S. Directed Self-Assembly of High χ Poly(styrene-b-(lactic acid-alt-glycolic acid)) Block Copolymers on Chemical Patterns via Thermal Annealing. ACS Macro Lett. 2018, 7, 751–756. [Google Scholar] [CrossRef]
- Azuma, K.; Sun, J.; Choo, Y.; Rokhlenko, Y.; Dwyer, J.H.; Schweitzer, B.; Hayakawa, T.; Osuji, C.O.; Gopalan, P. Self-Assembly of an Ultrahigh-χ Block Copolymer with Versatile Etch Selectivity. Macromolecules 2018, 51, 6460–6467. [Google Scholar] [CrossRef]
- Jo, S.; Jeon, S.; Jun, T.; Park, C.; Ryu, D.Y. Fluorine-Containing Styrenic Block Copolymers toward High χ and Perpendicular Lamellae in Thin Films. Macromolecules 2018, 51, 7152–7159. [Google Scholar] [CrossRef]
- Pang, Y.; Jin, X.; Huang, G.; Wan, L.; Ji, S. Directed Self-Assembly of Styrene-Methyl Acrylate Block Copolymers with Sub-7 nm Features via Thermal Annealing. Macromolecules 2019, 52, 2987–2994. [Google Scholar] [CrossRef]
- Park, J.; Staiger, A.; Mecking, S.; Winey, K.I. Sub-3-Nanometer Domain Spacings of Ultrahigh-χ Multiblock Copolymers with Pendant Ionic Groups. ACS Nano 2021, 15, 16738–16747. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Zhang, W.; Hong, S.; Chen, Z.; Liu, X.; Xiao, S.; Coughlin, E.B.; Russell, T.P. Using Block Copolymer Architecture to Achieve Sub-10 nm Periods. Polymer 2017, 121, 297–303. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, J.; Choe, Y.; Huh, J.; Bang, J. The Effect of Chain Architecture on the Phase Behavior of A4B4 Miktoarm Block Copolymers. Polym. Chem. 2019, 10, 3079–3087. [Google Scholar] [CrossRef]
- Español, P.; Warren, P.B. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Mukhyar, A.J.; Escobedo, F.A. Developing Local Order Parameters for Order-Disorder Transitions From Particles to Block Copolymers: Methodological Framework. Macromolecules 2018, 51, 9769–9780. [Google Scholar] [CrossRef]
- Kumar, A.; Molinero, V. Self-Assembly of Mesophases from Nanoparticles. J. Phys. Chem. Lett. 2017, 9, 5053–5058. [Google Scholar] [CrossRef]
- Andersona, J.A.; Glaser, J.; Glotzer, S.C. HOOMD-blue: A Python Package for High-Performance Molecular Dynamics and Hard Particle Monte Carlo Simulations. Comput. Mater. Sci. 2020, 173, 109363. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D.; Madden, T.J. Dynamic Simulation of Diblock Copolymer Microphase Separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Spenley, N.A. Scaling Laws for Polymers in Dissipative Particle Dynamics. Europhys. Lett. 2000, 49, 534–540. [Google Scholar] [CrossRef]
- Phillips, C.L.; Anderson, J.A.; Glotzer, S.C. Pseudo-Random Number Generation for Brownian Dynamics and Dissipative Particle Dynamics Simulations on GPU Devices. J. Comput. Phys. 2011, 230, 7191–7201. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Clarendon Press: Oxford, UK, 2017. [Google Scholar]

| Parameter | Value | Unit 1 | Equations |
|---|---|---|---|
| 25.0 | (11) | ||
| 4.5 | (12), (13) | ||
| K | 100.0 | (15) | |
| 1.5 | (15) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Shin, H.-W.; Bang, J.; Huh, J. Optimizing Chain Topology of Bottle Brush Copolymer for Promoting the Disorder-to-Order Transition. Int. J. Mol. Sci. 2022, 23, 5374. https://doi.org/10.3390/ijms23105374
Park J, Shin H-W, Bang J, Huh J. Optimizing Chain Topology of Bottle Brush Copolymer for Promoting the Disorder-to-Order Transition. International Journal of Molecular Sciences. 2022; 23(10):5374. https://doi.org/10.3390/ijms23105374
Chicago/Turabian StylePark, Jihoon, Hyun-Woo Shin, Joona Bang, and June Huh. 2022. "Optimizing Chain Topology of Bottle Brush Copolymer for Promoting the Disorder-to-Order Transition" International Journal of Molecular Sciences 23, no. 10: 5374. https://doi.org/10.3390/ijms23105374
APA StylePark, J., Shin, H. -W., Bang, J., & Huh, J. (2022). Optimizing Chain Topology of Bottle Brush Copolymer for Promoting the Disorder-to-Order Transition. International Journal of Molecular Sciences, 23(10), 5374. https://doi.org/10.3390/ijms23105374








