Exploring Nearest Neighbor Interactions and Their Influence on the Gibbs Energy Landscape of Unfolded Proteins and Peptides
Abstract
:1. Introduction
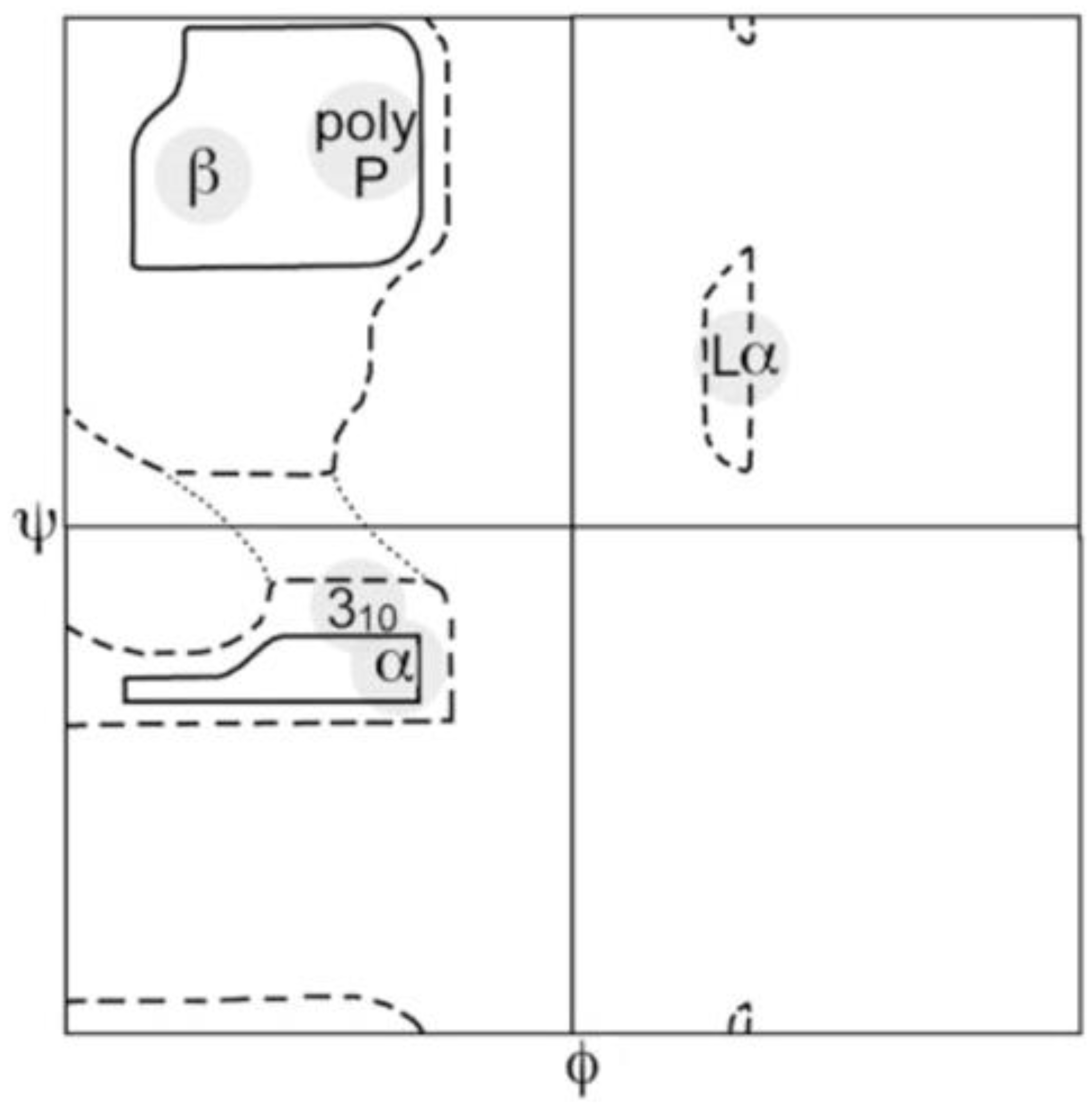
2. Thermodynamic Aspects of Nearest Neighbor Interactions
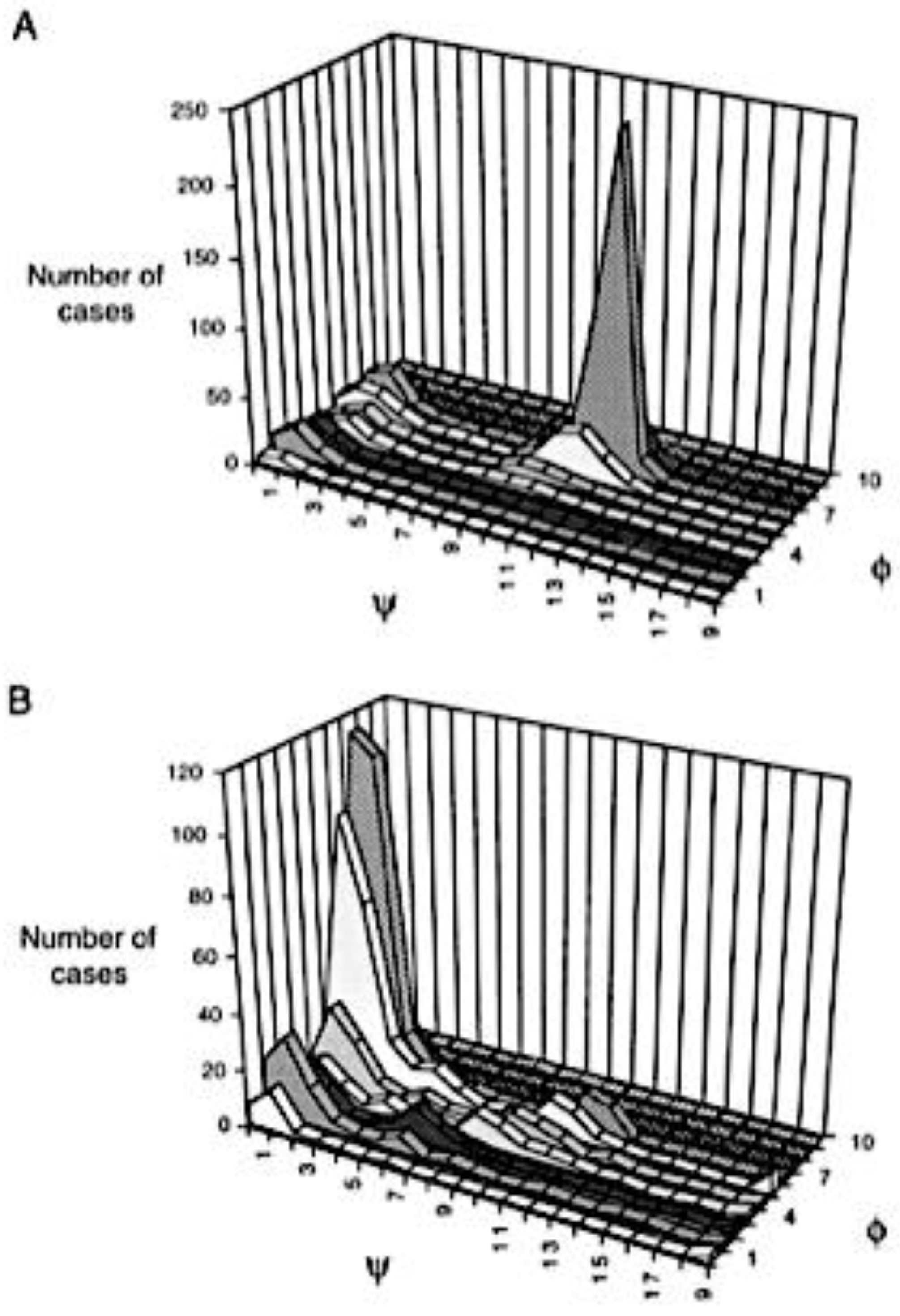
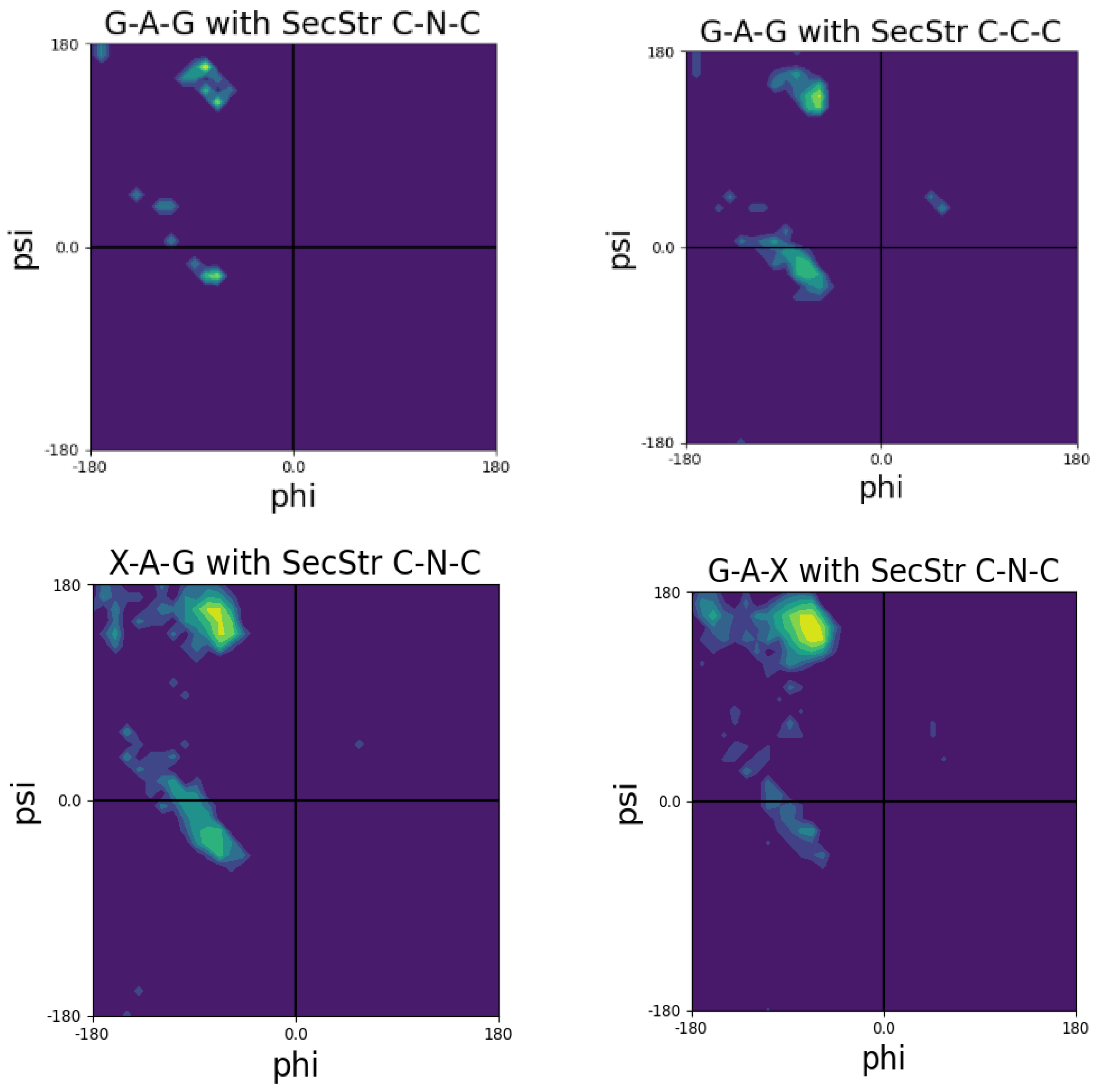
3. Coil Library Studies
4. Simulations
5. Experimental Results
5.1. NMR on Denatured Proteins
5.2. Structural Analysis of Homopeptides
5.3. Structural Analysis of Heteropeptides


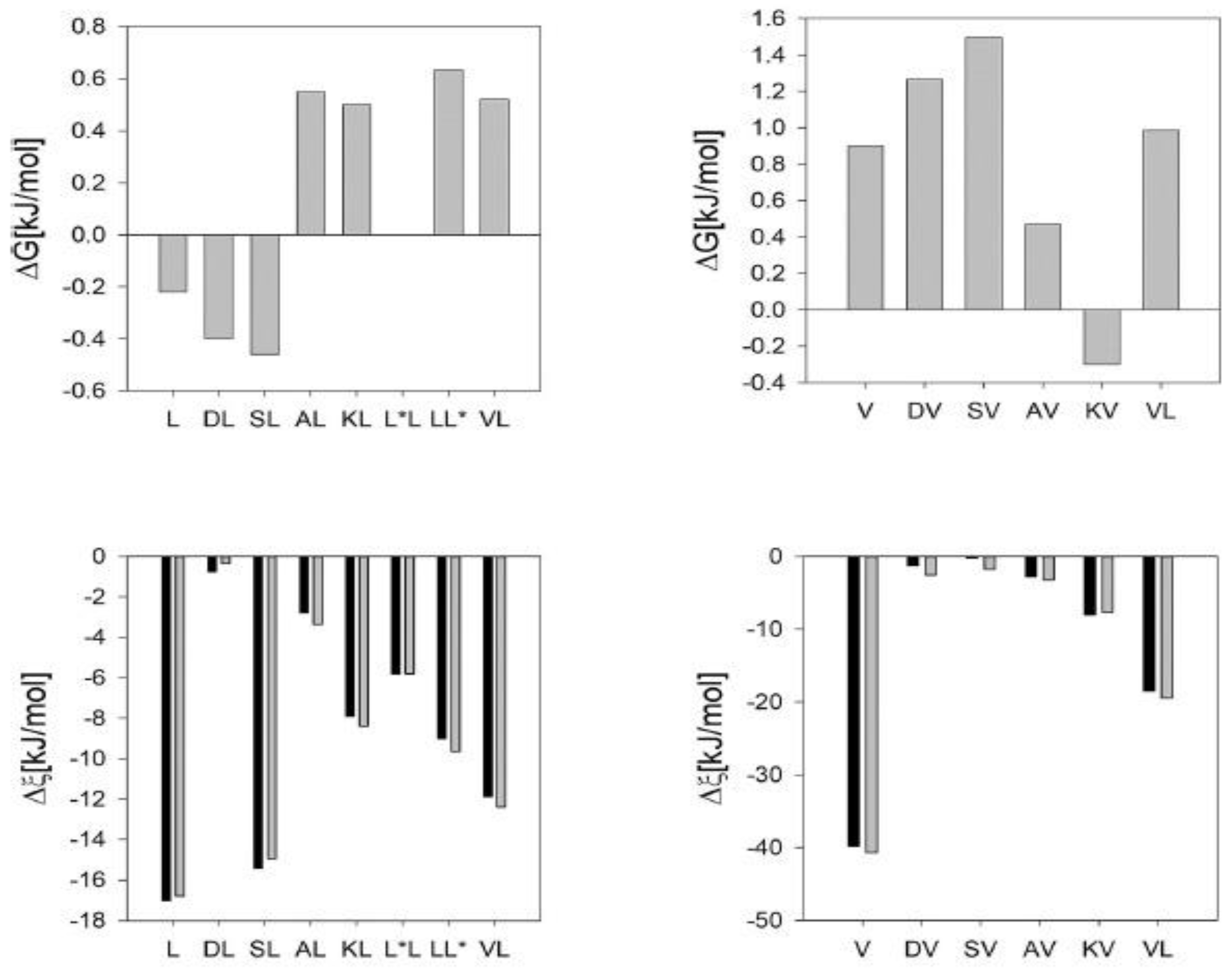
6. Summary and Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- Brant, D.A.; Flory, P.J. The Configuration of Random Polypeptide Chains. I. Experimental Results. J. Am. Chem. Soc. 1965, 87, 2788–2791. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Brant, D.A.; Flory, P.J. The Configuration of Random Polypeptide Chains. II. Theory. J. Am. Chem. Soc. 1965, 87, 2791–2800. [Google Scholar] [CrossRef]
- Uversky, V.N. What Does It Mean to Be Natively Unfolded? Eur. J. Biochem. 2002, 269, 2–12. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N.; Dunker, A.K. Why Are We Interested in the Unfolded Peptides and Proteins? In Protein Pept. Folding, Misfolding, Non-Folding; Schweitzer-Stenner, R., Ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 1–54. ISBN 978-0-470-59169-7. [Google Scholar]
- Romero, P.; Obradovic, Z.; Li, X.; Garner, E.C.; Brown, C.J.; Dunker, A.K. Sequence Complexity of Disordered Protein. Proteins Struct. Funct. Genet. 2001, 42, 38–48. [Google Scholar] [CrossRef]
- Dunker, A.K.; Obradovic, Z. The Protein Trinity-Linking Function and Disorder. Nat. Biotechnol. 2001, 19, 805–806. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, C.J.; Cue, B.; Dunker, A.K.; Uversky, V.N. Binding Promiscurity of Unfolded Peptides. In Protein and Peptide Folding, Misfolding and Non-Folding; Schweitzer-Stenner, R., Ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 241–278. ISBN 978-0-470-59169-7. [Google Scholar]
- Crick, S.L.; Pappu, R.V. Thermodynamic and Kinetic Models for Aggregation of Intrinsically Disordered Proteins. In Protein and Peptide Folding, Misfolding, and Non-Folding; Schweitzer-Stenner, R., Ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 413–440. ISBN 9780470591697. [Google Scholar]
- Vitale, R.M.; Andreotti, G.; Amodeo, P.; Motta, A. Structural Elements Regulating Interactions in the Early Stages of Fibrillogenesis: A Human Calcitonin Model System. In Protein and Peptide Folding, Misfolding, and Non-Folding; Schweitzer-Stenner, R., Ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 351–388. ISBN 978-0-470-59169-7. [Google Scholar]
- Dobson, C.M. Protein Misfolding, Evolution and Disease. Trends Biochem. Sci. 1999, 24, 329–332. [Google Scholar] [CrossRef]
- Rochet, J.C.; Lansbury, P.T. Amyloid Fibrillogenesis: Themes and Variations. Curr. Opin. Struct. Biol. 2000, 10, 60–68. [Google Scholar] [CrossRef]
- Bernadó, P.; Bertoncini, C.W.; Griesinger, C.; Zweckstetter, M.; Blackledge, M. Defining Long-Range Order and Local Disorder in Native α-Synuclein Using Residual Dipolar Couplings. J. Am. Chem. Soc. 2005, 127, 17968–17969. [Google Scholar] [CrossRef]
- Schwalbe, M.; Ozenne, V.; Bibow, S.; Jaremko, M.; Jaremko, L.; Gajda, M.; Jensen, M.R.; Biernat, J.; Becker, S.; Mandelkow, E.; et al. Predictive Atomic Resolution Descriptions of Intrinsically Disordered HTau40 and α-Synuclein in Solution from NMR and Small Angle Scattering. Structure 2014, 22, 238–249. [Google Scholar] [CrossRef] [Green Version]
- Swindells, M.B.; Macarthur, M.W.; Thornton, J.M. Intrinsic φ, ψ Propensities of Amino Acids, Derived from the Coil Regions of Known Structures. Nat. Struct. Biol. 1995, 2, 569–603. [Google Scholar] [CrossRef]
- Serrano, L. Comparison between the φ Distribution of the Amino Acids in the Protein Database and NMR Data Indicates That Amino Acids Have Various φ Propensities in the Random Coil Conformation. J. Mol. Biol. 1995, 254, 322–333. [Google Scholar] [CrossRef] [PubMed]
- Avbelj, F.; Grdadolnik, S.G.; Grdadolnik, J.; Baldwin, R.L. Intrinsic Backbone Preferences Are Fully Present in Blocked Amino Acids. Proc. Natl. Acad. Sci. USA 2006, 103, 1272–1277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jha, A.K.; Colubri, A.; Freed, K.F.; Sosnick, T.R. Statistical Coil Model of the Unfolded State: Resolving the Reconciliation Problem. Proc. Natl. Acad. Sci. USA 2005, 102, 13099–13104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ting, D.; Wang, G.; Shapovalov, M.; Mitra, R.; Jordan, M.I.; Dunbrack, R.L. Neighbor-Dependent Ramachandran Probability Distributions of Amino Acids Developed from a Hierarchical Dirichlet Process Model. PLoS Comput. Biol. 2010, 6, e1000763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Z.; Chen, K.; Liu, Z.; Kallenbach, N.R. Conformation of the Backbone in Unfolded Proteins. Chem. Rev. 2006, 106, 1877–1897. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer-Stenner, R. Conformational Propensities and Residual Structures in Unfolded Peptides and Proteins. Mol. Biosyst. 2012, 8, 122–133. [Google Scholar] [CrossRef]
- Toal, S.; Schweitzer-Stenner, R. Local Order in the Unfolded State: Conformational Biases and Nearest Neighbor Interactions. Biomolecules 2014, 4, 725–773. [Google Scholar] [CrossRef]
- Grdadolnik, J.; Mohacek-Grosev, V.; Baldwin, R.L.; Avbelj, F. Populations of the Three Major Backbone Conformations in 19 Amino Acid Dipeptides. Proc. Natl. Acad. Sci. USA 2011, 108, 1794–1798. [Google Scholar] [CrossRef] [Green Version]
- Toal, S.E.; Verbaro, D.J.; Schweitzer-Stenner, R. Role of Enthalpy-Entropy Compensation Interactions in Determining the Conformational Propensities of Amino Acid Residues in Unfolded Peptides. J. Phys. Chem. B 2014, 118, 1309–1318. [Google Scholar] [CrossRef]
- Meral, D.; Toal, S.; Schweitzer-Stenner, R.; Urbanc, B. Water-Centered Interpretation of Intrinsic PPII Propensities of Amino Acid Residues: In Vitro-Driven Molecular Dynamics Study. J. Phys. Chem. B 2015, 119, 13237–13251. [Google Scholar] [CrossRef]
- Zhang, S.; Schweitzer-Stenner, R.; Urbanc, B. Do Molecular Dynamics Force Fields Capture Conformational Dynamics of Alanine in Water? J. Chem. Theory Comput. 2020, 16, 510–527. [Google Scholar] [CrossRef] [PubMed]
- Garcia, A.E. Characterization of Non-Alpha Helical Conformations in Ala Peptides. Polymer 2004, 45, 669–676. [Google Scholar] [CrossRef]
- Kentsis, A.; Mezei, M.; Gindin, T.; Osman, R. Unfolded State of Polyalanine Is a Segmented Polyproline II Helix. Proteins Struct. Funct. Genet. 2004, 55, 493–501. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.S. Ramachandran Plot. Available online: https://commons.wikimedia.org/wiki/File:Ramachandran_plot_original_outlines.jpg (accessed on 15 April 2022).
- Plaxco, K.W.; Morton, C.J.; Grimshaw, S.B.; Jones, J.A.; Pitkeathly, M.; Campbell, L.D.; Dobson, C.M. The Effects of Guanidine Hydrochloride on the “random Coil” Conformations and NMR Chemical Shifts of the Peptide Series GGXGG. J. Biomol. NMR 1997, 10, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Natively Unfolded Proteins: A Point Where Biology Waits for Physics. Protein Sci. 2002, 11, 739–756. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, H.; Soranno, A.; Borgia, A.; Gast, K.; Nettels, D.; Schuler, B. Polymer Scaling Laws of Unfolded and Intrinsically Disordered Proteins Quantified with Single-Molecule Spectroscopy. Proc. Natl. Acad. Sci. USA 2012, 109, 16155–16160. [Google Scholar] [CrossRef] [Green Version]
- Müller-Späth, S.; Soranno, A.; Hirschfeld, V.; Hofmann, H.; Rüegger, S.; Reymond, L.; Nettels, D.; Schuler, B. Charge Interactions Can Dominate the Dimensions of Intrinsically Disordered Proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 14609–14614. [Google Scholar] [CrossRef] [Green Version]
- Mao, A.H.; Crick, S.L.; Vitalis, A.; Chicoine, C.L.; Pappu, R.V. Net Charge per Residue Modulates Conformational Ensembles of Intrinsically Disordered Proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8183–8188. [Google Scholar] [CrossRef] [Green Version]
- Holehouse, A.S.; Garai, K.; Lyle, N.; Vitalis, A.; Pappu, R.V. Quantitative Assessments of the Distinct Contributions of Polypeptide Backbone Amides versus Side Chain Groups to Chain Expansion via Chemical Denaturation. J. Am. Chem. Soc. 2015, 137, 2984–2995. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Paggi, D.; Hannibal, L.; Castro, M.A.; Oviedo-Rouco, S.; Demicheli, V.; Tórtora, V.; Tomasina, F.; Radi, R.; Murgida, D.H. Multifunctional Cytochrome c: Learning New Tricks from an Old Dog. Chem. Rev. 2017, 117, 13382–13460. [Google Scholar] [CrossRef]
- Schweitzer-Stenner, R.; Hagarman, A.; Verbaro, D.; Soffer, J.B. Conformational Stability of Cytochrome C Probed by Optical Spectroscopy. Methods Enzymol. 2009, 466, 109–153. [Google Scholar] [CrossRef] [PubMed]
- Schwalbe, H.; Fiebig, K.M.; Buck, M.; Jones, J.A.; Grimshaw, S.B.; Spencer, A.; Glaser, S.J.; Smith, L.J.; Dobson, C.M. Structural and Dynamical Properties of a Denatured Protein. Heteronuclear 3D NMR Experiments and Theoretical Simulations of Lysozyme in 8 M Urea. Biochemistry 1997, 36, 8977–8991. [Google Scholar] [CrossRef] [PubMed]
- Fitzkee, N.C.; Rose, G.D. Reassessing Random-Coil Statistics in Unfolded Proteins. Proc. Natl. Acad. Sci. USA 2004, 101, 12497–12502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Z.; Chen, K.; Liu, Z.; Ng, A.; Bracken, W.C.; Kallenbach, N.R. Polyproline II Propensities from GGXGG Peptides Reveal an Anticorrelation with β-Sheet Scales. Proc. Natl. Acad. Sci. USA 2005, 102, 17964–17968. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elam, W.A.; Schrank, T.P.; Hilser, V.J. Experimental and Computational Studies of Polyproline II Propensity. In Protein and Peptide Folding, Misfolding, and Non-Folding; Schweitzer-Stenner, R., Ed.; Wiley & Sons: Chichester, UK, 2012; pp. 159–185. ISBN 9780470591697. [Google Scholar]
- Hagarman, A.; Measey, T.J.; Mathieu, D.; Schwalbe, H.; Schweitzer-Stenner, R. Intrinsic Propensities of Amino Acid Residues in GxG Peptides Inferred from Amide I’ Band Profiles and NMR Scalar Coupling Constants. J. Am. Chem. Soc. 2010, 132, 540–551. [Google Scholar] [CrossRef]
- Hagarman, A.; Mathieu, D.; Toal, S.; Measey, T.J.; Schwalbe, H.; Schweitzer-Stenner, R. Amino Acids with Hydrogen-Bonding Side Chains Have an Intrinsic Tendency to Sample Various Turn Conformations in Aqueous Solution. Chem.-A Eur. J. 2011, 17, 6789–6797. [Google Scholar] [CrossRef]
- Schweitzer-Stenner, R.; Hagarman, A.; Toal, S.; Mathieu, D.; Schwalbe, H. Disorder and Order in Unfolded and Disordered Peptides and Proteins: A View Derived from Tripeptide Conformational Analysis. I. Tripeptides with Long and Predominantly Hydrophobic Side Chains. Proteins Struct. Funct. Bioinform. 2013, 81, 955–967. [Google Scholar] [CrossRef]
- Rybka, K.; Toal, S.E.; Verbaro, D.J.; Mathieu, D.; Schwalbe, H.; Schweitzer-Stenner, R. Disorder and Order in Unfolded and Disordered Peptides and Proteins: A View Derived from Tripeptide Conformational Analysis. II. Tripeptides with Short Side Chains Populating Asx and β-Type like Turn Conformations. Proteins Struct. Funct. Bioinform. 2013, 81, 968–983. [Google Scholar] [CrossRef]
- Meng, W.; Lyle, N.; Luan, B.; Raleigh, D.P.; Pappu, R.V. Experiments and Simulations Show How Long-Range Contacts Can Form in Expanded Unfolded Proteins with Negligible Secondary Structure. Proc. Natl. Acad. Sci. USA 2013, 110, 2123–2128. [Google Scholar] [CrossRef] [Green Version]
- Lyle, N.; Das, R.K.; Pappu, R.V. A Quantitative Measure for Protein Conformational Heterogneity. J. Chem. Phys. 2013, 139, 121907. [Google Scholar] [CrossRef]
- Das, R.K.; Pappu, R.V. Conformations of Intrinsically Disordered Proteins Are Influenced by Linear Sequence Distributions of Appositely Charged Residues. Proc. Natl. Acad. Sci. USA 2013, 110, 13392–13397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salmon, L.; Nodet, G.; Ozenne, V.; Yin, G.; Jensen, M.R.; Zweckstetter, M.; Blackledge, M. NMR Characterization of Long-Range Order in Intrinsically Disordered Proteins. J. Am. Chem. Soc. 2010, 132, 8407–8418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harmon, T.S.; Holehouse, A.S.; Rosen, M.K.; Pappu, R.V. Intrinsically Disordered Linkers Determine the Interplay between Phase Separation and Gelation in Multivalent Proteins. eLife 2017, 6, e30294. [Google Scholar] [CrossRef] [PubMed]
- Ho, B.K.; Thomas, A.; Brasseur, R. Revisiting the Ramachandran Plot: Hard-Sphere Repulsion, Electrostatics, and H-Bonding in the Alpha-Helix. Protein Sci. 2003, 12, 2508–2522. [Google Scholar] [CrossRef] [PubMed]
- Ilawe, N.V.; Raeber, A.E.; Schweitzer-Stenner, R.; Toal, S.E.; Wong, B.M. Assessing Backbone Solvation Effects in the Conformational Propensities of Amino Acid Residues in Unfolded Peptides. Phys. Chem. Chem. Phys. 2015, 17, 24917–24924. [Google Scholar] [CrossRef] [Green Version]
- Fleming, P.J.; Fitzkee, N.C.; Mezei, M.; Srinivasan, R.; Rose, G.D. A Novel Method Reveals That Solvent Water Favors Polyproline II over β-Strand Conformation in Peptides and Unfolded Proteins: Conditional Hydrophobic Accessible Surface Area (CHASA). Protein Sci. 2009, 14, 111–118. [Google Scholar] [CrossRef] [Green Version]
- Lanza, G.; Chiacchio, M.A. Interfacial Water at the Trialanine Hydrophilic Surface: A DFT Electronic Structure and Bottom-up Investigation. Phys. Chem. Chem. Phys. 2015, 17, 17101–17111. [Google Scholar] [CrossRef]
- Diguiseppi, D.; Milorey, B.; Lewis, G.; Kubatova, N.; Farrell, S.; Schwalbe, H.; Schweitzer-Stenner, R. Probing the Conformation-Dependent Preferential Binding of Ethanol to Cationic Glycylalanylglycine in Water/Ethanol by Vibrational and NMR Spectroscopy. J. Phys. Chem. B 2017, 121, 5744–5758. [Google Scholar] [CrossRef]
- Tanaka, S.; Scheraga, H.A. Statistical Mechanical Treatment of Protein Conformation. 4. A Four-State Model for Specific-Sequence Copolymers of Amino Acids. Macromolecules 1976, 9, 812–833. [Google Scholar] [CrossRef]
- Tanaka, S.; Scheraga, H.A. Statistical Mechanical Treatment of Protein Conformation. 5. A Multistate Model for Specific Sequence Copolymers of Amino Acids. Macromolecules 1977, 10, 9–20. [Google Scholar] [CrossRef]
- Karplus, M. Theoretical Calculation Links NMR Coupling Constant to Molecular Geometry. J. Chem. Phys. 1959, 30, 11. [Google Scholar] [CrossRef]
- Wang, A.C.; Bax, A. Determination of the Backbone Dihedral Angles Φ in Human Ubiquitin from Reparametrized Empirical Karplus Equations. J. Am. Chem. Soc. 1996, 118, 2483–2494. [Google Scholar] [CrossRef]
- Duddy, W.J.; Nissink, J.W.M.; Allen, F.H.; Milner-White, E.J. Mimicry by Asx- and ST-Turns of the Four Main Types of β-Turn in Proteins. Protein Sci. 2008, 13, 3051–3055. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Penkett, C.J.; Redfield, C.; Dodd, I.; Hubbard, J.; McBay, D.L.; Mossakowska, D.E.; Smith, R.A.G.; Dobson, C.M.; Smith, L.J. NMR Analysis of Main-Chain Conformational Preferences in an Unfolded Fibronectin-Binding Protein. J. Mol. Biol. 1997, 274, 152–159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, J.S.; Bax, A. Determination of φ and χ1 Angles in Proteins from 13C-13C Three-Bond J Couplings Measured by Three-Dimensional Heteronuclear NMR. How Planar Is the Peptide Bond? J. Am. Chem. Soc. 1997, 119, 6360–6368. [Google Scholar] [CrossRef]
- Vuister, G.W.; Bax, A. Quantitative J Correlation: A New Approach for Measuring Homonuclear Three-Bond J(HNHα) Coupling Constants in 15N-Enriched Proteins. J. Am. Chem. Soc. 1993, 115, 7772–7777. [Google Scholar] [CrossRef]
- Wirmer, J.; Schwalbe, H. Angular Dependence of 1J(Ni,Cαi) and 2J(Ni,Cα(i-1)} Couplings Constants Measured in J-Modulated HSQCs. J. Biomol. NMR 2002, 23, 47–55. [Google Scholar] [CrossRef]
- Hähnke, M.J.; Richter, C.; Heinicke, F.; Schwalbe, H. The HN(COCA)HAHB NMR Experiment for the Stereospecific Assignment of H β-Protons in Non-Native States of Proteins. J. Am. Chem. Soc. 2010, 132, 918–919. [Google Scholar] [CrossRef]
- Case, D.A.; Scheurer, C.; Bruschweiler, R. Static and Dynamic Effects on Vicinal Scalar J Couplings in Proteins and Peptides: A MD/DFT Analysis. J. Am. Chem. Soc. 2000, 122, 10390–10397. [Google Scholar] [CrossRef]
- Jha, A.K.; Colubri, A.; Zaman, M.H.; Koide, S.; Sosnick, T.R.; Freed, K.F. Helix, Sheet, and Polyproline II Frequencies and Strong Nearest Neighbor Effects in a Restricted Coil Library. Biochemistry 2005, 44, 9691–9702. [Google Scholar] [CrossRef] [Green Version]
- Pappu, R.V.; Srinivasan, R.; Rose, G.D. The Flory Isolated-Pair Hypothesis Is Not Valid for Polypeptide Chains: Implications for Protein Folding. Proc. Natl. Acad. Sci. USA 2000, 97, 12565–12570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of Polypeptide Chain Configurations. J. Mol. Biol. 1963, 7, 95–99. [Google Scholar] [CrossRef]
- Sosnick, T.R. Sampling Library. Available online: http://godzilla.uchicago.edu/cgi-bin/rama.cgi (accessed on 10 April 2022).
- de Gennes, P.-G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Schweitzer-Stenner, R. Distribution of Conformations Sampled by the Central Amino Acid Residue in Tripeptides Inferred from Amide i Band Profiles and NMR Scalar Coupling Constants. J. Phys. Chem. B 2009, 113, 2922–2932. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer-Stenner, R.; Toal, S.E. Construction and Comparison of the Statistical Coil States of Unfolded and Intrinsically Disordered Proteins from Nearest-Neighbor Corrected Conformational Propensities of Short Peptides. Mol. Biosyst. 2016, 12, 3294–3306. [Google Scholar] [CrossRef] [PubMed]
- Tran, H.T.; Wang, X.; Pappu, R.V. Reconciling Observations of Sequence-Specific Conformational Propensities with the Generic Polymeric Behavior of Denatured Proteins. Biochemistry 2005, 44, 11369–11380. [Google Scholar] [CrossRef]
- Gnanakaran, S.; Garcia, A.E. Validation of an All-Atom Protein Force Field: From Dipeptides to Larger Peptides. J. Phys. Chem. B 2003, 107, 12555–12557. [Google Scholar] [CrossRef]
- Avbelj, F.; Baldwin, R.L. Origin of the Neighboring Residue Effect on Peptide Backbone Conformation. Proc. Natl. Acad. Sci. USA 2004, 101, 10967–10972. [Google Scholar] [CrossRef] [Green Version]
- Baxa, M.C.; Haddadian, E.J.; Jha, A.K.; Freed, K.F.; Sosnick, T.R. Context and Force Field Dependence of the Loss of Protein Backbone Entropy upon Folding Using Realistic Denatured and Native State Ensembles. J. Am. Chem. Soc. 2012, 134, 15929–15936. [Google Scholar] [CrossRef] [Green Version]
- Zaman, M.H.; Shen, M.Y.; Berry, R.S.; Freed, K.F.; Sosnick, T.R. Investigations into Sequence and Conformational Dependence of Backbone Entropy, Inter-Basin Dynamics and the Flory Isolated-Pair Hypothesis for Peptides. J. Mol. Biol. 2003, 331, 693–711. [Google Scholar] [CrossRef]
- Toal, S.; Meral, D.; Verbaro, D.; Urbanc, B.; Schweitzer-Stenner, R. PH-Independence of Trialanine and the Effects of Termini Blocking in Short Peptides: A Combined Vibrational, NMR, UVCD, and Molecular Dynamics Study. J. Phys. Chem. B 2013, 117, 3689–3706. [Google Scholar] [CrossRef] [Green Version]
- Peti, W.; Smith, L.J.; Redfield, C.; Schwalbe, H. Chemical Shifts in Denatured Proteins: Resonance Assignments for Denatured Ubiquitin and Comparisons with Other Denatured Proteins. J. Biomol. NMR 2001, 19, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.J.; Bolin, K.A.; Schwalbe, H.; MacArthur, M.W.; Thornton, J.M.; Dobson, C.M. Analysis of Main Chain Torsion Angles in Proteins: Prediction of NMR Coupling Constants for Native and Random Coil Conformations. J. Mol. Biol. 1996, 255, 494–506. [Google Scholar] [CrossRef] [PubMed]
- Braun, D.; Wider, G.; Wüthrich, K. Sequence-Corrected $^15$N “Random Coil” Chemical Shifts. J. Am. Chem. Soc. 1994, 116, 8466–8469. [Google Scholar] [CrossRef]
- Peti, W.; Hennig, M.; Smith, L.J.; Schwalbe, H. NMR Spectroscopic Investigation of ψ Torsion Angle Distribution in Unfolded Ubiquitin from Analysis of 3J(Cα,Cα) Coupling Constants and Cross-Correlated Γ(HNN1CαHα)/(C) Relaxation Rates. J. Am. Chem. Soc. 2000, 122, 12017–12018. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.; Ponder, J.W. Consistent Treatment of Inter- and Intramolecular Polarization in Molecular Mechanics Calculations. J. Comput. Chem. 2002, 23, 1497–1506. [Google Scholar] [CrossRef] [PubMed]
- Mackerell, A.D.; Feig, M.; Brooks, C.L. Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of Gas-Phase Quantum Mechanics in Reproducing Protein Conformational Distributions in Molecular Dynamics Simulation. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Cruz, V.; Ramos, J.; Martínez-Salazar, J. Water-Mediated Conformations of the Alanine Dipeptide as Revealed by Distributed Umbrella Sampling Simulations, Quantum Mechanics Based Calculations, and Experimental Data. J. Phys. Chem. B 2011, 115, 4880–4886. [Google Scholar] [CrossRef]
- Kwac, K.; Lee, K.K.; Han, J.B.; Oh, K.I.; Cho, M. Classical and Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulations of Alanine Dipeptide in Water: Comparisons with IR and Vibrational Circular Dichroism Spectra. J. Chem. Phys. 2008, 128, 105106. [Google Scholar] [CrossRef]
- Kim, Y.S.; Wang, J.; Hochstrasser, R.M. Two-Dimensional Infrared Spectroscopy of the Alanine Dipeptide in Aqueous Solution. J. Phys. Chem. B 2005, 109, 7511–7521. [Google Scholar] [CrossRef] [PubMed]
- Poon, C.D.; Samulski, E.T.; Weise, C.F.; Weisshaar, J.C. Do Bridging Water Molecules Dictate the Structure of a Model Dipeptide in Aqueous Solution? J. Am. Chem. Soc. 2000, 122, 5642–5643. [Google Scholar] [CrossRef]
- Grdadolnik, J.; Grdadolnik, S.G.; Avbelj, F. Determination of Conformational Preferences of Dipeptides Using Vibrational Spectroscopy. J. Phys. Chem. B 2008, 112, 2712–2718. [Google Scholar] [CrossRef]
- Oh, K.-I.; Jung, Y.-S.; Hwang, G.-S.; Cho, M. Conformational Distributions of Denaturated and Unstructured Proteins Are Similar to Those of 20 × 20 Blocked Dipeptides. J. Biomol. NMR 2012, 53, 25–41. [Google Scholar] [CrossRef]
- Jung, Y.S.; Oh, K.I.; Hwang, G.S.; Cho, M. Neighboring Residue Effects in Terminally Blocked Dipeptides: Implications for Residual Secondary Structures in Intrinsically Unfolded/Disordered Proteins. Chirality 2014, 26, 443–452. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Navarro, A.E.; Shi, Z.; Kallenbach, N.R. End Effects Influence Short Model Peptide Conformation. J. Am. Chem. Soc. 2012, 134, 1571–1576. [Google Scholar] [CrossRef] [PubMed]
- Lee, O.; Roberts, G.M.; Diem, M. IR Vibrational CD in Alanyl Tripeptide: Indication of a Stable Solution Conformer. Biopolymers 1989, 28, 1759–1770. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Chen, K.; Santini, P.A.; Shi, Z.; Kallenbach, N.R. The Pentapeptide GGAGG Has PII Conformation. J. Am. Chem. Soc. 2003, 125, 8092–8093. [Google Scholar] [CrossRef]
- Chen, K.; Liu, Z.; Kallenbach, N.R. The Polyproline II Conformation in Short Alanine Peptides Is Noncooperative. Proc. Natl. Acad. Sci. USA 2004, 101, 15352–15357. [Google Scholar] [CrossRef] [Green Version]
- Toal, S.E.; Kubatova, N.; Richter, C.; Linhard, V.; Schwalbe, H.; Schweitzer-Stenner, R. Randomizing the Unfolded State of Peptides (and Proteins) by Nearest Neighbor Interactions between Unlike Residues. Chem. Eur. J. 2015, 21, 5173–5192, Erratum in Chemistry 2017, 23, 18084–18087. [Google Scholar] [CrossRef]
- Milorey, B.; Schweitzer-Stenner, R.; Andrews, B.; Schwalbe, H.; Urbanc, B. Short Peptides as Predictors for the Structure of Polyarginine Sequences in Disordered Proteins. Biophys. J. 2021, 120, 662–676. [Google Scholar] [CrossRef] [PubMed]
- Milorey, B.; Schwalbe, H.; O’Neill, N.; Schweitzer-Stenner, R. Repeating Aspartic Acid Residues Prefer Turn-like Conformations in the Unfolded State: Implications for Early Protein Folding. J. Phys. Chem. B 2021, 125, 11392–11407. [Google Scholar] [CrossRef] [PubMed]
- Makowska, J.; Rodziewicz-Motowidło, S.; Bagińska, K.; Vila, J.A.; Liwo, A.; Chmurzyński, L.; Scheraga, H.A. Polyproline II Conformation Is One of Many Local Conformational States and Is Not an Overall Conformation of Unfolded Peptides and Proteins. Proc. Natl. Acad. Sci. USA 2006, 103, 1744–1749. [Google Scholar] [CrossRef] [Green Version]
- Zagrovic, B.; Lipfert, J.; Sorin, E.J.; Millett, I.S.; Van Gunsteren, W.F.; Doniach, S.; Pande, V.S. Unusual Compactness of a Polyproline Type II Structure. Proc. Natl. Acad. Sci. USA 2005, 102, 11698–11703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Z.; Anders Olson, C.; Rose, G.D.; Baldwin, R.L.; Kallenbach, N.R. Polyproline II Structure in a Sequence of Seven Alanine Residues. Proc. Natl. Acad. Sci. USA 2002, 99, 9190–9195. [Google Scholar] [CrossRef] [Green Version]
- Tiffany, M.L.; Krimm, S. New Chain Conformations of Poly(Glutamic Acid) and Polylysine. Biopolymers 1968, 6, 1379–1382. [Google Scholar] [CrossRef] [Green Version]
- Dukor, R.K.; Keiderling, T.A. Reassessment of the Random Coil Conformation: Vibrational CD Study of Proline Oligopeptides and Related Polypeptides. Biopolymers 1991, 31, 1747–1761. [Google Scholar] [CrossRef]
- Makowska, J.; Rodziewicz-Motowidło, S.; Bagińska, K.; Makowski, M.; Vila, J.A.; Liwo, A.; Chmurzyński, L.; Scheraga, H.A. Further Evidence for the Absence of Polyproline II Stretch in the XAO Peptide. Biophys. J. 2007, 92, 2904–2917. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, H.; Roccatano, D.; Hennig, A.; Nau, W.M. A 10-Å Spectroscopic Ruler Applied to Short Polyprolines. J. Am. Chem. Soc. 2007, 129, 9762–9772. [Google Scholar] [CrossRef]
- Rucker, A.L.; Pager, C.T.; Campbell, M.N.; Qualls, J.E.; Creamer, T.P. Host-Guest Scale of Left-Handed Polyproline II Helix Formation. Proteins Struct. Funct. Genet. 2003, 53, 68–75. [Google Scholar] [CrossRef]
- Mikhonin, A.V.; Myshakina, N.S.; Bykov, S.V.; Asher, S.A. UV Resonance Raman Determination of Polyproline II, Extended 2.5 1-Helix, and β-Sheet ψ Angle Energy Landscape in Poly-L-Lysine and Poly-L-Glutamic Acid. J. Am. Chem. Soc. 2005, 127, 7712–7720. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer-Stenner, R.; Eker, F.; Griebenow, K.; Cao, X.; Nafie, L.A. The Conformation of Tetraalanine in Water Determined by Polarized Raman, FT-IR, and VCD Spectroscopy. J. Am. Chem. Soc. 2004, 126, 2768–2776. [Google Scholar] [CrossRef] [PubMed]
- McColl, I.H.; Blanch, E.W.; Hecht, L.; Kallenbach, N.R.; Barron, L.D. Vibrational Raman Optical Activity Characterization of Poly(l-Proline) II Helix in Alanine Oligopeptides. J. Am. Chem. Soc. 2004, 126, 5076–5077. [Google Scholar] [CrossRef] [PubMed]
- Verbaro, D.J.; Mathieu, D.; Toal, S.E.; Schwalbe, H.; Schweitzer-Stenner, R. Ionized Trilysine: A Model System for Understanding the Nonrandom Structure of Poly- l -Lysine and Lysine-Containing Motifs in Proteins. J. Phys. Chem. B 2012, 116, 8084–8094. [Google Scholar] [CrossRef]
- Graf, J.; Nguyen, P.H.; Stock, G.; Schwalbe, H. Structure and Dynamics of the Homologous Series of Alanine Peptides: A Joint Molecular Dynamics/NMR Study. J. Am. Chem. Soc. 2007, 129, 1179–1189. [Google Scholar] [CrossRef]
- Verbaro, D.; Ghosh, I.; Nau, W.M.; Schweitzer-Stenner, R. Discrepancies between Conformational Distributions of a Polyalanine Peptide in Solution Obtained from Molecular Dynamics Force Fields and Amide I′ Band Profiles. J. Phys. Chem. B 2010, 114, 17201–17208. [Google Scholar] [CrossRef]
- Schweitzer-Stenner, R.; Measey, T.J. The Alanine-Rich XAO Peptide Adopts a Heterogeneous Population, Including Turn-like and Polyproline II Conformations. Proc. Natl. Acad. Sci. USA 2007, 104, 6649–6654. [Google Scholar] [CrossRef] [Green Version]
- Eker, F.; Cao, X.; Nafie, L.; Schweitzer-Stenner, R. Tripeptides Adopt Stable Structures in Water. A Combined Polarized Visible Raman, FTIR, and VCD Spectroscopy Study. J. Am. Chem. Soc. 2002, 124, 14330–14341. [Google Scholar] [CrossRef]
- Eker, F.; Griebenow, K.; Schweitzer-Stenner, R. Stable Conformations of Tripeptides in Aqueous Solution Studied by UV Circular Dichroism Spectroscopy. J. Am. Chem. Soc. 2003, 125. [Google Scholar] [CrossRef]
- Rucker, A.L.; Creamer, T.P. Polyproline II Helical Structure in Protein Unfolded States: Lysine Peptides Revisited. Protein Sci. 2002, 11, 980–985. [Google Scholar] [CrossRef]
- Duitch, L.; Toal, S.; Measey, T.J.; Schweitzer-Stenner, R. Triaspartate: A Model System for Conformationally Flexible DDD Motifs in Proteins. J. Phys. Chem. B 2012, 116, 5160–5171. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer-Stenner, R.; Milorey, B.; Schwalbe, H. Randomizing of Oligopeptide Conformations by Nearest Neighbor Interactions between Amino Acid Residues. Biomolecules 2022, 12, 684. [Google Scholar] [CrossRef]
- Oh, K.-I.; Lee, K.-K.; Park, E.-K.; Jung, Y.-S.; Hwang, G.-S.; Cho, M. A Comprehensive Library of Blocked Dipeptides Reveals Intrinsic Backbone Conformational Propensities of Unfolded Proteins. Proteins Struct. Funct. Genet. 2012, 80, 977–990. [Google Scholar] [CrossRef] [PubMed]
- Lumry, R.; Shyamala, R. Enthalpy-Entropy Compensation Phenomena in Water Solutions of Proteins and Small M Olecules: A Ubiquitous Property of Water. Biopolymers 1970, 9, 1125–1227. [Google Scholar] [CrossRef]
- Dunitz, J.D. Win Some, Lose Some: Enthalpy-Entropy Compensation in Weak Intermolecular Interactions. Chem. Biol. 1995, 2, 709–712. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Guo, Q.X. Isokinetic Relationship, Isoequilibrium Relationship, and Enthalpy-Entropy Compensation. Chem. Rev. 2001, 101, 673–695. [Google Scholar] [CrossRef]
- Toal, S.E. Defining Local Order in the Unfolded State Using Short Peptide Model Systems and Spectroscopic Methods: Conformational Biases, Meditation by Solvation and Nearest Neighbor Effects. Ph.D. Thesis, Drexel University, Philadelphia, PA, USA, 2014. [Google Scholar]
- Schweitzer-Stenner, R.; Toal, S.E. Anticooperative Nearest-Neighbor Interactions between Residues in Unfolded Peptides and Proteins. Biophys. J. 2018, 114, 1046–1057. [Google Scholar] [CrossRef]
- Vitalis, A.; Pappu, R.V. ABSINTH: A New Continuum Solvation Model for Simulations of Polypeptides in Aqueous Solutions. J. Comput. Chem. 2009, 30, 673–699. [Google Scholar] [CrossRef] [Green Version]
- Dill, K.A. Additivity Principles in Biochemistry. J. Biol. Chem. 1997, 272, 701–704. [Google Scholar] [CrossRef] [Green Version]
- Andrews, B.; Guerra, J.; Schweitzer-Stenner, R.; Urbanc, B. Do Molecular Dynamics Force Fields Accurately Model Ramachandran Distributions of Amino Acid Residues in Water? Phys. Chem. Chem. Phys. 2022, 24, 3259–3279. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Intrinsically Unstructured Proteins: Re-Assessing the Protein Structure-Function Paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dyson, H.J.; Wright, P.E. Peptide Conformation and Protein Folding. Curr. Opin. Struct. Biol. 1993, 3, 60–65. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Defining Solution Conformations of Small Linear Peptides. Annu. Rev. Biophys. Biophys. Chem. 1991, 20, 519–538. [Google Scholar] [CrossRef] [PubMed]
- Zimm, B.H.; Bragg, J.K. Theory of the Phase Transition between Helix and Random Coil in Polypeptide Chains. J. Chem. Phys. 1959, 31, 526–535. [Google Scholar] [CrossRef] [Green Version]
- Lifson, S.; Roig, A. On the Theory of Helix-Coil Transitions in Polypeptides. J. Chem. Phys. 1961, 34, 1963–1974. [Google Scholar] [CrossRef]




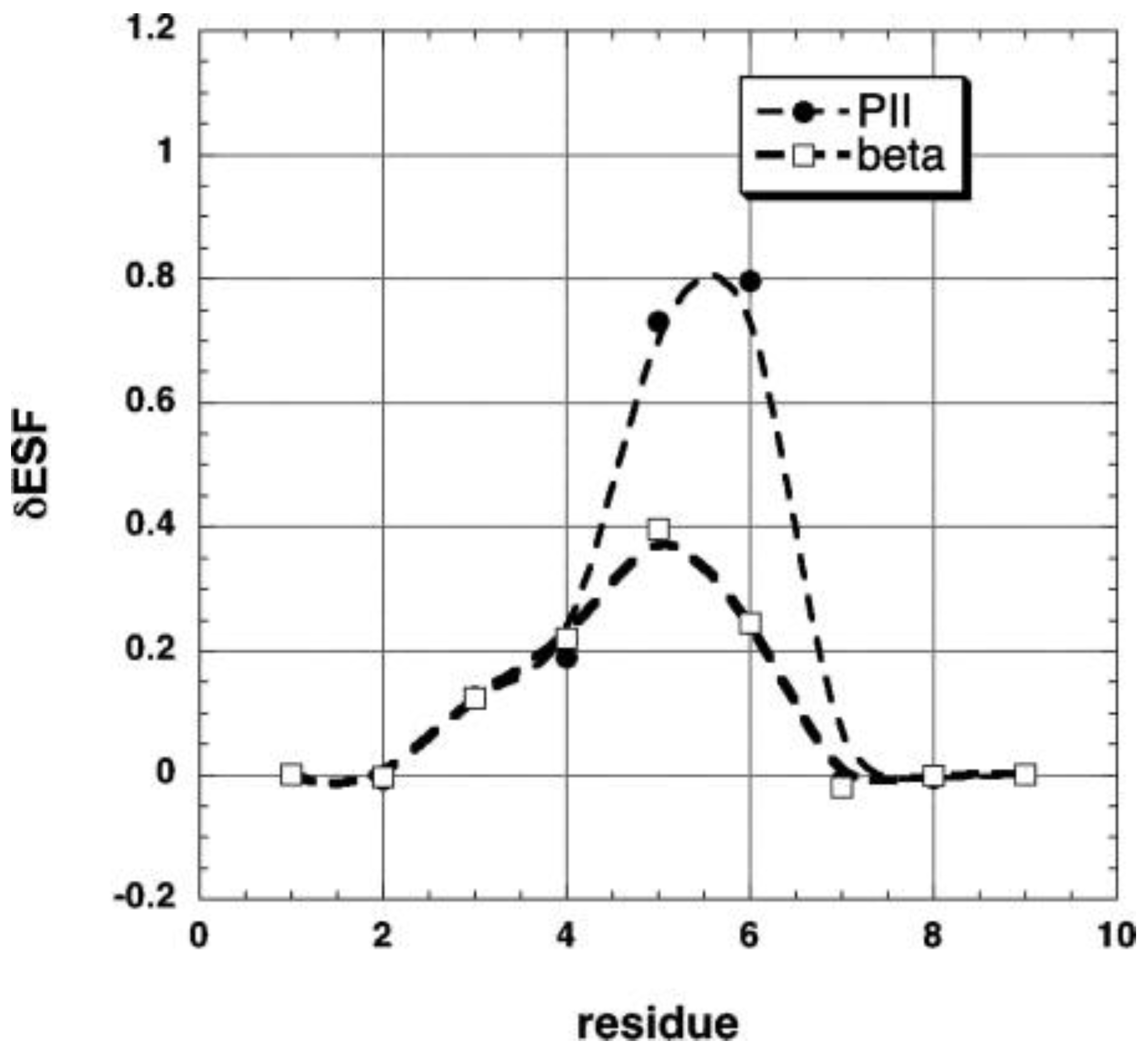

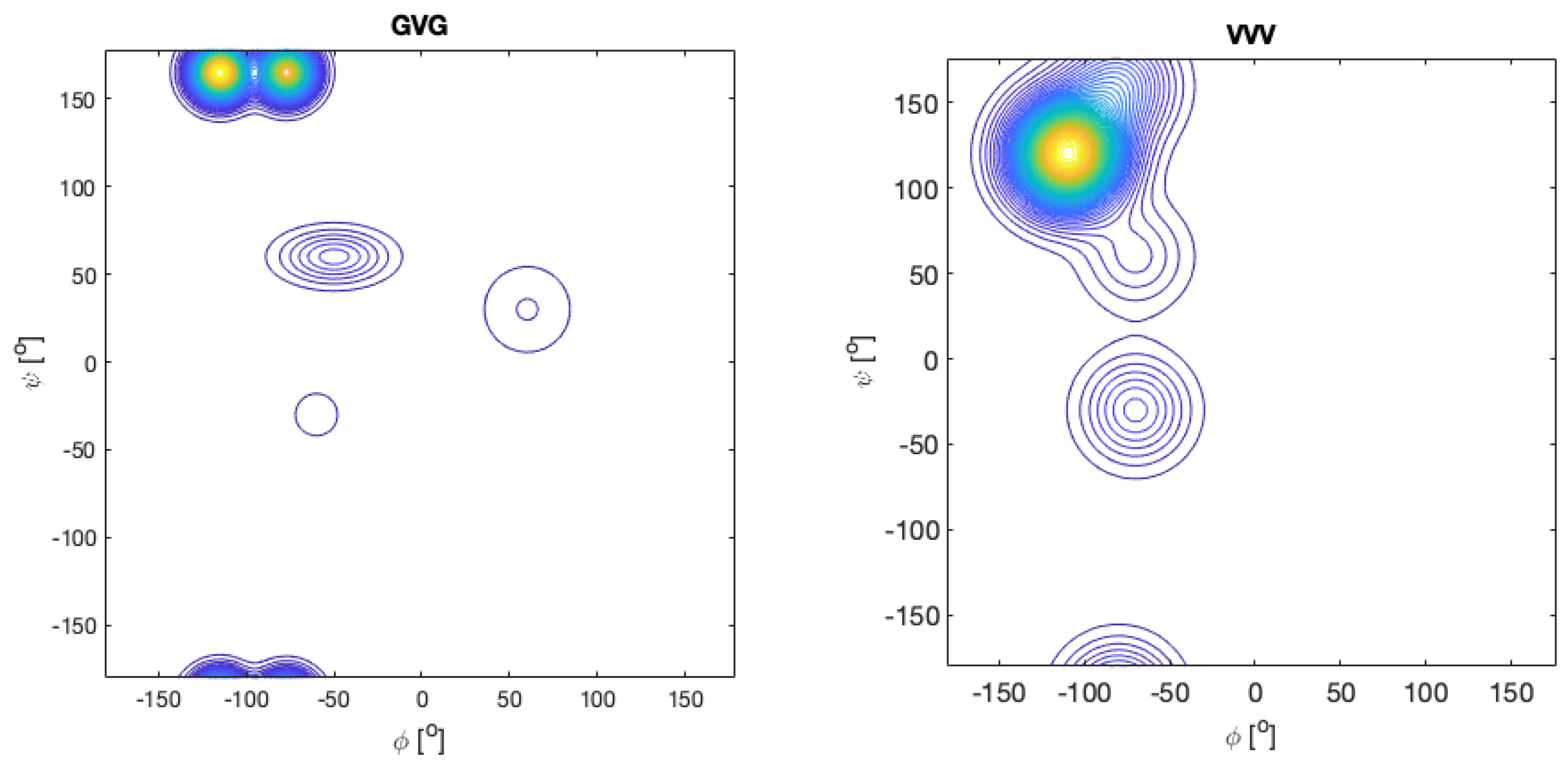
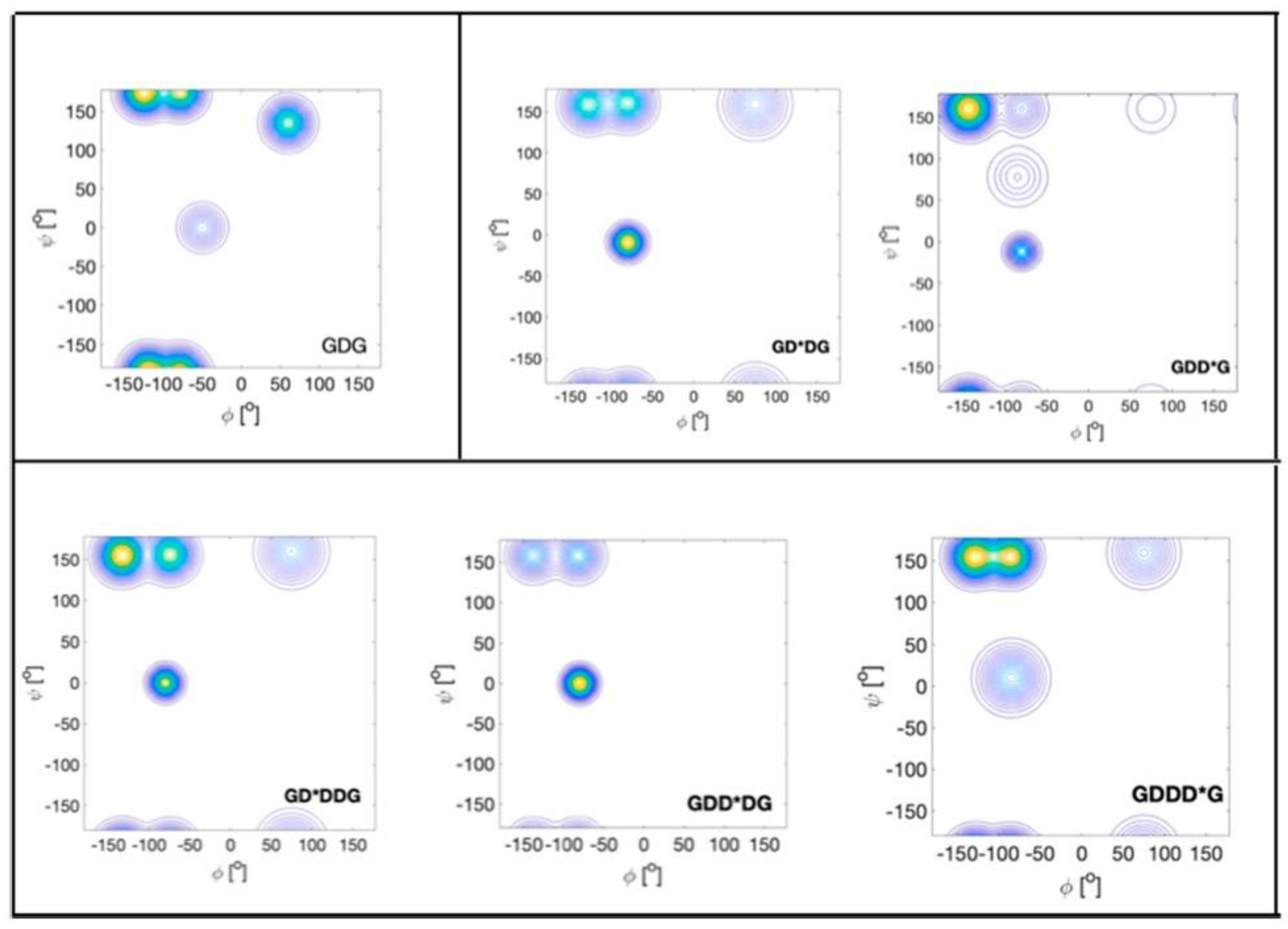
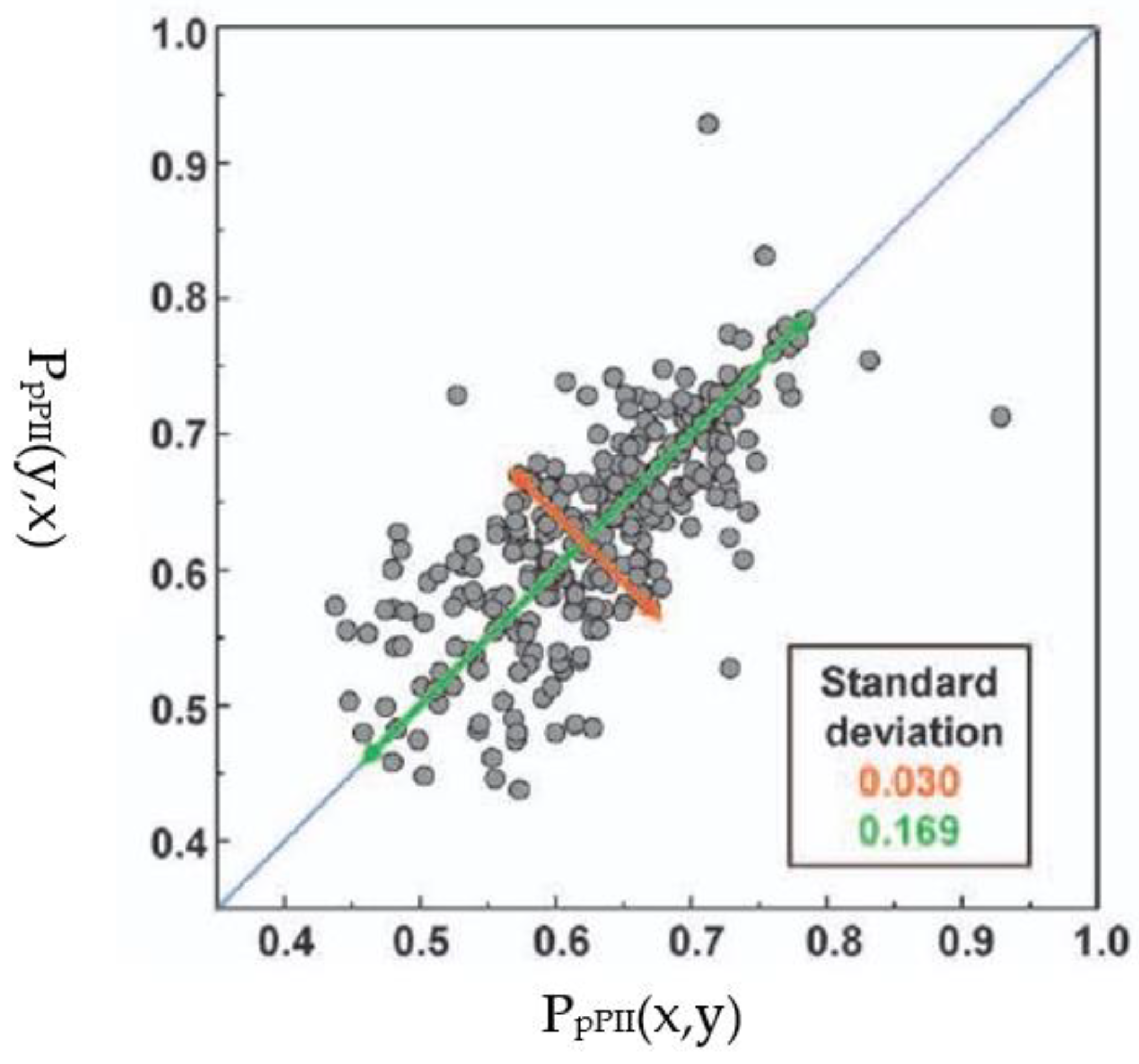
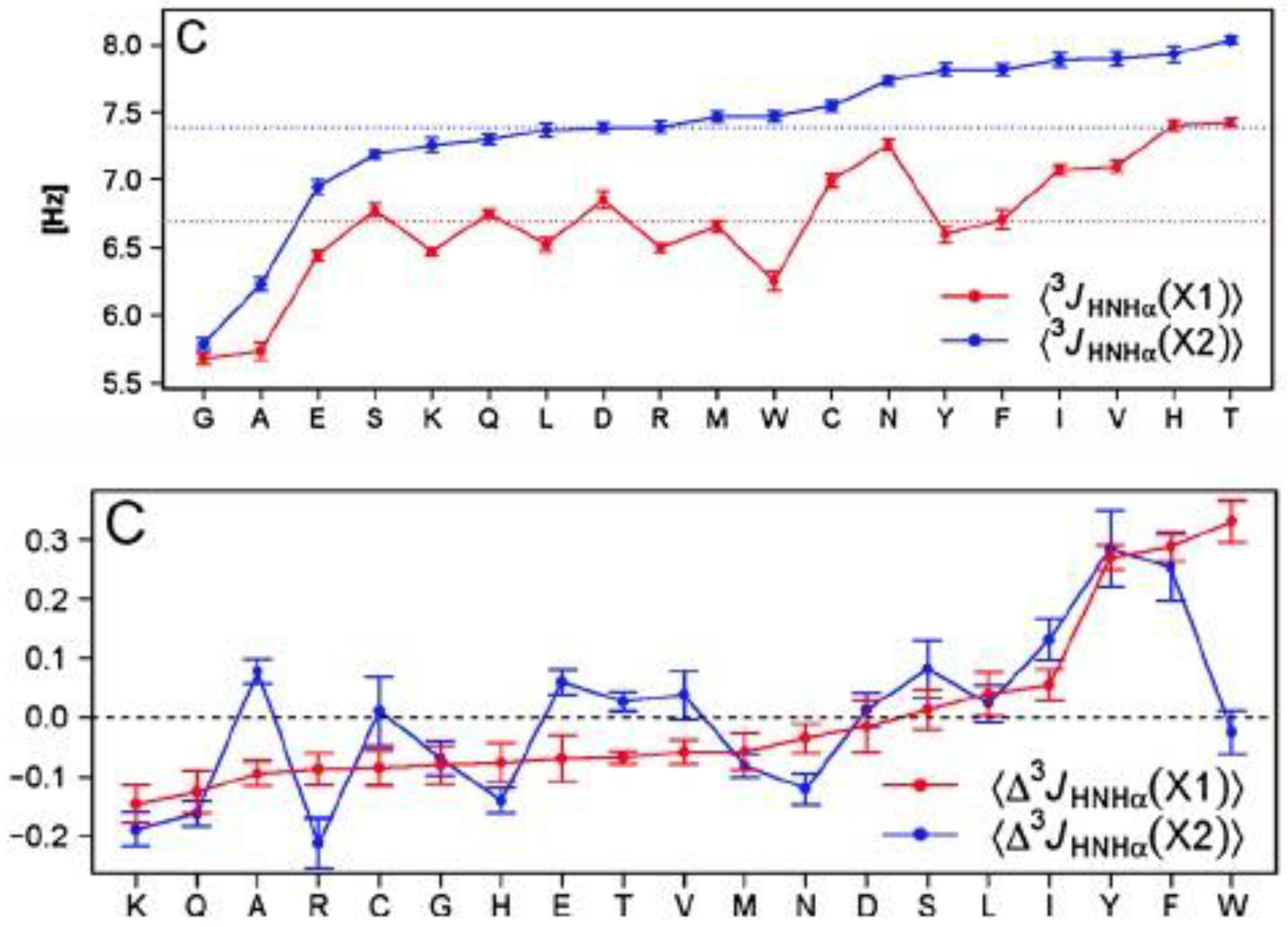
| F | Y | Q | K | V | I | A | N | |
|---|---|---|---|---|---|---|---|---|
| F | 1 | 0.08 | 0.1/0.15 | 0.12/0.16 | 0.21/0.14 | 0.22/0.17 | 0.19/0.15 | 0.19/0.12 |
| Y | 0.08 | 1 | 0.11/0.13 | 0.12/0.14 | 0.21/0.15 | 0.21/0.18 | 0.19/0.12 | 0.19/0.08 |
| Q | 0.10/0.15 | 0.11/0.13 | 1 | 0.09 | 0.21/0.09 | 0.22/0.11 | 0.16/0.07 | 0.18/0.09 |
| K | 0.12/0.16 | 0.12/0.14 | 0.09 | 1 | 0.20/0.09 | 0.20/0.12 | 0.16/0.08 | 0.22/0.09 |
| V | 0.21/0.14 | 0.21/0.15 | 0.21/0.09 | 0.20/0.09 | 1 | 0.09/0.10 | 0.28/0.12 | 0.32/0.11 |
| I | 0.22/0.17 | 0.21/0.18 | 0.22/0.11 | 0.20/0.12 | 0.09/0.10 | 1 | 0.16/0.13 | 0.32/0.13 |
| A | 0.19/0.15 | 0.19/0.12 | 0.16/0.07 | 0.16/0.08 | 0.28/0.12 | 0.16/0.13 | 1 | 0.25/0.09 |
| N | 0.19/0.12 | 0.190.08 | 0.18/0.09 | 0.22/0.09 | 0.32/0.11 | 0.32/0.13 | 0.25/0.09 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schweitzer-Stenner, R. Exploring Nearest Neighbor Interactions and Their Influence on the Gibbs Energy Landscape of Unfolded Proteins and Peptides. Int. J. Mol. Sci. 2022, 23, 5643. https://doi.org/10.3390/ijms23105643
Schweitzer-Stenner R. Exploring Nearest Neighbor Interactions and Their Influence on the Gibbs Energy Landscape of Unfolded Proteins and Peptides. International Journal of Molecular Sciences. 2022; 23(10):5643. https://doi.org/10.3390/ijms23105643
Chicago/Turabian StyleSchweitzer-Stenner, Reinhard. 2022. "Exploring Nearest Neighbor Interactions and Their Influence on the Gibbs Energy Landscape of Unfolded Proteins and Peptides" International Journal of Molecular Sciences 23, no. 10: 5643. https://doi.org/10.3390/ijms23105643
APA StyleSchweitzer-Stenner, R. (2022). Exploring Nearest Neighbor Interactions and Their Influence on the Gibbs Energy Landscape of Unfolded Proteins and Peptides. International Journal of Molecular Sciences, 23(10), 5643. https://doi.org/10.3390/ijms23105643





