Toward Real Real-Space Refinement of Atomic Models
Abstract
:1. Introduction
2. Results
2.1. Gaussian Atomic Model
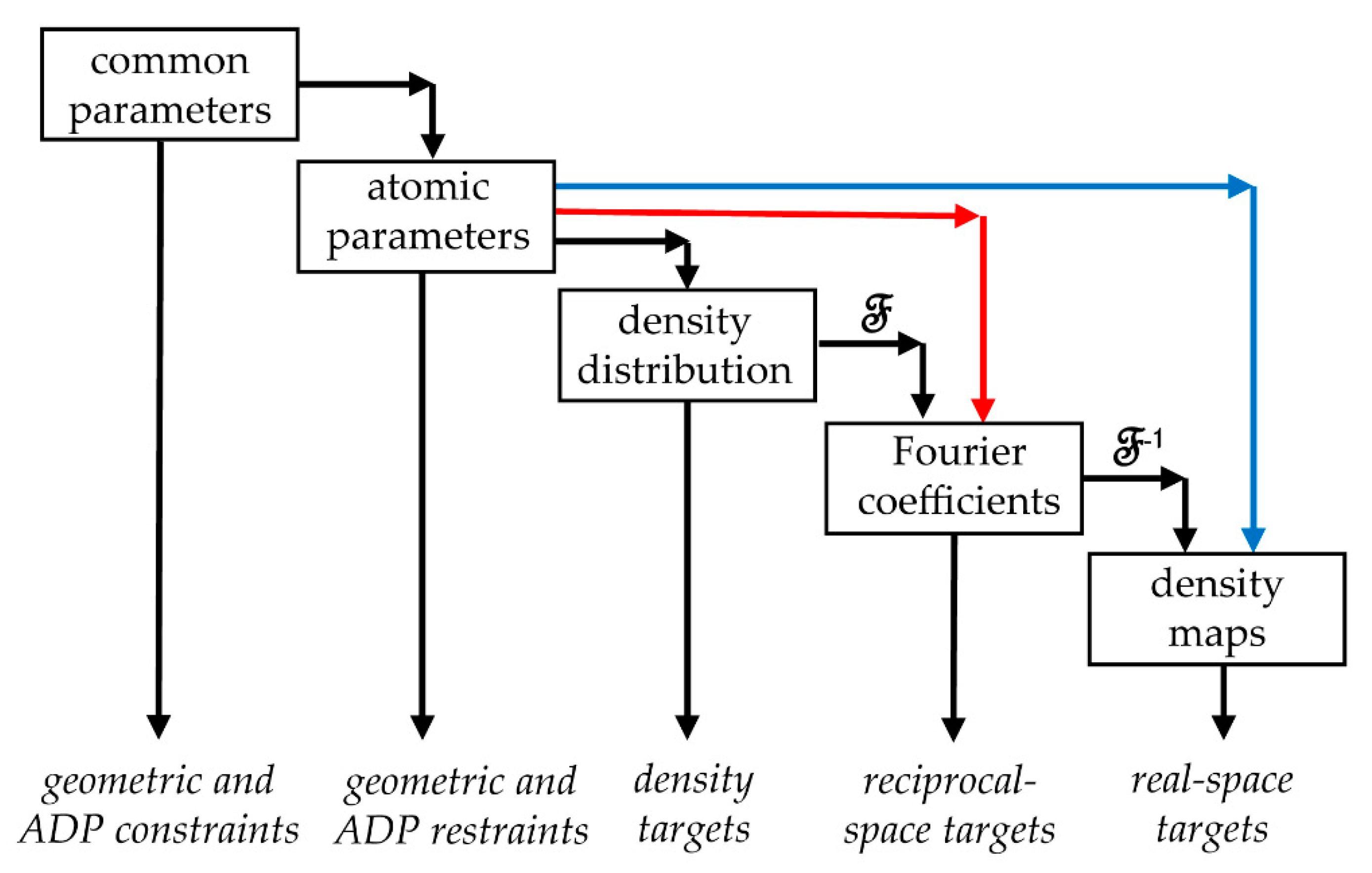
2.2. Schemes of Reciprocal-Space Refinement
2.3. Schemes of Real-Space Refinement
2.4. Map as an Analytic Function
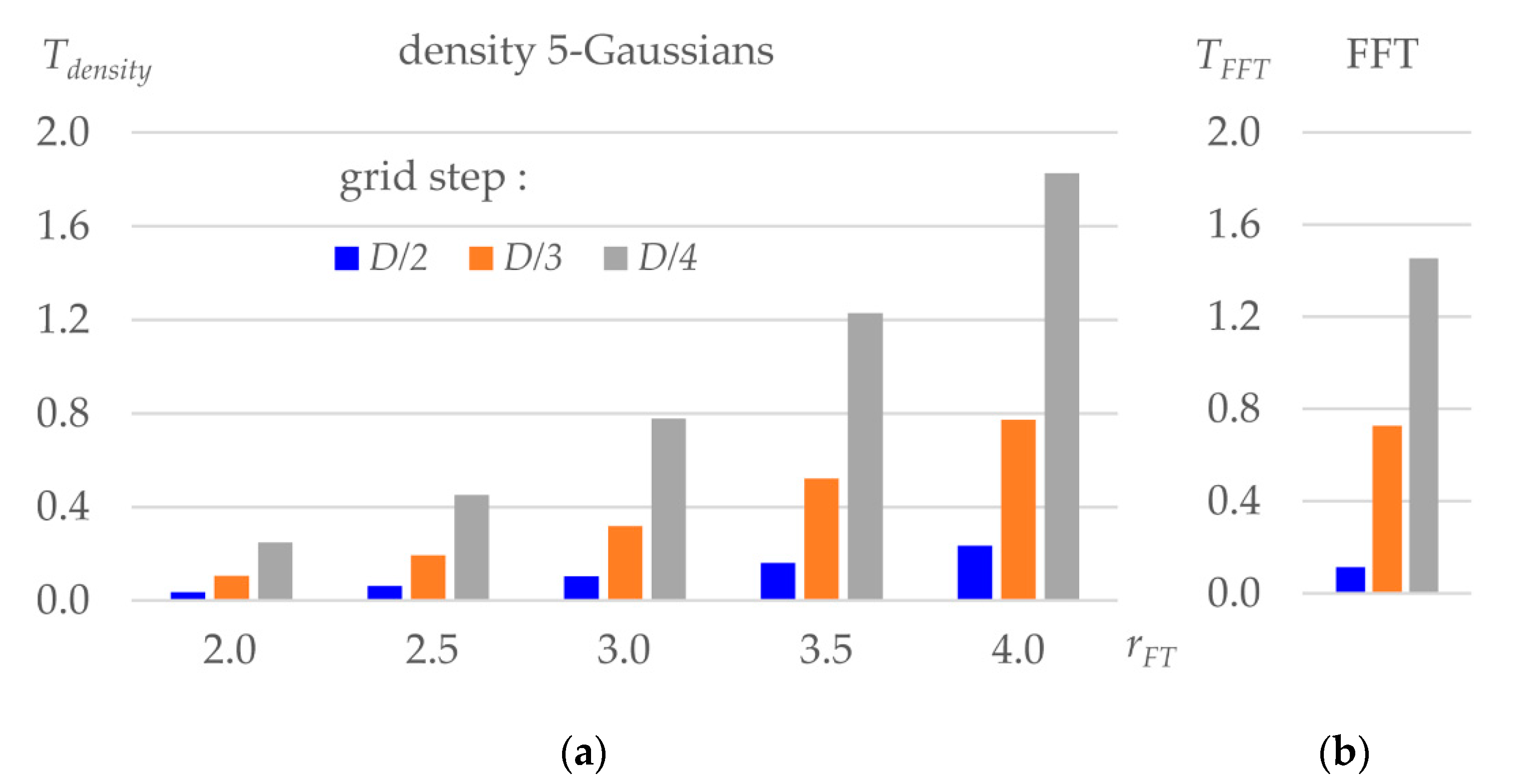
2.5. Comparison of Schemes of Real-Space Refinement
3. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cardone, G.; Heymann, J.B.; Steven, A.C. One number does not fit all: Mapping local variations in resolution in cryo-EM reconstructions. J. Struct. Biol. 2013, 184, 226–236. [Google Scholar] [CrossRef] [Green Version]
- Urzhumtsev, A.G.; Lunin, V.Y. Introduction to crystallographic refinement of macromolecular atomic models. Crystallogr. Rev. 2019, 25, 164–262. [Google Scholar] [CrossRef]
- Brown, A.; Long, F.; Nicholls, R.A.; Toots, I.; Emsley, P.; Murshudov, G. Tools for molecular model building and refinement into electron cryo-microscopy reconstructions. Acta Crystallogr. 2015, D71, 136–153. [Google Scholar]
- Lunin, V.Y.; Afonine, P.V.; Urzhumtsev, A.G. Likelihood-based refinement. I. Irremovable model errors. Acta Crystallogr. 2002, A58, 270–282. [Google Scholar] [CrossRef] [PubMed]
- Kostrewa, D. Bulk Solvent Correction: Practical Application and Effects in Reciprocal and Real Space. Jt. CCP4 ESF-EACBM Newsl. Protein Crystallogr. 1995, 34, 9–22. [Google Scholar]
- Afonine, P.V.; Adams, P.D.; Sobolev, O.V.; Urzhumtsev, A. A mosaic bulk-solvent model improves density maps and the fit between model and data. bioRxiv. 2021. Available online: https://www.biorxiv.org/content/10.1101/2021.12.09.471976v1.full (accessed on 6 October 2022).
- Afonine, P.V.; Urzhumtsev, A.; Adams, P.D. On the analysis of residual density distribution on an absolute scale. Comput. Cryst. Newsl. 2012, 3, 43–46. [Google Scholar]
- Palmer, C.M.; Aylett, C.H.S. Real space in cryo-EM: The future is local. Acta Crystallogr. 2022, D78, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Lunin, V.Y.; Urzhumtsev, A. Program construction for macromolecule atomic model refinement based on the fast Fourier transform and fast differentiation algorithms. Acta Crystallogr. 1985, A41, 327–333. [Google Scholar] [CrossRef]
- Urzhumtsev, A.G.; Lunin, V.Y. Fast differentiation algorithm and efficient calculation of the exact matrix of the second derivatives. Acta Crystallogr. 2001, A57, 451–460. [Google Scholar] [CrossRef] [Green Version]
- Diamond, R. A real-space procedure for proteins. Acta Crystallogr. 1971, A27, 436–451. [Google Scholar] [CrossRef]
- Abagyan, R.A.; Totrov, M.M.; Kuznetsov, D.A. Icm—A new method for protein modeling and design—Applications to docking and structure prediction from the distorted native conformation. J. Comput. Chem. 1994, 15, 488–506. [Google Scholar] [CrossRef]
- Rice, L.M.; Brünger, A.T. Torsion angle dynamics: Reduced variable conformational sampling enhances crystallographic structure refinement. Proteins Struct. Funct. Genet. 1994, 19, 277–290. [Google Scholar] [CrossRef] [PubMed]
- Afonine, P.V.; Grosse-Kunstleve, R.W.; Urzhumtsev, A.G.; Adams, P.D. Automatic multiple-zone rigid-body refinement with a large convergence radius. J. Appl. Crystallogr. 2009, 42, 607–615. [Google Scholar] [CrossRef]
- Merritt, E.A. To B or not to B: A question of resolution? Acta Crystallogr. 2012, D68, 468–477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cruickshank, D.W.J. The analysis of the anisotropic thermal motion of molecules in crystals. Acta Crystallogr. 1956, 9, 754–756. [Google Scholar] [CrossRef]
- Schomaker, V.; Trueblood, K.N. On the rigid-body motion of molecules in crystals. Acta Crystallogr. 1968, B24, 63–76. [Google Scholar] [CrossRef]
- Doyle, P.A.; Turner, P.S. Relativistic Hartree-Fock X-ray and electron scattering factors. Acta Crystallogr. 1968, A24, 390–397. [Google Scholar] [CrossRef]
- Agarwal, R.C. A new least-squares refinement technique based on the fast Fourier transform algorithm. Acta Crystallogr. 1978, A41, 327–333. [Google Scholar] [CrossRef]
- Waasmaier, D.; Kirfel, A. New analytical scattering-factor functions for free atoms and ions. Acta Crystallogr. 1985, A34, 791–809. [Google Scholar] [CrossRef]
- Peng, L.-M. Electron atomic scattering factors and scattering potentials of crystals. Micron 1999, 30, 625–648. [Google Scholar] [CrossRef]
- Grosse-Kunstleve, R.W.; Sauter, N.K.; Adams, P.D. CCTBX news. Newsl. IUCr Comm. Crystallogr. Comput. 2004, 3, 22–31. [Google Scholar]
- Brown, P.J.; Fox, A.G.; Maslen, E.N.; O’Keefe, M.A.; Willis, B.T.M. Intensity of diffracted intensities. In International Tables for X-ray Crystallography; Prince, E., Ed.; Springer: Dordrecht, The Netherlands, 2006; Volume C, pp. 554–595. [Google Scholar]
- Marques, M.A.; Purdy, M.D.; Yeager, M. CryoEM maps are full of potential. Curr. Opin. Struct. Biol. 2019, 58, 214–223. [Google Scholar] [CrossRef]
- Carugo, O. B-factor accuracy in protein crystal structures. Acta Crystallogr. 2022, D78, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Masmaliyeva, R.C.; Murshudov, G.N. Analysis and validation of macromolecular B values. Acta Crystallogr. 2019, D75, 505–518. [Google Scholar] [CrossRef] [PubMed]
- Sayre, D. The Calculation of Structure Factors by Fourier Summation. Acta Crystallogr. 1951, 4, 327–333. [Google Scholar] [CrossRef]
- Ten Eyck, L.F. Efficient structure-factor calculation for large molecules by the fast Fourier transform. Acta Crystallogr. 1977, A33, 486–492. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An algorithm for machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Navaza, J. On the computation of structure factors by FFT techniques. Acta Crystallogr. 2002, A58, 568–573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afonine, P.V.; Urzhumtsev, A. On a fast and accurate calculation of structure factors at a subatomic resolution. Acta Crystallogr. 2004, A60, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Rossmann, M.G. Fitting atomic models into electron-microscopy maps. Acta Crystallogr. 2000, D56, 1341–1349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossmann, M.G.; Bernal, R.; Pletnev, S.V. Combining electron microscopic with x-ray crystallographic structures. J. Struct. Biol. 2001, 136, 190–200. [Google Scholar] [CrossRef] [Green Version]
- Emsley, P.; Cowtan, K. Coot: Model-building tools for molecular graphics. Acta Crystallogr. 2004, D60, 2126–2132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afonine, P.V.; Poon, B.K.; Read, R.J.; Sobolev, O.V.; Terwilliger, T.C.; Urzhumtsev, A.G.; Adams, P.D. Real-space refinement in PHENIX for cryo-EM and crystallography. Acta Crystallogr. 2018, D74, 531–544. [Google Scholar]
- Lunin, V.Y.; Urzhumtsev, A. Improvement of protein phases by coarse model modification. Acta Crystallogr. 1984, A40, 269–277. [Google Scholar] [CrossRef]
- Mooij, W.T.M.; Hartshorn, M.J.; Tickle, I.J.; Sharff, A.J.; Verdonk, M.L.; Jhoti, H. Automated protein-ligand crystallography for structure-based drug design. ChemMedChem 2006, 1, 827–838. [Google Scholar] [CrossRef] [PubMed]
- DiMaio, F.; Song, Y.; Li, X.; Brunner, M.J.; Xu, C.; Conticello, V.; Egelman, E.; Marlovits, T.; Cheng, Y.; Baker, D. Atomic-accuracy models from 4.5-Å cryo-electron microscopy data with density-guided iterative local refinement. Nat. Methods 2015, 12, 361–365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chapman, M.S. Restrained real-space macromolecular atomic refinement using a new resolution-dependent electron-density function. Acta Crystallogr. 1995, A51, 69–80. [Google Scholar] [CrossRef]
- Chapman, M.S.; Trzynka, A.; Chapman, B.K. Atomic modeling of cryo-electron microscopy reconstructions—Joint refinement of model and imaging parameters. J. Struct. Biol. 2013, 182, 10–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afonine, P.V.; Lunin, V.Y.; Muzet, N.; Urzhumtsev, A. On the possibility of the observation of valence electron density for individual bonds in proteins in conventional difference maps. Acta Crystalogr. 2004, D60, 260–274. [Google Scholar] [CrossRef] [Green Version]
- Urzhumtsev, A.; Urzhumtseva, L.; Lunin, V.Y. Direct calculation of cryo EM and crystallographic model maps for real-space refinement. bioRxiv 2022. Available online: https://doi.org/10.1101/2022.07.17.500345 (accessed on 6 October 2022). [CrossRef]
- Urzhumtsev, A.G.; Lunin, V.Y. Analytic representation of inhomogeneous-resolution maps of three-dimensional scalar fields. bioRxiv 2022. Available online: https://doi.org/10.1101/2022.03.28.486044 (accessed on 6 October 2022). [CrossRef]
- Simonetti, A.; Marzi, S.; Fabbretti, A.; Myasnikov, A.G.; Hazemann, I.; Jenner, L.; Urzhumtsev, A.; Gualerzi, C.O.; Klaholz, B.P. Crystal structure of the protein core of translation initiation factor IF2 in apo, GTP and GDP forms. Acta Crystallogr. 2013, D69, 925–933. [Google Scholar]
- Schrödinger, L.; DeLano, W.L. Pymol. Version 2.5.2. 2020. Available online: http://www.pymol.org (accessed on 6 October 2022).
- Ten Eyck, L.F. Crystallographic fast Fourier transforms. Acta Crystallogr. 1973, A33, 183–191. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urzhumtsev, A.G.; Lunin, V.Y. Toward Real Real-Space Refinement of Atomic Models. Int. J. Mol. Sci. 2022, 23, 12101. https://doi.org/10.3390/ijms232012101
Urzhumtsev AG, Lunin VY. Toward Real Real-Space Refinement of Atomic Models. International Journal of Molecular Sciences. 2022; 23(20):12101. https://doi.org/10.3390/ijms232012101
Chicago/Turabian StyleUrzhumtsev, Alexandre G., and Vladimir Y. Lunin. 2022. "Toward Real Real-Space Refinement of Atomic Models" International Journal of Molecular Sciences 23, no. 20: 12101. https://doi.org/10.3390/ijms232012101
APA StyleUrzhumtsev, A. G., & Lunin, V. Y. (2022). Toward Real Real-Space Refinement of Atomic Models. International Journal of Molecular Sciences, 23(20), 12101. https://doi.org/10.3390/ijms232012101






