Ab Initio Study of Carrier Mobility, Thermodynamic and Thermoelectric Properties of Kesterite Cu2ZnGeS4
Abstract
1. Introduction
2. Results and Discussion
2.1. Electronic and Structural Properties
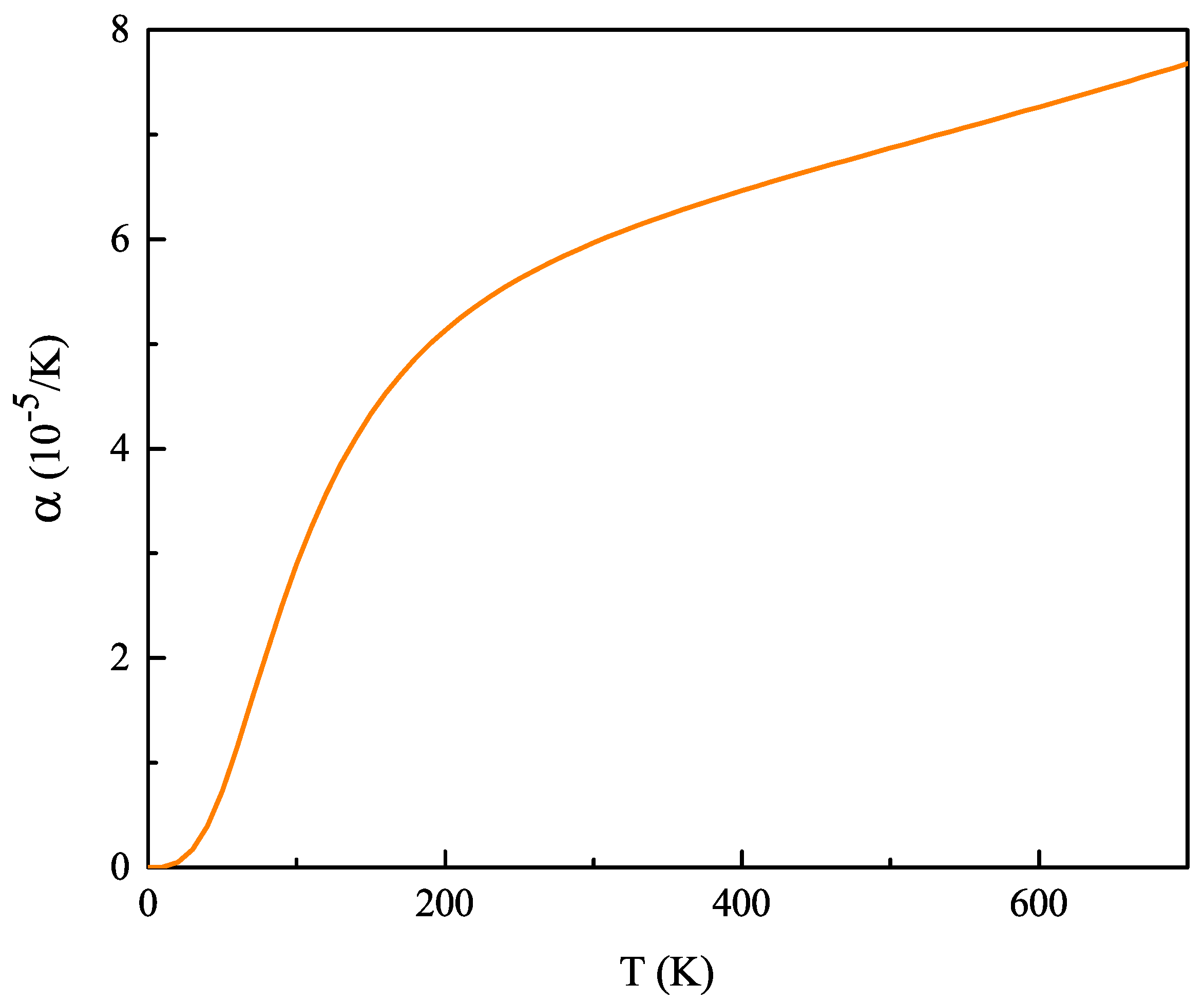
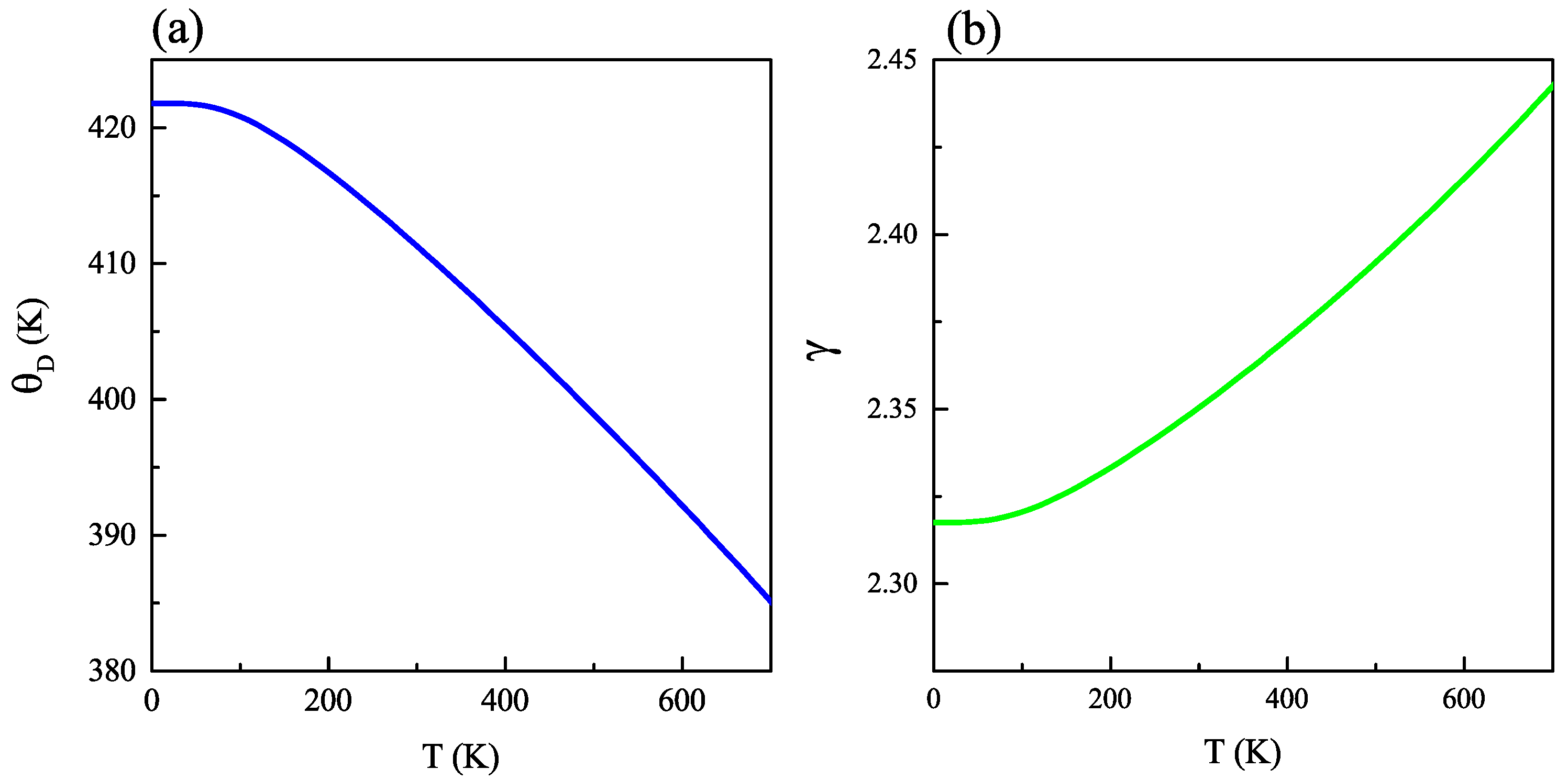
2.2. Thermodynamic Properties
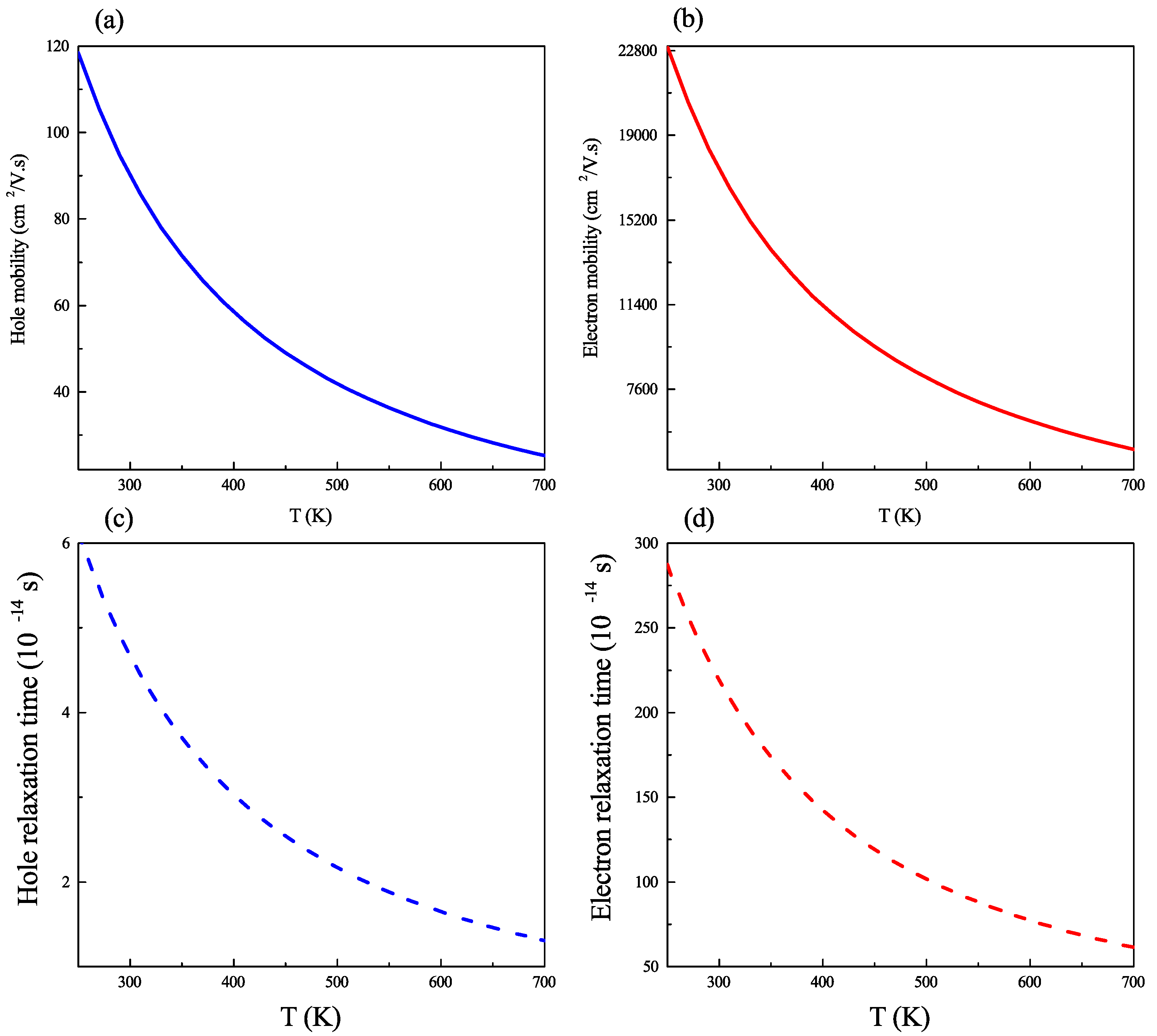
2.3. Carrier Mobility and Relaxation Time
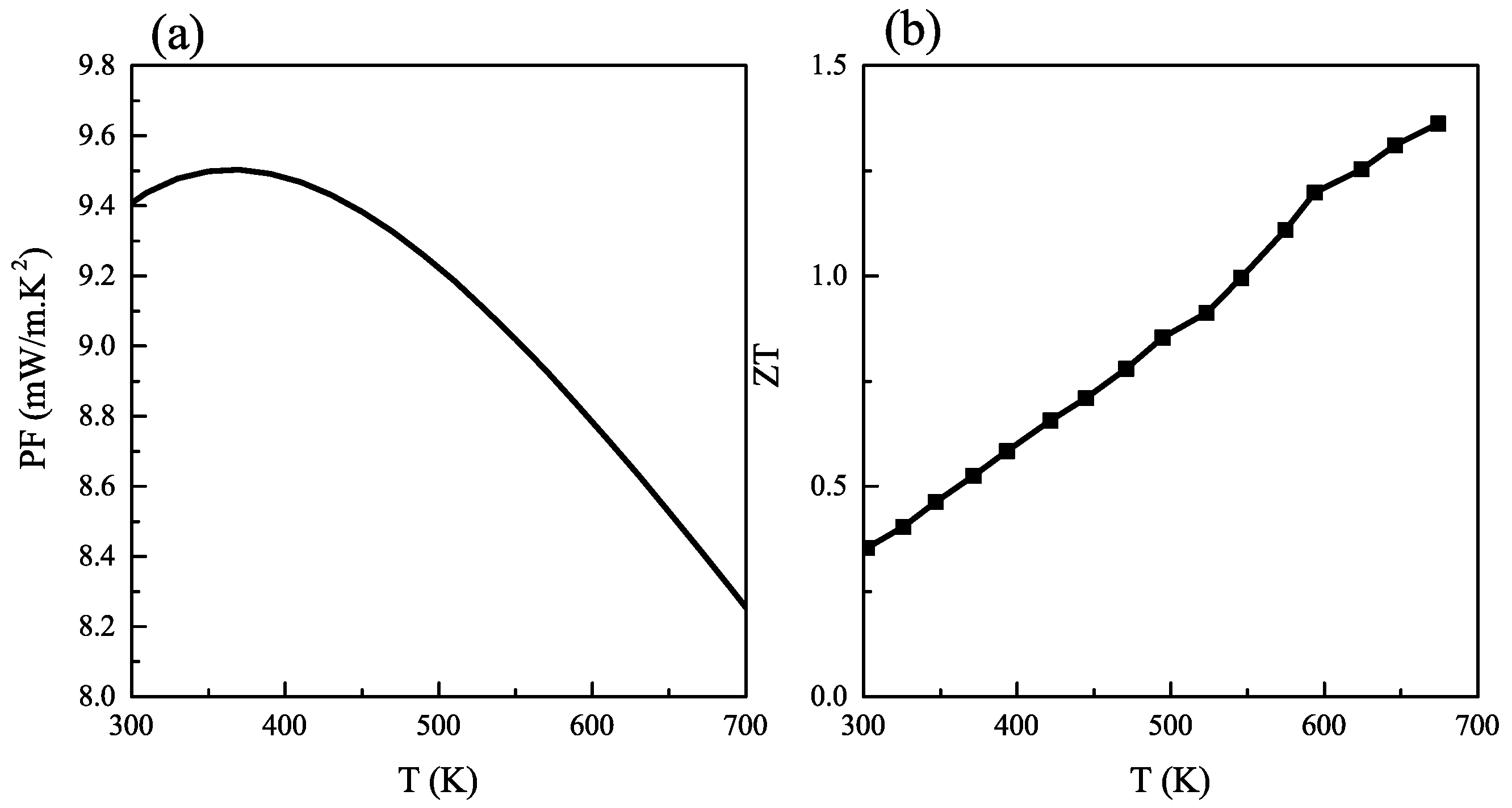
2.4. Thermoelectric Properties
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Siebentritt, S.; Schorr, S. Kesterites-a Challenging Material for Solar Cells. Prog. Photovoltaics Res. Appl. 2012, 20, 512–519. [Google Scholar] [CrossRef]
- Umehara, M.; Tajima, S.; Takeda, Y.; Motohiro, T. Wide bandgap Cu2ZnSn1-xGexS4 fabricated on transparent conductive oxide-coated substrates for top-cells of multi-junction solar cells. J. Alloys Compd. 2016, 689, 713–717. [Google Scholar] [CrossRef]
- Vermang, B.; Brammertz, G.; Meuris, M.; Schnabel, T.; Ahlswede, E.; Choubrac, L.; Harel, S.; Cardinaud, C.; Arzel, L.; Barreau, N.; et al. Wide band gap kesterite absorbers for thin film solar cells: Potential and challenges for their deployment in tandem devices. Sustain. Energy Fuels 2019, 3, 2246–2259. [Google Scholar] [CrossRef]
- Guc, M.; Lähderanta, E.; Hajdeu-Chicarosh, E.; Levcenko, S.; Shakhov, M.A.; Zakharchuk, I.; Arushanov, E.; Lisunov, K.G. Mechanisms of charge transfer and electronic properties of Cu2ZnGeS4 from investigations of the high-field magnetotransport. Sci. Rep. 2017, 7, 10685. [Google Scholar] [CrossRef]
- Shin, D.; Saparov, B.; Mitzi, D.B. Defect Engineering in Multinary EarthAbundan Chalcogenide Photovoltaic Materials. Adv. Energy Mater. 2017, 7, 1602366. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Zhang, P.; Yuan, X.; Huang, F.; Zhang, W. Structural properties and quasiparticle band structures of Cu-based quaternary semiconductors for photovoltaic applications. J. Appl. Phys. 2012, 111, 063709. [Google Scholar] [CrossRef]
- Khadka, D.B.; Kim, J. Study of Structural and Optical Properties of Kesterite Cu2ZnGeX4 (X = S, Se) Thin Films Synthesized by Chemical Spray Pyrolysis. CrystEngComm 2013, 15, 10500. [Google Scholar] [CrossRef]
- Huang, L.; Deng, H.; He, J.; Chen, L.; Yang, P.; Chu, J. Study of Structural and Optical Properties of Cu2ZnSnS4 and Cu2ZnGeS4 Thin Films Synthesized by Sulfurization of Stacked Metallic Layers. Mater. Sci. Forum 2015, 814, 44–48. [Google Scholar] [CrossRef]
- García-Llamas, E.; Merino, J.M.; Serna, R.; Fontané, X.; Victorov, I.A.; Pérez-Rodríguez, A.; León, M.; Bodnar, I.V.; Izquierdo-Roca, V.; Caballero, R. Wide band-gap tuning Cu2ZnSn1-xGexS4 single crystals: Optical and vibrational properties. Sol. Energy Mater. Sol. Cells 2016, 158, 147–153. [Google Scholar] [CrossRef]
- Schnabel, T.; Seboui, M.; Ahlswede, E. Band Gap Tuning of Cu2ZnGeSxSe4-x Absorbers for Thin-Film Solar Cells. Energies 2017, 10, 1813. [Google Scholar] [CrossRef]
- Tsuji, K.; Maeda, T.; Wada, T. Optical properties and electronic structures of Cu2ZnSnS4, Cu2ZnGeS4, and Cu2Zn(Sn,Ge)S4 and Cu2Zn(SnGe)Se4 solid solutions. Japn J. Appl. Phys. 2018, 57, 08RC21. [Google Scholar] [CrossRef]
- Zeier, W.G.; Zhu, H.; Gibbs, Z.M.; Ceder, G.; Tremel, W.; Snyder, G.J. Band convergence in the non-cubic chalcopyrite compounds Cu2MGeSe4. J. Mater. Chem. C 2014, 2, 10189. [Google Scholar] [CrossRef]
- Kodan, N.; Auluck, S.; Mehta, B.R. A DFT Study of the Electronic and Optical Properties of a Photovoltaic Absorber Material Cu2ZnGeS4 Using GGA and MBJ Exchange Correlation Potentials. J. Alloys Compd. 2016, 675, 236–243. [Google Scholar] [CrossRef]
- Mesbahi, M.; Serdouk, F.; Benkhedir, M. A DFT Study of the Electronic and Optical Properties of Kesterite Phase of Cu2ZnGeS4 Using GGA, TB-MBJ, and U Exchange Correlation Potentials. Acta Phys. Pol. A 2018, 134, 358–361. [Google Scholar] [CrossRef]
- Hamdaoui, J.E.; El-Yadri, M.; Lakaal, K.; Kria, M.; Courel, M.; Ojeda, M.; Pérez, L.M.; Laroze, D.; Feddi, E. Ab initio study on electronic and optical properties of Cu2NiGeS4 for photovoltaic applications. Solar Energy 2022, 237, 333–339. [Google Scholar] [CrossRef]
- Wexler, R.B.; Gautam, G.S.; Carter, E.A. Exchange-correlation functional challenges in modeling quaternary chalcogenides. Phys. Rev. B 2020, 102, 054101. [Google Scholar] [CrossRef]
- Hamdaoui, J.E.; El-Yadri, M.; Farkous, M.; Kria, M.; Courel, M.; Ojeda, M.; Pérez, L.M.; Tiutiunnyk, A.; Laroze, D.; Feddi, E.M. Strain Effects on the Electronic and Optical Properties of Kesterite Cu2ZnGeX4 (X = S, Se): First-Principles Study. Nanomaterials 2021, 11, 2692. [Google Scholar] [CrossRef]
- Kovacic, Z.; Blaz, L.; Hus, M. Photocatalytic CO2 reduction: A review of ab initio mechanism, kinetics, and multiscale modeling simulations. ACS Catal. 2020, 10, 14984–15007. [Google Scholar] [CrossRef]
- Ješić, D.; Jurković, D.L.; Pohar, A.; Suhadolnik, L.; Likozar, B. Engineering photocatalytic and photoelectrocatalytic CO2 reduction reactions: Mechanisms, intrinsic kinetics, mass transfer resistances, reactors and multi-scale modelling simulations. Chem. Eng. J. 2021, 407, 126799. [Google Scholar] [CrossRef]
- Kamal, K.M.; Narayan, R.; Chandran, N.; Popović, S.; Nazrulla, M.A.; Kovač, J.; Vrtovec, N.; Bele, M.; Hodnik, N.; Kržmanc, M.M.; et al. Synergistic enhancement of photocatalytic CO2 reduction by plasmonic Au nanoparticles on TiO2 decorated N-graphene heterostructure catalyst for high selectivity methane production. Appl. Catal. Environ. 2022, 307, 121181. [Google Scholar] [CrossRef]
- Ratz, T.; Raty, J.-Y.; Brammertz, G.; Vermang, B.; Nguyen, N.D. Optoelectronic properties and solar cell efficiency modelling of Cu2ZnXS4 (X = Sn,Ge,Si) kesterites. J. Phys. Energy 2021, 3, 035005. [Google Scholar] [CrossRef]
- Heinrich, C.P.; Day, T.W.; Zeier, W.G.; Snyder, G.J.; Tremel, W. Effect of isovalent substitution on the thermoelectric properties of the Cu2ZnGeSe4-xSx series of solid solutions. J. Am. Chem. Soc. 2014, 136, 442. [Google Scholar] [CrossRef]
- Yoshijama, H.; Kaneko, H. Design of thermoelectric materials with high electrical conductivity, high Seebeck coefficient, and low thermal conductivity. Anal. Sci. Adv. 2020, 2, 289–294. [Google Scholar] [CrossRef]
- Shibuya, T.; Skelton, J.M.; Jackson, A.J.; Yasuoka, K.; Togo, A.; Tanaka, I.; Walsh, A. Suppression of lattice thermal conductivity by mass-conserving cation mutation in multi-component semiconductors. APL Mater. 2016, 4, 104809. [Google Scholar] [CrossRef]
- Ibáñez, M.; Zamani, R.; LaLonde, A.; Cadavid, D.; Li, W.; Shavel, A.; Arbiol, J.; Morante, J.R.; Gorsse, S.; Snyder, G.J.; et al. Cu2ZnGeSe4 nanocrystals: Synthesis and thermoelectric properties. J. Am. Chem. Soc. 2012, 134, 4060–4063. [Google Scholar] [CrossRef]
- Shi, X.Y.; Huang, F.Q.; Liu, M.L.; Chen, L.D. Thermoelectric properties of tetrahedrally bonded wide-gap stannite compounds Cu2ZnSn1-xInxSe4. Appl. Phys. Lett. 2009, 94, 122103. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, Y.; Chen, Y.; Wang, B.; Wang, Y.; Zhou, J.; Liang, Z. Hot-Injection Synthesis of Cu-Doped Cu2ZnSnSe4 Nanocrystals to Reach Thermoelectric ZT of 0.70 at 450 ∘C. ACS Appl. Mater. Interfaces 2015, 7, 24403–24408. [Google Scholar] [CrossRef]
- Adachi, S. Earth-Abundant Materials for Solar Cells: Cu2–II–IV–VI4 Semiconductors; Wiley: Chichester, UK, 2015. [Google Scholar]
- Yang, Y.; Ma, L.; Gan, G.-Y.; Wang, W.; Tang, B.-Y. Investigation of thermodynamic properties of high entropy (TaNbHfTiZr)C and (TaNbHfTiZr)N. J. Alloys Compd. 2019, 788, 1076–1083. [Google Scholar] [CrossRef]
- Available online: https://www.msesupplies.com/pages/list-of-thermal-expansion-coefficients-cte-for-natural-and-engineered-materials (accessed on 2 May 2022).
- Yang, X.X.; Zhou, Z.F.; Wang, Y.; Jiang, R.; Zheng, W.T.; Sun, C.Q. Raman spectroscopy determination of the Debye temperature and atomic cohesive energy of CdS, CdSe, Bi2Se3, and Sb2Te3 nanostructures. J. Appl. Phys. 2012, 112, 083508. [Google Scholar] [CrossRef]
- Bao, W.; Liu, D.; Duan, Y. A first-principles prediction of anisotropic elasticity and thermal properties of potential superhard WB3. Ceram. Int. 2018, 44, 14053–14062. [Google Scholar] [CrossRef]
- Grüneisen, E. Theorie des festen Zustandes einatomiger Elemente. Ann. Phys. 1912, 344, 257–306. [Google Scholar] [CrossRef]
- MacDonald, D.K.C.; Roy, S.K. Vibrational Anharmonicity and Lattice Thermal Properties. II. Phys. Rev. 1995, 97, 673–676. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, J.; Yang, Z.; Yu, Y. Heat capacity and thermal expansion of metal crystalline materials based on dynamic thermal vibration. Comput. Mech. 2019, 63, 971–984. [Google Scholar] [CrossRef]
- Petit, A.-T.; Dulong, P.-L. Recherches sur quelques points importants de la Theorie de la Chaleur. Ann. Chim. Phys. 1819, 10, 395–413. [Google Scholar]
- Bardeen, J.; Shockley, W. Deformation potentials and mobilities in nonpolar crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Liu, H.-R.; Chen, S.; Zhai, Y.-T.; Xiang, H.J.; Gong, X.G.; Wei, S.-H. Firstprinciples study on the effective masses of zinc-blend-derived Cu2Zn-IV-VI4 (IV = Sn, Ge, Si and VI = S, Se). J. Appl. Phys. 2012, 112, 093717. [Google Scholar] [CrossRef]
- Vukmirović, N. Calculations of electron mobility in II-VI semiconductors. Phys. Rev. B 2021, 104, 085203. [Google Scholar] [CrossRef]
- Anselm, A. Introduction to Semiconductor Theory; Mir: Moscow, Russia, 1981. [Google Scholar]
- León, M.; Levcenko, S.; Serna, R.; Gurieva, G.; Nateprov, A.; Merino, J.M.; Friedrich, E.J.; Fillat, U.; Schorr, S.; Arushanov, E. Optical constants of Cu2ZnGeS4 bulk crystals. J. Appl. Phys. 2010, 108, 093502. [Google Scholar] [CrossRef]
- Slack, G.A. The Thermal Conductivity of Nonmetallic Crystals. Solid St. Phys. 1979, 34, 1. [Google Scholar]
- Morelli, D.T.; Slack, G.A. High Lattice Thermal Conductivity Solids; Shind, S.L., Goela, J.S., Eds.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Toberer, E.S.; Snyder, G.J. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar]
- Yumnam, G.; Pandey, T.; Singh, A.K. High temperature thermoelectric properties of Zr and Hf based transition metal dichalcogenides: A first principles study. J. Chem. Phys. 2015, 143, 234704. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Yang, L.; Ma, Z.; Song, P.; Zhang, M.; Ma, J.; Yang, F.; Wang, X. Review of current high-ZT thermoelectric materials. J. Mater. Sci. 2020, 55, 12642–12704. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-potential, linearized augmented plane wave programs for crystalline systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Schwarz, K.; Blaha, P.; Madsen, G.K.H. Electronic Structure Calculations of Solids Using the WIEN2k Package for Material Sciences. Comput. Phys. Commun. 2002, 147, 71–76. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef]
- Kirchner-Hall, N.E.; Zhao, W.; Xiong, Y.; Timrov, I.; Dabo, I. Extensive Benchmarking of DFT + U Calculations for Predicting Band Gaps. Appl. Sci. 2021, 11, 2395. [Google Scholar] [CrossRef]
- Perdew, J.P. Density functional theory and the band gap problem. Int. J. Quantum Chem. 2009, 28, 497–523. [Google Scholar] [CrossRef]
- Shokri, A.; Yazdani, A.; Rahimi, K. Tunable electronic and optical properties of g-ZnO/α-PtO2 van der Waals heterostructure: A density functional theory study. Mater. Chem. Phys. 2020, 225, 123617. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Abbasi-Perez, D.; Luana, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Zhang, Y.; Ke, X.; Chen, C.; Yang, J.; Kent, P.R.C. Thermodynamic properties of PbTe, PbSe, and PbS: First-principles study. Phys. Rev. B 2009, 80, 024304. [Google Scholar] [CrossRef]
- Feng, S.; Li, S.; Fu, H. First-principle calculation and quasi-harmonic Debye model prediction for elastic and thermodynamic properties of Bi2Te3. Comput. Mater. Sci. 2014, 82, 45–49. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef]



| Parameters | Values | Parameters | Parameters |
|---|---|---|---|
| a | 5.281 (Å) | 17,380.3 (cmVs) | |
| c | 10.51 (Å) | 90.2 (cmVs) | |
| 2.05 (eV) | 218.8 × 10 (s) | ||
| 5.9 × 10 (K | 4.53 × 10 (s) | ||
| 411 (K) | S | 149.4 (µV·K) | |
| 2.35 | 4.1 × 10 (m) | ||
| 181.9 (J molK) | 2.68 (WKm) | ||
| 212.17 (J molK) | 9.4 (mW K m) | ||
| 59.03 (meV) | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hamdaoui, J.; Kria, M.; Lakaal, K.; El-Yadri, M.; Feddi, E.M.; Pedraja Rejas, L.; Pérez, L.M.; Díaz, P.; Mora-Ramos, M.E.; Laroze, D. Ab Initio Study of Carrier Mobility, Thermodynamic and Thermoelectric Properties of Kesterite Cu2ZnGeS4. Int. J. Mol. Sci. 2022, 23, 12785. https://doi.org/10.3390/ijms232112785
El Hamdaoui J, Kria M, Lakaal K, El-Yadri M, Feddi EM, Pedraja Rejas L, Pérez LM, Díaz P, Mora-Ramos ME, Laroze D. Ab Initio Study of Carrier Mobility, Thermodynamic and Thermoelectric Properties of Kesterite Cu2ZnGeS4. International Journal of Molecular Sciences. 2022; 23(21):12785. https://doi.org/10.3390/ijms232112785
Chicago/Turabian StyleEl Hamdaoui, Jawad, Mohamed Kria, Kamal Lakaal, Mohamed El-Yadri, El Mustapha Feddi, Liliana Pedraja Rejas, Laura M. Pérez, Pablo Díaz, Miguel E. Mora-Ramos, and David Laroze. 2022. "Ab Initio Study of Carrier Mobility, Thermodynamic and Thermoelectric Properties of Kesterite Cu2ZnGeS4" International Journal of Molecular Sciences 23, no. 21: 12785. https://doi.org/10.3390/ijms232112785
APA StyleEl Hamdaoui, J., Kria, M., Lakaal, K., El-Yadri, M., Feddi, E. M., Pedraja Rejas, L., Pérez, L. M., Díaz, P., Mora-Ramos, M. E., & Laroze, D. (2022). Ab Initio Study of Carrier Mobility, Thermodynamic and Thermoelectric Properties of Kesterite Cu2ZnGeS4. International Journal of Molecular Sciences, 23(21), 12785. https://doi.org/10.3390/ijms232112785






