A Graph Neural Network Approach for the Analysis of siRNA-Target Biological Networks
Abstract
:1. Introduction
1.1. Related Work
2. Results and Discussion
2.1. Experimental Setup
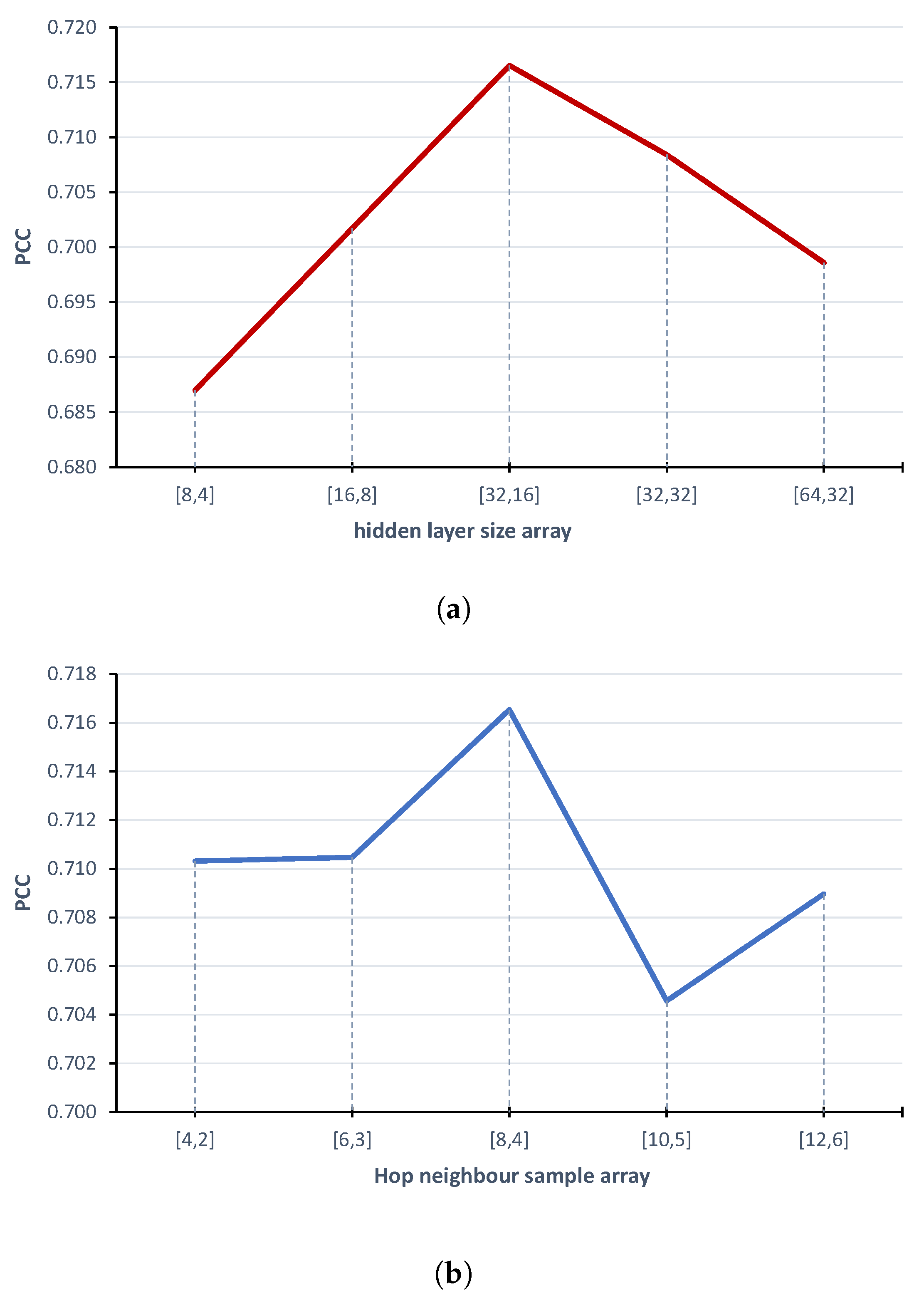
2.2. Model Parameters Fine-Tuning
2.3. Experimental Results and Comparison with Other Predictors
2.4. Biological Application of the Proposed siRNAs Efficacy Prediction Method
3. Materials and Methods
3.1. SiRNA Datasets
3.2. Sequence and Thermodynamic Features
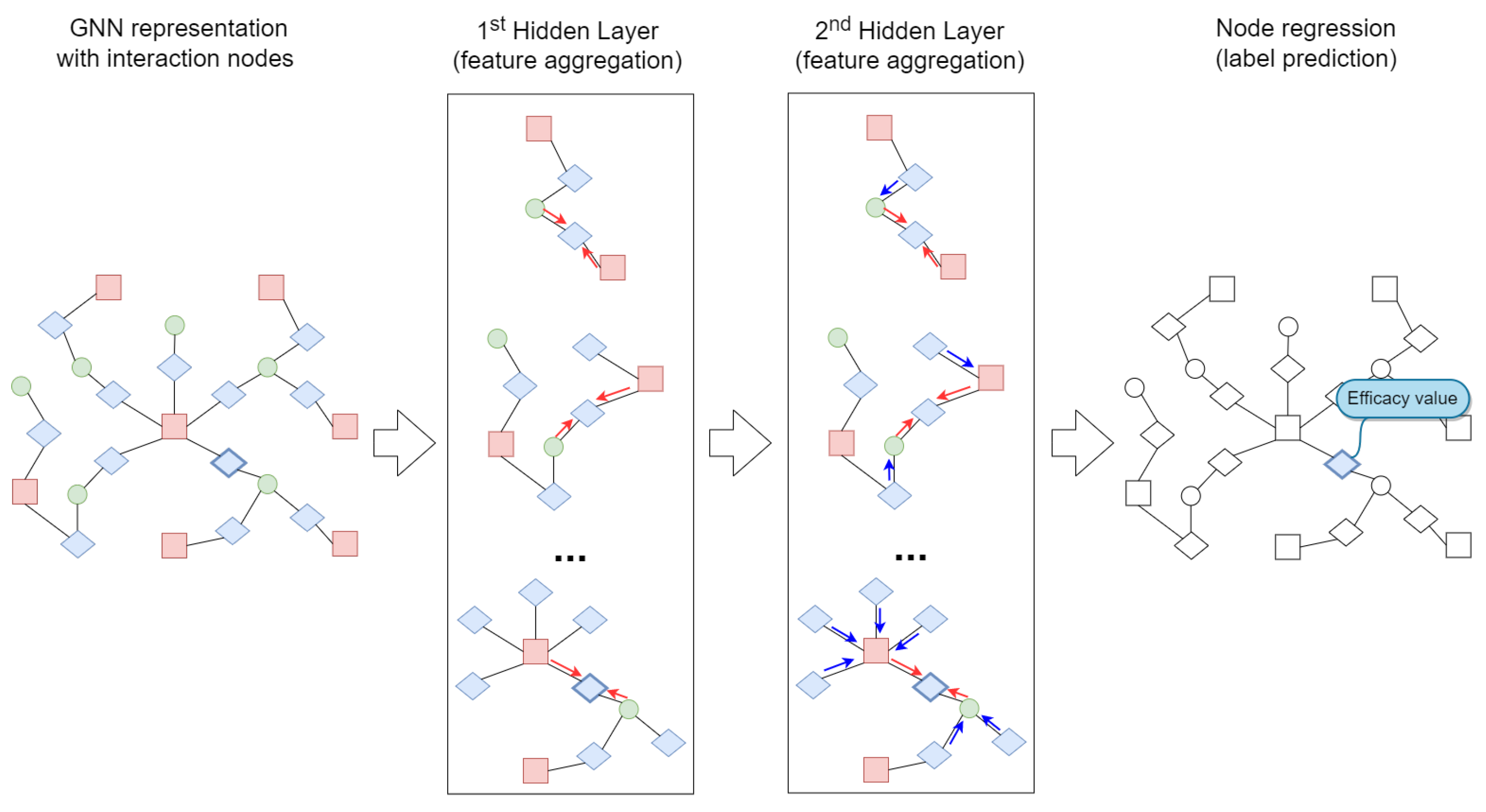
3.3. Graph Neural Networks
- Node classification/regression: in this case, we want to predict a label associated to a node of the graph. That label can be either categorical (classification) or numerical (regression). In a typical scenario, there are labelled and unlabelled nodes in the same graph, so the aim of task classification (regression) is to predict the label of the unknown nodes by means of a semi-supervised learning approach.
- Edge classification/regression: the same scenario as the node classification/regression, but we want to predict a label at edge level.
- Link prediction: in this case, we want to predict if a link exists between two nodes in the graph. In biological networks, in fact, there is often an incomplete knowledge of interactions among biological entities, such as in the protein–protein interaction networks or in the gene regulatory networks (GRNs). As in node classification, a typical scenario adopts a semi-supervised learning approach, where the knowledge of existing edges in the graph is used to predict new connections.
- Graph classification/regression: in this case, we want to predict a label, either categorical or numerical, that characterises the whole graph.
3.4. Proposed Approach
3.5. Baseline Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GNN | Graph neural network |
| ML | Machine learning |
| siRNA | Small interfering RNA |
| NPI | ncRNA–protein interaction |
| ZINB | Zero-inflated negative binomial |
| AUC | Area under curve |
| MCC | Matthews correlation coefficient |
| GRN | Gene regulatory network |
| GCN | Graph convolutional network |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| DNN | Dense neural network |
| RNN | Recurrent neural network |
| PCC | Pearson correlation coefficient |
| OOD | Out-of-distribution |
References
- Muzio, G.; O’Bray, L.; Borgwardt, K. Biological network analysis with deep learning. Briefings Bioinform. 2021, 22, 1515–1530. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.M.; Liang, L.; Liu, L.; Tang, M.J. Graph Neural Networks and Their Current Applications in Bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Tian, Y.; Zhang, Z. Network biology in medicine and beyond. Circulation. Cardiovasc. Genet. 2014, 7, 536–547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, S.; Pathak, K.; Vaidya, A. Molecular therapy using siRNA: Recent trends and advances of multi target inhibition of cancer growth. Int. J. Biol. Macromol. 2018, 116, 880–892. [Google Scholar] [CrossRef]
- Dana, H.; Chalbatani, G.M.; Mahmoodzadeh, H.; Karimloo, R.; Rezaiean, O.; Moradzadeh, A.; Mehmandoost, N.; Moazzen, F.; Mazraeh, A.; Marmari, V.; et al. Molecular mechanisms and biological functions of siRNA. Int. J. Biomed. Sci. IJBS 2017, 13, 48. [Google Scholar]
- Li, Z.; Rana, T.M. Molecular mechanisms of RNA-triggered gene silencing machineries. Accounts Chem. Res. 2012, 45, 1122–1131. [Google Scholar] [CrossRef]
- Vert, J.P.; Foveau, N.; Lajaunie, C.; Vandenbrouck, Y. An accurate and interpretable model for siRNA efficacy prediction. BMC Bioinform. 2006, 7, 520. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; He, F.; Chen, Y.; Liu, Y.; Yu, H. SiRNA silencing efficacy prediction based on a deep architecture. BMC Genom. 2018, 19, 669. [Google Scholar] [CrossRef]
- Shen, Z.A.; Luo, T.; Zhou, Y.K.; Yu, H.; Du, P.F. NPI-GNN: Predicting ncRNA–protein interactions with deep graph neural networks. Briefings Bioinform. 2021, 22, 51. [Google Scholar] [CrossRef]
- Ciortan, M.; Defrance, M. GNN-based embedding for clustering scRNA-seq data. Bioinformatics 2021, 38, 1037–1044. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Huang, X.; Zou, G.; Zhou, S.; Guan, J. Deep structural clustering for single-cell RNA-seq data jointly through autoencoder and graph neural network. Briefings Bioinform. 2022, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ma, A.; Chang, Y.; Gong, J.; Jiang, Y.; Qi, R.; Wang, C.; Fu, H.; Ma, Q.; Xu, D. scGNN is a novel graph neural network framework for single-cell RNA-Seq analyses. Nat. Commun. 2021, 12, 1882. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.; Yang, H.; Zhuang, X.; Liao, J.; Yang, P.; Cheng, J.; Lu, X.; Chen, H.; Fan, X. scDeepSort: A pre-trained cell-type annotation method for single-cell transcriptomics using deep learning with a weighted graph neural network. Nucleic Acids Res. 2021, 49, e122. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 1025–1035. [Google Scholar] [CrossRef]
- Yang, Y.; Li, D. NENN: Incorporate Node and Edge Features in Graph Neural Networks. In Proceedings of the 12th Asian Conference on Machine Learning, Bangkok, Thailand, 18–20 November 2020; Pan, S.J., Sugiyama, M., Eds.; Volume 129, pp. 593–608. [Google Scholar]
- Huesken, D.; Lange, J.; Mickanin, C.; Weiler, J.; Asselbergs, F.; Warner, J.; Meloon, B.; Engel, S.; Rosenberg, A.; Cohen, D.; et al. Design of a genome-wide siRNA library using an artificial neural network. Nat. Biotechnol. 2005, 23, 995–1001. [Google Scholar] [CrossRef]
- Shabalina, S.A.; Spiridonov, A.N.; Ogurtsov, A.Y. Computational models with thermodynamic and composition features improve siRNA design. BMC Bioinform. 2006, 7, 65. [Google Scholar] [CrossRef] [Green Version]
- He, F.; Han, Y.; Gong, J.; Song, J.; Wang, H.; Li, Y. Predicting siRNA efficacy based on multiple selective siRNA representations and their combination at score level. Sci. Rep. 2017, 7, 44836. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Wang, Y.; Lin, Y.; Shao, D.; He, K.; Huang, L. LncMirNet: Predicting LncRNA–miRNA Interaction Based on Deep Learning of Ribonucleic Acid Sequences. Molecules 2020, 25, 4372. [Google Scholar] [CrossRef]
- Miao, Y.R.; Liu, W.; Zhang, Q.; Guo, A.Y. lncRNASNP2: An updated database of functional SNPs and mutations in human and mouse lncRNAs. Nucleic Acids Res. 2017, 46, D276–D280. [Google Scholar] [CrossRef]
- Pearson’s Correlation Coefficient. Encyclopedia of Public Health; Springer: Dordrecht, The Netherlands, 2008; pp. 1090–1091. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 1 October 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 1 October 2022).
- Data61, C. StellarGraph Machine Learning Library. 2018. Available online: https://github.com/stellargraph/stellargraph (accessed on 1 October 2022).
- Park, H.; Yoon, K. Degree Matters: Assessing the Generalization of Graph Neural Network. In Proceedings of the 2021 7th IEEE International Conference on Network Intelligence and Digital Content (IC-NIDC), Beijing, China, 17–19 November 2021; pp. 71–75. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Zhang, Z.; Zhu, W. OOD-GNN: Out-of-Distribution Generalized Graph Neural Network. IEEE Trans. Knowl. Data Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Ray, K.K.; Landmesser, U.; Leiter, L.A.; Kallend, D.; Dufour, R.; Karakas, M.; Hall, T.; Troquay, R.; Turner, T.; Visseren, F.L.; et al. Inclisiran in patients at high cardiovascular risk with elevated LDL cholesterol. N. Engl. J. Med. 2017, 376, 1430–1440. [Google Scholar] [CrossRef] [Green Version]
- Raal, F.J.; Kallend, D.; Ray, K.K.; Turner, T.; Koenig, W.; Wright, R.S.; Wijngaard, P.L.; Curcio, D.; Jaros, M.J.; Leiter, L.A.; et al. Inclisiran for the treatment of heterozygous familial hypercholesterolemia. N. Engl. J. Med. 2020, 382, 1520–1530. [Google Scholar] [CrossRef] [PubMed]
- El Dika, I.; Lim, H.Y.; Yong, W.P.; Lin, C.C.; Yoon, J.H.; Modiano, M.; Freilich, B.; Choi, H.J.; Chao, T.Y.; Kelley, R.K.; et al. An open-label, multicenter, phase I, dose escalation study with phase II expansion cohort to determine the safety, pharmacokinetics, and preliminary antitumor activity of intravenous TKM-080301 in subjects with advanced hepatocellular carcinoma. Oncologist 2019, 24, 747.e218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, R.; Patil, S.; Zhao, X.; Miao, Z.; Qian, A. RNA Therapeutics-Research and Clinical Advancements. Front. Mol. Biosci. 2021, 913, S43–S59. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, X.; Zabkiewicz, C.; Ruge, F.; Xie, M.; Cai, S.; Sun, P.H.; Griffiths, P.; Pugh, M.R.; Ji, J.; et al. Noggin is associated with a poor prognosis of gastric cancer by promoting the proliferation of gastric cancer cells via the upregulation of EGFR. Int. J. Oncol. 2020, 57, 813–824. [Google Scholar] [CrossRef]
- Kozlow, W.; Guise, T.A. Breast cancer metastasis to bone: Mechanisms of osteolysis and implications for therapy. J. Mammary Gland Biol. Neoplasia 2005, 10, 169–180. [Google Scholar] [CrossRef]
- Secondini, C.; Wetterwald, A.; Schwaninger, R.; Thalmann, G.N.; Cecchini, M.G. The role of the BMP signaling antagonist noggin in the development of prostate cancer osteolytic bone metastasis. PLoS ONE 2011, 6, e16078. [Google Scholar] [CrossRef]
- Harborth, J.; Elbashir, S.M.; Vandenburgh, K.; Manninga, H.; Scaringe, S.A.; Weber, K.; Tuschl, T. Sequence, chemical, and structural variation of small interfering RNAs and short hairpin RNAs and the effect on mammalian gene silencing. Antisense Nucleic Acid Drug Dev. 2003, 13, 83–105. [Google Scholar] [CrossRef]
- Ui-Tei, K.; Naito, Y.; Takahashi, F.; Haraguchi, T.; Ohki-Hamazaki, H.; Juni, A.; Ueda, R.; Saigo, K. Guidelines for the selection of highly effective siRNA sequences for mammalian and chick RNA interference. Nucleic Acids Res. 2004, 32, 936–948. [Google Scholar] [CrossRef] [Green Version]
- Vickers, T.A.; Koo, S.; Bennett, C.F.; Crooke, S.T.; Dean, N.M.; Baker, B.F. Efficient reduction of target RNAs by small interfering RNA and RNase H-dependent antisense agents. A comparative analysis. J. Biol. Chem. 2003, 278, 7108–7118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khvorova, A.; Reynolds, A.; Jayasena, S.D. Functional siRNAs and miRNAs exhibit strand bias. Cell 2003, 115, 209–216. [Google Scholar] [CrossRef] [Green Version]
- Ichihara, M.; Murakumo, Y.; Masuda, A.; Matsuura, T.; Asai, N.; Jijiwa, M.; Ishida, M.; Shinmi, J.; Yatsuya, H.; Qiao, S.; et al. Thermodynamic instability of siRNA duplex is a prerequisite for dependable prediction of siRNA activities. Nucleic Acids Res. 2007, 35, e123. [Google Scholar] [CrossRef] [Green Version]
- Mysara, M.; Elhefnawi, M.; Garibaldi, J.M. MysiRNA: Improving siRNA efficacy prediction using a machine-learning model combining multi-tools and whole stacking energy (ΔG). J. Biomed. Inf. 2012, 45, 528–534. [Google Scholar] [CrossRef] [Green Version]
- Katoh, T.; Suzuki, T. Specific residues at every third position of siRNA shape its efficient RNAi activity. Nucleic Acids Res. 2007, 35, e27. [Google Scholar] [CrossRef] [PubMed]
- Chalk, A.M.; Warfinge, R.E.; Georgii-Hemming, P.; Sonnhammer, E.L.L. siRNAdb: A database of siRNA sequences. Nucleic Acids Res. 2005, 33, D131–D134. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Li, Q.Z.; Lin, H.; Zuo, Y.C. The effect of regions flanking target site on siRNA potency. Genomics 2013, 102, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Fiannaca, A.; La Rosa, M.; Rizzo, R.; Urso, A. A k-mer-based barcode DNA classification methodology based on spectral representation and a neural gas network. Artif. Intell. Med. 2015, 64, 173–184. [Google Scholar] [CrossRef]
- Schubert, S.; Grünweller, A.; Erdmann, V.A.; Kurreck, J. Local RNA Target Structure Influences siRNA Efficacy: Systematic Analysis of Intentionally Designed Binding Regions. J. Mol. Biol. 2005, 348, 883–893. [Google Scholar] [CrossRef]
- Xia, T.; SantaLucia, J.; Burkard, M.E.; Kierzek, R.; Schroeder, S.J.; Jiao, X.; Cox, C.; Turner, D.H. Thermodynamic Parameters for an Expanded Nearest-Neighbor Model for Formation of RNA Duplexes with Watson−Crick Base Pairs. Biochemistry 1998, 37, 14719–14735. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, R.; Bernhart, S.H.; Höner zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA Package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Gong, L.; Cheng, Q. Exploiting Edge Features for Graph Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9203–9211. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]


| Parameters | Values | |
|---|---|---|
| Input sequences | siRNA k-mer size | 3 |
| mRNA k-mer size | 4 | |
| number of thermodynamic features | 22 | |
| GNN model | batch size | 60 |
| hop neighbour samples | [8, 4] | |
| HinSAGE layer sizes | [32, 16] | |
| dropout | 0.15 | |
| Adamax learning rate | 0.005 */0.001 ** | |
| loss function | mean squared error |
| Algorithms | |||||||
|---|---|---|---|---|---|---|---|
| Proposed GNN | Baseline | CNN | LSTM | DNN | |||
| 10-fold Cross Validation | dataset_1 | PCC | 0.6918 | 0.5554 | 0.4996 | 0.4428 | 0.4723 |
| mse | 0.0253 | 0.0336 | 0.0455 | 0.043 | 0.0403 | ||
| 0.4459 | 0.2817 | 0.0243 | 0.0854 | 0.0275 | |||
| dataset_2 | PCC | 0.7361 | 0.6959 | 0.4975 | 0.4864 | 0.4797 | |
| mse | 0.0204 | 0.0228 | 0.0422 | 0.0351 | 0.0441 | ||
| 0.4882 | 0.4674 | −0.0124 | 0.1484 | −0.0302 | |||
| External Testset | dataset_1 vs. dataset_2 | PCC | 0.5740 | 0.5258 | 0.5477 | 0.5323 | 0.4744 |
| mse | 0.0336 | 0.0351 | 0.0299 | 0.0325 | 0.0337 | ||
| 0.2057 | 0.1741 | 0.2923 | 0.2313 | 0.2042 | |||
| siRNA Candidates for the Noggin Gene | Predicted Efficacy Value | |
|---|---|---|
| siRNA | Sequence | |
| 1 | UUUGAUCUCGCUCGGCAUG | 0.8078 |
| 2 | AUGUGGAGAUAGUGCUGGC | 0.7686 |
| 3 | AAUGUCUGCGACCACAGCC | 0.7858 |
| 4 | UUCAGAUCCUUUUCCUUGG | 0.8317 |
| 5 | AACUCUAGCCCUUUGAUCU | 0.8453 |
| 6 | AGCCACAUCUGUAACUUCC | 0.8106 |
| 7 | AACUUCCUCCGCAGCUUCU | 0.8324 |
| 8 | AUCUGUAACUUCCUCCGCA | 0.8408 |
| 9 | UUUUCCUUGGGGUCAAAGA | 0.7826 |
| 10 | AUGAAGCCUGGGUCGUAGU | 0.8261 |
| 11 | UCAGAUCCUUUUCCUUGGG | 0.7641 |
| 12 | UUCUUGCCCUGGGCCAAGC | 0.7843 |
| 13 | ACGUAGCGCGGCCAAAAGC | 0.7482 |
| 14 | AGAAUGUCUGCGACCACAG | 0.7767 |
| 15 | ACCUUCACGUAGCGCGGCC | 0.7248 |
| 16 | AAAGAUAGGGUCUGGGUGU | 0.8055 |
| 17 | AAAAGCGGCUGCCCAGGUC | 0.6789 |
| 18 | AGAUAGUGCUGGCCGCCGG | 0.7341 |
| 19 | AGAUCCUUUUCCUUGGGGU | 0.7616 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Rosa, M.; Fiannaca, A.; La Paglia, L.; Urso, A. A Graph Neural Network Approach for the Analysis of siRNA-Target Biological Networks. Int. J. Mol. Sci. 2022, 23, 14211. https://doi.org/10.3390/ijms232214211
La Rosa M, Fiannaca A, La Paglia L, Urso A. A Graph Neural Network Approach for the Analysis of siRNA-Target Biological Networks. International Journal of Molecular Sciences. 2022; 23(22):14211. https://doi.org/10.3390/ijms232214211
Chicago/Turabian StyleLa Rosa, Massimo, Antonino Fiannaca, Laura La Paglia, and Alfonso Urso. 2022. "A Graph Neural Network Approach for the Analysis of siRNA-Target Biological Networks" International Journal of Molecular Sciences 23, no. 22: 14211. https://doi.org/10.3390/ijms232214211
APA StyleLa Rosa, M., Fiannaca, A., La Paglia, L., & Urso, A. (2022). A Graph Neural Network Approach for the Analysis of siRNA-Target Biological Networks. International Journal of Molecular Sciences, 23(22), 14211. https://doi.org/10.3390/ijms232214211







