Dynamics of Ultrafast Phase Transitions in (001) Si on the Shock-Wave Front
Abstract
:1. Introduction
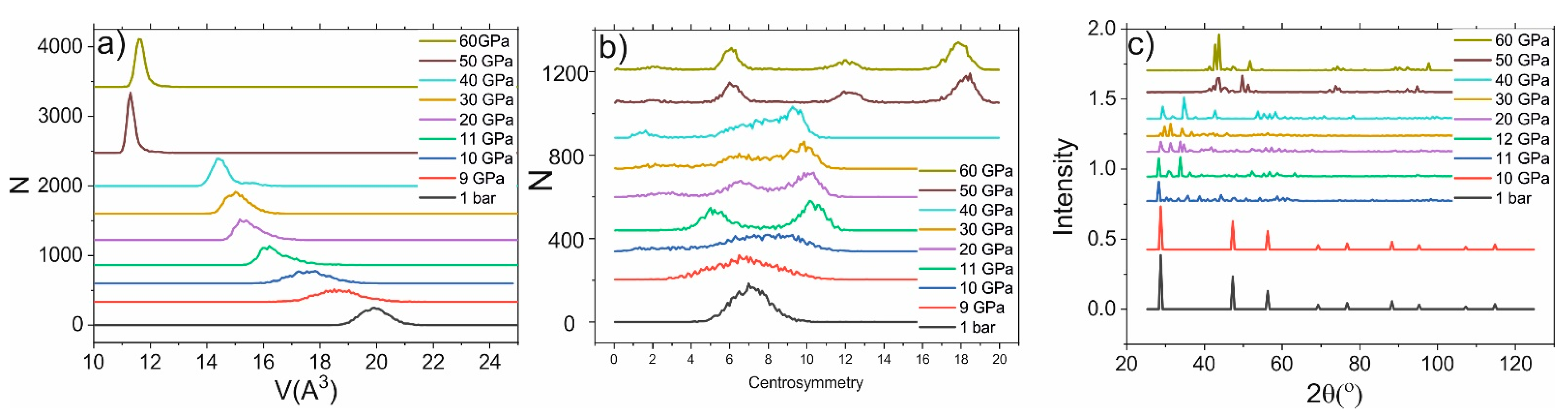
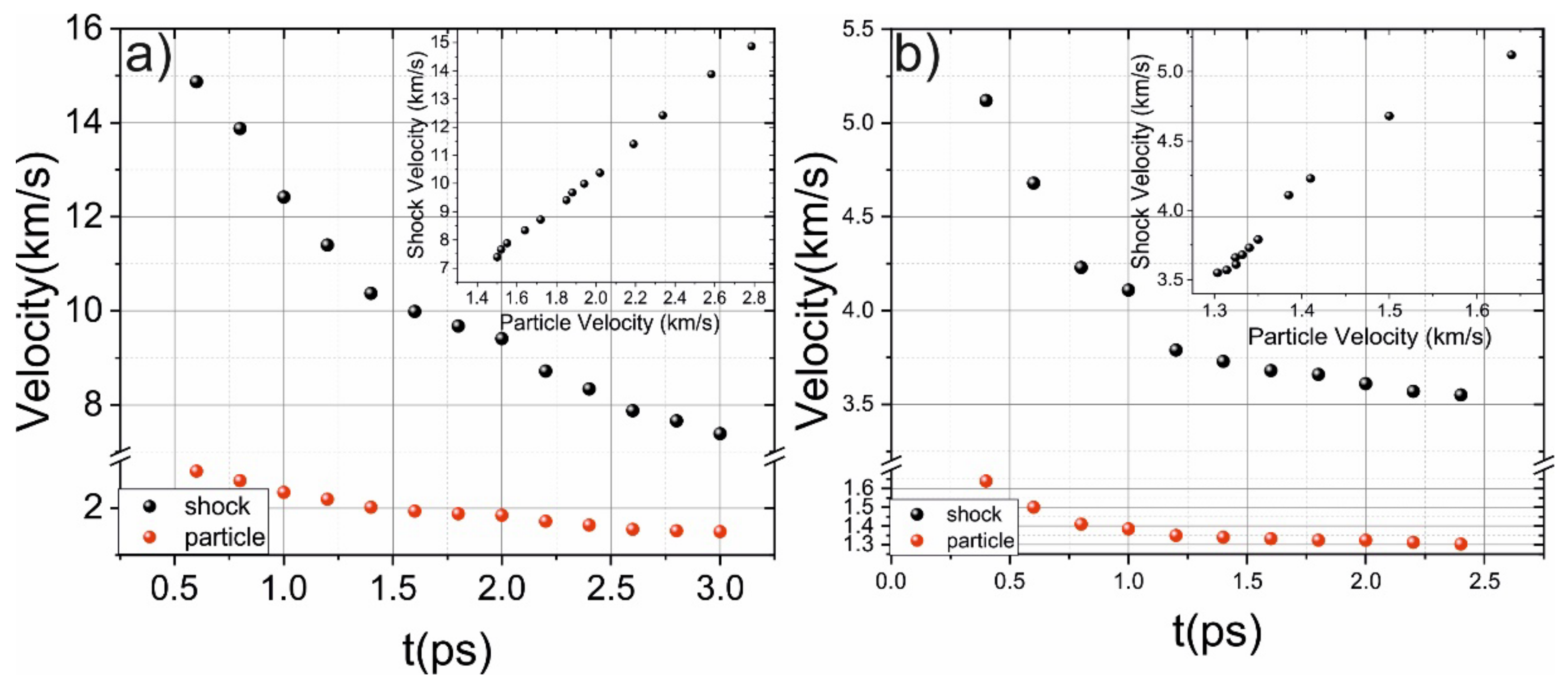
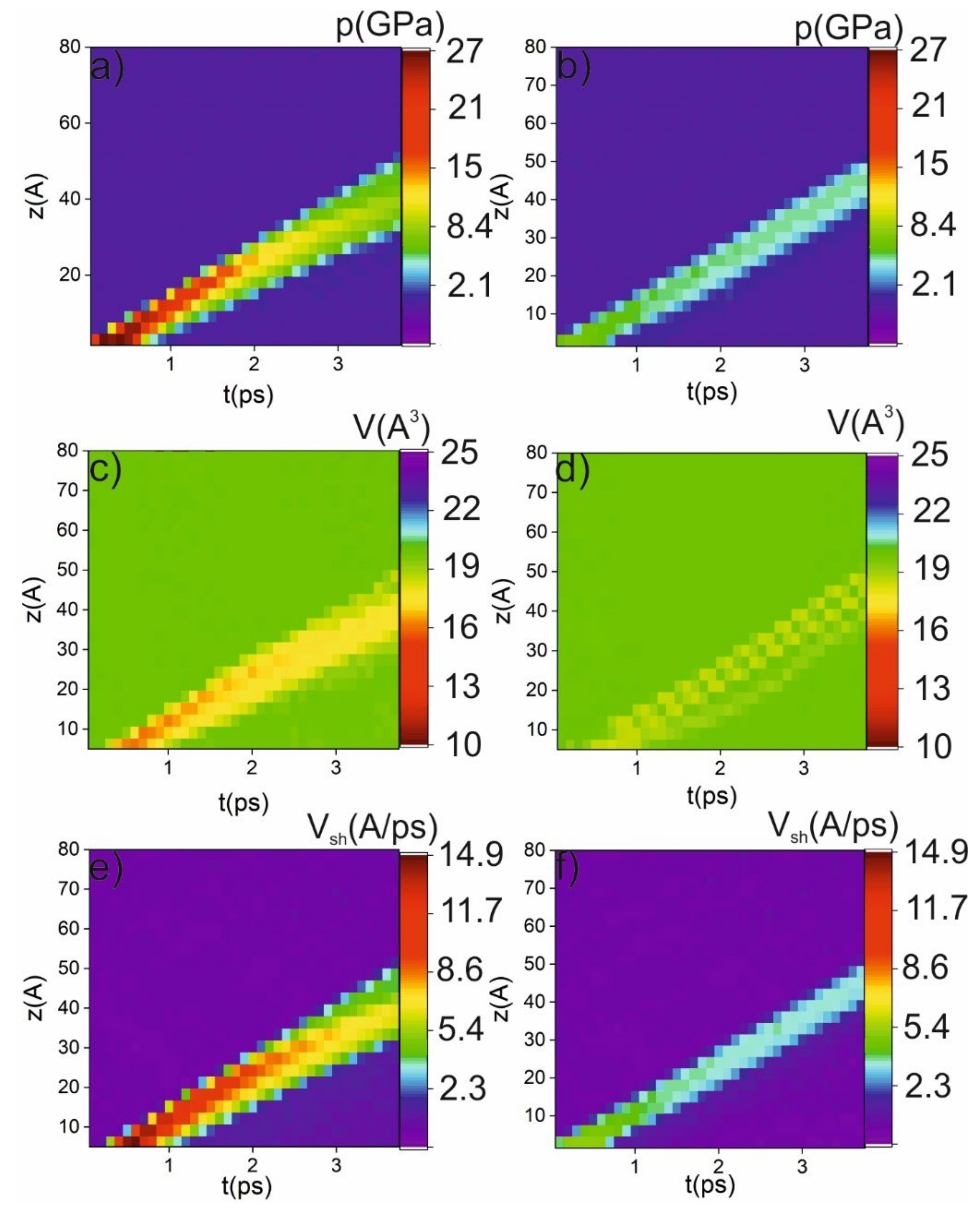
2. Results and Discussion
2.1. Stationary Conditions
2.2. Non-Stationary Conditions
3. Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Katzke, H.; Bismayer, U.; Tolédano, P. Theory of the high-pressure structural phase transitions in Si, Ge, Sn, and Pb. Phys. Rev. B 2006, 73, 134105. [Google Scholar] [CrossRef]
- Budnitzki, M.; Kuna, M. Stress induced phase transitions in silicon. J. Mech. Phys. Solids 2016, 95, 64–91. [Google Scholar] [CrossRef]
- Cheng, C. Uniaxial phase transition in Si:Ab initiocalculations. Phys. Rev. B 2003, 67, 134109. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef]
- Lee, I.-H.; Jeong, J.-W.; Chang, K.J. Invariant-molecular-dynamics study of the diamond-to-Β-Sn transition in Si under hydrostatic and uniaxial compressions. Phys. Rev. B 1997, 55, 5689–5693. [Google Scholar] [CrossRef]
- Hanfland, M.; Schwarz, U.; Syassen, K.; Takemura, K. Crystal Structure of the High-Pressure Phase Silicon VI. Phys. Rev. Lett. 1999, 82, 1197–1200. [Google Scholar] [CrossRef]
- Jeong, S.-M.; Kitamura, T. Atomistic Simulation on the Phase Transformation of Silicon under Nonhydrostatic Stress. Jpn. J. Appl. Phys. 2007, 46, 5924–5929. [Google Scholar] [CrossRef]
- Chang, K.J.; Cohen, M.L. Solid-solid phase transitions and soft phonon modes in highly condensed Si. Phys. Rev. B 1985, 31, 7819–7826. [Google Scholar] [CrossRef]
- Erhart, P.; Albe, K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef] [Green Version]
- Daisenberger, D.; Wilson, M.; McMillan, P.F.; Cabrera, R.Q.; Wilding, M.C.; Machon, D. High-pressure x-ray scattering and computer simulation studies of density-induced polyamorphism in silicon. Phys. Rev. B 2007, 75, 224118. [Google Scholar] [CrossRef] [Green Version]
- Mogni, G.; Higginbotham, A.; Gaál-Nagy, K.; Park, N.; Wark, J. Molecular dynamics simulations of shock-compressed single-crystal silicon. Phys. Rev. B 2014, 89, 1–10. [Google Scholar] [CrossRef]
- Mujica, A.; Rubio, A.; Muñoz, A.; Needs, R.J. High-pressure phases of group-IV, III–V, and II–VI compounds. Rev. Mod. Phys. 2003, 75, 863–912. [Google Scholar] [CrossRef] [Green Version]
- Wippermann, S.; He, Y.; Vörös, M.; Galli, G. Novel silicon phases and nanostructures for solar energy conversion. Appl. Phys. Rev. 2016, 3, 040807. [Google Scholar] [CrossRef] [Green Version]
- Pashaev, E.M.; Korchuganov, V.N.; Subbotin, I.A.; Likhachev, I.A.; Borisov, M.M.; Mareev, E.I.; Potemkin, F.V. Formation of Metastable Phase Si(III) in Silicon Exposed to Femtosecond Laser Radiation. Crystallogr. Rep. 2021, 66, 920–922. [Google Scholar] [CrossRef]
- Naghilou, A.; Armbruster, O.; Kautek, W. Femto- and nanosecond pulse laser ablation dependence on irradiation area: The role of defects in metals and semiconductors. Appl. Surf. Sci. 2017, 418, 487–490. [Google Scholar] [CrossRef]
- Norman, G.E.; Starikov, S.V.; Stegailov, V.V.; Saitov, I.M.; Zhilyaev, P.A. Atomistic Modeling of Warm Dense Matter in the Two-Temperature State. Contrib. Plasma Phys. 2013, 53, 129–139. [Google Scholar] [CrossRef]
- Smith, M.J.; Lin, Y.-T.; Sher, M.-J.; Winkler, M.T.; Mazur, E.; Gradečak, S. Pressure-induced phase transformations during femtosecond-laser doping of silicon. J. Appl. Phys. 2011, 110, 053524. [Google Scholar] [CrossRef]
- McBride, E.E.; Krygier, A.; Ehnes, A.; Galtier, E.; Harmand, M.; Konôpková, Z.; Lee, H.J.; Liermann, H.-P.; Nagler, B.; Pelka, A.; et al. Phase transition lowering in dynamically compressed silicon. Nat. Phys. 2018, 15, 89–94. [Google Scholar] [CrossRef]
- Weisshaupt, J.; Juvé, V.; Holtz, M.; Ku, S.; Woerner, M.; Elsaesser, T.; Ališauskas, S.; Pugzlys, A.; Baltuška, A. High-brightness table-top hard X-ray source driven by sub-100-femtosecond mid-infrared pulses. Nat. Photon. 2014, 8, 927–930. [Google Scholar] [CrossRef]
- Johnson, A.S.; Avni, T.; Larsen, E.W.; Austin, D.R.; Marangos, J.P. Attosecond soft X-ray high harmonic generation. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2019, 377, 20170468. [Google Scholar] [CrossRef] [Green Version]
- Murnane, M.M.; Kapteyn, H.C.; Rosen, M.D.; Falcone, R.W. Ultrafast X-ray Pulses from Laser-Produced Plasmas. Science 1991, 251, 531–536. [Google Scholar] [CrossRef]
- Lindenberg, A.M.; Johnson, S.L.; Reis, D.A. Visualization of Atomic-Scale Motions in Materials via Femtosecond X-Ray Scattering Techniques. Annu. Rev. Mater. Sci. 2017, 47, 425–449. [Google Scholar] [CrossRef]
- Lindenberg, A.M.; Larsson, J.; Sokolowski-Tinten, K.; Gaffney, K.J.; Blome, C.; Synnergren, O.; Sheppard, J.; Caleman, C.; MacPhee, A.G.; Weinstein, D.; et al. Atomic-Scale Visualization of Inertial Dynamics. Science 2005, 308, 392–395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wittenberg, J.S.; Miller, T.A.; Szilagyi, E.; Lutker, K.; Quirin, F.; Lu, W.; Lemke, H.T.; Zhu, D.; Chollet, M.; Robinson, J.; et al. Real-Time Visualization of Nanocrystal Solid–Solid Transformation Pathways. Nano Lett. 2014, 14, 1995–1999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, Q.-L.; Kitamura, T.; Li, Z. Transient phase transitions in single-crystal coppers under ultrafast lasers induced shock compression: A molecular dynamics study. J. Appl. Phys. 2019, 125, 194302. [Google Scholar] [CrossRef]
- Sokolowski-Tinten, K.; Blome, C.; Blums, J.; Cavalleri, A.; Dietrich, C.; Tarasevitch, A.; Uschmann, I.; Förster, E.; Kammler, M.; Horn-Von-Hoegen, M.; et al. Femtosecond X-ray measurement of coherent lattice vibrations near the Lindemann stability limit. Nature 2003, 422, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Schaffer, C.B.; Brodeur, A.; Mazur, E. Laser-induced breakdown and damage in bulk transparent materials induced by tightly focused femtosecond laser pulses. Meas. Sci. Technol. 2001, 12, 1784–1794. [Google Scholar] [CrossRef]
- Vailionis, A.; Gamaly, E.G.; Mizeikis, V.; Yang, W.; Rode, A.; Juodkazis, S. Evidence of superdense aluminium synthesized by ultrafast microexplosion. Nat. Commun. 2011, 2, 445. [Google Scholar] [CrossRef] [Green Version]
- Potemkin, F.; Mareev, E.; Bezsudnova, Y.; Platonenko, V.; Bravy, B.; Gordienko, V. Controlled energy deposition and void-like modification inside transparent solids by two-color tightly focused femtosecond laser pulses. Appl. Phys. Lett. 2017, 110, 163903. [Google Scholar] [CrossRef]
- Mareev, E.I.; Rumiantsev, B.V.; Potemkin, F.V. Study of the Parameters of Laser-Induced Shock Waves for Laser Shock Peening of Silicon. J. Exp. Theor. Phys. Lett. 2020, 112, 739–744. [Google Scholar] [CrossRef]
- Rethfeld, B.; Ivanov, D.S.; Garcia, M.E.; Anisimov, S.I. Modelling ultrafast laser ablation. J. Phys. D Appl. Phys. 2017, 50, 193001. [Google Scholar] [CrossRef]
- Ravelo, R.; Germann, T.C.; Guerrero, O.; An, Q.; Holian, B.L. Shock-induced plasticity in tantalum single crystals: Interatomic potentials and large-scale molecular-dynamics simulations. Phys. Rev. B 2013, 88, 134101. [Google Scholar] [CrossRef] [Green Version]
- Potemkin, F.V.; Mareev, E.I.; Garmatina, A.A.; Nazarov, M.M.; Fomin, E.A.; Stirin, A.I.; Korchuganov, V.N.; Kvardakov, V.V.; Gordienko, V.M.; Panchenko, V.Y.; et al. Hybrid x-ray laser-plasma/laser-synchrotron facility for pump–probe studies of the extreme state of matter at NRC “Kurchatov Institute”. Rev. Sci. Instrum. 2021, 92, 053101. [Google Scholar] [CrossRef] [PubMed]
- Oleynik, I.I.; Zybin, S.V.; Elert, M.L.; White, C.T. Nanoscale Molecular Dynamics Simulaton of Shock Compression of Silicon. AIP Conf. Proc. 2006, 845, 413–416. [Google Scholar] [CrossRef] [Green Version]
- Higginbotham, A.; Stubley, P.G.; Comley, A.J.; Eggert, J.H.; Foster, J.M.; Kalantar, D.H.; McGonegle, D.; Patel, S.; Peacock, L.J.; Rothman, S.D.; et al. Inelastic response of silicon to shock compression. Sci. Rep. 2016, 6, 24211. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991–7000. [Google Scholar] [CrossRef]
- Izumi, S.; Sakai, S. Internal Displacement and Elastic Properties of the Silicon Tersoff Model. JSME Int. J. Ser. A 2004, 47, 54–61. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Tang, Z.; Li, G.; Aluru, N.R. Quasiharmonic models for the calculation of thermodynamic properties of crystalline silicon under strain. J. Appl. Phys. 2006, 99, 64314. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Rycroft, C. VORO++: A three-dimensional Voronoi cell library in C++. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coleman, S.; Spearot, D.E.; Capolungo, L. Virtual diffraction analysis of Ni [0 1 0] symmetric tilt grain boundaries. Model. Simul. Mater. Sci. Eng. 2013, 21, 55020. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. J. Für Die Reine Und Angew. Math. 1908, 133, 97–178. [Google Scholar] [CrossRef]
- Finney, J.L. Random packings and the structure of simple liquids. I. The geometry of random close packing. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1970, 319, 479–493. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mareev, E.I.; Potemkin, F.V. Dynamics of Ultrafast Phase Transitions in (001) Si on the Shock-Wave Front. Int. J. Mol. Sci. 2022, 23, 2115. https://doi.org/10.3390/ijms23042115
Mareev EI, Potemkin FV. Dynamics of Ultrafast Phase Transitions in (001) Si on the Shock-Wave Front. International Journal of Molecular Sciences. 2022; 23(4):2115. https://doi.org/10.3390/ijms23042115
Chicago/Turabian StyleMareev, Evgenii Igorevich, and Fedor Viktorovich Potemkin. 2022. "Dynamics of Ultrafast Phase Transitions in (001) Si on the Shock-Wave Front" International Journal of Molecular Sciences 23, no. 4: 2115. https://doi.org/10.3390/ijms23042115
APA StyleMareev, E. I., & Potemkin, F. V. (2022). Dynamics of Ultrafast Phase Transitions in (001) Si on the Shock-Wave Front. International Journal of Molecular Sciences, 23(4), 2115. https://doi.org/10.3390/ijms23042115





