Self-Organization of Enzyme-Catalyzed Reactions Studied by the Maximum Entropy Production Principle
Abstract
:1. Introduction
2. Results and Discussion
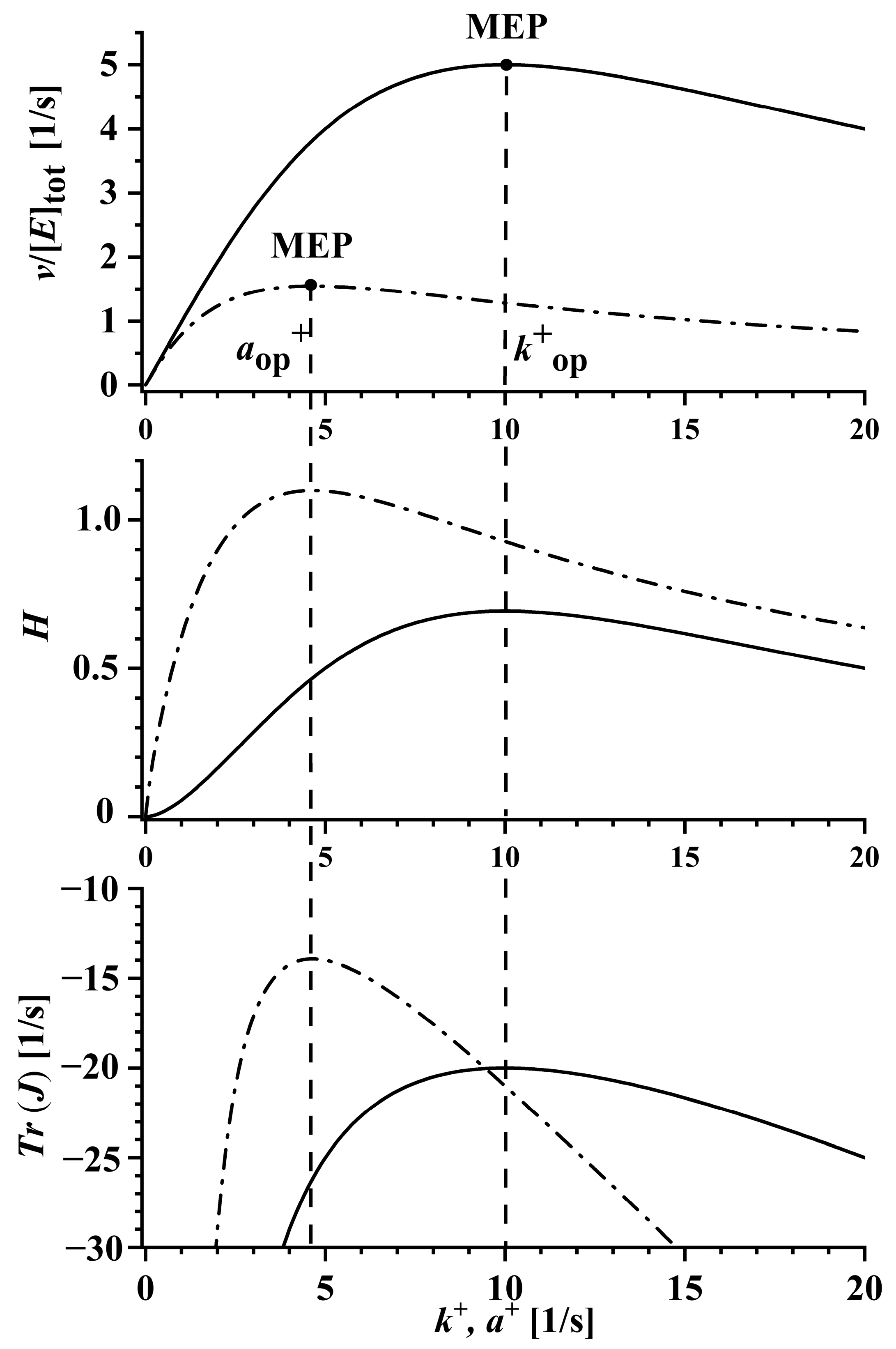
2.1. Optimal Enzyme State and Diffusion-Limited Enzymes
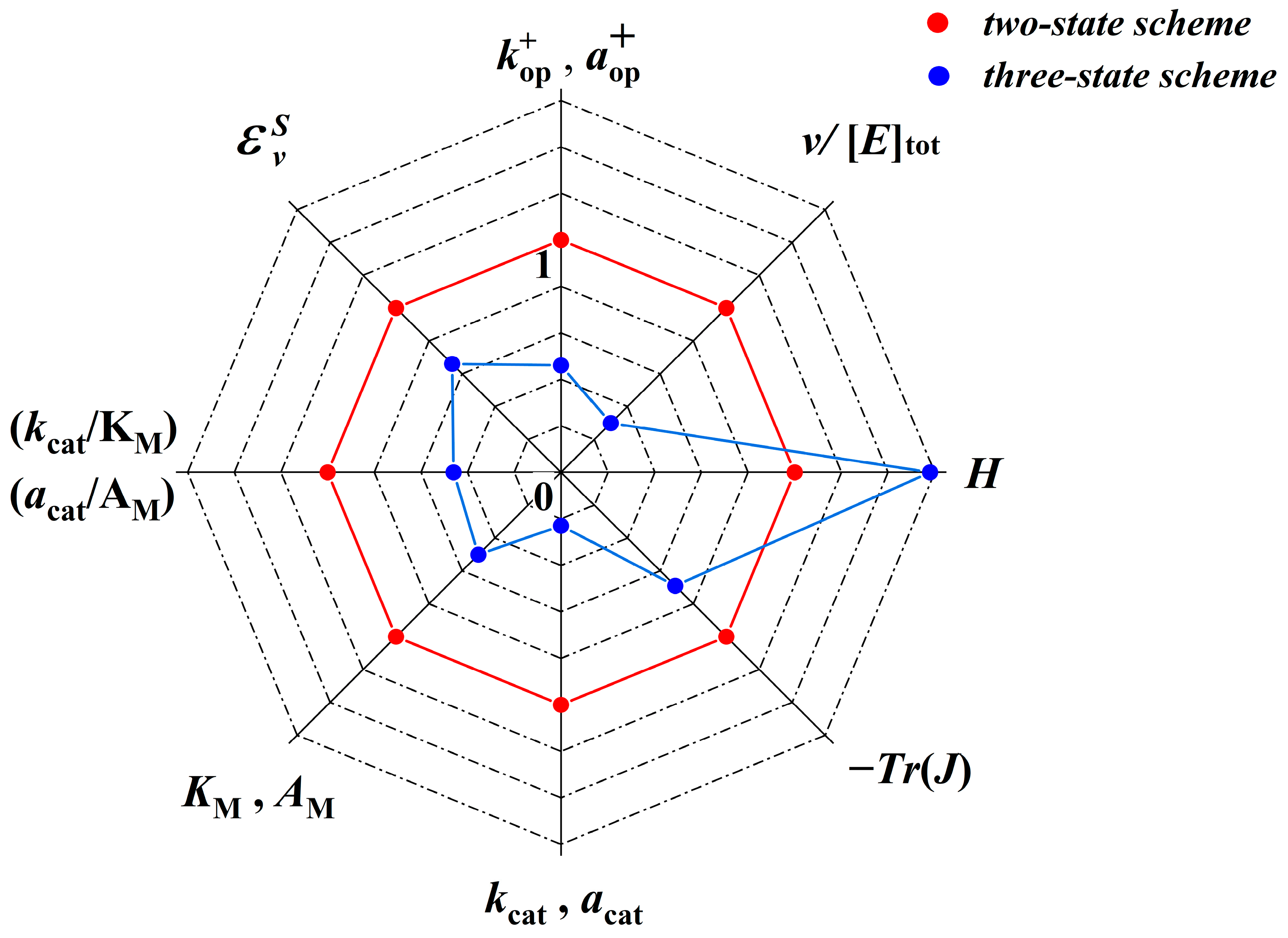
2.2. Broader Comparison of the Optimized Two- and Three-State Irreversible Kinetic Schemes
3. Methods and Materials: Theory, General Considerations and Basic Principles
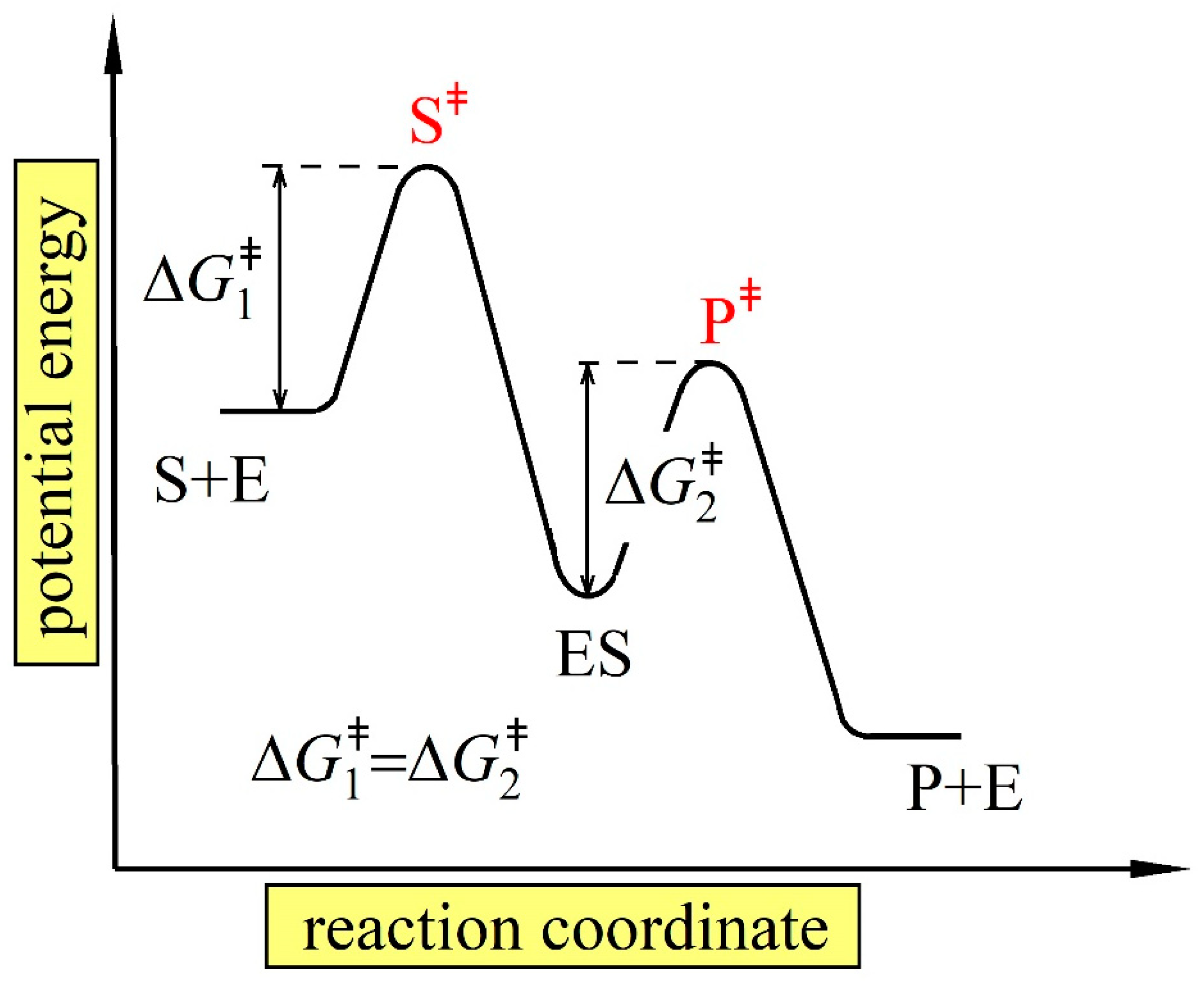
3.1. General Considerations
3.2. Entropy Production
3.3. Shannon Information Entropy
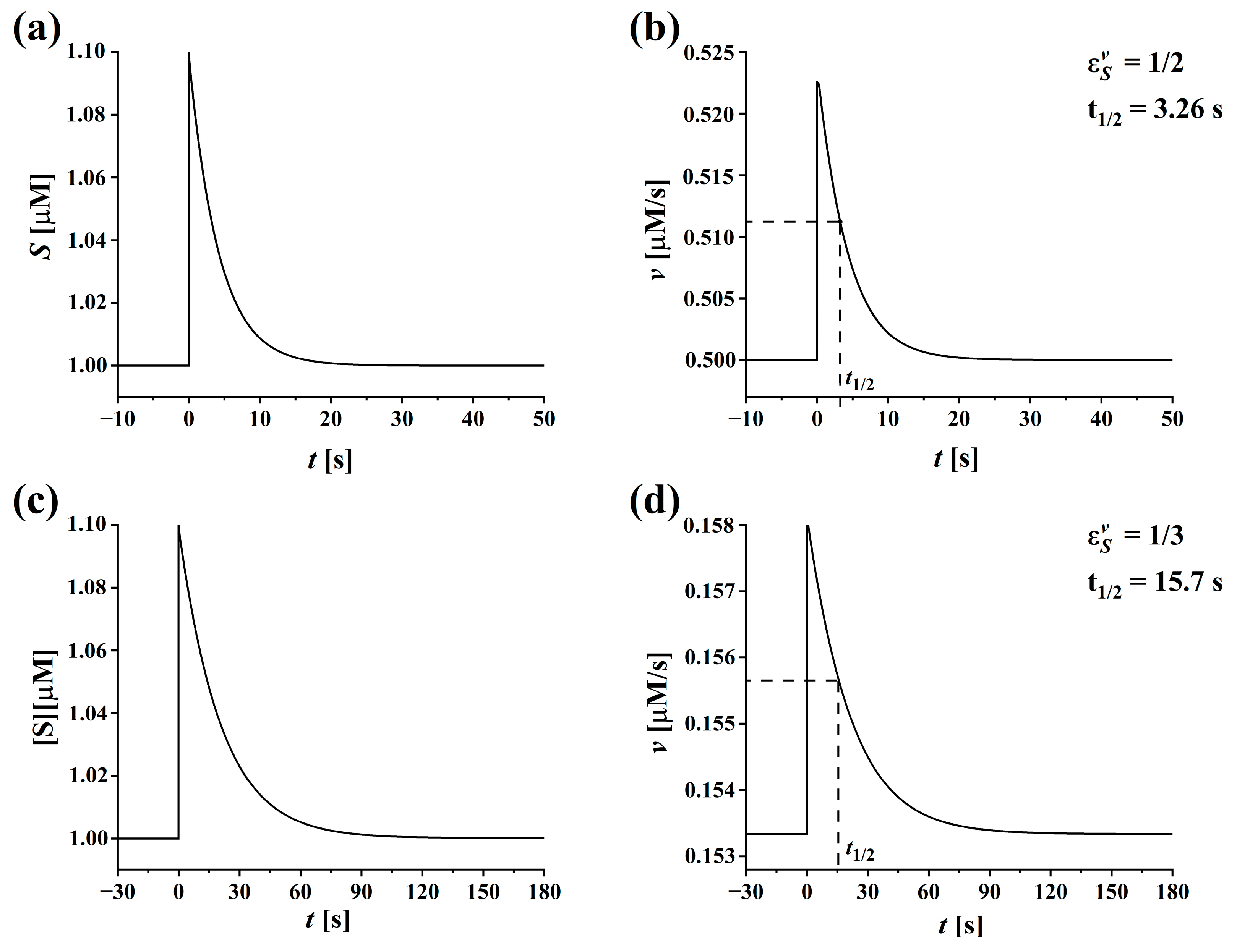
3.4. Sensitivity Analysis
3.5. Stability Analysis
3.6. Optimization Conditions
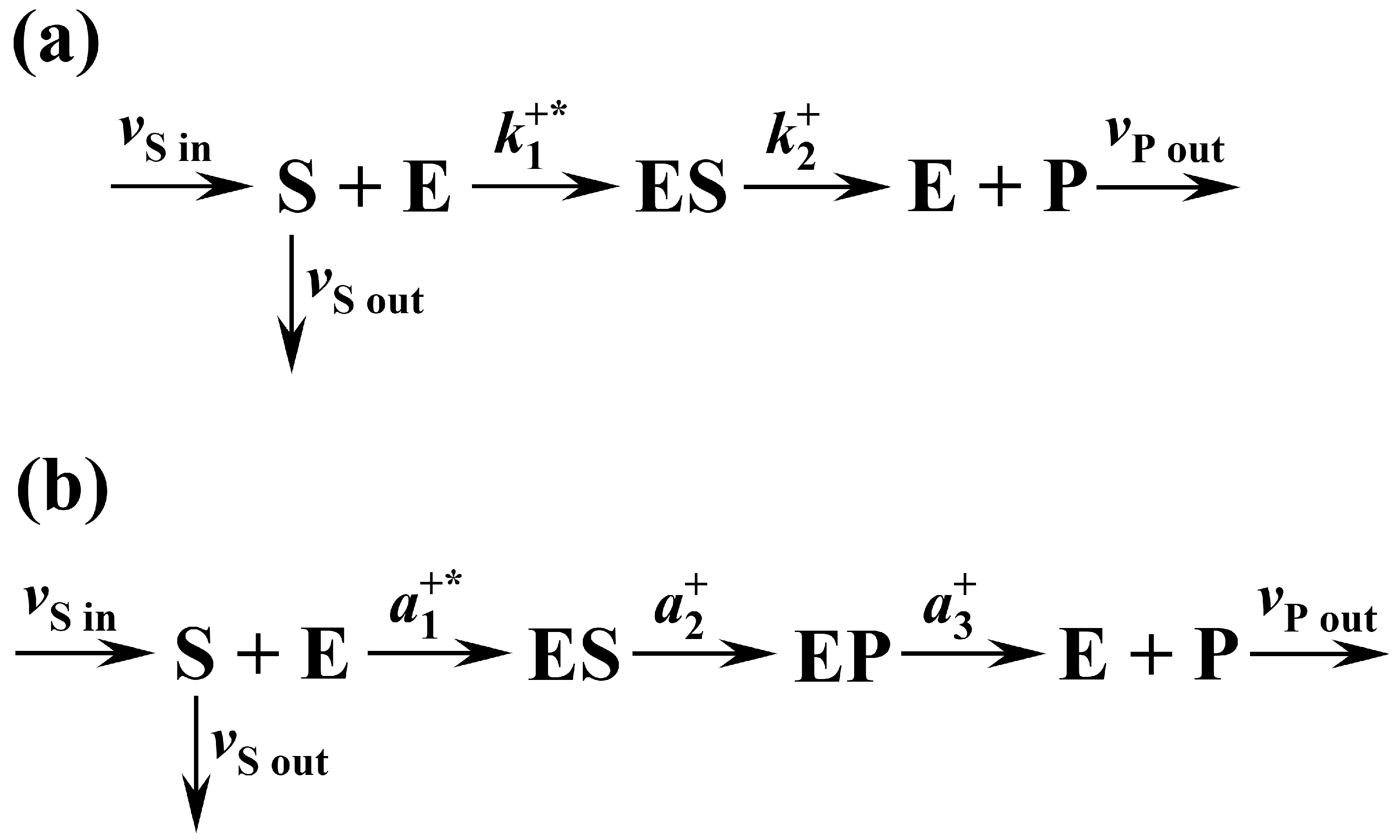
3.7. Kinetic and Thermodynamic Modeling of the Irreversible Two-State Kinetic Scheme
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Modeling of the Three-State Kinetic Scheme
References
- Heinrich, R.; Holzhütter, H.-G.; Schuster, S. A theoretical approach to the evolution and structural design of enzymatic networks; linear enzymatic chains, branched pathways and glycolysis of erythrocytes. Bull. Math. Biol. 1987, 49, 539–595. [Google Scholar] [CrossRef]
- Heinrich, R.; Hoffmann, E.; Holzhütter, H.-G. Calculation of kinetic parameters of a reversible enzymatic reaction in states of maximal activity. Biomed. Biochim. Acta 1990, 49, 891–902. [Google Scholar]
- Heinrich, R.; Schuster, S.; Holzhütter, H.-G. Mathematical analysis of enzymic reaction systems using optimization principles. Eur. J. Biochem. 1991, 201, 1–21. [Google Scholar] [CrossRef]
- Pettersson, C. Effect of evolution on the kinetic properties of enzymes. Eur. J. Biochem. 1989, 184, 561–566. [Google Scholar] [CrossRef]
- Salem, M.S.Z. Biological networks: An introductory review. J. Proteom. Genom. Res. 2018, 2, 41–111. [Google Scholar] [CrossRef]
- Kelleti, T.; Welch, G.R. The evolution of enzyme kinetic power. Biochem. J. 1984, 223, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Moles, C.G.; Mendes, P.; Banga, J.R. Parameter estimation in biochemical pathways: A comparison of global optimization methods. Genome Res. 2003, 13, 2467–2474. [Google Scholar] [CrossRef]
- Brocklehurst, K. Evolution of enzyme catalytic power. Characteristics of optimal catalysis evaluated for the simplest plausible kinetic model. Biochem. J. 1977, 163, 111–116. [Google Scholar] [CrossRef]
- Kacser, H.; Beeby, R. Evolution of catalytic proteins or on the origin of enzyme species by means of natural selection. J. Mol. Evol. 1984, 20, 38–51. [Google Scholar] [CrossRef] [PubMed]
- Dewar, R.C.; Juretić, D.; Županović, P. The functional design of the rotary enzyme ATP synthase is consistent with maximum entropy production. Chem. Phys. Lett. 2006, 430, 177–182. [Google Scholar] [CrossRef]
- Dobovišek, A.; Županović, P.; Brumen, M.; Lošić, Ž.B.; Kuić, D.; Juretić, D. Enzyme kinetics and the maximum entropy production principle. Biophys. Chem. 2011, 154, 49–55. [Google Scholar] [CrossRef]
- Dobovišek, A.; Županović, P.; Brumen, M.; Juretić, D. Maximum entropy production and maximum Shannon entropy as germane principles for the evolution of enzyme kinetics. In Beyond the Second Law: Entropy Production and Non-Equilibrium Systems; Dewar, R.C., Lineweaver, C.H., Niven, R.K., Regenauer-Lieb, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 361–382. [Google Scholar]
- Dobovišek, A.; Vitas, M.; Brumen, M.; Fajmut, A. Energy conservation and maximal entropy production in enzyme reactions. Biosystems 2017, 158, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Dobovišek, A.; Markovič, R.; Brumen, M.; Fajmut, A. The maximum entropy production and maximum Shannon information entropy in enzyme kinetics. Phys. A 2018, 496, 220–232. [Google Scholar] [CrossRef]
- Šterk, M.; Markovič, R.; Marhl, M.; Fajmut, A.; Dobovišek, A. Flexibility of enzymatic transitions as a hallmark of optimized enzyme steady-state kinetics and thermodynamics. Comput. Biol. Chem. 2021, 91, 107449. [Google Scholar] [CrossRef]
- Lošić, Ž.B.; Donđivić, T.; Juretić, D. Is the catalytic activity of trioseposphate isomerase fully optimized? An investigation based on maximization of entropy production. J. Biol. Phys. 2017, 43, 69–86. [Google Scholar] [CrossRef]
- Juretić, D.; Lošić, Ž.B.; Kuić, D.; Simunić, J.; Dobovišek, A. The maximum entropy production requirement for proton transfers enhances catalytic efficiency for β-lactamases. Biophys. Chem. 2019, 244, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Henry, M.; Schwartz, L. Entropy export as the driving force of evolution. Substantia 2021, 3, 29–56. [Google Scholar] [CrossRef]
- Prigogine, I.; Nicolis, G.; Babloyantz, A. Thermodynamics of evolution. Phys. Today 1972, 11, 23–28. [Google Scholar] [CrossRef]
- Ulusu, N.N. Evolution of enzyme kinetic mechanism. J. Mol. Evol. 2015, 80, 251–257. [Google Scholar] [CrossRef] [PubMed]
- Volk, T.; Pauluis, O. It is not the entropy you produce, rather, how you produce it. Philos. Trans. R. Soc. B 2010, 365, 1317–1322. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Dewar, R.C. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36, 631–641. [Google Scholar] [CrossRef]
- Attard, P. Theory for non-equilibrium statistical mechanics. Phys. Chem. Chem. Phys. 2006, 8, 3585–3611. [Google Scholar] [CrossRef] [PubMed]
- Niven, R.K. Steady state of a dissipative flow-controlled system and the maximum entropy production principle. Phys. Rev. E 2009, 80, 021113. [Google Scholar] [CrossRef] [PubMed]
- Županović, P.; Botrić, S.; Juretić, D.; Kuić, D. Relaxation processes and the maximum entropy production principle. Entropy 2010, 12, 473–479. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. The restrictions of the maximum entropy production principle. Phys. A 2014, 410, 17–21. [Google Scholar] [CrossRef]
- Unrean, P.; Srienc, F. Metabolic networks evolve towards states of maximum entropy production. Metab. Eng. 2011, 6, 666–673. [Google Scholar] [CrossRef]
- Vallino, J.J. Ecosystem biogeochemistry considered as a distributed metabolic network ordered by maximum entropy production. Philos. Trans. R. Soc. B 2010, 365, 1417–1427. [Google Scholar] [CrossRef]
- Virgo, N. From maximum entropy to maximum entropy production: A new approach. Entropy 2010, 12, 107–126. [Google Scholar] [CrossRef]
- Martyushev, L.M. Entropy and entropy production: Old misconceptions and new breakthroughs. Entropy 2013, 15, 1152–1170. [Google Scholar] [CrossRef]
- Benner, S. Enzyme kinetics and molecular evolution. Chem. Rev. 1989, 89, 789–806. [Google Scholar] [CrossRef]
- Fersht, A. Enzyme Structure and Mechanism; W.H. Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Hill, T.L. Free energy transduction in biology. In The Steady State Kinetics and Thermodynamic Formalism, 1st ed.; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Siddiq, M.A.; Hochberg, G.K.; Thornton, J.W. Evolution of protein specificity: Insights from ancestral protein reconstruction. Curr. Opin. Struct. Biol. 2017, 47, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry and Engineering; Perseus Book Publishing: New York, NY, USA, 1994. [Google Scholar]
- Gan, X.; Wang, H.; Yuan, R.; Ao, P. A new criterion beyond divergence for determining the dissipation of a system: Dissipative power. Front. Phys. 2021, 9, 1–8. [Google Scholar] [CrossRef]
- Marhl, M.; Schuster, S. Under what conditions signal transduction pathways are highly flexible in response to external forcing? A case study on calcium oscillations. J. Theor. Biol. 2003, 224, 491–500. [Google Scholar] [CrossRef]
- Perc, M.; Marhl, M. Sensitivity and flexibility of regular and chaotic calcium oscillations. Biophys. Chem. 2003, 104, 509–522. [Google Scholar] [CrossRef]
- Markovič, R.; Gosak, M.; Marhl, M. Broad-scale small-world network topology induces optimal synchronization of flexible oscillators. Chaos Solitons Fractals 2014, 69, 14–21. [Google Scholar] [CrossRef]
- Knowles, J.R.; Albery, W.J. Perfection in enzyme catalysis: The energetics of triosephosphate isomerase. Acc. Chem. Res. 1977, 10, 105–111. [Google Scholar] [CrossRef]
- Albery, W.J.; Knowles, J.R. Evolution of enzyme function and the development of catalytic efficiency. Biochem 1976, 15, 5631–5640. [Google Scholar] [CrossRef] [PubMed]
- Burbaum, J.J.; Raines, R.T.; Albery, W.J.; Knowles, J.R. Evolutionary optimization of the catalytic effectiveness of an enzyme. Biochemistry 1989, 28, 9293–9305. [Google Scholar] [CrossRef]
- Christensen, H.; Martin, M.T.; Waley, G. β-lactamases as fully efficient enzymes. Determination of all the rate constants in the acyl-enzyme mechanism. Biochem. J. 1990, 266, 853–861. [Google Scholar]
- Keener, J.; Sneyd, J. Mathematical physiology. In I: Cellular Physiology, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Aprahamian, I.; Goldrup, S.M. Off Detailed Balance: Non-Equilibrium Steady States in Catalysis, Molecular Motors and Supramolecular Materials, ChemRxiv; Cambridge Open Engage: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Sauro, H.M. Introduction to Metabolic Control Analysis, Version 0.22, 1st ed.; Ambrosius Publishing: Seattle, WA, USA, 2013. [Google Scholar]
- Heinrich, R.; Schuster, S.S. The Regulation of Cellular Systems, 1st ed.; Chapman & Hall: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Wilhelm, T.; Hoffmann-Klipp, E.; Heinrich, R. An evolutionary approach to enzyme kinetics: Optimization of ordered mechanisms. Bull. Math. Biol. 1994, 56, 65–106. [Google Scholar] [CrossRef]
- Gurdas, S.; Gülec, H.A.; Mutlu, M. Immobilization of aspergillus oryzae beta galactosidase onto duolite A568 resin via simple adsorption mechanism. Food Bioprocess Technol. 2012, 5, 904–911. [Google Scholar] [CrossRef]
- Kekenes-Huskey, P.M.; Scott, C.E.; Atalay, S. Quantifying the influence of the crowded cytoplasm on small molecule diffusion. J. Phys. Chem. B 2016, 120, 8696–8706. [Google Scholar] [CrossRef]
- Yadav, J.K.; Prakash, V. Thermal stability of α-amylase in aqueous cosolvent systems. J. Biosci. 2009, 34, 377–387. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, J.K.; Jiao, W.; Easter, A.D.; Parker, E.J.; Schipper, L.A.; Arcus, V.L. Change in heat capacity for enzyme catalysis determines temperature dependence of enzyme catalyzed rates. ACS Chem. Biol. 2013, 8, 2388–2393. [Google Scholar] [CrossRef]
- Arcus, V.L.; Prentice, E.J.; Hobbs, J.K.; Mulholland, A.J.; Van Der Kamp, M.W.; Pudney, C.R.; Parker, E.J.; Schipper, L.A. On the temperature dependence of enzyme-catalyzed rates. Biochem 2016, 55, 1681–1688. [Google Scholar] [CrossRef] [PubMed]
- DeLong, J.P.; Gibert, J.P.; Luhring, T.M.; Bachman, G.; Reed, B.; Neyer, A.; Montooth, K.L. The combined effects of reactant kinetics and enzyme stability explain the temperature dependence of metabolic rates. Ecol. Evol. 2017, 7, 3940–3950. [Google Scholar] [CrossRef]
- Nam, H.; Lewis, N.E.; Lerman, J.A.; Lee, D.-H.; Chang, R.L.; Kim, D.; Palsson, B.O. Network context and selection in the evolution to enzyme specificity. Science 2012, 337, 1101–1104. [Google Scholar] [CrossRef]
- Jensen, R.A. Enzyme recruitment in evolution of new function. Annu. Rev. Microbiol. 1976, 409, 409–425. [Google Scholar] [CrossRef]
- Aharoni, A.; Gaidukov, L.; Khersonsky, O.; Gould, S.M.; Roodveldt, C.; Tawfik, D.S. The ‘evolvability’ of promiscuous protein functions. Nat. Genet. 2005, 37, 73. [Google Scholar] [CrossRef] [PubMed]
| Quantity and Its Unit | Two-State Kinetic Scheme | Three-State Kinetic Scheme | ||
|---|---|---|---|---|
| Expression | Value | Expression | Value | |
| Equation (29) | Equation (A14) | |||
| 1 | ||||
| Equation (27) | Equation (27) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobovišek, A.; Vitas, M.; Blaževič, T.; Markovič, R.; Marhl, M.; Fajmut, A. Self-Organization of Enzyme-Catalyzed Reactions Studied by the Maximum Entropy Production Principle. Int. J. Mol. Sci. 2023, 24, 8734. https://doi.org/10.3390/ijms24108734
Dobovišek A, Vitas M, Blaževič T, Markovič R, Marhl M, Fajmut A. Self-Organization of Enzyme-Catalyzed Reactions Studied by the Maximum Entropy Production Principle. International Journal of Molecular Sciences. 2023; 24(10):8734. https://doi.org/10.3390/ijms24108734
Chicago/Turabian StyleDobovišek, Andrej, Marko Vitas, Tina Blaževič, Rene Markovič, Marko Marhl, and Aleš Fajmut. 2023. "Self-Organization of Enzyme-Catalyzed Reactions Studied by the Maximum Entropy Production Principle" International Journal of Molecular Sciences 24, no. 10: 8734. https://doi.org/10.3390/ijms24108734







