Self-Association of the Anion of 7-Oxodeoxycholic Acid (Bile Salt): How Secondary Micelles Are Formed
Abstract
:1. Introduction
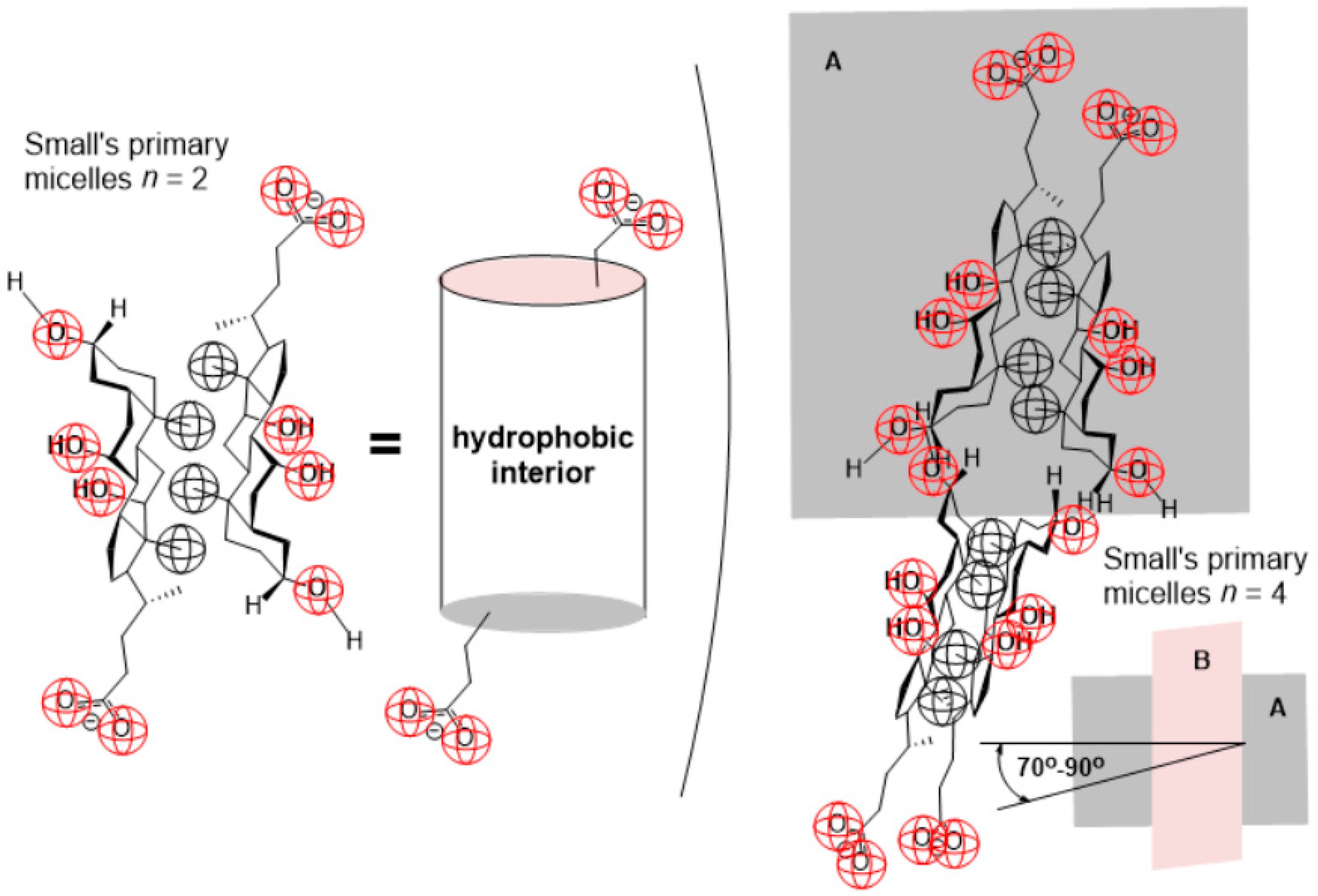
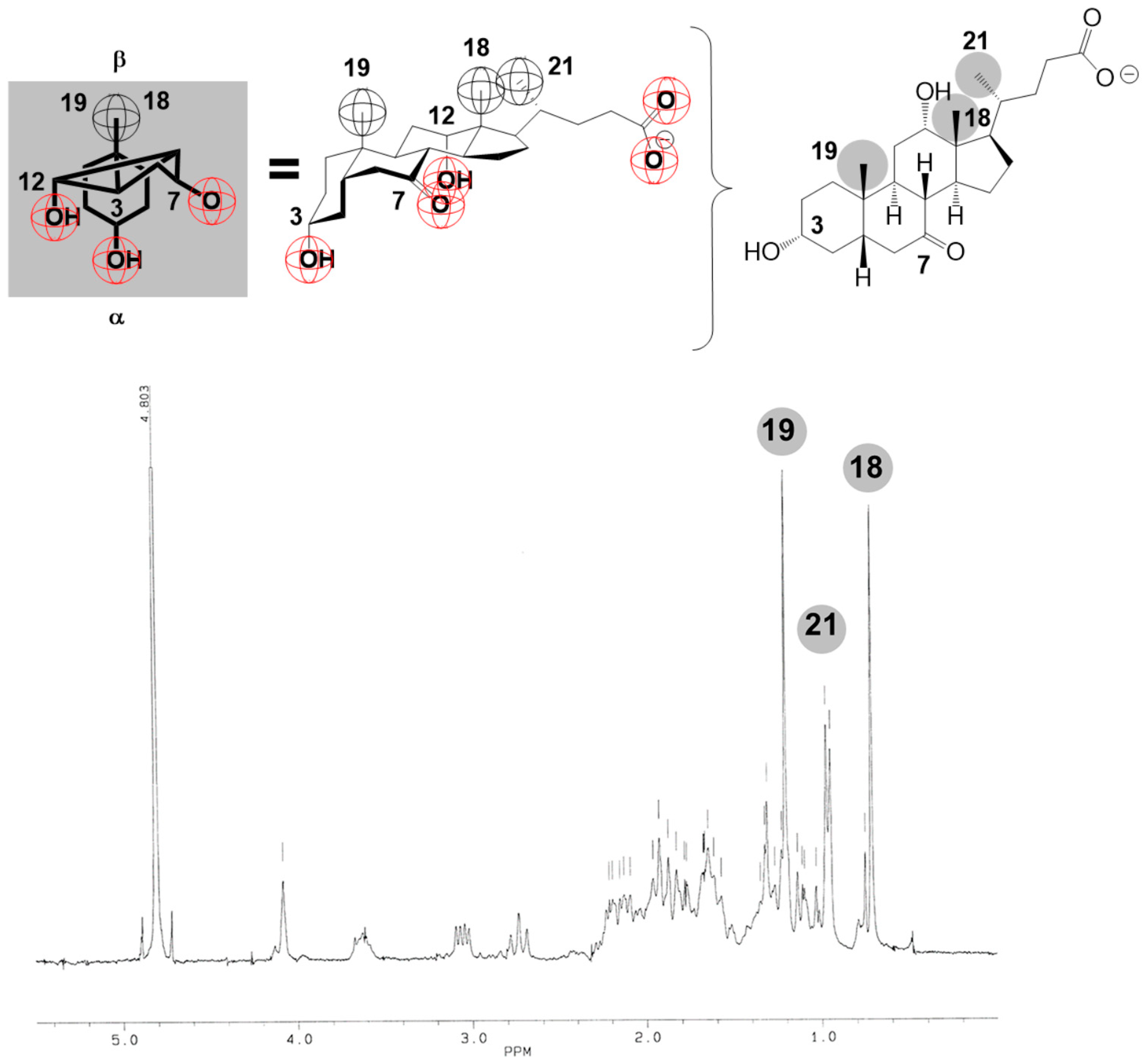
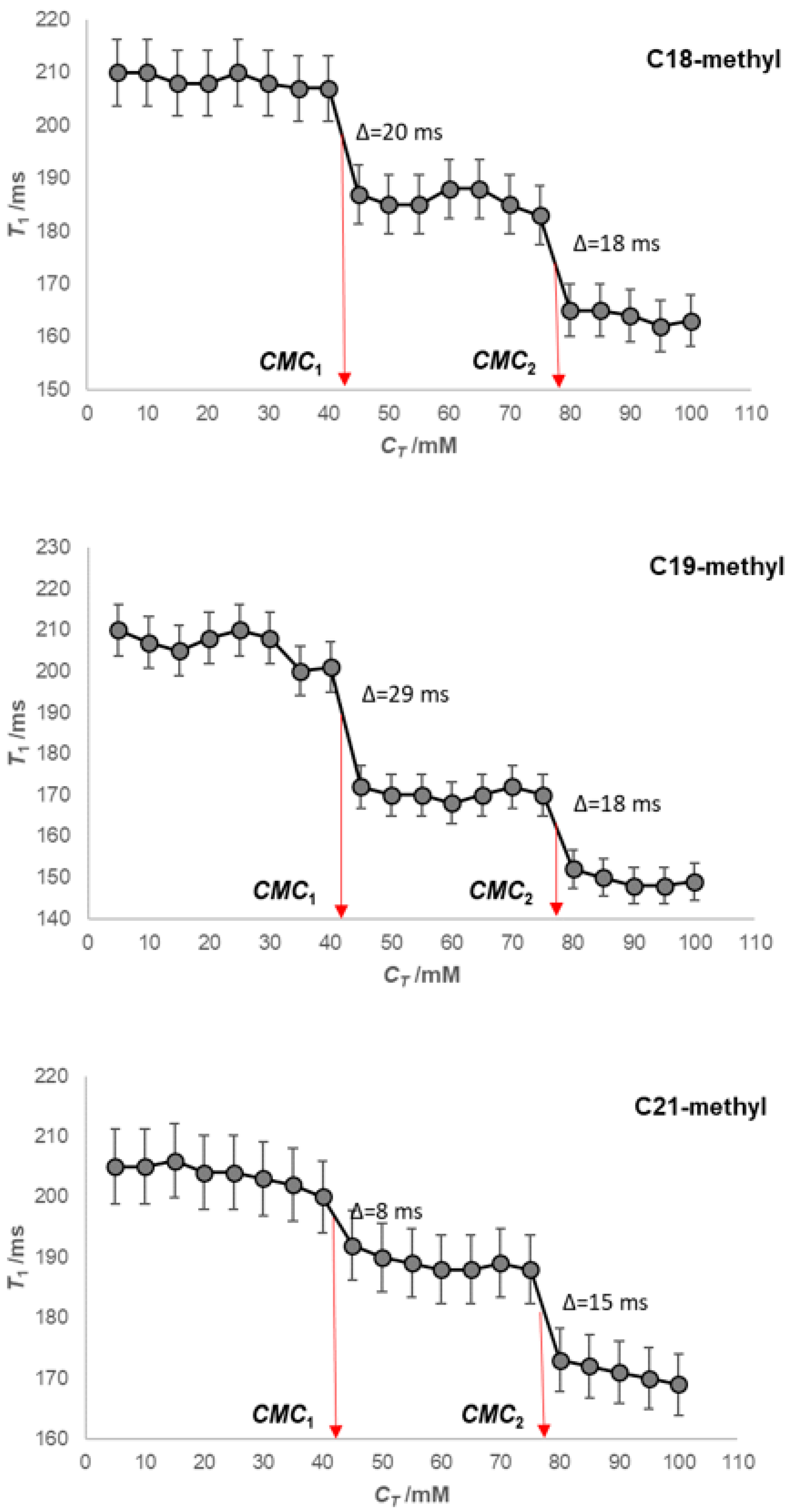
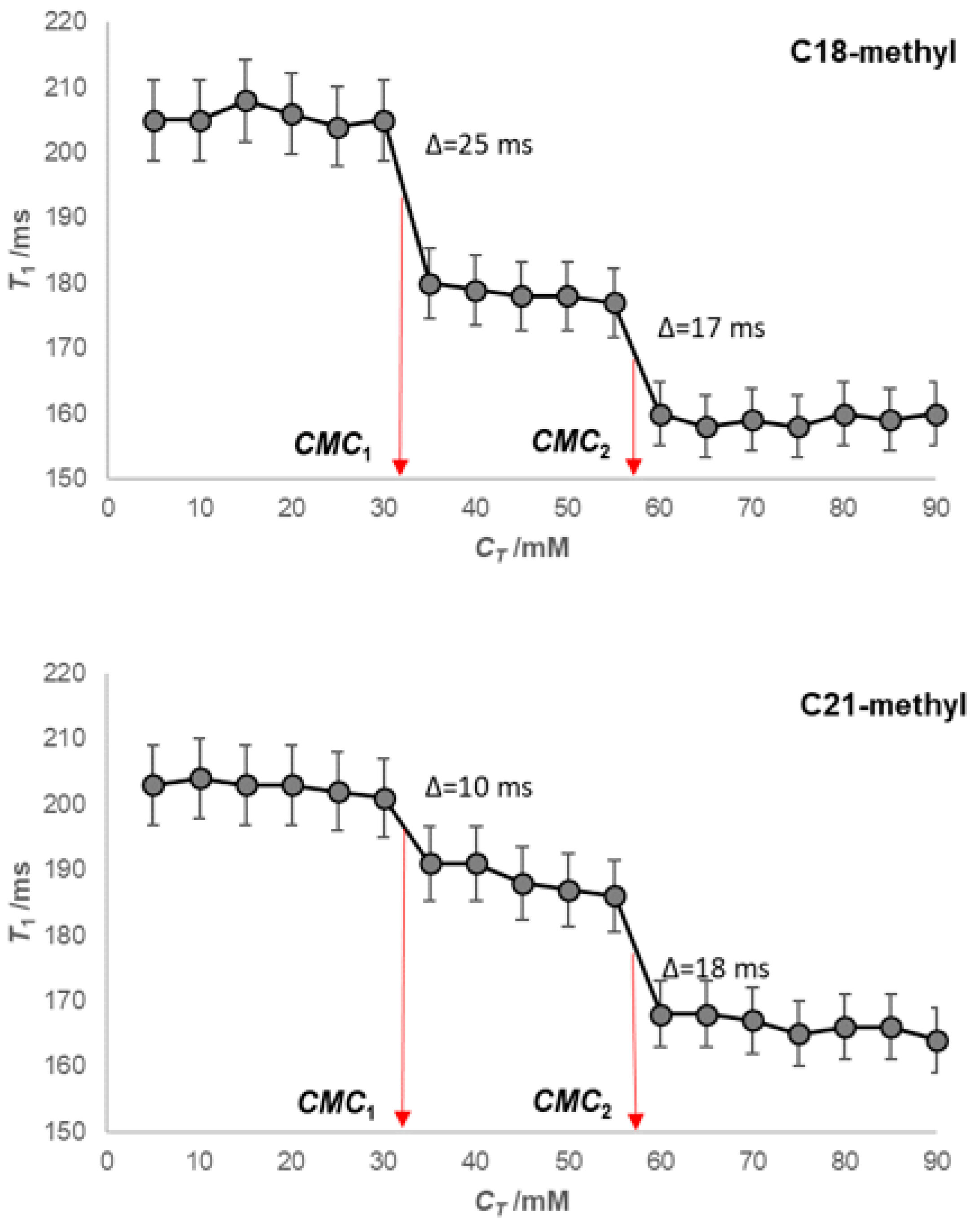
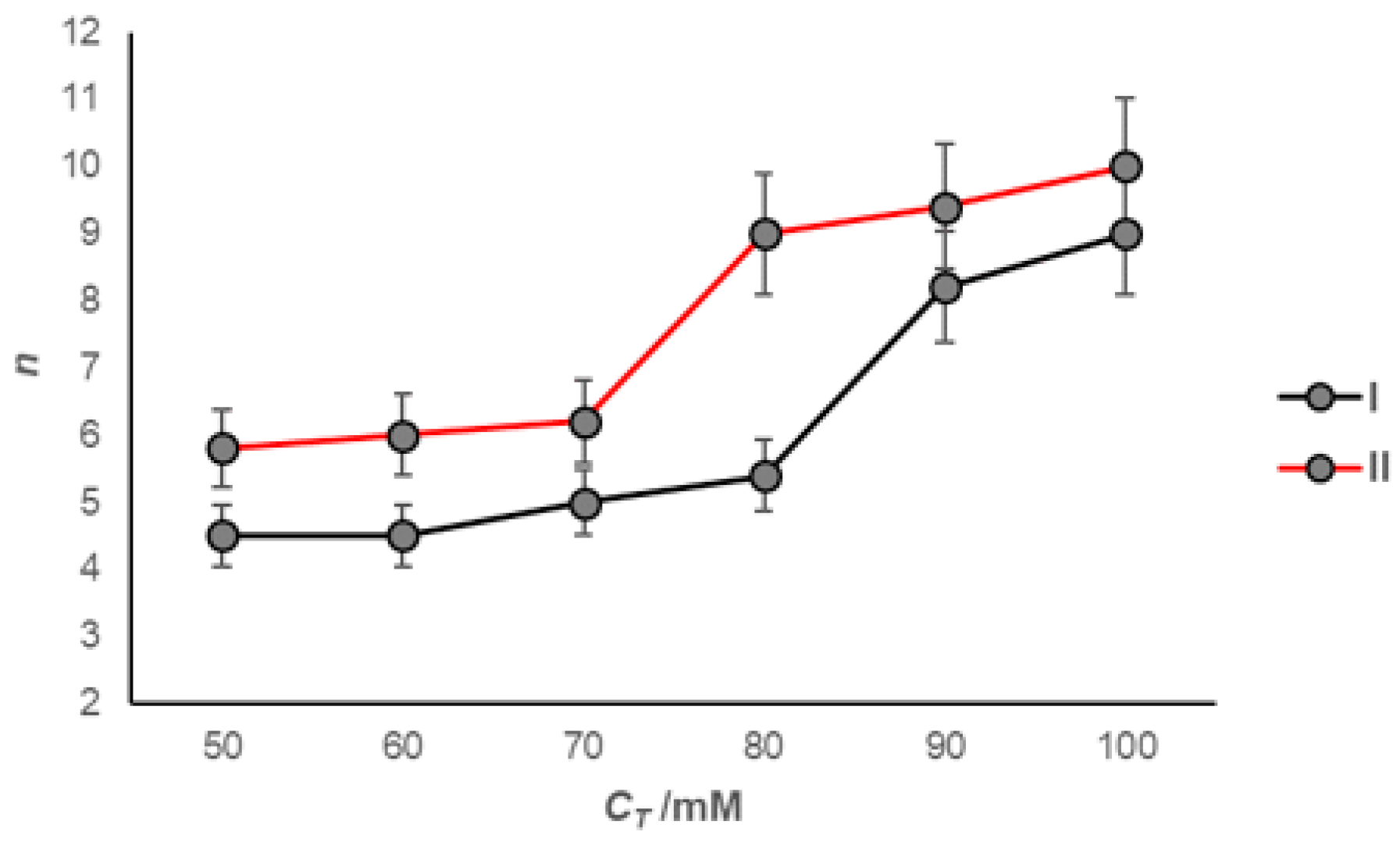
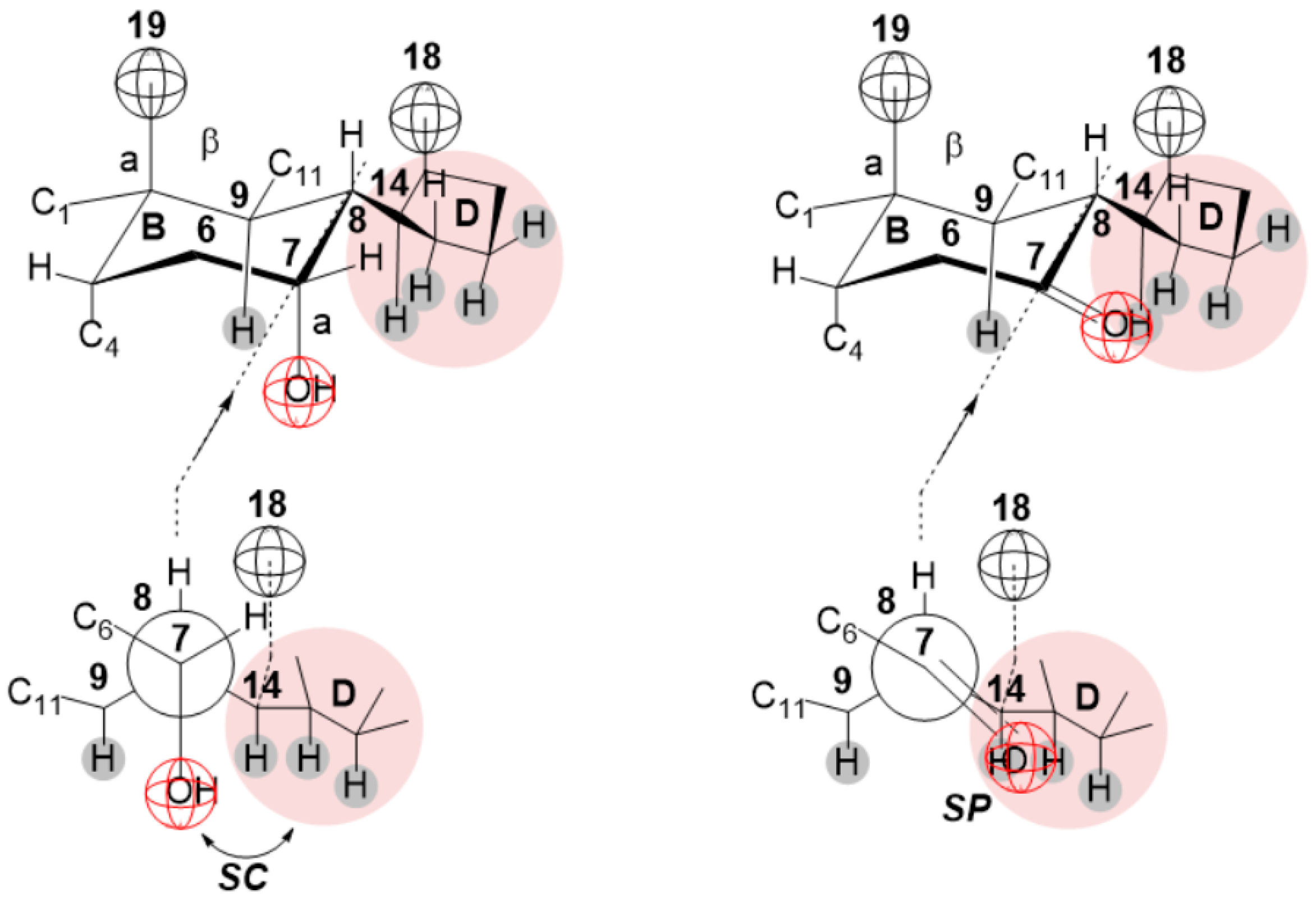
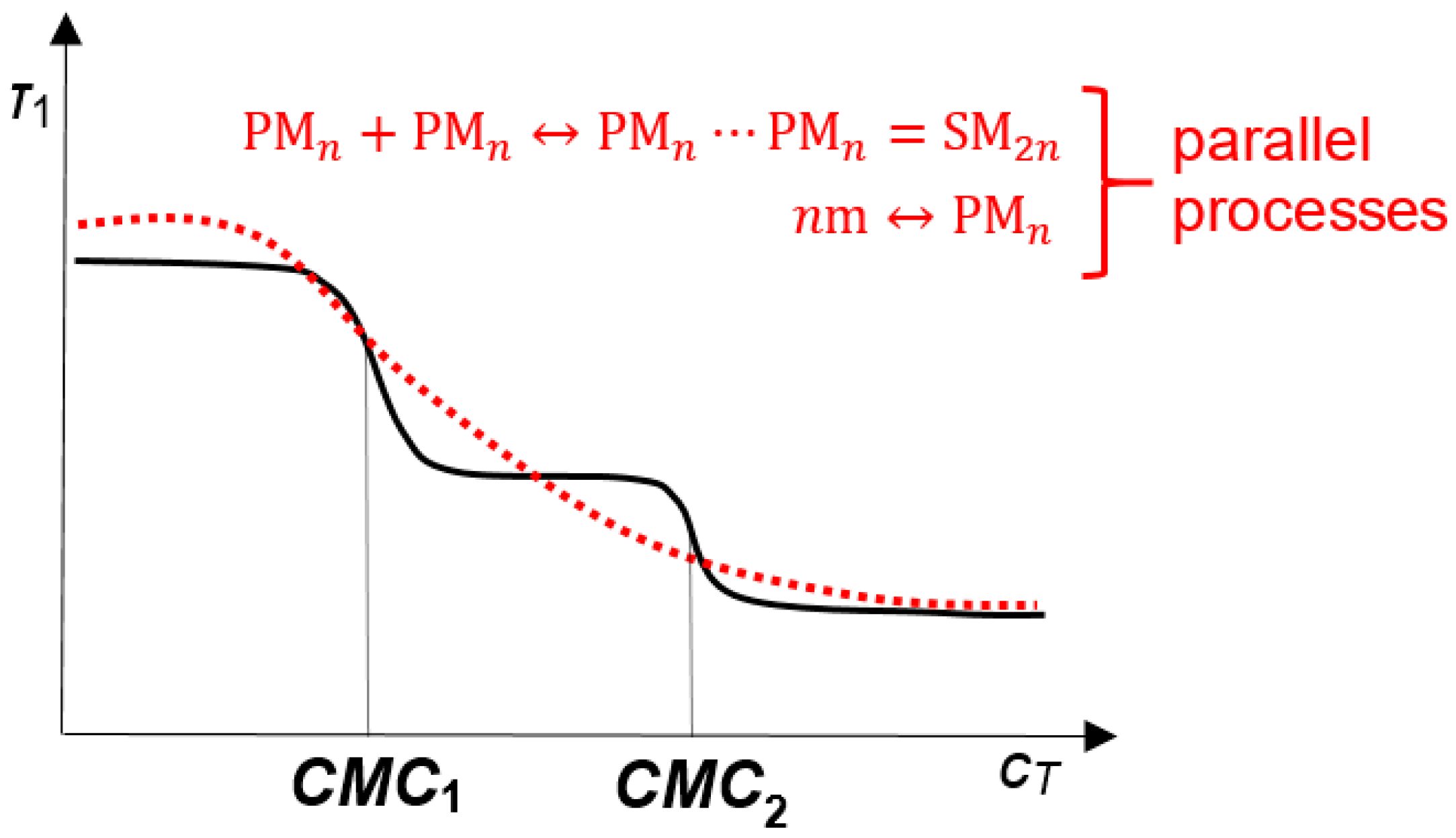
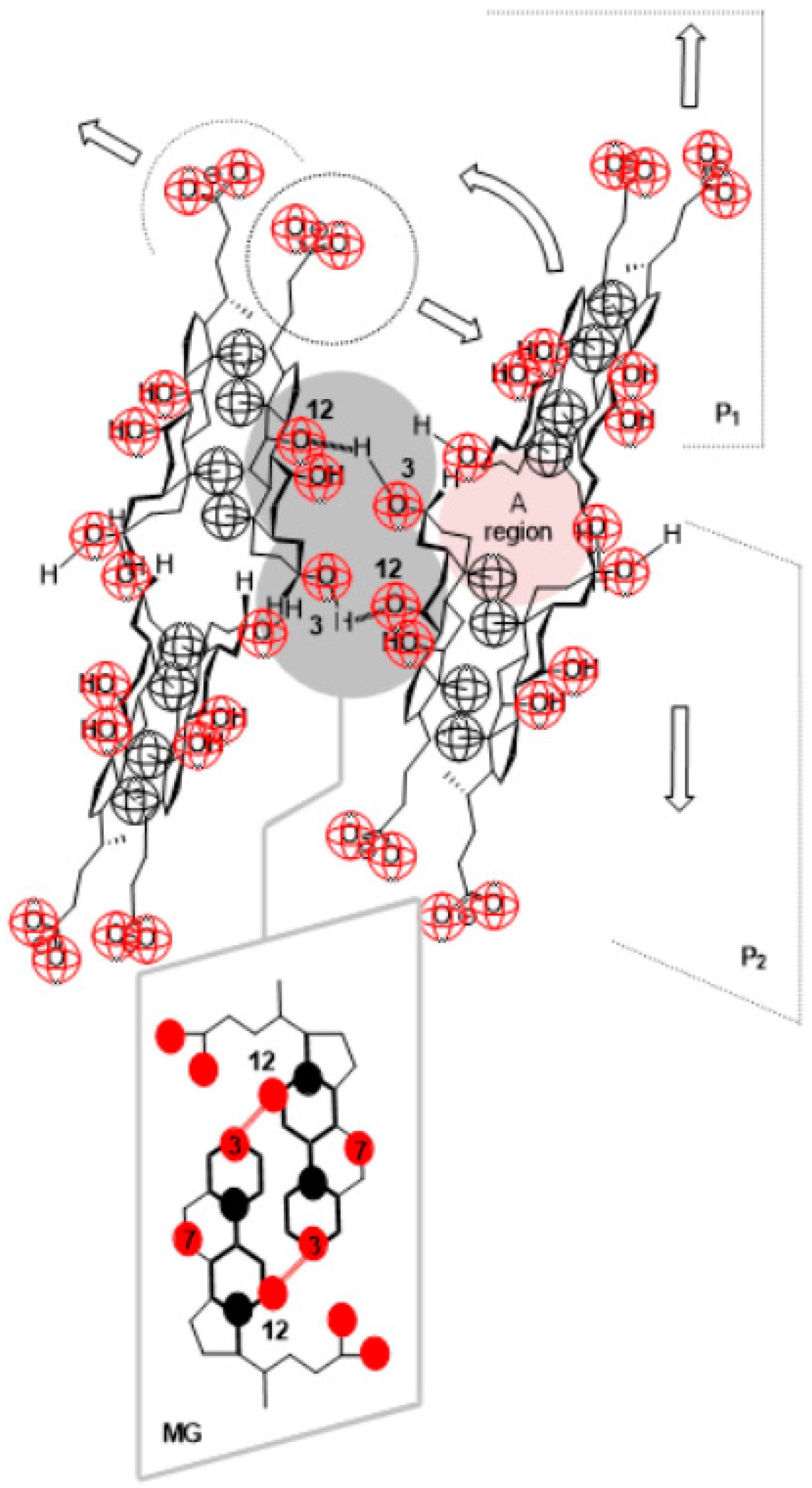
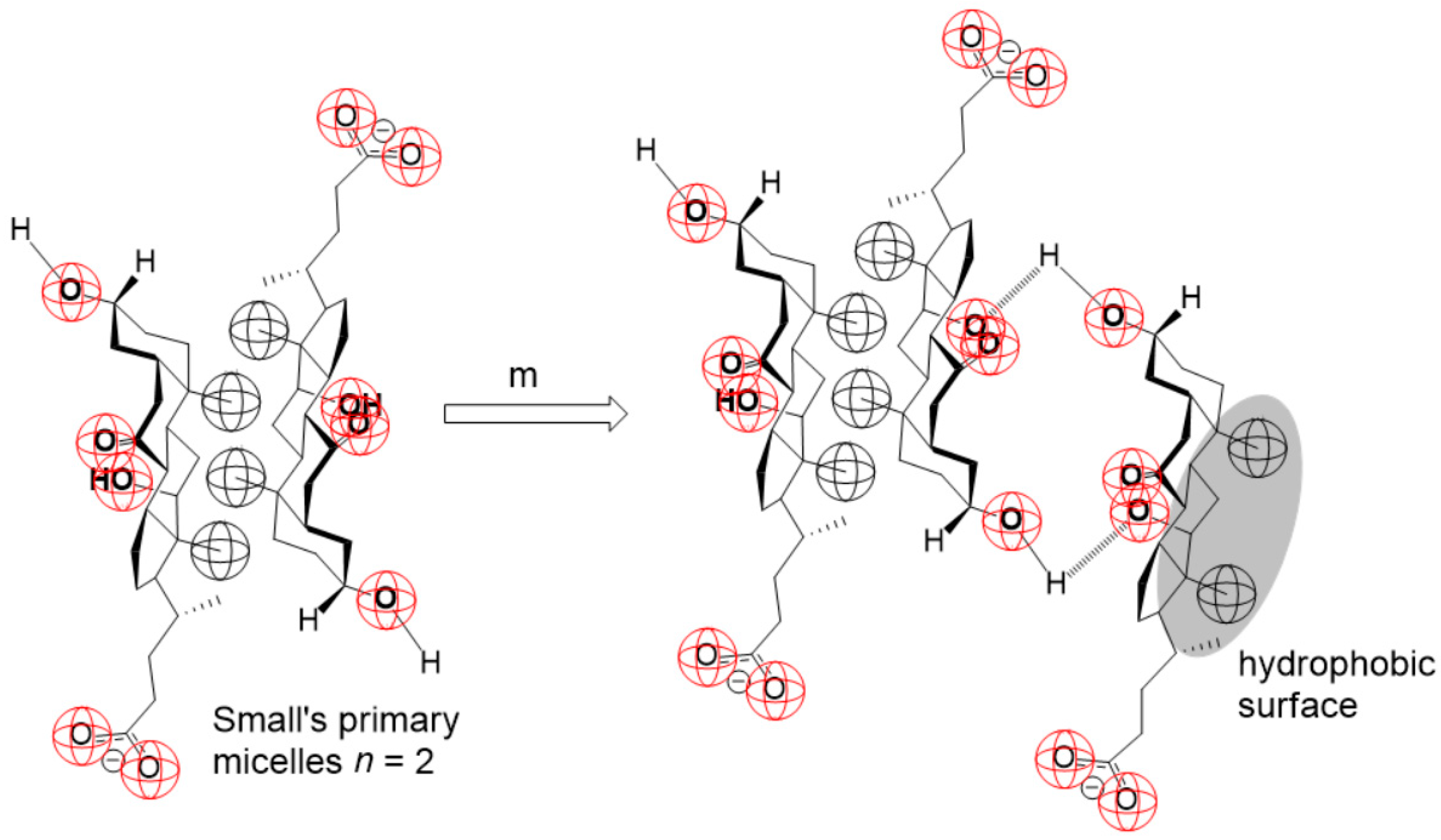
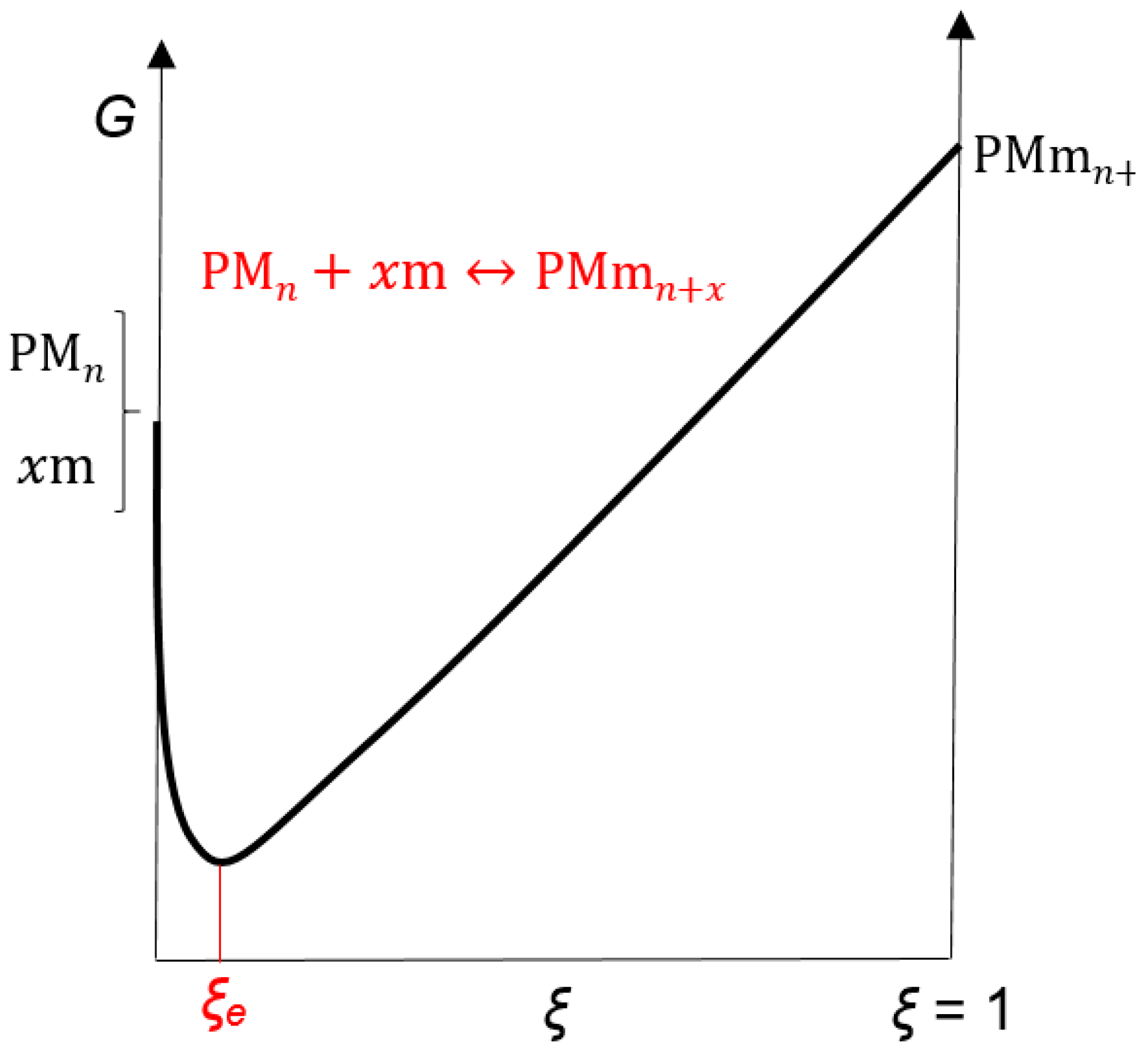
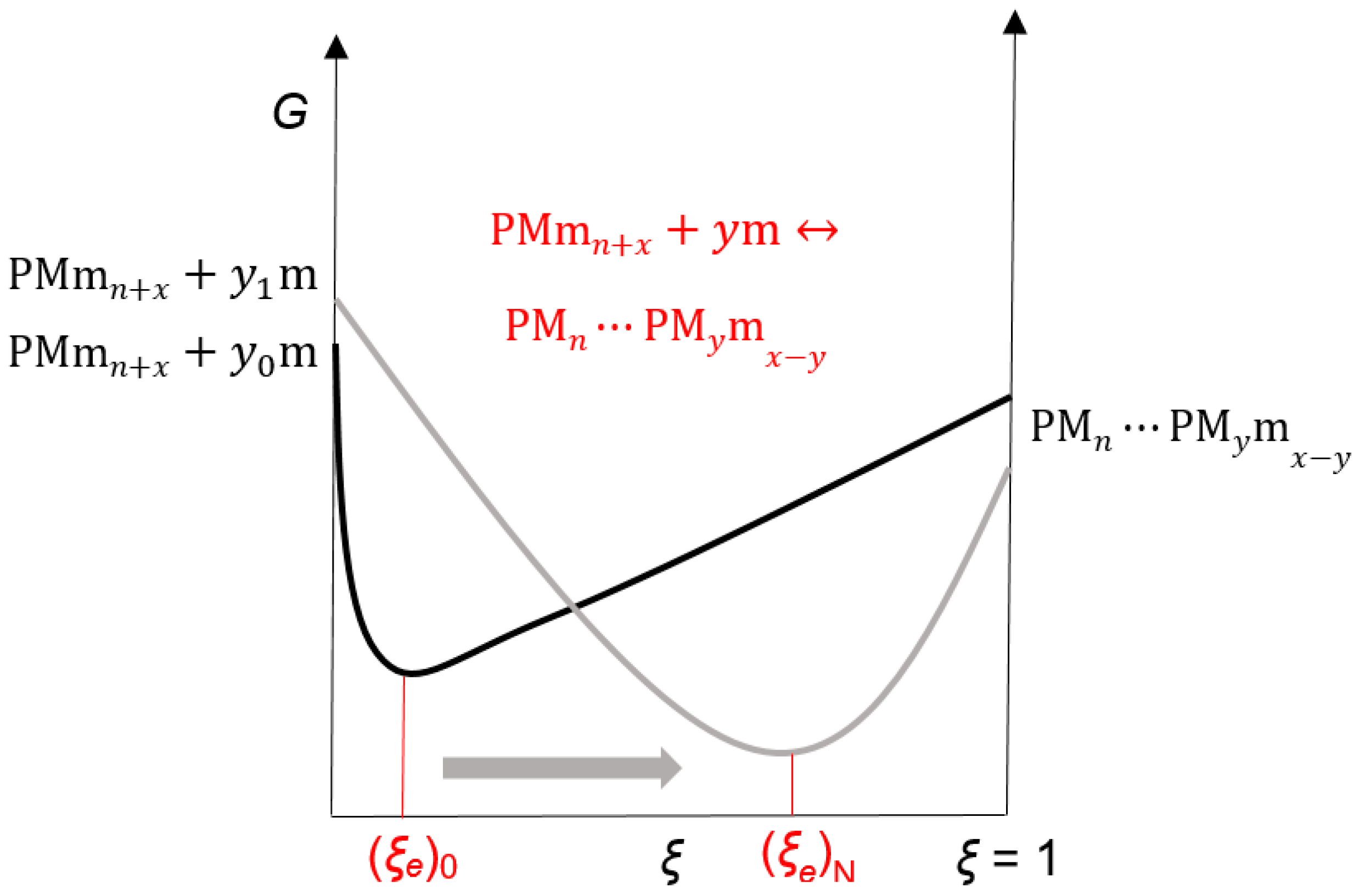
2. Results
3. Discussion
4. Materials and Methods
4.1. 1H NMR Studies
4.2. Fluorescence Measurements—Determination of the Micelle Aggregation Numbers
4.3. Dynamic Light Scattering (DLS) Measurements
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
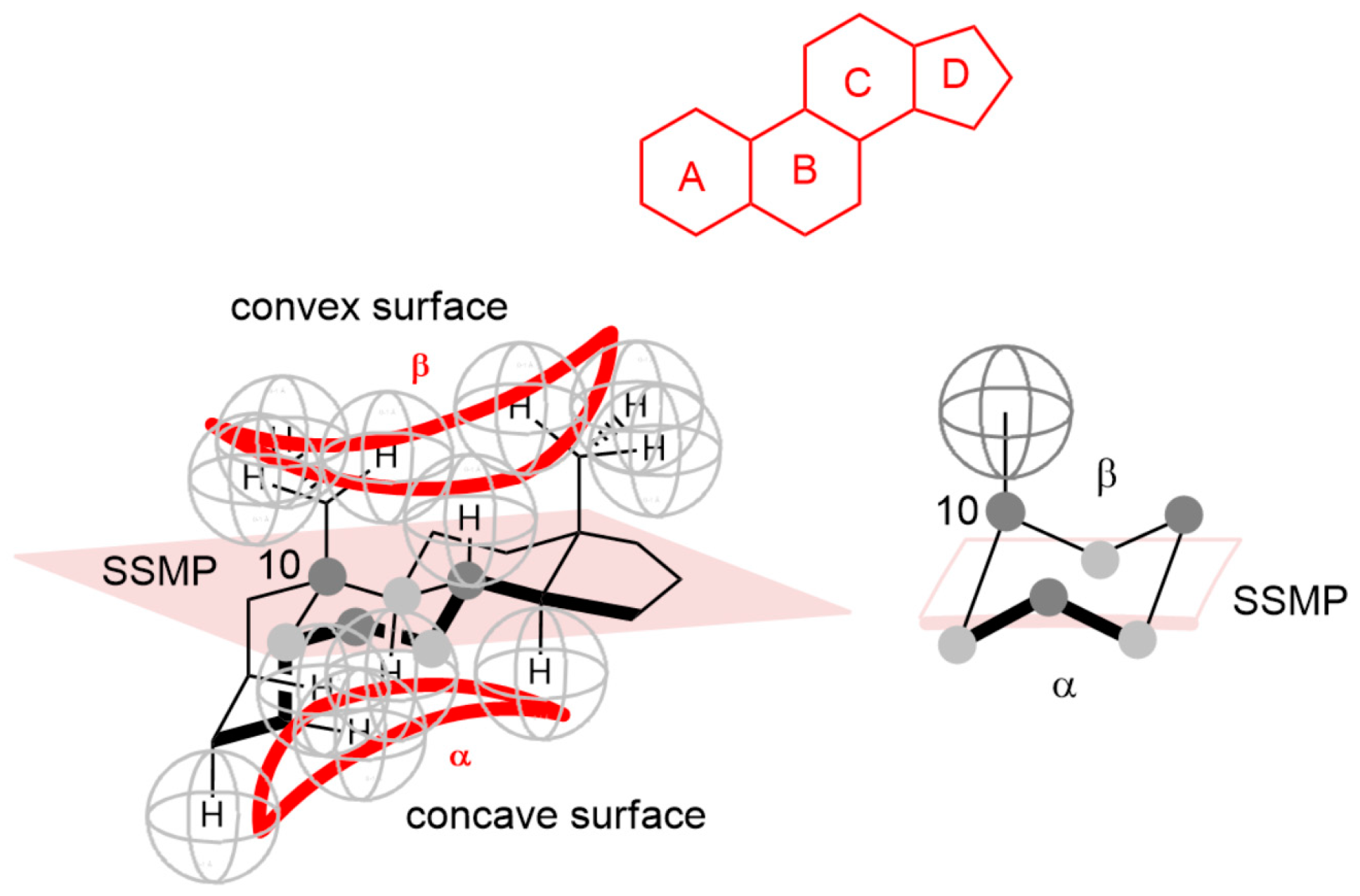
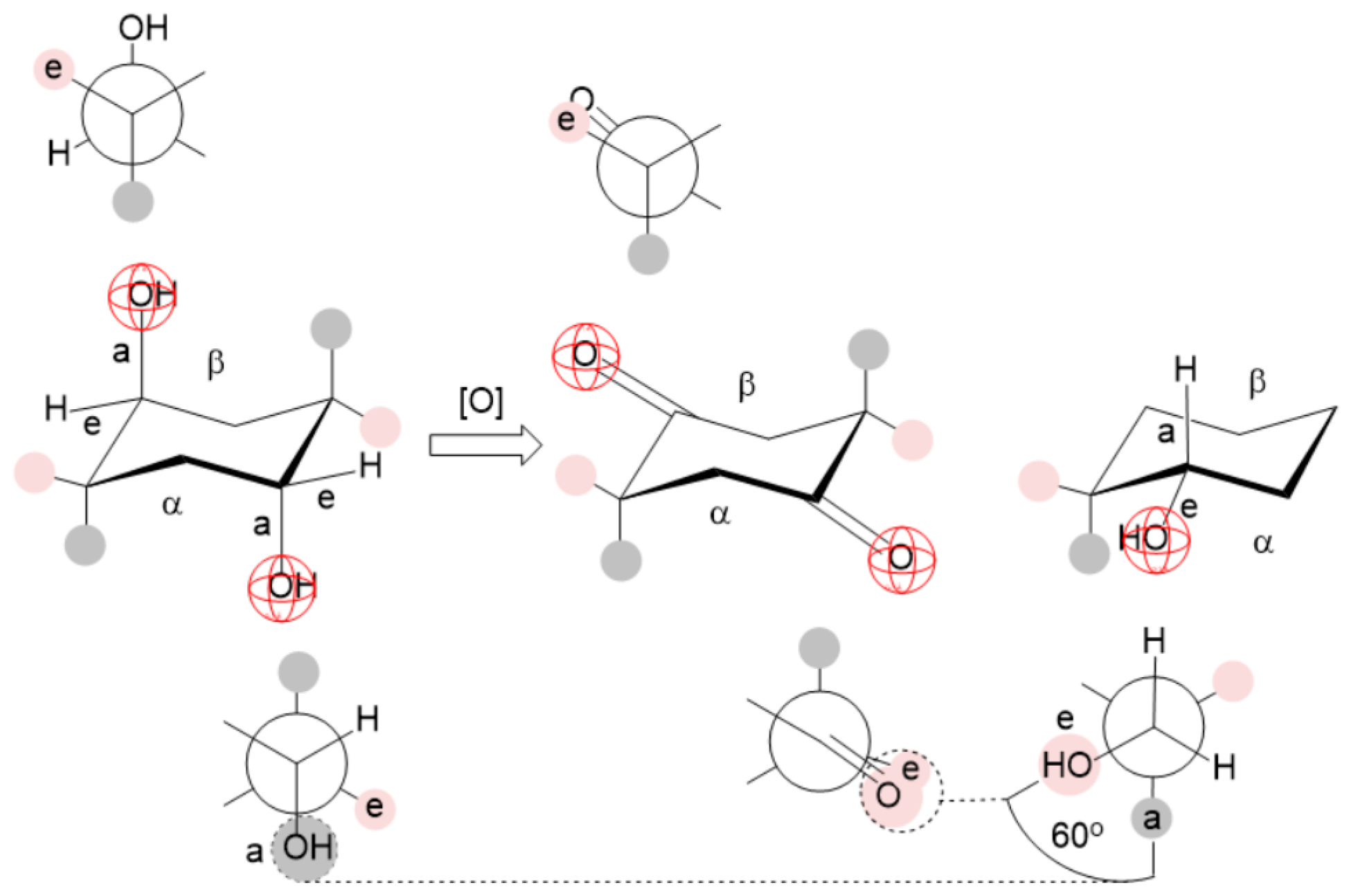
Appendix B

Appendix C
Appendix D
Appendix E
Appendix F
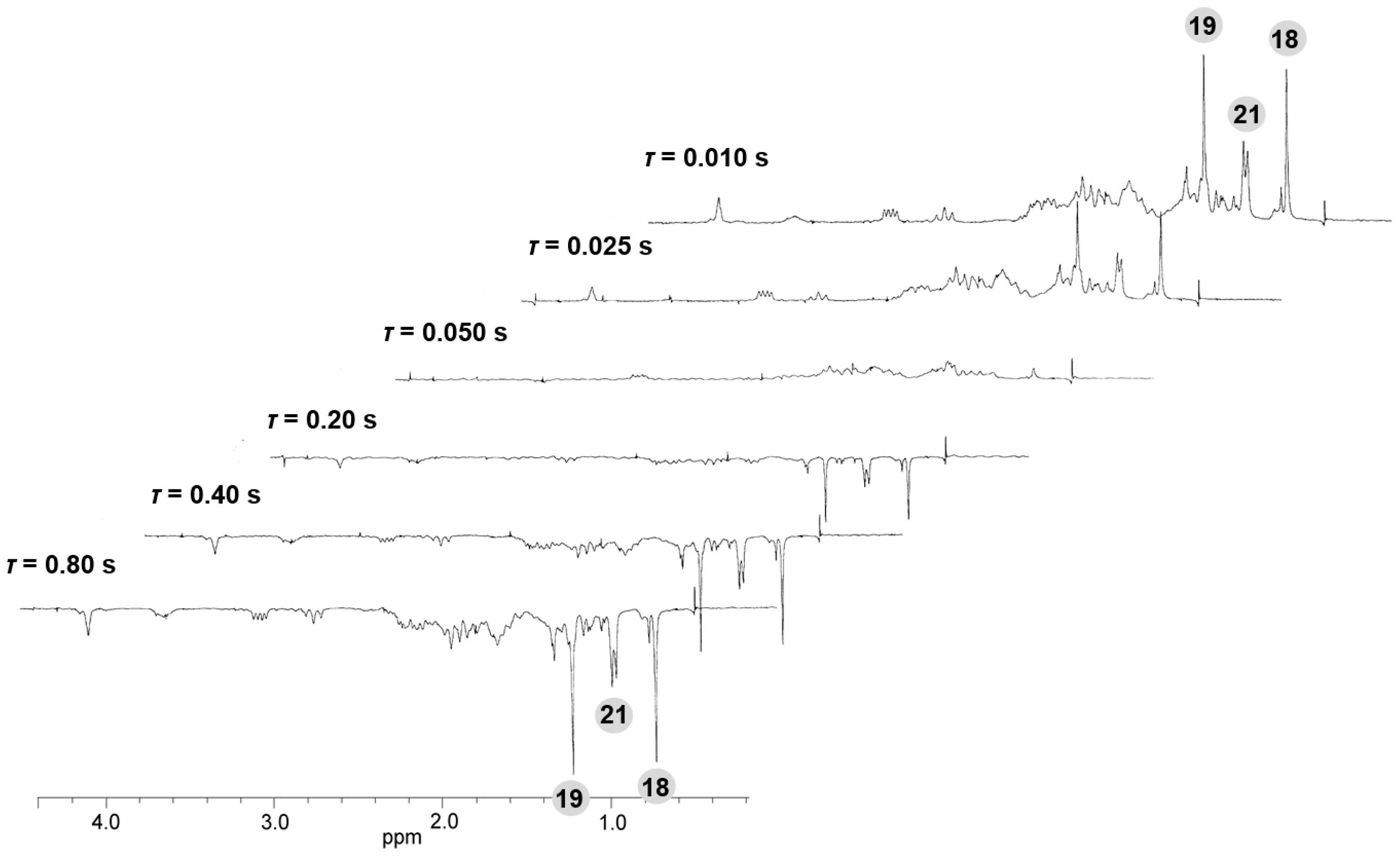
References
- Small, D.M. The physical chemistry of cholanic acids. In The Bile Acids: Chemistry, Physiology and Metabolism; Nair, P.P., Kritchevsky, D., Eds.; Plenum Press: New York, NY, USA, 1971; Volume 3, pp. 249–332. [Google Scholar]
- Hofmann, A.F.; Roda, A. Physicochemical properities of bile acids and their relationship to biological properties: An overview of the problem. J. Lipid Res. 1984, 25, 1477–1489. [Google Scholar] [CrossRef]
- Armstrong, M.J.; Carey, M.C. The hydrophobic-hydrophilic balance of bile salts. Inverse correlation between reverse-phase high performance liquid chromatographic mobilities and micellar cholesterol-solubilizing capacities. J. Lipid Res. 1982, 23, 70–80. [Google Scholar] [CrossRef]
- Poša, M. Heuman indices of hydrophobicity in bile acids and compared with new developed and conventional molecular descriptors. Biochimie 2014, 97, 28–38. [Google Scholar] [CrossRef]
- Poša, M.; Tepavčević, V.; Grbović, L.; Mikulić, M.; Pavlović, K. Hydrophobicity and self-association (micellisation) of bile salts with a lactone or lactam group in a steroid skeleton. J. Phys. Org. Chem. 2021, 34, e4133. [Google Scholar] [CrossRef]
- Roda, A.; Hofmann, A.F.; Mysels, K.J. The influence of bile salt structure on self-association in aqueous solutions. J. Biol. Chem. 1983, 258, 6362–6370. [Google Scholar] [CrossRef] [PubMed]
- Poša, M.; Farkaš, Z. Cholesterol solubilization by oxo derivatives of selected bile acids and their osmotic resistance. Collect. Czechoslov. Chem. Commun. 2010, 75, 767–784. [Google Scholar] [CrossRef]
- Mikov, M.; Fawcett, J.P. Bile Acids; Medishet Publisher: Geneva, Switzerland, 2007. [Google Scholar]
- Madenci, D.; Egelhaaf, U.S. Self-assembly in aqueous bile salt solutions. Curr. Opin. Colloid Interface Sci. 2010, 15, 109–115. [Google Scholar] [CrossRef]
- Roda, A.; Minutello, A.; Angellotti, M.A.; Fini, A. Bile acid structure-activity relationships: Evaluation of bile acids lipophilicity using 1-octanol/water partition coefficient and reverse phase HPLC. J. Lipid Res. 1990, 31, 1433–1443. [Google Scholar] [CrossRef]
- Poša, M. Symmetry (asymmetry) of the molar excess Gibbs free energy function of the binary mixed micelles of bile acid anion and classical cationic surfactant: Influence of sterically shielded and sterically unshielded polar groups of the steroid skeleton. Symmetry 2022, 14, 2337. [Google Scholar] [CrossRef]
- Heuman, D.M. Quantitative estimation of the hydrophilic-hydrophobic balance of mixed bile salt solutions. J. Lipid Res. 1989, 30, 719–730. [Google Scholar] [CrossRef]
- Natalini, B.; Sardella, R.; Camaioni, E.; Gioiello, A.; Pellicciari, R. Correlation between CMC and chromatographic index: Simple and effective evaluation of the hydrophobic/hydrophilic balance of bile acids. Anal. Bioanal. Chem. 2007, 388, 1681–1688. [Google Scholar] [CrossRef] [PubMed]
- Shaw, R.; Rivetna, M.; Elliot, W.H. Relationship between the mobility on reverse-phase high performance liquid chromatography and the structure of bile acids. J. Chromatogr. 1980, 21, 347–361. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, H.; Mikov, M.; Tucker, I.G. Physicochemical and biological characterization of monoketocholic acid, a novel permeability enhancer. Mol. Pharm. 2009, 6, 448–456. [Google Scholar] [CrossRef]
- Al-Salami, H.; Butt, G.; Tucker, I.G.; Mikov, M. Influence of the semisynthetic bile acid MKC on the ileal permeation of gliclazide in vitro in healthy and diabetic rats treated with probiotics. Methods Find. Exp. Clin. Pharmacol. 2008, 30, 107–113. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Fawcett, J.P.; Østergaard, J.; Zhang, H.; Tucker, I.G. Mechanistic studies of the effect of bile salts on rhodamine 123 uptake into RBE4 cells. Mol. Pharm. 2012, 9, 29–36. [Google Scholar] [CrossRef]
- Azum, N.; Rub, M.A.; Asiri, A.M. Bile salt–bile salt interaction in mixed monolayer and mixed micelle formation. J. Chem. Thermodyn. 2019, 128, 406–414. [Google Scholar] [CrossRef]
- Rub, M.A.; Azum, N.; Khan, F.; Asiri, A.M. Aggregation of sodium salt of ibuprofen and sodium taurocholate mixture in different media: A tensiometry and fluorometry study. J. Chem. Thermodyn. 2018, 121, 199–210. [Google Scholar] [CrossRef]
- Enache, M.; Toader, A.M.; Neacsu, V.; Ionita, G.; Enache, M.I. Spectroscopic investigation of the interaction of the anticancer drug mitoxantrone with sodium taurodeoxycholate (NaTDC) and sodium taurocholate (NaTC) bile salts. Molecules 2017, 22, 1079. [Google Scholar] [CrossRef] [Green Version]
- Toader, A.M.; Dascalu, I.; Neacsu, E.I.; Enache, M. Binding interactions of actinomycin D anticancer drug with bile salts micelles. J. Serb. Chem. Soc. 2023, 88, 367–379. [Google Scholar] [CrossRef]
- Wiedmann, T.S.; Kamel, L. Examination of the solubilization of drugs by bile salt micelles. J. Pharm. Sci. 2002, 91, 1743–1764. [Google Scholar] [CrossRef]
- Dongowski, G.; Fritzsch, B.; Giessler, J.; Hartl, A.; Kuhlmann, O.; Neubert, R.H.H. The influence of bile salts and mixed micelles on the pharmacokinetics of quinine in rabbits. Eur. J. Pharm. Biopharm. 2005, 60, 147–151. [Google Scholar] [CrossRef]
- di Gregorio, M.C.; Cautela, J.; Galantini, L. Physiology and physical chemistry of bile acids. Int. J. Mol. Sci. 2021, 22, 1780. [Google Scholar] [CrossRef]
- Garidel, P.; Hildebrand, A.; Knauf, K.; Blume, A. Membranolytic activity of bile salts: Influence of biological membrane properities and composition. Molecules 2007, 12, 2292–2326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poša, M.; Bjedov, S.; Tepavčević, V.; Mikulić, M.; Sakač, M. Physicochemical characterization of novel 3-carboxymethyl-bile salts, as permeability and solubility enhancers. J. Mol. Liq. 2020, 303, 112634. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A.; Bjedov, S.; Obradovic, S.; Tepavčević, V.; Sakač, M. Parameters of micellization and hydrophobicity of sodium salts of 7-buthyl (butylidene) and 7-octyl (octylidene) derivatives of the cholic and the deoxycholic acid in a water solution: Pattern recognition—Linear hydrophobic congeneric groups. J. Mol. Liq. 2016, 224, 9–18. [Google Scholar] [CrossRef]
- Small, D.M.; Penkett, S.A.; Chapman, D. Studies on simple and mixed bile salt micelles by nuclear magnetic resonance spectroscopy. Biochem. Biophys. Acta 1969, 176, 178–189. [Google Scholar] [CrossRef]
- Rovnyak, D.; He, J.; Kong, S.; Eckenroad, K.W.; Manley, G.A.; Geffert, R.M.; Krout, M.R.; Strein, T.G. Determining sequential micellization steps of bile salts with multi-CMC modeling. J. Colloid Interface Sci. 2023, 644, 496–508. [Google Scholar] [CrossRef]
- Gouin, S.; Zhu, X.X. Fluorescence and NMR studies of the effect of a bile acid dimer on the micellization of bile salts. Langmuir 1998, 14, 4025–4029. [Google Scholar] [CrossRef]
- Kawamura, H.; Murata, Y.; Yamaguchi, T.; Igimi, H.; Tanaka, M.; Sugihara, G.; Kratohvil, J.P. Spin-label studies of bile salt micelles. J. Phys. Chem. 1989, 93, 3321–3326. [Google Scholar] [CrossRef]
- Mazer, D.M.; Carey, M.C.; Kwasnick, R.F.; Benedek, G.B. Quasielastic light scattering studies of aqueous biliary lipid systems. Size, shape, and thermodynamics of bile salt micelles. Biochemistry 1979, 18, 3064–3075. [Google Scholar] [CrossRef]
- Pártai, L.B.; Jedlovszky, P.; Sega, M. Molecular aggregates in aqueous solutions of bile acid salts. Molecular dynamics simulation study. J. Phys. Chem. B 2007, 111, 9886–9896. [Google Scholar] [CrossRef]
- Pártai, L.B.; Sega, M.; Jedlovszky, P. Morphology of bile salts micelles as studied by computer simulation methods. Langmuir 2007, 23, 12322–12328. [Google Scholar] [CrossRef]
- Pártai, L.B.; Sega, M.; Jedlovszky, P. Counterion binding in the aqueous solutions of bile acid salts, as studied by computer simulation methods. Langmuir 2008, 24, 10729–10736. [Google Scholar] [CrossRef] [PubMed]
- Haustein, M.; Schiller, P.; Wahab, M.; Mogel, H.J. Computer simulations of the formation of bile salt micelles and bile salt/DPPC mixed micelles in aqueous solutions. J. Solution Chem. 2014, 43, 1755–1770. [Google Scholar] [CrossRef]
- Thomas, D.C.; Christian, S.D. Micellar and surface behavior of sodium deoxycholate characterized by surface tension and ellipsometric methods. J. Colloid Interface Sci. 1980, 78, 466–478. [Google Scholar] [CrossRef]
- Ekwall, P.; Fontelli, K.; Sten, A. Proceedings of the 2nd International Congress of Surface Activity: Solid/ Liquid Interface; Butterworth: London, UK, 1957; p. 357. [Google Scholar]
- Rusanov, A.I. The mass-action-law theory of micellization revisited. Langmuir 2014, 30, 14443–14451. [Google Scholar] [CrossRef]
- Meier, A.R.; Yehl, J.B.; Eckenroad, K.W.; Manley, G.A.; Strein, T.G.; Rovnyak, R. Stepwise aggregation of cholate and deoxycholate dictates the formation and loss of surface-available chirally selective binding sites. Langmuir 2018, 34, 6489–6501. [Google Scholar] [CrossRef]
- Matsuoka, K.; Moroi, Y. Micelle formation of sodium deoxycholate and sodium ursodeoxycholate. Biochim. Biophys. Acta 2002, 1580, 189–199. [Google Scholar] [CrossRef]
- Sugioka, H.; Moroi, Y. Micelle formation of sodium cholate and solubilization into the micelle. Biochim. Biophys. Acta 1998, 1394, 99–110. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, K.; Takagi, K.; Honda, C. Micelle formation of sodium hyodeoxycholate. Chem. Phys. Lipids 2013, 172–173, 6–13. [Google Scholar] [CrossRef]
- Coello, A.; Meijide, F.; Rodríguez Núñez, E.; Vázquez Tato, J. Aggregation behavior of bile salts in aqueous solution. J. Pharm. Sci. 1996, 85, 9–15. [Google Scholar] [CrossRef]
- Poša, M.; Sebenji, A. Determination of the number average aggregation numbers of bile salt micelles with a special emphasis on their oxo derivatives—The effect of the steroid skeleton. BBA-Gen. Subj. 2014, 1840, 1072–1082. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A.; Popović, K.; Kumar, D. Thermodynamics of trimethyltetradecylammonium bromide—Sodium deoxycholate binary mixed micelle formation in aqueous solution: Regular Solution Theory with mutual compensation of excess configurational and excess conformational entropy. J. Mol. Liq. 2022, 360, 119473. [Google Scholar] [CrossRef]
- Garidel, P.; Hildebrand, A. Thermodynamic properties of association of colloids. J. Therm. Anal. Calorim. 2005, 82, 483–489. [Google Scholar] [CrossRef]
- Garidel, P.; Hildebrand, A.; Neubert, R.; Blume, A. Thermodynamic characterization of bile salt aggregation as a function of temperature and ionic strength using isotermal titration calorimetry. Langmuir 2000, 16, 5267–5275. [Google Scholar] [CrossRef]
- Paula, S.; Süs, W.; Tuchtenhagen, J.; Blume, A. Thermodynamics of micelle formation as a function of temperature: A high sensitivity titration calorimetry study. J. Phys. Chem. 1995, 99, 11742–11751. [Google Scholar] [CrossRef]
- Anderson, S.L.; Rovnyak, D.; Strein, T.G. Direct measurement of the thermodynamics of chiral recognition in bile salt micelles. Chirality 2016, 28, 290–298. [Google Scholar] [CrossRef] [PubMed]
- Poša, M.; Pilipović, A. Self-association of C3 and C6 epimers of hyodeoxycholate anions in aqueous medium: Hydrophobicity, critical micelle concentration and aggregation number. J. Mol. Liq. 2017, 238, 48–57. [Google Scholar] [CrossRef]
- Singh, S.T.; Mitra, S. Fluorescence properties of trans-ethyl-p-(dimethylamino) cinnamate in presence of bile acid host. J. Photochem. Photobiol. A Biol. 2009, 96, 193–200. [Google Scholar] [CrossRef]
- Kroflic, A.; Sarac, B.; Bester-Rogac, M. Thermodynamic characterization of 3-[(3-cholamidopropyl)-dimethylammonium]-1-propanesulfonate (CHAPS) micellization using isothermal titration calorimetry: Temperature, salt, and pH dependence. Langmuir 2012, 28, 10363–10371. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Poša, M. Linear hydrophobic congeneric groups of bile acid anion derivatives based on the self-association (micellization) process and the phenomenon of enthalpy-entropy compensation. J. Mol. Liq. 2023, 382, 121925. [Google Scholar] [CrossRef]
- Privalov, P.L.; Gill, S.J. The hydrophobic effect: A reappraisal. Pure Appl. Chem. 1989, 61, 1097–1104. [Google Scholar] [CrossRef] [Green Version]
- Tepavčvić, V.; Pilipović, A.; Popović, K.; Farakaš Agatić, Z.; Poša, M. Self-association of sodium isoursodeoxycholate and sodium isohenodeoxycholate in water. Chem. Phys. Lipids 2019, 223, 104778. [Google Scholar] [CrossRef] [PubMed]
- Natalini, B.; Sardella, R.; Camaioni, E.; Macchiarulo, A.; Gioiello, A.; Carbone, G.; Pellicciari, R. Derived chromatographic indices as effective tools to study the self-aggregation process of bile acids. J. Pharm. Biomed. Anal. 2009, 50, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Natalini, B.; Sardella, R.; Gioiello, A.; Ianni, F.; Di Michele, A.; Marinozzia, M. Determination of bile salt critical micellization concentration on the road to drug discovery. J. Pharm. Biomed. Anal. 2014, 87, 62–81. [Google Scholar] [CrossRef] [PubMed]
- Poša, M.; Škorić, D.; Pilipović, A. Binary mixture (1:1) of Triton X100 and Propranolol hydrochloride in an aqueous solution of NaCl: Whether mixed micelles are formed, possible clarification in 1H DOSY NMR experiment. J. Mol. Liq. 2023, 369, 120870. [Google Scholar] [CrossRef]
- Akram, M.; Bhat, I.A.; Yaseen, Z.; Kabir-ud-Din. Physicochemical investigation of novel biodegradable dicationic ester bonded m-E2-m gemini surfactants with bile salts: Insights from surface tension, dynamic light scattering and fluorescence. Colloids Surf. A 2014, 444, 209–216. [Google Scholar] [CrossRef]
- Schurtenberger, P.; Mazer, N.; Kaenzig, W. Static and dynamic light scattering studies of micellar growth and interactions in bile salt solutions. J. Phys. Chem. 1983, 87, 308–315. [Google Scholar] [CrossRef]
- Poša, M.; Guzsvány, V.; Csanádi, J. Determination of critical micellar concentration of two monoketo derivatives of cholic acid. Colloids Surf. Biointerfaces 2009, 74, 84–90. [Google Scholar] [CrossRef]
- Kagan, H. Le Stéréochimie Organique; Presses Universitaires De France: Paris, France, 1975. [Google Scholar]
- Rusanov, A.I. The mass action law theory of micellar solutions. Adv. Colloid Interface Sci. 1993, 45, 1–78. [Google Scholar] [CrossRef]
- Rusanov, A.I. The wonderful world of micelles. Colloid J. 2014, 76, 121–126. [Google Scholar] [CrossRef]
- Vázquez-Gómez, S.; Pilar Vázquez-Tato, M.; Seijas, J.A.; Meijide, F.; de Frutos, S.; Vázquez Tato, J. Thermodynamics of the aggregation of the bile anions of obeticholic and chenodeoxycholic acids in aqueous solution. J. Mol. Liq. 2019, 296, 112092. [Google Scholar] [CrossRef]
- Deumie, M.; Boulil, B.; Henri-Rousseau, O. On the Minimum of the Gibbs free Energz Involved in chemical equilibrium. J. Chem. Educ. 1987, 64, 201–204. [Google Scholar] [CrossRef]
- Torres, E.M. Effect of a Perturbation on the chemical equilibrium: Comparison with Le Chatelier’s Principle. J. Chem. Educ. 2007, 84, 516–519. [Google Scholar] [CrossRef]
- De Heer, J. The principle of Le Chatelier and Braun. J. Chem. Educ. 1957, 34, 375–380. [Google Scholar] [CrossRef]
- Tullar, B.F. Hemi-Diethylene Glycol Adduct of 3,12-Dihydroxy-7-ketocjholanoicacid and Preparation Thereof. U.S. Patent 2,549,947, 24 April 1951. [Google Scholar]
- Pósa, M.; Guzsvány, V.; Csanádi, J.; Borbás, J.; Gaál, F. Study of association of 12-monoketocholic acid by 1H NMR relaxation method. Acta Chim. Slov. 2009, 56, 807–814. [Google Scholar]
- Hore, P.J. Nuclear Magnetic Resonance; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Sanders, J.K.M.; Hunter, B.K. Modern NMR Spectroscopy; Oxford University Press: Oxford, UK, 1995. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poša, M. Self-Association of the Anion of 7-Oxodeoxycholic Acid (Bile Salt): How Secondary Micelles Are Formed. Int. J. Mol. Sci. 2023, 24, 11853. https://doi.org/10.3390/ijms241411853
Poša M. Self-Association of the Anion of 7-Oxodeoxycholic Acid (Bile Salt): How Secondary Micelles Are Formed. International Journal of Molecular Sciences. 2023; 24(14):11853. https://doi.org/10.3390/ijms241411853
Chicago/Turabian StylePoša, Mihalj. 2023. "Self-Association of the Anion of 7-Oxodeoxycholic Acid (Bile Salt): How Secondary Micelles Are Formed" International Journal of Molecular Sciences 24, no. 14: 11853. https://doi.org/10.3390/ijms241411853
APA StylePoša, M. (2023). Self-Association of the Anion of 7-Oxodeoxycholic Acid (Bile Salt): How Secondary Micelles Are Formed. International Journal of Molecular Sciences, 24(14), 11853. https://doi.org/10.3390/ijms241411853





