Effective Dipole Moment Model for Axially Symmetric C3v Molecules: Application to the Precise Study of Absolute Line Strengths of the ν6 Fundamental of CH335Cl
Abstract
:1. Introduction
2. Methods and Materials
3. Results and Discussion
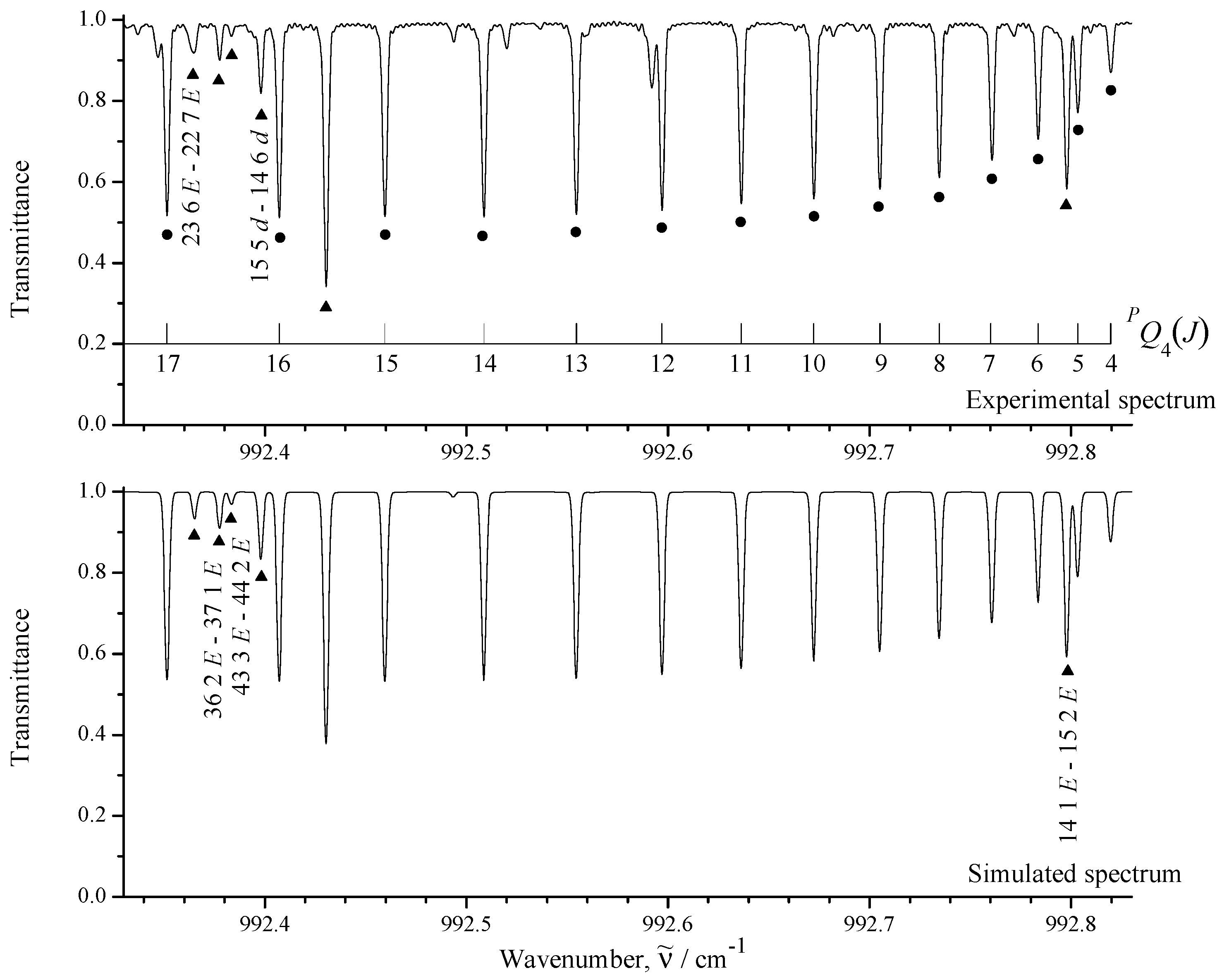
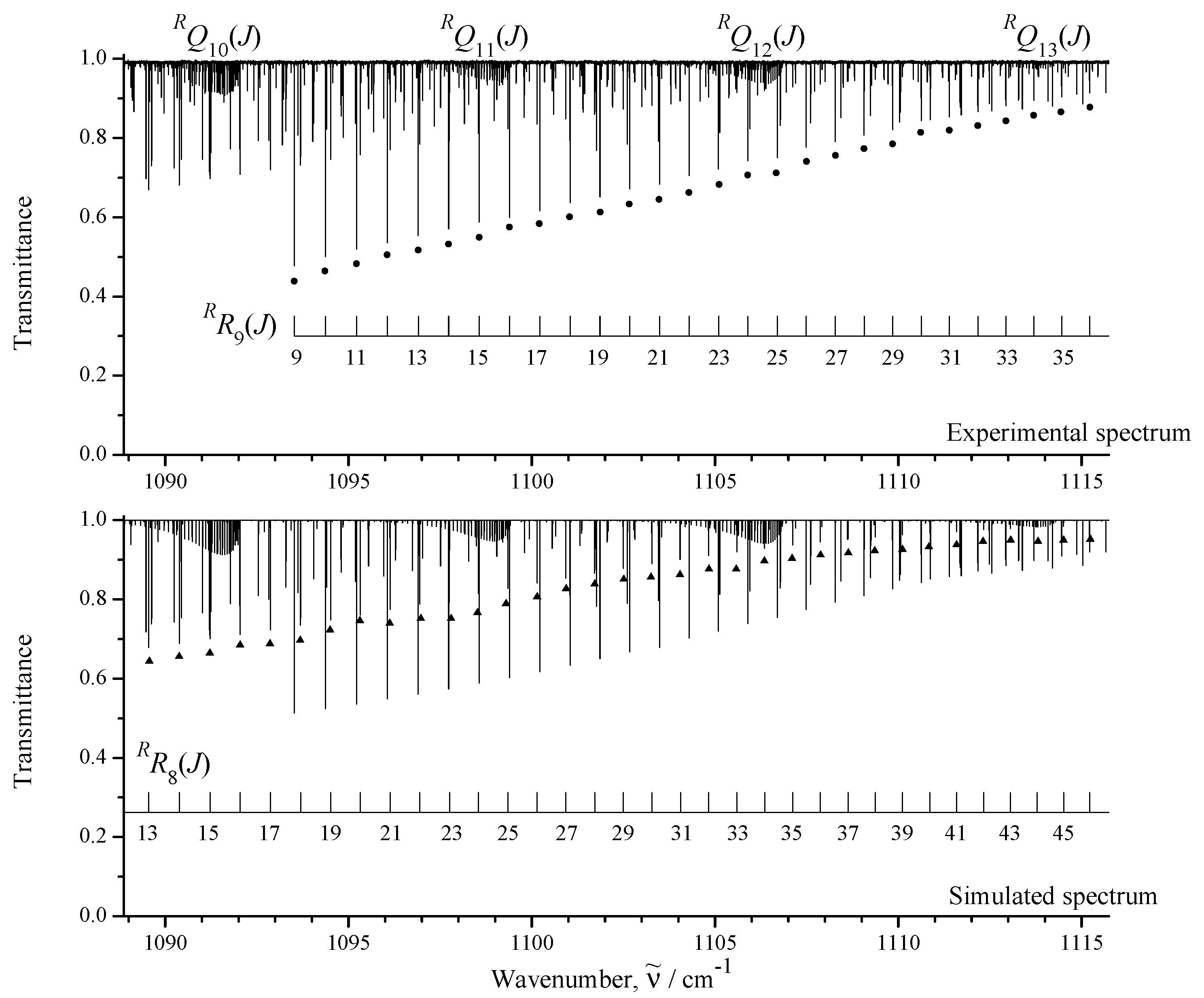
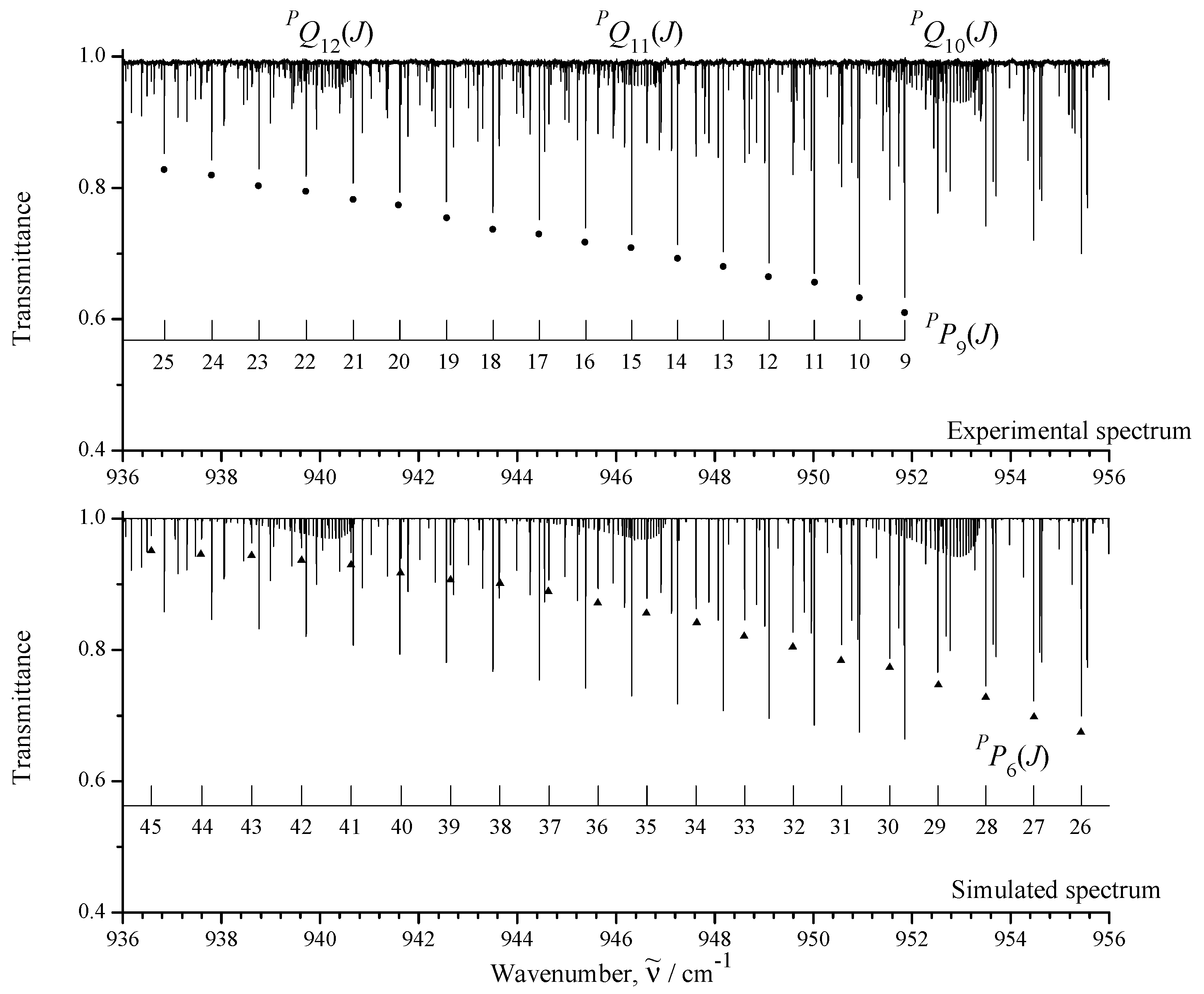
3.1. General Information and Assignment of Transitions
| Band | Center/cm | |||||||
|---|---|---|---|---|---|---|---|---|
| 1118.070790 | 68 | 21 | 5124 | 2077 | 88.9 | 8.8 | 2.3 | |
| J | K | (294.45) | (294.45) | R | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||
| 5 | 1 | E | 4 | 2 | E | 1010.81799 | 5 | 0.231768 | 0.5 | 0.2321 | −0.15 | 2.987 | −0.224 | −0.422 | 1.3 |
| 13 | 2 | 12 | 3 | 1010.83845 | 1 | 0.108382 | 0.2 | 0.5389 | 0.56 | 3.525 | −0.150 | −0.449 | 1.7 | ||
| 13 | 2 | 12 | 3 | 1010.83845 | −1 | 0.5389 | |||||||||
| 38 | 0 | E | 38 | 1 | E | 1010.88494 | 0 | 0.320599 | 3.9 | 0.2939 | 8.32 | 2.815 | 1.0 | ||
| 37 | 0 | E | 37 | 1 | E | 1011.00984 | 0 | 0.366556 | 0.4 | 0.3401 | 7.22 | 3.206 | 1.0 | ||
| 36 | 0 | E | 36 | 1 | E | 1011.13137 | −1 | 0.422301 | 0.6 | 0.3915 | 7.30 | 2.999 | 0.136 | 1.1 | |
| 30 | 4 | E | 29 | 5 | E | 1011.15162 | 8 | 0.206013 | 1.0 | 0.1975 | 4.11 | 2.808 | 1.0 | ||
| 24 | 3 | E | 25 | 2 | E | 1011.15634 | −2 | 0.499552 | 0.4 | 0.5107 | −2.23 | 3.976 | 1.0 | ||
| 9 | 1 | 10 | 0 | 1011.20573 | 1 | 0.157995 | 0.2 | 0.1596 | −0.99 | 4.175 | 1.0 | ||||
| 35 | 0 | E | 35 | 1 | E | 1011.24956 | −3 | 0.476969 | 0.3 | 0.4482 | 6.03 | 2.332 | −0.750 | −0.315 | 1.2 |
| 48 | 6 | E | 47 | 7 | E | 1011.30392 | −59 | 0.8773 | |||||||
| 39 | 5 | 38 | 6 | 1011.36055 | 12 | 0.109227 | 0.4 | 0.5266 | 3.57 | 2.970 | 1.0 | ||||
| 39 | 5 | 38 | 6 | 1011.36055 | 12 | 0.5266 | |||||||||
| 34 | 0 | E | 34 | 1 | E | 1011.36443 | −2 | 0.549711 | 0.4 | 0.5104 | 7.14 | 2.970 | 1.0 | ||
| 31 | 4 | 32 | 3 | 1011.44531 | −6 | 0.464102 | 0.6 | 0.2429 | −4.69 | 3.126 | −0.159 | 1.1 | |||
| 31 | 4 | 32 | 3 | 1011.44531 | −6 | 0.2429 | |||||||||
| 33 | 0 | E | 33 | 1 | E | 1011.47598 | 0 | 0.614718 | 0.2 | 0.5782 | 5.94 | 2.449 | −0.129 | −0.317 | 2.0 |
| 22 | 3 | E | 21 | 4 | E | 1011.50323 | 0 | 0.426391 | 0.6 | 0.4292 | −0.67 | 4.391 | 1.0 | ||
| 1 | 0 | E | 2 | 1 | E | 1011.53211 | −1 | 0.336528 | 0.5 | 0.3237 | 3.82 | 4.895 | 1.0 | ||
| 32 | 0 | E | 32 | 1 | E | 1011.58418 | −1 | 0.703075 | 0.4 | 0.6514 | 7.35 | 3.079 | 1.0 | ||
| 38 | 5 | E | 39 | 4 | E | 1011.64991 | −9 | 0.916940 | 2.7 | 0.8656 | 5.60 | 2.000 | 1.0 | ||
| 14 | 2 | 13 | 3 | 1011.67808 | 0 | 0.117754 | 0.3 | 0.5676 | 3.60 | 3.914 | 1.0 | ||||
| 14 | 2 | 13 | 3 | 1011.67808 | 2 | 0.5676 | |||||||||
| 6 | 1 | E | 5 | 2 | E | 1011.68498 | 7 | 0.323333 | 0.5 | 0.3157 | 2.37 | 3.697 | 1.0 | ||
| 31 | 0 | E | 31 | 1 | E | 1011.68904 | −2 | 0.781218 | 0.5 | 0.7299 | 6.57 | 3.697 | 1.0 | ||
| 16 | 2 | E | 17 | 1 | E | 1011.71876 | −1 | 0.789033 | 0.3 | 0.7925 | −0.44 | 4.412 | −0.549 | −0.266 | 1.1 |
| 45 | 6 | E | 46 | 5 | E | 1011.77417 | 24 | 0.2339 | |||||||
| 30 | 0 | E | 30 | 1 | E | 1011.79061 | −1 | 0.854407 | 0.5 | 0.8133 | 4.81 | 3.123 | 1.0 | ||
| 29 | 0 | E | 29 | 1 | E | 1011.88885 | −1 | 0.938728 | 0.5 | 0.9012 | 4.00 | 3.487 | 1.0 | ||
| Operator | Parameter | Value |
|---|---|---|
| 0.55712(72) | ||
| 0.1466(89) | ||
| −0.493(54) | ||
| −0.2249(25) | ||
| −0.3378(49) | ||
| −1.024(62) |
3.2. Theoretical Background for the Effective Hamiltonian Used
3.2.1. Effective Rotational–Vibrational Hamiltonian
- (1)
- The requirement is equivalent to fulfilling the conditions (which follow from Equations (11)–(13), etc):etc. These relations can be considered as equations for determining operators () (hence, ultimately, the unitary operator G, which transforms the operator matrix Equation (15) to the matrix in the form of Equation (16)).
- (2)
- All the above said allows us to present the Hamiltonian in the following form:
- (3)
- As was discussed above, if one is interested in the rotational structure of the only one vibrational state , then the second term on the right side of Equation (19) is insignificant and can be omitted from the further consideration. As for the first term, it obviously has the form of a function of coordinates of the second “y”-type (for vibrational–rotational problems, they are the Euler angles and ; in this case, the dependence of the effective Hamiltonian on the angular variables is manifested in the form of its dependence on the components , and of the angular momentum operator J.
- (a)
- Hermitian;
- (b)
- Totally symmetric (transformed in accordance with a symmetric irreducible representation of a molecule symmetry group);
- (c)
- Invariant according to the time reversal operation.
- (1)
- Provide splittings of ro–vibrational energies and for different values of the quantum number K (the operators and are responsible for the splittings for states with , operators and are responsible for the splittings for states with ).
- (2)
- Are responsible (the operators) for the borrowing of intensities from one sub-band to the other.
3.2.2. Symmetrized Ro–Vibrational Functions
- (1)
- The functions are also symmetrized functions, and any set of functions (for J fixed and ) is transformed in accordance with the irreducible representation of the SO(3) symmetry group (Ref. [104]).
- (2)
- Because the C symmetry group is a subgroup of the SO(3) group, any irreducible representation of the SO(3) group is divided into a set of irreducible representations ( and e) of the C group. In this case (in accordance with the general rules of the theory of group, see, e.g., [106]), one can construct superpositions of functions which will be transformed already in accordance with irreducible representations of the C group. Such pure rotational (symmetrized in the C group) functions have the form
3.2.3. Hamiltonian Matrix Elements
3.3. Ro–Vibrational Analysis and Parameters of the Effective Hamiltonian
3.4. Line Strengths: Experimental Intensities of Ro–Vibrational Lines of the Band
3.5. Line Strength Analysis: Improvement of the Model and Calculation Scheme
3.5.1. Effective Dipole Moment Operator for the -Type Band
3.5.2. Irreducible Rotational Operators of the SO(3) and Symmetry First-Order Operators
- (1)
- The rotational operators, Equations (56)–(58), satisfy the commutation relations; see, e.g., [95]:where is the totally antisymmetric tensor;
- (2)
- (3)
- As a consequence, three operators () can be constructed:andwhich satisfy the conditionsand, as a further consequence, they are nothing other than the first-rank irreducible rotational operators of the symmetry group. In Equation (42) , , and ; the values and are the well-known Clebsch–Gordan coefficients and the so-called reduced matrix elements [104]:Following the scheme of connection of irreducible tensorial operators of the and symmetry groups (see, e.g., [78]), one can obtain three first-order irreducible rotational operators that are symmetrized in accordance with irreducible representations of the point symmetry group:andTaking into account Equations (60)–(65), one can obtain
3.5.3. The and Irreducible Direction Cosines Operators
- (1)
- The direction cosines, which are obtained in such a way, satisfy the commutation relationsspecific to the components of the rotational angular momentum in the molecular-fixed coordinate system (Ref. [95]);
- (2)
- Their combinationsform the first rank irreducible tensor of the SO(3) symmetry group;
- (3)
- As a consequence, for the nonzero matrix elements , the following relations (analogous to Equation (64)) are valid:with
- (4)
- Analogously to Equations (66)–(68), it is possible to show that three irreducible operators of the point symmetry group areand the corresponding nonzero matrix elements of these operators on the functionsare
3.5.4. Effective Dipole Moment Operator: The Main Part
3.5.5. Effective Dipole Moment Operator: First Order Corrections
3.5.6. Effective Dipole Moment Operator: Second-Order Corrections
3.5.7. Effective Dipole Moment Operator: Higher-Order Corrections
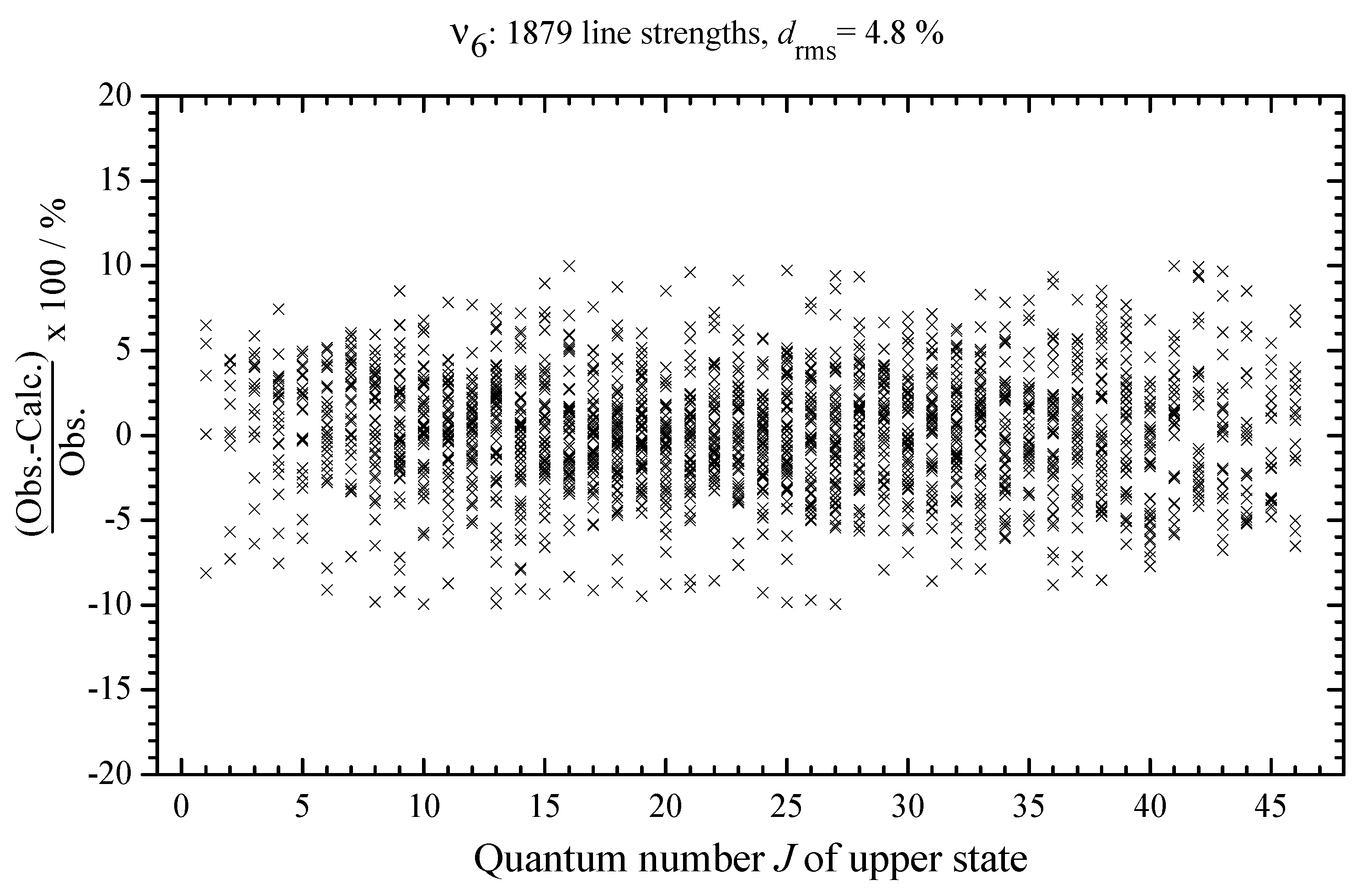
3.6. Line Strengths Analysis: Determination of Effective Dipole Moment Parameters and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flaud, J.; Camy-Peyret, C. Vibration–rotation intensities in H2O-type molecules application to the 2ν2, ν1, ν3 band of H216O. J. Mol. Spectrosc. 1975, 55, 278–310. [Google Scholar] [CrossRef]
- Loéte, M. Devéloppement complet du moment dipolaire des molécules tétraé. Application aux bandes triplement dégénéréet a la diade ν2 et ν4. Can. J. Phys. 1983, 61, 1242–1259. [Google Scholar] [CrossRef]
- Boudon, V.; Grigoryan, T.; Philipot, F.; Richard, C.; Tchana, F.K.; Manceron, L.; Rizopoulos, A.; Auwera, J.V.; Encrenaz, T. Line positions and intensities for the ν3 band of 5 isotopologues of germane for planetary applications. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 174–183. [Google Scholar] [CrossRef]
- Tarrago, J.; Ulenikov, O.; Poussigue, G. Dipole moment matrix for vibration–rotation transitions in C3v molecules. J. Phys. Paris 1984, 45, 1429–1447. [Google Scholar] [CrossRef]
- Saveliev, V.N.; Ulenikov, O.N. Calculation of vibration–rotation line intensities of polyatomic molecules based on the formalism of irreducible tensorial sets. J. Phys. B At. Mol. Phys. 1987, 20, 67–83. [Google Scholar] [CrossRef]
- Blanquet, G.; Walrand, J.; Mai, D. Absolute line intensities of the ν3 band of CH335Cl at 10 μm. J. Mol. Spectrosc. 1993, 159, 156–160. [Google Scholar] [CrossRef]
- Molina, M.J.; Rowland, F. Stratospheric sink for chlorofluoromethanes: Chlorine atom-catalysed destruction of ozone. Nature 1974, 249, 810–812. [Google Scholar] [CrossRef]
- Farman, J.; Gardiner, B.; Shanklin, J. Large losses of total ozone in Antarctica reveal seasonal ClOx/NOx interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- Kruger, A.; Stolarski, R. TOMS Antarctic ozone data for October–November 1985. EOS Trans. Am. Geophys. Union 1985, 66, 838–841. [Google Scholar] [CrossRef]
- Solomon, S.; Garcia, R.R.; Rowland, F.S.; Wuebbles, D.J. On the depletion of Antarctic ozone. Nature 1986, 321, 755–758. [Google Scholar] [CrossRef] [Green Version]
- Mcelroy, M.B.; Salawitch, R.J.; Wofsy, S.C.; Logan, J.A. Reductions of Antarctic ozone due to synergistic interactions of chlorine and bromine. Nature 1986, 321, 759–762. [Google Scholar] [CrossRef]
- Rasmussen, R.A.; Rasmussen, L.E.; Khalil, M.A.K.; Dalluge, R.W. Concentration distribution of methyl chloride in the atmosphere. J. Geophys. Res. Oceans 1980, 85, 7350–7356. Available online: https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/JC085iC12p07350 (accessed on 20 June 2023). [CrossRef]
- Singh, H.B.; Salas, L.J.; Stiles, R.E. Methyl halides in and over the eastern Pacific (40° N–32° S). J. Geophys. Res. Oceans 1983, 88, 3684–3690. Available online: https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/JC088iC06p03684 (accessed on 20 June 2023). [CrossRef]
- Crutzen, P.J.; Heidt, L.E.; Krasnec, J.P.; Pollock, W.H.; Seiler, W. Biomass burning as a source of atmospheric gases CO, H2, N2O, NO, CH3Cl and COS. Nature 1979, 282, 253–256. [Google Scholar] [CrossRef]
- Howard, C.J.; Evenson, K.M. Rate constants for the reactions of OH with CH4 and fluorine, chlorine, and bromine substituted methanes at 296 K. J. Chem. Phys. 1976, 64, 197–202. [Google Scholar] [CrossRef]
- Wallington, T.J.; Pivesso, B.P.; Lira, A.M.; Anderson, J.E.; Nielsen, C.J.; Andersen, N.H.; Hodnebrog, Ø. CH3Cl, CH2Cl2, CHCl3, and CCl4: Infrared spectra, radiative efficiencies, and global warming potentials. J. Quant. Spectrosc. Radiat. Transf. 2016, 174, 56–64. [Google Scholar] [CrossRef]
- Gutzeit, J. Effect of Organic Chloride Contamination of Crude Oil on Refinery Corrosion. Corrosion 2000, 21, 649–650. [Google Scholar]
- Morillon-Chapey, M.; Graner, G. Fine structure in the ν1 band of CH3Cl near 2970 cm−1. J. Mol. Spectrosc. 1969, 31, 155–169. [Google Scholar] [CrossRef]
- Di Lauro, C.; Lattanzi, F. Evidence for the 2ν3 overtone in the infrared spectrum of methyl chloride. Chem. Phys. Lett. 1979, 63, 464–466. [Google Scholar] [CrossRef]
- Imachi, M.; Tanaka, T.; Hirota, E. Microwave spectrum of methyl chloride in the excited vibrational states: Coriolis interaction between the ν2 and ν5 states. J. Mol. Spectrosc. 1976, 63, 265–280. [Google Scholar] [CrossRef]
- Derochf, J.C. Assignment of submillimeter laser lines in methyl chloride. J. Mol. Spectrosc. 1978, 69, 19–24. [Google Scholar] [CrossRef]
- Jensen, P.; Brodersen, S.; Guelachvili, G. Determination of A0 for CH335Cl and CH337Cl from the ν4 infrared and Raman bands. J. Mol. Spectrosc. 1981, 88, 378–393. [Google Scholar] [CrossRef]
- Dang-Nhu, M.; Morillon-Chapey, M.; Graner, G.; Guelachvili, G. Intensities of the ν1 bands of 12CH337Cl near 3 μm. J. Quant. Spectrosc. Radiat. Transf. 1981, 26, 515–521. [Google Scholar] [CrossRef]
- Morillon-Chapey, M.; Guelachvili, G.; Jensen, P. Analysis of the high resolution spectrum of the ν2 and ν5 bands of methyl chloride. Can. J. Phys. 1984, 62, 247–253. [Google Scholar] [CrossRef]
- Elkins, J.W.; Kagann, R.H.; Sams, R.L. Infrared band strengths for methyl chloride in the regions of atmospheric interest. J. Mol. Spectrosc. 1984, 105, 480–490. [Google Scholar] [CrossRef]
- Golby, J.; Butcher, R. 10-μm sub-doppler laser-stark spectroscopy of methyl chloride: Analysis of the ν6 bands of the CH335Cl and CH337Cl. J. Mol. Spectrosc. 1984, 107, 292–300. [Google Scholar] [CrossRef]
- Man, H.T.; Butcher, R. Laser-radiofrequency double-resonance spectroscopy of methyl chloride: Hyperfine structure of the ground and ν6 states. J. Mol. Spectrosc. 1985, 110, 19–26. [Google Scholar] [CrossRef]
- Wlodarczak, G.; Segard, B.; Legrand, J.; Demaison, J. The dipole moment of CH35Cl. J. Mol. Spectrosc. 1985, 111, 204–206. [Google Scholar] [CrossRef]
- Wlodarczak, G.; Herlemont, F.; Demaison, J.; Fayt, A.; Lahaye, J. Combined subdoppler laser-stark and millimeter-wave spectroscopies: Analysis of the ν6 band of CH335Cl. J. Mol. Spectrosc. 1985, 112, 401–412. [Google Scholar] [CrossRef]
- Henfrey, N.; Thrush, B. The analysis of high resolution spectra of the ν2 and ν5 bands of CH335Cl and CH337Cl. J. Mol. Struct. 1986, 146, 71–83. [Google Scholar] [CrossRef]
- Betrencourt, M.; Morillon-Chapey, M.; Blanquet, G.; Walrand, J. Diode laser spectroscopy of methyl chloride near 14 μm toward its detection in the stratosphere. J. Mol. Spectrosc. 1988, 128, 433–443. [Google Scholar] [CrossRef]
- Dang-Nhu, M.; Blanquet, G.; Walrand, J.; Derie, F. Spectral intensities in the ν3-band of 12CH3 35Cl at 13 µm. Mol.Phys. 1988, 65, 77–83. [Google Scholar] [CrossRef]
- Cappellani, F.; Restelli, G.; Tarrago, G. Absolute infrared intensities in the fundamentals ν2 and ν5 of 12CH3 35Cl. J. Mol. Spectrosc. 1991, 146, 326–333. [Google Scholar] [CrossRef]
- Blanquet, G.; Walrand, J.; Bouanich, J. Diode laser measurements of N2-broadening coefficients in the ν3 band of CH335Cl. J. Mol. Spectrosc. 1993, 159, 137–143. [Google Scholar] [CrossRef]
- Blanquet, G.; Walrand, J.; Bouanich, J. Diode laser measurements of O2-broadening coefficients in the ν3 band of CH335Cl. J. Mol. Spectrosc. 1993, 160, 253–257. [Google Scholar] [CrossRef]
- Bouanich, J.; Blanquet, G.; Walrand, J. Theoritical O2- and N2-broadening coefficients of CH335Cl spectral lines. J. Mol. Spectrosc. 1993, 161, 416–426. [Google Scholar] [CrossRef]
- Bouanich, J.P.; Blanquet, G.; Walrand, J. Diode laser measurements of self-broadening coefficients and line strengths in the ν3 band of CH335Cl. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 573–578. [Google Scholar] [CrossRef]
- Blanquet, G.; Coupe, P.; Walrand, J.; Bouanich, J.P. Determination of broadening coefficients and intensities for overlapping spectral lines with application to the QR(3,K) lines in the ν3 band of CH335Cl. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 671–678. [Google Scholar] [CrossRef]
- Blanquet, G.; Lance, B.; Walrand, J.; Bouanich, J. Absolute line intensities in the ν2 band of 12CH3 35Cl at 7.5 µm. J. Mol. Spectrosc. 1995, 170, 466–477. [Google Scholar] [CrossRef]
- Blanquet, G.; Walrand, J.; Populaire, J.C.; Bouanich, J.P. Self-broadening coefficients and line strengths in the ν3 band of CH335Cl at low temperature. J. Quant. Spectrosc. Radiat. Transf. 1995, 53, 211–219. [Google Scholar] [CrossRef]
- Chackerian, C.; Brown, L.; Lacome, N.; Tarrago, G. Methyl chloride ν5 region lineshape parameters and rotational constants for the ν2, ν5 and 2ν3 vibrational bands. J. Mol. Spectrosc. 1998, 191, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Bouanich, J.P.; Blanquet, G.; Populaire, J.C.; Walrand, J. N2-broadening for methyl chloride at low temperature by diode laser spectroscopy. J. Mol. Spectrosc. 2001, 208, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, A.; Fjard, L.; Champion, J.; Brger, H.; Litz, M.; Colmont, J.; Bakri, B. New measurements and global analysis of chloromethane in the region from 0 to 1800 cm−1. J. Mol. Spectrosc. 2003, 221, 199–212. [Google Scholar] [CrossRef]
- Nikitin, A.; Champion, J. New ground state constants of 12CH337Cl from global polyad analysis. J. Mol. Spectrosc. 2005, 230, 168–173. [Google Scholar] [CrossRef]
- Bray, C.; Perrin, A.; Jacquemart, D.; Lacome, N. The ν1, ν4 and 3ν6 bands of methyl chloride in the 3.4 μm region: Line positions and intensities. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2446–2462. [Google Scholar] [CrossRef] [Green Version]
- Guinet, M.; Rohart, F.; Buldyreva, J.; Gupta, V.; Eliet, S.; Motiyenko, R.; Marguls, L.; Cuisset, A.; Hindle, F.; Mouret, G. Experimental studies by complementary terahertz techniques and semi-classical calculations of N2-broadening coefficients of CH3Cl. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1113–1126. [Google Scholar] [CrossRef]
- Bray, C.; Jacquemart, D.; Buldyreva, J.; Lacome, N.; Perrin, A. N2-broadening coefficients of methyl chloride at room temperature. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1102–1112. [Google Scholar] [CrossRef] [Green Version]
- Barbouchi Ramchani, A.; Jacquemart, D.; Dhib, M.; Aroui, H. Line positions, intensities and self-broadening coefficients for the ν5 band of methyl chloride. J. Quant. Spectrosc. Radiat. Transf. 2013, 120, 1–15. [Google Scholar] [CrossRef]
- Kondo, S.; Koga, Y.; Nakanaga, T.; Saki, S. Calculation of the cubic symmetry force constants of methyl bromide and methyl chloride. J. Mol. Spectrosc. 1983, 100, 332–342. [Google Scholar] [CrossRef]
- Black, G.; Law, M. The general harmonic force field of methyl chloride. J. Mol. Spectrosc. 2001, 205, 280–285. [Google Scholar] [CrossRef]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J.; Thiel, W. A global ab initio dipole moment surface for methyl chloride. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 100–110. [Google Scholar] [CrossRef] [Green Version]
- Nikitin, A.V. Vibrational energy levels of methyl chloride calculated from full dimensional ab initio potential energy surface. J. Mol. Spectrosc. 2008, 252, 17–21. [Google Scholar] [CrossRef]
- Swarna Kumari, G.; Rajeswara Rao, N. Relation between electrooptical constants and polar tensors of CH3F, CD3F, CH3Cl, CD3Cl, CH3Br, CD3Br, CH3I, and CD3I. J. Mol. Spectrosc. 1984, 106, 1–11. [Google Scholar] [CrossRef]
- Duncan, J.; Law, M. A study of vibrational anharmonicity, fermi resonance interactions, and local mode behavior in CH3Cl. J. Mol. Spectrosc. 1990, 140, 13–30. [Google Scholar] [CrossRef]
- Hartmann, J.M.; Bouanich, J.P.; Boulet, C.; Blanquet, G.; Walrand, J.; Lacome, N. Simple modelling of Q-branch absorption—II. Application to molecules of atmospheric interest (CFC-22 and CH3Cl). J. Quant. Spectrosc. Radiat. Transf. 1995, 54, 723–735. [Google Scholar] [CrossRef]
- Grossman, A.S.; Grant, K.E.; Blass, W.E.; Wuebbles, D.J. Radiative forcing calculations for CH3Cl and CH3Br. J. Geophys. Res. Atmos. 1997, 102, 13651–13656. Available online: https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/97JD00611 (accessed on 20 June 2023). [CrossRef]
- Albert, S.; Albert-Keppler, K.; Quack, M. High-resolution Fourier transform infrared spectroscopy. In High-resolution Fourier Transform Infrared Spectroscopy, in Handbook of High-Resolution Spectroscopy; Quack, M., Merkt, F., Eds.; Wiley: New York, NY, USA, 2011; Volume 2, pp. 965–1019. [Google Scholar] [CrossRef]
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Maki, A.; Wells, J. Wavenumber Calibration Tables from Heterodyne Frequency Measurements (Version 1.3); National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998. [Google Scholar]
- Herzberg, G. Molecular Spectra and Molecular Structure, Volume 2: Infrared and Raman and Spectra of Polyatomic Molecules, 1st ed.; D. Van Nostrand Company: New York, NY, USA, 1945. [Google Scholar]
- Nielsen, H.H. The vibration–rotation energies of molecules. Rev. Mod. Phys. 1951, 23, 90–136. [Google Scholar] [CrossRef]
- Papoušek, D.; Aliev, M.R. Molecular Vibrational–Rotational Spectra; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Wang, X.H.; Ulenikov, O.; Onopenko, G.; Bekhtereva, E.; He, S.G.; Hu, S.M.; Lin, H.; Zhu, Q.S. High-Resolution Study of the First Hexad of D2O. J. Mol. Spectrosc. 2000, 200, 25–33. [Google Scholar] [CrossRef]
- Ulenikov, O.; Hu, S.M.; Bekhtereva, E.; Onopenko, G.; He, S.G.; Wang, X.H.; Zheng, J.J.; Zhu, Q.S. High-resolution Fourier transform spectrum of D2O in the region near 0.97 μm. J. Mol. Spectrosc. 2001, 210, 18–27. [Google Scholar] [CrossRef]
- Hu, S.M.; Ulenikov, O.; Bekhtereva, E.; Onopenko, G.; He, S.G.; Lin, H.; Cheng, J.X.; Zhu, Q.S. High-resolution Fourier-transform intracavity laser absorption spectroscopy of D2O in the region of the 4ν1+ν3 band. J. Mol. Spectrosc. 2002, 212, 89–95. [Google Scholar] [CrossRef] [Green Version]
- Ulenikov, O.N.; Bekhtereva, E.S.; Albert, S.; Bauerecker, S.; Hollenstein, H.; Quack, M. High-resolution near infrared spactroscopy and vibrational dynamics of dideuteromethane (CH2D2). J. Phys. Chem. A 2009, 113, 2218–2231. [Google Scholar] [CrossRef]
- Ulenikov, O.N.; Onopenko, G.A.; Bekhtereva, E.S.; Petrova, T.M.; Solodov, A.M.; Solodov, A.A. High resolution study of the ν5+ν12 band of C2H4. Mol. Phys. 2010, 108, 637–647. [Google Scholar] [CrossRef]
- Ulenikov, O.N.; Gromova, O.V.; Bekhtereva, E.S.; Belova, A.S.; Bauerecker, S.; Maul, C.; Sydow, C.; Horneman, V.M. High resolution analysis of the (111) vibrational state of SO2. J. Quant. Spectrosc. Radiat. Transf. 2014, 144, 1–10. [Google Scholar] [CrossRef]
- Ulenikov, O.N.; Gromova, O.V.; Bekhtereva, E.S.; Krivchikova, Y.V.; Sklyarova, E.A.; Buttersack, T.; Sydow, C.; Bauerecker, S. High resolution FTIR study of 34S16O2: The bands 2ν3, ν1+ν2 and 2ν1+ν2-ν2. J. Mol. Spectrosc. 2015, 318, 26–33. [Google Scholar] [CrossRef]
- Ulenikov, O.N.; Malikova, A.B.; Alanko, S.; Koivusaari, M.; Anttila, R. High-resolution study of the 2ν5 hybrid band of the CHD3 molecule. J. Mol. Spectrosc. 1996, 179, 175–194. [Google Scholar] [CrossRef]
- Han, J.X.; Ulenikov, O.N.; Yurchinko, S.; Hao, L.Y.; Wang, X.G.; Zhu, Q.S. High resolution photoacoustic spectrum of AsH3 (600A1/E) bands. Spectrochim. Acta–Part A Mol. Biomol. Spectrosc. 1997, 53, 1705–1712. [Google Scholar] [CrossRef]
- Lin, H.; Ulenikov, O.N.; Yurchinko, S.; Wang, X.G.; Zhu, Q.S. High-resolution spectroscopic study of the (310) local mode combination band system of AsH3. J. Mol. Spectrosc. 1998, 187, 89–96. [Google Scholar] [CrossRef]
- Ulenikov, O.; Bekhtereva, E.; Yuhnik, Y.; Bürger, H. High-resolution infrared study of the ν1 and ν3 bands, and the equilibrium structure of AsD3. J. Mol. Struct. 2006, 780–781, 115–123. [Google Scholar] [CrossRef]
- Ulenikov, O.; Bekhtereva, E.; Kozinskaia, V.; Zheng, J.J.; He, S.G.; Hu, S.M.; Zhu, Q.S.; Leroy, C.; Pluchart, L. On the study of resonance interactions and splittings in the PH3 molecule: ν1, ν3, ν2 + ν4, and 2ν4 bands. J. Mol. Spectrosc. 2002, 215, 295–308. [Google Scholar] [CrossRef]
- Ulenikov, O.; Bekhtereva, E.; Gromova, O.; Fomchenko, A.; Sydow, C.; Bauerecker, S. High-resolution re-investigation of the ν2 and ν4 bending bands of phosphine PH3. J. Quant. Spectrosc. Radiat. Transf. 2021, 272, 107795. [Google Scholar] [CrossRef]
- Ulenikov, O.; Yuhnik, Y.; Bekhtereva, E.; Tyabaeva, N.; Bürger, H.; Jerzembeck, W.; Fusina, L. High resolution fourier transform spectrum of PD3 in the region of the stretching overtone bands 2ν1 and ν1 + ν3. J. Mol. Spectrosc. 2003, 221, 250–260. [Google Scholar] [CrossRef]
- Bolotova, I.; Ulenikov, O.; Bekhtereva, E.; Albert, S.; Bauerecker, S.; Hollenstein, H.; Lerch, P.; Quack, M.; Peter, T.; Seyfang, G.; et al. High resolution analysis of the FTIR spectra of trifluoroamine NF3. J. Mol. Spectrosc. 2018, 348, 87–102. [Google Scholar] [CrossRef]
- Ulenikov, O.; Onopenko, G.; Tyabaeva, N.; Schroderus, J.; Alanko, S. Study on the Rovibrational Interactions and A1/A2 Splittings in the ν3/ν5/ν6 Triad of CH3D. J. Mol. Spectrosc. 2000, 200, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Ulenikov, O.; Bekhtereva, E.; Albert, S.; Bauerecker, S.; Hollenstein, H.; Quack, M. High resolution infrared spectroscopy and global vibrational analysis for the CH3D and CHD3 isotopomers of methane. Mol. Phys. 2010, 108, 1209–1240. [Google Scholar] [CrossRef]
- Ulenikov, O.; Onopenko, G.; Alanko, S.; Koivusaari, M.; Anttila, R. First High-resolution study of the 13CHD3 infrared spectrum: Rotational analysis of the ground state and the fundamentals v5 and v3/v6. J. Mol. Spectrosc. 1998, 191, 9–16. [Google Scholar] [CrossRef]
- Ulenikov, O.; Onopenko, G.; Tyabaeva, N.; Schroderus, J.; Alanko, S.; Koivusaari, M. High-resolution Fourier transform spectrum of the CHD3 molecule in the region of 1850–2450 cm−1: Assignment and preliminary analysis. J. Mol. Struct. 2000, 517–518, 25–40. [Google Scholar] [CrossRef]
- Kawashima, Y.; Ulenikov, O.; Hirota, E. The microwave spectrum of sodium tetrahydroborate NaBH4 in excited vibrational states: Coriolis interaction between the Na-BH4 stretching and the BH4 rocking vibrations. Mol. Phys. 2003, 101, 623–628. [Google Scholar] [CrossRef]
- Albert, S.; Bekhtereva, E.; Bolotova, I.; Chen, Z.; Fábri, C.; Hollenstein, H.; Quack, M.; Ulenikov, O. Isotope effects on the resonance interactions and vibrational quantum dynamics of fluoroform 12,13CHF3. Phys. Chem. Chem. Phys. 2017, 19, 26527–26534. [Google Scholar] [CrossRef]
- Albert, S.; Bauerecker, S.; Bekhtereva, E.; Bolotova, I.; Hollenstein, H.; Quack, M.; Ulenikov, O. High resolution FTIR spectroscopy of fluoroform 12CHF3 and critical analysis of the infrared spectrum from 25 to 1500 cm−1. Mol. Phys. 2018, 116, 1091–1107. [Google Scholar] [CrossRef]
- Fano, U.; Racah, G.D. Irreducible Tensorial Sets; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Hecht, T. The vibration–rotation energies of tetrahedral XY4 molecules. Part I. Theory of spherical top molecules. J. Mol. Spectrosc. 1960, 5, 355–389. [Google Scholar] [CrossRef] [Green Version]
- Moret-Bailly, J. Sur l’interpretation des spectres de vibration–rotation des molecules a symmetrie tetraedrique ou octaedrique. Cah. Phys. 1961, 15, 238–314. [Google Scholar]
- Wigner, E.P. Quantum Theory of Angular Momentum; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Silver, B.L. Irreducible Tensorial Methods; Academic Press: New York, NY, USA; London, UK, 1976. [Google Scholar]
- Champion, J.P. Developpement complet de l’hamiltonien de vibration-rotation adapte a l’etude des interactions dans les molecules toupies spheriques. Application aux bandes ν2 et ν4 de 12CH4. Can. J. Phys. 1977, 55, 1802–1828. [Google Scholar] [CrossRef]
- Zhilinskii, B.I. Method of Irreducible Tensorial Sets in Molecular Spectroscopy; Moscow State University Press: Moscow, Russia, 1981. (In Russian) [Google Scholar]
- Makushkin, Y.S.; Ulenikov, O.N.; Cheglokov, A.E. Symmetry and Its Applications to the Problems of Molecular Vibration–Rotation Spectroscopy, Parts I and II; Tomsk State University Press: Tomsk, Russia, 1990. (In Russian) [Google Scholar]
- Boudon, V.; Champion, J.P.; Gabard, T.; Loëte, M.; Rotger, M.; Wenger, E.P. Spherical Top Theory and Molecular Spectra. In Spherical Top Theory and Molecular Spectra, in Handbook of High-Resolution Spectroscopy; Quack, M., Merkt, F., Eds.; Wiley: New York, NY, USA, 2011; Volume 3, pp. 1437–1460. [Google Scholar] [CrossRef]
- Davydov, A.S. Quantum Mechanics, 1st ed.; Pergamon Press: Oxford, UK; London, UK; Edinburgh, UK; New York, NY, USA; Paris, France; Frankfurt, Germany, 1965; Volume 1. [Google Scholar]
- Van Vleck, J.H. The coupling of angular momentum vectors in molecules. Rev. Mod. Phys. 1951, 23, 213–227. [Google Scholar] [CrossRef]
- Amat, G.; Goldsmith, M.; Nielsen, H.H. Higher order rotation–vibration energies of polyatomic molecules. I. J. Chem. Phys. 1956, 24, 1178–1186. [Google Scholar] [CrossRef]
- Amat, G.; Goldsmith, M.; Nielsen, H.H. Higher order rotation–vibration energies of polyatomic molecules. II. J. Chem. Phys. 1957, 27, 838–844. [Google Scholar] [CrossRef]
- Amat, G.; Goldsmith, M.; Nielsen, H.H. Higher order rotation–vibration energies of polyatomic molecules. III. J. Chem. Phys. 1957, 27, 845–850. [Google Scholar] [CrossRef]
- Amat, G.; Nielsen, H.H. Higher order rotation–vibration energies of polyatomic molecules. IV. J. Chem. Phys. 1958, 29, 665–672. [Google Scholar] [CrossRef]
- Amat, G.; Nielsen, H.H. Higher order rotation–vibration energies of polyatomic molecules. V. J. Chem. Phys. 1962, 36, 1859–1865. [Google Scholar] [CrossRef]
- Jørgensen, F. Effective hamiltonians. Mol. Phys. 1975, 29, 1137–1164. [Google Scholar] [CrossRef]
- Jørgensen, F.; Pedersen, T.; Chedin, A. A projector formulation for the Van Vleck transformation. Generalization and relation to the contact transformation. Mol. Phys. 1975, 30, 1377–1395. [Google Scholar] [CrossRef]
- Cheglokov, A.; Ulenikov, O.; Zhilyakov, A.; Cherepanov, V.; Makushkin, Y.; Malikova, A. On the determination of spectroscopic constants as functions of intramolecular parameters. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 997–1015. [Google Scholar] [CrossRef]
- Varshalovitch, D.A.; Moskalev, A.N.; Khersonsky, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore; Hackensack, NJ, USA; Hong Kong, China, 1988. [Google Scholar]
- Urban, V.; Papoušek, D.; Garcia Hernandez, M. Effective Hamiltonian for degenerate vibrational states in symmetric top molecules. J. Mol. Spectrosc. 1987, 124, 272–284. [Google Scholar] [CrossRef]
- Lyubarsky, G.Y. The Application of Group Theory in Physics; Elsevier: Pergamon, Turkey, 2013. [Google Scholar]
- Kwan, Y.Y. The interacting states of an asymmetric top molecule XY2 of the group C2v. Application to five interacting states (101), (021), (120), (200), and (002) of H216O. J. Mol. Spectrosc. 1978, 71, 260–280. [Google Scholar] [CrossRef]
- Tran, H.; Ngo, N.H.; Hartmann, J.M. Efficient computation of some speed-dependent isolated line profiles. J. Quant. Spectrosc. Radiat. Transf. 2013, 129, 199–203. [Google Scholar] [CrossRef]
- Tran, H.; Ngo, N.H.; Hartmann, J.M.; Gamache, R.R.; Mondelain, D.; Kassi, S.; Campargue, A.; Gianfrani, L.; Castrillo, A.; Fasci, E.; et al. Velocity effects on the shape of pure H2O isolated lines: Complementary tests of the partially correlated speed-dependent Keilson–Storer model. J. Chem. Phys. 2013, 138, 034302. [Google Scholar] [CrossRef]
- Tennyson, J.; Bernath, P.F.; Campargue, A.; Csaszar, A.G.; Daumont, L.; Gamache, R.R. Recommended isolated-line profile for representing High-resolution spectroscopic transitions (IUPAC technical report). Pure Appl. Chem. 2014, 86, 1931–1943. [Google Scholar] [CrossRef] [Green Version]
- Davis, S.P.; Abrams, M.C.; Brault, J.W. Fourier Transform Spectrometry; Academic Press: San Diego, Chile, 2001. [Google Scholar]
- Dicke, R.H. The effect of collisions upon the Doppler width of spectral lines. Phys. Rev. 1953, 89, 472–473. [Google Scholar] [CrossRef]
- Galatry, L. Simultaneous effect of Doppler and foreign gas broadening on spectral lines. Phys Rev. 1961, 122, 1218–1223. [Google Scholar] [CrossRef]
- Nelkin, M.; Ghatak, A. Simple binary collision model for Van Hove’s Ge(r, t). Phys Rev. 1964, 135, A4–A9. [Google Scholar] [CrossRef]
- Armstrong, B.H. Spectrum line profiles: The Voigt function. J. Quant. Spectrosc. Radiat. Transf. 1967, 7, 61–88. [Google Scholar] [CrossRef]
- Rautian, S.G.; Sobelman, I.I. The effect of collisions on the Doppler broadening of spectral lines. Soviet Phys. Uspekhi 1967, 9, 701–716. [Google Scholar] [CrossRef]
- Berman, P.R. Speed-dependent collisional width and shift parameters in spectral profiles. J. Quant. Spectrosc. Radiat. Transf. 1972, 12, 1331–1342. [Google Scholar] [CrossRef]
- Murray, J.R.; Javan, A. Effects of collisions on Raman line profiles of hydrogen and deuterium gas. J. Mol. Spectrosc. 1972, 42, 1–26. [Google Scholar] [CrossRef]
- Eng, R.S.; Calawa, A.R.; Harman, T.C.; Kelley, P.L.; Javan, A. Collisional narrowing of infrared water vapor transitions. Appl. Phys. Lett. 1972, 21, 303–305. [Google Scholar] [CrossRef]
- Pickett, H.M. Effects of velocity averaging on the shapes of absorption lines. J. Chem. Phys. 1980, 73, 6090–6094. [Google Scholar] [CrossRef]
- Pine, A.S. Collisional narrowing of HF fundamental band spectral lines by neon and argon. J. Mol. Spectrosc. 1980, 82, 435–448. [Google Scholar] [CrossRef]
- Humlicek, J. Optimized computation of the Voigt and complex probability functions. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 437–444. [Google Scholar] [CrossRef]
- Varghese, P.L.; Hanson, R.K. Collisional narrowing effects on spectral line shapes measured at high resolution. Appl. Opt. 1984, 23, 2376–2385. [Google Scholar] [CrossRef]
- Lether, F.G.; Wenston, P.R. The numerical computation of the Voigt function by a corrected midpoint quadrature rule. J. Comput. Appl. Math. 1991, 34, 75–92. [Google Scholar] [CrossRef] [Green Version]
- Lance, B.; Blanquet, G.; Walrand, J.; Bouanich, J. On the speed-dependent hard collision lineshape models: Application to C2H2 Perturbed by Xe. J. Mol. Spectrosc. 1997, 185, 262–271. [Google Scholar] [CrossRef]
- Boone, C.D.; Walker, K.A.; Bernath, P.F. Speed-dependent Voigt profile for water vapor in infrared remote sensing applications. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 525–532. [Google Scholar] [CrossRef]
- Ulenikov, O.N.; Gromova, O.V.; Bekhtereva, E.S.; Kashirina, N.V.; Maul, C.; Bauerecker, S. Precise ro–vibrational analysis of molecular bands forbidden in absorption: The ν8+ν10 band of 13C2H4. J. Quant. Spectrosc. Radiat. Transf. 2015, 164, 117–128. [Google Scholar] [CrossRef]
- Ulenikov, O.N.; Bekhtereva, E.S.; Gromova, O.V.; Belova, A.S.; Bauerecker, S. On the method of precise abundance determination of isotopologues in a gas mixture. Phys. Chem. Chem. Phys. 2019, 21, 8464–8469. [Google Scholar] [CrossRef] [PubMed]
- Gamache, R.; Kennedy, S.; Hawkins, R.; Rothman, L. Total internal partition sums for molecules in the terrestrial atmosphere. J. Mol. Struct. 2000, 517–518, 407–425. [Google Scholar] [CrossRef]
- Griffits, D.J. Introduction to Quantum Mechanics; Prentice Hall, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Schmitt, M.; Meerts, L. Structures and dipole moments of molecules in their electronically excited states. In Structures and Dipole Moments of Molecules in Their Electronically Excited States, in Frontiers and Advances in Molecular Spectroscopy; Laane, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 143–193. [Google Scholar] [CrossRef]



| Spectrum | Region /cm | Resolution /cm | No. of Scans | Source | Detector | Beam- Splitter | Aperture /mm | Opt. Path- Length/m | Temp. /K | Pressure /Pa | Calibr. Gas |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 500–1700 | 0.0025 | 1000 | Globar | MCT | KBr | 1.5 | 4 | K | 50 | HO, CO |
| II | 500–5000 | 0.003 | 1860 | Globar | MCT | KBr | 1.0 | 24 | K | 300 | HO, CO |
| J | K | l | Value | |
|---|---|---|---|---|
| 0 | 0 | |||
| 0 | 1 | |||
| 3, 6, 9, … | 0 | |||
| 1 | ||||
| 1, 4, 7, … | 0 | |||
| 1 | ||||
| 2, 5, 8, … | 0 | |||
| 1 |
| Value | Value | ||||||
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 1 | |||||||
| J | K | ||||
|---|---|---|---|---|---|
| 1 | |||||
| 1 | |||||
| 1 | |||||
| 1 | |||||
| 1 | |||||
| k = 3, 6, 9,… | 1 | ||||
| 1 | |||||
| 1 | |||||
| 1 | |||||
| 1 | |||||
| 1 | |||||
| k = 0 | |||||
| k = 0 | |||||
| Parameter | Value |
|---|---|
| E | 1018.0707900(43) |
| B | 0.4417686446(97) |
| C | 5.23070591(17) |
| 0.6049990(56) | |
| 0.678610(25) | |
| 0.85663560(15) | |
| −0.33657(93) | |
| 0.14360(66) | |
| 0.1873(22) | |
| 0.13300(49) | |
| −0.1389(42) | |
| −0.2198(49) | |
| 2.6202558(10) | |
| −0.156270(14) | |
| −0.112648(17) | |
| 0.8931(92) | |
| −0.2986(22) | |
| 0.12944(56) | |
| −0.8241(79) | |
| −0.1205968(96) | |
| 0.5859(14) | |
| −0.4166(42) | |
| 0.145(15) | |
| −0.2327(92) | |
| 0.415(20) |
| Spectrum | CHCl | CHCl | HO | CO |
|---|---|---|---|---|
| I | 74.21 | 23.73 | 2.05 ± 0.22 | 0.013 ± 0.001 |
| Operator, | Parameter, | Coefficient, Equation (102) | |
|---|---|---|---|
| 1 | 1 | ||
| 2 | |||
| 3 | |||
| 4 | , | ||
| , | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulenikov, O.; Bekhtereva, E.; Gromova, O.; Fomchenko, A.; Morzhikova, Y.; Sidko, S.; Sydow, C.; Bauerecker, S. Effective Dipole Moment Model for Axially Symmetric C3v Molecules: Application to the Precise Study of Absolute Line Strengths of the ν6 Fundamental of CH335Cl. Int. J. Mol. Sci. 2023, 24, 12122. https://doi.org/10.3390/ijms241512122
Ulenikov O, Bekhtereva E, Gromova O, Fomchenko A, Morzhikova Y, Sidko S, Sydow C, Bauerecker S. Effective Dipole Moment Model for Axially Symmetric C3v Molecules: Application to the Precise Study of Absolute Line Strengths of the ν6 Fundamental of CH335Cl. International Journal of Molecular Sciences. 2023; 24(15):12122. https://doi.org/10.3390/ijms241512122
Chicago/Turabian StyleUlenikov, Oleg, Elena Bekhtereva, Olga Gromova, Anna Fomchenko, Yulia Morzhikova, Sergei Sidko, Christian Sydow, and Sigurd Bauerecker. 2023. "Effective Dipole Moment Model for Axially Symmetric C3v Molecules: Application to the Precise Study of Absolute Line Strengths of the ν6 Fundamental of CH335Cl" International Journal of Molecular Sciences 24, no. 15: 12122. https://doi.org/10.3390/ijms241512122
APA StyleUlenikov, O., Bekhtereva, E., Gromova, O., Fomchenko, A., Morzhikova, Y., Sidko, S., Sydow, C., & Bauerecker, S. (2023). Effective Dipole Moment Model for Axially Symmetric C3v Molecules: Application to the Precise Study of Absolute Line Strengths of the ν6 Fundamental of CH335Cl. International Journal of Molecular Sciences, 24(15), 12122. https://doi.org/10.3390/ijms241512122







