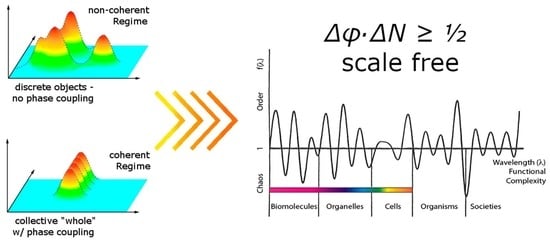
Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology
Abstract
1. Introduction
- (i)
- Living things exist as transduction devices of stimuli into responses, as transformers of inputs and outputs, according to deterministic, non-random, but not predeterminable causal relations [2];
- (ii)
- The theoretical tools commonly used to analyze the dynamics of living things are not capable of exhaustively describing the typical features of living things (from biochemical orders to energetic yields and biocommunication to morphogenesis, adaptation, non-random evolutionary pathways, as well as memory, behavior, choice, and teleology) [3,4,5].
2. Shifting from QM to QFT
2.1. Order, Symmetry Breaking, Dissipation, and Coherence
- (i)
- The manifold of possible configurations is made possible by the existence of the numerous (infinite) possible ground states in the scenario offered by QFT;
- (ii)
- The coexistence of these multiple configurations is given by the fact that these ground states are orthogonal to each other;
- (iii)
- Their temporal sequence is given by the dissipative dynamics, i.e., by their thermodynamic history (by all possible pairs of values of N(α) and N(β) obeying the relations N(α) − N(β) = 0);
- (iv)
- The succession of the states of the system is indeed a time-dependent thermodynamical (dissipative) history along which the following states depends on the previous ones in a deterministic, but a priori unpredictable, way because of the presence of its thermodynamical “double” (environment, inclusive of every possible quality and kind of stimuli).
2.2. Condensed Matter from a Field Perspective: Water, the Matrix of Life
2.3. Living Phase of Matter: Time-Dependent Order and Morphogenesis
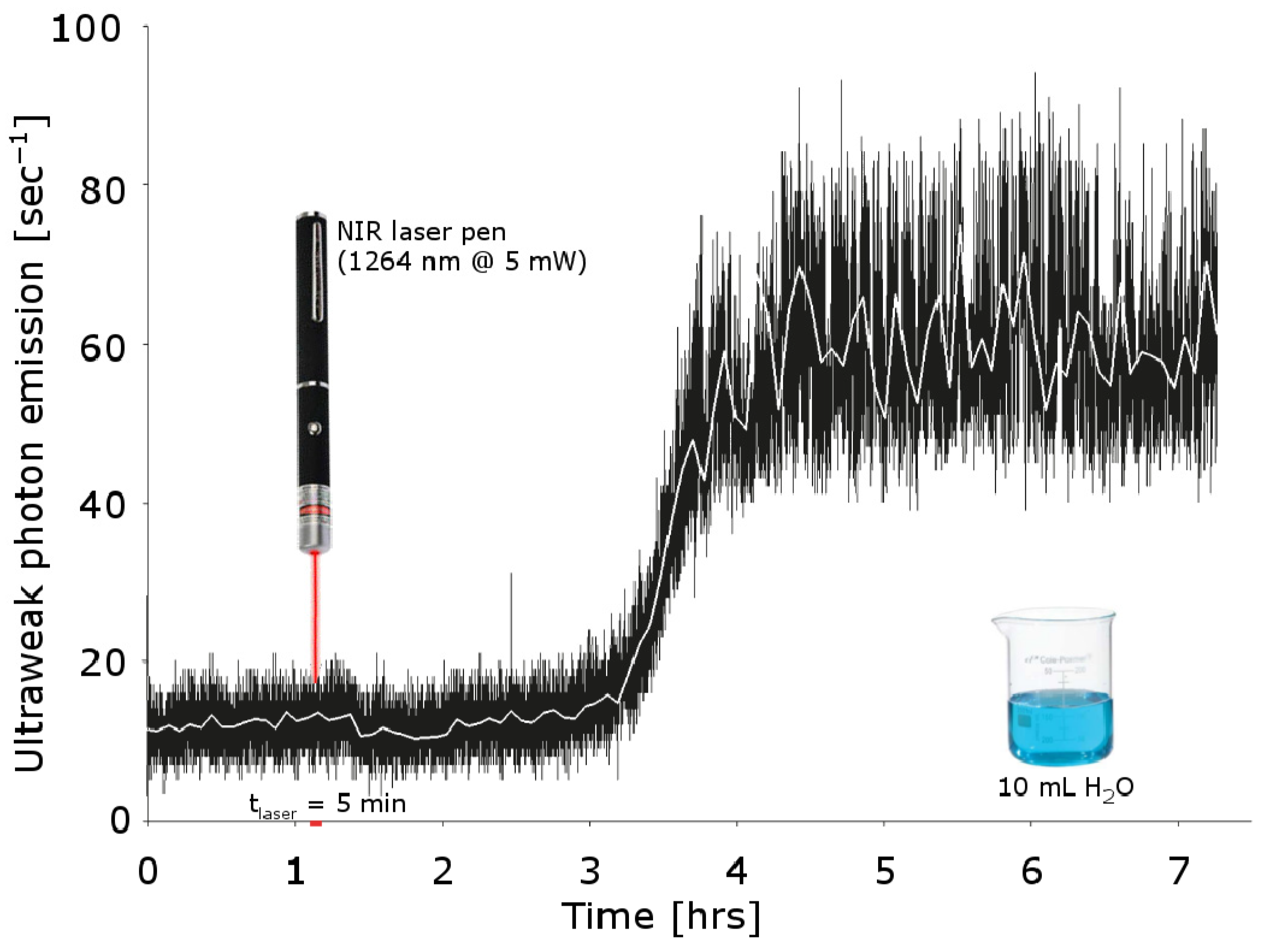
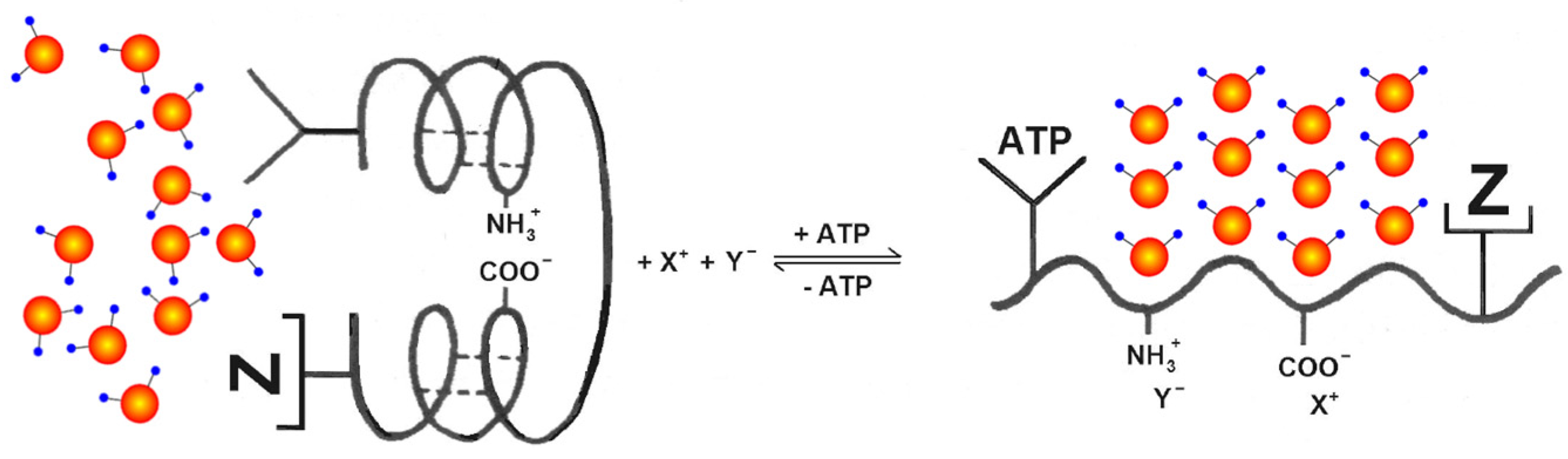
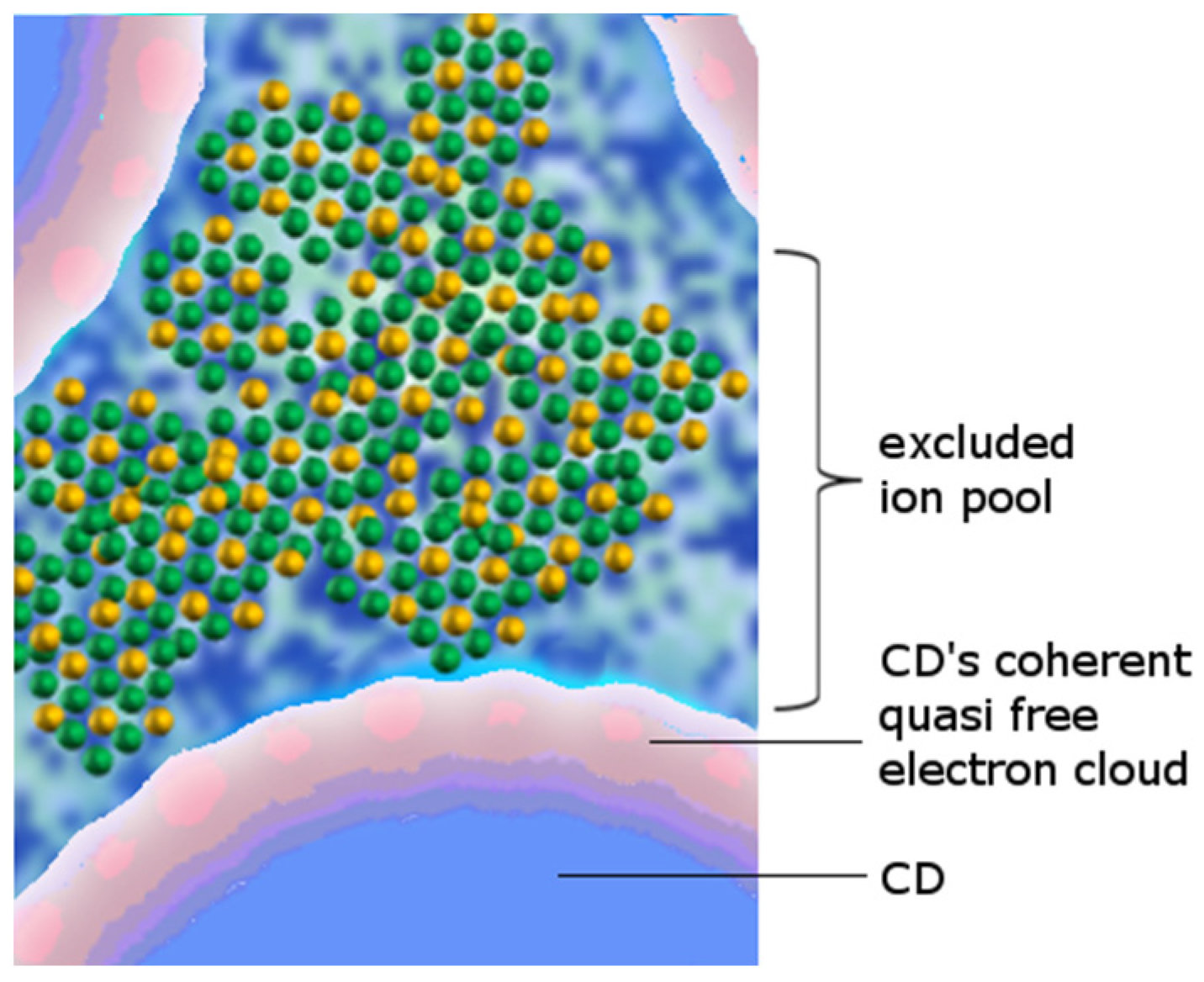
2.4. A Sensible Case: Ions and Ultraweak Fields
- -
- The “interface” zone, where self-trapped EM fields decay from inside water CDs, is the region between the ideal radius (RCD) of a CD at zero temperature and its actual radius due to thermal erosion from outside incoherent molecules. This zone has a temperature-dependent thickness δ. The effective radius r of a CD is thus given as r = RCD − δ(T). At normal temperatures (20 °C), δ(T)10 Å.
- -
- The “reservoir” zone corresponds to the interstices in-between CDs. Such zones are not occupied by EM field tails, and water is dense and vaporous there (Figure 7).
2.5. Hormesis: The Stimulus–Response Relationship
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
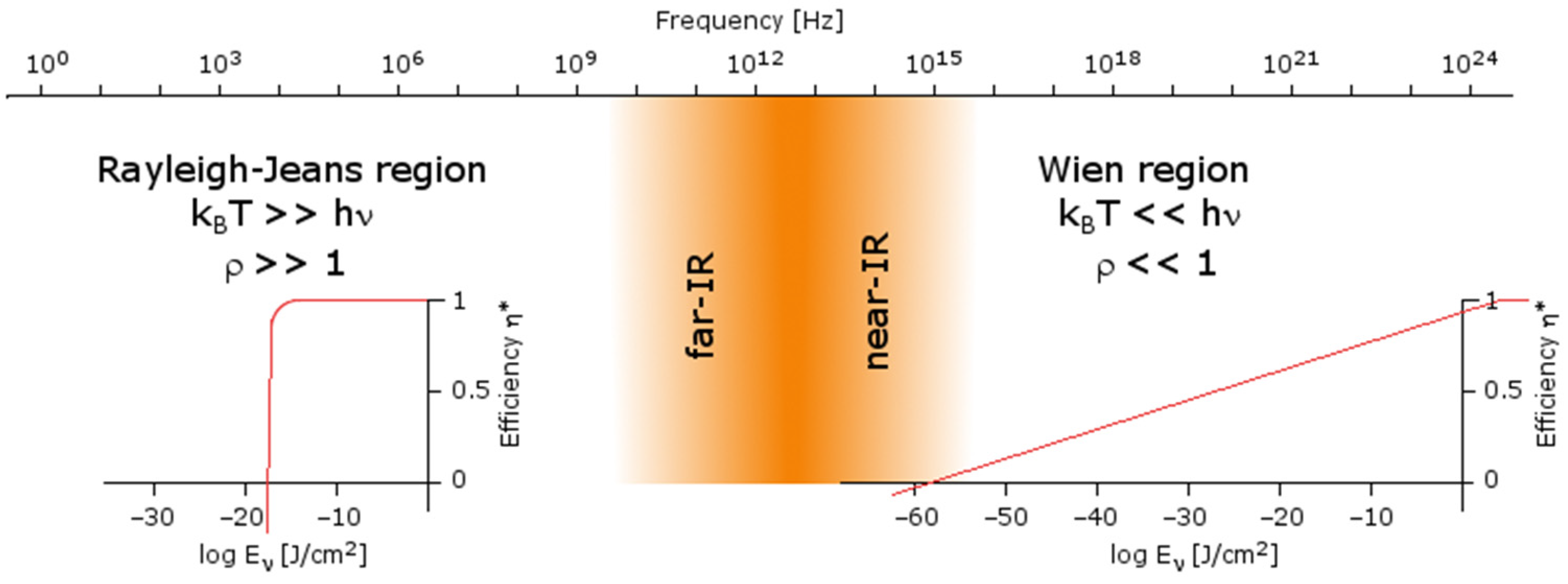
Appendix A. Radiation Hormesis and Quantum Thermodynamics
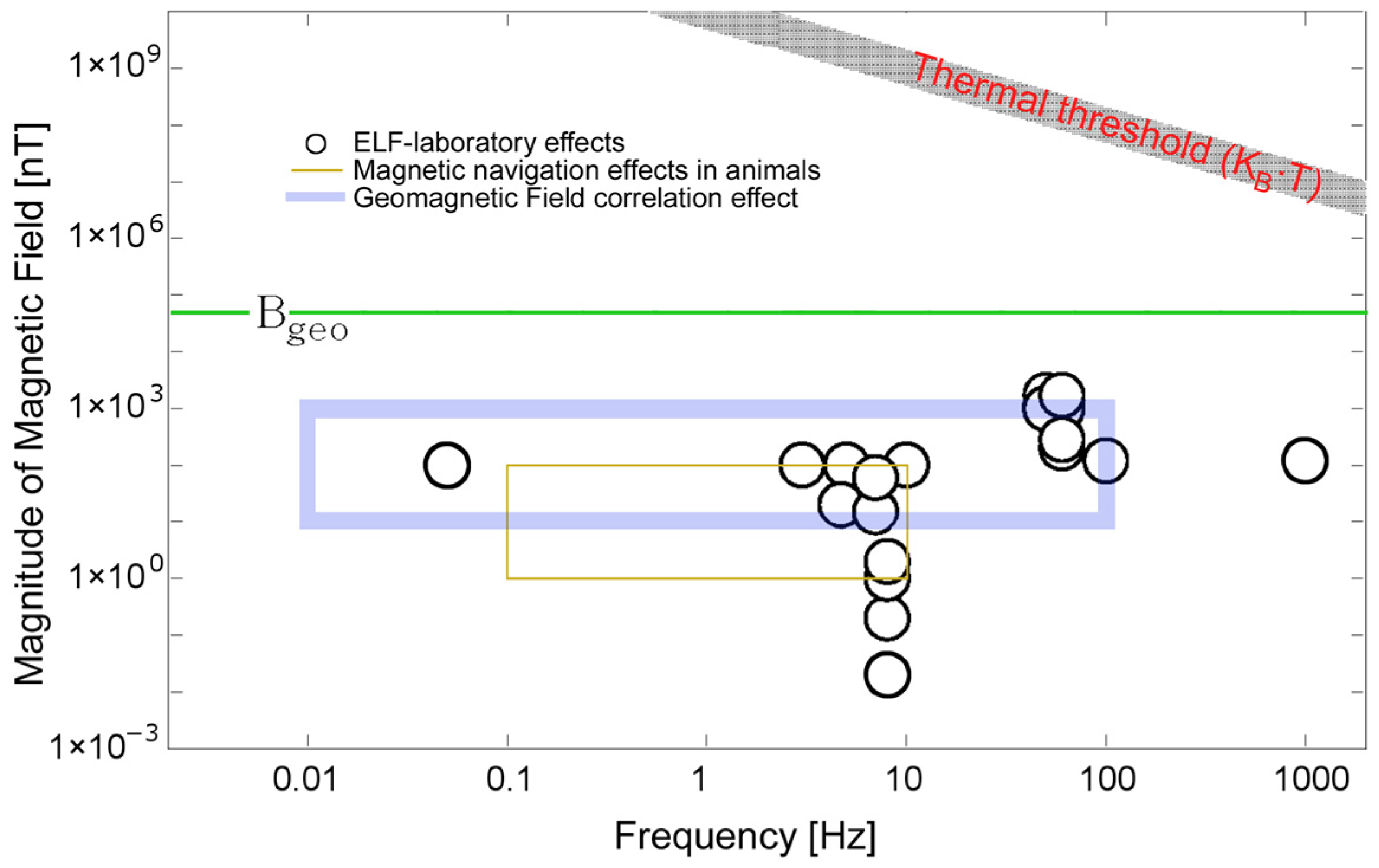
Appendix B. Effects of Weak-Field Exposure on Biota
Appendix C. The Theoretical Basis
Appendix C.1. How the Field Gradient Induces Order
Appendix C.2. Water with Various Dielectric Constants
Appendix C.3. Dissolution of Salts in Water
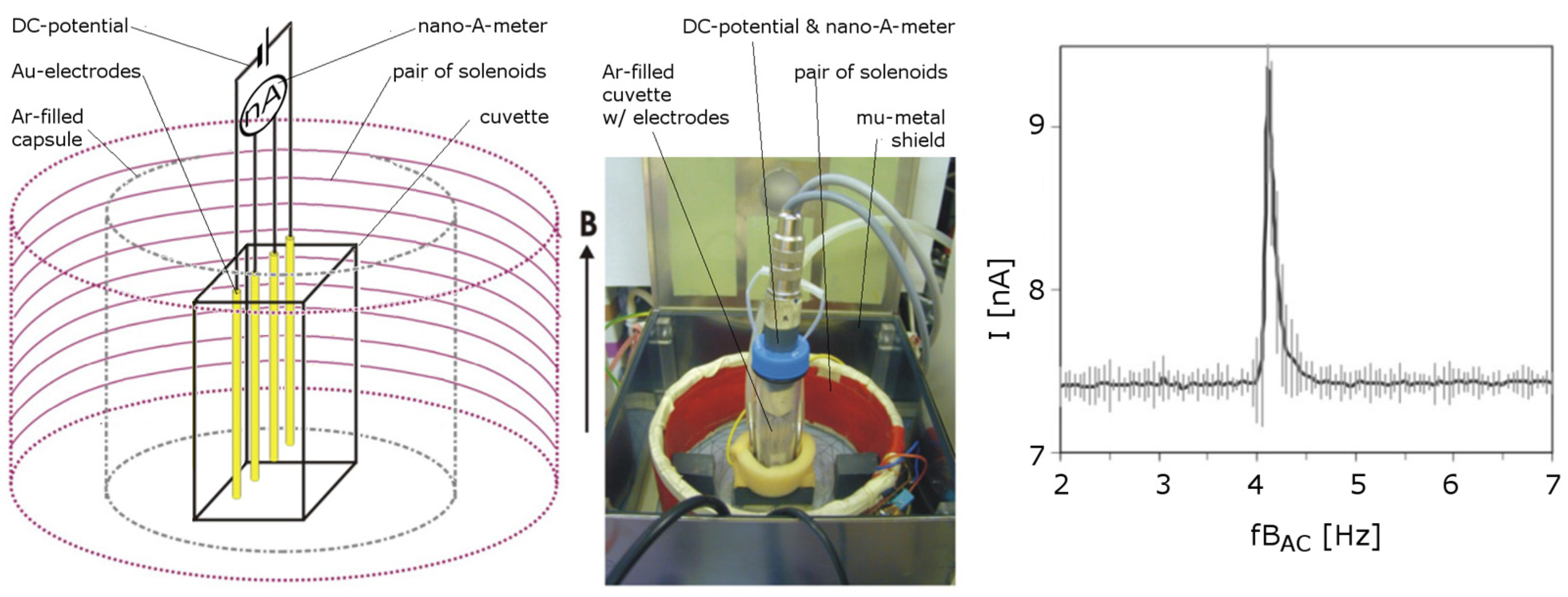
Appendix C.4. Current Spike as a Result of Interfacial Ion Cleansing


References
- Preparata, G. QED Coherence in Matter; World Scientific: Singapore, 1995. [Google Scholar] [CrossRef]
- Renati, P. Electrodynamic Coherence as a Physical Basis for Emergence of Perception, Semantics, and Adaptation in Living Systems. J. Genet. Mol. Cell. Biol. 2020, 7, 1–34. [Google Scholar] [CrossRef]
- Vitiello, G. Structure and function. Open letter to Patricia Churchland. In Toward a Science of Consciousness II; MIT Press: Boston, MA, USA, 1998; pp. 231–236. [Google Scholar]
- Del Giudice, E.; Stefanini, P.; Tedeschi, A.; Vitiello, G. The interplay of biomolecules and water at the origin of the active behaviour of living organisms. J. Phys. Conf. Ser. 2011, 329, 012001. [Google Scholar] [CrossRef]
- Renati, P. Relationships and Causation in Living Matter: Reframing Some Methods in Life Sciences? Phys. Sci. Biophys. J. 2022, 6, 1–25. [Google Scholar] [CrossRef]
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Krüger, T.P.J.; et al. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef] [PubMed]
- Preparata, G. An Introduction to a Realistic Quantum Physics; World Scientific: Singapore, 2002. [Google Scholar] [CrossRef]
- Perlman, H.S. Quantum Mechanics is Incomplete but it is Consistent with Locality. Found. Phys. 2017, 47, 1309–1316. [Google Scholar] [CrossRef]
- Umezawa, H. Advanced Field Theory: Micro, Macro and Thermal Concepts; American Institute of Physics: New York, NY, USA, 1993; ISBN 978-1-56396-456-5. [Google Scholar]
- Blasone, M.; Jizba, J.; Vitiello, G. Quantum Field Theory and Its Macroscopic Manifestations; Imperial College Press: London, UK, 2011. [Google Scholar]
- von Neumann, J. Mathematical Foundations of Quantum Theory; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Prigogine, I.; Stengers, I. La Nouvelle Alliance; Gallimard: Paris, France, 1979; ISBN 978-2-07032-324-1. [Google Scholar]
- Jorgensen, S.E.; Svirezhev, Y.M. Towards a Thermodynamic Theory for Ecological Systems; Elsevier: Amsterdam, The Netherlands, 2004; p. 366. [Google Scholar]
- Vernadsky, V. The Biosphere (Re-Edition of 1998); With introduction and annotations by Mark A.S.McMenamin and Jacques Grinevald., Leningrad: Copernicus Books (first published by GTI in Russian in 1926); Springer Science Business Media, LLC: Berlin/Heidelberg, Germany, 1926; ISBN 978-0-38798-268-7. [Google Scholar]
- Del Giudice, E.; Pulselli, R.M.; Tiezzi, E. Thermodynamics of irreversible processes and quantum field theory: An interplay for the understanding of ecosystem dynamics. Ecol. Model. 2009, 220, 1874–1879. [Google Scholar] [CrossRef]
- Marchettini, N.; Del Giudice, E.; Voeikov, V.; Tiezzi, E. Water: A medium where dissipative structures are produced by a coherent dynamics. J. Theor. Biol. 2010, 265, 511–516. [Google Scholar] [CrossRef]
- Vitiello, G. My Double Unveiled: The Dissipative Quantum Model of Brain; Benjamins Publisher Co.: Amsterdam, The Netherland, 2001. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. Electromagnetic field and spontaneous symmetry breakdown in biological matter. Nucl. Phys. B 1986, 275, 185. [Google Scholar] [CrossRef]
- Umezawa, H.; Vitiello, G. Quantum Mechanics; Bibliopolis: Naples, Italy, 1985; ISBN 8-870-881-326. [Google Scholar]
- Ricciardi, L.M.; Umezawa, H. Brain and physics of many-body problems. Kybernetik 1967, 4, 44–48. [Google Scholar] [CrossRef]
- Pitch, A. Effective Field Theory with Nambu–Goldstone Modes (Lectures). arXiv 2017, arXiv:1804.05664. [Google Scholar]
- Umezawa, H. Development in concepts in quantum field. Math. Jpn. 1995, 41, 109–124. [Google Scholar]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. A quantum field theoretical approach to the collective behavior of biological systems. Nucl. Phys. B 1985, 251, 375. [Google Scholar] [CrossRef]
- Freeman, W.; Vitiello, G. Dissipation, spontaneous breakdown of symmetry and brain dynamics. J. Phys. A Math. Theor. 2008, 41, 304042. [Google Scholar] [CrossRef]
- Bogoliubov, N.; Shirkov, D. Quantum Fields; Benjamin/Cummings Publ. Inc.: Massachusetts, MA, USA, 1983; ISBN 0-8053-0983-7. [Google Scholar]
- Wolfe, J. Imaging Phonons; Cambridge University Press: Cambridge, UK, 1998; ISBN 978-0-51166-542-4. [Google Scholar] [CrossRef]
- Preparata, G. Quantum field theory of ‘superradiance’. In Proceedings of the 4th Winter School on Hadronic Physics, Folgaria, Italy, 6–11 February 1989; p. 34. Available online: https://lib-extopc.kek.jp/preprints/PDF/1989/8910/8910032.pdf (accessed on 5 May 2023).
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Klauder, J.; Sudarshan, G. Fundamentals of Quantum Optics; WA Benjamin, Inc.: New York, NY, USA, 1968; ISBN 0-4864-5008-2. [Google Scholar]
- Renati, P. Physical Analogical Foundations of Conscious Reality; ININ Editions: Lugano, Switzerland, 2016; ISBN 978-8-89849-709-6. [Google Scholar]
- Bono, I.; Del Giudice, E.; Gamberale, L.; Henry, M. Emergence of the Coherent Structure of Liquid Water. Water 2012, 4, 510–532. [Google Scholar] [CrossRef]
- Renati, P.; Kovacs, Z.; De Ninno, A.; Tsenkova, R. Temperature dependence analysis of the NIR spectra of liquid water confirms the existence of two phases, one of which is in a coherent state. J. Mol. Liq. 2019, 292, 111449. [Google Scholar] [CrossRef]
- Tokushima, T.; Harada, Y.; Takahashi, O.; Senba, Y.; Ohashi, H.; Pettersson, L.; Nilsson, A.; Shin, S. High resolution X-ray emission spectroscopy of liquid water: The observation of two structural motifs. Chem. Phys. Lett. 2008, 460, 387–400. [Google Scholar] [CrossRef]
- Huang, C.; Wikfeldt, K.; Tokushima, T.; Nordlund, D.; Harada, Y.; Bergmann, U.; Niebuhr, M.; Weiss, T.; Horikawa, Y.; Leetmaa, M.; et al. The inhomogeneous structure of water at ambient conditions. Proc. Natl. Acad. Sci. USA 2009, 106, 15214–15218. [Google Scholar] [CrossRef]
- Taschin, A.; Bartolini, P.; Eramo, R.; Righini, R.; Torre, R. Evidence of two distinct local structures of water from ambient to supercooled conditions. Nat. Commun. 2013, 4, 2401. [Google Scholar] [CrossRef]
- Wikfeldt, K.; Nilsson, A.; Pettersson, L. Spatially inhomogeneous bimodal inherent structure of simulated liquid water. Phys. Chem. Chem. Phys. 2011, 13, 19918–19924. [Google Scholar] [CrossRef]
- Arani, R.; Bono, I.; Del Giudice, E.; Preparata, G. QED coherence and the thermodynamics of water. Int. J. Mod. Phys. B 1995, 9, 1813–1841. [Google Scholar] [CrossRef]
- Pollack, G.; Zheng, J.; Chin, W.; Khijniak, E.; Khijniak, E.J. Surfaces and interfacial water: Evidence that hydrophilic surfaces have long-range impact. Adv. Colloid Interface Sci. 2006, 23, 19–27. [Google Scholar] [CrossRef]
- Pollack, G.; Yoo, H.; Paranji, R. Impact of hydrophilic surfaces on interfacial water dynamics probed with NMR spectroscopy. J. Phys. Chem. Lett. 2011, 2, 532–536. [Google Scholar] [CrossRef]
- Del Giudice, E.; Preparata, G.; Vitiello, G. Water as a Free Electric Dipole Laser. Phys. Rev. Lett. 1988, 61, 1085–1088. [Google Scholar] [CrossRef] [PubMed]
- Persinger, M. The Modern Magnetotherapies. In Modern Bioelectricity; Dekker Inc.: New York, NY, USA, 1988; ISBN 978-1-0030-6582-1. [Google Scholar] [CrossRef]
- Del Giudice, E.; De Ninno, A.; Fleischmann, M.; Mengoli, G.; Milani, M.; Talpo, G.; Vitiello, G. Coherent Quantum Electrodynamics in Living Matter. Electromagn. Biol. Med. 2005, 24, 199–210. [Google Scholar] [CrossRef]
- Voeikov, V.L.; Del Giudice, E. Water Respiration: The Basis of the Living State. Water 2009, 1, 52–75. [Google Scholar] [CrossRef]
- Germano, R.; Tontodonato, V.; Hison, C.; Cirillo, D.; Tuccinardi, F. Oxhydroelectric Effect: Oxygen Mediated Electron Current Extraction from Water by Twin Electrodes. Key Eng. Mater. 2011, 495, 100–103. [Google Scholar] [CrossRef]
- Voeikov, V. Reactive Oxygen Species, Water, Photons, and Life. Riv. Biol. 2001, 94, 193–214. [Google Scholar]
- Voeikov, V. Mitogenetic radiation, biophotons and non-linear oxidative processes in aqueous media. In Integrative Bio-Physics–Biophotonics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 331–359. [Google Scholar] [CrossRef]
- Gudkov, S.; Bruskov, V.; Astashev, M.; Chernikov, A.; Yaguzhinsky, L.; Zakharov, S. Oxygen-dependent au-to-oscillations of water luminescence triggered by the 1264 nm radiation. J. Phys. Chem. B 2011, 115, 7693–7698. [Google Scholar] [CrossRef]
- Del Giudice, E.; Spinetti, P.R.; Tedeschi, A. Water Dynamics at the Root of Metamorphosis in Living Organisms. Water 2010, 2, 566–586. [Google Scholar] [CrossRef]
- Szent-Györgyi, A. The study of energy–levels in biochemistry. Nature 1941, 148, 157–159. [Google Scholar] [CrossRef]
- Szent-Györgyi, A. Bioenergetics; New York Academic Press: New York, NY, USA, 1957. [Google Scholar]
- Binhi, V. Magnetobiology; Academic Press: London, UK, 2002; p. 484. ISBN 200-109-59-15. [Google Scholar]
- Binhi, V. Principles of Electromagnetic Biophysics; FIZMATLIT: Moscow, Russia, 2011; p. 592. ISBN 978-5-9221-1333-5. (In Russian) [Google Scholar]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. Coherent Excited States in the Theory of Superconductivity: Gauge Invariance and the Meissner Effect. Phys. Rev. 1958, 110, 827–835. [Google Scholar] [CrossRef]
- Kibble, T. Some implications of a cosmological phase transition. Phys. Rep. 1980, 67, 183–199. [Google Scholar] [CrossRef]
- Del Giudice, E.; Vitiello, G. The Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions. Phys. Rev. A 2006, 74, 022105. [Google Scholar] [CrossRef]
- Celeghini, E.; De Martino, S.; De Siena, S.; Rasetti, M.; Vitiello, G. Quantum Groups, Coherent States, Squeezing and Lattice Quantum Mechanics. Ann. Phys. 1995, 241, 50–67. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Batelaan, T.A. The Aharonov–Bohm effects: Variations on a Subtle Theme. Phys. Today 2009, 62, 38–43. [Google Scholar] [CrossRef]
- Brizhik, L.; Del Giudice, E.; Jørgensen, S.E.; Marchettini, N.; Tiezzi, E. The role of electromagnetic potentials in the evolutionary dynamics of ecosystems. Ecol. Model. 2009, 220, 1865–1869. [Google Scholar] [CrossRef]
- Ho, M.-W.; Yu-Ming, Z.; Haffegee, J.; Watton, A.; Musumeci, F.; Privitera, G.; Scordino, A.; Triglia, A. The Liquid Crystalline Organism and Biological Water. In Water and the Cell; Springer: Dordrecht, The Netherland, 2006; pp. 219–234. [Google Scholar] [CrossRef]
- Ho, M.-W. Living Rainbow H2O; World Scientific: Singapore, 2012. [Google Scholar] [CrossRef]
- Garbelli, A. Proprietà Termodinamiche e Dielettriche Dell’acqua Alla Luce Della Teoria Complessa Delle Interazioni Molecolari Rlettrodinamiche ed Elettrostatiche (Thermodynamic and Dielectric Properties of Water in the Light of the Complex Theory of Electrodinamic and Electrostatic Molecular Interactions). Ph.D. Thesis, University of Milan, Milan, Italy, 2000. [Google Scholar]
- Del Giudice, E.; Tedeschi, A. Water and Autocatalysis in Living Matter. Electromagn. Biol. Med. 2009, 28, 46–52. [Google Scholar] [CrossRef]
- Ling, G. Life at the Cell and Below-Cell Level; Pacific Press: New York, NY, USA, 2001; ISBN 0-970-7322-0-1. [Google Scholar]
- Ling, G. What Is Life Answered in Terms of Properties and Activities of Auto-cooperativeAssemblies of Molecules, Atoms, Ions and Electrons Called Nano-protoplasm. Physiol. Chem. Phys. Med. NMR 2012, 42, 1–64. [Google Scholar]
- Henry, M. L’Eau et La Physique Quantique—Vers une Révolution de la Médecine (Water and Quantum Physics—Progres-Sing towards a Medical Revolution, in French); Éditions Dangles: Escalquens, France, 2016; ISBN 978-2-7033-1147-8. [Google Scholar]
- Ling, G. Nano-protoplasm: The Ultimate Unit of Life. Physiol. Chem. Phys. Med. NMR 2007, 39, 111–234. [Google Scholar]
- Sen, S.; Gupta, K.S.; Coey, J.M.D. Mesoscopic structure formation in condensed matter due to vacuum fluctuations. Phys. Rev. B 2015, 92, 155115. [Google Scholar] [CrossRef]
- Henry, M. L’eau Morphogenique—Sante, Information Et Champs de Coscience, Escalquens; Éditions Dangles: Escalquens, France, 2020; ISBN 978-2-7033-1269-7. [Google Scholar]
- Henry, M. The topological and quantum structure of zoemorphic water. In Aqua Incognita: Why Ice Floats on Water and Galileo 400 Years on; LoNostro, P.N.B.E., Ed.; Connor Court Publisher: Ballarat, Australia, 2014; pp. 197–239. ISBN 978-1925138214. [Google Scholar]
- Del Giudice, E. Old and new views on the structure of matter and the special case of living matter. J. Phys. Conf. Ser. 2007, 67, 012006. [Google Scholar] [CrossRef]
- Ho, M. Quantum coherence and conscious experience. Kybernetes 1997, 26, 653–674. [Google Scholar] [CrossRef][Green Version]
- Ho, M. Meaning of Life and the Universe; World Scientific: Singapore, 2017. [Google Scholar] [CrossRef]
- Ho, M.-W. Quantum Jazz—The Meaning of life, the Universe and Everything. September 2006. Available online: https://www.i-sis.org.uk/QuantumJazz.php (accessed on 5 June 2023).
- Roy, R.; Rao, M.; Kanzius, J. Observations of polarised RF radiation catalysis of dissociation of H2O-NaCl solutions. Mater. Res. Innov. 2008, 12, 3–6. [Google Scholar] [CrossRef]
- Popp, F.; Nagl, W.; Li, K.; Scholz, W.; Weingärtner, O.; Wolf, R. Biophoton emission. New evidence for coherence and DNA as source. Cell Biophys. 1984, 6, 33–52. [Google Scholar] [CrossRef]
- Li, K. Coherent Radiation from DNA Molecules. In Recent Advances in Biophoton Research and Its Applications; World Scientific: Singapore, 1992; pp. 157–195. [Google Scholar] [CrossRef]
- Bajpai, R.; Brizhik, L.; Del Giudice, E.; Finelli, F.; Popp, F.-A.; Schlebusch, K.-P. Light as a Trigger and a Probe of the Internal Dynamics of Living Organisms. J. Acupunct. Meridian Stud. 2010, 3, 291–297. [Google Scholar] [CrossRef]
- Blank, M.; Goodman, R. DNA is a fractal antenna in electromagnetic fields. Int. J. Radiat. Biol. 2011, 87, 409–415. [Google Scholar] [CrossRef]
- Calabrò, E.; Magazù, S. The α-helix alignment of proteins in water solution toward a high-frequency electromagnetic field: A FTIR spectroscopy study. Electromagn. Biol. Med. 2017, 36, 279–288. [Google Scholar] [CrossRef]
- Madl, P. The field and the photon from a physical point of view. In Fields of the Cell; Research Signpost: Kerala, India, 2015; pp. 29–53. ISBN 978-81-308-0544-3. [Google Scholar] [CrossRef]
- Celeghini, E.; Rasetti, M.; Vitiello, G. Quantum dissipation. Ann. Phys. 1992, 215, 156–170. [Google Scholar] [CrossRef]
- Del Giudice, E.; Preparata, G.; Fleischmann, M. QED coherence and electrolyte solutions. J. Electroanal. Chem. 2000, 482, 110–116. [Google Scholar] [CrossRef]
- Del Giudice, E.; Fleischmann, M.; Preparata, G.; Talpo, G. On the ‘unreasonable’ effects of ELF magnetic fields upon a system of ions. Bioelectromagnetics 2002, 23, 522–530. [Google Scholar] [CrossRef] [PubMed]
- Zhadin, M.N.; Novikov, V.V.; Barnes, F.S.; Pergola, N.F. Combined action of static and alternating magnetic fields on ionic current in aqueous glutamic acid solution. Bioelectromagnetics 1998, 19, 41–45. [Google Scholar] [CrossRef]
- Zhadin, M.; Giuliani, L. Some Problems in Modern Bioelectromagnetics. Electromagn. Biol. Med. 2006, 25, 227–243. [Google Scholar] [CrossRef]
- Pazur, A. Characterisation of weak magnetic field effects in an aqueous glutamic acid solution by nonlinear dielectric spectroscopy and voltammetry. Biomagn. Res. Technol. 2004, 2, 8. [Google Scholar] [CrossRef]
- Giuliani, L.; Grimaldi, S.; Lisi, A.; D’Emilia, E.; Bobkova, N.; Zhadin, M. Action of combined magnetic fields on aqueous solution of glutamic acid: The further development of investigations. Biomagn. Res. Technol. 2008, 6, 1. [Google Scholar] [CrossRef]
- Liboff, A. Cyclotron resonance in membrane transport. In Interaction between Electromagnetic Fields and Cells; Plenum Press: London, UK, 1985; pp. 281–296. ISBN 9-780-30642-083-2. [Google Scholar] [CrossRef]
- Liboff, A.; Smith, S. Experimental evidence for ion cyclotron resonance mediation of membrane transport. In Mechanistic Approaches to Interaction of Electric and Electromagnetic Fields with Living Systems; Plenum Press: New York, NY, USA, 1987; pp. 109–132. ISBN 978-1-4899-1970-0. [Google Scholar] [CrossRef]
- Adey, W. Frequency and power windowing in tissue interactions with weak electromagnetic fields. Proc. IEEE 1980, 68, 119–125. [Google Scholar] [CrossRef]
- Markov, M.S. “Biological Windows”: A Tribute to W. Ross Adey. Environmentalist 2005, 25, 67–74. [Google Scholar] [CrossRef]
- Southam, C.; Ehrlich, J. Effects of extract of western red-cedar heartwood on certain wood-decaying fungi in culture. Phytopathology 1943, 33, 517–524. [Google Scholar]
- Martins, I.; Galluzzi, L.; Kroemer, G. Hormesis, cell death and aging. Aging 2011, 3, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Kmecl, P.; Jerman, I. Biological effects of low-level environmental agents. Med. Hypotheses 2000, 54, 685–688. [Google Scholar] [CrossRef] [PubMed]
- Sanders, C. Accidents, Test and Incidents. In Radiation Hormesis and the Linear-No-Threshold Assumption; Springer: Berlin, Germany, 2010; pp. 43–50. ISBN 978-3-642-03720-7. [Google Scholar] [CrossRef]
- Chukova, Y. Radiation Hormesis in the Light of the Laws of Quantum Thermodynamics. In Proceedings of the 6th International Conference on Radiation and Applications in Various Fields of Research (RAD 2018), Ohrid, Macedonia, 18–22 June 2018. [Google Scholar]
- Calabrese, E.J. Hormesis: A fundamental concept in biology. Microb. Cell 2014, 1, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, E.; Baldwin, L. Hormesis: A generalizable and unifying hypothesis. Crit. Rev. Toxicol. 2001, 31, 353–424. [Google Scholar] [CrossRef]
- Calabrese, E.J.; Bachmann, K.A.; Bailer, A.J.; Bolger, P.M.; Borak, J.; Cai, L.; Cedergreen, N.; Cherian, M.G.; Chiueh, C.C.; Clarkson, T.W.; et al. Biological stress response terminology: Integrating the concepts of adaptive response and preconditioning stress within a hormetic dose-response frame-work. Toxicol. Appl. Pharmacol. 2007, 222, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Chisolm, H. Weber’s Law. In Encyclopaedia Britannica, 11th ed.; Cambridge University Press: Cambridge, UK, 1910; Available online: https://archive.org/details/EncyclopaediaBritannicaDict.a.s.l.g.i.11thed.chisholm.1910-1911-1922.33vols/01.EncycBrit.11th.1910.v.1.A-AND./page/n13/mode/2up (accessed on 5 May 2023).
- Madl, P.; De Filippis, A.; Tedeschi, A. Effects of ultra-weak fractal electromagnetic signals on the aqueous phase in living systems: A test-case analysis of molecular rejuvenation markers in fibroblasts. Electromagn. Biol. Med. 2020, 39, 227–238. [Google Scholar] [CrossRef]
- Madl, P.; Germano, R.; Tedeschi, A.; Lettner, H. Effects of Ultra-Weak Fractal Electromagnetic Signals on Malassezia furfur. Int. J. Mol. Sci. 2023, 24, 4099. [Google Scholar] [CrossRef]
- Chukova, Y. Fundamental Laws of Efficiency of Isothermal Processes under Ionising and Non-Ionising Electromagnetic Radiation. In Proceedings of the First International Conference on Radiation and Dosimetry in Various Fields of Research, Nis, Serbia, 25–27 April 2012; ISBN 978-86-6125-062-0. Available online: https://www.rad-conference.org/Proceedings-RAD_2012.pdf (accessed on 5 May 2023).
- Murray, R. The Ampullae of Lorenzini. In Electroreceptors and Other Specialized Receptors in Lower Vertebrates. Handbook of Sensory Physiology 3/3; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar] [CrossRef]
- Cope, F. Derivation of the Weber-Fechner law and the Loewenstein equation as the steady-state response of an Elovich solid state biological system. Bullettin Math. Biol. 1976, 38, 111–118. [Google Scholar] [CrossRef]
- Landy, M. Handout to Weber’s Law and Fechner’s Law; New York, 2014. Available online: https://www.cns.nyu.edu/~msl/courses/0044/handouts/Weber.pdf (accessed on 5 May 2023).
- Nutter, F.W.; Esker, P.D. The Role of Psychophysics in Phytopathology: The Weber–Fechner Law Revisited. Eur. J. Plant Pathol. 2006, 114, 199–213. [Google Scholar] [CrossRef]
- Tosi, M.; Del Giudice, E. The Principle of Minimum Stimulus in the Dynamics of the Living Organism. ISIS Rep. 2013, 60, 26–29. Available online: https://www.i-sis.org.uk/principle_of_minimal_stimulus.php (accessed on 5 May 2023).
- Becker, R.O.; Selden, G. The Body Electric: Electromagnetism and the Foundation of Life; William Morrow Paperbacks: New York, NY, USA, 1985; ISBN 0-688-06971-1. [Google Scholar]
- Binhi, V.N.; Rubin, A.B. Magnetobiology: The kT Paradox and Possible Solutions. Electromagn. Biol. Med. 2007, 26, 45–62. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, E.; Giuliani, L. Coherence in water and the kT problem in living matter. In Non-Thermal Effects and Mechanisms of Interaction between Electromagnetic Fields and Living Matter; Ramazzini Institute: Bologna, Italy, 2010; Available online: http://www.teslabel.be/PDF/ICEMS_Monograph_2010.pdf (accessed on 5 May 2023).
- Neidhardt, F.C.; Umbarger, H.E. Chemical Composition of Escherichia coli. In Escherichia Coli and Salmonella: Cellular and Molecular Biology, 2nd ed.; Neidhardt, F.C., Curtiss, R., Inghraham, J.L., Lin, C.C.E., Low, K.B., Magasanik, B., Rfznikopp, W.S., Riley, M., Schaechter, M., Umarger, H.E., Eds.; ASM Press: Washington, DC, USA, 1996; Volume I, Chapter 3; pp. 2788–2802. ISBN 1-55581-084-5. [Google Scholar]
- Sundararaj, S.; Guo, A.; Habibi-Nazhad, B.; Rouani, M.; Stothard, P.; Ellison, M.; Wishart, D. The CyberCell Database (CCDB): A comprehensive, self-updating, relational database to coordinate and facilitate in silico modeling of Escherichia coli. Nucleic Acids Res. 2004, 1, 32. [Google Scholar] [CrossRef]
- Milo, P.R. Cell Biology by the Numbers; Garland Science: New York, NY, USA, 2015; ISBN 978-0-8153-4163-5. [Google Scholar] [CrossRef]
- Giuliani, L.; (Bruxelles, Venice). Personal communication, 2001.
- Liboff, A. Local and holistic electromagnetic therapies. Electromagn. Biol. Med. 2007, 26, 315–325. [Google Scholar] [CrossRef] [PubMed]
- Ellis, K. Reference Man and Woman More Fully Characterized: Variations on the Basis of Body Size, Age, Sex, and Race. In Analytical Methods in the Life Sciences; Humana Press: Totowa, NJ, USA, 1990; pp. 385–400. ISBN 978-1-4612-6777-5. [Google Scholar] [CrossRef]
- Snyder, W.; Cook, M.; Nasset, E.; Karhausen, L.; Howells, G.; Tipton, T. Report of the Task Group on Reference Man (ICRP 23); Pergamon Press: Oxford, UK, 1975; ISBN 0-080-17024-2. Available online: https://www.icrp.org/publication.asp?id=ICRP%20Publication%2023 (accessed on 5 May 2023).
- Henry, M. The state of water in living systems: From the liquid to the jellyfish. Cell. Mol. Biol. 2005, 51, 677–702. [Google Scholar]
- Madl, P. Organisatiosnbionik—Die Natur als der Bessere Unternehmer! (Organisational Bionics—Nature: The Best Form of Economy Is Ecology). Lecture Held at the Technical University Puch-Urstein, Salzburg. December, 2006. Available online: http://edge-institute.org/talk/sprechstunde-2006.pdf (accessed on 15 August 2023).
- Brizhik, L.; Chiappini, E.; Stefanini, P.; Vitiello, G. Modeling Meridians Within the Quantum Field Theory. J. Acupunct. Meridian Stud. 2019, 12, 29–36. [Google Scholar] [CrossRef]
- Liboff, A. Subtle Electromagnetic Interactions in Living Things. In Bioelectromagnetic and Subtle Energy Medicine; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-1-4822-3320-9. [Google Scholar]
- Becker, R.O. Stimulation of Partial Limb Regeneration in Rats. Nature 1972, 235, 109–111. [Google Scholar] [CrossRef]
- Illingworth, C.M. Trapped fingers and amputated finger tips in children. J. Pediatr. Surg. 1974, 9, 853–858. [Google Scholar] [CrossRef]
- Leppik, L.; Froemel, D.; Slavici, A.; Ovadia, Z.N.; Hudak, L.; Henrich, D.; Marzi, I.; Barker, J.H. Effects of electrical stimula-tion on rat limb regeneration, a new look at an old model. Sci. Rep. 2016, 5, 18353. [Google Scholar] [CrossRef]
- Davidian, D.; Levin, M. Inducing Vertebrate Limb Regeneration: A Review of Past Advances and Future Outlook. Cold Spring Harb. Perspect. Biol. 2021, 14, a040782. [Google Scholar] [CrossRef]
- Ho, M.; French, A.; Haffegee, J.; Saunders, P. Can weak magnetic fields (or potentials) affect pattern formation? In Bioelectrodynamics and Biocommunication; World Scientific: Singapore, 1994; pp. 195–212. ISBN 978-981-4503-82-2. [Google Scholar] [CrossRef]
- De Ninno, A.; Pregnolato, M. Electromagnetic homeostasis and the role of low-amplitude electromagnetic fields on life organization. Electromagn. Biol. Med. 2016, 36, 115–122. [Google Scholar] [CrossRef]
- Cappucci, U.; Casale, A.M.; Proietti, M.; Marinelli, F.; Giuliani, L.; Piacentini, L. WiFi Related Radiofrequency Electromagnetic Fields Promote Transposable Element Dysregulation and Genomic Instability in Drosophila melanogaster. Cells 2022, 11, 4036. [Google Scholar] [CrossRef] [PubMed]
- Chukova, Y. The Weber-Fechner Law; To the 150th anniversary of the publication of the book “Elemente der Psycho-physik” by G.T. Fechner; Gigiena: Moscow, Russia, 2010; ISBN 978-5-9042-0707-6. [Google Scholar]
- Stevens, S. To Honor Fechner and Repeal His Law: A power function, not a log function, describes the operating characteristic of a sensory system. Science 1961, 133, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Devyatkov, N. Influence of millimeter- band electromagnetic radiation on biological objects. Sov. Phys. 1974, 16, 568–579. [Google Scholar] [CrossRef]
- Smolyanskaya, A.; Vilenskaya, R. Effects of Millimeter-band Electromagnetic Radiation on the Functional Activity of Certain Genetic Elements of Bacterial Cells. Sov. Phys. Usp. 1974, 16, 571–572. [Google Scholar] [CrossRef]
- Chukova, Y. The Devyatkov law (on the 40th anniversary of the discovery of non-thermal bioeffects of millimeter radia-tion). J. Biomed. Radioelectron. 2014, 5, 17–27. [Google Scholar]
- Chukova, Y. Radioactivity in the Light of the Fundamental Law of Physics. In RAD Conference Proceedings; Elsevier: Amsterdam, The Netherlands, 2017; ISSN 2466-4626. [Google Scholar] [CrossRef]
- Wertheimer, N.; Leeper, E. ELECTRICAL WIRING CONFIGURATIONS AND CHILDHOOD CANCER. Am. J. Epidemiology 1979, 109, 273–284. [Google Scholar] [CrossRef]
- Comisso, N.; Del Giudice, E.; De Ninno, A.; Fleischmann, M.; Giuliani, L.; Mengoli, G.; Merlo, F.; Talpo, G. Dynamics of the ion cyclotron resonance effect on amino acids adsorbed at the interfaces. Bioelectromagnetics 2005, 27, 16–25. [Google Scholar] [CrossRef]
- Novikov, V.V.; Yablokova, E.V.; Fesenko, E.E. A Decrease of the Respiratory Burst in Neutrophils after Exposure to Weak Combined Magnetic Fields of a Certain Duration. Biophysics 2020, 65, 82–87. [Google Scholar] [CrossRef]
- Grundler, W.; Kaiser, F. Experimental evidence for coherent excitations correlated with cell growth. Nanobiology 1992, 1, 163–176. [Google Scholar]
- Golant, M.B.; Mudrik, D.G.; Kruglyakova, O.P.; Izvol’Skaya, V.E. Effect of EHF-radiation polarization on yeast cells. Radiophys. Quantum Electron. 1994, 37, 82–84. [Google Scholar] [CrossRef]
- Garkusha, O.; Mazurenko, R.; Makhno, S.; Gorbik, P. Influence of low-intensity electromagnetic millimeter radia-tion on the vital activity of Saccharomyces cerevisiae cells. Biophysics 2008, 53, 402–405. [Google Scholar] [CrossRef]
- Sagripanti, J.; Swicord, M.; Davis, C. Microwave Effects on Plasmid DNA. Radiation Research. Radiat. Res. 1987, 110, 219–232. [Google Scholar] [CrossRef] [PubMed]
- Lai, H.; Singh, N. Acute Low-Intensity Microwave Exposure Increases DNA Single-Strand Breaks in Rat Brain Cells. Bioelectromagnetics 1997, 16, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Lai, H.; Singh, N.P. Acute exposure to a 60 Hz magnetic field increases DNA strand breaks in rat brain cells. Bioelectromagnetics 1997, 18, 156–165. [Google Scholar] [CrossRef]
- Lai, H.; Singh, N.P. Magnetic-field-induced DNA strand breaks in brain cells of the rat. Environ. Health Perspect. 2004, 112, 687–694. [Google Scholar] [CrossRef]
- Marino, A.A.; O Becker, R. Biological effects of extremely low frequency electric and magnetic fields: A review. Physiol. Chem. Phys. 1977, 9, 131–147. [Google Scholar]
- Marron, M.T.; Goodman, E.M.; Greenebaum, B. Mitotic delay in the slime mould Physarum polycephalum induced by low intensity 60 and 75 Hz electromagnetic fields. Nature 1975, 254, 66–67. [Google Scholar] [CrossRef]
- Liboff, A.R.; Williams, T.; Strong, D.M.; Wistar, R. Time-Varying Magnetic Fields: Effect on DNA Synthesis. Science 1984, 223, 818–820. [Google Scholar] [CrossRef]
- Liboff, A. The ‘cyclotron resonance’ hypothesis: Experimental evidence and theoretical constraints. In Interaction Mechanisms of Low-Level Electromagnetic Fields in Living Systems; Oxford University Press: Oxford, UK, 1992; pp. 130–147. ISBN 0-1985-7759-1. [Google Scholar]
- Goodman, R.; Bassett, C.H.A. Pulsing electromagnetic fields induce cellular transcription. Science 1983, 220, 1283–1285. [Google Scholar] [CrossRef]
- Ubeda, A.; Leal, J.; A Trillo, M.; A Jimenez, M.; Delgado, J.M. Pulse shape of magnetic fields influences chick embryogenesis. J. Anat. 1983, 137, 513–536. [Google Scholar]
- Berman, E.; Chacon, L.; House, D.; Koch, B.A.; Koch, W.E.; Leal, J.; Løvtrup, S.; Mantiply, E.; Martin, A.H.; Martucci, G.I.; et al. Development of chicken embryos in a pulsed magnetic field. Bioelectromagnetics 1990, 11, 169–187. [Google Scholar] [CrossRef] [PubMed]
- Juutilainen, J.; Harri, M.; Saali, K.; Lahtinen, T. Effects of 100-Hz magnetic fields with various waveforms on the develop-ment of chick embryos. Radiat. Env. Biophys. 1986, 25, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Juutilainen, J.; Läära, E.; Saali, K. Relationship between field strength and abnormal development in chick embryos exposed to 50 Hz magnetic fields. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 1987, 52, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Ubeda, A.; Trillo, M.; Chacón, L.; Blanco, M.; Leal, J. Chick embryo development can be irreversibly altered by early exposure to weak extremely-low-frequency magnetic fields. Bioelectromagnetics 1994, 15, 385–398. [Google Scholar] [CrossRef]
- Jenrow, K.; Smith, C.; Liboff, A. Weak extremely-low-frequency magnetic field-induced regeneration anomalies in the planarianDugesia tigrina. Bioelectromagnetics 1996, 17, 467–474. [Google Scholar] [CrossRef]
- Lednev, V. Possible mechanism for the influence of weak magnetic fields on biological systems. Bioelectromagnetics 1991, 12, 71–75. [Google Scholar] [CrossRef]
- Fuoss, R.M. Review of the theory of electrolytic conductance. J. Solut. Chem. 1978, 7, 771–782. [Google Scholar] [CrossRef]



| Matter | Molar Weight (Da) | Mass Fraction (%) | Moles (mM) | Number (−) | Mol Fr. (%) |
|---|---|---|---|---|---|
| Water | 18 | 70 | 3888.9 | 23,400,000,000 | 99.324 |
| Ions | 47 | 1 | 300 | 120,000,000 | 0.509 |
| Amino Acids | 110 (av.) | 2 | 1.5 | 6,000,000 | 0.025 |
| Nucleotides | 414 (av.) | 0.8 | 1.9 | 3,530,000 | 0.015 |
| Proteins | 40,000 (av.) | 15 | 0.34 | 3,600,000 | 0.015 |
| RNA | 33,500 | 6 | 0.18 | 222,000 | 0.001 |
| Polysaccharides | 1,000,000 (av.) | 3 | 0.003 | 39,000 | 0.001 |
| DNA | 2,840,000,000 | 1 | 0.000005 | 1 | 0.000 |
| Others | - | 0.4 | - | ||
| Total | 3,159,782 | 100 | 23,533,391,001 | 100.00 |
| Ion | Concentration (mM) | Number (−) | Number (%) | fICR/B (Hz/μT) |
|---|---|---|---|---|
| Potassium (K+) | 200–250 | 90,000,000 | 69.147 | 0.194 |
| Iron (Fe2+/Fe3+) | 18 | 7,000,000 | 5.378 | * 0.546 |
| Bicarbonate (HCO3−) | 12 | 5,670,000 | 4.356 | - |
| Chloride (Cl−) | 6 | 5,050,000 | 3.880 | - |
| Magnesium (Mg2+) | 10 | 4,000,000 | 3.073 | 1.255 |
| Hydronium (H3O+) | 10–4.2 | 3,000,000 | 2.305 | * 0.802 |
| Zündel cation (H3O+∙H2O) | * 0.477 | |||
| Trimer hydronium (H3O+∙2H2O) | * 0.277 | |||
| Tetramer hydronium (H3O+∙3H2O) | * 0.209 | |||
| Magic hydronium cation (H3O+∙20H2O) | * 0.167 | |||
| Calcium (Ca2+) | 6 | 2,300,000 | 1.767 | 0.761 |
| Dihydrogen phosphate (H2PO4−) | 5 | 2,107,700 | 1.619 | - |
| Sodium (Na+) | 5 | 2,000,000 | 1.573 | * 0.663 |
| Cuprum (Cu2+) | 4 | 1,700,000 | 1.306 | * 0.480 |
| Manganese (Mn2+) | 4 | 1,700,000 | 1.306 | * 0.555 |
| Molybdenium (Mo4+) | 4 | 1,700,000 | 1.306 | * 0.636 |
| Zincum (Zn2+) | 4 | 1,700,000 | 1.306 | * 0.466 |
| Phosphoenol-Pyruvate (PEP3−) | 2.8 | 1,100,000 | 0.845 | - |
| Pyruvate (CH3COCOO−) | 0.9 | 380,000 | 0.292 | - |
| Adenosin-Diphosphate (ADP3−) | 0.63 | 270,000 | 0.207 | - |
| Nicotinamide (NADP3−) | 0.63 | 240,000 | 0.184 | - |
| –”– (NADPH4−) | 0.56 | 220,060 | 0.169 | - |
| Ammonium (NH4+) | - | - | - | * 0.845 |
| Glucose-6-Phosphate (6GP2−) | 0.05 | 20,000 | 0.015 | - |
| Proton (H+) | 0.000063 | 30 | 0.000 | 15.13 |
| Total | 125,077,820 | 100.00 |
| m (g) | Molar Weight (Da) | Weight (%) | Mol (%) | Mol (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| ♀ | ♂ | ♀ | ♂ | ♀ | ♂ | ♀ | ♂ | ||
| Water (∑) | 30,900.0 | 45,000.0 | 18.0 | 52.32 | 55.14 | 96.07 | 96.49 | - | - |
| –”– intracellular | 15,400.0 | 24,900.0 | 18.0 | 26.07 | 30.51 | 47.88 | 53.39 | 96.71 | 97.39 |
| –”– extracellular | 15,500.0 | 20,100.0 | 18.0 | 26.24 | 24.63 | 48.19 | 43.10 | - | - |
| Lipids | 15,900.0 | 19,800.0 | 600.0 | 26.92 | 24.26 | 1.48 | 1.27 | 3.00 | 2.32 |
| Proteins | 9720.0 | 13,070.0 | 40,000.0 | 15.70 | 16.01 | 0.01 | 0.01 | 0.03 | 0.02 |
| Phosphates | 1372.0 | 1704.0 | 98.0 | 2.32 | 2.09 | 0.78 | 0.67 | - | - |
| Calcium | 905.5 | 1230.0 | 40.1 | 1.53 | 1.51 | 1.26 | 1.18 | - | - |
| Carbohydrates | 500.0 | 500.0 | 1,000,000.0 | 0.85 | 0.61 | 0.00 | 0.00 | - | - |
| Potassium | 88.5 | 149.0 | 39.1 | 0.15 | 0.18 | 0.13 | 0.15 | 0.26 | 0.27 |
| Sodium | 63.5 | 82.0 | 23.0 | 0.11 | 0.10 | 0.15 | 0.14 | - | - |
| Chlor | 61.5 | 77.5 | 35.5 | 0.10 | 0.09 | 0.01 | 0.08 | - | - |
| Total | 59,511.0 | 81,612.5 | 99.99 | 99.99 | 99.93 | 100.00 | 100.00 | 100.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madl, P.; Renati, P. Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology. Int. J. Mol. Sci. 2023, 24, 14003. https://doi.org/10.3390/ijms241814003
Madl P, Renati P. Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology. International Journal of Molecular Sciences. 2023; 24(18):14003. https://doi.org/10.3390/ijms241814003
Chicago/Turabian StyleMadl, Pierre, and Paolo Renati. 2023. "Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology" International Journal of Molecular Sciences 24, no. 18: 14003. https://doi.org/10.3390/ijms241814003
APA StyleMadl, P., & Renati, P. (2023). Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology. International Journal of Molecular Sciences, 24(18), 14003. https://doi.org/10.3390/ijms241814003