Warm Cells, Hot Mitochondria: Achievements and Problems of Ultralocal Thermometry
Abstract
:1. Introduction
2. Review Chapters
2.1. Nonoptical Methods
2.2. Optical Methods
2.3. Local Intracellular Temperature
2.3.1. Whole Cell, Cell Surface, and Cytosol
| Cell Type * | Assay ** | Thermosensor *** | Stimulus **** | , ***** | Ref. |
|---|---|---|---|---|---|
| COS-7 | Fluorescence microscopy | 1, nanogel polyNIPAM-MBAM-DBD-AA | 100 M FCCP | 28 C/+0.45 (0–2) C | [43] |
| COS-7 | TCSPC system-based FLIM | FPT, polyNNPAM- SPA- DBD-AA | (NA M) FCCP (30 min) | 30 C/+1.02 ± 0.17 C average; +1–4 C around mitochondria | [39] |
| NIH/3T3 | Fluorescence microscopy | QD, quantum dots (QD655, Invitrogen, Waltham, MA, USA) | 1 M ionomycin-Ca2+ | 37 C/+1.84 ± 0.27 C (from −2 to +8 C) | [26] |
| HeLa, COS-7, NIH/3T3 | FLIM | AP4-FPT, nanogel, polyNNPAM- APTMA- DBThD-AA | 10 mM CCCP | 30 C/+1.57 ± 1.41 C (HeLa) | [37] |
| HeLa | Confocal fluorescence microscopy, single-photon detection | RFP, two-component ratiometric fluorescent polymer PolyNIPAM-co-NBDAA:PolyNIPAM-co-RhBAM (100:1) | (NA M) FCCP | 33.3 C/+2.0–2.4 C | [42] |
| HeLa | ODMR technique | FND, fluorescent nanodiamonds | No stimulus | 32 C/+1.5 ± 0.5 C | [22] |
| HeLa | Confocal microscopy | tsGFP1, GFP-TlpA fusion protein | 10 M CCCP | 37 C/ | [29] |
| HeLa | Confocal microscopy | RNT, ratiometric nanothermometer, Eu-TTA and rhodamine 101 embedded in PMMA nanoparticle covered by PAH | No stimulusIonomycin (high) | 37 C/(+2 (0.5–3.5) C (transient peak within ∼100–150 s) | [77] |
| HeLa | Fluorescence microscopy | Pipette filled with Eu-TTA | 2 M ionomycin 2 M thapsigargin 1 h prior to ionomycin | 22 C/≤+1 C Suppression of warming | [49] |
| HEK293T | TCSPC system-based FLIM | FPT, linear cationic fluorescent polymeric thermometer, polyNNPAM- APTMA- DBD-AA | A42 (for 24 h) A42 + MJ040X FCCP A42 + MJ040X + FCCP | 37 C/+2.8 ± 0.6 C / /+10.0 ± 1.2 C /+10.0 ± 1.2 C | [80] |
| J774A.1 HEK293T | Thermography in cell suspension | Thermography catheter | +100 M NaCN (10 min) UCP2 overexpression (>95% cells) | 23 C/+0.13 ± 0.048 C (J774A.1) 23 C/+0.16 ± 0.068 C (HEK293T) | [81] |
| HeLa HEK293 BA Rat neonatal cardiomyocytes Rat hippocampal neurons | Phase contrast (DIC) fluorescent microscopy | Nanosheets fluorescent thermometer containing EuTTA and rhodamine 101 (thickness ∼ 50 nm) | No stimulus 2 M ionomycin Type 1 ryanodine receptor mutation 10 M CCCP 2 Hz electrical stimulation 0.25 Hz electrical stimulation | 36 ± 1 C/+ 0.12–0.19 C (HEK293) / (±0.15 C , HeLa) /≤+0.1 C (HEK293) / (±0.1 C , cardiomyocytes, BA) / (±0.01 C , cardiomyocytes) / (±0.03 C , neurons) | [66] |
| C2C12 myoblasts and differentiated myotubes | Time-domain FLIM, frequency-domain FLIM, confocal laser scanning microscopy | mCherry, fluorescent protein | 1 mM caffeine | 37 C/−0.07 ± 0.18 C | [67] |
| BA, pre-BA | Confocal microscopy | R-CFPT, ratiometric–cationic fluorescent polymeric thermometer, polyNNPAM-APTMA-DBThD-AA-BODIPY-AA | No stimulus 10 M FCCP 30 M FCCP NE CL316.243 | 30 C/+2.3 ± 0.2 C (pre-BA) /+4.4 ± 0.2 C (BA)/+1.5 C (10 min, BA); (20–30 min, pre-BA) /+2.5 and +3.5 C (10 and 30 min, BA) /+1.25 ± 0.25 C /+1.39 ± 0.38 C (at 31 min, BA) | [78] |
| BA, BA-ASK1-KO | Fluorescence microscopy | 1, nanogel polyNIPAM- MBAM- DBD-AA | 0.5 M CL316.243 ASK1-KO + CL316.243 | NA C/ +1.29 C (at 30 min) NA C/ +0.52 C (at 30 min) | [82] |
| BA | Bright-field microscopy | Microcantilever (cell–sensor distance ∼2–7 m) | No stimulus 1 M NE (30 min) | 25 ± 1 C/ /+0.217 ± 0.120 C | [17] |
| BA | Microvoltmetry | Si pn junction diode thermal sensor | 1 M NE | 23 C/+0.1 C (in 5–20 min interval) | [18] |
| BA | TCSPC system-based FLIM | DTG, lipid droplets thermo green, BODIPY-n-undecanoyl fusion | 1 mM ISO (50 min) | 37 C/−0.24 ± 1.0 C | [35] |
| Aplysia californica neurons | Microvoltmetry | Au/Pd thermocouple with silicon nitride cantilever | 10 M BAM15 | 23 C/+7.5 ± 2.0 C (relaxation within 33 s)/+0.1–0.2 C (external thermometer) | [83] |
| U251 | Microvoltmetry | Thermocouple, W/polyurethane/Pt sandwich | 12 M camptothecin 50 M doxorubicin | 23 C/+ 0.6 ± 0.2 C (30 min) 23 C/+ 0.1 ± 0.1 C (30 min) | [15] |
| SH-SY5Y | Confocal fluorescent laser scanning microscopy | QD, quantum dots (Qtracker nanocrystals, Invitrogen) | No stimulus 10 M CCCP | 37 C/+0.8 C (neurites), +1.4 C (cell body) /+0.94 C average (−2.5–+5.5 C) | [24] |
| CHO-K1 | TCSPC system-based FLIM | NPs_Eu2, Eu-TTA complex embedded in latex nanoparticles | 10–30 M FCCP | 25 C/+3–4 C (endosomes/lysosomes) | [48] |
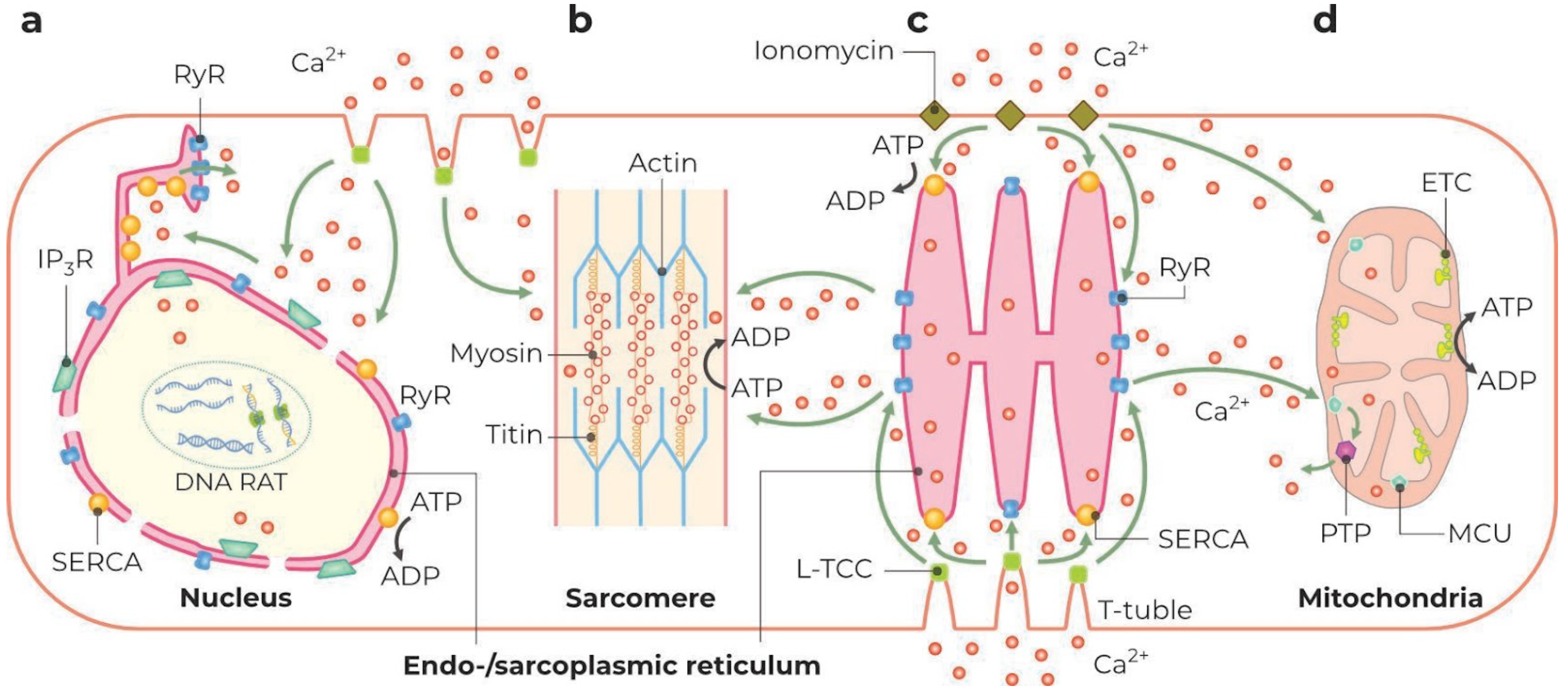
2.3.2. ER and SR
2.3.3. Nuclei
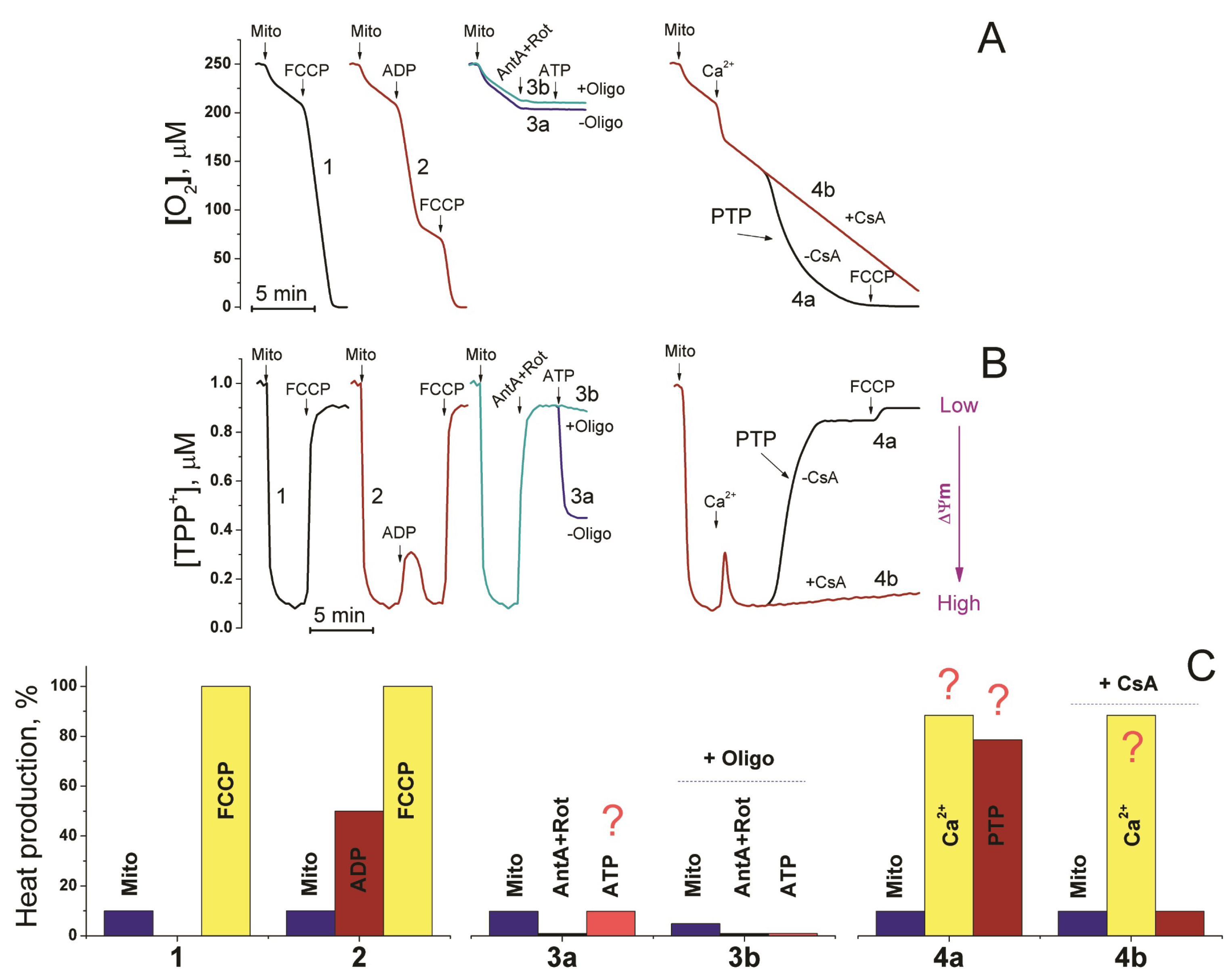
2.3.4. Mitochondria
| Cell Type * | Assay | Thermosensor ** | Stimulus *** | **** | Ref. |
|---|---|---|---|---|---|
| HeLa | Confocal fluorescence microscopy | MTY, mito thermo yellow | 5 M FCCP | Dye release (−0.4F within 4 min) matching to C (our estimation) | [111] |
| HeLa | Confocal fluorescence microscopy | Mito-TEM 2, rhodamine B-BODIPY construct bearing formaldehyde anchor | No stimulus 10 L/mL S. aureus (60 min) 20 g/mL LPS (30 min) | C (heterogeneous = 35–40 C) /+6 C (Heterogeneous = 40–46 C) /+6 C (heterogeneous = 40–46 C) | [33] |
| HeLa | Fluorescence microscopy | Mito-RTP, mitochondrial ratiometric temperature probe, rhodamine B-CS NIR dye construct | 10 M FCCP | C/+3 ± 1 C (our estimation) | [109] |
| HeLa | Fluorescence intensity, microplate reader | T sensing probe, polyNIPAm-VBC-DACC-CTPP | 200 M FCCP removal of FCCP | C/+2.4 C ; C/−2 C (our estimation) | [108] |
| HeLa | Confocal fluorescence microscopy, peak fraction analysis | emGFP-Mito, mitochondria-targeted GFP (CellLight BacMam 2.0) | 10 M FCCP | C/+3–5 C (duration of maximum rise ∼300 s) organelle thermal heterogeneity (from 15 C to 57 C). | [30] |
| HeLa | Fluorescence microscopy | gTEMP, coupled fluorescent proteins | 10 M FCCP | C/+6–9 C organelle thermal heterogeneity. | [28] |
| HeLa, BA | Confocal fluorescence microscopy | tsGFP1-mito, mitochondria-targeted GFP-TlpA construct | No stimulus 10 M rothenone 10 M CCCP CCCP+ rothenone 10 M CCCP 10 M NE | Organelle thermal heterogeneity (25–45 C) C/−10 C (HeLa, our estimation) /+4–6 C (HeLa, our estimation) /−2 C (HeLa, our estimation) C/+5–6 C (BA) /+3–5 C (BA) | [29] |
| BA | TCSPC system-based FLIM | MTG, mitochondria thermo green, BODIPY-TPP+ fusion | 1 mM ISO (50 min) | C/+2.8 ± 2.7 C | [35] |
| BA | Confocal fluorescence microscopy | Ratiometric rhodamine B/rhodamine 800 pair | 10 M CCCP (30 min) 100 nM NE | Tmed = 33 C/+15 C /+4 C (Our estimation) | [58] |
| MCF-7 | Confocal fluorescence microscopy | Mito-TEM, rhodamine B bearing targeting and anchoring moieties | 50 M PMA (30 min) 50 M CCCP (30 min) | C/+3 C C/(brighter fluorescence) | [110] |
| HEK 293, primary skin fibroblasts | Fluorescence | MTY, mito thermo yellow | No stimulus Anoxia 0.8 mM KCN 3 M rotenone 1 M antimycin A 5 M oligomycin | C /−10.5 C /∼−10.5 C /∼−10.5 C /∼−10.5 C /∼−9 C | [32] |
2.3.5. Physiologic and Pathophysiologic Thermal Limits for Mitochondria
2.3.6. Avoidance of Thermal Damage
3. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tattersall, G.J.; Sinclair, B.J.; Withers, P.C.; Fields, P.A.; Seebacher, F.; Cooper, C.E.; Maloney, S.K. Coping with thermal challenges: Physiological adaptations to environmental temperatures. Compr. Physiol. 2012, 2, 2151–2202. [Google Scholar] [PubMed]
- Wendering, P.; Nikoloski, Z. Model-driven insights into the effects of temperature on metabolism. Biotechnol. Adv. 2023, 67, 108203. [Google Scholar] [CrossRef]
- Daniel, R.M.; Danson, M.J. Temperature and the catalytic activity of enzymes: A fresh understanding. FEBS Lett. 2013, 587, 2738–2743. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Zhang, Z.; Grubner, S.; Yurkovich, J.T.; Palsson, B.O.; Zielinski, D.C. Temperature-Dependent Estimation of Gibbs Energies Using an Updated Group-Contribution Method. Biophys. J. 2018, 114, 2691–2702. [Google Scholar] [CrossRef] [PubMed]
- Almeida, P.F.F.; Vaz, W.L.C.; Thompson, T.E. Lateral diffusion in the liquid phases of dimyristoylphosphatidylcholine/cholesterol lipid bilayers: A free volume analysis. Biochemistry 1992, 31, 6739–6747. [Google Scholar] [CrossRef] [PubMed]
- Zakim, D.; Kavecansky, J.; Scarlata, S. Are membrane enzymes regulated by the viscosity of the membrane environment. Biochemistry 1992, 31, 11589–11594. [Google Scholar] [CrossRef]
- Ng, T.W.; Chan, W.L.; Lai, K.M. Influence of membrane fatty acid composition and fluidity on airborne survival of Escherichia coli. Appl. Microbiol. Biotechnol. 2018, 102, 3327–3336. [Google Scholar] [CrossRef]
- Reszczyńska, E.; Hanaka, A. Lipids Composition in Plant Membranes. Cell Biochem. Biophys. 2020, 78, 401–414. [Google Scholar] [CrossRef]
- Ritchie, M.E. Reaction and diffusion thermodynamics explain optimal temperatures of biochemical reactions. Sci. Rep. 2018, 8, 11105. [Google Scholar] [CrossRef]
- Chen, J.; Nolte, V.; Schlötterer, C. Temperature-Related Reaction Norms of Gene Expression: Regulatory Architecture and Functional Implications. Mol. Biol. Evol. 2015, 32, 2393–2402. [Google Scholar] [CrossRef]
- Van Dijk, E.; Hoogeveen, A.; Abeln, S. The Hydrophobic Temperature Dependence of Amino Acids Directly Calculated from Protein Structures. PLoS Comput. Biol. 2015, 11, e1004277. [Google Scholar] [CrossRef] [PubMed]
- Jarzab, A.; Kurzawa, N.; Hopf, T.; Moerch, M.; Zecha, J.; Leijten, N.; Bian, Y.; Musiol, E.; Maschberger, M.; Stoehr, G.; et al. Meltome atlas—Thermal proteome stability across the tree of life. Nat. Methods 2020, 17, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Okabe, K.; Uchiyama, S. Intracellular thermometry uncovers spontaneous thermogenesis and associated thermal signaling. Commun. Biol. 2021, 4, 1377. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Li, G.; Yang, J.; Wang, Z.; Han, D.; Zheng, F.; Xu, S. Measurement of local temperature increments induced by cultured HepG2 cells with micro-thermocouples in a thermally stabilized system. Sci. Rep. 2017, 7, 1721. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Xu, R.; Tian, W.; Jiang, X.; Cui, Z.; Wang, M.; Sun, H.; Fang, K.; Gu, N. Determining intracellular temperature at single-cell level by a novel thermocouple method. Cell Res. 2011, 21, 1517–1519. [Google Scholar] [CrossRef] [PubMed]
- Tian, W.; Wang, C.; Wang, J.; Chen, Q.; Sun, J.; Li, C.; Wang, X.; Gu, N. A high precision apparatus for intracellular thermal response at single-cell level. Nanotechnology 2015, 26, 355501. [Google Scholar] [CrossRef] [PubMed]
- Sato, M.; Toda, M.; Inomata, N.; Maruyama, H.; Okamatsu-Ogura, Y.; Arai, F.; Ono, T.; Ishijima, A.; Inoue, Y. Temperature Changes in Brown Adipocytes Detected with a Bimaterial Microcantilever. Biophys. J. 2014, 106, 2458–2464. [Google Scholar] [CrossRef]
- Yamada, T.; Inomata, N.; Ono, T. Sensitive thermal microsensor with pn junction for heat measurement of a single cell. Jpn. J. Appl. Phys. 2016, 55, 027001. [Google Scholar] [CrossRef]
- Fujiwara, M.; Sun, S.; Dohms, A.; Nishimura, Y.; Suto, K.; Takezawa, Y.; Oshimi, K.; Zhao, L.; Sadzak, N.; Umehara, Y.; et al. Real-time nanodiamond thermometry probing in vivo thermogenic responses. Sci. Adv. 2020, 6, eaba9636. [Google Scholar] [CrossRef]
- Kucsko, G.; Maurer, P.C.; Yao, N.Y.; Kubo, M.; Noh, H.J.; Lo, P.K.; Park, H.; Lukin, M.D. Nanometre-scale thermometry in a living cell. Nature 2013, 500, 54–58. [Google Scholar] [CrossRef]
- Petrini, G.; Tomagra, G.; Bernardi, E.; Moreva, E.; Traina, P.; Marcantoni, A.; Picollo, F.; Kvaková, K.; Cígler, P.; Degiovanni, I.P.; et al. Nanodiamond–Quantum Sensors Reveal Temperature Variation Associated to Hippocampal Neurons Firing. Adv. Sci. 2022, 9, 2202014. [Google Scholar] [CrossRef] [PubMed]
- Sekiguchi, T.; Sotoma, S.; Harada, Y. Fluorescent nanodiamonds as a robust temperature sensor inside a single cell. Biophys. Physicobiol. 2018, 15, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Romshin, A.M.; Osypov, A.A.; Popova, I.Y.; Zeeb, V.E.; Sinogeykin, A.G.; Vlasov, I.I. Heat Release by Isolated Mouse Brain Mitochondria Detected with Diamond Thermometer. Nanomaterials 2022, 13, 98. [Google Scholar] [CrossRef] [PubMed]
- Tanimoto, R.; Hiraiwa, T.; Nakai, Y.; Shindo, Y.; Oka, K.; Hiroi, N.; Funahashi, A. Detection of Temperature Difference in Neuronal Cells. Sci. Rep. 2016, 6, 22071. [Google Scholar] [CrossRef] [PubMed]
- Albers, A.E.; Chan, E.M.; McBride, P.M.; Ajo-Franklin, C.M.; Cohen, B.E.; Helms, B.A. Dual-Emitting Quantum Dot/Quantum Rod-Based Nanothermometers with Enhanced Response and Sensitivity in Live Cells. J. Am. Chem. Soc. 2012, 134, 9565–9568. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.M.; Yang, H.; Lin, L. Quantum Dot Nano Thermometers Reveal Heterogeneous Local Thermogenesis in Living Cells. ACS Nano 2011, 5, 5067–5071. [Google Scholar] [CrossRef] [PubMed]
- Ye, F.; Wu, C.; Jin, Y.; Chan, Y.H.; Zhang, X.; Chiu, D.T. Ratiometric Temperature Sensing with Semiconducting Polymer Dots. J. Am. Chem. Soc. 2011, 133, 8146–8149. [Google Scholar] [CrossRef]
- Nakano, M.; Arai, Y.; Kotera, I.; Okabe, K.; Kamei, Y.; Nagai, T. Genetically encoded ratiometric fluorescent thermometer with wide range and rapid response. PLoS ONE 2017, 12, e0172344. [Google Scholar] [CrossRef]
- Kiyonaka, S.; Kajimoto, T.; Sakaguchi, R.; Shinmi, D.; Omatsu-Kanbe, M.; Matsuura, H.; Imamura, H.; Yoshizaki, T.; Hamachi, I.; Morii, T.; et al. Genetically encoded fluorescent thermosensors visualize subcellular thermoregulation in living cells. Nat. Methods 2013, 10, 1232–1238. [Google Scholar] [CrossRef]
- Savchuk, O.A.; Silvestre, O.F.; Adão, R.M.R.; Nieder, J.B. GFP fluorescence peak fraction analysis based nanothermometer for the assessment of exothermal mitochondria activity in live cells. Sci. Rep. 2019, 9, 7535. [Google Scholar] [CrossRef]
- Donner, J.S.; Thompson, S.A.; Kreuzer, M.P.; Baffou, G.; Quidant, R. Mapping Intracellular Temperature Using Green Fluorescent Protein. Nano Lett. 2012, 12, 2107–2111. [Google Scholar] [CrossRef] [PubMed]
- Chrétien, D.; Bénit, P.; Ha, H.H.; Keipert, S.; El-Khoury, R.; Chang, Y.T.; Jastroch, M.; Jacobs, H.T.; Rustin, P.; Rak, M. Mitochondria are physiologically maintained at close to 50 °C. PLoS Biol. 2018, 16, e2003992. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Li, N.; Zhang, X.; Xiao, Y. Mitochondria-Anchored Molecular Thermometer Quantitatively Monitoring Cellular Inflammations. Anal. Chem. 2021, 93, 5081–5088. [Google Scholar] [CrossRef] [PubMed]
- Arai, S.; Lee, S.C.; Zhai, D.; Suzuki, M.; Chang, Y.T. A Molecular Fluorescent Probe for Targeted Visualization of Temperature at the Endoplasmic Reticulum. Sci. Rep. 2014, 4, 6701. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Yamazaki, T.; Kwon, H.Y.; Arai, S.; Chang, Y.T. A palette of site-specific organelle fluorescent thermometers. Mater. Today Bio 2022, 16, 100405. [Google Scholar] [CrossRef]
- Tsuji, T.; Yoshida, S.; Yoshida, A.; Uchiyama, S. Cationic Fluorescent Polymeric Thermometers with the Ability to Enter Yeast and Mammalian Cells for Practical Intracellular Temperature Measurements. Anal. Chem. 2013, 85, 9815–9823. [Google Scholar] [CrossRef]
- Hayashi, T.; Fukuda, N.; Uchiyama, S.; Inada, N. A Cell-Permeable Fluorescent Polymeric Thermometer for Intracellular Temperature Mapping in Mammalian Cell Lines. PLoS ONE 2015, 10, e0117677. [Google Scholar] [CrossRef]
- Gong, D.; Cao, T.; Han, S.C.; Zhu, X.; Iqbal, A.; Liu, W.; Qin, W.; Guo, H. Fluorescence enhancement thermoresponsive polymer luminescent sensors based on BODIPY for intracellular temperature. Sens. Actuators B Chem. 2017, 252, 577–583. [Google Scholar] [CrossRef]
- Okabe, K.; Inada, N.; Gota, C.; Harada, Y.; Funatsu, T.; Uchiyama, S. Intracellular temperature mapping with a fluorescent polymeric thermometer and fluorescence lifetime imaging microscopy. Nat. Commun. 2012, 3, 705. [Google Scholar] [CrossRef]
- Uchiyama, S.; Tsuji, T.; Ikado, K.; Yoshida, A.; Kawamoto, K.; Hayashi, T.; Inada, N. A cationic fluorescent polymeric thermometer for the ratiometric sensing of intracellular temperature. Analyst 2015, 140, 4498–4506. [Google Scholar] [CrossRef]
- Uchiyama, S.; Gota, C.; Tsuji, T.; Inada, N. Intracellular temperature measurements with fluorescent polymeric thermometers. Chem. Commun. 2017, 53, 10976–10992. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Chen, C.; Qi, L.; Liu, M.; Dong, P.; Jiang, Q.; Yang, X.; Mu, X.; Mao, L. Intracellular temperature sensing by a ratiometric fluorescent polymer thermometer. J. Mater. Chem. B 2014, 2, 7544–7550. [Google Scholar] [CrossRef] [PubMed]
- Gota, C.; Okabe, K.; Funatsu, T.; Harada, Y.; Uchiyama, S. Hydrophilic Fluorescent Nanogel Thermometer for Intracellular Thermometry. J. Am. Chem. Soc. 2009, 131, 2766–2767. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, S.; Tsuji, T.; Kawamoto, K.; Okano, K.; Fukatsu, E.; Noro, T.; Ikado, K.; Yamada, S.; Shibata, Y.; Hayashi, T.; et al. A Cell-Targeted Non-Cytotoxic Fluorescent Nanogel Thermometer Created with an Imidazolium-Containing Cationic Radical Initiator. Angew. Chem. Int. Ed. 2018, 57, 5413–5417. [Google Scholar] [CrossRef]
- Wang, C.; Ling, L.; Yao, Y.; Song, Q. One-step synthesis of fluorescent smart thermo-responsive copper clusters: A potential nanothermometer in living cells. Nano Res. 2015, 8, 1975–1986. [Google Scholar] [CrossRef]
- Shang, L.; Stockmar, F.; Azadfar, N.; Nienhaus, G.U. Intracellular Thermometry by Using Fluorescent Gold Nanoclusters. Angew. Chem. Int. Ed. 2013, 52, 11154–11157. [Google Scholar] [CrossRef]
- Vetrone, F.; Naccache, R.; Zamarrón, A.; Juarranz De La Fuente, A.; Sanz-Rodríguez, F.; Martinez Maestro, L.; Martín Rodriguez, E.; Jaque, D.; García Solé, J.; Capobianco, J.A. Temperature Sensing Using Fluorescent Nanothermometers. ACS Nano 2010, 4, 3254–3258. [Google Scholar] [CrossRef]
- Kuznetsov, K.M.; Baigildin, V.A.; Solomatina, A.I.; Galenko, E.E.; Khlebnikov, A.F.; Sokolov, V.V.; Tunik, S.P.; Shakirova, J.R. Polymeric Nanoparticles with Embedded Eu(III) Complexes as Molecular Probes for Temperature Sensing. Molecules 2022, 27, 8813. [Google Scholar] [CrossRef]
- Suzuki, M.; Tseeb, V.; Oyama, K.; Ishiwata, S. Microscopic Detection of Thermogenesis in a Single HeLa Cell. Biophys. J. 2007, 92, L46–L48. [Google Scholar] [CrossRef]
- Wei, L.; Ma, Y.; Shi, X.; Wang, Y.; Su, X.; Yu, C.; Xiang, S.; Xiao, L.; Chen, B. Living cell intracellular temperature imaging with biocompatible dye-conjugated carbon dots. J. Mater. Chem. B 2017, 5, 3383–3390. [Google Scholar] [CrossRef]
- Kalytchuk, S.; Poláková, K.; Wang, Y.; Froning, J.P.; Cepe, K.; Rogach, A.L.; Zbořil, R. Carbon Dot Nanothermometry: Intracellular Photoluminescence Lifetime Thermal Sensing. ACS Nano 2017, 11, 1432–1442. [Google Scholar] [CrossRef] [PubMed]
- Inomata, N.; Toda, M.; Sato, M.; Ishijima, A.; Ono, T. Pico calorimeter for detection of heat produced in an individual brown fat cell. Appl. Phys. Lett. 2012, 100, 154104. [Google Scholar] [CrossRef]
- Inomata, N.; Toda, M.; Ono, T. Highly sensitive thermometer using a vacuum-packed Si resonator in a microfluidic chip for the thermal measurement of single cells. Lab Chip 2016, 16, 3597–3603. [Google Scholar] [CrossRef] [PubMed]
- Herth, S.; Giesguth, M.; Wedel, W.; Reiss, G.; Dietz, K.J. Thermomicrocapillaries as temperature biosensors in single cells. Appl. Phys. Lett. 2013, 102, 103505. [Google Scholar] [CrossRef]
- Jaque, D.; Vetrone, F. Luminescence nanothermometry. Nanoscale 2012, 4, 4301. [Google Scholar] [CrossRef] [PubMed]
- Brites, C.D.S.; Lima, P.P.; Silva, N.J.O.; Millán, A.; Amaral, V.S.; Palacio, F.; Carlos, L.D. Thermometry at the nanoscale. Nanoscale 2012, 4, 4799. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Del Rosal, B.; Jaque, D.; Uchiyama, S.; Jin, D. Advances and challenges for fluorescence nanothermometry. Nat. Methods 2020, 17, 967–980. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.R.; Liu, C.F.; Kang, J.S. Dye-based mito-thermometry and its application in thermogenesis of brown adipocytes. Biophys. Rep. 2017, 3, 85–91. [Google Scholar] [CrossRef]
- Kriszt, R.; Arai, S.; Itoh, H.; Lee, M.H.; Goralczyk, A.G.; Ang, X.M.; Cypess, A.M.; White, A.P.; Shamsi, F.; Xue, R.; et al. Optical visualisation of thermogenesis in stimulated single-cell brown adipocytes. Sci. Rep. 2017, 7, 1383. [Google Scholar] [CrossRef]
- Li, S.; Zhang, K.; Yang, J.M.; Lin, L.; Yang, H. Single Quantum Dots as Local Temperature Markers. Nano Lett. 2007, 7, 3102–3105. [Google Scholar] [CrossRef]
- Vlasov, I.I.; Shiryaev, A.A.; Rendler, T.; Steinert, S.; Lee, S.Y.; Antonov, D.; Vörös, M.; Jelezko, F.; Fisenko, A.V.; Semjonova, L.F.; et al. Molecular-sized fluorescent nanodiamonds. Nat. Nanotechnol. 2014, 9, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Fahimi, P.; Matta, C.F. The hot mitochondrion paradox: Reconciling theory and experiment. Trends Chem. 2022, 4, 96–110. [Google Scholar] [CrossRef]
- Macherel, D.; Haraux, F.; Guillou, H.; Bourgeois, O. The conundrum of hot mitochondria. Biochim. Biophys. Acta (BBA) Bioenerg. 2021, 1862, 148348. [Google Scholar] [CrossRef] [PubMed]
- Baffou, G.; Rigneault, H.; Marguet, D.; Jullien, L. A critique of methods for temperature imaging in single cells. Nat. Methods 2014, 11, 899–901. [Google Scholar] [CrossRef]
- Suzuki, M.; Zeeb, V.; Arai, S.; Oyama, K.; Ishiwata, S. The 105 gap issue between calculation and measurement in single-cell thermometry. Nat. Methods 2015, 12, 802–803. [Google Scholar] [CrossRef]
- Oyama, K.; Gotoh, M.; Hosaka, Y.; Oyama, T.G.; Kubonoya, A.; Suzuki, Y.; Arai, T.; Tsukamoto, S.; Kawamura, Y.; Itoh, H.; et al. Single-cell temperature mapping with fluorescent thermometer nanosheets. J. Gen. Physiol. 2020, 152, e201912469. [Google Scholar] [CrossRef]
- Itoh, H.; Arai, S.; Sudhaharan, T.; Lee, S.C.; Chang, Y.T.; Ishiwata, S.; Suzuki, M.; Lane, E.B. Direct organelle thermometry with fluorescence lifetime imaging microscopy in single myotubes. Chem. Commun. 2016, 52, 4458–4461. [Google Scholar] [CrossRef]
- Nath, S. The thermodynamic efficiency of ATP synthesis in oxidative phosphorylation. Biophys. Chem. 2016, 219, 69–74. [Google Scholar] [CrossRef]
- Mazat, J.; Ransac, S.; Heiske, M.; Devin, A.; Rigoulet, M. Mitochondrial energetic metabolism—some general principles. IUBMB Life 2013, 65, 171–179. [Google Scholar] [CrossRef]
- Nicholls, D.G.; Ferguson, S.J. Quantitative bioenergetics. In Bioenergetics; Elsevier: Amsterdam, The Netherlands, 2003; pp. 31–55. [Google Scholar] [CrossRef]
- Nowack, J.; Giroud, S.; Arnold, W.; Ruf, T. Muscle Non-shivering Thermogenesis and Its Role in the Evolution of Endothermy. Front. Physiol. 2017, 8, 889. [Google Scholar] [CrossRef]
- Oyama, K.; Zeeb, V.; Yamazawa, T.; Kurebayashi, N.; Kobirumaki-Shimozawa, F.; Murayama, T.; Oyamada, H.; Noguchi, S.; Inoue, T.; Inoue, Y.U.; et al. Heat-hypersensitive mutants of ryanodine receptor type 1 revealed by microscopic heating. Proc. Natl. Acad. Sci. USA 2022, 119, e2201286119. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Marinov, G.K. The bioenergetic costs of a gene. Proc. Natl. Acad. Sci. USA 2015, 112, 15690–15695. [Google Scholar] [CrossRef] [PubMed]
- Mathews, C.K. Deoxyribonucleotides as genetic and metabolic regulators. FASEB J. 2014, 28, 3832–3840. [Google Scholar] [CrossRef] [PubMed]
- Hohendanner, F.; McCulloch, A.D.; Blatter, L.A.; Michailova, A.P. Calcium and IP3 dynamics in cardiac myocytes: Experimental and computational perspectives and approaches. Front. Pharmacol. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, P.L.; Pedersen, P.A. Structure–function relationships of Na+, K+, ATP, or Mg2+ binding and energy transduction in Na,K-ATPase. Biochim. Biophys. Acta (BBA) Bioenerg. 2001, 1505, 57–74. [Google Scholar] [CrossRef]
- Takei, Y.; Arai, S.; Murata, A.; Takabayashi, M.; Oyama, K.; Ishiwata, S.; Takeoka, S.; Suzuki, M. A nanoparticle-based ratiometric and self-calibrated fluorescent thermometer for single living cells. ACS Nano 2014, 8, 198–206. [Google Scholar] [CrossRef]
- Tsuji, T.; Ikado, K.; Koizumi, H.; Uchiyama, S.; Kajimoto, K. Difference in intracellular temperature rise between matured and precursor brown adipocytes in response to uncoupler and β-adrenergic agonist stimuli. Sci. Rep. 2017, 7, 12889. [Google Scholar] [CrossRef]
- Sotoma, S.; Zhong, C.; Kah, J.C.Y.; Yamashita, H.; Plakhotnik, T.; Harada, Y.; Suzuki, M. In situ measurements of intracellular thermal conductivity using heater-thermometer hybrid diamond nanosensors. Sci. Adv. 2021, 7, eabd7888. [Google Scholar] [CrossRef]
- Chung, C.W.; Stephens, A.D.; Konno, T.; Ward, E.; Avezov, E.; Kaminski, C.F.; Hassanali, A.A.; Kaminski Schierle, G.S. Intracellular Aβ42 Aggregation Leads to Cellular Thermogenesis. J. Am. Chem. Soc. 2022, 144, 10034–10041. [Google Scholar] [CrossRef]
- Van De Parre, T.J.; Martinet, W.; Verheye, S.; Kockx, M.M.; Van Langenhove, G.; Herman, A.G.; De Meyer, G.R. Mitochondrial uncoupling protein 2 mediates temperature heterogeneity in atherosclerotic plaques. Cardiovasc. Res. 2007, 77, 425–431. [Google Scholar] [CrossRef]
- Hattori, K.; Naguro, I.; Okabe, K.; Funatsu, T.; Furutani, S.; Takeda, K.; Ichijo, H. ASK1 signalling regulates brown and beige adipocyte function. Nat. Commun. 2016, 7, 11158. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, M.C.; Brown, J.W.; Gelda, D.; Valavala, K.V.; Wang, H.; Llano, D.A.; Gillette, R.; Sinha, S. Transient heat release during induced mitochondrial proton uncoupling. Commun. Biol. 2019, 2, 279. [Google Scholar] [CrossRef] [PubMed]
- Consolini, A.E.; Ragone, M.I.; Bonazzola, P.; Colareda, G.A. Mitochondrial Bioenergetics During Ischemia and Reperfusion. In Mitochondrial Dynamics in Cardiovascular Medicine; Santulli, G., Ed.; Series Title: Advances in Experimental Medicine and Biology; Springer International Publishing: Cham, Switzerland, 2017; Volume 982, pp. 141–167. [Google Scholar] [CrossRef]
- Boyman, L.; Karbowski, M.; Lederer, W.J. Regulation of Mitochondrial ATP Production: Ca2+ Signaling and Quality Control. Trends Mol. Med. 2020, 26, 21–39. [Google Scholar] [CrossRef] [PubMed]
- Periasamy, M.; Herrera, J.L.; Reis, F.C.G. Skeletal Muscle Thermogenesis and Its Role in Whole Body Energy Metabolism. Diabetes Metab. J. 2017, 41, 327. [Google Scholar] [CrossRef] [PubMed]
- Block, B.A. Thermogenesis in Muscle. Annu. Rev. Physiol. 1994, 56, 535–577. [Google Scholar] [CrossRef] [PubMed]
- Blondin, D.P.; Haman, F. Shivering and nonshivering thermogenesis in skeletal muscles. In Handbook of Clinical Neurology; Elsevier: Amsterdam, The Netherlands, 2018; Volume 156, pp. 153–173. [Google Scholar] [CrossRef]
- Sentex, E.; Laurent, A.; Martine, L.; Gregoire, S.; Rochette, L.; Demaison, L. Calcium- and ADP-magnesium-induced respiratory uncoupling in isolated cardiac mitochondria: Influence of cyclosporin A. Mol. Cell. Biochem. 1999, 202, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Halestrap, A.P. Mitochondria and reperfusion injury of the heart—A holey death but not beyond salvation. J. Bioenerg. Biomembr. 2009, 41, 113–121. [Google Scholar] [CrossRef]
- Javadov, S.; Karmazyn, M.; Escobales, N. Mitochondrial Permeability Transition Pore Opening as a Promising Therapeutic Target in Cardiac Diseases. J. Pharmacol. Exp. Ther. 2009, 330, 670–678. [Google Scholar] [CrossRef]
- Reynolds, I.J. Mitochondrial Membrane Potential and the Permeability Transition in Excitotoxicity. Ann. N. Y. Acad. Sci. 1999, 893, 33–41. [Google Scholar] [CrossRef]
- Nguyen, K.T.; García-Chacón, L.E.; Barrett, J.N.; Barrett, E.F.; David, G. The ΔΨm depolarization that accompanies mitochondrial Ca2+ uptake is greater in mutant SOD1 than in wild-type mouse motor terminals. Proc. Natl. Acad. Sci. USA 2009, 106, 2007–2011. [Google Scholar] [CrossRef]
- Van Eyk, J.E.; Thomas, L.T.; Tripet, B.; Wiesner, R.J.; Pearlstone, J.R.; Farah, C.S.; Reinach, F.C.; Hodges, R.S. Distinct Regions of Troponin I Regulate Ca2+-dependent Activation and Ca2+ Sensitivity of the Acto-S1-TM ATPase Activity of the Thin Filament. J. Biol. Chem. 1997, 272, 10529–10537. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, H.L.; Hammers, D.W. Muscle Contraction. Cold Spring Harb. Perspect. Biol. 2018, 10, a023200. [Google Scholar] [CrossRef] [PubMed]
- Herzog, W.; Schappacher-Tilp, G. Molecular mechanisms of muscle contraction: A historical perspective. J. Biomech. 2023, 155, 111659. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Emerson, D.J.; Gilgenast, T.G.; Titus, K.R.; Lan, Y.; Huang, P.; Zhang, D.; Wang, H.; Keller, C.A.; Giardine, B.; et al. Chromatin structure dynamics during the mitosis-to-G1 phase transition. Nature 2019, 576, 158–162. [Google Scholar] [CrossRef] [PubMed]
- Kupriyanov, V.V.; Lakomkin, V.L.; Kapelko, V.I.; Saks, V.A. Myoplasmic phosphate metabolites in the integration of oxidative phosphorylation and contractile function in the myocardium. Biomed. Sci. 1990, 1, 113–121. [Google Scholar] [PubMed]
- Moreno-Loshuertos, R.; Movilla, N.; Marco-Brualla, J.; Soler-Agesta, R.; Ferreira, P.; Enríquez, J.A.; Fernández-Silva, P. A Mutation in Mouse MT-ATP6 Gene Induces Respiration Defects and Opposed Effects on the Cell Tumorigenic Phenotype. Int. J. Mol. Sci. 2023, 24, 1300. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.F.; Latorre-Muro, P.; Puigserver, P. Mechanisms of mitochondrial respiratory adaptation. Nat. Rev. Mol. Cell Biol. 2022, 23, 817–835. [Google Scholar] [CrossRef]
- Nielsen, J.; Gejl, K.D.; Hey-Mogensen, M.; Holmberg, H.C.; Suetta, C.; Krustrup, P.; Elemans, C.P.; Ørtenblad, N. Plasticity in mitochondrial cristae density allows metabolic capacity modulation in human skeletal muscle. J. Physiol. 2017, 595, 2839–2847. [Google Scholar] [CrossRef]
- Paital, B.; Samanta, L. A comparative study of hepatic mitochondrial oxygen consumption in four vertebrates by using Clark-type electrode. Acta Biol. Hung. 2013, 64, 152–160. [Google Scholar] [CrossRef]
- Long, J.; Xia, Y.; Qiu, H.; Xie, X.; Yan, Y. Respiratory substrate preferences in mitochondria isolated from different tissues of three fish species. Fish Physiol. Biochem. 2022, 48, 1555–1567. [Google Scholar] [CrossRef]
- Latorre-Muro, P.; O’Malley, K.E.; Bennett, C.F.; Perry, E.A.; Balsa, E.; Tavares, C.D.; Jedrychowski, M.; Gygi, S.P.; Puigserver, P. A cold-stress-inducible PERK/OGT axis controls TOM70-assisted mitochondrial protein import and cristae formation. Cell Metab. 2021, 33, 598–614. [Google Scholar] [CrossRef] [PubMed]
- Wolf, D.M.; Segawa, M.; Kondadi, A.K.; Anand, R.; Bailey, S.T.; Reichert, A.S.; van der Bliek, A.M.; Shackelford, D.B.; Liesa, M.; Shirihai, O.S. Individual cristae within the same mitochondrion display different membrane potentials and are functionally independent. EMBO J. 2019, 38, e101056. [Google Scholar] [CrossRef] [PubMed]
- Nedergaard, J.; Cannon, B. Brown adipose tissue as a heat-producing thermoeffector. Handb. Clin. Neurol. 2018, 156, 137–152. [Google Scholar] [PubMed]
- Kiyonaka, S.; Sakaguchi, R.; Hamachi, I.; Morii, T.; Yoshizaki, T.; Mori, Y. Validating subcellular thermal changes revealed by fluorescent thermosensors. Nat. Methods 2015, 12, 801–802. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C.; Shangguan, D.; Mu, X.; Wang, S.; Jiang, L.; Qi, L. Simultaneous Monitoring of Mitochondrial Temperature and ATP Fluctuation Using Fluorescent Probes in Living Cells. Anal. Chem. 2018, 90, 12553–12558. [Google Scholar] [CrossRef] [PubMed]
- Homma, M.; Takei, Y.; Murata, A.; Inoue, T.; Takeoka, S. A ratiometric fluorescent molecular probe for visualization of mitochondrial temperature in living cells. Chem. Commun. 2015, 51, 6194–6197. [Google Scholar] [CrossRef]
- Huang, Z.; Li, N.; Zhang, X.; Wang, C.; Xiao, Y. Fixable Molecular Thermometer for Real-Time Visualization and Quantification of Mitochondrial Temperature. Anal. Chem. 2018, 90, 13953–13959. [Google Scholar] [CrossRef]
- Arai, S.; Suzuki, M.; Park, S.J.; Yoo, J.S.; Wang, L.; Kang, N.Y.; Ha, H.H.; Chang, Y.T. Mitochondria-targeted fluorescent thermometer monitors intracellular temperature gradient. Chem. Commun. 2015, 51, 8044–8047. [Google Scholar] [CrossRef]
- Jilkina, O.; Bhullar, R.P. A serine kinase associates with the RAL GTPase and phosphorylates RAL-interacting protein 1. Biochim. Biophys. Acta (BBA) Mol. Cell Res. 2006, 1763, 948–957. [Google Scholar] [CrossRef]
- Awasthi, K.; Yamamoto, K.; Furuya, K.; Nakabayashi, T.; Li, L.; Ohta, N. Fluorescence Characteristics and Lifetime Images of Photosensitizers of Talaporfin Sodium and Sodium Pheophorbide a in Normal and Cancer Cells. Sensors 2015, 15, 11417–11430. [Google Scholar] [CrossRef]
- Mottram, L.F.; Forbes, S.; Ackley, B.D.; Peterson, B.R. Hydrophobic analogues of rhodamine B and rhodamine 101: Potent fluorescent probes of mitochondria in living C. elegans. Beilstein J. Org. Chem. 2012, 8, 2156–2165. [Google Scholar] [CrossRef] [PubMed]
- Grasmick, K.A.; Hu, H.; Hone, E.A.; Farooqi, I.; Rellick, S.L.; Simpkins, J.W.; Ren, X. Uncoupling of the Electron Transport Chain Compromises Mitochondrial Oxidative Phosphorylation and Exacerbates Stroke Outcomes. J. Neuroinfect. Dis. 2018, 09. [Google Scholar] [CrossRef] [PubMed]
- Chrétien, D.; Bénit, P.; Leroy, C.; El-Khoury, R.; Park, S.; Lee, J.Y.; Chang, Y.T.; Lenaers, G.; Rustin, P.; Rak, M. Pitfalls in monitoring mitochondrial temperature using charged thermosensitive fluorophores. Chemosensors 2020, 8, 124. [Google Scholar] [CrossRef]
- Zhang, R.; Ji, J.; Blaženović, I.; Pi, F.; Wang, T.; Zhang, Y.; Sun, X. Investigation into Cellular Glycolysis for the Mechanism Study of Energy Metabolism Disorder Triggered by Lipopolysaccharide. Toxins 2018, 10, 441. [Google Scholar] [CrossRef] [PubMed]
- De Vente, J.E.; Kukoly, C.A.; Bryant, W.O.; Posekany, K.J.; Chen, J.; Fletcher, D.J.; Parker, P.J.; Pettit, G.J.; Lozano, G.; Cook, P.P. Phorbol esters induce death in MCF-7 breast cancer cells with altered expression of protein kinase C isoforms. Role for p53-independent induction of gadd-45 in initiating death. J. Clin. Investig. 1995, 96, 1874–1886. [Google Scholar] [CrossRef]
- Moreno-Loshuertos, R.; Marco-Brualla, J.; Meade, P.; Soler-Agesta, R.; Enriquez, J.A.; Fernández-Silva, P. How hot can mitochondria be? Incubation at temperatures above 43 °C induces the degradation of respiratory complexes and supercomplexes in intact cells and isolated mitochondria. Mitochondrion 2023, 69, 83–94. [Google Scholar] [CrossRef]
- Marino, A.; Arai, S.; Hou, Y.; Degl’Innocenti, A.; Cappello, V.; Mazzolai, B.; Chang, Y.T.; Mattoli, V.; Suzuki, M.; Ciofani, G. Gold Nanoshell-Mediated Remote Myotube Activation. ACS Nano 2017, 11, 2494–2508. [Google Scholar] [CrossRef]
- Kannadorai, R.K.; Chiew, G.G.Y.; Luo, K.Q.; Liu, Q. Dual functions of gold nanorods as photothermal agent and autofluorescence enhancer to track cell death during plasmonic photothermal therapy. Cancer Lett. 2015, 357, 152–159. [Google Scholar] [CrossRef]
- Ventura, B.; Genova, M.L.; Bovina, C.; Formiggini, G.; Lenaz, G. Control of oxidative phosphorylation by Complex I in rat liver mitochondria: Implications for aging. Biochim. Biophys. Acta (BBA) Bioenerg. 2002, 1553, 249–260. [Google Scholar] [CrossRef]
- Grivennikova, V.G.; Kapustin, A.N.; Vinogradov, A.D. Catalytic Activity of NADH-ubiquinone Oxidoreductase (Complex I) in Intact Mitochondria. J. Biol. Chem. 2001, 276, 9038–9044. [Google Scholar] [CrossRef]
- Gostimskaya, I.S.; Grivennikova, V.G.; Cecchini, G.; Vinogradov, A.D. Reversible dissociation of flavin mononucleotide from the mammalian membrane-bound NADH:ubiquinone oxidoreductase (complex I). FEBS Lett. 2007, 581, 5803–5806. [Google Scholar] [CrossRef] [PubMed]
- M. Abrantes, A.; Serra, E.; Goncalves, C.; Oliveiros, B.; Laranjo, M.; B. Sarmento-Ribeiro, A.; Rocha-Gonsalves, A.; F. Botelho, M. Tumour Hypoxia and Technetium Tracers: In Vivo Studies. Curr. Radiopharm. 2012, 5, 99–105. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Prado, E.; Dunn, J.F.; Vasconez, J.; Castillo, D.; Viscor, G. Partial pressure of oxygen in the human body: A general review. Am. J. Blood Res. 2019, 9, 1–14. [Google Scholar] [PubMed]
- Matthewman, C.; Miller-Fleming, T.W.; Miller, D.M.; Bianchi, L. Ca2+ permeability and Na+ conductance in cellular toxicity caused by hyperactive DEG/ENaC channels. Am. J. Physiol.-Cell Physiol. 2016, 311, C920–C930. [Google Scholar] [CrossRef] [PubMed]
- Žūkienė, R.; Naučienė, Z.; Šilkūnienė, G.; Vanagas, T.; Gulbinas, A.; Zimkus, A.; Mildažienė, V. Contribution of mitochondria to injury of hepatocytes and liver tissue by hyperthermia. Medicina 2017, 53, 40–49. [Google Scholar] [CrossRef]
- Nikiforova, A.B.; Baburina, Y.L.; Borisova, M.P.; Surin, A.K.; Kharechkina, E.S.; Krestinina, O.V.; Suvorina, M.Y.; Kruglova, S.A.; Kruglov, A.G. Mitochondrial F-ATP Synthase Co-Migrating Proteins and Ca2+-Dependent Formation of Large Channels. Cells 2023, 12, 2414. [Google Scholar] [CrossRef]
- Kruglov, A.G.; Kharechkina, E.S.; Nikiforova, A.B.; Odinokova, I.V.; Kruglova, S.A. Dynamics of the permeability transition pore size in isolated mitochondria and mitoplasts. FASEB J. 2021, 35, e21764. [Google Scholar] [CrossRef]
- Khaliulin, I.; Clarke, S.J.; Lin, H.; Parker, J.; Suleiman, M.; Halestrap, A.P. Temperature preconditioning of isolated rat hearts – a potent cardioprotective mechanism involving a reduction in oxidative stress and inhibition of the mitochondrial permeability transition pore. J. Physiol. 2007, 581, 1147–1161. [Google Scholar] [CrossRef]
- Zorova, L.D.; Popkov, V.A.; Plotnikov, E.Y.; Silachev, D.N.; Pevzner, I.B.; Jankauskas, S.S.; Babenko, V.A.; Zorov, S.D.; Balakireva, A.V.; Juhaszova, M.; et al. Mitochondrial membrane potential. Anal. Biochem. 2018, 552, 50–59. [Google Scholar] [CrossRef]
- Nesci, S.; Trombetti, F.; Pagliarani, A. Nicotinamide Nucleotide Transhydrogenase as a Sensor of Mitochondrial Biology. Trends Cell Biol. 2020, 30, 1–3. [Google Scholar] [CrossRef]
- Rydström, J. Mitochondrial NADPH, transhydrogenase and disease. Biochim. Biophys. Acta (BBA) Bioenerg. 2006, 1757, 721–726. [Google Scholar] [CrossRef] [PubMed]
- Hillman, S.S.; Hancock, T.V.; Hedrick, M.S. A comparative meta-analysis of maximal aerobic metabolism of vertebrates: Implications for respiratory and cardiovascular limits to gas exchange. J. Comp. Physiol. B 2013, 183, 167–179. [Google Scholar] [CrossRef]
- Lee, M.P.; Gear, A.R. The effect of temperature on mitochondrial membrane-linked reactions. J. Biol. Chem. 1974, 249, 7541–7549. [Google Scholar] [CrossRef] [PubMed]
- Lemieux, H.; Blier, P.U.; Gnaiger, E. Remodeling pathway control of mitochondrial respiratory capacity by temperature in mouse heart: Electron flow through the Q-junction in permeabilized fibers. Sci. Rep. 2017, 7, 2840. [Google Scholar] [CrossRef] [PubMed]
- Mitov, M.I.; Harris, J.W.; Alstott, M.C.; Zaytseva, Y.Y.; Evers, B.M.; Butterfield, D.A. Temperature induces significant changes in both glycolytic reserve and mitochondrial spare respiratory capacity in colorectal cancer cell lines. Exp. Cell Res. 2017, 354, 112–121. [Google Scholar] [CrossRef] [PubMed]
- Chung, D.J.; Sparagna, G.C.; Chicco, A.J.; Schulte, P.M. Patterns of mitochondrial membrane remodeling parallel functional adaptations to thermal stress. J. Exp. Biol. 2018, 221, jeb174458. [Google Scholar] [CrossRef] [PubMed]
- Sokolova, I. Mitochondrial adaptations to variable environments and their role in animals’ stress tolerance. Integr. Comp. Biol. 2018, 58, 519–531. [Google Scholar] [CrossRef]
- Michaelsen, J.; Fago, A.; Bundgaard, A. High temperature impairs mitochondrial function in rainbow trout cardiac mitochondria. J. Exp. Biol. 2021, 224, jeb242382. [Google Scholar] [CrossRef]
- Vinogradov, A.D. NADH/NAD+ interaction with NADH: Ubiquinone oxidoreductase (complex I). Biochim. Biophys. Acta (BBA) Bioenerg. 2008, 1777, 729–734. [Google Scholar] [CrossRef]
- Miyazono, Y.; Hirashima, S.; Ishihara, N.; Kusukawa, J.; Nakamura, K.i.; Ohta, K. Uncoupled mitochondria quickly shorten along their long axis to form indented spheroids, instead of rings, in a fission-independent manner. Sci. Rep. 2018, 8, 350. [Google Scholar] [CrossRef]
- Golombek, M.; Tsigaras, T.; Schaumkessel, Y.; Hänsch, S.; Weidtkamp-Peters, S.; Anand, R.; Reichert, A.S.; Kondadi, A.K. Cristae dynamics is modulated in bioenergetically compromised mitochondria. Life Sci. Alliance 2024, 7, 2. [Google Scholar] [CrossRef] [PubMed]
- Jevzek, P.; Jaburek, M.; Holendov, B.; Engstov, H.; Dlaskov, A. Mitochondrial cristae morphology reflecting metabolism, superoxide formation, redox homeostasis, and pathology. Antioxid. Redox Signal. 2023, 39, 635–683. [Google Scholar] [CrossRef] [PubMed]
- Dlasková, A.; Špaček, T.; Engstová, H.; Špačková, J.; Schröfel, A.; Holendová, B.; Smolková, K.; Plecitá-Hlavatá, L.; Ježek, P. Mitochondrial cristae narrowing upon higher 2-oxoglutarate load. Biochim. Biophys. Acta (BBA) Bioenerg. 2019, 1860, 659–678. [Google Scholar] [CrossRef] [PubMed]
- Mannella, C.A. Structure and dynamics of the mitochondrial inner membrane cristae. Biochim. Biophys. Acta (BBA) Mol. Cell Res. 2006, 1763, 542–548. [Google Scholar] [CrossRef] [PubMed]
- Qian, L.; Song, X.; Ren, H.; Gong, J.; Cheng, S. Mitochondrial mechanism of heat stress-induced injury in rat cardiomyocyte. Cell Stress Chaperones 2004, 9, 281. [Google Scholar] [CrossRef]
- Carraro, M.; Bernardi, P. The mitochondrial permeability transition pore in Ca2+ homeostasis. Cell Calcium 2023, 111, 102719. [Google Scholar] [CrossRef]
- Gupta, A.; Sharma, D.; Gupta, H.; Singh, A.; Chowdhury, D.; Meena, R.C.; Ganju, L.; Kumar, B. Heat precondition is a potential strategy to combat hepatic injury triggered by severe heat stress. Life Sci. 2021, 269, 119094. [Google Scholar] [CrossRef]
- Jaworek, W.; Sylvester, M.; Cenini, G.; Voos, W. Elucidation of the interaction proteome of mitochondrial chaperone Hsp78 highlights its role in protein aggregation during heat stress. J. Biol. Chem. 2022, 298. [Google Scholar] [CrossRef]
- El-Gammal, Z.; Nasr, M.A.; Elmehrath, A.O.; Salah, R.A.; Saad, S.M.; El-Badri, N. Regulation of mitochondrial temperature in health and disease. Pflügers Archiv-Eur. J. Physiol. 2022, 474, 1043–1051. [Google Scholar] [CrossRef]
- Kabakov, A.; Molotkov, A.; Budagova, K.; Makarova, Y.M.; Mosin, A.; Gabai, V. Adaptation of Ehrlich ascites carcinoma cells to energy deprivation in vivo can be associated with heat shock protein accumulation. J. Cell. Physiol. 1995, 165, 1–6. [Google Scholar] [CrossRef]
- MATZ, J.M.; LaVOI, K.P.; Moen, R.; BLAKE, M.J. Cold-induced heat shock protein expression in rat aorta and brown adipose tissue. Physiol. Behav. 1996, 60, 1369–1374. [Google Scholar] [CrossRef] [PubMed]
- Bouillaud, F.; Ricquier, D.; Mory, G.; Thibault, J. Increased level of mRNA for the uncoupling protein in brown adipose tissue of rats during thermogenesis induced by cold exposure or norepinephrine infusion. J. Biol. Chem. 1984, 259, 11583–11586. [Google Scholar] [CrossRef] [PubMed]
- Samelman, T.; Shiry, L.; Cameron, D. Endurance training increases the expression of mitochondrial and nuclear encoded cytochrome c oxidase subunits and heat shock proteins in rat skeletal muscle. Eur. J. Appl. Physiol. 2000, 83, 22–27. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, V.; Scapagnini, G.; Ravagna, A.; Colombrita, C.; Spadaro, F.; Butterfield, D.; Stella, A.G. Increased expression of heat shock proteins in rat brain during aging: Relationship with mitochondrial function and glutathione redox state. Mech. Ageing Dev. 2004, 125, 325–335. [Google Scholar] [CrossRef]
- Tu, R.H.; Li, Q.J.; Huang, Z.; He, Y.; Meng, J.J.; Zheng, H.L.; Zeng, Z.Y.; Zhong, G.Q. Novel functional role of heat shock protein 90 in mitochondrial connexin 43-mediated hypoxic postconditioning. Cell. Physiol. Biochem. 2017, 44, 982–997. [Google Scholar] [CrossRef]
- Chen, H.W.; Hsu, C.; Lu, T.S.; Wang, S.J.; Yang, R.C. Heat shock pretreatment prevents cardiac mitochondrial dysfunction during sepsis. Shock 2003, 20, 274–279. [Google Scholar] [CrossRef]
- Duan, Y.; Tang, H.; Mitchell-Silbaugh, K.; Fang, X.; Han, Z.; Ouyang, K. Heat shock protein 60 in cardiovascular physiology and diseases. Front. Mol. Biosci. 2020, 7, 73. [Google Scholar] [CrossRef]

| Cell Type | Assay | Thermosensor * | Stimulus | ** | Ref. |
|---|---|---|---|---|---|
| HeLa | Fluorescent microscopy | ER thermo yellow | 10 M FCCP 2 M ionomycin | Rotenone-insensitive nonthermal effects 36 ± 1 C/+∼3 C | [66] |
| HeLa | Fluorescent microscopy | ER thermo yellow | 1 M ionomycin | 37 C/+1.7 ± 0.4 C (duration 200–250 s) | [34] |
| HeLa, C2C12 myoblasts, and differentiated myotubes | Time-domain FLIM, frequency-domain FLIM, confocal laser scanning microscopy | ER thermo yellow | 2 M ionomycin 1 mM caffeine 1 mM thapsigargin thapsigargin (30 min) + caffeine | 37 C/+0.93 ± 0.68 C (HeLa) +1.6 ± 0.6 C (duration > 150 s; myotubes) (myoblasts) +0.38 ± 0.34 C +0.41 ± 0.48 C | [67] |
| C2C12 myoblasts and differentiated myotubes | Confocal microscopy | tsGFP1-ER, ER-targeted GFP-TlpA fusion protein | 50 M cyclopiazonic acid (SERCA inhibitor) | 37 C/−12 C (our estimation, +0.1R, myotubes) (myoblasts) | [29] |
| BA | TCSPC system-based FLIM | ETG, ER Thermo Green, unsymmetrical BODIPY derivative | 1 mM ISO (50 min) | 37 C/+0.64 ± 1.8 C | [35] |
| Mouse WT-1 pre-BA, human BA | Confocal fluorescence microscopy | ERtherm-AC, ER thermo yellow acetyl derivative | 10 M ISO 10 M FCCP 10 M forskolin | 25 C/+19.8 C (our estimation, −0.5F) (pre-BA) 25 C/+17.5 C (our estimation, −0.4F) (BA) | [59] |
| Cell Type * | Assay | Thermosensor ** | Stimulus | , *** | Ref. |
|---|---|---|---|---|---|
| HeLa | Fluorescent microscopy | gTEMP, coupled fluorescent proteins | No stimulus | C , C | [28] |
| HeLa | TCSPC system-based FLIM | AP4-FPT, nanogel, polyNNPAM- APTMA- DBThD-AA | No stimulus | C , C | [37] |
| COS-7, HeLa | TCSPC system-based FLIM | FPT, polyNNPAM- SPA- DBD-AA | No stimulus | C , C , C (COS-7) and −0.03 C in G1 and S/G2 cell cycle phase, respectively (COS-7) C , C (HeLa) Nuclei and centrosomes bind more FPT than cytosol | [39] |
| MOLT-4 and HEK293T cells | Flow cytometry, confocal microscopy (MOLT-4) Confocal spectrofluorometry (HEK293T) | 1, NNPAM-APTMA-DBThD-AA-BODIPY-AA | No stimulus | Cell cycle-dependent sensor accumulation (MOLT-4) C , C (HEK293T) | [40] |
| BA | TCSPC system-based FLIM | NTG, nucleus thermo green, BODIPY-Hoechst 33258 fusion | 1 mM ISO (50 min) | C , C | [35] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruglov, A.G.; Romshin, A.M.; Nikiforova, A.B.; Plotnikova, A.; Vlasov, I.I. Warm Cells, Hot Mitochondria: Achievements and Problems of Ultralocal Thermometry. Int. J. Mol. Sci. 2023, 24, 16955. https://doi.org/10.3390/ijms242316955
Kruglov AG, Romshin AM, Nikiforova AB, Plotnikova A, Vlasov II. Warm Cells, Hot Mitochondria: Achievements and Problems of Ultralocal Thermometry. International Journal of Molecular Sciences. 2023; 24(23):16955. https://doi.org/10.3390/ijms242316955
Chicago/Turabian StyleKruglov, Alexey G., Alexey M. Romshin, Anna B. Nikiforova, Arina Plotnikova, and Igor I. Vlasov. 2023. "Warm Cells, Hot Mitochondria: Achievements and Problems of Ultralocal Thermometry" International Journal of Molecular Sciences 24, no. 23: 16955. https://doi.org/10.3390/ijms242316955
APA StyleKruglov, A. G., Romshin, A. M., Nikiforova, A. B., Plotnikova, A., & Vlasov, I. I. (2023). Warm Cells, Hot Mitochondria: Achievements and Problems of Ultralocal Thermometry. International Journal of Molecular Sciences, 24(23), 16955. https://doi.org/10.3390/ijms242316955








