Next Article in Journal
Natural Alkaloids in Cancer Therapy: Berberine, Sanguinarine and Chelerythrine against Colorectal and Gastric Cancer
Next Article in Special Issue
Preparation and Molecular Dynamic Simulation of Superfine CL−20/TNT Cocrystal Based on the Opposite Spray Method
Previous Article in Journal
H3K27me3 and EZH Are Involved in the Control of the Heat-Stress-Elicited Morphological Changes in Diatoms
Previous Article in Special Issue
Ab Initio Molecular Dynamics Insight to Structural Phase Transition and Thermal Decomposition of InN
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 25
Issue 15
10.3390/ijms25158374
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Molecular Insights into Adhesion at Interface of Geopolymer Binder and Cement Mortar

by
Anton S. Kasprzhitskii
* and
Alexander A. Kruglikov
Laboratory of Fuel Energy Waste Recycling, Platov South-Russian State Polytechnic University (NPI), Prosveshcheniya St., 132, Rostov Region, Novocherkassk 346428, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2024, 25(15), 8374; https://doi.org/10.3390/ijms25158374
Submission received: 10 June 2024 / Revised: 27 July 2024 / Accepted: 28 July 2024 / Published: 31 July 2024
(This article belongs to the Special Issue Molecular Simulation and Modeling)
Browse Figures
Versions Notes

Abstract

:
The degradation of concrete and reinforced concrete structures is a significant technical and economic challenge, requiring continuous repair and rehabilitation throughout their service life. Geopolymers (GPs), known for their high mechanical strength, low shrinkage, and durability, are being increasingly considered as alternatives to traditional repair materials. However, there is currently a lack of understanding regarding the interface bond properties between new geopolymer layers and old concrete substrates. In this paper, using advanced computational techniques, including quantum mechanical calculations and stochastic modeling, we explored the adsorption behavior and interaction mechanism of aluminosilicate oligomers with different Si/Al ratios forming the geopolymer gel structure and calcium silicate hydrate as the substrate at the interface bond region. We analyzed the electron density distributions of the highest occupied and lowest unoccupied molecular orbitals, examined the reactivity indices based on electron density functional theory, performed Mulliken charge population analysis, and evaluated global reactivity descriptors for the considered oligomers. The results elucidate the mechanisms of local and global reactivity of the oligomers, the equilibrium low-energy configurations of the oligomer structures adsorbed on the surface of C-(A)-S-H(I) (100), and their adsorption energies. These findings contribute to a better understanding of the adhesion properties of geopolymers and their potential as effective repair materials.

1. Introduction

Degradation of concrete and reinforced concrete structures is a serious technical and economic problem, requiring timely and effective preventive measures, as well as repair and rehabilitation throughout their service life [1,2]. Repair materials (RMs) play an important role in extending the service life and durability of engineering infrastructure, providing a reduction in operating costs and improving safety [3,4,5]. Such materials are commonly used in engineering practice to repair large cracks, fill hollows or cavities, and coat surfaces for repairing deteriorated and damaged concrete structures. In the context of concrete repair, cement mortar plays a crucial role as it forms the interface between the existing concrete substrate and new repair materials. The adhesion and compatibility of repair materials with the cement mortar substrate are critical factors determining the effectiveness and longevity of concrete repairs. This study focuses on the interaction between geopolymer-based repair materials and the cement mortar substrate, specifically investigating the molecular-level processes at this interface.
Recently, geopolymers (GPs) produced by low-temperature alkaline activation of aluminosilicate materials, including industrial solid wastes and by-products (red mud [6], granulated blast furnace slag [7], fly ash [8], electric furnace nickel slag [9], and binary and ternary waste blends [10,11,12]), have been increasingly considered as an alternative to conventional repair materials. Geopolymers are characterized by their relatively high mechanical strength [13], low shrinkage [14], and durability [15], making them potentially attractive as a base for repair mixtures. The presence of reactive phases with relatively low Al2O3 content but large amounts of reactive SiO2 and CaO in some waste materials suitable for geopolymers promotes the formation of N(C)-A-S-H type gel phases, thus reducing the shrinkage of the material upon drying [16,17], which is critical for repair materials.
In order to perform their functions effectively, repair mixtures must have good adhesion to the substrate surface, sufficient flexibility and strength to withstand mechanical stresses, and the ability to endure internal stress changes caused by volume changes and chemical and electrochemical factors [18]. Due to differences in elastic properties, thermal coefficients, and shrinkage between the substrate and overlay, the interface bond region is usually the weakest link in the system [19,20]. This makes it difficult to form a tightly bonded interfacial layer between the old concrete substrate and the new repair material, which, over time, leads to crack formation, reducing the filling efficiency and load transfer capability. In some cases, the repair material may delaminate from the substrate, making repairs ineffective. The addition of granulated blast furnace slag to metakaolin-based geopolymer is an option to improve the interfacial chemical bonding force due to the secondary hydration reaction of GP, as observed by Fan et al. [7]. With increasing calcium content, more C-S-H and/or C-A-S-H at the interface is formed, promoting better adhesion [21]. In turn, an increase in the Si/Al ratio in geopolymer mixes can lead to an increase in substrate-to-overlay interfacial bond strength in concrete repairs, as reported by Asayesh et al. [22].
Although more and more papers have reported on the prospects of using geopolymer mortars as sustainable repair materials [23], there is currently a gap in understanding the interface bond properties at the site of a new geopolymer layer on the old concrete substrate. The influence of material factors controlling adhesive failure, in particular the chemical composition of the geopolymer binder, remains understudied. A better understanding of interfacial bonding mechanisms is important to assess the potential of geopolymers as repair materials.
In the present work, utilizing quantum mechanical approaches and stochastic simulations, we examined the adsorption characteristics and bonding mechanisms of aluminosilicate oligomers with varying Si/Al ratios. These oligomers, which form the geopolymer gel structure, were studied in relation to calcium silicate hydrate, which served as a substrate at the interface bond region. We analyzed the spatial distribution of electron density for frontier molecular orbitals, evaluated reactivity indicators derived from electron density functional theory, conducted Mulliken charge distribution analysis, and calculated global reactivity parameters for the oligomers under consideration. We determined the stable configurations of oligomers adsorbed on the C-(A)-S-H(I) (100) surface that minimize energy, and computed their respective adsorption energies. This approach allows us to gain insights into the molecular-level interactions between geopolymer-based repair materials and the cement mortar substrate, which is crucial for understanding and improving the adhesion in concrete repair applications.

2. Results and Discussion

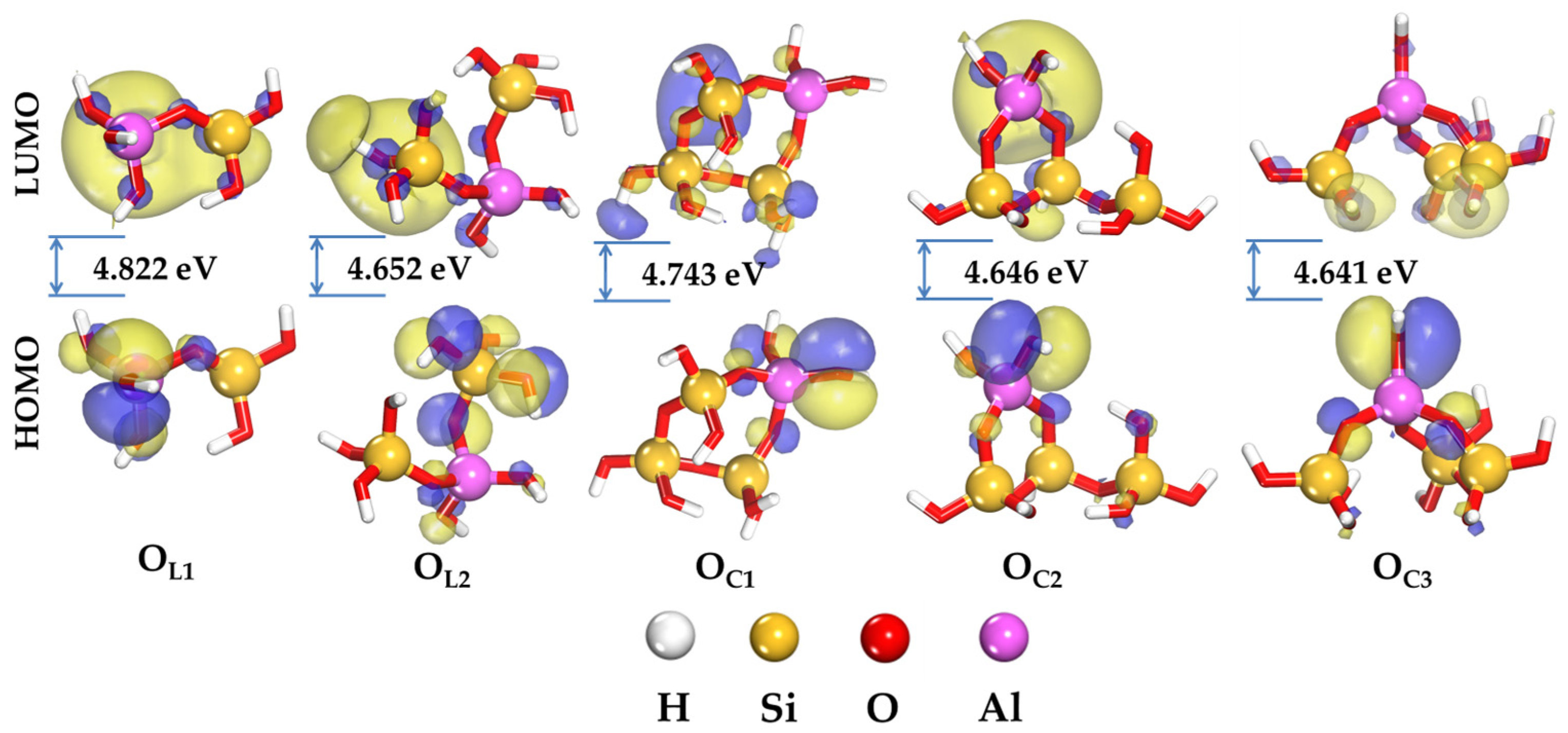
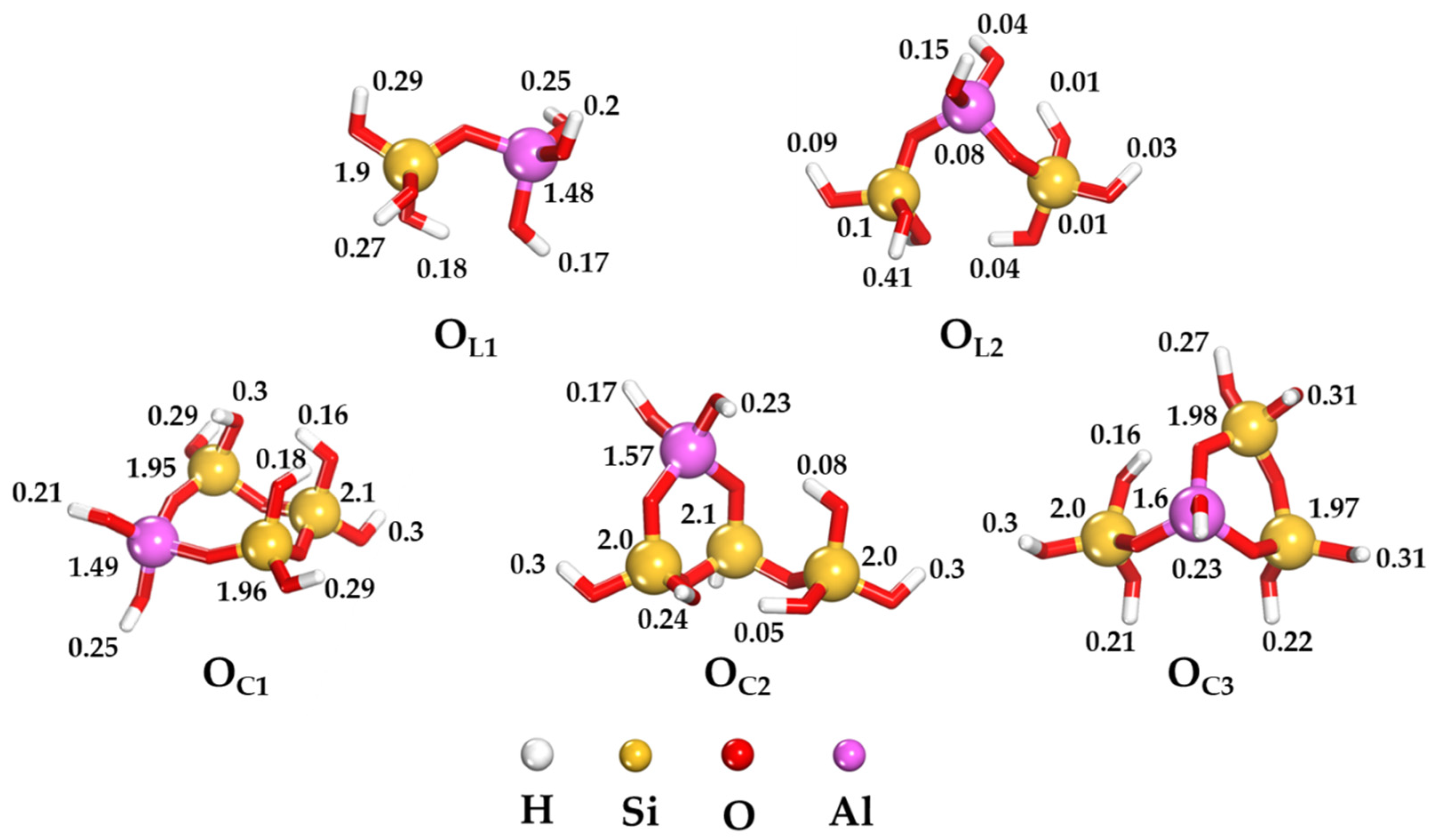
2.1. Local Reactivity of Aluminosilicate Oligomers

The study of the local reactivity of linear (OL)- and ring (OC)-type aluminosilicate oligomers is crucial for understanding their interaction with the cement mortar substrate at the molecular level. This analysis is performed for the equilibrium structures of the oligomers, simulating their state when in contact with the cement mortar surface during the application of geopolymer repair materials. The assessment of reactivity for these multi-atomic complexes is founded on Fukui’s frontier orbital theory, which is particularly relevant for predicting chemical interactions at the geopolymer–cement mortar interface. It is dependent on the energetic positions of the frontier molecular orbitals, namely, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), which govern the nature of donor–acceptor interactions between the oligomers and the cement mortar surface [24]. The maximum value of EHOMO corresponds to the highest propensity of multi-atomic systems to release electrons. Conversely, a low ELUMO value indicates an enhanced capability to accept electrons into the unoccupied electronic levels of polyatomic systems [25]. These energetic criteria are commonly employed to assess their interaction with atomic surfaces [26]. In this context, an increase in the EHOMO value coupled with a decrease in ELUMO is expected to yield the most favorable adhesion effect with the surface. A crucial energetic parameter characterizing the activity of a multi-atomic system is the energy gap (ΔE = ELUMO − EHOMO) between ELUMO and EHOMO. This parameter allows us to elucidate the reactivity of oligomers during adsorption onto the atomic surface [27], simulating their behavior when applied to cement mortar. A reduction in ΔE signifies an enhancement in the reactivity of the oligomer, which promotes improved adhesion to the cement mortar substrate. The computational results presented in Figure 1 demonstrate that for linear aluminosilicate oligomers, ΔE ranges from 4.822 to 4.652 eV for OL1 and OL2, respectively. Thus, the OL reactivity increases with the growing number of silicon-containing octahedra. This implies an increase in atomic surface affinity for the oligomers with increasing aluminosilicate framework Si/Al ratio. This trend is consistent with observations reported for other polyatomic systems [28,29].
The presence of ring structures in the aluminosilicate framework of OC oligomers leads to an increase in their reactivity. The energy gap values shown in Figure 1 for these oligomers decrease from 4.743 to 4.641 eV for OC1 and OC3, respectively. The EHOMO value for the linear oligomers OL1 and OL2 changes from −6.310 eV to −6.284 eV, respectively. A larger effect is observed for oligomers with OC ring structures, for which the EHOMO value increases by 0.18 eV when going to OC3. The increase in Si/Al changes the ELUMO level by 0.14 eV and 0.30 eV for linear and ring-shaped oligomers, respectively. This observation suggests an enhanced electron-accepting capacity for oligomers with increasing Si/Al ratio when alumino- and silica-containing tetrahedrons are integrated into a common framework.
Figure 1 illustrates the spatial arrangement of frontier molecular orbitals for oligomers with linear and ring forms at an isosurface value of 0.03. The localization of electron density associated with the HOMO and LUMO frontier orbitals on specific atomic groups indicates reactive sites involved in donor–acceptor interactions with the mineral surface [25]. As can be seen in Figure 1, the spatial distribution of electron density for the frontier orbitals is influenced by the structure of the aluminosilicate framework. For the linear oligomer OL1, the electron density is distributed throughout the framework, whereas for the ring oligomers OC, it is concentrated on specific functional molecular groups. In this case, due to OH groups, which can establish additional chemical bonds with the surface atoms of calcium silicate hydrate, a parallel interaction of OC with the mineral surface can be postulated. These findings are corroborated by the adsorption configurations obtained from stochastic simulations presented in the subsequent section of this work. For the linear form of OL oligomers, the electron-donor and electron-acceptor sites are primarily associated with the OH groups of the silicic-oxygen or alumino-oxygen tetrahedra. In contrast, for the ring forms of OC oligomers, the electron-donor sites are predominantly located in the vicinity of the aluminosilicate tetrahedron, while the electron-acceptor sites are mainly found in the region of the silica/silicate tetrahedron. The overall comparative analysis suggests that OC ring oligomers have a greater propensity for electron exchange with multiple sites on the cement mortar surface, potentially facilitating the formation of stronger chemical bonds at the geopolymer–cement mortar interface. This implies their efficient adsorption onto the surface of the cement mortar substrate, potentially resulting in the formation of a stable and strongly adhered geopolymer repair layer.
Further insights into the local reactivity of aluminosilicate oligomers can be gained through the application of Fukui’s concept [24]. The Fukui function, f r , is mathematically defined as the first derivative of the electron density ρ r with respect to the number of electrons N. This function enables the identification of atoms within the molecule that are prone to nucleophilic and electrophilic reactions. Employing the finite difference approximation and utilizing the charge of the atom in its neutral state q N and its cationic state q N − 1 , the Fukui functions can be computed as follows [29]:
f + = q N + 1 − q N   for   nucleophilic   attack ; f − = q N − q N − 1   for   electrophilic   attack
Figure 2 depicts the spatial distribution of f +     and f −     for oligomers in linear and ring conformations at an isosurface value of 0.01. For oligomers in linear form, there is a notable prevalence of sites susceptible to electrophilic attack compared to those prone to nucleophilic attack. In the case of ring-form oligomers, the nucleophilic attack centers are primarily localized on OH groups of organosilicon tetrahedra, while the regions vulnerable to electrophilic attack are predominantly associated with OH groups of alumina tetrahedra.
The comprehensive analysis reveals a proliferation of reactive sites within the framework structure as the Si/Al ratio increases, attributed to the emergence of additional OH groups. The ring conformation of the oligomer exhibits enhanced reactivity compared to its linear counterpart. The observed increase in potential reaction sites capable of interacting with the mineral surface suggests an improved likelihood of achieving effective adhesion.
To further elucidate the atomic-level adsorption mechanisms of the oligomers, we conducted a Mulliken population analysis on the framework structure [30]. It is well-established that atoms with more negative charge exhibit a higher propensity for surface adsorption through donor–acceptor interactions. The outcomes of this analysis for both linear and ring conformations of the oligomers are summarized in Figure 3. The graphical representation clearly demonstrates that the ring structure possesses a higher concentration of negative charge on its heteroatoms compared to the linear configuration. This observation lends support to the enhanced reactivity of the ring forms of OC1, OC2, and OC3 oligomers.

2.2. Global Reactivity of Aluminosilicate Oligomers

Global reactivity indicators serve as crucial parameters for predicting the adhesive properties of multi-atomic systems, which is particularly relevant when considering the interaction between geopolymer repair materials and cement mortar substrates. The quantification of these descriptors was carried out in accordance with the principles outlined in Koopmans’ theorem [31], utilizing the energetic values associated with the HOMO and LUMO. The outcomes of these calculations for OL and OC oligomers in both linear and ring conformations, which represent different structural components of geopolymers, are presented in Figure 4. These results provide insights into how different geopolymer structures might interact with the cement mortar surface at a molecular level.
The assessment of global hardness (softness) is illustrated in Figure 4a,b. These parameters are evaluated in alignment with the hard and soft acids and bases (HSABs) principle [32]. This principle posits that compounds preferentially react with systems exhibiting comparable hardness (softness) characteristics. In the context of concrete repair, this suggests that geopolymer components with softness values closer to those of the cement mortar surface are likely to form stronger bonds. The strength of interaction is expected to increase as the hardness (softness) of the reactants decreases [33]. Consequently, the interaction with the mineral surface is enhanced for softer polyatomic systems (characterized by lower hardness and higher softness values) compared to harder polyatomic systems (exhibiting higher hardness and lower softness values). The data presented in Figure 4a,b indicate an enhancement in global softness associated with the formation of the OC ring structure (OC1, OC2, and OC3). Notably higher global softness values are observed for the ring-form oligomers relative to their linear counterparts. These findings suggest that the ring configuration of the oligomer exhibits superior reactivity compared to the linear form.
The concept of electrophilicity provides a measure of a polyatomic system’s capacity to accept electrons. In this context, a higher electrophilicity value corresponds to an increased propensity for electron acceptance, thus indicating stronger electrophilic behavior, and vice versa. The results depicted in Figure 4c demonstrate an intensification of electron-accepting processes with increasing Si/Al ratio for linear oligomers. Conversely, for ring-shaped oligomers, an increase in Si/Al ratio is associated with enhanced electron-donating capabilities.
The exchange of charge between the oligomer and the mineral surface, characteristic of donor–acceptor processes, can be evaluated through the analysis of energy variations [26]. The energy change calculations, as shown in Figure 4d, yield negative values for all oligomers. This observation indicates that both the forward donation and reverse donation processes are energetically favorable. The magnitude of this energy parameter increases with rising Si/Al ratio, suggesting enhanced adsorption of oligomers at higher Si/Al ratios. It is noteworthy that this trend is more pronounced for ring-form oligomers compared to their linear counterparts.

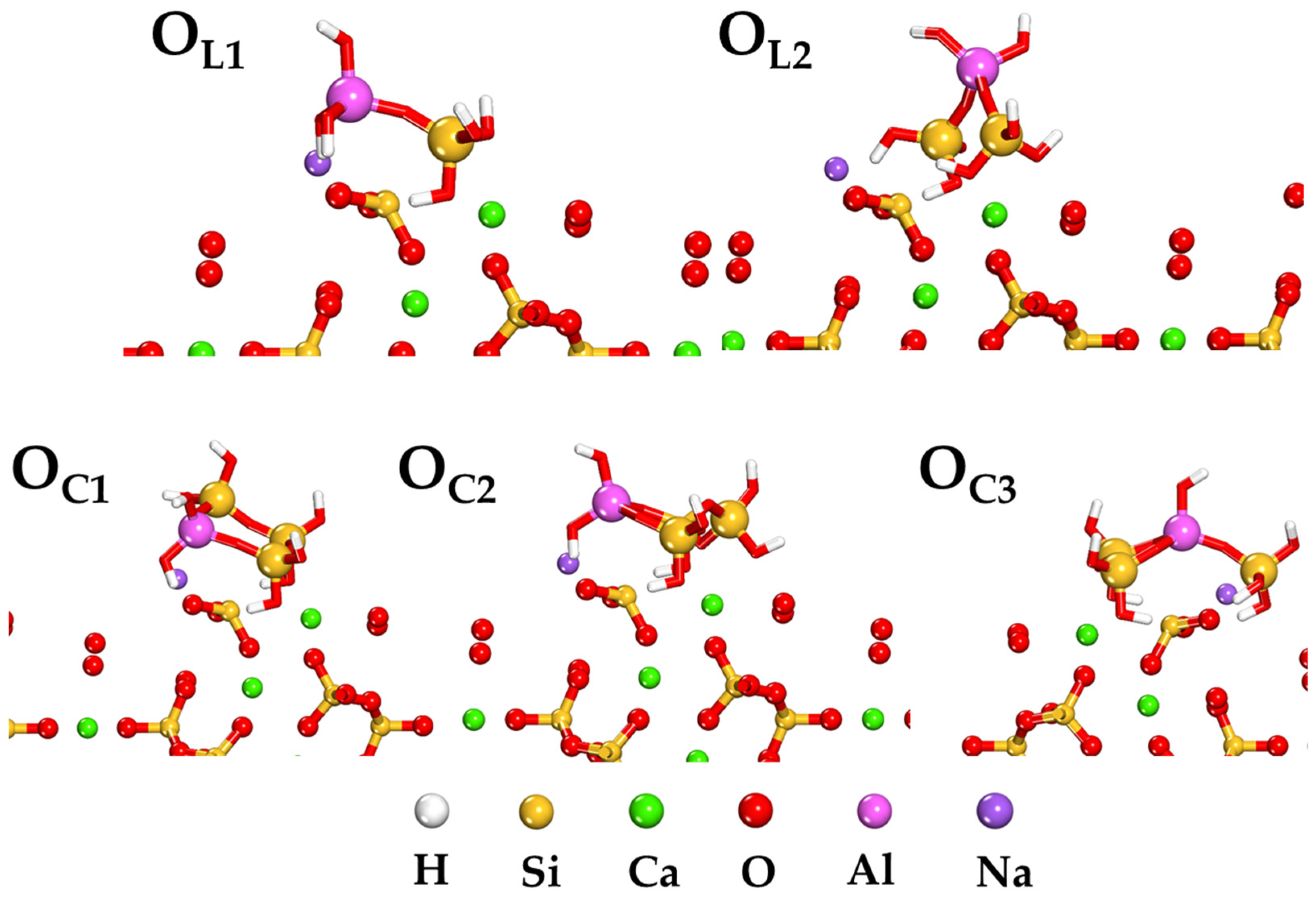
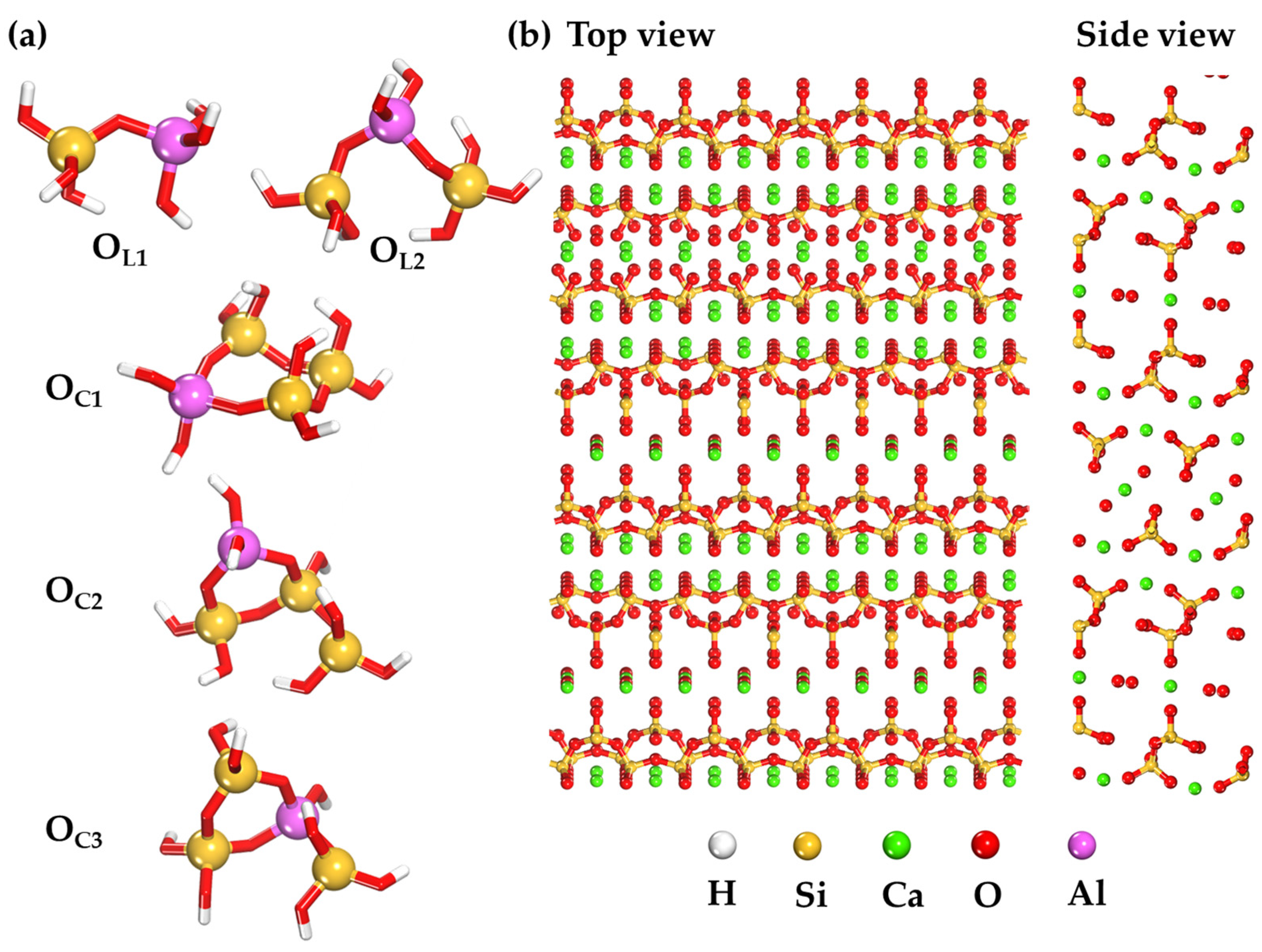
2.3. Adsorption Behavior of Aluminosilicate Oligomers

The adhesion efficacy of OL and OC oligomers was investigated in relation to calcium silicate hydrate, a widely used model for the primary binding phase in concrete. This approach allows us to simulate and understand the interactions between geopolymer repair materials and the cement mortar substrate at a molecular level. This investigation was conducted through a comprehensive examination of the adsorption characteristics derived from stochastic modeling techniques. We evaluated the energetically favorable adsorption configurations of the oligomers on the C-S-H surface and quantified their corresponding adsorption energies. The energy released during the adsorption process (Eads) when the relaxed adsorbate components interact with the substrate was determined using the following equation:
Eads = ETotal − (EAdsorbate + ESubstrate)
where Eads represents the energy of the substrate–adsorbate system, while EAdsorbate and ESubstrate denote the energies of the isolated oligomer and mineral surface, respectively.
The computationally derived low-energy structural arrangements of OL and OC oligomers adsorbed onto the C-(A)-S-H(I) (100) surface are illustrated in Figure 5. The simulations reveal that all oligomers adopt a parallel orientation with respect to the mineral surface upon adsorption. This behavior is consistent across both linear and ring conformations of the oligomers. The observed spatial arrangement relative to the C-(A)-S-H(I) (100) surface can be attributed to the distribution of HOMO and LUMO electron densities within the oligomers. This suggests that the adsorption process involves bidirectional electron transfer between the oligomers and the investigated mineral surface. The parallel alignment indicates enhanced adhesive capabilities of the oligomers and promotes maximal coverage of the mineral surface.
The predominant types of adsorbate–substrate interactions can be inferred through an analysis of bond lengths. Typical intermolecular distances associated with van der Waals interactions, mineral complexation, and hydrogen bonding fall within the ranges of 5–10 Å, 2–3 Å, and 2–3.5 Å, respectively. Table 1 presents the minimum distances between the surface metal atoms and the nearest aluminum and silicon atoms of the adsorbed oligomers in their equilibrium configurations. The majority of these interatomic distances are less than 3.5 Å, indicating the formation of robust chemical bonds between the chemisorbed oligomers and the mineral surface. Exceptions to this trend are observed in the Al-O bond lengths of the linear oligomer OL2 and the Si-O bond lengths in the ring-form oligomer OC1. The data in Table 1 demonstrates that the adsorption process results in a progressive decrease in the analyzed bond lengths, following the sequence: OC3 > OC2 > OC1. This trend suggests that ring-shaped oligomers exhibit stronger adsorption characteristics on the investigated mineral surface compared to their linear counterparts.
Figure 6 illustrates that an increase in the Si/Al ratio of the aluminosilicate framework correlates with a significant reduction in Eads. The observed high negative values of adsorption energy for the oligomers are indicative of their enhanced adsorption capacity and, by extension, their adhesion efficiency. These computational results align well with existing experimental studies [34,35,36,37]. Research by [34] established that the Si/Al ratio in geopolymers plays a crucial role in determining both compressive strength and adhesion strength, which are essential properties for the material’s effectiveness as a coating. While a higher Si/Al ratio generally enhances the compressive strength of the geopolymer, its impact on adhesion strength can vary depending on factors such as substrate type and surface roughness.
A study conducted by [35] demonstrated that elevated Si/Al ratios strengthen the bonding between the geopolymer binder and the substrate, resulting in improved durability and effectiveness in high-temperature and aggressive environments. The research showed that an appropriate Si/Al ratio contributes to the chemical stability of the geopolymer matrix, which in turn influences the longevity and adhesion strength of coatings. The formation of stable chemical bonds leads to increased adhesion [36].
Furthermore, a higher Si/Al ratio has been associated with the development of a denser and more cohesive microstructure, which can enhance the adhesion strength of geopolymer coatings by reducing porosity and improving interfacial bonding [36]. In a study by [37], it was revealed that the Si/Al ratio significantly influences the adhesion strength of geopolymer coatings. Higher ratios generally lead to improved adhesion, attributed to the increased silicon dioxide content, which enhances the geopolymerization process and results in a more condensed structure. Notably, the maximum adhesion strength was observed at a Si/Al ratio of 3, which aligns closely with the computational results obtained in this work. The highest negative adsorption energy is associated with OC3 ring-shaped oligomers (Si/Al = 3), indicating their superior potential for adhesion. This finding is in agreement with the quantum chemical calculations presented in the preceding sections of this study.

3. Materials and Methods

A cross-linked three-dimensional N-A-S-H structure is formed during the geopolymerization of oligomers containing silicon and aluminum [38]. These oligomers (monomers), containing Si and Al, are structurally represented as oxygen tetrahedral complexes [39]. During bond formation between monomers, the Loewenstein principle is observed, meaning that two Al tetrahedra cannot be linked by a single oxygen bridge. Therefore, each Al tetrahedron is always connected to four Si tetrahedra [40]. The formation of dimers and trimers, as a reaction between monomers containing Si and Al(OH)4−, and their existence in isolated form, is consistent with nuclear magnetic resonance (NMR) experimental data [41,42,43]. Increasing the pH of the alkaline solution further facilitates the reaction between monomers, making the environment more favorable for the formation of complex structures such as dimers and trimers at the initial stage of geopolymerization, as discussed in studies [38,39,44]. However, it is acknowledged that aluminum coordination can vary in real-world silicate-containing systems. Recent literature, such as [45], has found that Al coordination varies and Al-IV facilitates oligomerization in neutral conditions. Models may not fully account for the effects of various reaction conditions, such as temperature, pH, and concentration, which can significantly influence the behavior of aluminosilicate oligomers [46]. The transition from oligomers to larger structures, including nucleation and growth processes, is difficult to capture accurately in current models [46,47]. This highlights the complexity of real-world systems compared to the pure, ordered models used in this study. In this work, five oligomers (Figure 7a) with different spatial configurations and Si/Al ratios (1 to 3) were investigated. Linear-type aluminosilicate oligomers with Si/Al ratios from 1 to 2 (OL1 and OL2) were considered, as well as aluminosilicate oligomers in the form of OC1, OC2, and OC3, presented with a Si/Al ratio of 3, as shown in Figure 7a. The coordination of aluminum in our models was tetrahedral (Al-IV), which is commonly observed in high-pH conditions characteristic of geopolymerization.
The C-(A)-S-H(I) (100) surface (Figure 7b) was chosen to model the adsorption behavior of the oligomers (OL1, OL2, OC1, OC2, and OC3) (see supplementary materials). Calcium silicate hydrate is widely used as a model of the basic binding phase in concrete. It is a structurally imperfect form of tobermorite, which has a variable composition and length of (alumo) silicate anions [48]. To ensure the isolation of the modeled system and prevent unintended interactions, a buffer zone of 40 Å was incorporated into the model. This approach effectively negates the influence of periodic boundary conditions on the atomic layers within the simulation.
Quantum chemical computations for the gas phase were executed using the DMol3 computational package [49]. The structural optimization of OL and OC oligomers was performed employing an exchange-correlation functional within the framework of the generalized gradient approximation (GGA) [50], specifically utilizing the Perdew–Burke–Ernzerhof (PBE) formulation [51]. PBE offers a good balance between accuracy and computational efficiency. The accuracy of PBE can vary depending on the system being studied. For metallic bulk and surface systems, the PBEsol variant has been shown to provide improved accuracy for some properties. It provides reasonably accurate results for many properties without requiring excessive computational resources, making it a popular choice for various applications [52,53]. Hybrid functionals that incorporate a fraction of Hartree–Fock exchange, such as PBE0, HSE, and B3LYP, can offer improved accuracy for certain properties, particularly for molecular systems [54,55,56]. However, this comes at the cost of increased computational demands. In summary, the PBE functional offers a good compromise between accuracy and computational efficiency for many systems. While more advanced functionals or methods may provide higher accuracy in some cases, they often come with increased computational costs.
The electron density was calculated using a comprehensive set of numerical basis functions with dual polarization capabilities (DNP+) [57]. To enhance the accuracy in describing hydrogen bonding and van der Waals dispersion forces, which are crucial in the hydration process of mineral surfaces [58], a DFT-D correction functional was applied. In this study, the dispersion correction (DFT-D2) was implemented using the method developed by Grimme [59]. The optimization procedure adhered to the following convergence criteria: the energy convergence threshold was set at 1 ×10 −6 Ha, the maximum force tolerance was 2 × 10−3 Ha×Å−1, and the maximum displacement was limited to 5 × 10−3 Å. The self-consistent field (SCF) calculations were performed with a precision of 1 × 10−6.
The adsorption process of oligomers on the C-(A)-S-H(I) (100) surface was investigated using stochastic modeling techniques in the gas phase. Optimized structures of oligomers were used for the calculation. During the modeling process, the C-(A)-S-H(I) (100) surface is considered non-deformable. These simulations were carried out using the Adsorption Locator module within the Materials Studio software suite [49]. The computational framework for the model is grounded in the Metropolis algorithm [60]. For the stochastic modeling, a simulated annealing protocol was employed, consisting of 20 temperature cycles with 2 × 105 steps per cycle. The COMPASS force field was utilized to compute energies and identify equilibrium configurations [61,62]. Electrostatic interactions were described using the Ewald summation method, with a precision of 1 × 10−4 kcal/mol [63]. The van der Waals interaction energies were evaluated using an atom-based approach. The cutoff radius for Lennard–Jones interactions was set at 14.5 Å. To achieve system equilibrium, an initial 1 × 105 steps were performed, followed by an additional 1 × 106 steps for subsequent calculations.

4. Conclusions

In this study, quantum mechanical calculations and stochastic modeling techniques were used to investigate the adsorption behavior and interaction mechanisms of aluminosilicate oligomers with varying Si/Al ratios forming the geopolymer gel structure and calcium silicate hydrate as a substrate at the interface bond region. These oligomers, characterized by varying Si/Al ratios, form the geopolymer gel structure and were studied in relation to calcium silicate hydrate, which served as a substrate at the interface bond region. Furthermore, we determined the energetically favorable structural configurations of oligomers adsorbed onto the C-(A)-S-H(I) (100) surface and computed their respective adsorption energies. The quantum mechanical assessment of local and global reactivity descriptors for aluminosilicate oligomers revealed an increasing adhesion effect correlating with higher Si/Al ratios. This enhancement can be attributed to a proliferation of reactive sites within the atomic structure. Notably, ring-form oligomers demonstrated superior activity compared to their linear counterparts. Our stochastic simulations indicated that the oligomers can be effectively adsorbed onto the calcium silicate hydrate surface through chemisorption processes. We observed that the magnitude of adsorption energies for these oligomers on the studied surface increased proportionally with higher Si/Al ratios, following the sequence: OC3 > OC2 > OC1 > OL2 > OL1. Ring-shaped oligomers exhibited the highest adsorption capacity with respect to the calcium silicate hydrate surface, suggesting their potential for achieving the most pronounced adhesion effect.
It is worth noting that these computational findings align well with existing experimental studies in the field. This congruence between theoretical predictions and empirical observations lends credence to the validity and practical applicability of our results.
In conclusion, this study provides valuable molecular-level insights into the adhesion mechanisms at the interface between geopolymer binders and cement mortar. These results contribute to a deeper understanding of the adhesion properties of geopolymers and underscore their potential as effective repair materials in concrete applications.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms25158374/s1.

Author Contributions

Conceptualization, A.S.K.; methodology, A.S.K.; software, A.S.K.; validation, A.S.K. and A.A.K.; formal analysis, A.A.K.; investigation, A.A.K.; writing—original draft preparation, A.S.K.; writing—review and editing, A.A.K.; visualization, A.S.K.; supervision, A.S.K.; project administration, A.S.K.; funding acquisition, A.S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by a grant from the Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-15-2022-1111; “Carbon-neutral technologies for recycling large-tonnage fuel energy waste with the production of functional geopolymer materials”).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Wang, R.; Zhang, Q.; Li, Y. Deterioration of concrete under the coupling effects of freeze–thaw cycles and other actions. Constr. Build. Mater. 2022, 319, 126045. [Google Scholar] [CrossRef]
  2. Qu, F.; Li, W.; Dong, W.; Tam, V.W.Y.; Yu, T. Durability deterioration of concrete under marine environment from material to structure. Build. Eng. 2021, 35, 102074. [Google Scholar] [CrossRef]
  3. Song, X.; Song, X.; Liu, H.; Huang, H.; Anvarovna, K.G.; Ugli, N.A.D.; Huang, Y.; Hu, J.; Wei, J.; Yu, Q. Cement-Based Repair Materials and the Interface with Concrete Substrates: Characterization, Evaluation and Improvement. Polymers 2022, 14, 1485. [Google Scholar] [CrossRef]
  4. Fang, B.; Hu, Z.; Shi, T.; Liu, Y.; Wang, X.; Yang, D.; Zhu, K.; Zhao, X.; Zhao, Z. Research progress on the properties and applications of magnesium phosphate cement. Ceram. Int. 2023, 49, 4001–4016. [Google Scholar] [CrossRef]
  5. Mechtcherine, V. Novel cement-based composites for the strengthening and repair of concrete structures. Constr. Build. Mater. 2013, 41, 365–373. [Google Scholar] [CrossRef]
  6. Hai, R.; Zheng, J.; Li, J.; Hui, C.; Liu, J. Preparation mechanism and properties of thermal activated red mud and its geopolymer repair mortar. Case Stud. Constr. Mater. 2024, 20, e02853. [Google Scholar] [CrossRef]
  7. Fan, L.F.; Chen, D.K.; Zhong, W.L. Effects of slag and alkaline solution contents on bonding strength of geopolymer-concrete composites. Constr. Build. Mater. 2023, 406, 133391. [Google Scholar] [CrossRef]
  8. Mohd Tahir, M.F.; Ahmad Zailani, W.W.; Ghazali Abd, A.; Miltiadis, S.K. Morphological analysis of fly ash based geopolymer with different concentration of NaOH as repair material. AIP Conf. Proc. 2021, 2339, 020244. [Google Scholar] [CrossRef]
  9. Shen, Y.; Kang, S.; Cheng, G.; Wang, J.; Wu, W.; Wang, X.; Zhao, Y.; Li, Q. Effects of silicate modulus and alkali dosage on the performance of one-part electric furnace nickel slag-based geopolymer repair materials. Case Stud. Constr. Mater. 2023, 19, e02224. [Google Scholar] [CrossRef]
  10. Zhang, B. Repair of ordinary concrete using alkali activated slag/fly ash: High temperature resistance and micro structure evolution of adhesive interface. Constr. Build. Mater. 2023, 386, 131559. [Google Scholar] [CrossRef]
  11. Wang, B.; Feng, H.; Huang, H.; Guo, A.; Zheng, Y.; Wang, Y. Bonding Properties between Fly Ash/Slag-Based Engineering Geopolymer Composites and Concrete. Materials 2023, 16, 4232. [Google Scholar] [CrossRef] [PubMed]
  12. Song, L.; Li, Z.; Duan, P.; Huang, M.; Hao, X.; Yu, Y. Novel low cost and durable rapid-repair material derived from industrial and agricultural by-products. Minerals 2019, 9, 14516. [Google Scholar] [CrossRef]
  13. Ng, C.; Alengaram, U.J.; Wong, L.S.; Mo, K.H.; Jumaat, M.Z.; Ramesh, S. A review on microstructural study and compressive strength of geopolymer mortar, paste and concrete. Constr. Build. Mater. 2018, 186, 550–576. [Google Scholar] [CrossRef]
  14. Zhang, B.; Zhu, H.; Feng, P.; Zhang, P. A review on shrinkage-reducing methods and mechanisms of alkali-activated/geopolymer systems: Effects of chemical additives. Build. Eng. 2022, 49, 104056. [Google Scholar] [CrossRef]
  15. Wasim, M.; Ngo, T.D.; Law, D. A state-of-the-art review on the durability of geopolymer concrete for sustainable structures and infrastructure. Constr. Build. Mater. 2021, 291, 123381. [Google Scholar] [CrossRef]
  16. Frasson, B.J.; Rocha, J.C. Drying shrinkage behavior of geopolymer mortar based on kaolinitic coal gangue. Case Stud. Constr. Mater. 2023, 18, e01957. [Google Scholar] [CrossRef]
  17. Pacheco-Torgal, F.; Castro-Gomes, J.P.; Jalali, S. Adhesion characterization of tungsten mine waste geopolymeric binder. Influence of OPC concrete substrate surface treatment. Constr. Build. Mater. 2008, 22, 154–161. [Google Scholar] [CrossRef]
  18. Baloch, W.L.; Siad, H.; Lachemi, M.; Sahmaran, M. A review on the durability of concrete-to-concrete bond in recent rehabilitated structures. Build. Eng. 2021, 44, 103315. [Google Scholar] [CrossRef]
  19. Daneshvar, D.; Behnood, A.; Robisson, A. Interfacial bond in concrete-to-concrete composite. Constr. Build. Mater. 2022, 359, 129195. [Google Scholar] [CrossRef]
  20. Feng, S.; Xiao, H.; Liu, R.; Liu, M. The bond properties between ultra-high-performance concrete and normal strength concrete substrate: Bond macro-performance and overlay transition zone microstructure. Cem. Concr. Compos. 2022, 128, 104436. [Google Scholar] [CrossRef]
  21. Wang, Y.-S.; Peng, K.-D.; Alrefaei, Y.; Dai, J.-G. The bond between geopolymer repair mortars and OPC concrete substrate: Strength and microscopic interactions. Cem. Concr. Compos. 2021, 119, 103991. [Google Scholar] [CrossRef]
  22. Asayesh, S.; Shirzadi Javid, A.A.; Ziari, H.; Mehri, B. Evaluating fresh state, hardened State, thermal expansion and bond properties of geopolymers for the repairing of concrete pavements under restrained conditions. Constr. Build. Mater. 2021, 292, 123398. [Google Scholar] [CrossRef]
  23. Fahim Huseien, G.; Mirza, J.; Ismail, M.; Ghoshal, S.K.; Abdulameer Hussein, A. Geopolymer mortars as sustainable repair material: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 80, 54–74. [Google Scholar] [CrossRef]
  24. Fukui, K. Role of frontier orbitals in chemical reactions. Science 1982, 218, 747–754. [Google Scholar] [CrossRef]
  25. Gece, G. The use of quantum chemical methods in corrosion inhibitor studies. Corros. Sci. 2008, 50, 2981–2992. [Google Scholar] [CrossRef]
  26. Ebenso, E.E.; Kabanda, M.M.; Murulana, L.C.; Singh, A.K.; Shukla, S.K. Electrochemical and quantum chemical investigation of some azine and thiazine dyes as potential corrosion inhibitors for mild steel in hydrochloric acid solution. Ind. Eng. Chem. Res. 2012, 51, 12940–12958. [Google Scholar] [CrossRef]
  27. Obot, I.B.; Macdonald, D.D.; Gasem, Z.M. Density functional theory (DFT) as a powerful tool for designing new organic corrosion inhibitors: Part 1: An overview. Corros. Sci. 2015, 99, 1–30. [Google Scholar] [CrossRef]
  28. Anupama, K.K.; Ramya, K.; Joseph, A. Electrochemical measurements and theoretical calculations on the inhibitive interaction of Plectranthus amboinicus leaf extract with mild steel in hydrochloric acid. Meas. J. Int. Meas. Confed. 2017, 95, 297–305. [Google Scholar] [CrossRef]
  29. Yang, W.; Mortier, W.J. The Use of Global and Local Molecular Parameters for the Analysis of the Gas-Phase Basicity of Amines. J. Am. Chem. Soc. 1986, 108, 5708–5711. [Google Scholar] [CrossRef]
  30. Mulliken, R.S. Electronic population analysis on LCAO-MO molecular wave functions. II. Overlap populations, bond orders, and covalent bond energies. J. Chem. Phys. 1955, 23, 1841–1846. [Google Scholar] [CrossRef]
  31. Koopmans, T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
  32. Pearson, R.G. Hard and Soft Acids and Bases. J. Am. Chem. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
  33. Moretti, G.; Guidi, F.; Grion, G. Tryptamine as a green iron corrosion inhibitor in 0.5 M deaerated sulphuric acid. Corros. Sci. 2004, 46, 387–403. [Google Scholar] [CrossRef]
  34. Rong, X.; Wang, Z.; Xing, X.; Zhao, L. Review on the Adhesion of Geopolymer Coatings. ACS Omega 2021, 6, 5108–5112. [Google Scholar] [CrossRef] [PubMed]
  35. Wang, Z.; Rong, X.; Zhao, L.; Xing, X.; Ma, H. Effects of Substrate Surface Characteristics on the Adhesion Properties of Geopolymer Coatings. ACS Omega 2022, 7, 11988–11994. [Google Scholar] [CrossRef] [PubMed]
  36. Słomka-Słupik, B.; Wiśniewska, P.; Bargieł, W. Multicomponent Low Initial Molar Ratio of SiO2/Al2O3 Geopolymer Mortars: Pilot Research. Materials 2022, 15, 5943. [Google Scholar] [CrossRef] [PubMed]
  37. Khan, M.I.; Azizi, K.; Sufian, S.; Man, Z. Effect of Na/Al and Si/Al Ratios on Adhesion Strength of Geopolymers as Coating Material. Appl. Mech. Mater. 2014, 625, 85–89. [Google Scholar] [CrossRef]
  38. Guan, X.; Jiang, L.; Fan, D.; Garcia Hernandez, A.; Li, B.; Do, H. Molecular simulations of the structure-property relationships of N-A-S-H gels. Constr. Build. Mater. 2022, 329, 127166. [Google Scholar] [CrossRef]
  39. Yang, H.; Ma, S.; Zhao, S.; Wang, Q.; Liu, X.; He, P.; Jia, D.; Colombo, P.; Zhou, Y. Mechanistic understanding of geopolymerization at the initial stage: Ab initio molecular dynamics simulations. J. Am. Ceram. Soc. 2023, 106, 4425–4442. [Google Scholar] [CrossRef]
  40. Loewenstein, W. The distribution of aluminum in the tetrahedra of silicates and aluminates. Am. Mineral. 1954, 39, 92–96. [Google Scholar]
  41. North, M.R.; Swaddle, T.W. Kinetics of silicate exchange in alkaline aluminosilicate solutions. Inorg. Chem. 2000, 39, 2661–2665. [Google Scholar] [CrossRef]
  42. Duxson, P.; Provis, J.L.; Lukey, G.C.; Separovic, F.; van Deventer, J.S.J. 29Si NMR study of structural ordering in aluminosilicate geopolymer gels. Langmuir 2005, 21, 3028–3036. [Google Scholar] [CrossRef]
  43. Favier, A.; Habert, G.; Roussel, N.; D’Espinosede Lacaillerie, J.-B. A multinuclear static NMR study of geopolymerisation. Cem. Concr. Res. 2015, 75, 104–109. [Google Scholar] [CrossRef]
  44. Koleżyński, A.; Król, M.; Żychowicz, M. The structure of geopolymers—Theoretical studies. J. Mol. Struct. 2018, 1163, 465–471. [Google Scholar] [CrossRef]
  45. Salha, M.S.; Yada, R.Y.; Farrar, D.H.; Chass, G.A.; Tian, K.V.; Bodo, E. Aluminium catalysed oligomerisation in cement-forming silicate systems. Phys. Chem. Chem. Phys. 2022, 25, 455–461. [Google Scholar] [CrossRef]
  46. Siyal, A.A.; Mohamed, R.M.S.R.; Shamsuddin, R.; Ridzuan, M.B. A comprehensive review of synthesis kinetics and formation mechanism of geopolymers. RSC Adv. 2024, 14, 446–462. [Google Scholar] [CrossRef]
  47. Freeman, E.E.; Neeway, J.J.; Motkuri, R.K.; Rimer, J.D.; Mpourmpakis, G. Understanding initial zeolite oligomerization steps with first principles calculations. AIChE J. 2020, 66, e17107. [Google Scholar] [CrossRef]
  48. Bonaccorsi, E.; Merlino, S.; Kampf, A.R. The Crystal Structure of Tobermorite 14 Å (Plombierite), a C-S-H Phase. Am. Ceram. Soc. 2005, 88, 505–512. [Google Scholar] [CrossRef]
  49. BIOVIA. Dassault Systemes, Materials Studio; Dassault Systemes: San Diego, CA, USA, 2020. [Google Scholar]
  50. Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
  51. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  52. Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
  53. Willand, A.; Kvashnin, Y.O.; Genovese, L.; Vázquez-Mayagoitia, Á.; Deb, A.K.; Sadeghi, A.; Deutsch, T.; Goedecker, S. Norm-conserving pseudopotentials with chemical accuracy compared to all-electron calculations. J. Chem. Phys. 2013, 138, 104109. [Google Scholar] [CrossRef]
  54. Sancho-García, J.; Brédas, J.; Cornil, J. Assessment of the reliability of the Perdew–Burke–Ernzerhof functionals in the determination of torsional potentials in π-conjugated molecules. Chem. Phys. Lett. 2003, 377, 63–68. [Google Scholar] [CrossRef]
  55. Saßnick, H.-D.; Cocchi, C. Electronic structure of cesium-based photocathode materials from density functional theory: Performance of PBE, SCAN, and HSE06 functionals. Electron. Struct. 2021, 3, 027001. [Google Scholar] [CrossRef]
  56. Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
  57. Inada, Y.; Orita, H. Efficiency of numerical basis sets for predicting the binding energies of hydrogen bonded complexes: Evidence of small basis set superposition error compared to Gaussian basis sets. J. Comput. Chem. 2008, 29, 225–232. [Google Scholar] [CrossRef]
  58. Wu, X.; Vargas, M.C.; Nayak, S. Towards extending the applicability of density functional theory to weakly bound systems. Chem. Phys. 2001, 115, 8748–8757. [Google Scholar] [CrossRef]
  59. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  60. Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
  61. Sun, H. The COMPASS force field: Parameterization and validation for phosphazenes. Comput. Theor. Polym. Sci. 1998, 8, 229–246. [Google Scholar] [CrossRef]
  62. Sun, H. Compass: An ab initio force-field optimized for condensed-phase applications—Overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
  63. Yeh, I.-C.; Berkowitz, M.L. Ewald summation for systems with slab geometry. J. Phys. Chem. 1999, 111, 3155–3162. [Google Scholar] [CrossRef]
Ijms 25 08374 g001
Figure 1. HOMO and LUMO isosurface densities of OL and OC oligomers in the gas phase (value for isosurface: 0.03 e∙Å−2).
Figure 1. HOMO and LUMO isosurface densities of OL and OC oligomers in the gas phase (value for isosurface: 0.03 e∙Å−2).
Ijms 25 08374 g001
Ijms 25 08374 g002
Figure 2. Spatial distribution of reactivity indicators derived from electron density functional theory for aluminosilicate oligomers in the gas phase (isosurface value: 0.01).
Figure 2. Spatial distribution of reactivity indicators derived from electron density functional theory for aluminosilicate oligomers in the gas phase (isosurface value: 0.01).
Ijms 25 08374 g002
Ijms 25 08374 g003
Figure 3. Mulliken charges for aluminosilicate oligomers in the gas phase.
Figure 3. Mulliken charges for aluminosilicate oligomers in the gas phase.
Ijms 25 08374 g003
Ijms 25 08374 g004
Figure 4. Descriptors of global reactivity of aluminosilicate oligomers in the gas phase. (a) global hardness, (b) global softness, (c) electrophilicity (d) ΔEb-d′, L- linear form of the oligomer, C- ring form of the oligomer.
Figure 4. Descriptors of global reactivity of aluminosilicate oligomers in the gas phase. (a) global hardness, (b) global softness, (c) electrophilicity (d) ΔEb-d′, L- linear form of the oligomer, C- ring form of the oligomer.
Ijms 25 08374 g004
Ijms 25 08374 g005
Figure 5. Energetically favorable configurations determined through stochastic simulations for the adsorption of OL and OC oligomers on the C-(A)-S-H(I) surface (100).
Figure 5. Energetically favorable configurations determined through stochastic simulations for the adsorption of OL and OC oligomers on the C-(A)-S-H(I) surface (100).
Ijms 25 08374 g005
Ijms 25 08374 g006
Figure 6. Adsorption energies obtained from stochastic simulations for the adsorption of OL and OC oligomers onto the C-(A)-S-H(I) surface (100) in the gas phase.
Figure 6. Adsorption energies obtained from stochastic simulations for the adsorption of OL and OC oligomers onto the C-(A)-S-H(I) surface (100) in the gas phase.
Ijms 25 08374 g006
Ijms 25 08374 g007
Figure 7. (a) OL and OS oligomers defining the structure of N-A-S-H aluminosilicate gel; (b) surface model of the C-(A)-S-H(I) surface (100).
Figure 7. (a) OL and OS oligomers defining the structure of N-A-S-H aluminosilicate gel; (b) surface model of the C-(A)-S-H(I) surface (100).
Ijms 25 08374 g007
Table 1. Interatomic distances (Å) between the surface layer atoms and the nearest oligomer atoms, as determined by stochastic modeling.
Table 1. Interatomic distances (Å) between the surface layer atoms and the nearest oligomer atoms, as determined by stochastic modeling.
AlSiSiSi
OL12.8551.690
OL24.2271.8972.036
OC12.8591.6772.4144.0241
OC23.1231.9412.3532.5287
OC33.2342.3331.8211.7913
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kasprzhitskii, A.S.; Kruglikov, A.A. Molecular Insights into Adhesion at Interface of Geopolymer Binder and Cement Mortar. Int. J. Mol. Sci. 2024, 25, 8374. https://doi.org/10.3390/ijms25158374

AMA Style

Kasprzhitskii AS, Kruglikov AA. Molecular Insights into Adhesion at Interface of Geopolymer Binder and Cement Mortar. International Journal of Molecular Sciences. 2024; 25(15):8374. https://doi.org/10.3390/ijms25158374

Chicago/Turabian Style

Kasprzhitskii, Anton S., and Alexander A. Kruglikov. 2024. "Molecular Insights into Adhesion at Interface of Geopolymer Binder and Cement Mortar" International Journal of Molecular Sciences 25, no. 15: 8374. https://doi.org/10.3390/ijms25158374

APA Style

Kasprzhitskii, A. S., & Kruglikov, A. A. (2024). Molecular Insights into Adhesion at Interface of Geopolymer Binder and Cement Mortar. International Journal of Molecular Sciences, 25(15), 8374. https://doi.org/10.3390/ijms25158374

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop