Ab Initio Molecular Dynamics Insight to Structural Phase Transition and Thermal Decomposition of InN
Abstract
1. Introduction
Phase Diagram of InN
- At the lower pressure range (up to 7–10 GPa), InN decomposes when heated above approx. 710 °C [9] (green arrow in Figure 1). It was also confirmed by our earlier differential thermal analysis (DTA) experiments up to 2 GPa [13] at high pressure of N2 gas. The independence of decomposition temperature on pressure suggests that the equilibrium temperatures in the InN–In–N2 system can be even lower than the measured ones.
- At 12 GPa (low T) to 7–10 GPa (high T), a structural phase transition from hexagonal wurtzite to cubic rocksalt phase induced by increasing pressure is observed (blue arrow in Figure 1). The borderline between the two solid phases is inclined towards lower pressures; however, the different linear or non-linear character of this line follows from XRD experiments reported in [15,16], respectively. A possible verification could be checking if at, i.e., 8 GPa the InN crystal in its wurtzite phase transforms into rocksalt at heating to 800–1000 K (red arrow in Figure 1).
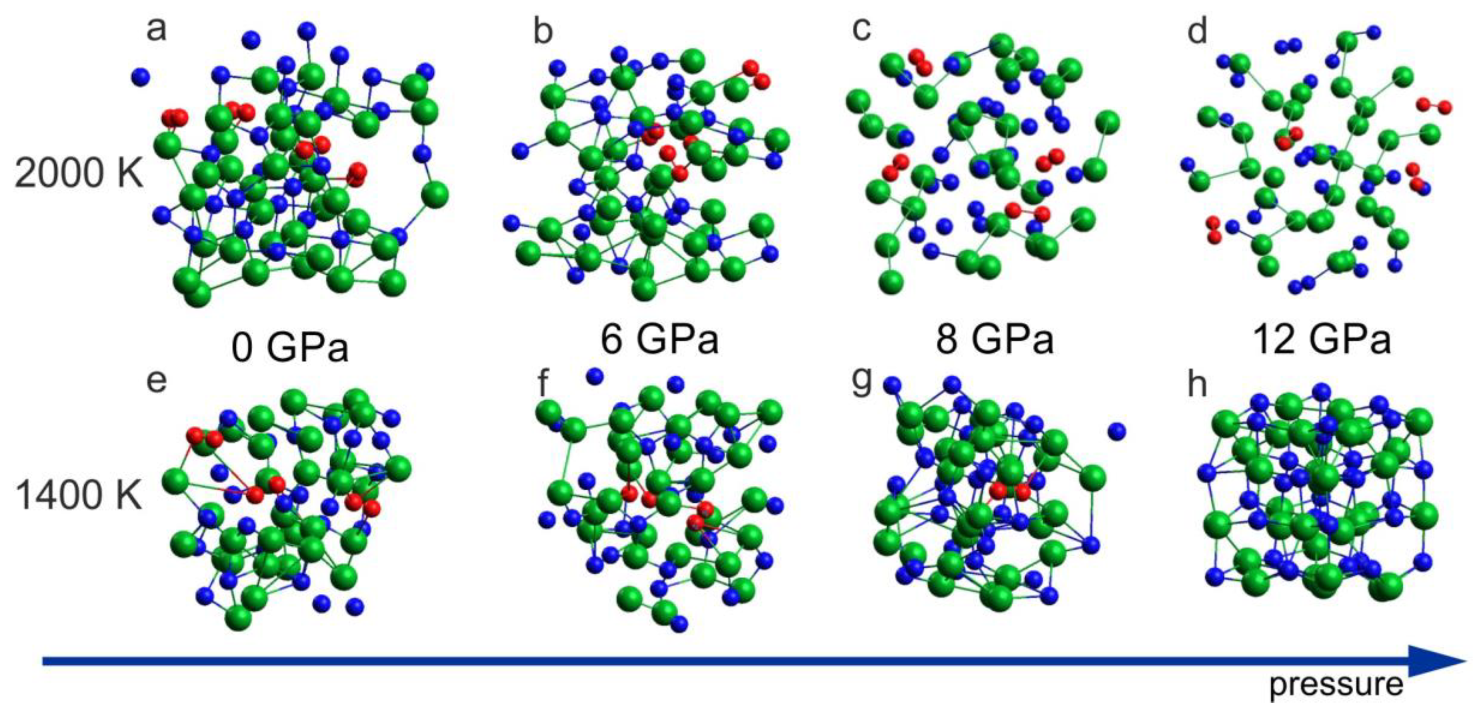
- The InN crystal in its high pressure rocksalt phase also decomposes at high temperatures, but the decomposition temperature strongly increases with increasing pressure (violet arrow in Figure 1).
- The decomposition is suppressed only at pressure as high as >16 GPa and then the congruent melting of InN (without formation of N2, thus reversible) is possible (magenta arrow in Figure 1).
- wurtzite-to-rocksalt structural phase transition induced by high pressure (blue arrow);
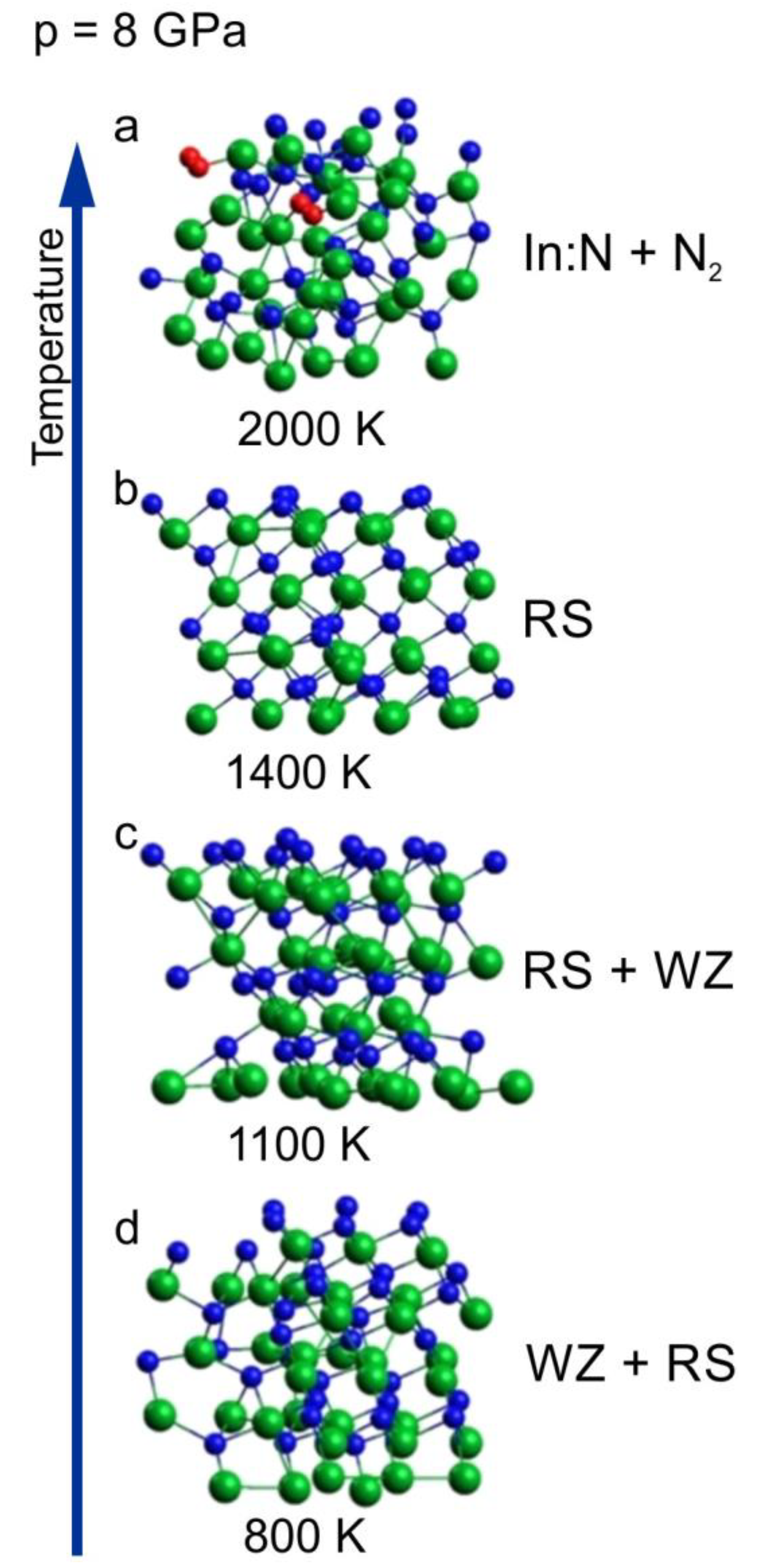
- wurtzite-to-rocksalt structural phase transition induced by high temperature at 8 GPa (red arrow);
- thermal decomposition of InN crystal in both wurtzite and rocksalt phases (green and violet arrow, respectively).
2. Result and Discussion
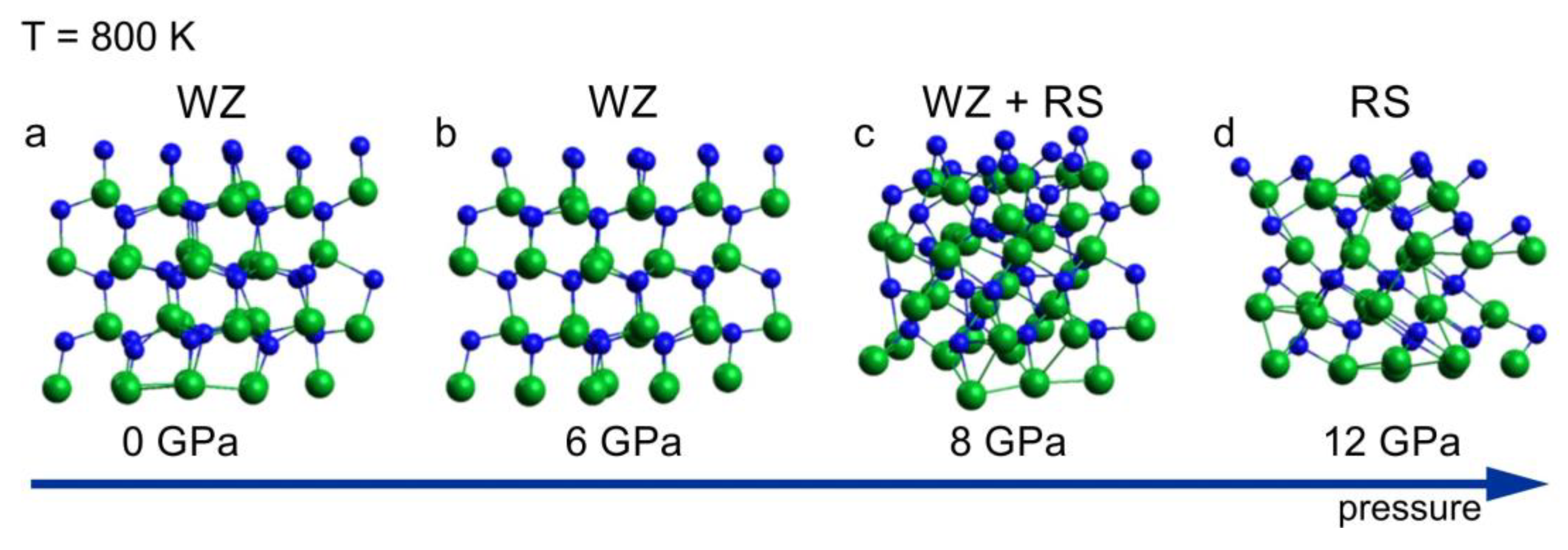
2.1. Pressure Induced Solid–Solid Phase Transition at Low Temperature
- A RMSD ≤ 1.0 Å if no phase transition takes place;
- A 2.0 Å < RMSD < 3.0 Å in the case of structural phase transition (e.g., wurtzite → rocksalt);
- A RMSD ≥ 3.0 Å in the case of melting of the system.
2.2. Temperature Induced Solid–Solid Phase Transition at 8 GPa
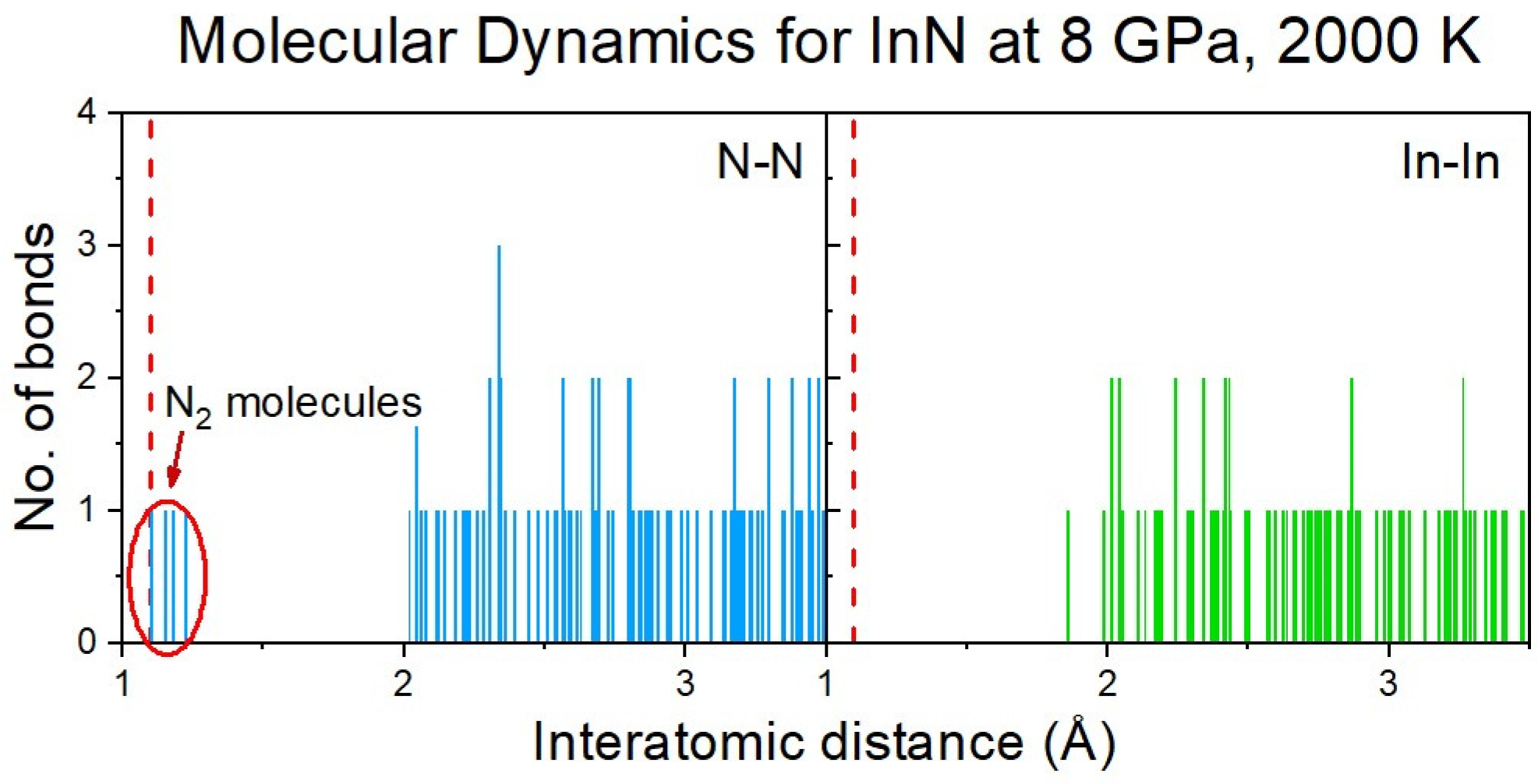
2.3. Decomposition of InN
3. The Simulation Method
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kour, R.; Arya, S.; Verma, S.; Singh, A.; Mahajan, P.; Khosla, A. Review—Recent Advances and Challenges in Indium Gallium Nitride (InxGa1-xN) Materials for Solid State Lighting. ECS J. Solid Stat. Sci. Technol. 2019, 9, 015011. [Google Scholar] [CrossRef]
- Nobelprize.org. The Nobel Prize in Physics. 2014. Available online: https://www.nobelprize.org/prizes/physics/2014/summary/ (accessed on 15 July 2024).
- Davydov, V.Y.; Klochikhin, A.A.; Emtsev, V.V.; Kurdyukov, D.A.; Ivanov, S.V.; Vekshin, V.A.; Bechstedt, F.; Furthmuller, J.; Aderhold, J.; Graul, J.; et al. Band Gap of Hexagonal InN and InGaN Alloys. Phys. Stat. Sol. (b) 2002, 234, 787–795. [Google Scholar] [CrossRef]
- Wu, J. When group-III nitrides go infrared: New properties and perspectives. J. Appl. Phys. 2009, 106, 011101. [Google Scholar] [CrossRef]
- Davydov, V.Y.; Klochikhin, A.; Seisyan, R.; Emtsev, V.; Ivanov, S.; Bechstedt, F.; Furthmüller, J.; Harima, H.; Mudryi, A.; Aderhold, J.; et al. Absorption and Emission of Hexagonal InN. Evidence of Narrow Fundamental Bandgap. Phys. Stat. Sol. (b) 2002, 229, R1–R3. [Google Scholar] [CrossRef]
- Bougrov, V.; Levinshtein, M.E.; Rumyantsev, S.L.; Zubrilov, A. Gallium Nitride (GaN). In Properties of Advanced Semiconductor Materials GaN, AlN, InN, BN, SiC, SiGe; Levinshtein, M.E., Rumyantsev, S.L., Shur, M.S., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; book Section 1; pp. 1–30. [Google Scholar]
- Zubrilov, A. Indium Nitride (InN). In Properties of Advanced Semiconductor Materials GaN, AlN, InN, BN, SiC, SiGe; Levinshtein, M.E., Rumyantsev, S.L., Shur, M.S., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; book Section 3; pp. 45–66. [Google Scholar]
- Silveira, E.; Freitas, J.A.; Schujman, S.B.; Schowalter, L.J. AlN bandgap temperature dependence from its optical properties. J. Cryst. Growth 2008, 310, 4007–4010. [Google Scholar] [CrossRef]
- Ahmed, R.; Aleem, F.; Hashemifar, S.J.; Akbarzadeh, H. First principles study of structural and electronic properties of different phases of boron nitride. Phys. B Condens. Matter. 2007, 400, 297–306. [Google Scholar] [CrossRef]
- Krukowski, S.; Witek, A.; Adamczyk, J.; Jun, J.; Bockowski, M.; Grzegory, I.; Lucznik, B.; Nowak, G.; Wroblewski, M.; Presz, A.; et al. Thermal properties of indium nitride. J. Phys. Chem. Solids 1998, 59, 289–295. [Google Scholar] [CrossRef]
- Kumar, V.; Roy, D.R. Structure, bonding, stability, electronic, thermodynamic and thermoelectric properties of six different phases of indium nitride. J. Mater. Sci. 2018, 53, 8302–8313. [Google Scholar] [CrossRef]
- Grzegory, I.; Jun, J.; Bockowski, M.; Krukowski, S.; Wroblewski, M.; Lucznik, B.; Porowski, S. III–V Nitrides—Thermodynamics and crystal growth at high N2 pressure. J. Phys. Chem. Solids 1995, 56, 639–647. [Google Scholar] [CrossRef]
- Grzegory, I.; Jun, J.; Krukowski, S.; Perlin, P.; Porowski, S. InN Thermodynamics and Crystal-Growth at High-Pressure of N2. Jpn. J. Appl. Phys. 1993, 32, 343–345. [Google Scholar] [CrossRef]
- Piechota, J.; Krukowski, S.; Sadovyi, B.; Sadovyi, P.; Porowski, S.; Grzegory, I. Melting versus Decomposition of GaN: Ab Initio Molecular Dynamics Study and Comparison to Experimental Data. Chem. Mater. 2023, 35, 7694–7707. [Google Scholar] [CrossRef]
- Saitoh, H.; Utsumi, W.; Kaneko, H.; Aoki, K. The phase and crystal-growth study of group-III nitrides in a 2000 °C at 20 GPa region. J. Cryst. Growth 2007, 300, 26–31. [Google Scholar] [CrossRef]
- Soignard, E.; Shen, G.; Sata, N.; McMillan, P.F. Indium Nitride at High Pressures and High Temperatures; Report; The Advanced Photon Source—Argonne National Laboratory: Lemont, IL, USA, 2000. [Google Scholar]
- Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis As Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; van Gunsteren, W.F. Practical algorithms for dynamic simulations. In Molecular-Dynamics Simulations of Statistical-Mechanical Systems, Proc. Int. School Phys. “Enrico Rermi”, Course 97; Giccotti, G., Hoover, W.G., Eds.; North-Holland Physics Publishing: Amsterdam, The Netherlands, 1986; pp. 43–65. [Google Scholar]
- Hayes, E.F.; Parr, R.G. Time-Dependent Hellmann-Feynman Theorems. J. Chem. Phys. 1965, 43, 1831–1832. [Google Scholar] [CrossRef]
- Gamaly, E. Ultra-fast disordering by fs-lasers: Lattice superheating prior to the entropy catastrophe. Appl. Phys. A 2010, 101, 205–208. [Google Scholar] [CrossRef]
- Muñoz, G.A.D.; Correa, A.A.; Yang, S.; Delaire, O.; Huang, Y.J.; Johnson, A.S.; Katayama, T.; Krapivin, V.; Pastor, E.; Reis, D.A.; et al. Ultrafast lattice disordering can be accelerated by electronic collisional forces. Nat. Phys. 2023, 19, 1489–1494. [Google Scholar] [CrossRef]
- Zier, T.; Zijlstra, E.S.; Garcia, M.E.; Strubbe, D.A. Pausing ultrafast melting by multiple femtosecond-laser pulses. arXiv 2023, arXiv:2306.08159. [Google Scholar]
- Garcia, A.; Papior, N.; Akhtar, A.; Artacho, E.; Blum, V.; Bosoni, E.; Brandimarte, P.; Brandbyge, M.; Cerda, J.I.; Corsetti, F.; et al. Siesta: Recent developments and applications. J. Chem. Phys. 2020, 152, 204108. [Google Scholar] [CrossRef]
- Sankey, O.F.; Niklewski, D.J. Ab initio multicenter tight-binding model for molecular-dynamics simulations and other applications in covalent systems. Phys. Rev. B 1989, 40, 3979–3995. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. II. Operators for fast iterative diagonalization. Phys. Rev. B 1991, 43, 8861–8869. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Paszkowicz, W.; Adamczyk, J.; Krukowski, S.; Leszczynski, M.; Porowski, S.; Sokolowski, J.A.; Michalec, M.; Lasocha, W. Lattice parameters, density and thermal expansion of InN microcrystals grown by the reaction of nitrogen plasma with liquid indium. Philos. Mag. A 1999, 79, 1145–1154. [Google Scholar] [CrossRef]
- Stirling, A.; Papai, I.; Mink, J.; Salahub, D.R. Density functional study of nitrogen oxides. J. Chem. Phys. 1994, 100, 2910–2923. [Google Scholar] [CrossRef]
- Awasthi, N.; Ritschel, T.; Lipowsky, R.; Knecht, V. Standard Gibbs energies of formation and equilibrium constants from ab-initio calculations: Covalent dimerization of NO2 and synthesis of NH3. J. Chem. Thermodyn. 2013, 62, 211–221. [Google Scholar] [CrossRef]
- Barin, I. Thermochemical Data of Pure Substances, 3rd ed.; VCH: Weinheim, Germany, 1995; p. 1936. [Google Scholar] [CrossRef]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Yang, J.Z.; Wu, X.; Li, X. A generalized Irving-Kirkwood formula for the calculation of stress in molecular dynamics models. J. Chem. Phys. 2012, 137, 134104. [Google Scholar] [CrossRef]
- Sadovyi, B.; Wierzbowska, M.; Stelmakh, S.; Boccato, S.; Gierlotka, S.; Porowski, S.; Grzegory, I. Experimental and theoretical evidence of the temperature-induced wurtzite to rocksalt phase transition in GaN under high pressure. Phys. Rev. B 2020, 102, 235109. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piechota, J.; Krukowski, S.; Sadovyi, B.; Sadovyi, P.; Porowski, S.; Grzegory, I. Ab Initio Molecular Dynamics Insight to Structural Phase Transition and Thermal Decomposition of InN. Int. J. Mol. Sci. 2024, 25, 8281. https://doi.org/10.3390/ijms25158281
Piechota J, Krukowski S, Sadovyi B, Sadovyi P, Porowski S, Grzegory I. Ab Initio Molecular Dynamics Insight to Structural Phase Transition and Thermal Decomposition of InN. International Journal of Molecular Sciences. 2024; 25(15):8281. https://doi.org/10.3390/ijms25158281
Chicago/Turabian StylePiechota, Jacek, Stanislaw Krukowski, Bohdan Sadovyi, Petro Sadovyi, Sylwester Porowski, and Izabella Grzegory. 2024. "Ab Initio Molecular Dynamics Insight to Structural Phase Transition and Thermal Decomposition of InN" International Journal of Molecular Sciences 25, no. 15: 8281. https://doi.org/10.3390/ijms25158281
APA StylePiechota, J., Krukowski, S., Sadovyi, B., Sadovyi, P., Porowski, S., & Grzegory, I. (2024). Ab Initio Molecular Dynamics Insight to Structural Phase Transition and Thermal Decomposition of InN. International Journal of Molecular Sciences, 25(15), 8281. https://doi.org/10.3390/ijms25158281






