Mathematical Modeling and Inference of Epidermal Growth Factor-Induced Mitogen-Activated Protein Kinase Cell Signaling Pathways
Abstract
:1. Introduction
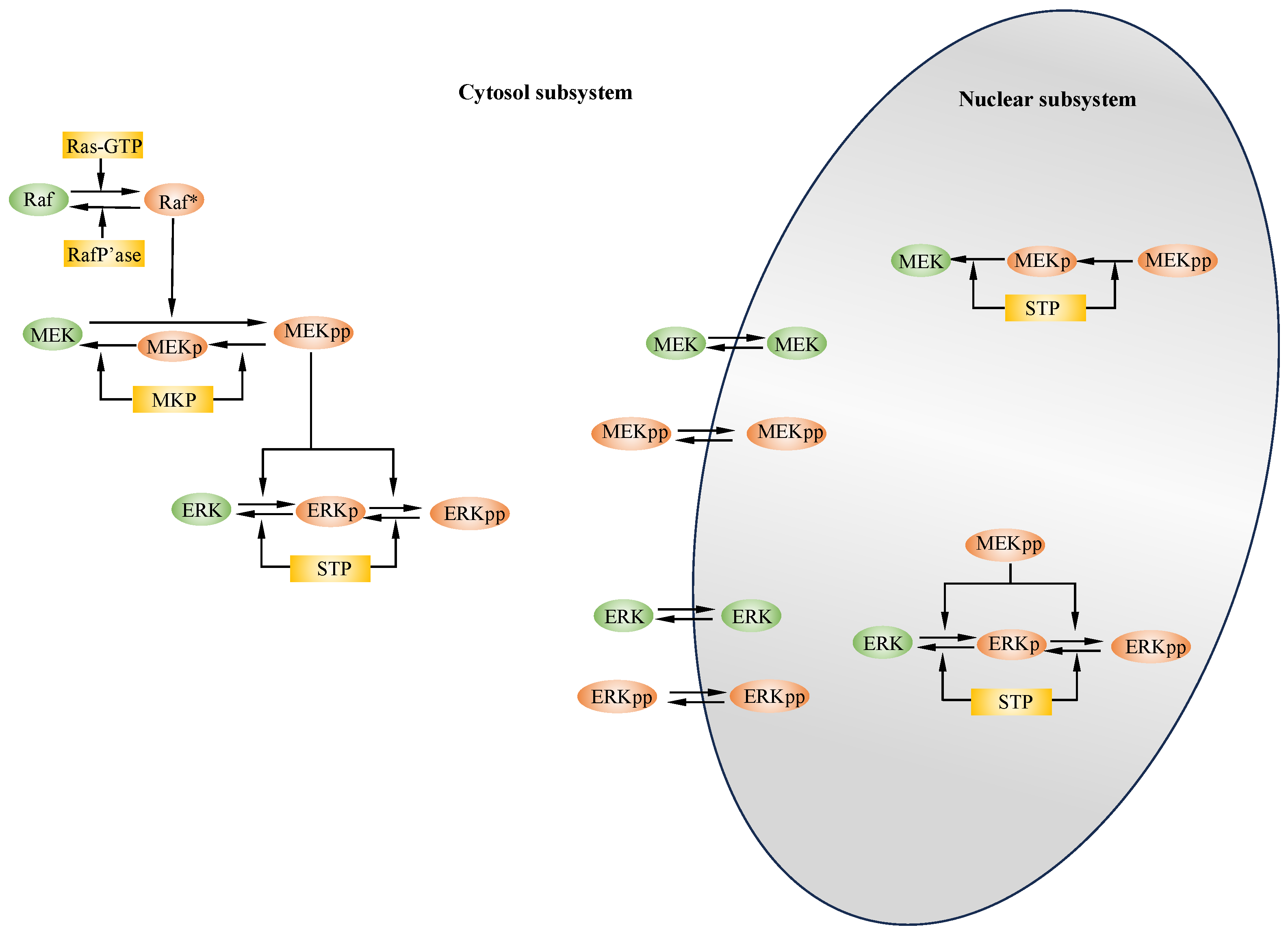
2. Modeling of MAP Kinase Modules
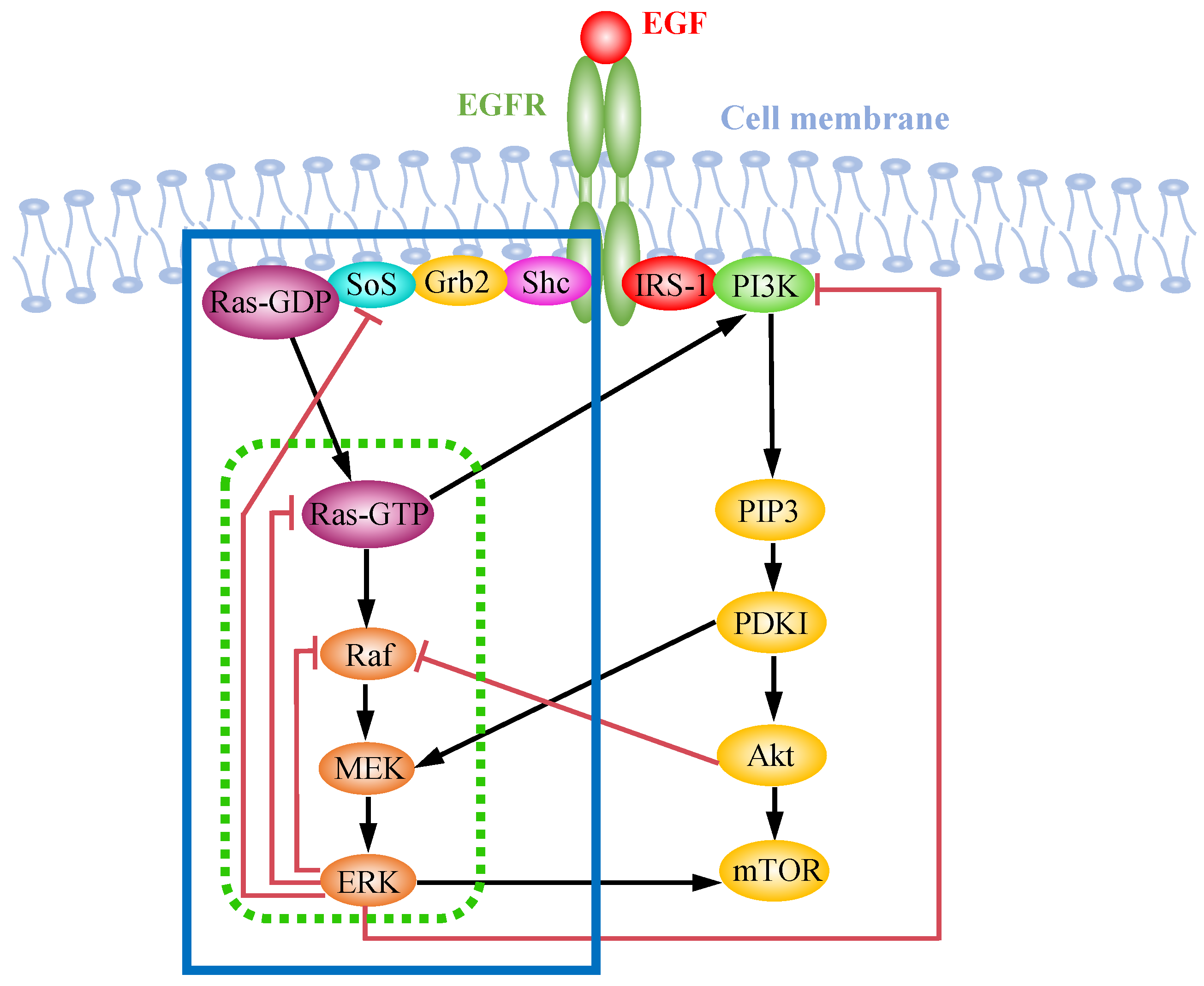
3. EGFR-Induced MAPK Pathway
4. Crosstalk within MAPK and AKT Pathways
5. Data-Driven Modeling of Signaling Pathways
- Non-parametric approaches, which include signaling Petri net-based simulations [158].
- Discrete dynamic modeling, which does not require kinetic parameters [159].
- The BowTieBuilder pipeline, which is used to infer signal transduction pathways [164].
- Information theory-based methods, which analyze signaling pathways [165].
- Extended Boolean network models, which incorporate stochastic processes [169].
- cSTAR (Cell-State Transition Assessment and Regulation), which transforms omics data into input for mechanistic models [170].
- Non-Markovian signaling processes, which account for signaling intermediates with random time delays [171].
6. Stochastic Models for Cell Signaling Pathways
7. Parameter Inference
8. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAPK | mitogen-activated protein kinase |
| JNK | c-Jun N-terminal kinase |
| PI3K | phosphoinositide 3-kinase |
| mTOR | mammalian target of rapamycin |
| EGFR | epidermal growth factor receptor |
| MEK | MAP/ERK kinase |
| ERK | extracellular signal-regulated kinase |
| AKT | protein kinase B |
| ODE | ordinary differential equation |
| SDE | stochastic differential equation |
| NLMEM | nonlinear mixed-effect model |
| ABC | approximate Bayesian computation |
References
- Marshall, C. Specificity of receptor tyrosine kinase signaling: Transient versus sustained extracellular signal-regulated kinase activation. Cell 1995, 80, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Karin, M. Mammalian MAP kinase signalling cascades. Nature 2001, 410, 37–40. [Google Scholar] [CrossRef] [PubMed]
- Yue, J.; López, J.M. Understanding MAPK signaling pathways in apoptosis. Int. J. Mol. Sci. 2020, 21, 2346. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Liu, W.Z.; Liu, T.; Feng, X.; Yang, N.; Zhou, H.F. Signaling pathway of MAPK/ERK in cell proliferation, differentiation, migration, senescence and apoptosis. J. Recept. Signal Transduct. 2015, 35, 600–604. [Google Scholar] [CrossRef]
- Braicu, C.; Buse, M.; Busuioc, C.; Drula, R.; Gulei, D.; Raduly, L.; Rusu, A.; Irimie, A.; Atanasov, A.G.; Slaby, O.; et al. A comprehensive review on MAPK: A promising therapeutic target in cancer. Cancers 2019, 11, 1618. [Google Scholar] [CrossRef]
- Dong, C.; Davis, R.J.; Flavell, R.A. MAP kinases in the immune response. Annu. Rev. Immunol. 2002, 20, 55–72. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.; Corrêa, S.A.; Müller, J. Negative feedback regulation of the ERK1/2 MAPK pathway. Cell. Mol. Life Sci. 2016, 73, 4397–4413. [Google Scholar] [CrossRef]
- Sommariva, S.; Caviglia, G.; Ravera, S.; Frassoni, F.; Benvenuto, F.; Tortolina, L.; Castagnino, N.; Parodi, S.; Piana, M. Computational quantification of global effects induced by mutations and drugs in signaling networks of colorectal cancer cells. Sci. Rep. 2021, 11, 19602. [Google Scholar] [CrossRef]
- Bahar, M.E.; Kim, H.J.; Kim, D.R. Targeting the RAS/RAF/MAPK pathway for cancer therapy: From mechanism to clinical studies. Signal Transduct. Target. Ther. 2023, 8, 455. [Google Scholar] [CrossRef]
- Kestler, H.A.; Wawra, C.; Kracher, B.; Kühl, M. Network modeling of signal transduction: Establishing the global view. Bioessays 2008, 30, 1110–1125. [Google Scholar] [CrossRef]
- Oda, K.; Matsuoka, Y.; Funahashi, A.; Kitano, H. A comprehensive pathway map of epidermal growth factor receptor signaling. Mol. Syst. Biol. 2005, 1, 2005-0010. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Hancock, J.F.; Kolch, W. Signalling ballet in space and time. Nat. Rev. Mol. Cell Biol. 2010, 11, 414–426. [Google Scholar] [CrossRef] [PubMed]
- Hancock, J.F. Ras proteins: Different signals from different locations. Nat. Rev. Mol. Cell Biol. 2003, 4, 373–385. [Google Scholar] [CrossRef] [PubMed]
- Kolch, W.; Berta, D.; Rosta, E. Dynamic regulation of RAS and RAS signaling. Biochem. J. 2023, 480, 1–23. [Google Scholar] [CrossRef]
- Kholodenko, B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006, 7, 165–176. [Google Scholar] [CrossRef]
- Ram, A.; Murphy, D.; DeCuzzi, N.; Patankar, M.; Hu, J.; Pargett, M.; Albeck, J.G. A guide to ERK dynamics, part 1: Mechanisms and models. Biochem. J. 2023, 480, 1887–1907. [Google Scholar] [CrossRef]
- Atay, O.; Skotheim, J.M. Spatial and temporal signal processing and decision making by MAPK pathways. J. Cell Biol. 2017, 216, 317–330. [Google Scholar] [CrossRef]
- Lemmon, M.A.; Schlessinger, J. Cell signaling by receptor tyrosine kinases. Cell 2010, 141, 1117–1134. [Google Scholar] [CrossRef] [PubMed]
- Wagner, E.F.; Nebreda, A.R. Signal integration by JNK and p38 MAPK pathways in cancer development. Nat. Rev. Cancer 2009, 9, 537–549. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, M.C.; Er, E.E.; Blenis, J. The Ras-ERK and PI3K-mTOR pathways: Cross-talk and compensation. Trends Biochem. Sci. 2011, 36, 320–328. [Google Scholar] [CrossRef]
- Cuesta, C.; Arévalo-Alameda, C.; Castellano, E. The importance of being PI3K in the RAS signaling network. Genes 2021, 12, 1094. [Google Scholar] [CrossRef] [PubMed]
- Shorning, B.Y.; Dass, M.S.; Smalley, M.J.; Pearson, H.B. The PI3K-AKT-mTOR pathway and prostate cancer: At the crossroads of AR, MAPK, and WNT signaling. Int. J. Mol. Sci. 2020, 21, 4507. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Li, S.; Chepeha, D.B.; Giordano, T.J.; Li, J.; Zhang, H.; Polverini, P.J.; Nor, J.; Kitajewski, J.; Wang, C.Y. Crosstalk between tumor and endothelial cells promotes tumor angiogenesis by MAPK activation of Notch signaling. Cancer Cell 2005, 8, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Hlavacek, W.S.; Faeder, J.R.; Blinov, M.L.; Perelson, A.S.; Goldstein, B. The complexity of complexes in signal transduction. Biotechnol. Bioeng. 2003, 84, 783–794. [Google Scholar] [CrossRef]
- Gilbert, D.; Fuss, H.; Gu, X.; Orton, R.; Robinson, S.; Vyshemirsky, V.; Kurth, M.J.; Downes, C.S.; Dubitzky, W. Computational methodologies for modelling, analysis and simulation of signalling networks. Briefings Bioinform. 2006, 7, 339–353. [Google Scholar] [CrossRef]
- Le Novere, N. Quantitative and logic modelling of molecular and gene networks. Nat. Rev. Genet. 2015, 16, 146–158. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Tian, T. Bayesian inference of stochastic dynamic models using early-rejection methods based on sequential stochastic simulations. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 19, 1484–1494. [Google Scholar] [CrossRef]
- Wang, S.; Wu, R.; Lu, J.; Jiang, Y.; Huang, T.; Cai, Y.D. Protein-protein interaction networks as miners of biological discovery. Proteomics 2022, 22, 2100190. [Google Scholar] [CrossRef] [PubMed]
- Casadio, R.; Martelli, P.L.; Savojardo, C. Machine learning solutions for predicting protein–protein interactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1618. [Google Scholar] [CrossRef]
- Robin, V.; Bodein, A.; Scott-Boyer, M.P.; Leclercq, M.; Périn, O.; Droit, A. Overview of methods for characterization and visualization of a protein–protein interaction network in a multi-omics integration context. Front. Mol. Biosci. 2022, 9, 962799. [Google Scholar] [CrossRef]
- Kolch, W.; Halasz, M.; Granovskaya, M.; Kholodenko, B.N. The dynamic control of signal transduction networks in cancer cells. Nat. Rev. Cancer 2015, 15, 515–527. [Google Scholar] [CrossRef] [PubMed]
- Sommariva, S.; Berra, S.; Biddau, G.; Caviglia, G.; Benvenuto, F.; Piana, M. In-silico modelling of the mitogen-activated protein kinase (MAPK) pathway in colorectal cancer: Mutations and targeted therapy. Front. Syst. Biol. 2023, 3, 1207898. [Google Scholar] [CrossRef]
- Aldridge, B.B.; Burke, J.M.; Lauffenburger, D.A.; Sorger, P.K. Physicochemical modelling of cell signalling pathways. Nat. Cell Biol. 2006, 8, 1195–1203. [Google Scholar] [CrossRef] [PubMed]
- Ying, T.; Alexander, H. Quantifying information of intracellular signaling: Progress with machine learning. Rep. Prog. Physics. Phys. Soc. (Great Britain) 2022, 85, 086602. [Google Scholar]
- Azeloglu, E.U.; Iyengar, R. Signaling networks: Information flow, computation, and decision making. Cold Spring Harb. Perspect. Biol. 2015, 7, a005934. [Google Scholar] [CrossRef]
- Choudhary, C.; Mann, M. Decoding signalling networks by mass spectrometry-based proteomics. Nat. Rev. Mol. Cell Biol. 2010, 11, 427–439. [Google Scholar] [CrossRef]
- Lun, X.K.; Bodenmiller, B. Profiling cell signaling networks at single-cell resolution. Mol. Cell. Proteom. 2020, 19, 744–756. [Google Scholar] [CrossRef]
- Rosenberger, F.A.; Thielert, M.; Mann, M. Making single-cell proteomics biologically relevant. Nat. Methods 2023, 20, 320–323. [Google Scholar] [CrossRef]
- Lähnemann, D.; Köster, J.; Szczurek, E.; McCarthy, D.J.; Hicks, S.C.; Robinson, M.D.; Vallejos, C.A.; Campbell, K.R.; Beerenwinkel, N.; Mahfouz, A.; et al. Eleven grand challenges in single-cell data science. Genome Biol. 2020, 21, 31. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, W.; Jin, H.; Chen, X. A review of single-cell rna-seq annotation, integration, and cell–cell communication. Cells 2023, 12, 1970. [Google Scholar] [CrossRef]
- Madsen, R.R.; Toker, A. PI3K signaling through a biochemical systems lens. J. Biol. Chem. 2023, 299, 105224. [Google Scholar] [CrossRef] [PubMed]
- Leduc, A.; Harens, H.; Slavov, N. Modeling and interpretation of single-cell proteogenomic data. arXiv 2023, arXiv:2308.07465v2. [Google Scholar]
- Pillai, M.; Hojel, E.; Jolly, M.K.; Goyal, Y. Unraveling non-genetic heterogeneity in cancer with dynamical models and computational tools. Nat. Comput. Sci. 2023, 3, 301–313. [Google Scholar] [CrossRef] [PubMed]
- AlMusawi, S.; Ahmed, M.; Nateri, A.S. Understanding cell-cell communication and signaling in the colorectal cancer microenvironment. Clin. Transl. Med. 2021, 11, e308. [Google Scholar] [CrossRef]
- Bijman, E.Y.; Kaltenbach, H.M.; Stelling, J. Experimental analysis and modeling of single-cell time-course data. Curr. Opin. Syst. Biol. 2021, 28, 100359. [Google Scholar] [CrossRef]
- Zhao, M.; He, W.; Tang, J.; Zou, Q.; Guo, F. A comprehensive overview and critical evaluation of gene regulatory network inference technologies. Briefings Bioinform. 2021, 22, bbab009. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, T.; Tian, T. Integrated Pipelines for Inferring Gene Regulatory Networks from Single-Cell Data. Curr. Bioinform. 2022, 17, 559–564. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef]
- Raj, A.; Van Oudenaarden, A. Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell 2008, 135, 216–226. [Google Scholar] [CrossRef]
- Tian, T.; Burrage, K. Stochastic models for regulatory networks of the genetic toggle switch. Proc. Natl. Acad. Sci. USA 2006, 103, 8372–8377. [Google Scholar] [CrossRef]
- Lei, X.; Tian, W.; Zhu, H.; Chen, T.; Ao, P. Biological sources of intrinsic and extrinsic noise in cI expression of lysogenic phage lambda. Sci. Rep. 2015, 5, 13597. [Google Scholar] [CrossRef] [PubMed]
- Ladbury, J.E.; Arold, S.T. Noise in cellular signaling pathways: Causes and effects. Trends Biochem. Sci. 2012, 37, 173–178. [Google Scholar] [CrossRef]
- Albeck, J.G.; Mills, G.B.; Brugge, J.S. Frequency-modulated pulses of ERK activity transmit quantitative proliferation signals. Mol. Cell 2013, 49, 249–261. [Google Scholar] [CrossRef] [PubMed]
- Kunz, M.; Vera, J. Modelling of protein kinase signaling pathways in melanoma and other cancers. Cancers 2019, 11, 465. [Google Scholar] [CrossRef] [PubMed]
- Myers, P.J.; Lee, S.H.; Lazzara, M.J. Mechanistic and data-driven models of cell signaling: Tools for fundamental discovery and rational design of therapy. Curr. Opin. Syst. Biol. 2021, 28, 100349. [Google Scholar] [CrossRef]
- Valls, P.O.; Esposito, A. Signalling dynamics, cell decisions, and homeostatic control in health and disease. Curr. Opin. Cell Biol. 2022, 75, 102066. [Google Scholar] [CrossRef]
- Loos, C.; Hasenauer, J. Mathematical modeling of variability in intracellular signaling. Curr. Opin. Syst. Biol. 2019, 16, 17–24. [Google Scholar] [CrossRef]
- Huang, C.Y.; Ferrell, J.E., Jr. Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc. Natl. Acad. Sci. USA 1996, 93, 10078–10083. [Google Scholar] [CrossRef]
- Kholodenko, B.N. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. Eur. J. Biochem. 2000, 267, 1583–1588. [Google Scholar] [CrossRef]
- Markevich, N.I.; Hoek, J.B.; Kholodenko, B.N. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 2004, 164, 353–359. [Google Scholar] [CrossRef]
- Ferrell, J.E.; Ha, S.H. Ultrasensitivity part III: Cascades, bistable switches, and oscillators. Trends Biochem. Sci. 2014, 39, 612–618. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Pryciak, P.M. Membrane localization of scaffold proteins promotes graded signaling in the yeast MAP kinase cascade. Curr. Biol. 2008, 18, 1184–1191. [Google Scholar] [CrossRef] [PubMed]
- Dyjack, N.; Azeredo-Tseng, C.; Yildirim, N. Mathematical modeling reveals differential regulation of MAPK activity by phosphatase proteins in the yeast pheromone response pathway. Mol. BioSyst. 2017, 13, 1323–1335. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, A.; Bruck, J.; Sternberg, P.W. Scaffold proteins may biphasically affect the levels of mitogen-activated protein kinase signaling and reduce its threshold properties. Proc. Natl. Acad. Sci. USA 2000, 97, 5818–5823. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, R.; Neel, B.G.; Rapoport, T.A. Mathematical models of protein kinase signal transduction. Mol. Cell 2002, 9, 957–970. [Google Scholar] [CrossRef]
- Tian, T.; Harding, A. How MAP kinase modules function as robust, yet adaptable, circuits. Cell Cycle 2014, 13, 2379–2390. [Google Scholar] [CrossRef]
- Sturm, O.E.; Orton, R.; Grindlay, J.; Birtwistle, M.; Vyshemirsky, V.; Gilbert, D.; Calder, M.; Pitt, A.; Kholodenko, B.; Kolch, W. The mammalian MAPK/ERK pathway exhibits properties of a negative feedback amplifier. Sci. Signal. 2010, 3, ra90. [Google Scholar] [CrossRef]
- Aoki, K.; Yamada, M.; Kunida, K.; Yasuda, S.; Matsuda, M. Processive phosphorylation of ERK MAP kinase in mammalian cells. Proc. Natl. Acad. Sci. USA 2011, 108, 12675–12680. [Google Scholar] [CrossRef]
- Qiao, L.; Nachbar, R.B.; Kevrekidis, I.G.; Shvartsman, S.Y. Bistability and oscillations in the Huang-Ferrell model of MAPK signaling. PLoS Comput. Biol. 2007, 3, e184. [Google Scholar] [CrossRef]
- Yeung, E.; McFann, S.; Marsh, L.; Dufresne, E.; Filippi, S.; Harrington, H.A.; Shvartsman, S.Y.; Wühr, M. Inference of multisite phosphorylation rate constants and their modulation by pathogenic mutations. Curr. Biol. 2020, 30, 877–882. [Google Scholar] [CrossRef]
- Qi, M.; Elion, E.A. MAP kinase pathways. J. Cell Sci. 2005, 118, 3569–3572. [Google Scholar] [CrossRef] [PubMed]
- Haugh, J.M. A unified model for signal transduction reactions in cellular membranes. Biophys. J. 2002, 82, 591–604. [Google Scholar] [CrossRef] [PubMed]
- Harding, A.; Tian, T.; Westbury, E.; Frische, E.; Hancock, J.F. Subcellular localization determines MAP kinase signal output. Curr. Biol. 2005, 15, 869–873. [Google Scholar] [CrossRef] [PubMed]
- Tian, T.; Harding, A.; Inder, K.; Plowman, S.; Parton, R.G.; Hancock, J.F. Plasma membrane nanoswitches generate high-fidelity Ras signal transduction. Nat. Cell Biol. 2007, 9, 905–914. [Google Scholar] [CrossRef]
- Tian, T.; Plowman, S.J.; Parton, R.G.; Kloog, Y.; Hancock, J.F. Mathematical modeling of K-Ras nanocluster formation on the plasma membrane. Biophys. J. 2010, 99, 534–543. [Google Scholar] [CrossRef]
- Yue, T.; Zhang, X. Signal transduction across cellular membranes can be mediated by coupling of the clustering of anchored proteins in both leaflets. Phys. Rev. E 2012, 85, 011917. [Google Scholar] [CrossRef]
- Kozer, N.; Barua, D.; Orchard, S.; Nice, E.C.; Burgess, A.W.; Hlavacek, W.S.; Clayton, A.H. Exploring higher-order EGFR oligomerisation and phosphorylation—a combined experimental and theoretical approach. Mol. BioSyst. 2013, 9, 1849–1863. [Google Scholar] [CrossRef]
- Ryu, H.; Chung, M.; Dobrzyński, M.; Fey, D.; Blum, Y.; Lee, S.S.; Peter, M.; Kholodenko, B.N.; Jeon, N.L.; Pertz, O. Frequency modulation of ERK activation dynamics rewires cell fate. Mol. Syst. Biol. 2015, 11, 838. [Google Scholar] [CrossRef]
- Shankaran, H.; Ippolito, D.L.; Chrisler, W.B.; Resat, H.; Bollinger, N.; Opresko, L.K.; Wiley, H.S. Rapid and sustained nuclear–cytoplasmic ERK oscillations induced by epidermal growth factor. Mol. Syst. Biol. 2009, 5, 332. [Google Scholar] [CrossRef]
- Regot, S.; Hughey, J.J.; Bajar, B.T.; Carrasco, S.; Covert, M.W. High-sensitivity measurements of multiple kinase activities in live single cells. Cell 2014, 157, 1724–1734. [Google Scholar] [CrossRef]
- Hadač, O.; Muzika, F.; Nevoral, V.; Přibyl, M.; Schreiber, I. Minimal oscillating subnetwork in the Huang-Ferrell model of the MAPK cascade. PLoS ONE 2017, 12, e0178457. [Google Scholar] [CrossRef] [PubMed]
- Fujioka, A.; Terai, K.; Itoh, R.E.; Aoki, K.; Nakamura, T.; Kuroda, S.; Nishida, E.; Matsuda, M. Dynamics of the Ras/ERK MAPK cascade as monitored by fluorescent probes. J. Biol. Chem. 2006, 281, 8917–8926. [Google Scholar] [CrossRef] [PubMed]
- Shindo, Y.; Iwamoto, K.; Mouri, K.; Hibino, K.; Tomita, M.; Kosako, H.; Sako, Y.; Takahashi, K. Conversion of graded phosphorylation into switch-like nuclear translocation via autoregulatory mechanisms in ERK signalling. Nat. Commun. 2016, 7, 10485. [Google Scholar] [CrossRef]
- Gerosa, L.; Chidley, C.; Fröhlich, F.; Sanchez, G.; Lim, S.K.; Muhlich, J.; Chen, J.Y.; Vallabhaneni, S.; Baker, G.J.; Schapiro, D.; et al. Receptor-driven ERK pulses reconfigure MAPK signaling and enable persistence of drug-adapted BRAF-mutant melanoma cells. Cell Syst. 2020, 11, 478–494. [Google Scholar] [CrossRef] [PubMed]
- Jorissen, R.N.; Walker, F.; Pouliot, N.; Garrett, T.P.; Ward, C.W.; Burgess, A.W. Epidermal growth factor receptor: Mechanisms of activation and signalling. EGF Recept. Fam. 2003, 33–55. [Google Scholar] [CrossRef] [PubMed]
- Kiyatkin, A.; van Alderwerelt van Rosenburgh, I.K.; Klein, D.E.; Lemmon, M.A. Kinetics of receptor tyrosine kinase activation define ERK signaling dynamics. Sci. Signal. 2020, 13, eaaz5267. [Google Scholar] [CrossRef]
- Avraham, R.; Yarden, Y. Feedback regulation of EGFR signalling: Decision making by early and delayed loops. Nat. Rev. Mol. Cell Biol. 2011, 12, 104–117. [Google Scholar] [CrossRef]
- Bhalla, U.S.; Iyengar, R. Emergent properties of networks of biological signaling pathways. Science 1999, 283, 381–387. [Google Scholar] [CrossRef]
- Bhalla, U.S.; Ram, P.T.; Iyengar, R. MAP kinase phosphatase as a locus of flexibility in a mitogen-activated protein kinase signaling network. Science 2002, 297, 1018–1023. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Demin, O.V.; Moehren, G.; Hoek, J.B. Quantification of short term signaling by the epidermal growth factor receptor. J. Biol. Chem. 1999, 274, 30169–30181. [Google Scholar] [CrossRef]
- Schoeberl, B.; Eichler-Jonsson, C.; Gilles, E.D.; Müller, G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat. Biotechnol. 2002, 20, 370–375. [Google Scholar] [CrossRef] [PubMed]
- Freed, D.M.; Bessman, N.J.; Kiyatkin, A.; Salazar-Cavazos, E.; Byrne, P.O.; Moore, J.O.; Valley, C.C.; Ferguson, K.M.; Leahy, D.J.; Lidke, D.S.; et al. EGFR ligands differentially stabilize receptor dimers to specify signaling kinetics. Cell 2017, 171, 683–695. [Google Scholar] [CrossRef] [PubMed]
- Blum, Y.; Mikelson, J.; Dobrzyński, M.; Ryu, H.; Jacques, M.A.; Jeon, N.L.; Khammash, M.; Pertz, O. Temporal perturbation of ERK dynamics reveals network architecture of FGF2/MAPK signaling. Mol. Syst. Biol. 2019, 15, e8947. [Google Scholar] [CrossRef] [PubMed]
- Oyarzún, D.A.; Bramhall, J.L.; López-Caamal, F.; Richards, F.M.; Jodrell, D.I.; Krippendorff, B.F. The EGFR demonstrates linear signal transmission. Integr. Biol. 2014, 6, 736–742. [Google Scholar] [CrossRef] [PubMed]
- Bardwell, L.; Zou, X.; Nie, Q.; Komarova, N.L. Mathematical models of specificity in cell signaling. Biophys. J. 2007, 92, 3425–3441. [Google Scholar] [CrossRef]
- Zou, X.; Peng, T.; Pan, Z. Modeling specificity in the yeast MAPK signaling networks. J. Theor. Biol. 2008, 250, 139–155. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Niepel, M.; McDermott, J.E.; Gao, Y.; Nicora, C.D.; Chrisler, W.B.; Markillie, L.M.; Petyuk, V.A.; Smith, R.D.; Rodland, K.D.; et al. Conservation of protein abundance patterns reveals the regulatory architecture of the EGFR-MAPK pathway. Sci. Signal. 2016, 9, rs6. [Google Scholar] [CrossRef]
- Yi, L.; Shi, T.; Gritsenko, M.A.; X’avia Chan, C.Y.; Fillmore, T.L.; Hess, B.M.; Swensen, A.C.; Liu, T.; Smith, R.D.; Wiley, H.S.; et al. Targeted quantification of phosphorylation dynamics in the context of EGFR-MAPK pathway. Anal. Chem. 2018, 90, 5256–5263. [Google Scholar] [CrossRef]
- Schlessinger, J. Ligand-induced, receptor-mediated dimerization and activation of EGF receptor. Cell 2002, 110, 669–672. [Google Scholar] [CrossRef]
- Klein, P.; Mattoon, D.; Lemmon, M.A.; Schlessinger, J. A structure-based model for ligand binding and dimerization of EGF receptors. Proc. Natl. Acad. Sci. USA 2004, 101, 929–934. [Google Scholar] [CrossRef]
- Hajdu, T.; Váradi, T.; Rebenku, I.; Kovács, T.; Szöllösi, J.; Nagy, P. Comprehensive model for epidermal growth factor receptor ligand binding involving conformational states of the extracellular and the kinase domains. Front. Cell Dev. Biol. 2020, 8, 776. [Google Scholar] [CrossRef] [PubMed]
- Mac Gabhann, F.; Popel, A.S. Dimerization of VEGF receptors and implications for signal transduction: A computational study. Biophys. Chem. 2007, 128, 125–139. [Google Scholar] [CrossRef]
- Mayawala, K.; Vlachos, D.G.; Edwards, J.S. Computational modeling reveals molecular details of epidermal growth factor binding. BMC Cell Biol. 2005, 6, 41. [Google Scholar] [CrossRef] [PubMed]
- Claas, A.M.; Atta, L.; Gordonov, S.; Meyer, A.S.; Lauffenburger, D.A. Systems modeling identifies divergent receptor tyrosine kinase reprogramming to MAPK pathway inhibition. Cell. Mol. Bioeng. 2018, 11, 451–469. [Google Scholar] [CrossRef] [PubMed]
- Resat, H.; Ewald, J.A.; Dixon, D.A.; Wiley, H.S. An integrated model of epidermal growth factor receptor trafficking and signal transduction. Biophys. J. 2003, 85, 730–743. [Google Scholar] [CrossRef] [PubMed]
- Monast, C.S.; Furcht, C.M.; Lazzara, M.J. Computational analysis of the regulation of EGFR by protein tyrosine phosphatases. Biophys. J. 2012, 102. [Google Scholar] [CrossRef]
- Hendriks, B.S.; Orr, G.; Wells, A.; Wiley, H.S.; Lauffenburger, D.A. Parsing ERK activation reveals quantitatively equivalent contributions from epidermal growth factor receptor and HER2 in human mammary epithelial cells. J. Biol. Chem. 2005, 280, 6157–6169. [Google Scholar] [CrossRef]
- Barua, D.; Faeder, J.R.; Haugh, J.M. Structure-based kinetic models of modular signaling protein function: Focus on Shp2. Biophys. J. 2007, 92, 2290–2300. [Google Scholar] [CrossRef]
- Li, H.; Ung, C.Y.; Ma, X.H.; Li, B.W.; Low, B.C.; Cao, Z.W.; Chen, Y.Z. Simulation of crosstalk between small GTPase RhoA and EGFR-ERK signaling pathway via MEKK1. Bioinformatics 2009, 25, 358–364. [Google Scholar] [CrossRef]
- Gagliardi, P.A.; Pertz, O. The mitogen-activated protein kinase network, wired to dynamically function at multiple scales. Curr. Opin. Cell Biol. 2024, 88, 102368. [Google Scholar] [CrossRef]
- Kamioka, Y.; Yasuda, S.; Fujita, Y.; Aoki, K.; Matsuda, M. Multiple decisive phosphorylation sites for the negative feedback regulation of SOS1 via ERK. J. Biol. Chem. 2010, 285, 33540–33548. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.Y.; Cardelli, L.; Phillips, A.; Piterman, N.; Fisher, J. Computational modeling of the EGFR network elucidates control mechanisms regulating signal dynamics. BMC Syst. Biol. 2009, 3, 118. [Google Scholar] [CrossRef] [PubMed]
- Ogura, Y.; Wen, F.L.; Sami, M.M.; Shibata, T.; Hayashi, S. A switch-like activation relay of EGFR-ERK signaling regulates a wave of cellular contractility for epithelial invagination. Dev. Cell 2018, 46, 162–172. [Google Scholar] [CrossRef] [PubMed]
- De Simone, A.; Evanitsky, M.N.; Hayden, L.; Cox, B.D.; Wang, J.; Tornini, V.A.; Ou, J.; Chao, A.; Poss, K.D.; Di Talia, S. Control of osteoblast regeneration by a train of Erk activity waves. Nature 2021, 590, 129–133. [Google Scholar] [CrossRef]
- Arkun, Y.; Yasemi, M. Dynamics and control of the ERK signaling pathway: Sensitivity, bistability, and oscillations. PLoS ONE 2018, 13, e0195513. [Google Scholar] [CrossRef]
- Fritsche-Guenther, R.; Witzel, F.; Sieber, A.; Herr, R.; Schmidt, N.; Braun, S.; Brummer, T.; Sers, C.; Blüthgen, N. Strong negative feedback from Erk to Raf confers robustness to MAPK signalling. Mol. Syst. Biol. 2011, 7, 489. [Google Scholar] [CrossRef]
- Manning, B.D.; Toker, A. AKT/PKB signaling: Navigating the network. Cell 2017, 169, 381–405. [Google Scholar] [CrossRef]
- Aksamitiene, E.; Kiyatkin, A.; Kholodenko, B.N. Cross-talk between mitogenic Ras/MAPK and survival PI3K/Akt pathways: A fine balance. Biochem. Soc. Trans. 2012, 40, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Sulaimanov, N.; Klose, M.; Busch, H.; Boerries, M. Understanding the mTOR signaling pathway via mathematical modeling. Wiley Interdiscip. Rev. Syst. Biol. Med. 2017, 9, e1379. [Google Scholar] [CrossRef]
- Glaviano, A.; Foo, A.S.; Lam, H.Y.; Yap, K.C.; Jacot, W.; Jones, R.H.; Eng, H.; Nair, M.G.; Makvandi, P.; Geoerger, B.; et al. PI3K/AKT/mTOR signaling transduction pathway and targeted therapies in cancer. Mol. Cancer 2023, 22, 138. [Google Scholar] [CrossRef]
- Hatakeyama, M.; Kimura, S.; Naka, T.; Kawasaki, T.; Yumoto, N.; Ichikawa, M.; Kim, J.H.; Saito, K.; Saeki, M.; Shirouzu, M.; et al. A computational model on the modulation of mitogen-activated protein kinase (MAPK) and Akt pathways in heregulin-induced ErbB signalling. Biochem. J. 2003, 373, 451–463. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Yuan, J.M. Time-dependent sensitivity analysis of biological networks: Coupled MAPK and PI3K signal transduction pathways. J. Phys. Chem. A 2006, 110, 5361–5370. [Google Scholar] [CrossRef] [PubMed]
- Lebedeva, G.; Sorokin, A.; Faratian, D.; Mullen, P.; Goltsov, A.; Langdon, S.P.; Harrison, D.J.; Goryanin, I. Model-based global sensitivity analysis as applied to identification of anti-cancer drug targets and biomarkers of drug resistance in the ErbB2/3 network. Eur. J. Pharm. Sci. 2012, 46, 244–258. [Google Scholar] [CrossRef] [PubMed]
- Koh, G.; Teong, H.F.C.; Clement, M.V.; Hsu, D.; Thiagarajan, P. A decompositional approach to parameter estimation in pathway modeling: A case study of the Akt and MAPK pathways and their crosstalk. Bioinformatics 2006, 22, e271–e280. [Google Scholar] [CrossRef]
- Babu, C.; Babar, S.M.E.; Song, E.J.; Oh, E.; Yoo, Y.S. Kinetic analysis of the MAPK and PI3K/Akt signaling pathways. Mol. Cells (Springer Sci. Bus. Media BV) 2008, 25, 397–406. [Google Scholar]
- Kiyatkin, A.; Aksamitiene, E.; Markevich, N.I.; Borisov, N.M.; Hoek, J.B.; Kholodenko, B.N. Scaffolding protein Grb2-associated binder 1 sustains epidermal growth factor-induced mitogenic and survival signaling by multiple positive feedback loops. J. Biol. Chem. 2006, 281, 19925–19938. [Google Scholar] [CrossRef]
- Chen, W.W.; Schoeberl, B.; Jasper, P.J.; Niepel, M.; Nielsen, U.B.; Lauffenburger, D.A.; Sorger, P.K. Input–output behavior of ErbB signaling pathways as revealed by a mass action model trained against dynamic data. Mol. Syst. Biol. 2009, 5, 239. [Google Scholar] [CrossRef]
- Arkun, Y. Dynamic modeling and analysis of the cross-talk between insulin/AKT and MAPK/ERK signaling pathways. PLoS ONE 2016, 11, e0149684. [Google Scholar] [CrossRef]
- Hu, H.; Goltsov, A.; Bown, J.L.; Sims, A.H.; Langdon, S.P.; Harrison, D.J.; Faratian, D. Feedforward and feedback regulation of the MAPK and PI3K oscillatory circuit in breast cancer. Cell. Signal. 2013, 25, 26–32. [Google Scholar] [CrossRef]
- Tasaki, S.; Nagasaki, M.; Kozuka-Hata, H.; Semba, K.; Gotoh, N.; Hattori, S.; Inoue, J.i.; Yamamoto, T.; Miyano, S.; Sugano, S.; et al. Phosphoproteomics-based modeling defines the regulatory mechanism underlying aberrant EGFR signaling. PLoS ONE 2010, 5, e13926. [Google Scholar] [CrossRef]
- Birtwistle, M.R.; Hatakeyama, M.; Yumoto, N.; Ogunnaike, B.A.; Hoek, J.B.; Kholodenko, B.N. Ligand-dependent responses of the ErbB signaling network: Experimental and modeling analyses. Mol. Syst. Biol. 2007, 3, 144. [Google Scholar] [CrossRef] [PubMed]
- Borisov, N.; Aksamitiene, E.; Kiyatkin, A.; Legewie, S.; Berkhout, J.; Maiwald, T.; Kaimachnikov, N.P.; Timmer, J.; Hoek, J.B.; Kholodenko, B.N. Systems-level interactions between insulin–EGF networks amplify mitogenic signaling. Mol. Syst. Biol. 2009, 5, 256. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.C.; Cirit, M.; Haugh, J.M. PI3K-dependent cross-talk interactions converge with Ras as quantifiable inputs integrated by Erk. Mol. Syst. Biol. 2009, 5, 246. [Google Scholar] [CrossRef]
- Padala, R.R.; Karnawat, R.; Viswanathan, S.B.; Thakkar, A.V.; Das, A.B. Cancerous perturbations within the ERK, PI3K/Akt, and Wnt/β-catenin signaling network constitutively activate inter-pathway positive feedback loops. Mol. BioSyst. 2017, 13, 830–840. [Google Scholar] [CrossRef] [PubMed]
- Samaga, R.; Saez-Rodriguez, J.; Alexopoulos, L.G.; Sorger, P.K.; Klamt, S. The logic of EGFR/ErbB signaling: Theoretical properties and analysis of high-throughput data. PLoS Comput. Biol. 2009, 5, e1000438. [Google Scholar] [CrossRef]
- Han, J.; Lin, K.; Zhang, X.; Yan, L.; Liu, J.; Liu, J. PTEN-mediated AKT/β-catenin signaling enhances the proliferation and expansion of Lgr5+ hepatocytes. Int. J. Biol. Sci. 2021, 17, 861. [Google Scholar] [CrossRef]
- He, J.; Han, J.; Lin, K.; Wang, J.; Li, G.; Li, X.; Gao, Y. PTEN/AKT and Wnt/β-catenin signaling pathways regulate the proliferation of Lgr5+ cells in liver cancer. Biochem. Biophys. Res. Commun. 2023, 683, 149117. [Google Scholar] [CrossRef]
- Han, J.; Lin, K.; Choo, H.; Chen, Y.; Zhang, X.; Xu, R.H.; Wang, X.; Wu, Y. Distinct bulge stem cell populations maintain the pilosebaceous unit in a β-catenin-dependent manner. IScience 2023, 26, 105805. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Tian, R.; Zhang, Y.; Drutskaya, M.S.; Wang, C.; Ge, J.; Fan, Z.; Kong, D.; Wang, X.; et al. Macrophages induce AKT/β-catenin-dependent Lgr5+ stem cell activation and hair follicle regeneration through TNF. Nat. Commun. 2017, 8, 14091. [Google Scholar] [CrossRef]
- Olsen, J.V.; Blagoev, B.; Gnad, F.; Macek, B.; Kumar, C.; Mortensen, P.; Mann, M. Global, in vivo, and site-specific phosphorylation dynamics in signaling networks. Cell 2006, 127, 635–648. [Google Scholar] [CrossRef]
- Tian, T.; Song, J. Mathematical Modelling of the MAP Kinase Pathway Using Proteomic Datasets. PLoS ONE 2012, 7, e42230. [Google Scholar] [CrossRef] [PubMed]
- Kulak, N.A.; Pichler, G.; Paron, I.; Nagaraj, N.; Mann, M. Minimal, encapsulated proteomic-sample processing applied to copy-number estimation in eukaryotic cells. Nat. Methods 2014, 11, 319–324. [Google Scholar] [CrossRef] [PubMed]
- Geiger, T.; Wehner, A.; Schaab, C.; Cox, J.; Mann, M. Comparative proteomic analysis of eleven common cell lines reveals ubiquitous but varying expression of most proteins. Mol. Cell. Proteom. 2012, 11, M111.014050. [Google Scholar] [CrossRef] [PubMed]
- Stites, E.C.; Aziz, M.; Creamer, M.S.; Von Hoff, D.D.; Posner, R.G.; Hlavacek, W.S. Use of mechanistic models to integrate and analyze multiple proteomic datasets. Biophys. J. 2015, 108, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, F.; Gerosa, L.; Muhlich, J.; Sorger, P.K. Mechanistic model of MAPK signaling reveals how allostery and rewiring contribute to drug resistance. Mol. Syst. Biol. 2023, 19, e10988. [Google Scholar] [CrossRef] [PubMed]
- Bessette, D.C.; Tilch, E.; Seidens, T.; Quinn, M.C.; Wiegmans, A.P.; Shi, W.; Cocciardi, S.; McCart-Reed, A.; Saunus, J.M.; Simpson, P.T.; et al. Using the MCF10A/MCF10CA1a breast cancer progression cell line model to investigate the effect of active, mutant forms of EGFR in breast cancer development and treatment using gefitinib. PLoS ONE 2015, 10, e0125232. [Google Scholar] [CrossRef]
- Bouhaddou, M.; Barrette, A.M.; Stern, A.D.; Koch, R.J.; DiStefano, M.S.; Riesel, E.A.; Santos, L.C.; Tan, A.L.; Mertz, A.E.; Birtwistle, M.R. A mechanistic pan-cancer pathway model informed by multi-omics data interprets stochastic cell fate responses to drugs and mitogens. PLoS Comput. Biol. 2018, 14, e1005985. [Google Scholar] [CrossRef]
- Erdem, C.; Mutsuddy, A.; Bensman, E.M.; Dodd, W.B.; Saint-Antoine, M.M.; Bouhaddou, M.; Blake, R.C.; Gross, S.M.; Heiser, L.M.; Feltus, F.A.; et al. A scalable, open-source implementation of a large-scale mechanistic model for single cell proliferation and death signaling. Nat. Commun. 2022, 13, 3555. [Google Scholar] [CrossRef]
- Zhao, C.; Medeiros, T.X.; Sové, R.J.; Annex, B.H.; Popel, A.S. A data-driven computational model enables integrative and mechanistic characterization of dynamic macrophage polarization. Iscience 2021, 24, 102112. [Google Scholar] [CrossRef]
- Lee, D.; Jayaraman, A.; Kwon, J.S. Development of a hybrid model for a partially known intracellular signaling pathway through correction term estimation and neural network modeling. PLoS Comput. Biol. 2020, 16, e1008472. [Google Scholar] [CrossRef]
- Liu, F.; Heiner, M.; Gilbert, D. Hybrid modelling of biological systems: Current progress and future prospects. Briefings Bioinform. 2022, 23, bbac081. [Google Scholar] [CrossRef] [PubMed]
- Cruz, D.A.; Kemp, M.L. Hybrid computational modeling methods for systems biology. Prog. Biomed. Eng. 2021, 4, 012002. [Google Scholar] [CrossRef]
- Walpole, J.; Papin, J.A.; Peirce, S.M. Multiscale computational models of complex biological systems. Annu. Rev. Biomed. Eng. 2013, 15, 137–154. [Google Scholar] [CrossRef] [PubMed]
- Schweidtmann, A.M.; Zhang, D.; von Stosch, M. A review and perspective on hybrid modelling methodologies. Digit. Chem. Eng. 2023, 10, 100136. [Google Scholar] [CrossRef]
- Mahanty, B. Hybrid modeling in bioprocess dynamics: Structural variabilities, implementation strategies, and practical challenges. Biotechnol. Bioeng. 2023, 120, 2072–2091. [Google Scholar] [CrossRef]
- Erdem, C.; Birtwistle, M.R. MEMMAL: A tool for expanding large-scale mechanistic models with machine learned associations and big datasets. Front. Syst. Biol. 2023, 3, 1099413. [Google Scholar] [CrossRef]
- Myers, P.; Lee, S.H.; Lazzara, M. An integrated mechanistic and data-driven computational model predicts cell responses to high-and low-affinity EGFR ligands. bioRxiv 2023, 2023-06. [Google Scholar] [CrossRef]
- Ruths, D.; Muller, M.; Tseng, J.T.; Nakhleh, L.; Ram, P.T. The signaling petri net-based simulator: A non-parametric strategy for characterizing the dynamics of cell-specific signaling networks. PLoS Comput. Biol. 2008, 4, e1000005. [Google Scholar] [CrossRef]
- Albert, R.; Wang, R.S. Discrete dynamic modeling of cellular signaling networks. Methods Enzymol. 2009, 467, 281–306. [Google Scholar]
- Henriques, D.; Villaverde, A.F.; Rocha, M.; Saez-Rodriguez, J.; Banga, J.R. Data-driven reverse engineering of signaling pathways using ensembles of dynamic models. PLoS Comput. Biol. 2017, 13, e1005379. [Google Scholar] [CrossRef]
- Grieco, L.; Calzone, L.; Bernard-Pierrot, I.; Radvanyi, F.; Kahn-Perles, B.; Thieffry, D. Integrative modelling of the influence of MAPK network on cancer cell fate decision. PLoS Comput. Biol. 2013, 9, e1003286. [Google Scholar] [CrossRef]
- Aldridge, B.B.; Saez-Rodriguez, J.; Muhlich, J.L.; Sorger, P.K.; Lauffenburger, D.A. Fuzzy logic analysis of kinase pathway crosstalk in TNF/EGF/insulin-induced signaling. PLoS Comput. Biol. 2009, 5, e1000340. [Google Scholar] [CrossRef] [PubMed]
- Bernardo-Faura, M.; Massen, S.; Falk, C.S.; Brady, N.R.; Eils, R. Data-derived modeling characterizes plasticity of MAPK signaling in melanoma. PLoS Comput. Biol. 2014, 10, e1003795. [Google Scholar] [CrossRef] [PubMed]
- Supper, J.; Spangenberg, L.; Planatscher, H.; Dräger, A.; Schröder, A.; Zell, A. BowTieBuilder: Modeling signal transduction pathways. BMC Syst. Biol. 2009, 3, 67. [Google Scholar] [CrossRef]
- Waltermann, C.; Klipp, E. Information theory based approaches to cellular signaling. Biochim. Biophys. Acta (BBA)-Gen. Subj. 2011, 1810, 924–932. [Google Scholar] [CrossRef]
- Krantz, M.; Ahmadpour, D.; Ottosson, L.G.; Warringer, J.; Waltermann, C.; Nordlander, B.; Klipp, E.; Blomberg, A.; Hohmann, S.; Kitano, H. Robustness and fragility in the yeast high osmolarity glycerol (HOG) signal-transduction pathway. Mol. Syst. Biol. 2009, 5, 281. [Google Scholar] [CrossRef] [PubMed]
- Blüthgen, N.; Legewie, S. Robustness of signal transduction pathways. Cell. Mol. Life Sci. 2013, 70, 2259–2269. [Google Scholar] [CrossRef]
- Kardynska, M.; Smieja, J.; Paszek, P.; Puszynski, K. Application of sensitivity analysis to discover potential molecular drug targets. Int. J. Mol. Sci. 2022, 23, 6604. [Google Scholar] [CrossRef]
- Kim, M.; Kim, E. Mathematical model of the cell signaling pathway based on the extended Boolean network model with a stochastic process. BMC Bioinform. 2022, 23, 515. [Google Scholar] [CrossRef]
- Rukhlenko, O.S.; Halasz, M.; Rauch, N.; Zhernovkov, V.; Prince, T.; Wynne, K.; Maher, S.; Kashdan, E.; MacLeod, K.; Carragher, N.O.; et al. Control of cell state transitions. Nature 2022, 609, 975–985. [Google Scholar] [CrossRef]
- Kim, D.W.; Hong, H.; Kim, J.K. Systematic inference identifies a major source of heterogeneity in cell signaling dynamics: The rate-limiting step number. Sci. Adv. 2022, 8, eabl4598. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Tian, T.; Burrage, K. Binomial leap methods for simulating stochastic chemical kinetics. J. Chem. Phys. 2004, 121, 10356–10364. [Google Scholar] [CrossRef]
- Chen, A.; Ren, Q.; Zhou, T.; Burrage, P.; Tian, T.; Burrage, K. Balanced implicit Patankar–Euler methods for positive solutions of stochastic differential equations of biological regulatory systems. J. Chem. Phys. 2024, 160, 064117. [Google Scholar] [CrossRef] [PubMed]
- Iwamoto, K.; Shindo, Y.; Takahashi, K. Modeling cellular noise underlying heterogeneous cell responses in the epidermal growth factor signaling pathway. PLoS Comput. Biol. 2016, 12, e1005222. [Google Scholar] [CrossRef]
- Filippi, S.; Barnes, C.P.; Kirk, P.D.; Kudo, T.; Kunida, K.; McMahon, S.S.; Tsuchiya, T.; Wada, T.; Kuroda, S.; Stumpf, M.P. Robustness of MEK-ERK dynamics and origins of cell-to-cell variability in MAPK signaling. Cell Rep. 2016, 15, 2524–2535. [Google Scholar] [CrossRef]
- Aoki, K.; Kumagai, Y.; Sakurai, A.; Komatsu, N.; Fujita, Y.; Shionyu, C.; Matsuda, M. Stochastic ERK activation induced by noise and cell-to-cell propagation regulates cell density-dependent proliferation. Mol. Cell 2013, 52, 529–540. [Google Scholar] [CrossRef]
- Jurado, M.; Castaño, Ó.; Zorzano, A. Stochastic modulation evidences a transitory EGF-Ras-ERK MAPK activity induced by PRMT5. Comput. Biol. Med. 2021, 133, 104339. [Google Scholar] [CrossRef]
- Jeschke, M.; Baumgärtner, S.; Legewie, S. Determinants of cell-to-cell variability in protein kinase signaling. PLoS Comput. Biol. 2013, 9, e1003357. [Google Scholar] [CrossRef]
- Marquez-Lago, T.T.; Steinberg, S. Stochastic model of ERK-mediated progesterone receptor translocation, clustering and transcriptional activity. Sci. Rep. 2022, 12, 11791. [Google Scholar] [CrossRef]
- Kolbe, N.; Hexemer, L.; Bammert, L.M.; Loewer, A.; Lukáčová-Medvid’ová, M.; Legewie, S. Data-based stochastic modeling reveals sources of activity bursts in single-cell TGF-β signaling. PLoS Comput. Biol. 2022, 18, e1010266. [Google Scholar] [CrossRef] [PubMed]
- Strasen, J.; Sarma, U.; Jentsch, M.; Bohn, S.; Sheng, C.; Horbelt, D.; Knaus, P.; Legewie, S.; Loewer, A. Cell-specific responses to the cytokine TGF β are determined by variability in protein levels. Mol. Syst. Biol. 2018, 14, e7733. [Google Scholar] [CrossRef] [PubMed]
- Bajikar, S.S.; Janes, K.A. Multiscale models of cell signaling. Ann. Biomed. Eng. 2012, 40, 2319–2327. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, H.; Oliveira, R.H.M.; Zhao, C.; Popel, A.S. Systems biology of angiogenesis signaling: Computational models and omics. WIREs Mech. Dis. 2022, 14, e1550. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.C.; Georgopoulos, N.T.; Southgate, J. From pathway to population—A multiscale model of juxtacrine EGFR-MAPK signalling. BMC Syst. Biol. 2008, 2, 102. [Google Scholar] [CrossRef]
- Hsieh, M.y.; Yang, S.; Raymond-Stinz, M.A.; Edwards, J.S.; Wilson, B.S. Spatio-temporal modeling of signaling protein recruitment to EGFR. BMC Syst. Biol. 2010, 4, 57. [Google Scholar] [CrossRef]
- Shalom-Feuerstein, R.; Plowman, S.J.; Rotblat, B.; Ariotti, N.; Tian, T.; Hancock, J.F.; Kloog, Y. K-ras nanoclustering is subverted by overexpression of the scaffold protein galectin-3. Cancer Res. 2008, 68, 6608–6616. [Google Scholar] [CrossRef]
- Lindstrom, M.J.; Bates, D.M. Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef]
- Davidian, M.; Giltinan, D.M. Nonlinear models for repeated measurement data: An overview and update. J. Agric. Biol. Environ. Stat. 2003, 8, 387–419. [Google Scholar] [CrossRef]
- Lee, S.Y. Bayesian nonlinear models for repeated measurement data: An overview, implementation, and applications. Mathematics 2022, 10, 898. [Google Scholar] [CrossRef]
- Karlsson, M.; Janzén, D.L.; Durrieu, L.; Colman-Lerner, A.; Kjellsson, M.C.; Cedersund, G. Nonlinear mixed-effects modelling for single cell estimation: When, why, and how to use it. BMC Syst. Biol. 2015, 9, 52. [Google Scholar] [CrossRef] [PubMed]
- Almquist, J.; Bendrioua, L.; Adiels, C.B.; Goksör, M.; Hohmann, S.; Jirstrand, M. A nonlinear mixed effects approach for modeling the cell-to-cell variability of Mig1 dynamics in yeast. PLoS ONE 2015, 10, e0124050. [Google Scholar] [CrossRef]
- Straube, J.; Gorse, A.D.; PROOF Centre of Excellence Team; Huang, B.E.; Lê Cao, K.A. A linear mixed model spline framework for analysing time course ‘omics’ data. PLoS ONE 2015, 10, e0134540. [Google Scholar] [CrossRef]
- Wade, J.D.; Lun, X.K.; Bodenmiller, B.; Voit, E.O. Multidimensional single-cell modeling of cellular signaling. bioRxiv 2020, 2020-11. [Google Scholar] [CrossRef]
- Hasenauer, J.; Hasenauer, C.; Hucho, T.; Theis, F.J. ODE constrained mixture modelling: A method for unraveling subpopulation structures and dynamics. PLoS Comput. Biol. 2014, 10, e1003686. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, F.; Reiser, A.; Fink, L.; Woschée, D.; Ligon, T.; Theis, F.J.; Rädler, J.O.; Hasenauer, J. Multi-experiment nonlinear mixed effect modeling of single-cell translation kinetics after transfection. NPJ Syst. Biol. Appl. 2018, 4, 42. [Google Scholar] [CrossRef]
- Alamoudi, E.; Schälte, Y.; Müller, R.; Starruss, J.; Bundgaard, N.; Graw, F.; Brusch, L.; Hasenauer, J. FitMultiCell: Simulating and parameterizing computational models of multi-scale and multi-cellular processes. bioRxiv 2023, 2023-02. [Google Scholar] [CrossRef]
- Starruß, J.; De Back, W.; Brusch, L.; Deutsch, A. Morpheus: A user-friendly modeling environment for multiscale and multicellular systems biology. Bioinformatics 2014, 30, 1331–1332. [Google Scholar] [CrossRef]
- Klinger, E.; Rickert, D.; Hasenauer, J. pyABC: Distributed, likelihood-free inference. Bioinformatics 2018, 34, 3591–3593. [Google Scholar] [CrossRef]
- Erdem, C.; Bensman, E.M.; Mutsuddy, A.; Saint-Antoine, M.M.; Bouhaddou, M.; Blake, R.C.; Dodd, W.; Gross, S.M.; Heiser, L.M.; Feltus, F.A.; et al. A Simple and Efficient Pipeline for Construction, Merging, Expansion, and Simulation of Large-Scale, Single-Cell Mechanistic Models. bioRxiv 2020. [Google Scholar] [CrossRef]
- Tejero-Cantero, A.; Boelts, J.; Deistler, M.; Lueckmann, J.M.; Durkan, C.; Gonçalves, P.J.; Greenberg, D.S.; Macke, J.H. SBI–A toolkit for simulation-based inference. arXiv 2020, arXiv:2007.09114. [Google Scholar] [CrossRef]
- Cranmer, K.; Brehmer, J.; Louppe, G. The frontier of simulation-based inference. Proc. Natl. Acad. Sci. USA 2020, 117, 30055–30062. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Sierra, M.A.; Sokolowski, T.R. Comparing AI versus Optimization Workflows for Simulation-Based Inference of Spatial-Stochastic Systems. arXiv 2024, arXiv:2407.10938. [Google Scholar]
- Jacques, M.A.; Dobrzyński, M.; Gagliardi, P.A.; Sznitman, R.; Pertz, O. CODEX, a neural network approach to explore signaling dynamics landscapes. Mol. Syst. Biol. 2021, 17, e10026. [Google Scholar] [CrossRef] [PubMed]
- Jo, H.; Hong, H.; Hwang, H.J.; Chang, W.; Kim, J.K. Density physics-informed neural networks reveal sources of cell heterogeneity in signal transduction. Patterns 2024, 5, 100899. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Bennett, J.J.; Stern, A.D.; Zhang, X.; Birtwistle, M.R.; Pandey, G. Low-frequency ERK and Akt activity dynamics are predictive of stochastic cell division events. Npj Syst. Biol. Appl. 2024, 10, 65. [Google Scholar] [CrossRef]
- Stern, A.D.; Smith, G.R.; Santos, L.C.; Sarmah, D.; Zhang, X.; Lu, X.; Iuricich, F.; Pandey, G.; Iyengar, R.; Birtwistle, M.R. Relating individual cell division events to single-cell ERK and Akt activity time courses. Sci. Rep. 2022, 12, 18077. [Google Scholar] [CrossRef]
- Yang, C.; Tian, C.; Hoffman, T.E.; Jacobsen, N.K.; Spencer, S.L. Melanoma subpopulations that rapidly escape MAPK pathway inhibition incur DNA damage and rely on stress signalling. Nat. Commun. 2021, 12, 1747. [Google Scholar] [CrossRef] [PubMed]
- Dessauges, C.; Mikelson, J.; Dobrzyński, M.; Jacques, M.A.; Frismantiene, A.; Gagliardi, P.A.; Khammash, M.; Pertz, O. Optogenetic actuator–ERK biosensor circuits identify MAPK network nodes that shape ERK dynamics. Mol. Syst. Biol. 2022, 18, e10670. [Google Scholar] [CrossRef]
- Loos, C.; Moeller, K.; Fröhlich, F.; Hucho, T.; Hasenauer, J. A hierarchical, data-driven approach to modeling single-cell populations predicts latent causes of cell-to-cell variability. Cell Syst. 2018, 6, 593–603. [Google Scholar] [CrossRef] [PubMed]
- Ryu, H.; Chung, M.; Song, J.; Lee, S.S.; Pertz, O.; Jeon, N.L. Integrated platform for monitoring single-cell MAPK kinetics in computer-controlled temporal stimulations. Sci. Rep. 2018, 8, 11126. [Google Scholar] [CrossRef] [PubMed]
- Miura, H.; Kondo, Y.; Matsuda, M.; Aoki, K. Cell-to-cell heterogeneity in p38-mediated cross-inhibition of JNK causes stochastic cell death. Cell Rep. 2018, 24, 2658–2668. [Google Scholar] [CrossRef] [PubMed]
- Chavez-Abiega, S.; Grönloh, M.L.; Gadella, T.W., Jr.; Bruggeman, F.J.; Goedhart, J. Single-cell imaging of ERK and Akt activation dynamics and heterogeneity induced by G-protein-coupled receptors. J. Cell Sci. 2022, 135, jcs259685. [Google Scholar] [CrossRef]
- Davies, A.E.; Pargett, M.; Siebert, S.; Gillies, T.E.; Choi, Y.; Tobin, S.J.; Ram, A.R.; Murthy, V.; Juliano, C.; Quon, G.; et al. Systems-level properties of EGFR-RAS-ERK signaling amplify local signals to generate dynamic gene expression heterogeneity. Cell Syst. 2020, 11, 161–175. [Google Scholar] [CrossRef]
- Hucka, M.; Finney, A.; Bornstein, B.J.; Keating, S.M.; Shapiro, B.E.; Matthews, J.; Kovitz, B.L.; Schilstra, M.J.; Funahashi, A.; Doyle, J.C.; et al. Evolving a lingua franca and associated software infrastructure for computational systems biology: The Systems Biology Markup Language (SBML) project. Syst. Biol. 2004, 1, 41–53. [Google Scholar] [CrossRef] [PubMed]
- Keating, S.M.; Waltemath, D.; König, M.; Zhang, F.; Dräger, A.; Chaouiya, C.; Bergmann, F.T.; Finney, A.; Gillespie, C.S.; Helikar, T.; et al. SBML Level 3: An extensible format for the exchange and reuse of biological models. Mol. Syst. Biol. 2020, 16, e9110. [Google Scholar] [CrossRef]
- Keating, S.M.; Bornstein, B.J.; Finney, A.; Hucka, M. SBMLToolbox: An SBML toolbox for MATLAB users. Bioinformatics 2006, 22, 1275–1277. [Google Scholar] [CrossRef]
- Schmidt, H.; Jirstrand, M. Systems Biology Toolbox for MATLAB: A computational platform for research in systems biology. Bioinformatics 2006, 22, 514–515. [Google Scholar] [CrossRef]
- Radivoyevitch, T. A two-way interface between limited Systems Biology Markup Language and R. BMC Bioinform. 2004, 5, 190. [Google Scholar] [CrossRef]
- Welsh, C.; Xu, J.; Smith, L.; König, M.; Choi, K.; Sauro, H.M. libRoadRunner 2.0: A high performance SBML simulation and analysis library. Bioinformatics 2023, 39, btac770. [Google Scholar] [CrossRef] [PubMed]
- Tusek, A.; Kurtanjek, Z. Systems Biology Markup Language: Case Study of T-Cell Signal Transduction Network. In Proceedings of the 2007 29th International Conference on Information Technology Interfaces, Cavtat, Croatia, 25–28 June 2007; pp. 651–656. [Google Scholar]
- Pinto, J.; Costa, R.S.; Alexandre, L.; Ramos, J.; Oliveira, R. SBML2HYB: A Python interface for SBML compatible hybrid modeling. Bioinformatics 2023, 39, btad044. [Google Scholar] [CrossRef] [PubMed]
- Hamis, S.J.; Kapelyukh, Y.; McLaren, A.; Henderson, C.J.; Roland Wolf, C.; Chaplain, M.A. Quantifying ERK activity in response to inhibition of the BRAFV600E-MEK-ERK cascade using mathematical modelling. Br. J. Cancer 2021, 125, 1552–1560. [Google Scholar] [CrossRef] [PubMed]
- Santra, T. Fitting mathematical models of biochemical pathways to steady state perturbation response data without simulating perturbation experiments. Sci. Rep. 2018, 8, 11679. [Google Scholar] [CrossRef] [PubMed]
- Ji, B.; Bai, J.; Mur, L.A.; Zou, M.; Han, J.; Gao, R.; Yang, Q. Mathematical modelling of Her2 (ErbB2) PI3K/AKT signalling pathways during breast carcinogenesis to include PTPD2. AIMS Math. 2020, 5, 4946–4958. [Google Scholar] [CrossRef]
- Plaugher, D.; Aguilar, B.; Murrugarra, D. Uncovering potential interventions for pancreatic cancer patients via mathematical modeling. J. Theor. Biol. 2022, 548, 111197. [Google Scholar] [CrossRef]
- Tavenard, R.; Faouzi, J.; Vandewiele, G.; Divo, F.; Androz, G.; Holtz, C.; Payne, M.; Yurchak, R.; Rußwurm, M.; Kolar, K.; et al. Tslearn, a machine learning toolkit for time series data. J. Mach. Learn. Res. 2020, 21, 1–6. [Google Scholar]
- Imoto, H.; Zhang, S.; Okada, M. A computational framework for prediction and analysis of cancer signaling dynamics from RNA sequencing data—application to the ErbB receptor signaling pathway. Cancers 2020, 12, 2878. [Google Scholar] [CrossRef]
- Nałęcz-Jawecki, P.; Gagliardi, P.A.; Kochańczyk, M.; Dessauges, C.; Pertz, O.; Lipniacki, T. The MAPK/ERK channel capacity exceeds 6 bit/hour. PLoS Comput. Biol. 2023, 19, e1011155. [Google Scholar] [CrossRef]
- Smart, B.; de Cesare, I.; Renson, L.; Marucci, L. Model predictive control of cancer cellular dynamics: A new strategy for therapy design. Front. Control Eng. 2022, 3, 935018. [Google Scholar] [CrossRef]
- Calzone, L.; Noël, V.; Barillot, E.; Kroemer, G.; Stoll, G. Modeling signaling pathways in biology with MaBoSS: From one single cell to a dynamic population of heterogeneous interacting cells. Comput. Struct. Biotechnol. J. 2022, 20, 5661–5671. [Google Scholar] [CrossRef] [PubMed]
- Perampalam, P.; MacDonald, J.I.; Zakirova, K.; Passos, D.T.; Wasif, S.; Ramos-Valdes, Y.; Hervieu, M.; Mehlen, P.; Rottapel, R.; Gibert, B.; et al. Netrin signaling mediates survival of dormant epithelial ovarian cancer cells. Elife 2024, 12, RP91766. [Google Scholar] [CrossRef] [PubMed]
- Dimitriou, N.M.; Flores-Torres, S.; Kyriakidou, M.; Kinsella, J.M.; Mitsis, G.D. Cancer cell sedimentation in 3D cultures reveals active migration regulated by self-generated gradients and adhesion sites. PLoS Comput. Biol. 2024, 20, e1012112. [Google Scholar] [CrossRef] [PubMed]
- Bosdriesz, E.; Neto, J.M.F.; Sieber, A.; Bernards, R.; Blüthgen, N.; Wessels, L.F. Identifying mutant-specific multi-drug combinations using comparative network reconstruction. Iscience 2022, 25, 104760. [Google Scholar] [CrossRef]
- Dokmegang, J.; Nguyen, H.; Kardash, E.; Savy, T.; Cavaliere, M.; Peyriéras, N.; Doursat, R. Quantification of cell behaviors and computational modeling show that cell directional behaviors drive zebrafish pectoral fin morphogenesis. Bioinformatics 2021, 37, 2946–2954. [Google Scholar] [CrossRef]
- Fröhlich, F.; Loos, C.; Hasenauer, J. Scalable inference of ordinary differential equation models of biochemical processes. Gene Regul. Netw. Methods Protoc. 2019, 385–422. [Google Scholar] [CrossRef]
- Needham, C.J.; Bradford, J.R.; Bulpitt, A.J.; Westhead, D.R. A primer on learning in Bayesian networks for computational biology. PLoS Comput. Biol. 2007, 3, e129. [Google Scholar] [CrossRef]
- Toni, T.; Stumpf, M.P. Simulation-based model selection for dynamical systems in systems and population biology. Bioinformatics 2010, 26, 104–110. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wu, Q.; Hu, X.T.; Tian, T. An integrated approach to infer dynamic protein-gene interactions–a case study of the human p53 protein. Methods 2016, 110, 3–13. [Google Scholar] [CrossRef]
- Wei, J.; Hu, X.; Zou, X.; Tian, T. Reverse-engineering of gene networks for regulating early blood development from single-cell measurements. BMC Med Genom. 2017, 10, 31–43. [Google Scholar] [CrossRef]
- Arisi, I.; Cattaneo, A.; Rosato, V. Parameter estimate of signal transduction pathways. BMC Neurosci. 2006, 7, S6. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Jin, L.; Xiong, M. Extended Kalman filter for estimation of parameters in nonlinear state-space models of biochemical networks. PLoS ONE 2008, 3, e3758. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, F.; Kessler, T.; Weindl, D.; Shadrin, A.; Schmiester, L.; Hache, H.; Muradyan, A.; Schütte, M.; Lim, J.H.; Heinig, M.; et al. Efficient parameter estimation enables the prediction of drug response using a mechanistic pan-cancer pathway model. Cell Syst. 2018, 7, 567–579. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, F.; Sorger, P.K. Fides: Reliable trust-region optimization for parameter estimation of ordinary differential equation models. PLoS Comput. Biol. 2022, 18, e1010322. [Google Scholar] [CrossRef]
- Stapor, P.; Schmiester, L.; Wierling, C.; Merkt, S.; Pathirana, D.; Lange, B.M.; Weindl, D.; Hasenauer, J. Mini-batch optimization enables training of ODE models on large-scale datasets. Nat. Commun. 2022, 13, 34. [Google Scholar] [CrossRef]
- Brown, K.S.; Hill, C.C.; Calero, G.A.; Myers, C.R.; Lee, K.H.; Sethna, J.P.; Cerione, R.A. The statistical mechanics of complex signaling networks: Nerve growth factor signaling. Phys. Biol. 2004, 1, 184. [Google Scholar] [CrossRef]
- Xu, T.R.; Vyshemirsky, V.; Gormand, A.; von Kriegsheim, A.; Girolami, M.; Baillie, G.S.; Ketley, D.; Dunlop, A.J.; Milligan, G.; Houslay, M.D.; et al. Inferring signaling pathway topologies from multiple perturbation measurements of specific biochemical species. Sci. Signal. 2010, 3, ra20. [Google Scholar] [CrossRef]
- Toni, T.; Ozaki, Y.i.; Kirk, P.; Kuroda, S.; Stumpf, M.P. Elucidating the in vivo phosphorylation dynamics of the ERK MAP kinase using quantitative proteomics data and Bayesian model selection. Mol. BioSyst. 2012, 8, 1921–1929. [Google Scholar] [CrossRef]
- Liepe, J.; Kirk, P.; Filippi, S.; Toni, T.; Barnes, C.P.; Stumpf, M.P. A framework for parameter estimation and model selection from experimental data in systems biology using approximate Bayesian computation. Nat. Protoc. 2014, 9, 439–456. [Google Scholar] [CrossRef]
- Wu, Q.; Smith-Miles, K.; Tian, T. Approximate Bayesian computation schemes for parameter inference of discrete stochastic models using simulated likelihood density. BMC Bioinform. 2014, 15, S3. [Google Scholar] [CrossRef]
- He, W.; Xia, P.; Zhang, X.; Tian, T. Bayesian Inference Algorithm for Estimating Heterogeneity of Regulatory Mechanisms Based on Single-Cell Data. Mathematics 2022, 10, 4748. [Google Scholar] [CrossRef]
- Oates, C.J.; Dondelinger, F.; Bayani, N.; Korkola, J.; Gray, J.W.; Mukherjee, S. Causal network inference using biochemical kinetics. Bioinformatics 2014, 30, i468–i474. [Google Scholar] [CrossRef] [PubMed]
- Dixit, P.D.; Lyashenko, E.; Niepel, M.; Vitkup, D. Maximum entropy framework for predictive inference of cell population heterogeneity and responses in signaling networks. Cell Syst. 2020, 10, 204–212. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, E.; Lavielle, M. Maximum likelihood estimation in nonlinear mixed effects models. Comput. Stat. Data Anal. 2005, 49, 1020–1038. [Google Scholar] [CrossRef]
- Dharmarajan, L.; Kaltenbach, H.M.; Rudolf, F.; Stelling, J. A simple and flexible computational framework for inferring sources of heterogeneity from single-cell dynamics. Cell Syst. 2019, 8, 15–26. [Google Scholar] [CrossRef]
- Lambert, B.; Gavaghan, D.J.; Tavener, S.J. A Monte Carlo method to estimate cell population heterogeneity from cell snapshot data. J. Theor. Biol. 2021, 511, 110541. [Google Scholar] [CrossRef]
- Augustin, D.; Lambert, B.; Wang, K.; Walz, A.C.; Robinson, M.; Gavaghan, D. Filter inference: A scalable nonlinear mixed effects inference approach for snapshot time series data. PLoS Comput. Biol. 2023, 19, e1011135. [Google Scholar] [CrossRef] [PubMed]
- Loos, C.; Hasenauer, J. Robust calibration of hierarchical population models for heterogeneous cell populations. J. Theor. Biol. 2020, 488, 110118. [Google Scholar] [CrossRef]
- Persson, S.; Welkenhuysen, N.; Shashkova, S.; Wiqvist, S.; Reith, P.; Schmidt, G.W.; Picchini, U.; Cvijovic, M. Scalable and flexible inference framework for stochastic dynamic single-cell models. PLoS Comput. Biol. 2022, 18, e1010082. [Google Scholar] [CrossRef]
- Browning, A.P.; Ansari, N.; Drovandi, C.; Johnston, A.P.; Simpson, M.J.; Jenner, A.L. Identifying cell-to-cell variability in internalization using flow cytometry. J. R. Soc. Interface 2022, 19, 20220019. [Google Scholar] [CrossRef]
- Hsu, I.S.; Moses, A.M. Stochastic models for single-cell data: Current challenges and the way forward. FEBS J. 2022, 289, 647–658. [Google Scholar] [CrossRef] [PubMed]
- Prangle, D. Lazy abc. Stat. Comput. 2016, 26, 171–185. [Google Scholar] [CrossRef]
- Yazdani, A.; Lu, L.; Raissi, M.; Karniadakis, G.E. Systems biology informed deep learning for inferring parameters and hidden dynamics. PLoS Comput. Biol. 2020, 16, e1007575. [Google Scholar] [CrossRef]


| Name | Web Link | Language | Ref/Comment |
|---|---|---|---|
| MAPKcascades | https://github.com/SJHamis/MAPKcascades | MATLAB | [224] |
| MARM1 | https://github.com/labsyspharm/marm1-supplement | Python | [84] |
| MRA-SMC-ABC | https://github.com/SBIUCD/MRA_SMC_ABC1 | MATLAB | [225] |
| Modeling | https://github.com/Jia-V/modeling | MATLAB | [226] |
| PCC-Mutation | https://github.com/drplaugher/PCC_Mutations | MATLAB& Python | [227] |
| Tslearn | https://github.com/tslearn-team/tslearn | Python | [228] |
| Biomass | https://github.com/okadalabipr/biomass | Python | [229] |
| pulsatile-information | https://github.com/pawelnalecz/pulsatile-information | Python | [230] |
| Adaptive MPC | https://github.com/Ben-Smart/Adaptive_MPC_on_NSCLC | MATLAB | [231] |
| MaBoss | https://github.com/sysbio-curie/MaBoSS_test | Python | [232] |
| TRACT | https://github.com/developerpiru/TRACS | Python | [233] |
| HyMetaGrowthXTreat | https://github.com/NMDimitriou/HyMetaGrowthXTreat | MATLAB | [234] |
| MixedIC50 | https://github.com/NKI-CCB/MixedIC50 | R | [235] |
| MaSoFin | https://github.com/guijoe/MaSoFin | C | [236] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Zhang, X.; Tian, T. Mathematical Modeling and Inference of Epidermal Growth Factor-Induced Mitogen-Activated Protein Kinase Cell Signaling Pathways. Int. J. Mol. Sci. 2024, 25, 10204. https://doi.org/10.3390/ijms251810204
Feng J, Zhang X, Tian T. Mathematical Modeling and Inference of Epidermal Growth Factor-Induced Mitogen-Activated Protein Kinase Cell Signaling Pathways. International Journal of Molecular Sciences. 2024; 25(18):10204. https://doi.org/10.3390/ijms251810204
Chicago/Turabian StyleFeng, Jinping, Xinan Zhang, and Tianhai Tian. 2024. "Mathematical Modeling and Inference of Epidermal Growth Factor-Induced Mitogen-Activated Protein Kinase Cell Signaling Pathways" International Journal of Molecular Sciences 25, no. 18: 10204. https://doi.org/10.3390/ijms251810204
APA StyleFeng, J., Zhang, X., & Tian, T. (2024). Mathematical Modeling and Inference of Epidermal Growth Factor-Induced Mitogen-Activated Protein Kinase Cell Signaling Pathways. International Journal of Molecular Sciences, 25(18), 10204. https://doi.org/10.3390/ijms251810204







