Adsorption of Carbon Dioxide and Nitrogen in Co3(ndc)3(dabco) Metal–Organic Framework
Abstract
1. Introduction
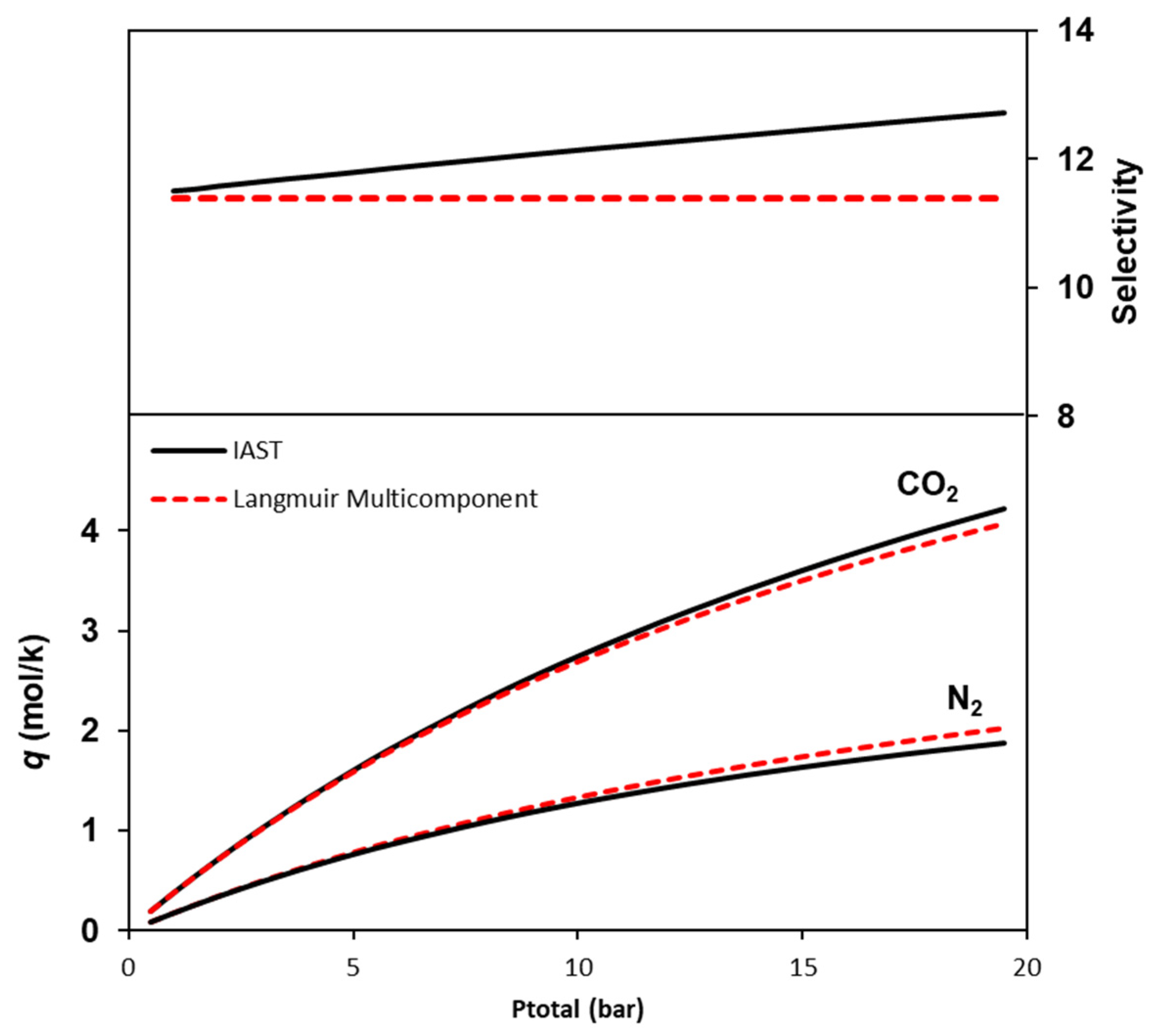
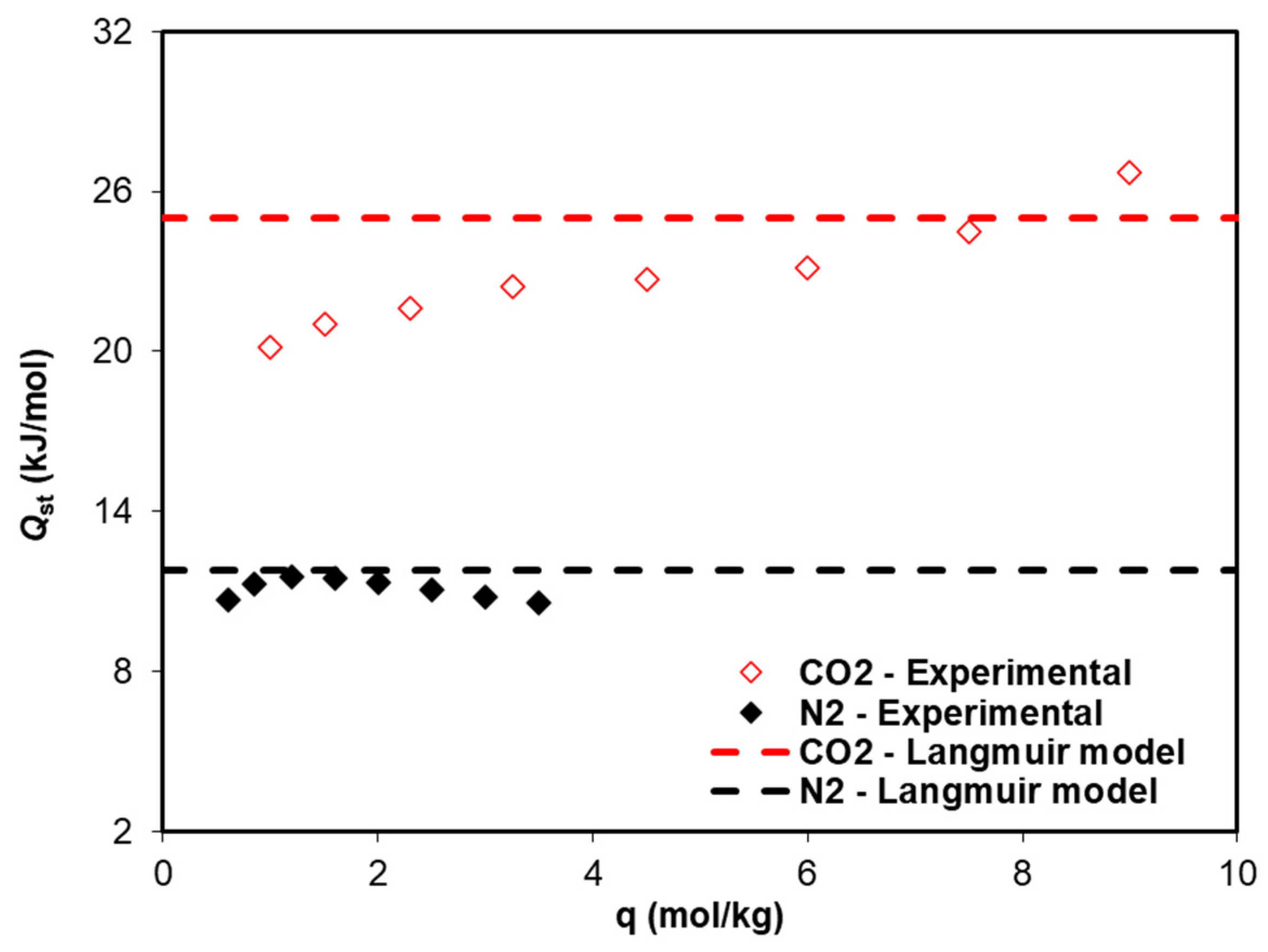
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commision. Stepping Up Europe’s 2030 Climate Ambition. Investing in a Climate-Neutral Future for the Benefit of Our People; European Commision: Brussels, Belgium, 2020. [Google Scholar]
- Ebner, A.D.; Ritter, J.A. State-of-the-art Adsorption and Membrane Separation Processes for Carbon Dioxide Production from Carbon Dioxide Emitting Industries. Sep. Sci. Technol. 2009, 44, 1273–1421. [Google Scholar] [CrossRef]
- Joss, L.; Gazzani, M.; Mazzotti, M. Rational design of temperature swing adsorption cycles for post-combustion CO2 capture. Chem. Eng. Sci. 2017, 158, 381–394. [Google Scholar] [CrossRef]
- Ribeiro, R.P.P.L.; Grande, C.A.; Rodrigues, A.E. Activated Carbon Honeycomb Monolith—Zeolite 13X Hybrid System to Capture CO2 from Flue Gases employing Electric Swing Adsorption. Chem. Eng. Sci. 2013, 104, 304–318. [Google Scholar] [CrossRef]
- Santos, M.P.S.; Grande, C.A.; Rodrigues, A.E. Pressure Swing Adsorption for Biogas Upgrading. Effect of Recycling Streams in Pressure Swing Adsorption Design. Ind. Eng. Chem. Res. 2011, 50, 974–985. [Google Scholar] [CrossRef]
- Grande, C.A. Biogas Upgrading by Pressure Swing Adsorption. In Biofuel’s Engineering Process Technology; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Ribeiro, R.P.; Sauer, T.P.; Lopes, F.V.; Moreira, R.F.; Grande, C.A.; Rodrigues, A.E. Adsorption of CO2, CH4, and N2 in Activated Carbon Honeycomb Monolith. J. Chem. Eng. Data 2008, 53, 2311–2317. [Google Scholar] [CrossRef]
- Plaza, M.G.; González, A.S.; Pevida, C.; Rubiera, F. Green Coffee Based CO2 Adsorbent with High Performance in Postcombustion Conditions. Fuel 2015, 140, 633–648. [Google Scholar] [CrossRef]
- Surra, E.; Ribeiro, R.P.P.L.; Santos, T.; Bernardo, M.; Mota, J.P.B.; Lapa, N.; Esteves, I.A.A.C. Evaluation of activated carbons produced from Maize Cob Waste for adsorption-based CO2 separation and biogas upgrading. J. Environ. Chem. Eng. 2022, 10, 107065. [Google Scholar] [CrossRef]
- Xiao, P.; Zhang, J.; Webley, P.; Li, G.; Singh, R.; Todd, R. Capture of CO2 from flue gas streams with zeolite 13X by vacuum-pressure swing adsorption. Adsorption 2008, 14, 575–582. [Google Scholar] [CrossRef]
- Merel, J.; Clausse, M.; Meunier, F. Experimental Investigation on CO2 Post-Combustion Capture by Indirect Thermal Swing Adsorption using 13X and 5A Zeolites. Ind. Eng. Chem. Res. 2008, 47, 209–215. [Google Scholar] [CrossRef]
- Zelenak, V.; Halamova, D.; Gaberova, L.; Bloch, E.; Llewellyn, P. Amine-Modified SBA-12 Mesoporous Silica for Carbon Dioxide Capture: Effect of Amine Basicity on Sorption Properties. Microporous Mesoporous Mater. 2008, 116, 358–364. [Google Scholar] [CrossRef]
- Heydari-Gorji, A.; Belmabkhout, Y.; Sayari, A. Polyethylenimine-Impregnated Mesoporous Silica: Effect of Amine Loading and Surface Alkyl Chains on CO2 Adsorption. Langmuir 2011, 27, 12411–12416. [Google Scholar] [CrossRef] [PubMed]
- Camacho, B.C.R.; Ribeiro, R.P.P.L.; Esteves, I.A.A.C.; Mota, J.P.B. Adsorption Equilibrium of Carbon Dioxide and Nitrogen on the MIL-53(Al) Metal Organic Framework. Sep. Purif. Technol. 2015, 141, 150–159. [Google Scholar] [CrossRef]
- Joss, L.; Hefti, M.; Bjelobrk, Z.; Mazzotti, M. On the Potential of Phase-change Adsorbents for CO2 Capture by Temperature Swing Adsorption. Energy Procedia 2017, 114, 2271–2278. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, Y.; Shah, B.B.; Zhao, D. CO2 Capture in Metal–Organic Framework Adsorbents: An Engineering Perspective. Adv. Sustain. Syst. 2019, 3, 1800080. [Google Scholar] [CrossRef]
- Ribeiro, R.P.P.L.; Mota, J.P.B. Surface Area and Porosity of Co3(ndc)3(dabco) Metal–Organic Framework and Its Methane Storage Capacity: A Combined Experimental and Simulation Study. J. Phys. Chem. C 2021, 125, 2411–2423. [Google Scholar] [CrossRef]
- Ribeiro, R.P.P.L.; Esteves, I.A.A.C.; Mota, J.P.B. Adsorption of Carbon Dioxide, Methane, and Nitrogen on Zn(dcpa) Metal-Organic Framework. Energies 2021, 14, 5598. [Google Scholar] [CrossRef]
- Rowsell, J.L.C.; Yaghi, O.M. Metal–Organic Frameworks: A New Class of Porous Materials. Microporous Mesoporous Mater. 2004, 73, 3–14. [Google Scholar] [CrossRef]
- Ferey, G. Hybrid Porous Solids: Past, Present, Future. Chem. Soc. Rev. 2008, 37, 191–214. [Google Scholar] [CrossRef]
- Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. [Google Scholar] [CrossRef]
- Czaja, A.U.; Trukhan, N.; Muller, U. Industrial Applications of Metal-Organic Frameworks. Chem. Soc. Rev. 2009, 38, 1284–1293. [Google Scholar] [CrossRef]
- Ribeiro, R.P.P.L.; Antunes, C.L.; Garate, A.U.; Portela, A.F.; Plaza, M.G.; Mota, J.P.B.; Esteves, I.A.A.C. Binderless shaped metal-organic framework particles: Impact on carbon dioxide adsorption. Microporous Mesoporous Mater. 2019, 275, 111–121. [Google Scholar] [CrossRef]
- Pons Picart, J.; Sanchez, F.J.; Casabó, J.; Rius, J.; Alvarez-Larena, A.; Ros, J. Synthesis and structural characterisation of a new cobalt(II) pentanuclear complex with a tetranucleating pyrazole-derived ligand. Inorg. Chem. Commun. 2002, 5, 130–133. [Google Scholar] [CrossRef]
- Chadghan, A.; Pons, J.; Caubet, A.; Casabó, J.; Ros, J.; Alvarez-Larena, A.; Francesc Piniella, J. Cobalt(II) complexes with pyrazole-derived ligands: Crystal structure of {bis[3-phenyl-5-(2-pyridyl) pyrazole]aquachlorocobalt(II)}chloride monohydrate. Polyhedron 2000, 19, 855–862. [Google Scholar] [CrossRef]
- Soldevila-Sanmartín, J.; Calvet, T.; Font-Bardia, M.; Choquesillo-Lazarte, D.; Pons, J. Variable behaviour of a flexible bispyrazole ligand: A Co(II) polymer and a unique Cu(II) penta-coordinated dimer. J. Mol. Struct. 2023, 1284, 135419. [Google Scholar] [CrossRef]
- Chun, H.; Jung, H.; Koo, G.; Jeong, H.; Kim, D.K. Efficient hydrogen sorption in 8-connected MOFs based on trinuclear pinwheel motifs. Inorg. Chem. 2008, 47, 5355–5359. [Google Scholar] [CrossRef]
- Ribeiro, R.P.P.L.; Barreto, J.; Grosso Xavier, M.D.; Martins, D.; Esteves, I.A.A.C.; Branco, M.; Tirolien, T.; Mota, J.P.B.; Bonfait, G. Cryogenic neon adsorption on Co3(ndc)3(dabco) metal-organic framework. Microporous Mesoporous Mater. 2020, 298, 110055. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark Alexander, V.; Olivier James, P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing Kenneth, S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051. [Google Scholar] [CrossRef]
- Nabais, A.R.; Ribeiro, R.P.P.L.; Mota, J.P.B.; Alves, V.D.; Esteves, I.A.A.C.; Neves, L.A. CO2/N2 gas separation using Fe(BTC)-based mixed matrix membranes: A view on the adsorptive and filler properties of metal-organic frameworks. Sep. Purif. Technol. 2018, 202, 174–184. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Ribeiro, R.P.P.L.; Camacho, B.C.R.; Lyubchyk, A.; Esteves, I.A.A.C.; Cruz, F.J.A.L.; Mota, J.P.B. Experimental and Computational Study of Ethane and Ethylene Adsorption in the MIL-53(Al) Metal Organic Framework. Microporous Mesoporous Mater. 2016, 230, 154–165. [Google Scholar] [CrossRef]
- Gumma, S.; Talu, O. Net Adsorption: A Thermodynamic Framework for Supercritical Gas Adsorption and Storage in Porous Solids. Langmuir 2010, 26, 17013–17023. [Google Scholar] [CrossRef]
- Brandani, S.; Mangano, E.; Sarkisov, L. Net, Excess and Absolute Adsorption and Adsorption of Helium. Adsorption 2016, 22, 261–276. [Google Scholar] [CrossRef] [PubMed]
- Myers, A.L. Adsorption of Gas Mixtures—A Thermodynamic Approach. Ind. Eng. Chem. 1968, 60, 45–49. [Google Scholar] [CrossRef]
- Myers, A.L.; Prausnitz, J.M. Thermodynamics of Mixed-Gas Adsorption. AIChE J. 1965, 11, 121–127. [Google Scholar] [CrossRef]

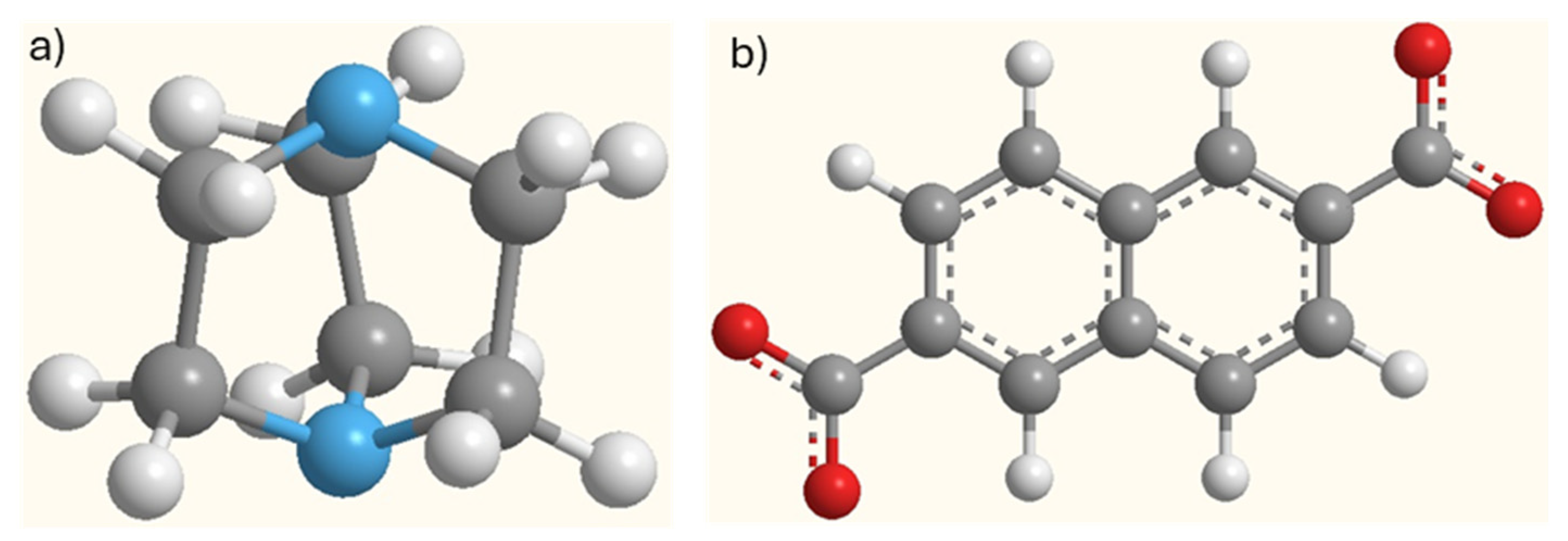

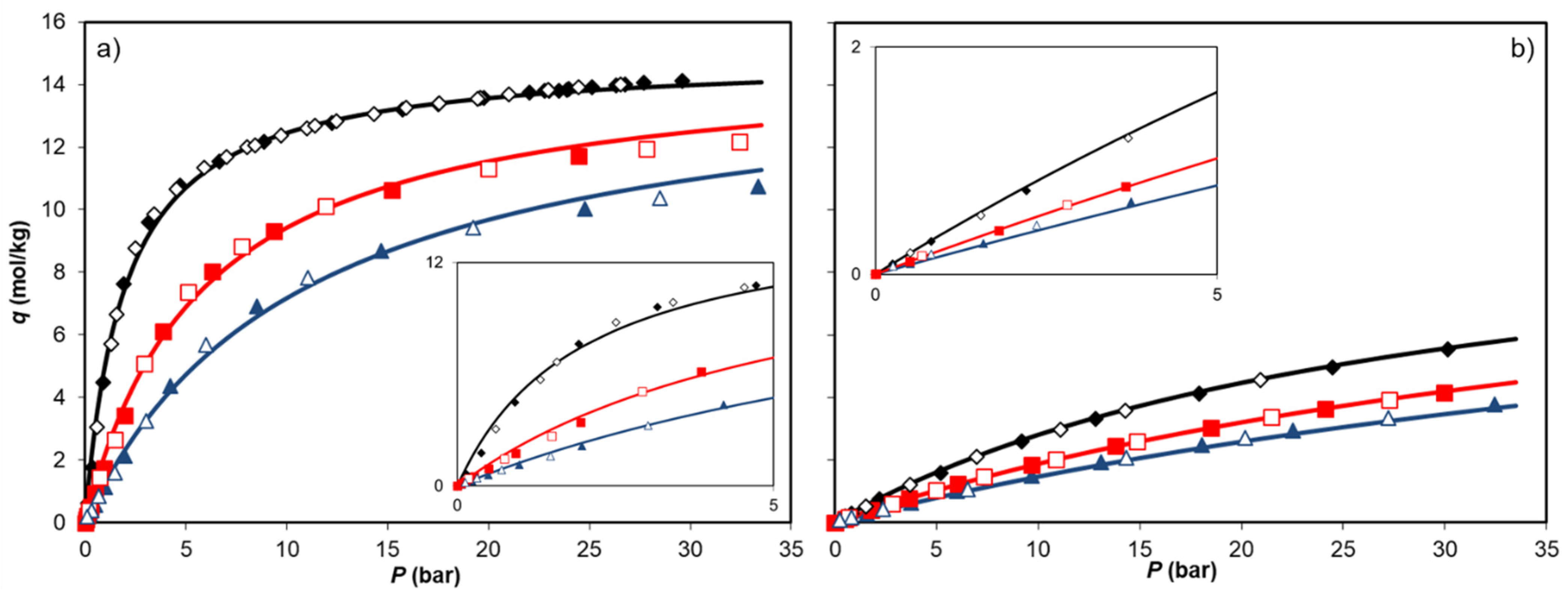
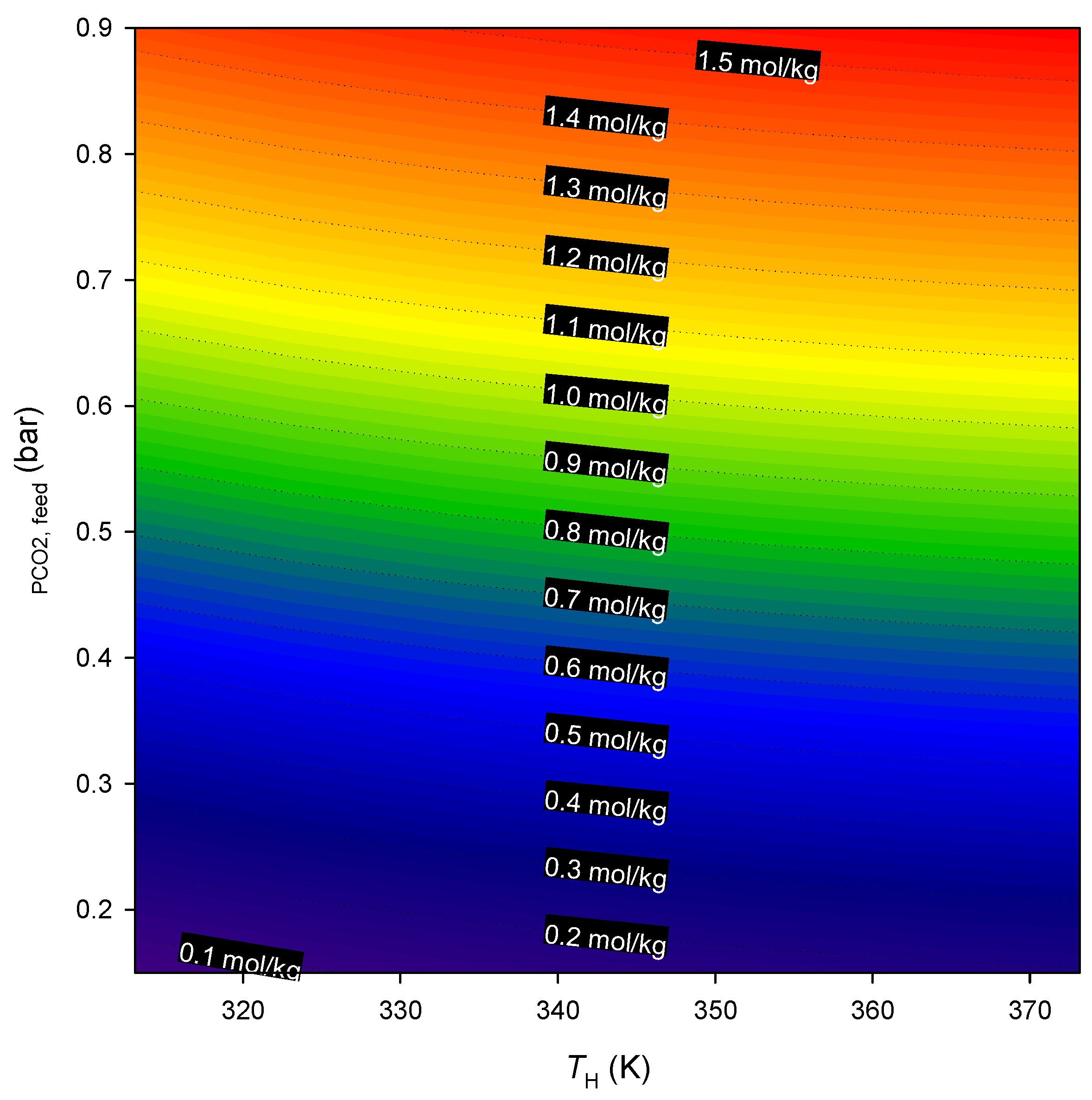
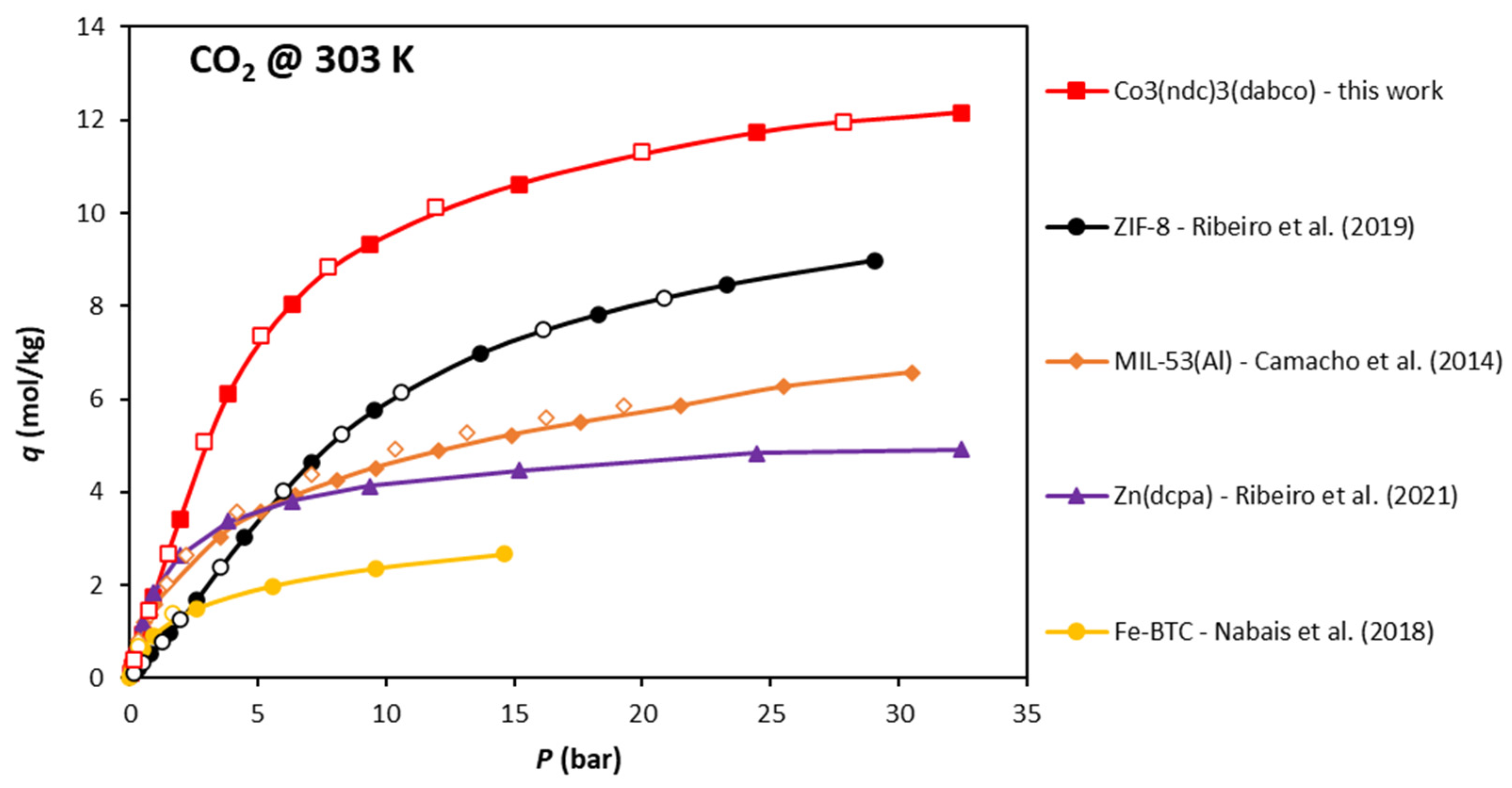
| T = 273 K | T = 303 K | T = 323 K | ||||||
|---|---|---|---|---|---|---|---|---|
(bar) | (mol/kg) | (mol/kg) | (bar) | (mol/kg) | (mol/kg) | (bar) | (mol/kg) | (mol/kg) |
| 0.04 | 0.13 | 0.13 | 0.06 | 0.11 | 0.11 | 0.07 | 0.08 | 0.09 |
| 0.15 | 0.61 | 0.62 | 0.13 | 0.23 | 0.24 | 0.23 | 0.26 | 0.27 |
| 0.38 | 1.74 | 1.76 | 0.27 | 0.49 | 0.50 | 0.49 | 0.55 | 0.58 |
| 0.91 | 4.43 | 4.48 | 0.50 | 0.91 | 0.93 | 0.98 | 1.09 | 1.14 |
| 1.92 | 7.51 | 7.63 | 0.93 | 1.69 | 1.74 | 1.97 | 2.04 | 2.14 |
| 3.16 | 9.41 | 9.60 | 1.95 | 3.31 | 3.42 | 4.21 | 4.15 | 4.36 |
| 4.73 | 10.47 | 10.76 | 3.86 | 5.91 | 6.12 | 8.52 | 6.47 | 6.91 |
| 6.66 | 11.14 | 11.55 | 6.31 | 7.69 | 8.04 | 14.66 | 7.90 | 8.68 |
| 8.87 | 11.61 | 12.18 | 9.36 | 8.79 | 9.32 | 24.79 | 8.65 | 10.04 |
| 12.26 | 11.98 | 12.78 | 15.20 | 9.74 | 10.62 | 33.37 | 8.79 | 10.74 |
| 15.73 | 12.14 | 13.20 | 24.46 | 10.23 | 11.73 | 28.48 | 8.76 | 10.37 |
| 17.50 | 12.19 | 13.38 | 32.46 | 10.06 | 12.16 | 19.22 | 8.38 | 9.43 |
| 19.75 | 12.19 | 13.57 | 27.81 | 10.21 | 11.95 | 11.04 | 7.24 | 7.82 |
| 22.03 | 12.17 | 13.75 | 19.97 | 10.13 | 11.32 | 6.02 | 5.37 | 5.68 |
| 22.80 | 12.15 | 13.79 | 11.94 | 9.44 | 10.12 | 3.02 | 3.10 | 3.25 |
| 22.99 | 12.14 | 13.80 | 7.75 | 8.41 | 8.84 | 1.48 | 1.53 | 1.60 |
| 23.49 | 12.10 | 13.80 | 5.13 | 7.08 | 7.36 | 0.70 | 0.83 | 0.86 |
| 23.89 | 12.08 | 13.83 | 2.93 | 4.91 | 5.07 | 0.31 | 0.39 | 0.41 |
| 23.99 | 12.11 | 13.86 | 1.49 | 2.58 | 2.66 | 0.12 | 0.18 | 0.19 |
| 25.11 | 12.06 | 13.92 | 0.74 | 1.42 | 1.46 | |||
| 26.34 | 12.00 | 13.98 | 0.18 | 0.38 | 0.39 | |||
| 26.78 | 11.99 | 14.01 | ||||||
| 27.71 | 11.92 | 14.05 | ||||||
| 29.62 | 11.79 | 14.12 | ||||||
| 26.54 | 12.00 | 14.00 | ||||||
| 24.46 | 12.11 | 13.90 | ||||||
| 22.97 | 12.16 | 13.82 | ||||||
| 21.02 | 12.20 | 13.69 | ||||||
| 19.57 | 12.21 | 13.57 | ||||||
| 19.48 | 12.19 | 13.55 | ||||||
| 17.56 | 12.21 | 13.41 | ||||||
| 15.93 | 12.19 | 13.26 | ||||||
| 14.34 | 12.11 | 13.06 | ||||||
| 12.46 | 12.02 | 12.83 | ||||||
| 11.39 | 11.94 | 12.68 | ||||||
| 11.01 | 11.90 | 12.61 | ||||||
| 9.73 | 11.76 | 12.38 | ||||||
| 8.41 | 11.54 | 12.06 | ||||||
| 8.04 | 11.49 | 12.00 | ||||||
| 7.03 | 11.26 | 11.70 | ||||||
| 5.92 | 10.97 | 11.34 | ||||||
| 4.54 | 10.38 | 10.66 | ||||||
| 3.41 | 9.64 | 9.85 | ||||||
| 2.51 | 8.63 | 8.78 | ||||||
| 1.58 | 6.56 | 6.66 | ||||||
| 1.31 | 5.63 | 5.71 | ||||||
| 0.61 | 3.01 | 3.04 | ||||||
| T = 273 K | T = 303 K | T = 323 K | ||||||
|---|---|---|---|---|---|---|---|---|
(bar) | (mol/kg) | (mol/kg) | (bar) | (mol/kg) | (mol/kg) | (bar) | (mol/kg) | (mol/kg) |
| 0.25 | 0.08 | 0.09 | 0.01 | 0.003 | 0.003 | 0.01 | 0.004 | 0.004 |
| 0.81 | 0.24 | 0.29 | 0.50 | 0.09 | 0.110 | 0.51 | 0.070 | 0.090 |
| 2.21 | 0.60 | 0.74 | 1.81 | 0.29 | 0.390 | 1.58 | 0.190 | 0.270 |
| 5.21 | 1.26 | 1.57 | 3.66 | 0.57 | 0.770 | 3.74 | 0.450 | 0.640 |
| 9.18 | 2.03 | 2.58 | 6.05 | 0.90 | 1.220 | 6.01 | 0.690 | 0.990 |
| 12.81 | 2.54 | 3.30 | 9.68 | 1.31 | 1.830 | 9.67 | 1.020 | 1.500 |
| 17.93 | 3.06 | 4.14 | 13.80 | 1.70 | 2.440 | 13.09 | 1.280 | 1.940 |
| 24.45 | 3.49 | 4.96 | 18.49 | 2.03 | 3.030 | 18.03 | 1.580 | 2.480 |
| 30.13 | 3.74 | 5.55 | 24.10 | 2.33 | 3.620 | 22.52 | 1.800 | 2.930 |
| 20.95 | 3.29 | 4.55 | 29.96 | 2.54 | 4.150 | 32.46 | 2.140 | 3.770 |
| 14.28 | 2.71 | 3.57 | 27.28 | 2.46 | 3.920 | 27.22 | 1.980 | 3.340 |
| 11.08 | 2.31 | 2.98 | 21.46 | 2.21 | 3.360 | 20.18 | 1.690 | 2.700 |
| 6.99 | 1.67 | 2.09 | 14.87 | 1.78 | 2.580 | 14.32 | 1.350 | 2.070 |
| 3.70 | 0.98 | 1.20 | 10.89 | 1.44 | 2.020 | 6.54 | 0.740 | 1.070 |
| 1.54 | 0.42 | 0.52 | 7.32 | 1.07 | 1.460 | 2.36 | 0.310 | 0.430 |
| 0.51 | 0.16 | 0.19 | 5.00 | 0.77 | 1.040 | 0.81 | 0.140 | 0.180 |
| 2.80 | 0.46 | 0.610 | 0.26 | 0.060 | 0.070 | |||
| 0.68 | 0.13 | 0.160 | ||||||
| CO2 | N2 | |
|---|---|---|
| (mol/kg) | 14.9 | 11.0 |
| (bar−1) | 8.47 × 10−6 | 1.09 × 10−4 |
| Q (kJ/mol) | 25.00 | 11.78 |
| ARE (%) | 7.3 | 5.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, R.P.P.L.; Mota, J.P.B. Adsorption of Carbon Dioxide and Nitrogen in Co3(ndc)3(dabco) Metal–Organic Framework. Int. J. Mol. Sci. 2024, 25, 9951. https://doi.org/10.3390/ijms25189951
Ribeiro RPPL, Mota JPB. Adsorption of Carbon Dioxide and Nitrogen in Co3(ndc)3(dabco) Metal–Organic Framework. International Journal of Molecular Sciences. 2024; 25(18):9951. https://doi.org/10.3390/ijms25189951
Chicago/Turabian StyleRibeiro, Rui Pedro Pinto Lopes, and José Paulo Barbosa Mota. 2024. "Adsorption of Carbon Dioxide and Nitrogen in Co3(ndc)3(dabco) Metal–Organic Framework" International Journal of Molecular Sciences 25, no. 18: 9951. https://doi.org/10.3390/ijms25189951
APA StyleRibeiro, R. P. P. L., & Mota, J. P. B. (2024). Adsorption of Carbon Dioxide and Nitrogen in Co3(ndc)3(dabco) Metal–Organic Framework. International Journal of Molecular Sciences, 25(18), 9951. https://doi.org/10.3390/ijms25189951







