Tunable Optical Properties of Cu/VSe2 from the Visible to Terahertz Spectral Range: A First-Principles Study
Abstract
1. Introduction
2. Results and Discussion
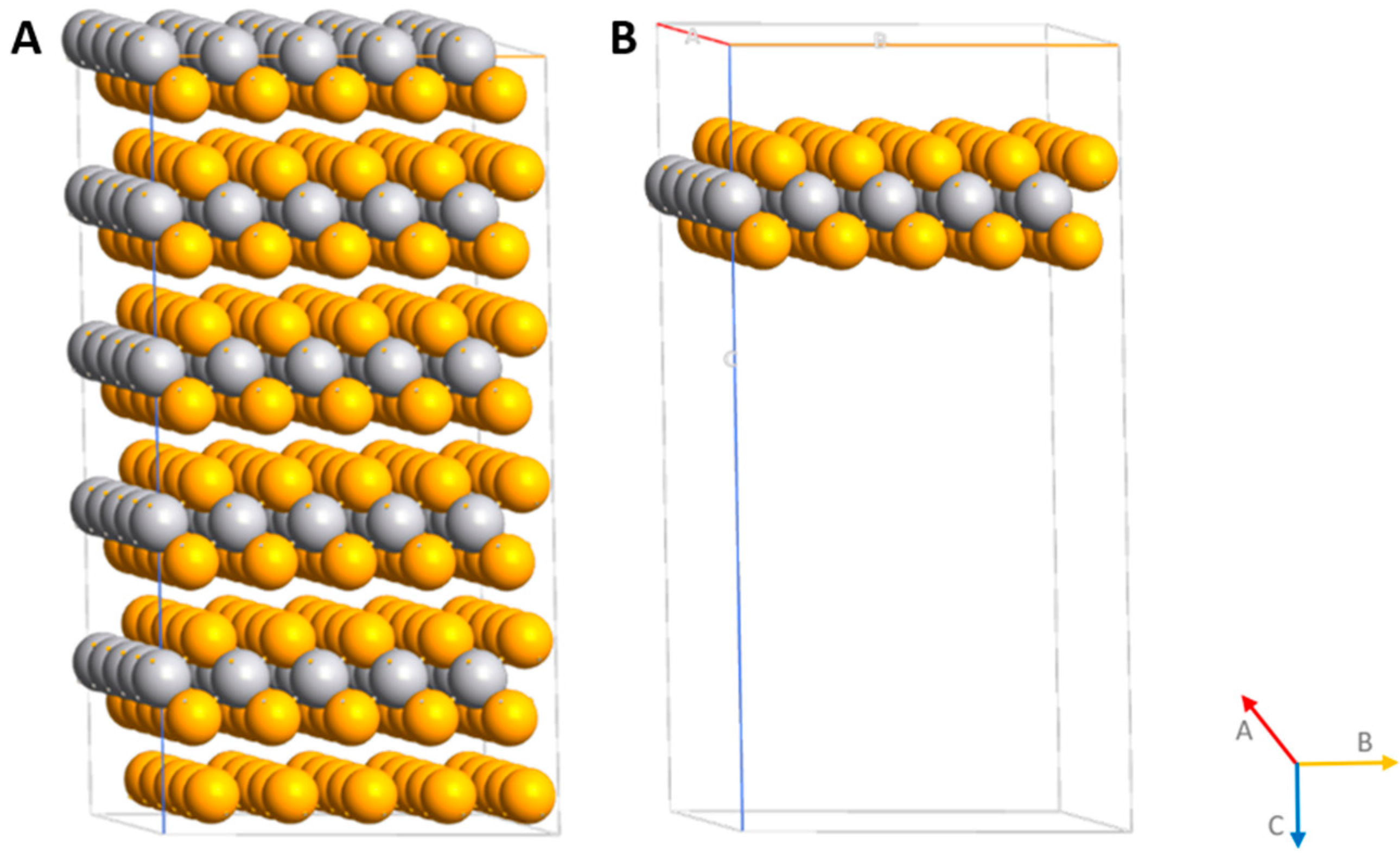
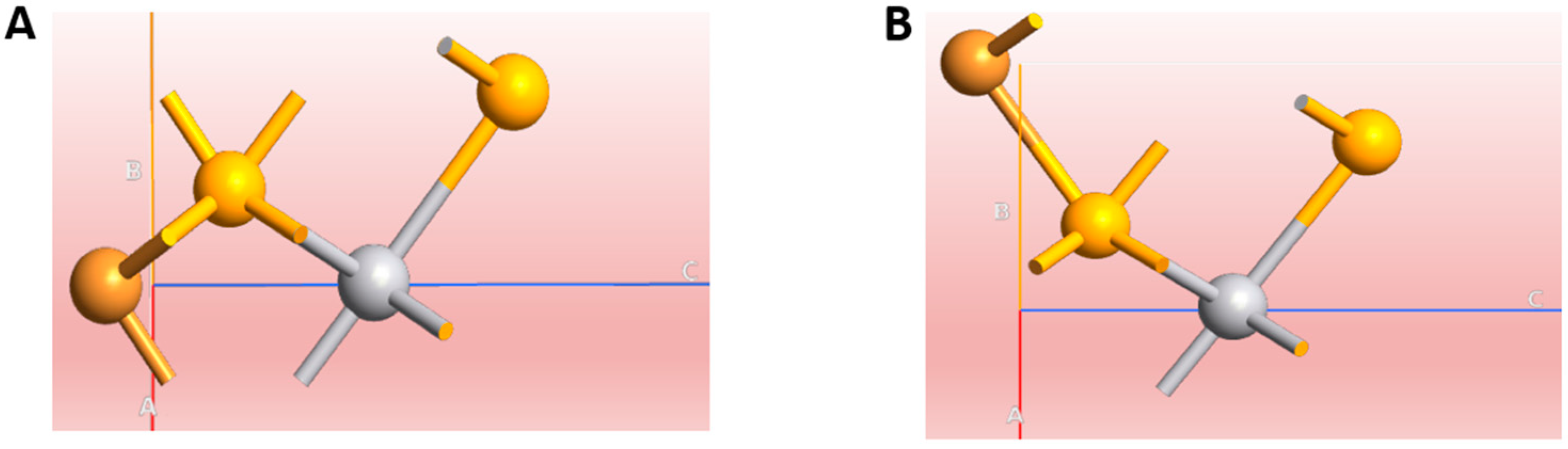
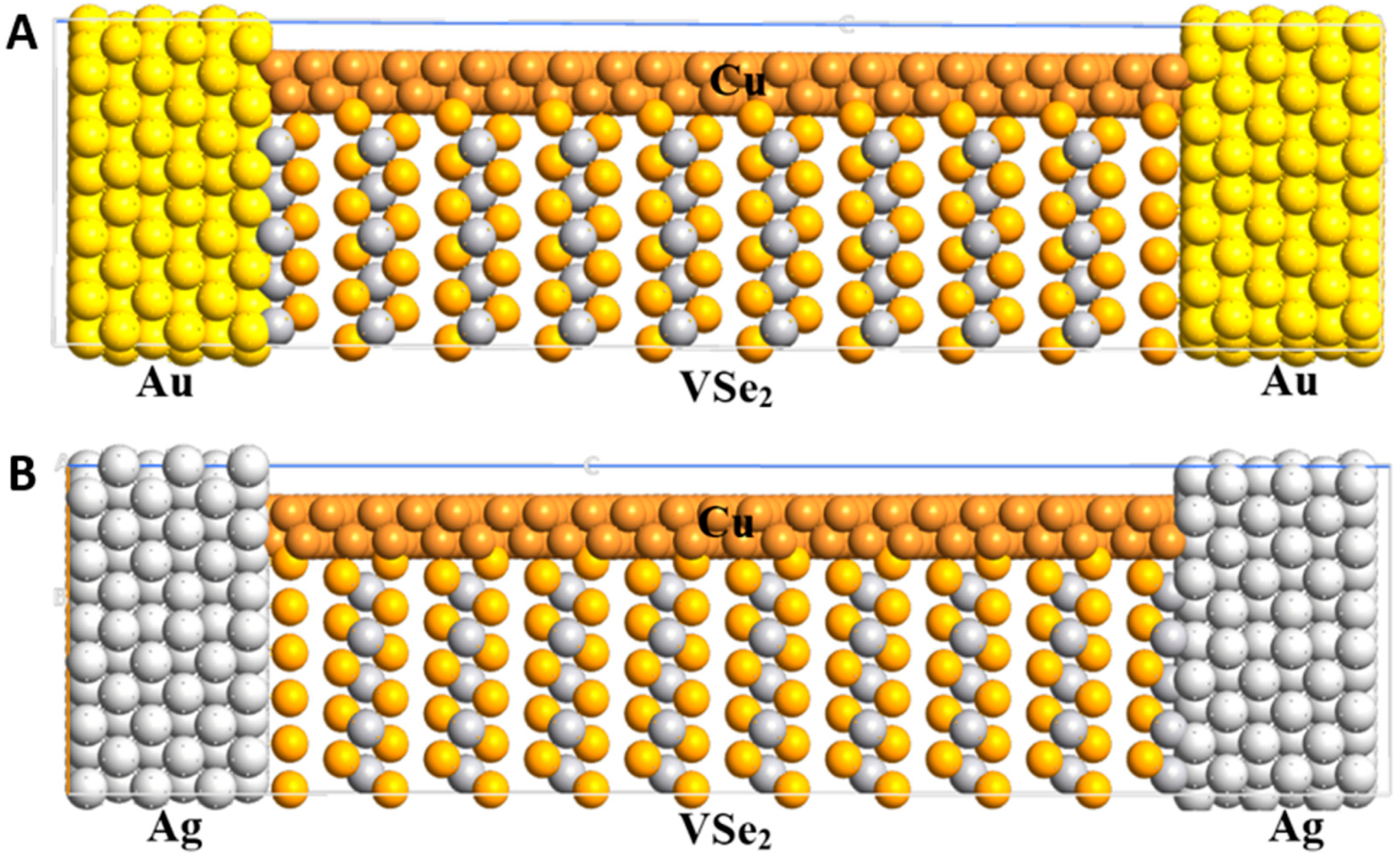
2.1. Structural Parameters and Binding Energy
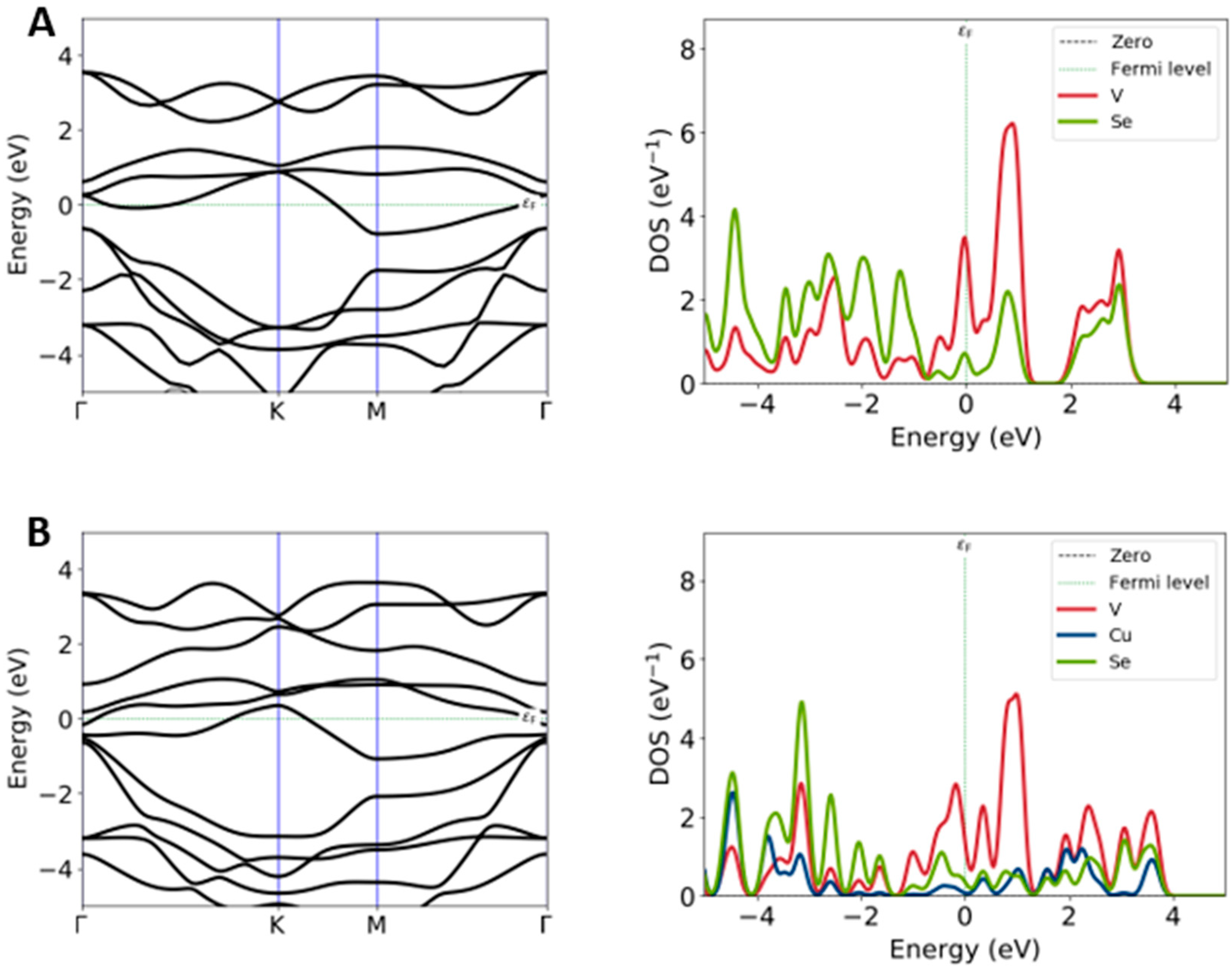
2.2. Electronic Structure Calculations
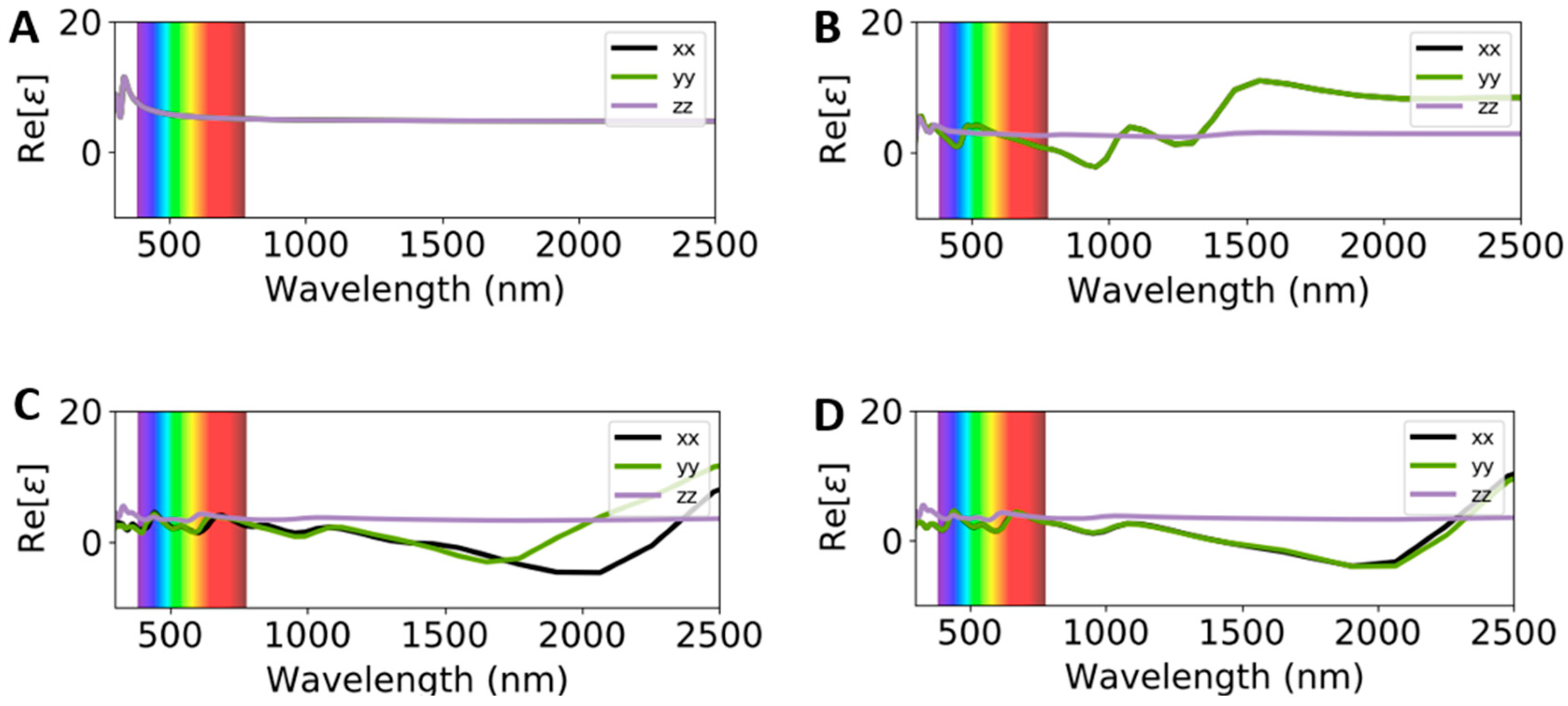
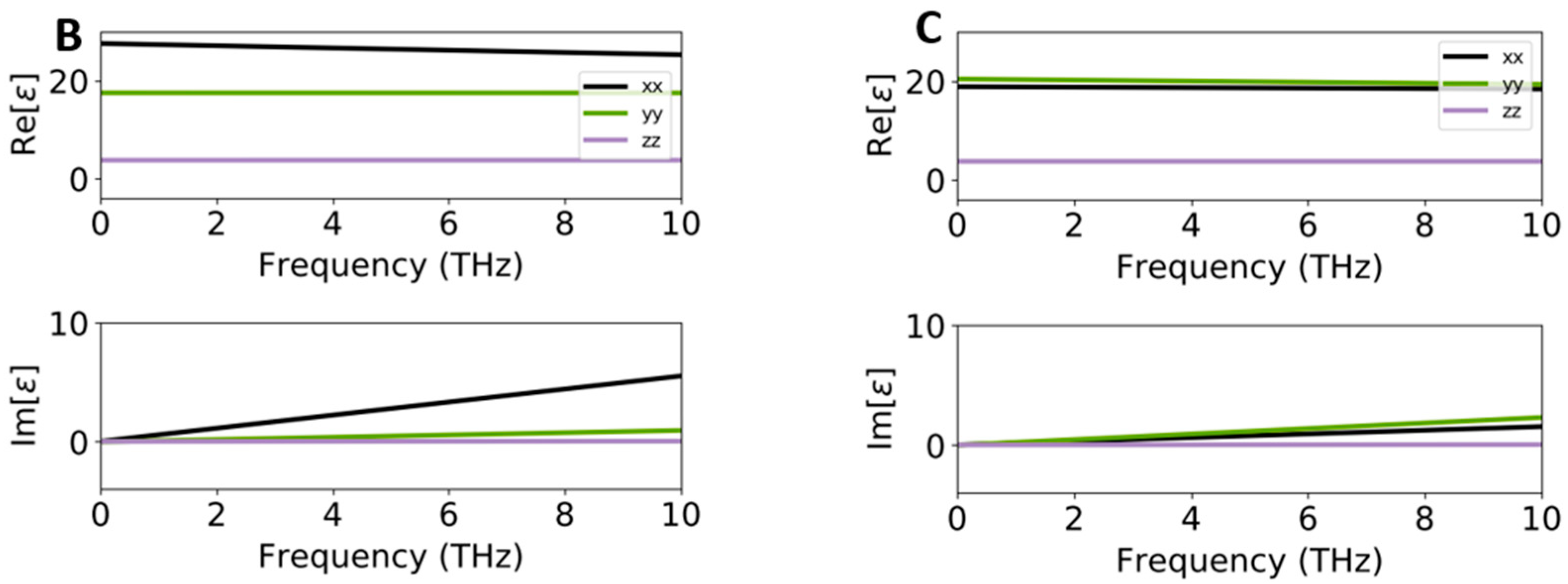
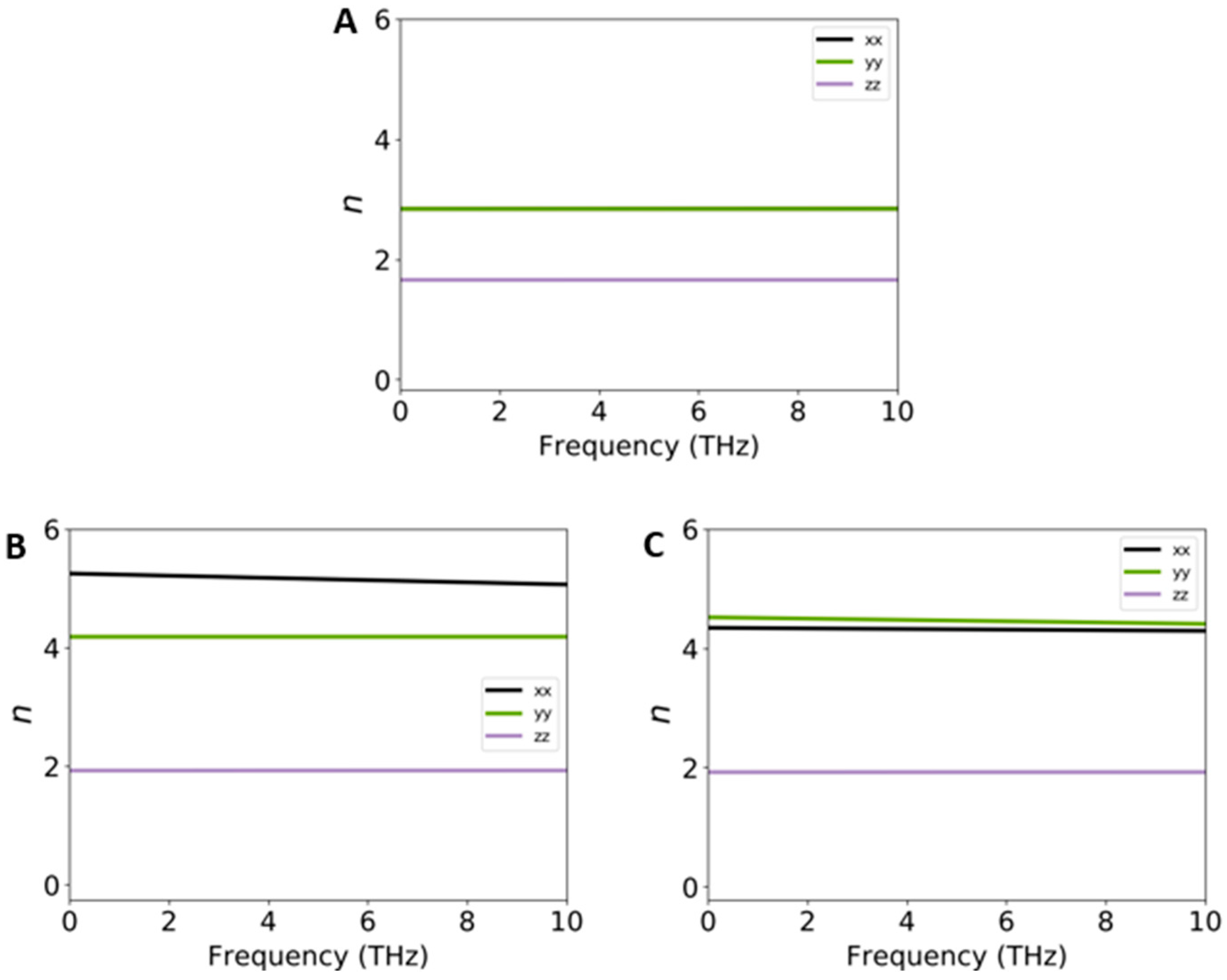
2.3. Optical Properties
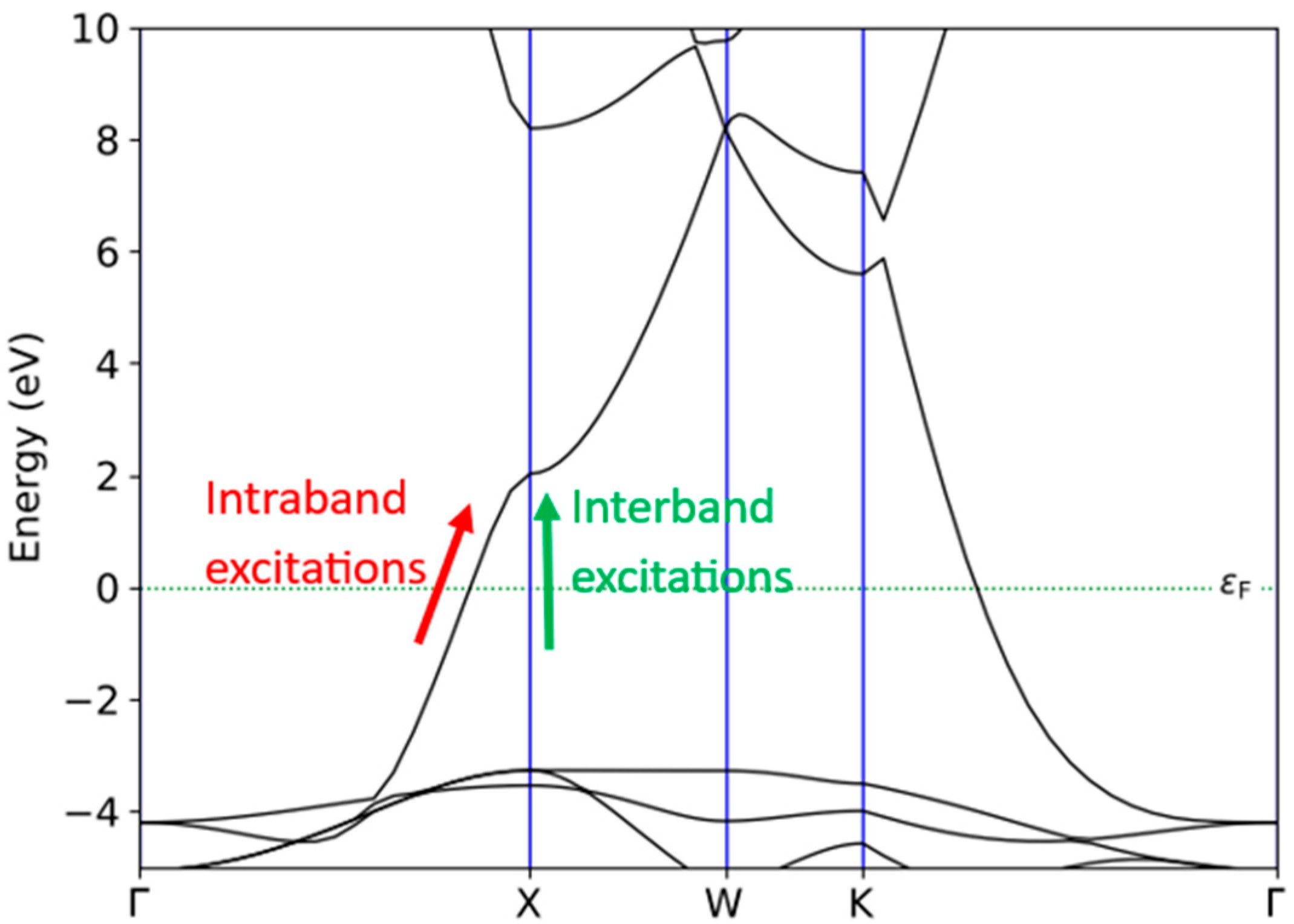
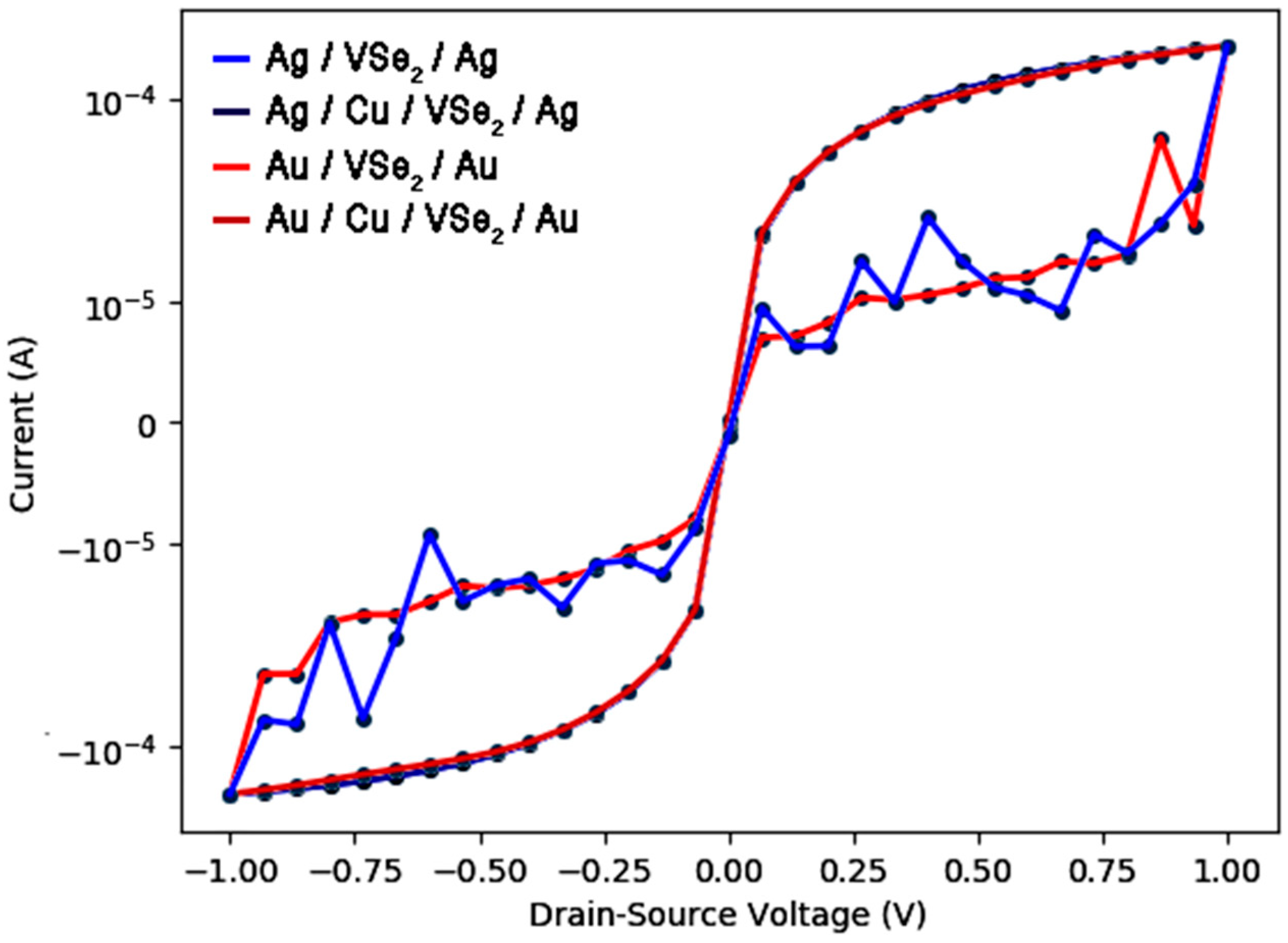
2.4. I(V) Characteristics
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chhowalla, M.; Liu, Z.; Zhang, H. Two-Dimensional Transition Metal Dichalcogenide (TMD) Nanosheets. Chem. Soc. Rev. 2015, 44, 2584–2586. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent Development of Two-Dimensional Transition Metal Dichalcogenides and Their Applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Mohebbi, E.; Pavoni, E.; Pierantoni, L.; Stipa, P.; Laudadio, E.; Mencarelli, D. Effect of Different Pseudopotentials on the Phonon Frequencies, Dielectric Constant, and Born Effective Charge of SnSe and SnSe2 Nanostructures: A Density Functional Perturbation Theory Study. J. Phys. Chem. Solids 2024, 185, 111755. [Google Scholar] [CrossRef]
- Li, J.; Jiang, L.; Ma, W.; Wu, T.; Qiu, Q.; Shi, Y.; Zhou, W.; Yao, N.; Huang, Z. VSe2 Nanosheets for Broadband Photodetection from Visible to Terahertz. ACS Appl. Nano Mater. 2022, 5, 5158–5167. [Google Scholar] [CrossRef]
- Pataniya, P.M.; Patel, V.; Sumesh, C.K. MoS2/WSe2 Nanohybrids for Flexible Paper-Based Photodetectors. Nanotechnology 2021, 32, 315709. [Google Scholar] [CrossRef] [PubMed]
- Mohebbi, E.; Pavoni, E.; Pierantoni, L.; Stipa, P.; Zampa, G.M.; Laudadio, E.; Mencarelli, D. Band Gap and THz Optical Adsorption of SnSe and SnSe2 Nanosheets on Graphene: Negative Dielectric Constant of SnSe. Results Phys. 2024, 57, 107415. [Google Scholar] [CrossRef]
- Guan, X.; Yu, X.; Periyanagounder, D.; Benzigar, M.R.; Huang, J.; Lin, C.; Kim, J.; Singh, S.; Hu, L.; Liu, G. Recent Progress in Short-to Long-wave Infrared Photodetection Using 2D Materials and Heterostructures. Adv. Opt. Mater. 2021, 9, 2001708. [Google Scholar] [CrossRef]
- Chowdhury, T.; Sadler, E.C.; Kempa, T.J. Progress and Prospects in Transition-Metal Dichalcogenide Research beyond 2D. Chem. Rev. 2020, 120, 12563–12591. [Google Scholar] [CrossRef]
- Pavoni, E.; Mohebbi, E.; Zampa, G.M.; Stipa, P.; Pierantoni, L.; Laudadio, E.; Mencarelli, D. First Principles Study of WSe2 and the Effect of V Doping on the Optical and Electronic Properties. Mater. Adv. 2024, 5, 2230–2237. [Google Scholar] [CrossRef]
- Zhang, Z.; Niu, J.; Yang, P.; Gong, Y.; Ji, Q.; Shi, J.; Fang, Q.; Jiang, S.; Li, H.; Zhou, X.; et al. Van Der Waals Epitaxial Growth of 2D Metallic Vanadium Diselenide Single Crystals and Their Extra-high Electrical Conductivity. Adv. Mater. 2017, 29, 1702359. [Google Scholar] [CrossRef]
- Brauer, H.E.; Starnberg, H.I.; Holleboom, L.J.; Strocov, V.N.; Hughes, H.P. Electronic Structure of Pure and Alkali-Metal-Intercalated VSe2. Phys. Rev. B 1998, 58, 10031. [Google Scholar] [CrossRef]
- Ma, Y.; Dai, Y.; Guo, M.; Niu, C.; Zhu, Y.; Huang, B. Evidence of the Existence of Magnetism in Pristine VX2 Monolayers (X= S, Se) and Their Strain-Induced Tunable Magnetic Properties. ACS Nano 2012, 6, 1695–1701. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Biswas, D.; Rajan, A.; Watson, M.D.; Mazzola, F.; Clark, O.J.; Underwood, K.; Markovic, I.; McLaren, M.; Hunter, A.; et al. Electronic Structure and Enhanced Charge-Density Wave Order of Monolayer VSe2. Nano Lett. 2018, 18, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
- Strocov, V.N.; Shi, M.; Kobayashi, M.; Monney, C.; Wang, X.; Krempasky, J.; Schmitt, T.; Patthey, L.; Berger, H.; Blaha, P.; et al. Three-Dimensional Electron Realm in VSe2 by Soft-x-Ray Photoelectron Spectroscopy: Origin of Charge-Density Waves. Phys. Rev. Lett. 2012, 109, 086401. [Google Scholar] [CrossRef]
- Awazu, K.; Fujimaki, M.; Rockstuhl, C.; Tominaga, J.; Murakami, H.; Ohki, Y.; Yoshida, N.; Watanabe, T. A Plasmonic Photocatalyst Consisting of Silver Nanoparticles Embedded in Titanium Dioxide. J. Am. Chem. Soc. 2008, 130, 1676–1680. [Google Scholar] [CrossRef]
- Ramakrishna, G.; Ghosh, H.N. Effect of Particle Size on the Reactivity of Quantum Size ZnO Nanoparticles and Charge-Transfer Dynamics with Adsorbed Catechols. Langmuir 2003, 19, 3006–3012. [Google Scholar] [CrossRef]
- Qin, Y.; Kong, X.-T.; Wang, Z.; Govorov, A.O.; Kortshagen, U.R. Near-Infrared Plasmonic Copper Nanocups Fabricated by Template-Assisted Magnetron Sputtering. ACS Photonics 2017, 4, 2881–2890. [Google Scholar] [CrossRef]
- Grubisic, A.; Schweikhard, V.; Baker, T.A.; Nesbitt, D.J. Multiphoton Photoelectron Emission Microscopy of Single Au Nanorods: Combined Experimental and Theoretical Study of Rod Morphology and Dielectric Environment on Localized Surface Plasmon Resonances. Phys. Chem. Chem. Phys. 2013, 15, 10616–10627. [Google Scholar] [CrossRef]
- Takahata, R.; Yamazoe, S.; Koyasu, K.; Imura, K.; Tsukuda, T. Gold Ultrathin Nanorods with Controlled Aspect Ratios and Surface Modifications: Formation Mechanism and Localized Surface Plasmon Resonance. J. Am. Chem. Soc. 2018, 140, 6640–6647. [Google Scholar] [CrossRef]
- Seh, Z.W.; Liu, S.; Low, M.; Zhang, S.; Liu, Z.; Mlayah, A.; Han, M. Janus Au-TiO2 Photocatalysts with Strong Localization of Plasmonic Near-fields for Efficient Visible-light Hydrogen Generation. Adv. Mater. 2012, 24, 2310–2314. [Google Scholar] [CrossRef]
- Qiao, L.; Wang, D.; Zuo, L.; Ye, Y.; Qian, J.; Chen, H.; He, S. Localized Surface Plasmon Resonance Enhanced Organic Solar Cell with Gold Nanospheres. Appl. Energy 2011, 88, 848–852. [Google Scholar] [CrossRef]
- Mascaretti, L.; Dutta, A.; Kment, Š.; Shalaev, V.M.; Boltasseva, A.; Zbořil, R.; Naldoni, A. Plasmon-enhanced Photoelectrochemical Water Splitting for Efficient Renewable Energy Storage. Adv. Mater. 2019, 31, 1805513. [Google Scholar] [CrossRef] [PubMed]
- Homola, J. Surface Plasmon Resonance Sensors for Detection of Chemical and Biological Species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef]
- Gawande, M.B.; Goswami, A.; Felpin, F.-X.; Asefa, T.; Huang, X.; Silva, R.; Zou, X.; Zboril, R.; Varma, R.S. Cu and Cu-Based Nanoparticles: Synthesis and Applications in Catalysis. Chem. Rev. 2016, 116, 3722–3811. [Google Scholar] [CrossRef]
- Linic, S.; Aslam, U.; Boerigter, C.; Morabito, M. Photochemical Transformations on Plasmonic Metal Nanoparticles. Nat. Mater. 2015, 14, 567–576. [Google Scholar] [CrossRef]
- Yao, G.-Y.; Zhao, Z.-Y.; Liu, Q.-L.; Dong, X.-D.; Zhao, Q.-M. Theoretical Calculations for Localized Surface Plasmon Resonance Effects of Cu/TiO2 Nanosphere: Generation, Modulation, and Application in Photocatalysis. Sol. Energy Mater. Sol. Cells 2020, 208, 110385. [Google Scholar] [CrossRef]
- Bayliss, S.C.; Liang, W.Y. Reflectivity and Band Structure of 1T-VSe2. J. Phys. C Solid State Phys. 1984, 17, 2193. [Google Scholar] [CrossRef]
- Wilson, J.A.; Yoffe, A.D. The Transition Metal Dichalcogenides Discussion and Interpretation of the Observed Optical, Electrical and Structural Properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Reshak, A.H.; Auluck, S. Theoretical Investigations of the Electronic and Optical Properties of Pure and Alkali Metal Intercalated 1T-VSe2. Phys. B Condens. Matter 2004, 349, 310–315. [Google Scholar] [CrossRef]
- Chazarin, U.; Lezoualc’h, M.; Chou, J.; Pai, W.W.; Karn, A.; Sankar, R.; Chacon, C.C.; Girard, Y.; Repain, V.; Bellec, A.; et al. Formation of Monolayer Charge Density Waves and Anomalous Edge Doping in Na Doped Bulk VSe2. Adv. Mater. Interfaces 2023, 10, 2201680. [Google Scholar] [CrossRef]
- Sita, Z.; Sedlakova, V.; Majzner, J.; Sedlak, P.; Sikula, J.; Grmela, L. Analysis of Noise and Non-Linearity of IV Characteristics of Positive Temperature Coefficient Chip Thermistors. Metrol. Meas. Syst. 2013, 20, 635–644. [Google Scholar] [CrossRef]
- Lee, C.; Park, Y.; Park, J.Y. Hot Electrons Generated by Intraband and Interband Transition Detected Using a Plasmonic Cu/TiO2 Nanodiode. RSC Adv. 2019, 9, 18371–18376. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An Integrated Platform of Electronic and Atomic-Scale Modelling Tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef]
- Pavoni, E.; Mohebbi, E.; Stipa, P.; Pierantoni, L.; Mencarelli, D.; Dragoman, M.; Aldrigo, M.; Laudadio, E. First-Principles Investigation of Interface Phenomena in Hafnium-Based Metal–Insulator–Metal Diodes. Nanoscale Adv. 2023, 5, 2748–2755. [Google Scholar] [CrossRef]
- Laudadio, E.; Mohebbi, E.; Pavoni, E.; Minnelli, C.; Sabbatini, S.; Stipa, P. Density Functional Theory and Molecular Dynamics Studies on Electrical, Mechanical, and Thermal Properties of TiO2 Nanoparticles Interacting with Poly Lactic-Co-Glycolic Acid. Colloids Surf. A Physicochem. Eng. Asp. 2023, 667, 131388. [Google Scholar] [CrossRef]
- Mohebbi, E.; Pavoni, E.; Pierantoni, L.; Stipa, P.; Laudadio, E.; Mencarelli, D. Insights Into a New Geometric Graphene Diode with Ultrahigh Asymmetry Ratio: A Computational Approach. In Proceedings of the 2023 IEEE 23rd International Conference on Nanotechnology (NANO), Jeju Island, Republic of Korea, 2–5 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 238–242. [Google Scholar]
- Ernzerhof, M.; Scuseria, G.E. Perspective on “Inhomogeneous Electron Gas” Hohenberg P, Kohn W (1964) Phys Rev 136: B864. Theor. Chem. Acc. 2000, 103, 259–262. [Google Scholar] [CrossRef]
- Sánchez-Portal, D.; Ordejon, P.; Artacho, E.; Soler, J.M. Density-functional Method for Very Large Systems with LCAO Basis Sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar] [CrossRef]
- van Setten, M.J.; Giantomassi, M.; Bousquet, E.; Verstraete, M.J.; Hamann, D.R.; Gonze, X.; Rignanese, G.-M. The PseudoDojo: Training and Grading a 85 Element Optimized Norm-Conserving Pseudopotential Table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Ehrlich, S.; Moellmann, J.; Reckien, W.; Bredow, T.; Grimme, S. System-dependent Dispersion Coefficients for the DFT-D3 Treatment of Adsorption Processes on Ionic Surfaces. ChemPhysChem 2011, 12, 3414–3420. [Google Scholar] [CrossRef] [PubMed]
- Sedona, F.; Fakhrabadi, M.M.S.; Carlotto, S.; Mohebbi, E.; De Boni, F.; Casalini, S.; Casarin, M.; Sambi, M. On-Surface Synthesis of Extended Linear Graphyne Molecular Wires by Protecting the Alkynyl Group. Phys. Chem. Chem. Phys. 2020, 22, 12180–12186. [Google Scholar] [CrossRef] [PubMed]
- Henderson, T.M.; Paier, J.; Scuseria, G.E. Accurate Treatment of Solids with the HSE Screened Hybrid. Phys. Status Solidi 2011, 248, 767–774. [Google Scholar] [CrossRef]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2020; ISBN 1108657478. [Google Scholar]
- Mohebbi, E.; Pavoni, E.; Pierantoni, L.; Stipa, P.; Hemmetter, A.; Laudadio, E.; Mencarelli, D. Towards Graphene-Based Asymmetric Diodes: A Density Functional Tight-Binding Study. Nanoscale Adv. 2024, 6, 1548–1555. [Google Scholar] [CrossRef]
- Seifert, G.; Eschrig, H.; Bieger, W. An Approximation Variant of LCAO-X-ALPHA Methods. Z. Fur Phys. Chem.-Leipz. 1986, 267, 529–539. [Google Scholar]
- Foulkes, W.M.C.; Haydock, R. Tight-Binding Models and Density-Functional Theory. Phys. Rev. B 1989, 39, 12520. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Ammeter, J.H.; Bürgi, H.-B.; Thibeault, J.C.; Hoffmann, R. Counterintuitive Orbital Mixing in Semiempirical and Ab Initio Molecular Orbital Calculations. J. Am. Chem. Soc. 1978, 100, 3686–3692. [Google Scholar] [CrossRef]
- Eschrig, H. Optimized LCAO Method and the Electronic Structure of Extended Systems; Walter de Gruyter GmbH &, Co., KG: Berlin, Germany, 2022; ISBN 3112483464. [Google Scholar]
- Stokbro, K.; Petersen, D.E.; Smidstrup, S.; Blom, A.; Ipsen, M.; Kaasbjerg, K. Semiempirical Model for Nanoscale Device Simulations. Phys. Rev. B 2010, 82, 075420. [Google Scholar] [CrossRef]
- Ozaki, T.; Nishio, K.; Kino, H. Efficient Implementation of the Nonequilibrium Green Function Method for Electronic Transport Calculations. Phys. Rev. B 2010, 81, 035116. [Google Scholar] [CrossRef]
- Zampa, G.M.; Mencarelli, D.; Pierantoni, L. A Full-Wave Time-Dependent Schrödinger Equation Approach for the Modeling of Asymmetric Transport in Geometric Diodes. Phys. B Condens. Matter 2023, 661, 414917. [Google Scholar] [CrossRef]
- Haug, H.; Jauho, A.-P. Quantum Kinetics in Transport and Optics of Semiconductors; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohebbi, E.; Pavoni, E.; Stipa, P.; Pierantoni, L.; Laudadio, E.; Mencarelli, D. Tunable Optical Properties of Cu/VSe2 from the Visible to Terahertz Spectral Range: A First-Principles Study. Int. J. Mol. Sci. 2025, 26, 2527. https://doi.org/10.3390/ijms26062527
Mohebbi E, Pavoni E, Stipa P, Pierantoni L, Laudadio E, Mencarelli D. Tunable Optical Properties of Cu/VSe2 from the Visible to Terahertz Spectral Range: A First-Principles Study. International Journal of Molecular Sciences. 2025; 26(6):2527. https://doi.org/10.3390/ijms26062527
Chicago/Turabian StyleMohebbi, Elaheh, Eleonora Pavoni, Pierluigi Stipa, Luca Pierantoni, Emiliano Laudadio, and Davide Mencarelli. 2025. "Tunable Optical Properties of Cu/VSe2 from the Visible to Terahertz Spectral Range: A First-Principles Study" International Journal of Molecular Sciences 26, no. 6: 2527. https://doi.org/10.3390/ijms26062527
APA StyleMohebbi, E., Pavoni, E., Stipa, P., Pierantoni, L., Laudadio, E., & Mencarelli, D. (2025). Tunable Optical Properties of Cu/VSe2 from the Visible to Terahertz Spectral Range: A First-Principles Study. International Journal of Molecular Sciences, 26(6), 2527. https://doi.org/10.3390/ijms26062527









