ICVAE: Interpretable Conditional Variational Autoencoder for De Novo Molecular Design
Abstract
:1. Introduction
2. Results
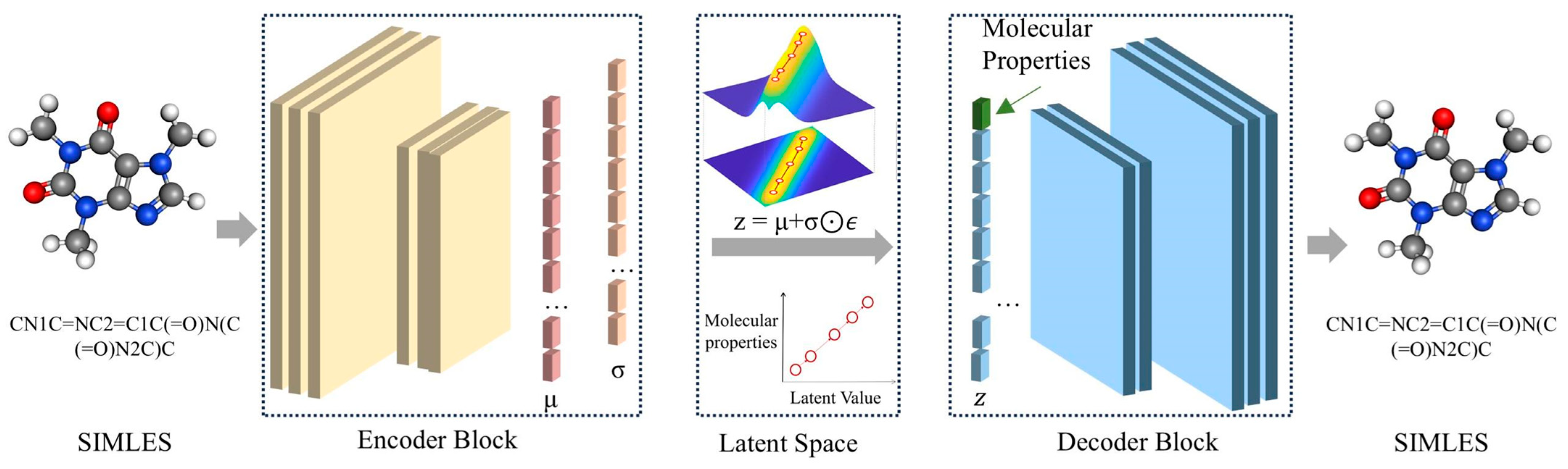
2.1. Workflow Summary
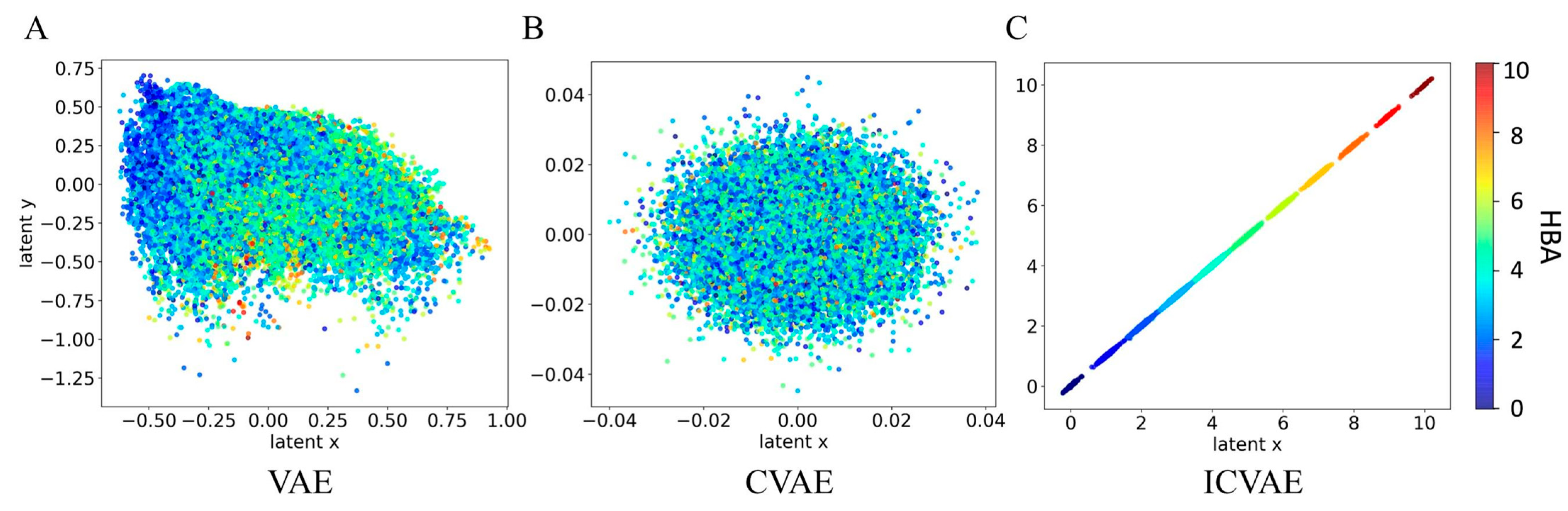
2.2. The Interpretability of ICVAE
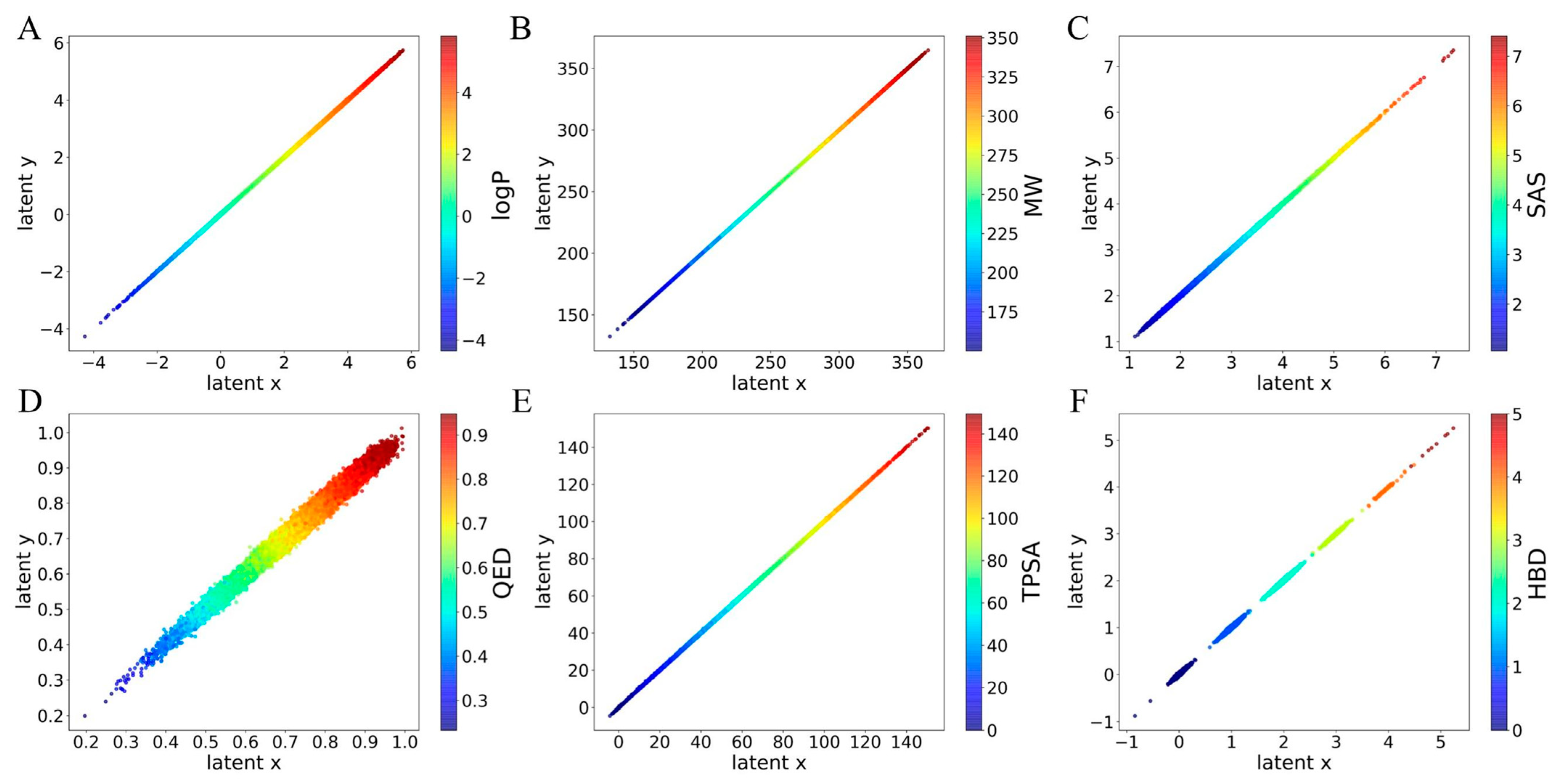
2.3. The Latent Space of ICVAE with Single Property
2.4. The Latent Space of ICVAE with Multiple Properties
2.5. The Performances of Molecular Generation
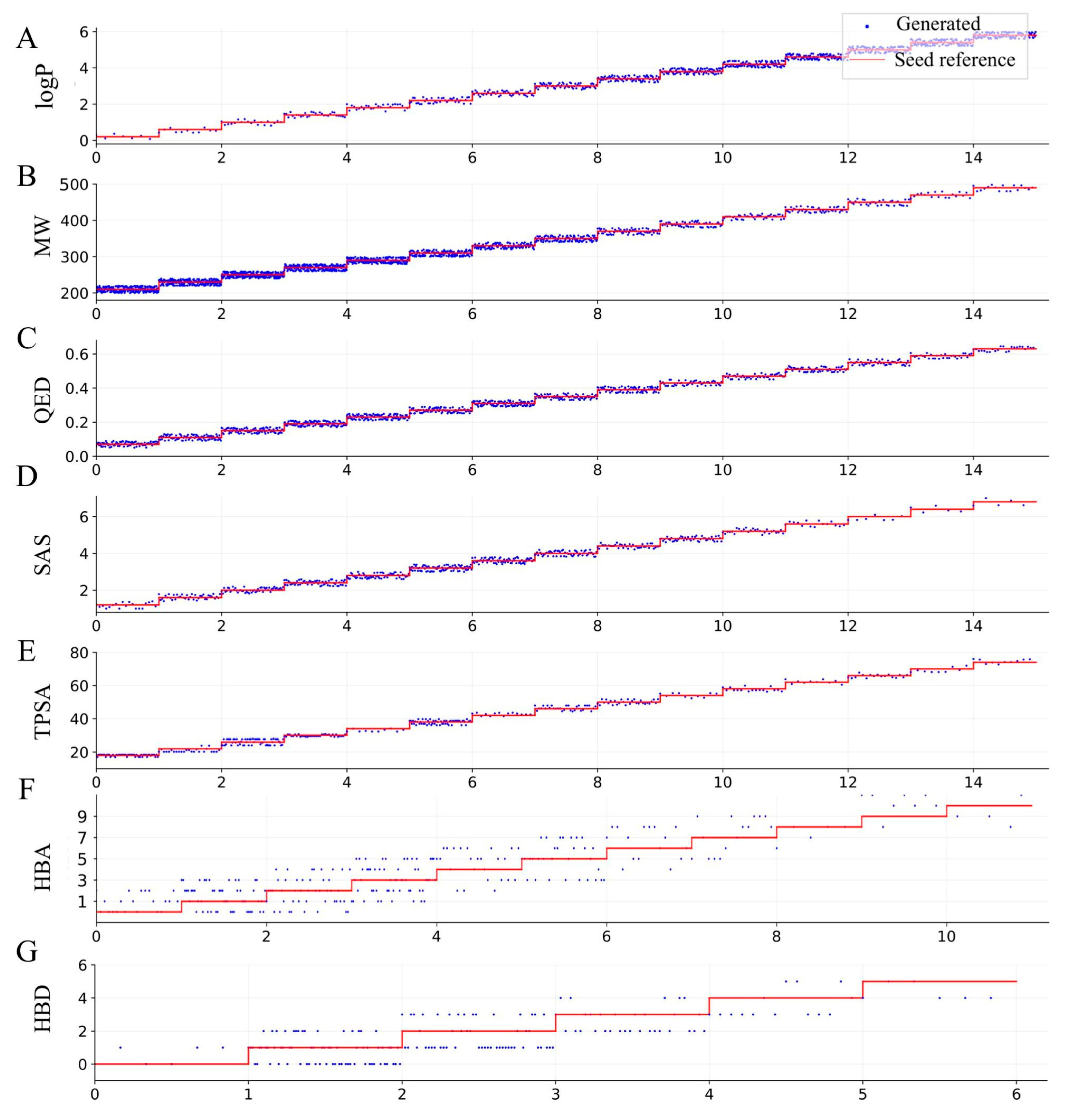
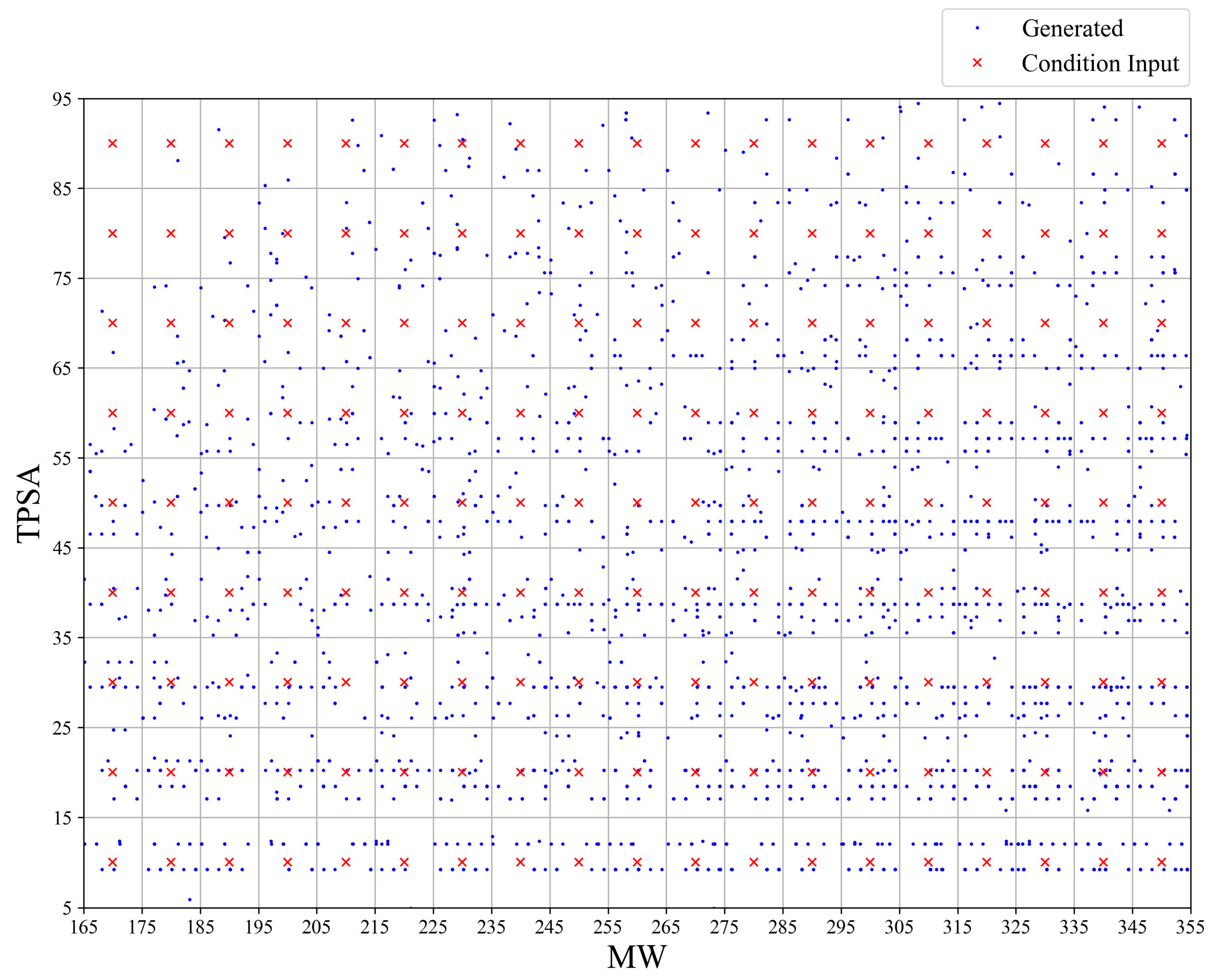
2.6. Molecular Generation with Target Properties
3. Discussion
Limitations and Future Work
4. Materials and Methods
4.1. Dataset
4.2. Data Processing
4.3. Algorithm of ICVAE
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fleming, N. How artificial intelligence is changing drug discovery. Nature 2018, 577, S55–S57. [Google Scholar] [CrossRef] [PubMed]
- Schneider, P.; Walters, W.P.; Plowright, A.T.; Sieroka, N.; Listgarten, J.; Goodnow, R.A., Jr.; Fisher, J.; Jansen, J.M.; Duca, J.S.; Rush, T.S. Rethinking drug design in the artificial intelligence era. Nat. Rev. Drug Discov. 2020, 19, 353–364. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, F.; Luo, Y.; Kang, S.-g.; Tang, J.; Lightstone, F.C.; Fang, E.F.; Cornell, W.; Nussinov, R.; Cheng, F. Deep generative molecular design reshapes drug discovery. Cell Rep. Med. 2022, 3, 100794. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Liu, X.; Tan, X.; Li, X.; Jiang, J.; Xiong, Z.; Xu, T.; Jiang, H.; Qiao, N.; Zheng, M. Generative models for de novo drug design. J. Med. Chem. 2021, 64, 14011–14027. [Google Scholar] [CrossRef]
- Zhavoronkov, A.; Ivanenkov, Y.A.; Aliper, A.; Veselov, M.S.; Aladinskiy, V.A.; Aladinskaya, A.V.; Terentiev, V.A.; Polykovskiy, D.A.; Kuznetsov, M.D.; Asadulaev, A. Deep learning enables rapid identification of potent DDR1 kinase inhibitors. Nat. Biotechnol. 2019, 37, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Wang, L.; Meng, J.; Zhao, Q.; Zhang, L.; Liu, H. De Novo design of potential inhibitors against SARS-CoV-2 Mpro. Comput. Biol. Med. 2022, 147, 105728. [Google Scholar] [CrossRef]
- Gupta, A.; Müller, A.T.; Huisman, B.J.; Fuchs, J.A.; Schneider, P.; Schneider, G. Generative recurrent networks for de novo drug design. Mol. Inform. 2018, 37, 1700111. [Google Scholar] [CrossRef]
- Pogány, P.; Arad, N.; Genway, S.; Pickett, S.D. De novo molecule design by translating from reduced graphs to SMILES. J. Chem. Inf. Model. 2018, 59, 1136–1146. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Yoshizoe, K.; Terayama, K.; Tsuda, K. ChemTS: An efficient python library for de novo molecular generation. Sci. Technol. Adv. Mater. 2017, 18, 972–976. [Google Scholar] [CrossRef]
- Segler, M.H.; Kogej, T.; Tyrchan, C.; Waller, M.P. Generating focused molecule libraries for drug discovery with recurrent neural networks. ACS Cent. Sci. 2018, 4, 120–131. [Google Scholar] [CrossRef]
- Liu, X.; Ye, K.; Van Vlijmen, H.W.; IJzerman, A.P.; Van Westen, G.J. An exploration strategy improves the diversity of de novo ligands using deep reinforcement learning: A case for the adenosine A2A receptor. J. Cheminform. 2019, 11, 35. [Google Scholar] [CrossRef]
- Merk, D.; Friedrich, L.; Grisoni, F.; Schneider, G. De novo design of bioactive small molecules by artificial intelligence. Mol. Inform. 2018, 37, 1700153. [Google Scholar] [CrossRef] [PubMed]
- Grisoni, F.; Moret, M.; Lingwood, R.; Schneider, G. Bidirectional molecule generation with recurrent neural networks. J. Chem. Inf. Model. 2020, 60, 1175–1183. [Google Scholar] [CrossRef]
- Li, C.; Wang, C.; Sun, M.; Zeng, Y.; Yuan, Y.; Gou, Q.; Wang, G.; Guo, Y.; Pu, X. Correlated RNN framework to quickly generate molecules with desired properties for energetic materials in the low data regime. J. Chem. Inf. Model. 2022, 62, 4873–4887. [Google Scholar] [CrossRef]
- Stravs, M.A.; Dührkop, K.; Böcker, S.; Zamboni, N. MSNovelist: De novo structure generation from mass spectra. Nat. Methods 2022, 19, 865–870. [Google Scholar] [CrossRef]
- Kadurin, A.; Nikolenko, S.; Khrabrov, K.; Aliper, A.; Zhavoronkov, A. druGAN: An advanced generative adversarial autoencoder model for de novo generation of new molecules with desired molecular properties in silico. Mol. Pharm. 2017, 14, 3098–3104. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Cho, K. Conditional molecular design with deep generative models. J. Chem. Inf. Model. 2018, 59, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.; Ryu, S.; Kim, J.W.; Kim, W.Y. Molecular generative model based on conditional variational autoencoder for de novo molecular design. J. Cheminform. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef]
- Colby, S.M.; Nuñez, J.R.; Hodas, N.O.; Corley, C.D.; Renslow, R.R. Deep learning to generate in silico chemical property libraries and candidate molecules for small molecule identification in complex samples. Anal. Chem. 2019, 92, 1720–1729. [Google Scholar] [CrossRef]
- Joo, S.; Kim, M.S.; Yang, J.; Park, J. Generative model for proposing drug candidates satisfying anticancer properties using a conditional variational autoencoder. ACS Omega 2020, 5, 18642–18650. [Google Scholar] [CrossRef]
- Bjerrum, E.J.; Sattarov, B. Improving chemical autoencoder latent space and molecular de novo generation diversity with heteroencoders. Biomolecules 2018, 8, 131. [Google Scholar] [CrossRef] [PubMed]
- Kotsias, P.-C.; Arús-Pous, J.; Chen, H.; Engkvist, O.; Tyrchan, C.; Bjerrum, E.J. Direct steering of de novo molecular generation with descriptor conditional recurrent neural networks. Nat. Mach. Intell. 2020, 2, 254–265. [Google Scholar] [CrossRef]
- Bagal, V.; Aggarwal, R.; Vinod, P.; Priyakumar, U.D. MolGPT: Molecular generation using a transformer-decoder model. J. Chem. Inf. Model. 2021, 62, 2064–2076. [Google Scholar] [CrossRef]
- Popova, M.; Isayev, O.; Tropsha, A. Deep reinforcement learning for de novo drug design. Sci. Adv. 2018, 4, eaap7885. [Google Scholar] [CrossRef] [PubMed]
- Ståhl, N.; Falkman, G.; Karlsson, A.; Mathiason, G.; Bostrom, J. Deep reinforcement learning for multiparameter optimization in de novo drug design. J. Chem. Inf. Model. 2019, 59, 3166–3176. [Google Scholar] [CrossRef]
- Wang, J.; Hsieh, C.-Y.; Wang, M.; Wang, X.; Wu, Z.; Jiang, D.; Liao, B.; Zhang, X.; Yang, B.; He, Q. Multi-constraint molecular generation based on conditional transformer, knowledge distillation and reinforcement learning. Nat. Mach. Intell. 2021, 3, 914–922. [Google Scholar] [CrossRef]
- Korshunova, M.; Huang, N.; Capuzzi, S.; Radchenko, D.S.; Savych, O.; Moroz, Y.S.; Wells, C.I.; Willson, T.M.; Tropsha, A.; Isayev, O. Generative and reinforcement learning approaches for the automated de novo design of bioactive compounds. Commun. Chem. 2022, 5, 129. [Google Scholar] [CrossRef]
- Olivecrona, M.; Blaschke, T.; Engkvist, O.; Chen, H. Molecular de-novo design through deep reinforcement learning. J. Cheminform. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Guo, J.; Fialková, V.; Arango, J.D.; Margreitter, C.; Janet, J.P.; Papadopoulos, K.; Engkvist, O.; Patronov, A. Improving de novo molecular design with curriculum learning. Nat. Mach. Intell. 2022, 4, 555–563. [Google Scholar] [CrossRef]
- Wan, C.; Jones, D.T. Improving protein function prediction with synthetic feature samples created by generative adversarial networks. bioRxiv 2019. [Google Scholar] [CrossRef]
- Bian, Y.; Wang, J.; Jun, J.J.; Xie, X.-Q. Deep convolutional generative adversarial network (dcGAN) models for screening and design of small molecules targeting cannabinoid receptors. Mol. Pharm. 2019, 16, 4451–4460. [Google Scholar] [CrossRef] [PubMed]
- Prykhodko, O.; Johansson, S.V.; Kotsias, P.-C.; Arús-Pous, J.; Bjerrum, E.J.; Engkvist, O.; Chen, H. A de novo molecular generation method using latent vector based generative adversarial network. J. Cheminform. 2019, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Sousa, T.; Correia, J.; Pereira, V.; Rocha, M. Generative deep learning for targeted compound design. J. Chem. Inf. Model. 2021, 61, 5343–5361. [Google Scholar] [CrossRef]
- De Cao, N.; Kipf, T. MolGAN: An implicit generative model for small molecular graphs. arXiv 2018, arXiv:1805.11973. [Google Scholar]
- Griffiths, R.-R.; Hernández-Lobato, J.M. Constrained Bayesian optimization for automatic chemical design using variational autoencoders. Chem. Sci. 2020, 11, 577–586. [Google Scholar] [CrossRef] [PubMed]
- Leguy, J.; Cauchy, T.; Glavatskikh, M.; Duval, B.; Da Mota, B. EvoMol: A flexible and interpretable evolutionary algorithm for unbiased de novo molecular generation. J. Cheminform. 2020, 12, 1–19. [Google Scholar] [CrossRef]
- Krishnan, S.R.; Bung, N.; Bulusu, G.; Roy, A. Accelerating de novo drug design against novel proteins using deep learning. J. Chem. Inf. Model. 2021, 61, 621–630. [Google Scholar] [CrossRef]
- Noutahi, E.; Beaini, D.; Horwood, J.; Giguère, S.; Tossou, P. Towards interpretable sparse graph representation learning with laplacian pooling. arXiv 2019, arXiv:1905.11577. [Google Scholar]
- Polykovskiy, D.; Zhebrak, A.; Sanchez-Lengeling, B.; Golovanov, S.; Tatanov, O.; Belyaev, S.; Kurbanov, R.; Artamonov, A.; Aladinskiy, V.; Veselov, M. Molecular sets (MOSES): A benchmarking platform for molecular generation models. Front. Pharmacol. 2020, 11, 565644. [Google Scholar] [CrossRef]
- Irwin, J.J.; Sterling, T.; Mysinger, M.M.; Bolstad, E.S.; Coleman, R.G. ZINC: A free tool to discover chemistry for biology. J. Chem. Inf. Model. 2012, 52, 1757–1768. [Google Scholar] [CrossRef] [PubMed]


| Model | Unique@1k↑ a | Valid↑ | SNN↑ | Frag↑ | Novelty↑ | IntDiv↑ |
|---|---|---|---|---|---|---|
| VAE | 1.000 | 0.977 | 0.626 | 0.999 | 0.695 | 0.856 |
| CVAE | 0.975 | 0.971 | 0.315 | 0.925 | 0.985 | 0.832 |
| ICVAE | 1.000 | 0.979 | 0.339 | 0.843 | 1.000 | 0.869 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Fang, S.; Li, Z.; Ji, H.; Yue, M.; Li, J.; Ren, X. ICVAE: Interpretable Conditional Variational Autoencoder for De Novo Molecular Design. Int. J. Mol. Sci. 2025, 26, 3980. https://doi.org/10.3390/ijms26093980
Fan X, Fang S, Li Z, Ji H, Yue M, Li J, Ren X. ICVAE: Interpretable Conditional Variational Autoencoder for De Novo Molecular Design. International Journal of Molecular Sciences. 2025; 26(9):3980. https://doi.org/10.3390/ijms26093980
Chicago/Turabian StyleFan, Xiaqiong, Senlin Fang, Zhengyan Li, Hongchao Ji, Minghan Yue, Jiamin Li, and Xiaozhen Ren. 2025. "ICVAE: Interpretable Conditional Variational Autoencoder for De Novo Molecular Design" International Journal of Molecular Sciences 26, no. 9: 3980. https://doi.org/10.3390/ijms26093980
APA StyleFan, X., Fang, S., Li, Z., Ji, H., Yue, M., Li, J., & Ren, X. (2025). ICVAE: Interpretable Conditional Variational Autoencoder for De Novo Molecular Design. International Journal of Molecular Sciences, 26(9), 3980. https://doi.org/10.3390/ijms26093980











