Ab Initio Study of the Prototropic Tautomerism of Cytosine and Guanine and Their Contribution to Spontaneous Point Mutations
Abstract
:Introduction

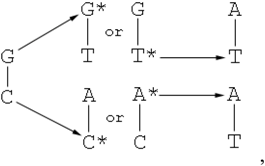
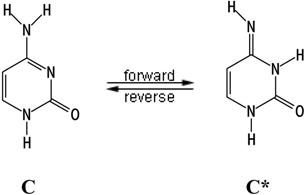
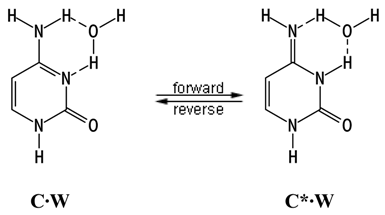
- The equilibrium in the tautomeric transformations is reached during the synthesis of DNA (equation (2) for cytosine and analogous one for guanine [33]). Topal and Fresco [35] were the first to propose this scheme. They suggested that the value of the equilibrium constant should be in the range of 10-4 – 10-5 if the same equilibrium is also governing the “proof-reading” reaction [35].
- The second mechanism was first discussed by Löwdin [9]. He suggested that the equilibrium is not reached during the DNA synthesis due to the fact that the forward reaction in (2) is too slow. This suggests that the forward reaction rate constant is a limited factor rather than the equilibrium constant. Therefore, this constant should be large enough to be able to generate a concentration of rare form significant enough to reproduce the frequency of point mutations after the proofreading step of the DNA synthesis.
Details of Calculations
Results and Discussion
| Cytosine | Guanine† | |||||||
| Level of Theory | C↔C* | C∙W↔C*∙W | G↔G* | G∙W↔G*∙W | ||||
| ∆G298 | K | ∆G298 | K | ∆G298 | K | ∆G298 | K | |
| MP2/6-31G(d)‡ | 1.58 | 7.0 × 10-2 | 2.57 | 1.3 × 10-2 | 2.38 | 1.8 × 10-2 | 3.65 | 2.1 × 10-3 |
| MP2/6-31G(d) | 0.82 | 2.5 × 10-1 | 2.07 | 3.0 × 10-2 | — | — | — | — |
| MP2/6-31++G(d,p)// MP2/6-31G(d)‡ | — | — | — | — | 0.39 | 5.2 × 10-1 | 2.30 | 2.1 × 10-2 |
| MP4(SDQ)/6-31G(d)// MP2/6-31G(d)‡ | 1.40 | 9.4 × 10-2 | 2.90 | 7.5 × 10-3 | 3.35 | 3.5 × 10-3 | 4.73 | 3.5 × 10-4 |
| MP2/aug-cc-pVTZ// MP2/6-31G(d) | 1.27 | 1.2 × 10-1 | 2.35 | 1.9 × 10-2 | — | — | — | — |
| CCSD(T)/aug-cc-pVDZ// MP2/6-31G(d) | 0.48 | 4.4 × 10-1 | 1.54 | 7.4 × 10-2 | — | — | — | — |
| Cytosine | Guanine† | |||
| C↔C* | C∙W↔C*∙W | G↔G* | G∙W↔G*∙W | |
| MP2/6-31G(d)‡ | ||||
| Uf | 44.41 | 20.38 | 36.15 | 14.74 |
| ∆Er | 0.90 | 1.87 | 2.39 | 3.64 |
| kf | 1.0 × 10-10 | 1.8 × 102 | 1.5 × 10-7 | 9.5 × 104 |
| kr | 4.4 × 10-10 | 5.7 × 103 | 8.6 × 10-6 | 4.5 × 107 |
| MP2/6-31G(d)§ | ||||
| Uf | 44.41 | 20.38 | ||
| ∆Er | 0.90 | 1.87 | ||
| kf | 5.7 × 10-11 | 4.3 × 105 | ||
| kr | 2.4 × 10-10 | 9.7 × 106 | ||
| MP2/aug-cc-pVTZ§ | ||||
| Uf | 41.84 | 17.29 | ||
| ∆Er | 1.35 | 2.15 | ||
| kf | 1.5 × 10-9 | 1.2 × 107 | ||
| kr | 1.3 × 10-8 | 4.2 × 108 | ||
| CCSD(T)/aug-cc-pVDZ§ | ||||
| Uf | 43.67 | 19.32 | ||
| ∆Er | 0.56 | 1.34 | ||
| kf | 1.8 × 10-10 | 1.9 × 106 | ||
| kr | 4.1 × 10-10 | 1.8 × 107 | ||
Conclusions
Acknowledgement
References
- Watson, J. D.; Crick, F. H. C. Nature 1953, 171, 964.
- Elguero, J.; Marzin, C.; Katritzky, A.R.; Linda, P. The Tautomerism of Heterocycles. Adv. Heterocycl. Chem. Suppl. I 1976. [Google Scholar]
- Dreyfus, M.; Bensaude, O.; Dodin, G.; Dubois, J.E. J. Am.Chem. Soc. 1976, 98, 6338.
- Stolarski, R.; Remin, M.; Shugar, D. Z. Naturforsch. C. 1977, 32, 894.
- Lin, J.; Yu, C.; Peng, S.; Akiyama, I.; Li, K.; Lee, L.K.; LeBreton, P.R. J. Phys. Chem. 1980, 84, 1006.
- Norton, R.S.; Gregson, R.P.; Quinn, R.J. J. Chem. Soc. Chem. Commun. 1980, 339. [CrossRef]
- Nowak, M.J.; Szczepaniak, K.; Barski, A.; Shugar, D. Z. Naturforsch. C. 1978, 33, 876.
- Löwdin, P.O. Adv. Quant. Chem. 1965, 2, 213.
- Löwdin, P.O. Quantum Genetics and Aperiodic Solids. Some Aspects of the Biological Problems of Heredity, Mutations, Ageing, and Tumors in View of Quantum Theory of the DNA Molecule. In Preprint No 32. Quantum Theory Project for Research in Atomic, Molecular and Solid state, Chemistry and Physics; University of Florida: Gainesville, Florida, 1962. [Google Scholar]
- Computational Molecular Biology of “Theoretical and Computational Chemistry Book Series”; Leszczynski, J. (Ed.) Elsevier; Volume v. 8, 1999.
- Kwiatkowski, S.; Leszczynski, J. J. Mol. Structure (Theochem) 1990, 208, 35. [CrossRef]
- Leszczynski, J. J. Phys. Chem. A 1998, 102, 2357.
- Radchenko, E. D.; Plohotnichenko, A. M.; Sheina, G. G.; Blagoi, Yu. P. Biophysics (Engl. Ed.) 1983, 28, 559.
- Szczepaniak, K.; Szczepaniak, M. J. Mol. Struct. 1987, 156, 29.
- Nir, E.; Janzen, Ch.; Imhof, P.; Kleinermanns, K.; de Vries, M.S. J. Chem. Phys. 2001, 115, 4604.
- Saenger, W. Principles of Nucleic Acid Structure; Springer-Verlag: New York, 1983. [Google Scholar]
- Nowak, M.J.; Lapinski, L.; Fulara, J. Spectrochim. Acta 1989, 45A, 229.
- Gould, I.R.; Vincent, M.A.; Hiller, I.H.; Lapinski, L.; Nowak, M.J. Spectrochim. Acta 1992, A48, 811.
- Jaworski, A.; Szczepaniak, M.; KiBulat, K.; Person, W.B. J. Mol. Struct. 1990, 63, 223.
- Radchenko, E. D.; Sheina, G.G.; Smorygo, N.; Blagoi, Yu.P. J. Mol. Struct. 1984, 116, 387.
- Kobayashi, R. J. Phys. Chem. A 1998, 102, 10813.
- Les, A.; Adamowicz, L.; Bartlett, R. J. J. Phys. Chem. 1989, 93, 4001.
- Gorb, L.; Podolyan, Y.; Leszczynski, J. J. Mol. Struct. (Theochem) 1999, 487, 47. [CrossRef]
- Brown, R. D.; Godfrey, P. D.; Mc.Naughton, D.; Pierlot, A. P. J. J. Am. Chem. Soc. 1987, 111, 2308.
- Kwiatkowski, J.S.; Pullman, B. Adv. Heterocycl. Chem. 1975, 18, 199.
- Sharma, B.D.; McConnel, J.F. Acta Crystallogr. 1965, 19, 797.
- Lowe, P.R.; Schwalbe, C.H.; Williams, G.J.B. Acta Crystallogr. 1987, C43, 330.
- Helene, C.; Dozou, P. C. R. C. R. Acad. Sci. (Paris) 1964, 259, 4387.
- Brown, D.J.; Teitei, T. Aust. J. Chem. 1965, 18, 559.
- Morita, H.; Nagakura, S. Teor. Chim. Acta 1968, 11, 279. [CrossRef]
- Kaito, A.; Hatano, M.; Ueda, T.; Shibuya, S. Bull. Chem. Soc. Jpn. 1980, 53, 3073. [CrossRef]
- Drake, J. W. Molecular Basis of Mutations; San Francisco: Holden-Day, 1970. [Google Scholar]
- Gorb, L.; Podolyan, Y.; Leszczynski, J.; Siebrand, W.; Fernandez-Ramos, A.; Smedarchina, Z. Biopolymers 2002, 61, 77.
- Fowler, R. G.; Degnen, G. E.; Cox, E. C. Molec. Gen. Gene. 1974, 133, 179. [CrossRef]
- Topal, M. D.; Fresco, J. R. Nature 1976, 263, 285.
- Petrushka, J.; Sowers, L. C.; Goodman, M. Proc. Natl. Acad. Sci. 1986, 83, 1559. [CrossRef]
- Dewar, M. J. S.; Storoch, D. M. Proc. Natl. Acad. Sci. 1985, 82, 2225. [CrossRef]
- Benderskii, V. A.; Goldanskii, V. I.; Makarov, D. E. Chem. Phys. 1991, 154, 407.
- Benderskii, V. A.; Makarov, D. E.; Wight, C. H. Adv. Chem. Phys. 1994, 88, 1.
- Bell, R. L.; Truong, T. N. J. Phys. Chem. 1994, 101, 10442.
- Bell, R. L.; Taveras, D. L.; Truong, T. N.; Simons, J. Int. J. Quant. Chem. 1997, 63, 861.
- Podolyan, Y.; Gorb, L.; Leszczynski, J. J. Phys. Chem. A 2000, 104, 7346.
- Smedarchina, Z.; Siebrand, W.; Fernandez-Ramos, A.; Gorb, L.; Leszczynski, J. J. Chem. Phys. 2000, 112, 566.
- Smedarchina, Z.; Fernandez-Ramos, A.; Siebrand, W. J. Comp. Chem. 2001, 22, 787.
- Stent, G. S.; Calendar, B. Molecular Genetics. An Introductory Narrative; W. H. Freedman & Co: San Francisco, 1978. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; Dapprich, S.; Millam, J.M.; Daniels, A.D.; Kudin, K.N.; Strain, M.C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G.A.; Ayala, P.Y.; Cui, Q.; Morokuma, K.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Cioslowski, J.; Ortiz, J.V.; Baboul, A.G.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Andres, J.L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E.S.; Pople, J.A. Gaussian 98, Revision A.7; Gaussian: Pittsburgh PA, 1998. [Google Scholar]
- Møller, C.; Plesset, M.S. Phys. Rev. 1934, 46, 618. [CrossRef] [Green Version]
- Hehre, W. H.; Radom, L.; Schleyer, P. v. R.; Pople, J. A. Ab initio Molecular Orbital Theory; Wiley: New York, 1986. [Google Scholar]
- Scott, A.P.; Radom, L. J. Phys. Chem. 1996, 100, 16502.
- Siebrand, W.; Smedarchina, Z.; Zgierski, M. Z.; Fernandez-Ramos, A. Int. Rev. Phys. Chem. 1999.
- Smedarchina, Z.; Fernandez-Ramos, A.; Zgierski, M.Z.; Siebrand, W. DOIT 1.2, A computer program to calculate hydrogen tunneling rate constants and splittings, National Research Council of Canada (2000).
- Moore, W. J. Basic Physical Chemistry; Prentice-Hall: Englewood Cliffs, NJ, 1983. [Google Scholar]
- Gorb, L.; Leszczynski, J. J. Am. Chem. Soc. 1998, 120, 5024.
- Kornberg, A. DNA Synthesis; Freeman & Co.: San Francisco, 1974. [Google Scholar]
- Watson, J. D. Molecular Biology of Gene; Benjamin, Inc.: New York, 1970. [Google Scholar]
© 2003 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Podolyan, Y.; Gorb, L.; Leszczynski, J. Ab Initio Study of the Prototropic Tautomerism of Cytosine and Guanine and Their Contribution to Spontaneous Point Mutations. Int. J. Mol. Sci. 2003, 4, 410-421. https://doi.org/10.3390/i4070410
Podolyan Y, Gorb L, Leszczynski J. Ab Initio Study of the Prototropic Tautomerism of Cytosine and Guanine and Their Contribution to Spontaneous Point Mutations. International Journal of Molecular Sciences. 2003; 4(7):410-421. https://doi.org/10.3390/i4070410
Chicago/Turabian StylePodolyan, Yevgeniy, Leonid Gorb, and Jerzy Leszczynski. 2003. "Ab Initio Study of the Prototropic Tautomerism of Cytosine and Guanine and Their Contribution to Spontaneous Point Mutations" International Journal of Molecular Sciences 4, no. 7: 410-421. https://doi.org/10.3390/i4070410
APA StylePodolyan, Y., Gorb, L., & Leszczynski, J. (2003). Ab Initio Study of the Prototropic Tautomerism of Cytosine and Guanine and Their Contribution to Spontaneous Point Mutations. International Journal of Molecular Sciences, 4(7), 410-421. https://doi.org/10.3390/i4070410




