Theoretical Study of Multidimensional Proton Tunnelling in Benzoic Acid Dimer

Marek J. Wójcik; Krzysztof Szczeponek; Marek Boczar

doi:10.3390/i4070422

Abstract

Ab initio B3LYP/6-311++G** calculations have been carried out for the benzoic acid dimer for the stable and saddle point structures. The energy barrier for the proton tunneling amounts to 6.5 kcal/mol. The normal mode frequencies have been computed including modes coupled to the proton tunneling mode. Two-dimensional model potentials, formed from symmetric mode coupling potential and squeezed double well potential, have been fitted to the calculated energy barrier, geometries and frequencies, and used to analyze proton dynamics. The calculated proton tunneling energy splitting in the vibrationally ground states of the low-frequency modes is ~230 cm^-1. The two-dimensional model PES predict monotonic increase of the tunneling splitting with the excitation of the planar modes. Depending of the sign of the coupling parameter out-of-plane modes can either suppress or promote the splittings.

Keywords:

proton tunnelling; energy barrier; tunnelling splittings

Introduction

The importance of proton tunneling in chemical and biological systems is well known, e.g. for the DNA base pairing, as discussed by Löwdin [1]. The phenomenon of potential barrier penetration plays an important role in many branches of physics: quantum field theory, fission of atomic nuclei, scanning tunneling microscopy and solid state physics [2]. Theoretical studies of proton tunneling require the knowledge of multi-dimensional potential energy surfaces (PES’s) which are difficult to obtain from ab initio calculations, especially for electronically excited states. From the theoretical point of view proton transfer in the ground electronic state is more easily tractable. Extensive experimental and theoretical studies have been reported for multidimensional proton tunneling in tropolone [3,4,5,6,7,8,9,10,11,12,13]. Vener et al. [10] studied theoretically multidimensional proton tunneling in tropolone by using adiabatic separation of variables. Smedarchina et al. [11] used the instanton approach to account for tunnelling splittings. Takada and Nakamura [12] on the base of high accuracy ab initio calculations proposed a model potential energy surface (PES) for the electronically ground

\tilde{X}

state and employed it to analyze the proton tunnelling dynamics. Wójcik et al. [13] reported the results of the high accuracy ab initio MO calculations of the potential energy surfaces in the excited Ã state of tropolone, and by fitting the two- and three-dimensional analytical model potentials to these surfaces and solving the multidimensional vibrational problems, interpreted the existing experimental data. Other systems for which tunnelling have been studied include malonaldehyde [14,15,16,17], formic acid [18], hydrogen-oxalate anion [16], substituted tropolone [19,20] and 5-methyl-9-hydroxyphenalenone (OH and OD) [21], methanol tetramer [22] and hydrogen carbonate dimer ion [23]. Recently a mixed quantum-classical approach has been used to study dynamics of hydrogen-bonded systems [24,25].

System which draws our attention in the present paper is benzoic acid dimer. It is present in the structure of the crystal [26,27,28]. Its proton transfer has been recently studied by inelastic neutron scattering by Plazanet et al. [29] and Fillaux et al. [30]. Vibrational spectra of benzoic acid have been reported in Refs. [31,32]. In this article we present the results of high accuracy ab initio MO and DFT calculations of the potential energy surfaces for the ground state of benzoic acid dimer in the stable and saddle point structures, and by fitting the two-dimensional analytical model potentials to these surfaces and solving the multidimensional vibrational problems, we predict the effects of excitations of the low-frequency in- and out-of-plane modes on the proton tunnelling splittings.

This paper is organized as follows. The results of our quantum chemical calculations for the ground state of benzoic acid dimer are presented in Sec. II. Model studies of the tunnelling are discussed in Sec. III. Concluding remarks are given in Sec. IV.

Quantum Chemical Calculations

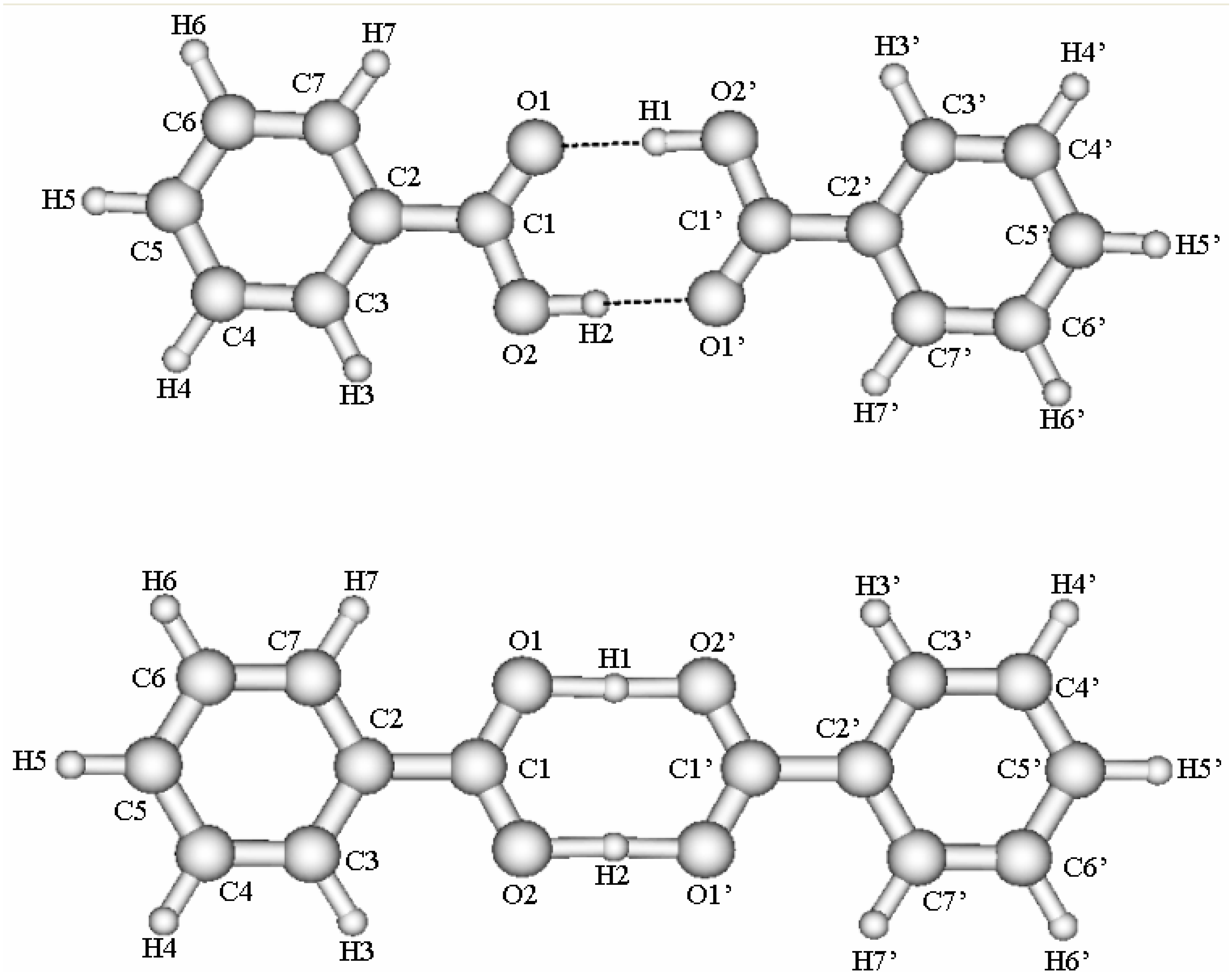
We performed ab initio B3LYP/6-311++G** calculations for the ground state of benzoic acid dimer using the Gaussian 98 program package [33]. The calculations have been done in the Computer Center of Hokkaido University in Sapporo, Japan and the Department of Materials Chemistry, Uppsala University in Sweden. The calculations have been performed for the stable and the saddle point structures. The geometry of benzoic acid dimer in the stable and the saddle point structures, calculated by the B3LYP/6-311++G** method is shown in Fig. 1. Optimized geometry is summarized in Table 1. The complex is planar in the stable and the saddle point structures. The calculated values reproduce the experimental bond lengths and angles reasonably well. There are small discrepancies for C₁-O₂ and some C-C distances. Experimental C-H distances taken from Ref. [26] are only estimates. The angles are well reproduced except O₂C₁C₂. The influence of the saddle point structure on geometry in hydrogen-bonded cyclic structure is considerable.

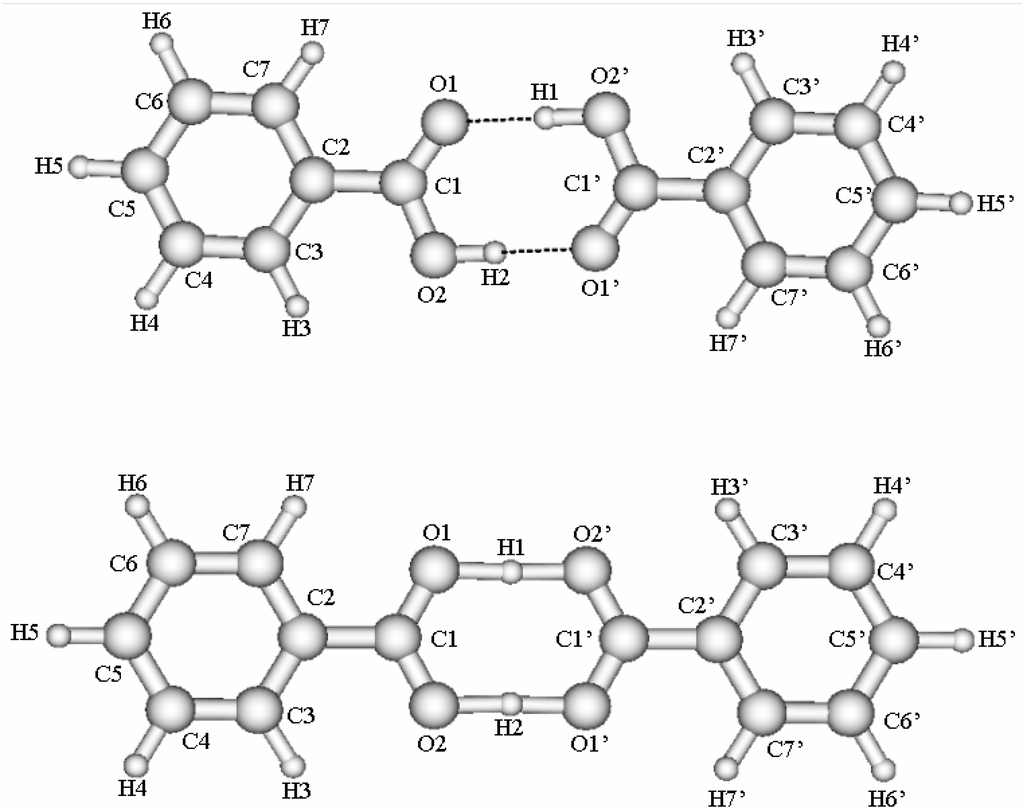
Figure 1. Benzoic acid in the stable and saddle point structures.

The calculated frequencies and symmetries of the normal modes at the stable and the saddle point structure are summarized in Table 2. The modes calculated by the B3LYP/6-311++G** method and used in the model calculations are pictured in Fig. 2.. The frequencies have not been scaled. The agreement between experimental and calculated frequencies is generally good, especially in the low and medium-frequency regions. The calculated frequencies in the region of O-H and C-H stretchings are overestimated by about 100-150 cm^-1 and the frequency of the O-H symmetric stretching mode ν₇₃ is overestimated by ~500 cm^-1. This is partly due to harmonic approximation and effects of intermolecular interactions on this mode in the crystal.

Table 1. Optimized geometries of the stable and saddle point structures of benzoic acid by the B3LYP/6-311++G** (DFT) method.

**Table 1.** Optimized geometries of the stable and saddle point structures of benzoic acid by the B3LYP/6-311++G** (DFT) method.
	Stable structure		Saddle point structure
	DFT	EXP.	DFT
Bond lengths (Å)
O₁··· O₂’	2,663	2,64^a; 2,629^b; 2,633^c	2,410
O₁ – H₁	1,663	1,64^b	1,205
O₂ – H₂	1,000	0,988^b	1,205
C₁ – O₁	1,230	1,24^a; 1,268^b; 1,263 ^c	1,272
C₁ – O₂	1,323	1,29^a; 1,275^b; 1,275 ^c	1,271
C₂ – C₁	1,486	1,48^a; 1,484 ^c	1,486
C₂ – C₃	1,400	1,39^a; 1,390 ^c	1,400
C₃ – C₄	1,391	1,42^a; 1,387 ^c	1,391
C₄ – C₅	1,395	1,36^a; 1,379 ^c	1,395
C₅ – C₆	1,395	1,37^a; 1,384 ^c	1,395
C₆ – C₇	1,390	1,41^a; 1,401 ^c	1,391
C₇ – C₂	1,400	1,39^a; 1,392 ^c	1,400
C₃ – H₃	1,082	0,79^a	1,082
C₄ – H₄	1,084	0,96^a	1,084
C₅ – H₅	1,084	0,91^a	1,084
C₆ – H₆	1,084	0,96^a	1,084
C₇ – H₇	1,083	0,79^a	1,082

Bond angles (^o)
O₁H₁O₂’	177,14		179,63
C₁O₁H₁	126,84		116,66
C₁O₂H₂	110,27		116,71
O₁C₁O₂	123,26	122 ^a; 123,2^c	123,78
O₂C₁C₂	114,50	118 ^a; 119,9 ^c	118,12
C₂C₁O₁	122,24	122 ^a; 120,2 ^c	118,11
C₁C₂C₃	121,40	122 ^a; 118,0 ^c	120,04
C₃C₂C₇	119,90	119 ^a; 119,9 ^c	119,92
C₇C₂C₁	118,70	119 ^a; 118,8 ^c	120,04
C₂C₃C₄	119,86	118 ^a; 120,1 ^c	119,94
C₃C₄C₅	120,02	123 ^a; 119,9 ^c	120,03
C₄C₅C₆	120,15	118 ^a; 120,3 ^c	120,16
C₅C₆C₇	119,98	122 ^a; 119,7 ^c	120,03
C₆C₇C₂	120,02	120 ^a; 119,8 ^c	119,94
C₂C₃H₃	119,48		119,11
H₃C₃C₄	120,66		120,95
C₃C₄H₄	119,85		119,89
H₄C₄C₅	120,07		120,08
C₄C₅H₅	119,91		119,92
H₅C₅C₆	119,94		119,92
C₅C₆H₆	120,09		120,08
H₆C₆C₇	119,93		119,89
C₆C₇H₇	121,12		120,95
H₇C₇C₂	118,86		119,12

^a Ref. 26, ^b Ref. 27, ^c Ref. 28.

Table 2. Calculated normal mode frequencies for the stable and saddle point structures of benzoic acid by the B3LYP/6-311++G** (DFT) method.

**Table 2.** Calculated normal mode frequencies for the stable and saddle point structures of benzoic acid by the B3LYP/6-311++G** (DFT) method.
No.	Symmetry	Frequency (cm^-1)
No.	Symmetry	Stable structure	Saddle point structure	Literature Infrared
1	AU	22	22	25^b
2	AU	33	35	35^b
3	BG	41	17	41^b
4	BU	60	75	71^b
5	BG	64	62	79^b
6	AU	87	79	94^a
7	AG	106	120	110^b
8	AG	114	201	127^b
9	AU	172	174	146^a
10	BG	179	177
11	AG	259	294
12	BU	283	363
13	BU	389	385
14	BG	414	413
15	AU	415	415
16	AG	423	588
17	AU	446	448	421^a
18	BG	448	451
19	AG	512	529
20	BU	546	723	491^a
21	AG	632	632
22	BU	632	631	615^a
23	AG	669	729
24	BU	679	698	669^a
25	BG	694	699
26	AU	696	697	687^a
27	BG	707	680
28	AU	724	729	711^a
29	BG	804	788
30	AG	804	824
31	BU	816	866	767^a
32	AU	831	838	813^a
33	AU	866	865
34	BG	866	865	856^a
35	BG	886	1203
36	BG	961	961
37	AU	963	965	937^a
38	AU	982	1327	960^a
39	BG	1000	999
40	AU	1000	999	974^a
41	BG	1010	1009	998^a
42	AU	1011	1009
43	BU	1018	1015	1002^a
44	AG	1018	1018
45	BU	1046	1044	1027^a
46	AG	1046	1047
47	AG	1101	1101
48	BU	1101	1101	1066^a
49	BU	1146	1121	1027^a
50	AG	1150	1173
51	BU	1184	1184	1164^a
52	AG	1184	1184
53	BU	1198	1185	1185^a
54	AG	1199	1202
55	AG	1309	1436	1316^a
56	BU	1317	1563	1322^a
57	AG	1344	1337
58	BU	1346	1338	1297^a
59	AG	1350	1350
60	BU	1350	1350	1380^a
61	BU	1453	1449	1430^a
62	AG	1474	1477
63	BU	1480	1478	1456^a
64	AG	1486	1697
65	AG	1524	1523
66	BU	1524	1526	1496^a
67	BU	1620	1616	1590^a
68	AG	1621	1614
69	BU	1643	1642	1606^a
70	AG	1643	1641
71	AG	1686	1696	1699^a
72	BU	1731	1690	1738^a
73	AG	3102	1194 i	2605^a
74	BU	3166	3167	3012^a
75	AG	3166	3167
76	BU	3179	3179	3041^a
77	AG	3179	3179
78	BU	3187	3189	3068^a
79	AG	3188	3189
80	BU	3197	1216	3312^a
81	AG	3203	3206
82	BU	3203	3206	3079^a
83	BU	3210	3207	3098^a
84	AG	3210	3207

^a Ref. 30, ^b Ref. 31.

In Table 3 we present the calculated energies and potential barriers. The energy barrier for the proton transfer amounts to 6.497 kcal/mol, no ZPE and only 1.867 kcal/mol, with ZPE.

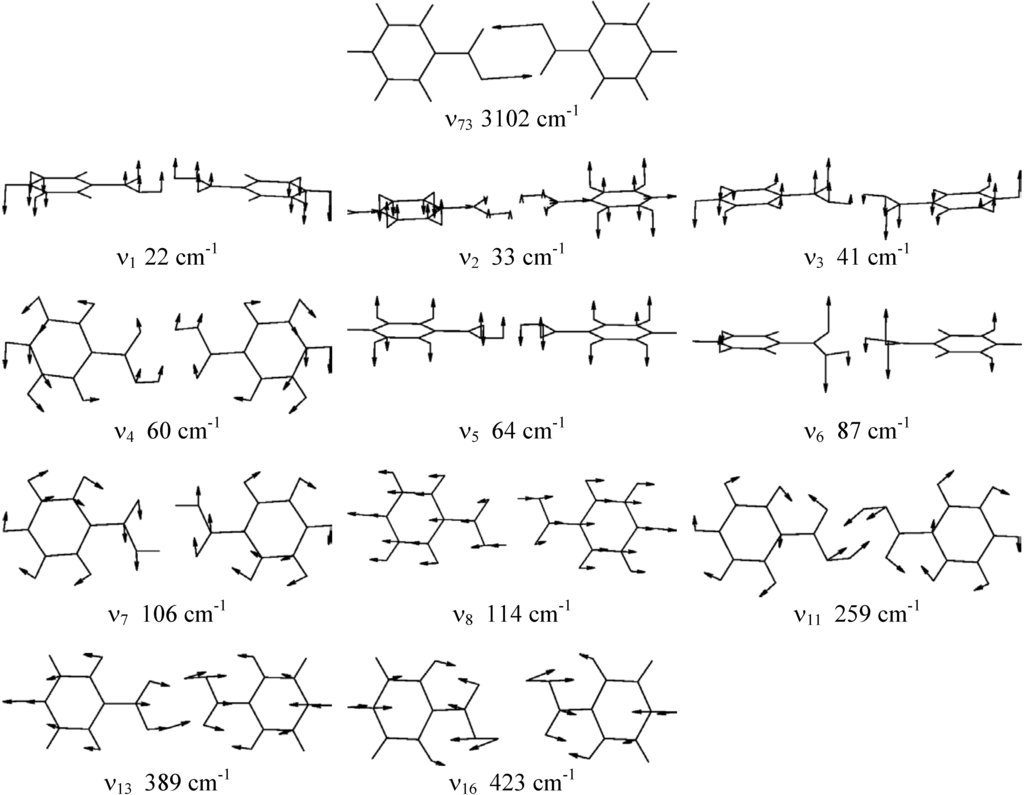
Figure 2. Normal modes of benzoic acid calculated by the B3LYP/6-311++G** method.

Table 3. Calculated energies and barrier for benzoic acid by the B3LYP/6-311++G** (DFT) method.

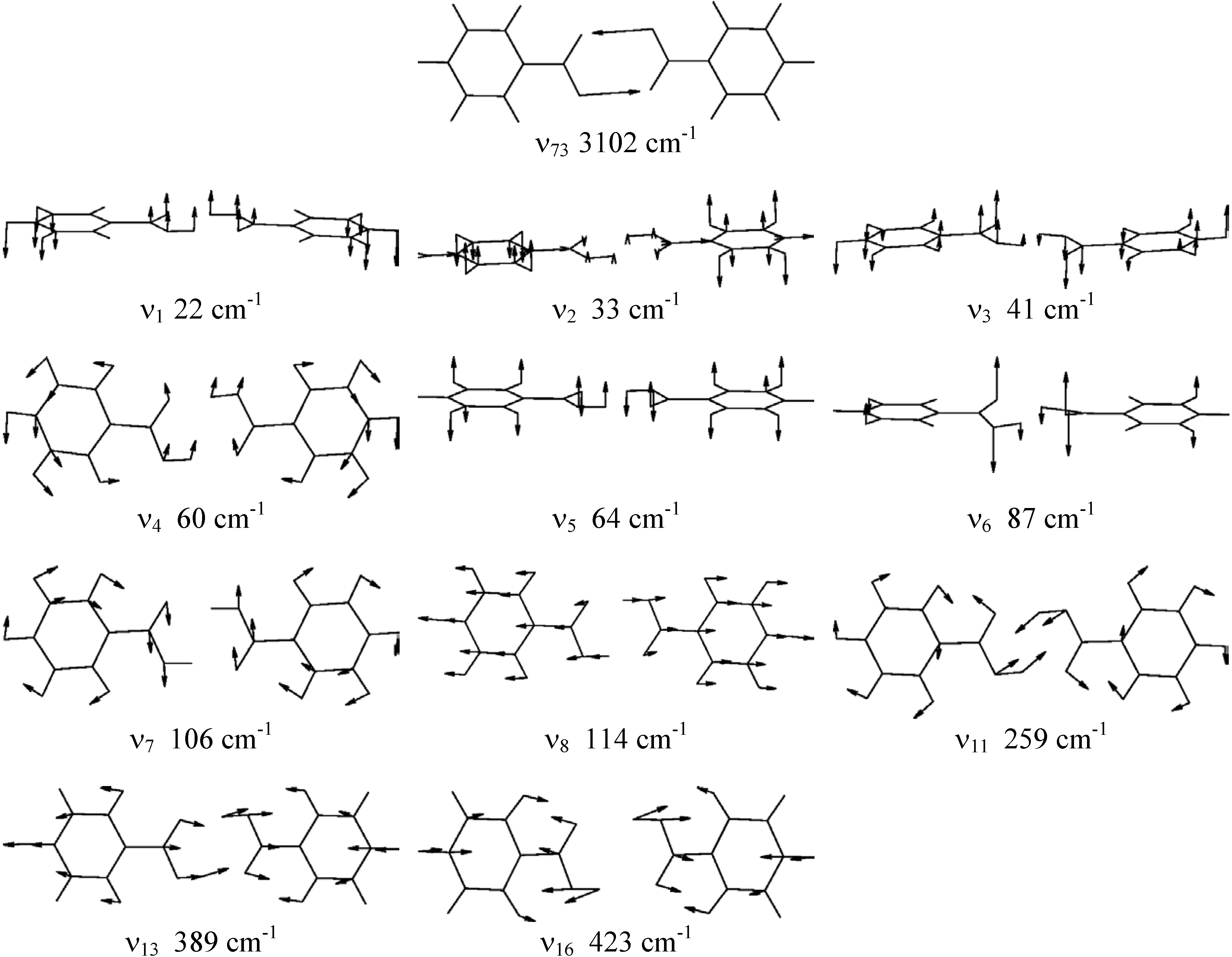
**Table 3.** Calculated energies and barrier for benzoic acid by the B3LYP/6-311++G** (DFT) method.
	DFT
Energy, stable structure	No ZPE, a.u.	-841,923
	With ZPE, a.u.	-841,691
Energy, saddle point structure	No ZPE, a.u.	-841,912
	With ZPE, a.u.	-841,688
Energy barrier	No ZPE, kcal/mol	6,497
	No ZPE, cm^-1	2272
	With ZPE, kcal/mol	1,867
	With ZPE, cm^-1	653

Model Calculations

On the basis of the ab initio calculations we constructed two-dimensional model PES for the proton tunnelling ν₇₃ coupled to chosen low-frequency modes of benzoic acid dimer which largely affect the tunnelling. These are the low-frequency planar hydrogen-bond stretching and bending modes ν₄, ν₇, ν₈, ν₁₁, ν₁₃ and ν₁₆ and the lowest-frequency out-of-plane modes ν₁, ν₂, ν₃, ν₅ and ν₆. They are shown in Fig. 2 and their calculated vibrational frequencies are listed in Table 2. We assumed the symmetric (synchronous) double proton transfer in benzoic acid dimer in accordance with the results of ref. [18].

The two-dimensional model potentials used to simulate the couplings are [12,13]:

(a) the symmetric mode coupling potential (SMC) describing couplings of the proton tunneling mode ν₁ with the planar modes ν₈, ν₉ and ν₂₁:

V_{S M C} = \frac{1}{8 x_{0}^{2}} {(x - x_{0})}^{2} {(x + x_{0})}^{2} + \frac{1}{2} \frac{ω_{y}}{ω_{x}} {[y + α (x^{2} - x_{0}^{2})]}^{2}

(1)

and

(b) the squeezed double well potential (SQZ) describing couplings of the proton tunneling mode ν₁ with the out-of-plane modes ν₁₂, ν₁₃ and ν₂₄:

V_{S Q Z} = \frac{1}{8 x_{0}^{2}} {(x - x_{0})}^{2} {(x + x_{0})}^{2} + \frac{1}{2 x_{0}^{2}} [\frac{ω_{z}}{ω_{x}} x_{0}^{2} - γ (x^{2} - x_{0}^{2}) / (\frac{ω_{z}}{ω_{x}})] z^{2},

(2)

where x and y and z, denote the coordinates of the proton tunneling and the low-frequency modes, respectively, ω_x, ω_y and ω_z are the angular frequencies, 2x_o the distance between the two minima, α and γ the coupling strengths. In the formulas (1) and (2) the potentials are expressed in the units of the quantum ћω_x and the coordinates x, y and z are dimensionless:

\begin{array}{l} x = \tilde{x} \sqrt{\frac{m_{x} ω_{x}}{ћ}}, \\ y = \tilde{y} \sqrt{\frac{m_{y} ω_{y}}{ћ}}, \\ z = \tilde{z} \sqrt{\frac{m_{z} ω_{z}}{ћ}} . \end{array}

(3)

\tilde{x}, \tilde{y}

and

\tilde{z}

denote the dimensional coordinates and m_x, m_y and m_z are the effective masses.

The parameters x_o, α and γ of the potentials (1) and (2) were estimated from the formulas:

\begin{array}{l} Δ E = \frac{x_{0}^{2}}{8} ћ ω_{x}, \\ y_{s} = α x_{0}^{2}, \\ γ = \frac{(ω_{z}^{s} - ω_{z}) ω_{z}}{ω_{x}^{2}}, \end{array}

(4)

where ΔE, y_s and

ω_{z}^{s}

denote the energy barrier, the value of the normal coordinate y of the coupled mode of the SMC potential at the saddle point structure and the angular frequency of the mode z at the saddle point structure, respectively. We used no ZPE energy barriers. The parameters used in subsequent calculations of the energy splittings have been calculated from the results of the B3LYP/6-311++G** data and are listed in Table 4. The parameter α describing coupling between the O-H stretching mode ν₇₃ and the mode ν₄, ν₇, ν₈, ν₁₁, ν₁₃ or ν₁₆ represent an analogue of linear distortion parameters b used for theoretical reproduction of the X-H infrared band shapes of tropolone [34], salicylaldehyde [35] or aspirin [36]. Both different spectroscopic facts thus have the same origin, the anharmonic coupling in the potential energy between the two X-H and X...Y vibrations.

Tunnelling energy splittings have been calculated variationally. The convergence has been confirmed by reproducing exactly the energy splittings reported by Takada and Nakamura [12] and calculated by the DVR method [37,38]. The results are presented in Table 5 for the two-dimensional model potentials (1) and (2). The proton tunnelling energy splitting in the vibrationally ground states of the low-frequency modes is ca. 230 cm^-1. This compares reasonably well with the experimental value 172 cm^-1 obtained from the inelastic neutron scattering measurements for benzoic acid - D₅H and recently reported by Fillaux et al. [30]. The two-dimensional model PES qualitatively explain increase of the tunnelling splitting with the excitation of the planar ν₄, ν₇, ν₈,ν₁₁, ν₁₃ and ν₁₆ modes. For the out-of-plane modes the monotonic change depend on a sign of the coupling parameter γ. When the sign is positive (for modes ν₁ and ν₂) one obtains monotonic decrease of the splitting with the excitation, and when it is negative (for the ν₃, ν₅ and ν₆ mode) the excitations cause increase of the splittings. This remains in agreement with our previous theoretical results for the excited state of tropolone [13] and hydrogen carbonate dimer [23]. Experimentally observed in tropolone promotion of the tunnelling by the excitation of the planar modes and its suppression by the excitation of the out-of-plane modes [7,8] are qualitatively confirmed in the present two-dimensional model calculations. Our previous results on the excited state of tropolone [13], hydrogen carbonate dimer ion [23] and the present ones do not require any adjustments and present pure quantum-mechanical approach to the problem of tunnelling splittings.

Table 4. Parameters of the two-dimensional models.

**Table 4.** Parameters of the two-dimensional models.
Mode		x_o	α	γ
Stable	Saddle point	x_o	α	γ
ν₄		2,42	0,178
ν₇		2,42	0,096
ν₈		2,42	0,122
ν₁₁		2,42	0,040
ν₁₃		2,42	0,056
ν₁₆		2,42	0,138
	ν₁	2,42		0,00000017
	ν₂	2,42		0,00000597
	ν₃	2,42		-0,00010000
	ν₅	2,42		-0,00000807
	ν₆	2,42		-0,00007099

Table 5. Energy splittings (cm^-1) calculated for two-dimensional model potentials.

**Table 5.** Energy splittings (cm^-1) calculated for two-dimensional model potentials.
Quantum number	SMC						SQZ
Quantum number	ν₄	ν₇	ν₈	ν₁₁	ν₁₃	ν₁₆	ν₁	ν₂	ν₃	ν₅	ν₆
0	229,24	229,50	229,36	229,67	229,65	229,54	229,71	229,63	230,99	229,78	230,10
1	229,43	229,68	229,69	229,86	230,52	235,50	229,71	229,47	233,54	229,89	230,87
2	229,62	229,86	230,02	230,05	231,38	241,32	229,70	229,30	236,12	230,01	231,64
3	229,82	230,04	230,35	230,25	232,23	247,01	229,69	229,14	238,74	230,13	232,41
4	230,01	230,22	230,68	230,44	233,09	252,57	229,69	228,97	241,39	230,25	233,18
5	230,20	230,40	231,01	230,63	233,94	258,02	229,68	228,81	244,08	230,37	233,96
6	230,39	230,57	231,34	230,82	234,79	263,36	229,67	228,64	246,80	230,49	234,74
7	230,58	230,75	231,67	231,02	235,63	268,59	229,66	228,48	249,55	230,60	235,52
8	230,77	230,93	231,99	231,21	236,48	273,72	229,66	228,31	252,34	230,72	236,30
9	230,96	231,11	232,32	231,40	237,31	278,76	229,65	228,15	255,16	230,84	237,09
10	231,15	231,29	232,65	231,59	238,15	283,70	229,64	227,98	258,01	230,96	237,88

Conclusions

The proton tunnelling dynamics in benzoic acid dimer in the ground electronic state has been studied by performing quantum mechanical calculations of the potential energy surface and fitting it by two-dimensional model potentials. The tunnelling energy splittings for different vibrationally excited states have been calculated. The calculated proton tunnelling energy splitting in the vibrationally ground states of the low-frequency modes (~230 cm^-1) compares reasonably well with the experimental value 172 cm^-1 obtained from the inelastic neutron scattering measurements for benzoic acid - D₅H [29]. Our model calculations predict the promotion of the proton tunnelling by the excitation of the planar modes. Depending of the sign of the coupling parameter γ, out-of-plane modes can either supress or promote the tunnelling. This results are confirmed by existing experimental data [7,8]. Our model presents a pure quantum-mechanical approach to the problem of the proton tunnelling splittings.

References

Löwdin, P.O. Rev. Mod. Phys. 1963, 35, 724. [CrossRef]
Nakamura, H. Ann. Rev. Phys. Chem. 1997, 48, 299. [CrossRef]
Alves, A.C.P.; Hollas, J.M. Mol. Phys. 1973, 25, 1305.
Redington, R.L.; Redington, T.E. J. Mol. Spectr. 1979, 78, 229. [CrossRef]
Tomioka, Y.; Ito, M.; Mikami, N. J. Phys. Chem. 1983, 87, 4401. [CrossRef]
Redington, R.L.; Chen, Y.; Scherer, G.J.; Field, R.W. J. Chem. Phys. 1988, 88, 627. [CrossRef]
Sekiya, H.; Nagashima, Y.; Nishimura, Y. J. Chem. Phys. 1990, 92, 5761.
Sekiya, H.; Nagashima, Y.; Tsuji, T.; Nishimura, Y.; Mori, A.; Takeshita, H. J. Phys. Chem. 1991, 95, 10311. [CrossRef]
Nishi, K.; Sekiya, H.; Kawakami, H.; Mori, A.; Nishimura, Y. J. Chem. Phys. 1998, 109, 1589.
Vener, M.V.; Scheiner, S.; Sokolov, N.D. J. Chem. Phys. 1994, 101, 9755.
Smedarchina, Z.; Siebrand, W.; Zgierski, M.Z. J. Chem. Phys. 1996, 104, 1203.
Takada, S.; Nakamura, H. J. Chem. Phys. 1995, 102, 3977.
Wójcik, M.J.; Nakamura, H.; Iwata, S.; Tatara, W. J. Chem. Phys. 2000, 112, 6322.
Carrington, T. Jr.; Miller, W.H. J. Chem. Phys. 1986, 84, 4364.
Shida, N.; Barbara, P.F.; Almlof, J.E. J. Chem. Phys. 1989, 91, 4061.
Smedarchina, Z.; Siebrand, W.; Zgierski, M.Z. J. Chem. Phys. 1995, 103, 5326.
Sewell, T.D.; Guo, Y.; Thompson, D.L. J. Chem. Phys. 1995, 103, 8557.
Shida, N.; Barbara, P.; Almlof, J.E. J. Chem. Phys. 1991, 94, 3633.
Nishi, K.; Sekiya, H.; Kawakami, H.; Mori, A.; Nishimura, Y. J. Chem. Phys. 1998, 109, 1589.
Nishi, K.; Sekiya, H.; Kawakami, H.; Mori, A.; Nishimura, Y. J. Chem. Phys. 1999, 111, 3961.
Nishi, K.; Sekiya, H.; Mochida, T.; Sugawara, T.; Nishimura, Y. J. Chem. Phys. 2000, 112, 5002.
Vener, M.V.; Sauer, J. J. Chem. Phys. 2001, 114, 2623.
Wójcik, M.J.; Tatara, W.; Ikeda, S. J. Mol. Struct. 2002, 614, 109. [CrossRef]
Decornez, M.; Drukker, H.; Hammes-Schiffer, S. J. Phys. Chem. A 1999, 103, 2891. [CrossRef]
Mavri, S.; Grdadolnik, J. J. Phys. Chem. A 2001, 105, 2045. [CrossRef]
Sim, G.A.; Monteath Robertson, J.; Goodwin, T.H. Acta Cryst. 1955, 8, 157.
Wilson, C.C.; Shanklandnd, N.; Florence, A.J. Chem. Phys. Lett. 1996, 253, 103.
Bruno, G.; Randaccio, L. Acta Cryst. 1980, B36, 1711.
Plazanet, M.; Fukushima, N.; Johnson, M.R.; Horsewill, A.J.; Trommsdorf, H.P. J. Chem. Phys. 2001, 115, 3241.
Fillaux, F.; Limage, M.H.; Romain, F. Chem. Phys. 2002, 276, 181.
Stepanian, S.G.; Reva, I.D.; Radchenko, E.D.; Sheina, G.G. Vibrat. Spectrosc. 1996, 11, 123. [CrossRef]
Zelsmann, H.R.; Mielke, Z. Chem. Phys. Lett. 1991, 186, 501. [CrossRef]
Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; Dapprich, S.; Millam, J.M.; Daniels, A.D.; Kudin, K.N.; Strain, M.C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G.A.; Ayala, P.Y.; Cui, Q.; Morokuma, K.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Cioslowski, J.; Ortiz, J.V.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, W.; Johnson, B.; Chen, W.; Wong, M.W.; Andres, J.L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E.S.; Pople, J.A. Gaussian 98, Revision A.6; Gaussian: Pittsburgh PA, 1998. [Google Scholar]
Wójcik, M.J.; Boczar, M.; Stoma, M. Int. J. Quant. Chem. 1999, 73, 275.
Boczar, M.; Wójcik, J.M.; Szczeponek, K.; Jamróz, D.; Ikeda, S. Int. J. Quant. Chem. 2002, 90, 689. [CrossRef]
Boczar, M.; Wójcik, M.J.; Szczeponek, K.; Jamróz, D.; Zieba, A.; Kawałek, B. Chem. Phys. 2002, 286, 63. [CrossRef]
Light, J.C.; Hamilton, I.P.; Lill, J.V. J. Chem. Phys. 1985, 82, 1400.
Whitnell, R.M.; Light, J.C. J. Chem. Phys. 1989, 90, 1774.

Article Metrics

Citations

Article Access Statistics

Journal Statistics

Multiple requests from the same IP address are counted as one view.