Inductive QSAR Descriptors. Distinguishing Compounds with Antibacterial Activity by Artificial Neural Networks

Artem Cherkasov

doi:10.3390/i6010063

Abstract

On the basis of the previous models of inductive and steric effects, ‘inductive’ electronegativity and molecular capacitance, a range of new ‘inductive’ QSAR descriptors has been derived. These molecular parameters are easily accessible from electronegativities and covalent radii of the constituent atoms and interatomic distances and can reflect a variety of aspects of intra- and intermolecular interactions. Using 34 ‘inductive’ QSAR descriptors alone we have been able to achieve 93% correct separation of compounds with- and without antibacterial activity (in the set of 657). The elaborated QSAR model based on the Artificial Neural Networks approach has been extensively validated and has confidently assigned antibacterial character to a number of trial antibiotics from the literature.

Keywords:

QSAR; antibiotics; descriptors; substituent effect; electronegativity

Introduction.

Nowadays, rational drug design efforts widely rely on building extensive QSAR models which currently represent a substantial part of modern ‘in silico’ research. Due to inability of the fundamental laws of chemistry and physics to directly quantify biological activities of compounds, computational chemists are led to research for simplified but efficient ways of dealing with the phenomenon, such as by the means of molecular descriptors [1]. The QSAR descriptors came to particular demand during last decades when the amounts of chemical information started to grow explosively. Nowadays, scientists routinely work with collections of hundreds of thousands of molecular structures which cannot be efficiently processed without use of diverse sets of QSAR parameters. Modern QSAR science uses a broad range of atomic and molecular properties varying from merely empirical to quantum-chemical. The most commonly used QSAR arsenals can include up to hundreds and even thousands of descriptors readily computable for extensive molecular datasets. Such varieties of available descriptors in combination with numerous powerful statistical and machine learning techniques allow creating effective and sophisticated structure-bioactivity relationships [1,2,3]. Nevertheless, although even the most advanced QSAR models can be great predictive instruments, often they remain purely formal and do not allow interpretation of individual factors influencing activity of drugs [3]. Many molecular descriptors (in particular derived from molecular topology alone) lack defined physical justification. The creation of efficient QSAR descriptors also possessing much defined physical meaning still remains one of the most important tasks for the QSAR research.

In a series of previous works we introduced a number of reactivity indices derived from the Linearity of Free Energy Relationships (LFER) principle [4]. All of these atomic and group parameters could be easily calculated from the fundamental properties of bound atoms and possess much defined physical meaning [5,6,7,8]. It should be noted that, historically, the entire field of the QSAR has been originated by such LFER descriptors as inductive, resonance and steric substituent constants [4]. As the area progressed further, the substituent parameters remained recognized and popular quantitative descriptors making lots of intuitive chemical sense, but their applicability was limited for actual QSAR studies [9]. To overcome this obstacle, we have utilized the extensive experimental sets of inductive and steric substituent constants to build predictive models for inductive and steric effects [5]. The developed mathematical apparatus not only allowed quantification of inductive and steric interactions between any substituent and reaction centre, but also led to a number of important equations such as those for partial atomic charges [8], analogues of chemical hardness-softness [7] and electronegativity [6].

Notably, all of these parameters (also known as ‘inductive’ reactivity indices) have been expressed through the very basic and readily accessible parameters of bound atoms: their electronegativities (χ), covalent radii (R) and intramolecular distances (r). Thus, steric Rs and inductive σ* influence of n - atomic group G on a single atom j can be calculated as:

R s_{G \to j} = α \sum_{i \subset G, i \neq j}^{n} \frac{R_{i}^{2}}{r_{i - j}^{2}}

(1)

σ_{G \to j}^{*} = β \sum_{i \subset G, i \neq j}^{n} \frac{(χ_{i}^{0} - χ_{j}^{0}) R_{i}^{2}}{r_{i - j}^{2}}

(2)

In those cases when the inductive and steric interactions occur between a given atom j and the rest of N-atomic molecule (as sub-substituent) the summation in (1) and (2) should be taken over N-1 terms. Thus, the group electronegativity of (N-1)-atomic substituent around atom j has been expressed as the following:

χ_{N - 1 \to j}^{0} = \frac{\sum_{i \neq j}^{N - 1} \frac{χ_{i}^{0} (R_{i}^{2} + R_{j}^{2})}{r_{i - j}^{2}}}{\sum_{i \neq j}^{N - 1} \frac{R_{i}^{2} + R_{j}^{2}}{r_{i - j}^{2}}}

(3)

Similarly we have defined steric and inductive effects of a singe atom onto a group of atoms (the rest of the molecule):

R s_{j \to N - 1} = α \sum_{i \neq j}^{N - 1} \frac{R_{j}^{2}}{r_{j - i}^{2}} = α R_{j}^{2} \sum_{i \neq j}^{N - 1} \frac{1}{r_{j - i}^{2}}

(4)

σ_{j \to N - 1}^{*} = β \sum_{i \neq j}^{N - 1} \frac{(χ_{j}^{0} - χ_{i}^{0}) R_{j}^{2}}{r_{j - i}^{2}} = β R_{j}^{2} \sum_{i \neq j}^{N - 1} \frac{(χ_{j}^{0} - χ_{i}^{0})}{r_{j - i}^{2}}

(5)

In the works [7,8] an iterative procedure for calculating a partial charge on j-th atom in a molecule has been developed:

Δ N_{j} = Q_{j} + γ \sum_{i \neq j}^{N - 1} \frac{(χ_{j} - χ_{i}) (R_{j}^{2} + R_{i}^{2})}{r_{j - i}^{2}}

(6)

(where Q_j reflects the formal charge of atom j).

Initially, the parameter χ in (6) corresponds to χ⁰ - an absolute, unchanged electronegativity of an atom; as the iterative calculation progresses the equalized electronegativity χ’ gets updated according to (7):

χ' \approx χ^{0} + η^{0} Δ N

(7)

where the local chemical hardness η⁰ reflects the “resistance” of electronegativity to a change of the atomic charge. The parameters of ‘inductive’ hardness η_i and softness s_i of a bound atom i have been elaborated as the following:

η_{i} = \frac{1}{2 \sum_{j \neq i}^{N - 1} \frac{R_{j}^{2} + R_{i}^{2}}{r_{j - i}^{2}}}

(8)

s_{i} = 2 \sum_{j \neq i}^{N - 1} \frac{R_{j}^{2} + R_{i}^{2}}{r_{j - i}^{2}}

(9)

The corresponding group parameters have been expressed as

η_{M O L} = \frac{1}{s_{M O L}} = \frac{1}{2 \sum_{j \neq i}^{N - 1} \frac{R_{j}^{2} + R_{i}^{2}}{r_{j - i}^{2}}}

(10)

s_{M O L} = \sum_{j \neq i}^{N} \sum_{j \neq i}^{N} \frac{R_{j}^{2} + R_{i}^{2}}{r_{j - i}^{2}} = \sum_{j \neq i}^{N} 2 \frac{R_{j}^{2} + R_{i}^{2}}{r_{j - i}^{2}} = \sum_{i}^{N} s_{i}

(11)

The interpretation of the physical meaning of ‘inductive’ indices has been developed by considering a neutral molecule as an electrical capacitor formed by charged atomic spheres [8]. This approximation related inductive chemical softness and hardness of bound atom(s) with the total area of the facings of electrical capacitor formed by the atom(s) and the rest of the molecule.

We have also conducted very extensive validation of ‘inductive’ indices on experimental data. Thus, it has been established that R_S steric parameters calculated for common organic substituents form a high quality correlation with Taft’s empirical E_S -steric constants (r²=0.985) [10]. The theoretical inductive σ* constants calculated for 427 substituents correlated with the corresponding experimental numbers with coefficient r = 0.990 [5]. The group inductive parameters χ computed by the method (3) have agreed with a number of known electronegativity scales [6]. The inductive charges produced by the iterative procedure (6) have been verified by experimental C-1s Electron Core Binding Energies [8] and dipole moments [6]. A variety of other reactivity and physical-chemical properties of organic, organometallic and free radical substances has been quantified within equations (1)-(11) [11,12,13,14,15,16]. It should be noted, however, that in our previous studies we have always considered different classes of ‘inductive’ indices (substituent constants, charges or electronegativity) in separate contexts and tended to use the canonical LFER methodology of correlation analysis in dealing with the experimental data. At the same time, a rather broad range of methods of computing ‘inductive’ indices has already been developed to the date and it is feasible to use these approaches to derive a new class of QSAR descriptors. In the present work we introduce 50 such QSAR descriptors (we called ‘inductive’) and will test their applicability for building QSAR model of “antibiotic-likeness”.

Results

QSAR models for drug-likeness in general and for antibiotic-likeness in particular are the emerging topics of the ‘in silico’ chemical research. These binary classifiers serve as invaluable tools for automated pre-virtual screening, combinatorial library design and data mining. A variety of QSAR descriptors and techniques has been applied to drug/non-drug classification problem. The latest series of QSAR works report effective separation of bioactive substances from the non-active chemicals by applying the methods of Support Vector Machines (SVM) [17,18], probability-based classification [19], the Artificial Neural Networks (ANN) [20,21,22] and the Bayesian Neural Networks (BNN) [23,24] among others. Several groups used datasets of antibacterial compounds to build the binary classifiers of general antibacterial activity (antibiotic-likeness models) utilizing the ANN algorithm [25,26,27], linear discriminant analysis (LDA) [28,29], binary logistic regression [29] or k-means cluster method [30]. Thus, in the study [31] the LDA has been used to relate anti-malarial activity of a series of chemical compounds to molecular connectivity QSAR indices. The results clearly demonstrate that creation of QSAR approaches for classification of molecules active against broad range of infective agents represents an important and valuable tack for the modern QSAR research.

Dataset

To investigate the possibility of using the inductive QSAR descriptors for creation an effective model of antibiotic-likeness, we have considered a dataset of Vert and co-authors [27] containing the total of 657 structurally heterogeneous compounds including 249 antibiotics and 408 general drugs. This dataset has been used in the previous studies [27,29] and therefore could allow us to comparatively evaluate the performance of QSAR model built upon the inductive descriptors.

Descriptors

50 inductive QSAR descriptors introduced on the basis of formulas (1)-(11) have been described in the greater details in Table 1. Those include various local parameters calculated for certain kinds of bound atoms (for instance for most positively/negatively charges, etc), groups of atoms (say, for substituent with the largest/smallest inductive or steric effect within a molecule, etc) or computed for the entire molecule. One common feature for all of the introduced inductive descriptors is that they all produce a single value per compound. Another similarity between them is in their relation to atomic electronegativity, covalent radii and interatomic distances. It should also be noted, that all descriptors (except the total formal charge) depend on the actual spatial structure of molecules. The choice of particular inductive descriptors in Table 1 was driven by our expectation to have a limited set of QSAR parameters reflecting the greatest variety of different aspects of intra- and intermolecular interactions a molecule can be engaged into. It should be mentioned, however, that some inductive descriptors may reflect related or similar molecular/atomic properties and therefore can be correlated in certain cases (even though the analytical representation of those descriptors does not directly imply their co-linearity). Thus, a special precaution should be taken when using such parameters for QSAR modeling. The procedure of selection of appropriate inductive descriptors has been outlined in the following section.

Table 1. Inductive QSAR descriptors introduced on the basis of equations (1)-(11).

**Table 1.** Inductive QSAR descriptors introduced on the basis of equations (1)-(11).
Descriptor	Characterization	Parental formula(s)
χ (electronegativity) – based
EO_Equalized^a	Iteratively equalized electronegativity of a molecule	Calculated iteratively by (7) where charges get updated according to (6); an atomic hardness in (7) is expressed through (8)
Average_EO_Pos^a	Arithmetic mean of electronegativities of atoms with positive partial charge	$\frac{\sum_{i}^{n^{+}} χ_{i}^{0}}{n^{+}}$ where $n^{+}$ is the number of atoms i in a molecule with positive partial charge
Average_EO_Neg^a	Arithmetic mean of electronegativities of atoms with negative partial charge	$\frac{\sum_{i}^{n^{-}} χ_{i}^{0}}{n^{-}}$ where $n^{-}$ is the number of atoms i in a molecule with negative partial charge
η (hardness) – based
Global_Hardness^a	Molecular hardness - reversed softness of a molecule	(10)
Sum_Hardness^a	Sum of hardnesses of atoms of a molecule	Calculated as a sum of inversed atomic softnesses in turn computed within (9)
Sum_Pos_Hardness^a	Sum of hardnesses of atoms with positive partial charge	Obtained by summing up the contributions from atoms with positive charge computed by (8)
Sum_Neg_Hardness^a	Sum of hardnesses of atoms with negative partial charge	Obtained by summing up the contributions from atoms with negative charge computed by (8)
Average_Hardness^a	Arithmetic mean of hardnesses of all atoms of a molecule	Estimated by dividing quantity (10) by the number of atoms in a molecule
Average_Pos_Hardness	Arithmetic mean of hardnesses of atoms with positive partial charge	$\frac{\sum_{i}^{n^{+}} η_{i}}{n^{+}}$ where $n^{+}$ is the number of atoms i with positive partial charge.
Average_Neg_Hardness^a	Arithmetic mean of hardnesses of atoms with negative partial charge	$\frac{\sum_{i}^{n^{-}} η_{i}}{n^{-}}$ where $n^{-}$ is the number of atoms i with negative partial charge.
Smallest_Pos_Hardness^a	Smallest atomic hardness among values for positively charged atoms	(8)
Smallest_Neg_Hardness^a	Smallest atomic hardness among values for negatively charged atoms.	(8)
Largest_Pos_Hardness	Largest atomic hardness among values for positively charged atoms	(8)
Largest_Neg_Hardness	Largest atomic hardness among values for negatively charged atoms	(8)
Hardness_of_Most_Pos	Atomic hardness of an atom with the most positive charge	(8)
Hardness_of_Most_Neg^a	Atomic hardness of an atom with the most negative charge	(8)
s (softness) - based
Global_Softness	Molecular softness – sum of constituent atomic softnesses	(11)
Total_Pos_Softness^a	Sum of softnesses of atoms with positive partial charge	Obtained by summing up the contributions from atoms with positive charge computed by (9)
Total_Neg_Softness^a	Sum of softnesses of atoms with negative partial charge	Obtained by summing up the contributions from atoms with negative charge computed by (9)
Average_Softness	Arithmetic mean of softnesses of all atoms of a molecule	(11) divided by the number of atoms in molecule
Average_Pos_Softness	Arithmetic mean of softnesses of atoms with positive partial charge	$\frac{\sum_{i}^{n^{+}} s_{i}}{n^{+}}$ where $n^{+}$ is the number of atoms i with positive partial charge.
Average_Neg_Softness	Arithmetic mean of softnesses of atoms with negative partial charge	$\frac{\sum_{i}^{n^{-}} s_{i}}{n^{-}}$ where $n^{-}$ is the number of atoms i with negative partial charge.
Smallest_Pos_Softness^a	Smallest atomic softness among values for positively charged atoms	(9)
Smallest_Neg_Softness^a	Smallest atomic softness among values for negatively charged atoms	(9)
Largest_Pos_Softness	Largest atomic softness among values for positively charged atoms	(9)
Largest_Neg_Softness	Largest atomic softness among values for positively charged atoms	(9)
Softness_of_Most_Pos^a	Atomic softness of an atom with the most positive charge	(9)
Softness_of_Most_Neg^a	Atomic softness of an atom with the most negative charge	(9)
q (charge)- based
Total_Charge	Sum of absolute values of partial charges on all atoms of a molecule	$\sum_{i}^{N} \| Δ N_{i} \|$ where all the contributions $Δ N_{i}$ derived within (6)
Total_Charge_Formal^a	Sum of charges on all atoms of a molecule (formal charge of a molecule)	Sum of all contributions (6)
Average_Pos_Charge^a	Arithmetic mean of positive partial charges on atoms of a molecule	$\frac{\sum_{i}^{n^{+}} Δ N_{i}}{n^{+}}$ where $n^{+}$ is the number of atoms i with positive partial charge
Average_Neg_Charge^a	Arithmetic mean of negative partial charges on atoms of a molecule	$\frac{\sum_{i}^{n^{-}} Δ N_{i}}{n^{-}}$ where $n^{-}$ is the number of atoms i with negative partial charge
Most_Pos_Charge^a	Largest partial charge among values for positively charged atoms	(6)
Most_Neg_Charge	Largest partial charge among values for negatively charged atoms	(6)
σ* (inductive parameter) – based
Total_Sigma_mol_i^a	Sum of inductive parameters σ*(molecule→atom) for all atoms within a molecule	$\sum_{i}^{N} σ_{G \to i}^{}$ where contributions $σ_{G \to i}^{}$ are computed by equation (2) with n=N-1 – i.e. each atom j is considered against the rest of the molecule G
Total_Abs_Sigma_mol_i	Sum of absolute values of group inductive parameters σ*(molecule→atom) for all atoms within a molecule	$\sum_{i}^{N} \| σ_{G \to i}^{*} \|$
Most_Pos_Sigma_mol_i^a	Largest positive group inductive parameter σ*(molecule→atom) for atoms in a molecule	(2)
Most_Neg_Sigma_mol_i^a	Largest (by absolute value) negative group inductive parameter σ*(molecule→atom) for atoms in a molecule	(2)
Most_Pos_Sigma_i_mol^a	Largest positive atomic inductive parameter σ*(atom→molecule) for atoms in a molecule	(5)
Most_Neg_Sigma_i_mol^a	Largest negative atomic inductive parameter σ*(atom→molecule) for atoms in a molecule	(5)
Sum_Pos_Sigma_mol_i	Sum of all positive group inductive parameters σ*( molecule →atom) within a molecule	$\sum_{i}^{n^{+}} \| σ_{G \to i}^{} \|$ where $σ_{G \to i}^{}$ >0 and $n^{+}$ is the number of N-1 atomic substituents in a molecule with positive inductive effect (electron acceptors)
Sum_Neg_Sigma_mol_i^a	Sum of all negative group inductive parameters σ*( molecule →atom) within a molecule	$\sum_{i}^{n^{-}} \| σ_{G \to i}^{} \|$ where $σ_{G \to i}^{}$ <0 and $n^{-}$ is the number of N-1 atomic substituents in a molecule with negative inductive effect (electron donors)
Rs (steric parameter) – based
Largest_Rs_mol_i^a	Largest value of steric influence Rs(molecule→atom) in a molecule	(1) where n=N-1 - each atom j is considered against the rest of the molecule G
Smallest_Rs_mol_i^a	Smallest value of group steric influence Rs(molecule→atom) in a molecule	(1) where n=N-1 - each atom j is considered against the rest of the molecule G
Largest_Rs_i_mol	Largest value of atomic steric influence Rs(atom→molecule) in a molecule	(4)
Smallest_Rs_i_mol^a	Smallest value of atomic steric influence Rs(atom→molecule) in a molecule	(4)
Most_Pos_Rs_mol_i^a	Steric influence Rs(molecule→atom) ON the most positively charged atom in a molecule	(1)
Most_Neg_Rs_mol_i^a	Steric influence Rs(molecule→atom) ON the most negatively charged atom in a molecule	(1)
Most_Pos_Rs_i_mol	Steric influence Rs(atom→molecule) OF the most positively charged atom to the rest of a molecule	(4)
Most_Neg_Rs_i_mol^a	Steric influence Rs(atom→molecule) OF the most negatively charged atom to the rest of a molecule	(4)

^a – descriptors selected for building the antibiotic-likeness QSAR model.

Selection of variables

To build a binary QSAR model enabling effective separation of antibacterials we have initially calculated all 50 individual inductive descriptors for each molecule from the Vert’s dataset. We have used the hydrogen suppressed representation of the molecular structures – i.e. only the heavy atoms have been taken into account. The inductive QSAR descriptors have been calculated within the MOE package [32] from values of atomic electronegativities and radii taken from our previous publications [5]. To avoid the mentioned cross-correlation among the independent variables we have computed pair wise regressions between all 50 sets of the QSAR parameters and removed those inductive descriptors which formed any linear dependence with R≥0.9. As the result of this procedure, only 34 inductive QSAR descriptors have been selected for the further processing (see the legend to Table 1). The average values of these 34 parameters independently calculated for antibacterial and non- antibacterial compounds have been plotted onto Figure 1. As it can be seen, the corresponding curves for two classes of compounds are clearly separated on the graph and, hence, the selected 34 inductive descriptors should allow building an effective QSAR model of “antibiotic likeness”.

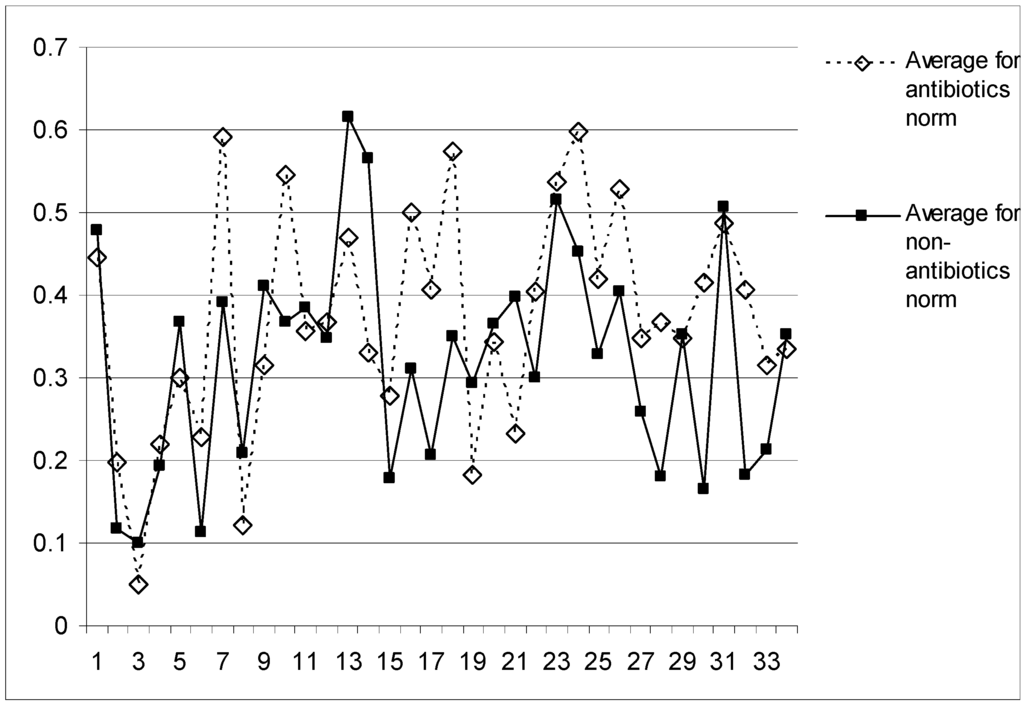
Figure 1. Averaged values of 34 selected inductive QSAR descriptors calculated independently within studied sets of antibiotics (dashed line) and non-antibiotics (solid line).

QSAR model

In order to relate the inductive descriptors to antibiotic activity of the studied molecules we have employed the Artificial Neural Networks (ANN) method – one of the most effective pattern recognition techniques. During the last decades the machine-learning approaches have became an essential part of the QSAR research; the detailed description of the ANN’s fundamentals can be found in numerous sources [33 for example].

In our study we have used the standard back-propagation ANN configuration consisting of 34 input and 1 output nodes. The number of nodes in the hidden layer was varied from 2 to 14 in order to find the optimal network that allows most accurate separation of antibacterials from other compounds in the training sets. For effective training of the ANN (to avoid its over fitting) we have used the training sets of 592 compounds (including 197 antibiotics) randomly derived as 90 percent of the total of 657 molecules. In each training run the remaining 10 percents of the compounds were used as the testing set to assess the predictive ability of the model. It should be noted, that we the condition of non-correlation amongst the descriptors has been monitored within the training and the testing sets of compounds as well.

During the learning phase, a value of 1 has been assigned to the training set’s molecules possessing antibacterial activity and value 0 to the others. For each configuration of the ANN (with 2, 3, 4, 6, 8, 10, 12, and 14 hidden nodes respectively) we have conducted 20 independent training runs to evaluate the average predictive power of the network. Table 2 contains the resulting values of specificity, sensitivity and accuracy of separation of antibacterial and non-antibacterial compounds in the testing sets. The corresponding counts of the false/true positive- and negative predictions have been estimated using 0.4 and 0.6 cut-off values for non-antibacterials and antibacterials respectively. Thus, an antibiotic compound from the testing set, has been considered correctly classified by the ANN only when its output value ranged from 0.6 to 1.0. For each non-antibiotic entry of the testing set the correct classification has been assumed if the corresponding ANN output lay between 0 and 0.4. Thus, all network output values ranging from 0.4 to 0.6 have been ultimately considered as incorrect predictions (rather than undetermined or non-defined).

Table 2. Parameters of specificity, sensitivity, accuracy and positive predictive values for prediction of antibiotic and non-antibiotic compounds by the artificial neural networks with the varying number of hidden nodes. The cut-off values 0.4 and 0.6 have been used for negative and positive predictions respectively.

**Table 2.** Parameters of specificity, sensitivity, accuracy and positive predictive values for prediction of antibiotic and non-antibiotic compounds by the artificial neural networks with the varying number of hidden nodes. The cut-off values 0.4 and 0.6 have been used for negative and positive predictions respectively.
Hidden nodes	Specificity	Sensitivity	Accuracy	PPV
2	0.8	0.92	0.846	0.751
3	0.926	0.928	0.923	0.884
4	0.925	0.92	0.923	0.884
6	0.9	1	0.938	0.862
8	0.9	0.92	0.907	0.851
10	0.9	0.92	0.907	0.851
12	0.9	0.92	0.907	0.851
14	0.815	1	0.923	0.833

Considering that one of the most important implications for the “antibiotic-likeness” model is its potential use for identification of novel antibiotic candidates from electronic databases, we have calculated the parameters of the Positive Predictive Values (PPV) for the networks while varying the number of hidden nodes. Taking into account the PPV values for the networks with the varying number of the hidden nodes along with the corresponding values of sensitivity, specificity and general accuracy we have selected neural network with three hidden nodes as the most efficient among the studied. The ANN with 34 input-, 3 hidden- and 1 output nodes has allowed the recognition of 93% of antibiotic and 93% of non-antibiotic compounds, on average. The output from this 34-3-1 network has also demonstrated very good separation on positive (antibiotics) and negative (non-antibiotics) predictions. Figure 2 features frequencies of the output values for the training and testing sets consisting of ⅓ of antibiotic and ⅔ of non-antibiotics compounds. As it can readily be seen from the graph, the vast majority of the predictions has been contained within [0.0°0.4] and [0.6°1.0] ranges what also illustrates that 0.4 and 0.6 cut-offs values provide very adequate separation of two bioactivity classes (Table 3 and Table 4 feature the outputs values from the 34-3-1 ANN for the training and testing sets respectively).

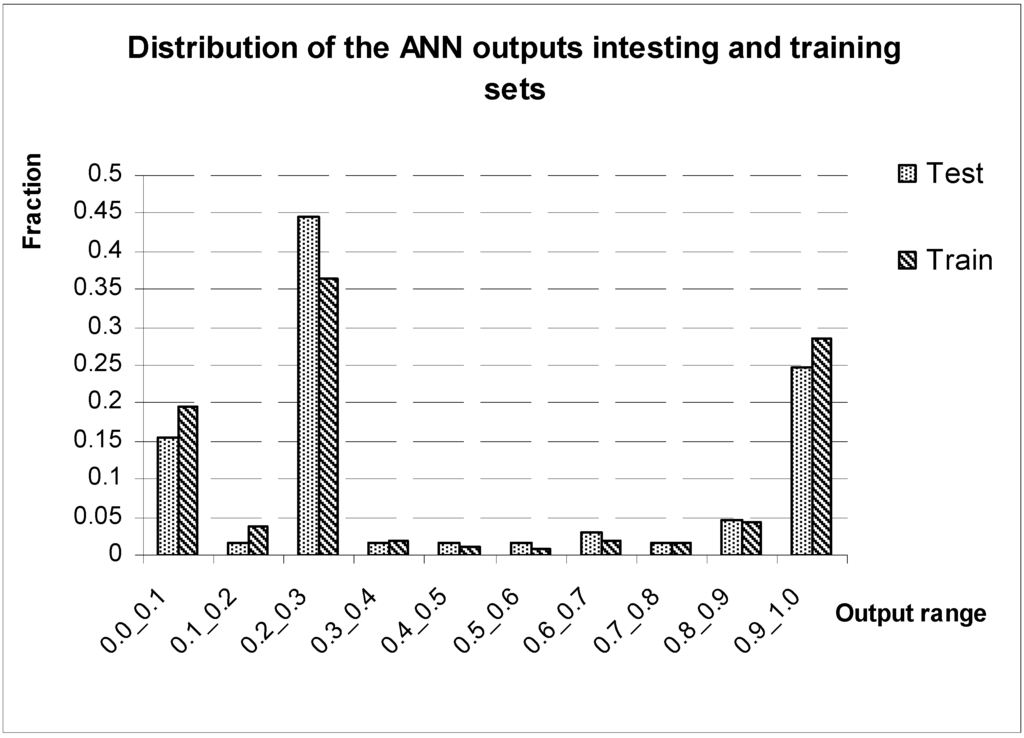
Figure 2. Distribution of the output values from the ANN with three nodes in the hidden layer and trained on the set containing 90% of the studied compounds

It should be mentioned, that the estimated 93% accuracy of the prediction by the 34-3-1 ANN is similar or superior to the results by several similar ‘antibiotic-likeness’ studies where the overall cross—validated accuracy can range from 78 [20] to 98% [26] depending of the QSAR methodology, size of antibiotics/non-antibiotics dataset, cross-correlation technique and statistics utilized.

We have also applied the developed techniques on the non-hydrogen suppressed molecular structures. The estimated accuracy of antibiotic/non-antibiotic classification was very close to the results for the hydrogen suppressed molecules. In contrast, the time for the calculation of the inductive QSAR descriptors in the former case is much shorter as the total number of all atoms nearly doubles.

Discussion

The accuracy of discrimination of antibiotic compounds by the artificial neural networks built upon the ‘inductive’ descriptors clearly demonstrates an adequacy and good predictive power of the developed QSAR model. There is strong evidence, that the introduced inductive descriptors do adequately reflect the structural properties of chemicals, which are relevant for their antibacterial activity. This observation is not surprising considering that the inductive QSAR descriptors calculated within (1)–(11) should cover a very broad range of proprieties of bound atoms and molecules related to their size, polarizability, electronegativity, compactness, mutual inductive and steric influence and distribution of electronic density, etc. The results of the study demonstrate that not extensive sets of inductive QSAR descriptors having much defined physical meaning can be sufficient for creating useful models of “antibiotic-likeness”. The accuracy of the developed QSAR model is superior or similar compared to other binary classifiers on the same set of molecules but using much more extensive collections of QSAR descriptors [27,29].

Presumably, accuracy of the approach operating by the inductive descriptors can be improved even further by expanding the QSAR descriptors or by applying more powerful classification techniques such as Support Vector Machines or Bayesian Neural Networks. Use of merely statistical techniques in conjunction with the inductive QSAR descriptors would also be beneficial, as they will allow interpreting individual descriptor contributions into molecular “antibiotic-likeness”. The selection of drugs used for the simulation can also be extended and/or refined. For instance, it has been experimentally confirmed that several non-antibacterial compounds from Vert’s dataset can, in fact, possess definite antibacterial activity. Thus, anti-inflammatory drugs diclofenac [34,35], piroxicam, mefenamic acid and naproxen [35], antihistamines – bromodiphenhydramine [36] diphenhydramine [36] and triprolidine [37], anti-psychotics – chlorpromazine [38,39] and fluphenazine [40,41], the tranquilizer promazine [42] and anti-hypertensive methyldopa [43] all exhibit moderate to powerful potential against microbes. It is obvious, that having all these compounds as the negative control can interfere with the training of efficient antibiotic-likeness model. We, however, did not remove these substances from the e training and testing sets for the sake of comparison of our results with the previous data. Nonetheless, despite the certain drawbacks, it is obvious that the developed ANN-based QSAR model operating by the inductive descriptors has demonstrated very high accuracy and can be used for mining electronic collections of chemical structures for novel antibiotic candidates.

An application of the model

We have decided to test the developed model of “antibiotic-likeness” on the series of early-stage antibiotic compounds featured in the free issue of the Drug Data Report – a journal presenting preliminary drug research results appearing for the first time in patent literature [44]. The “experimental” antibiotic compounds cited by the issue included one penicillin- and two cephalosporin- derivatives as well as a number of high molecular weight chemicals with complex spatial structures such as five C11-carbamate azalides and four eremomycin carboxamides (the corresponding structural formulas are presented on Figure 3).

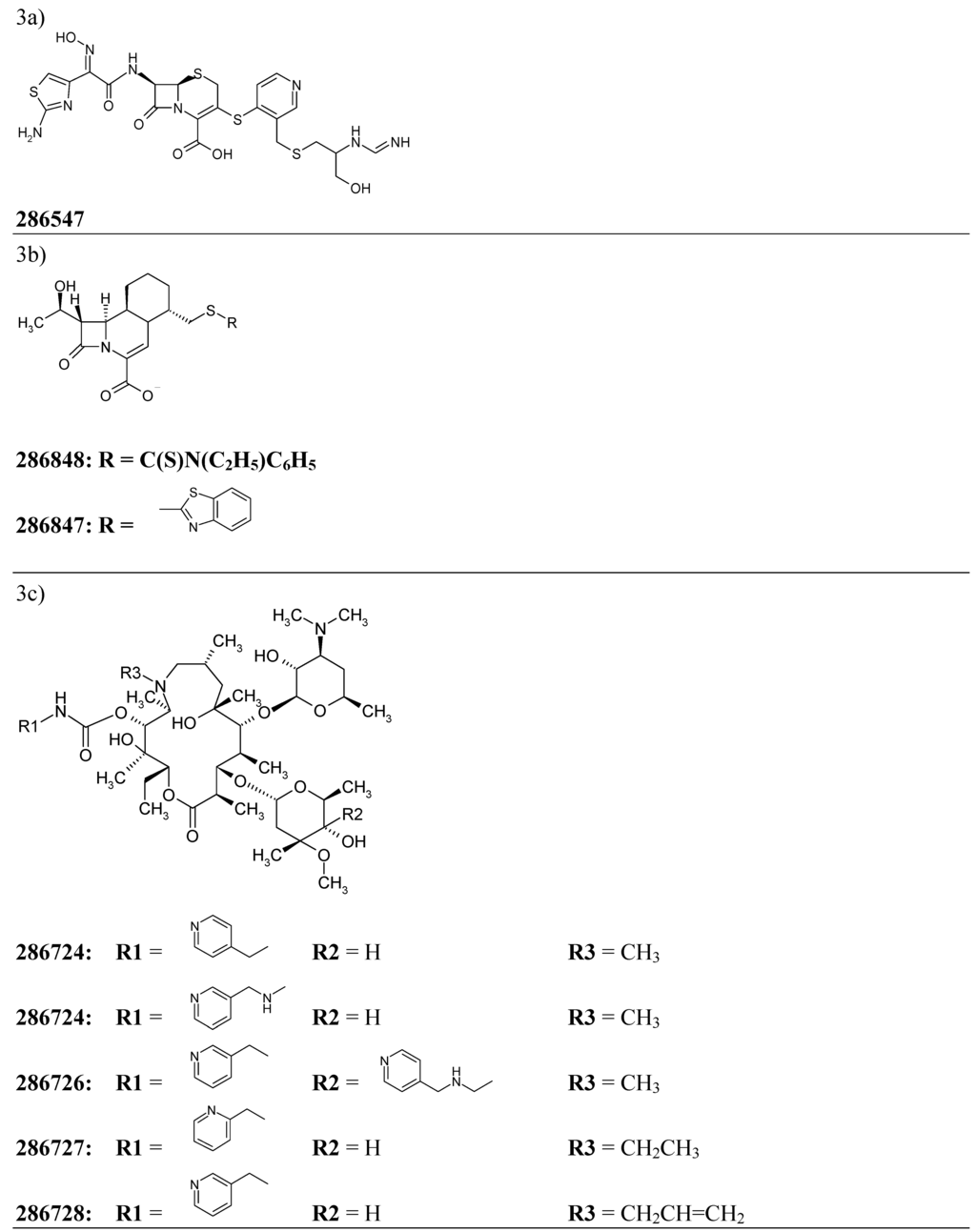
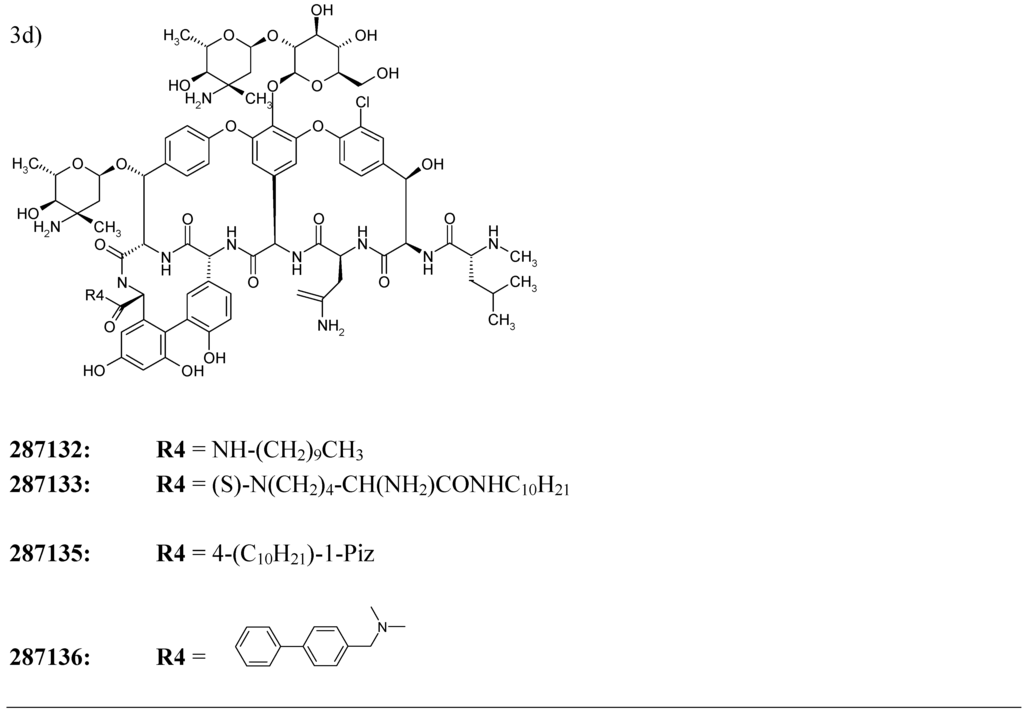
Figure 3. Chemical structures of twelve early stage antibiotics from the Drug Data Report used for validation for the developed ANN – based QSAR model.

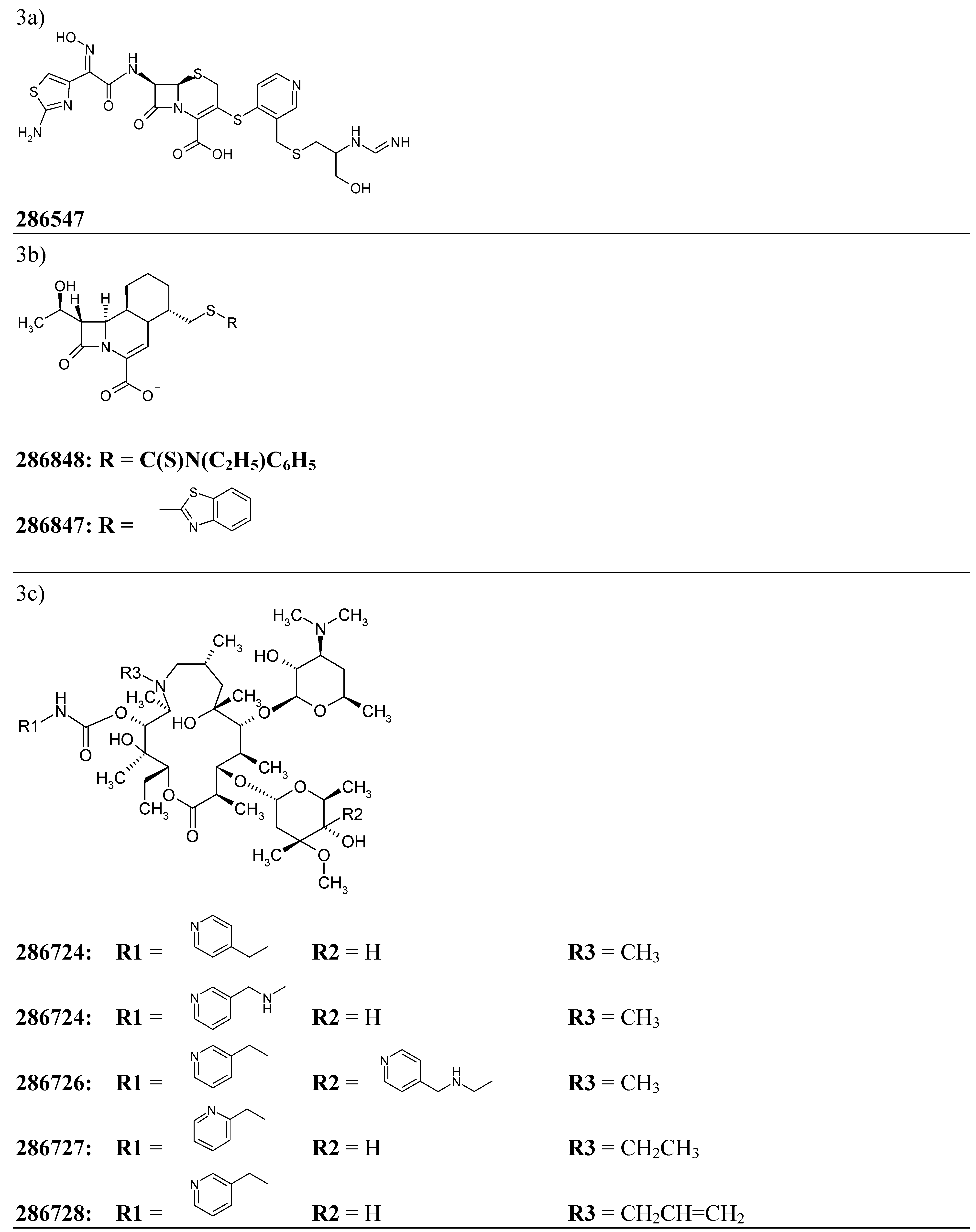
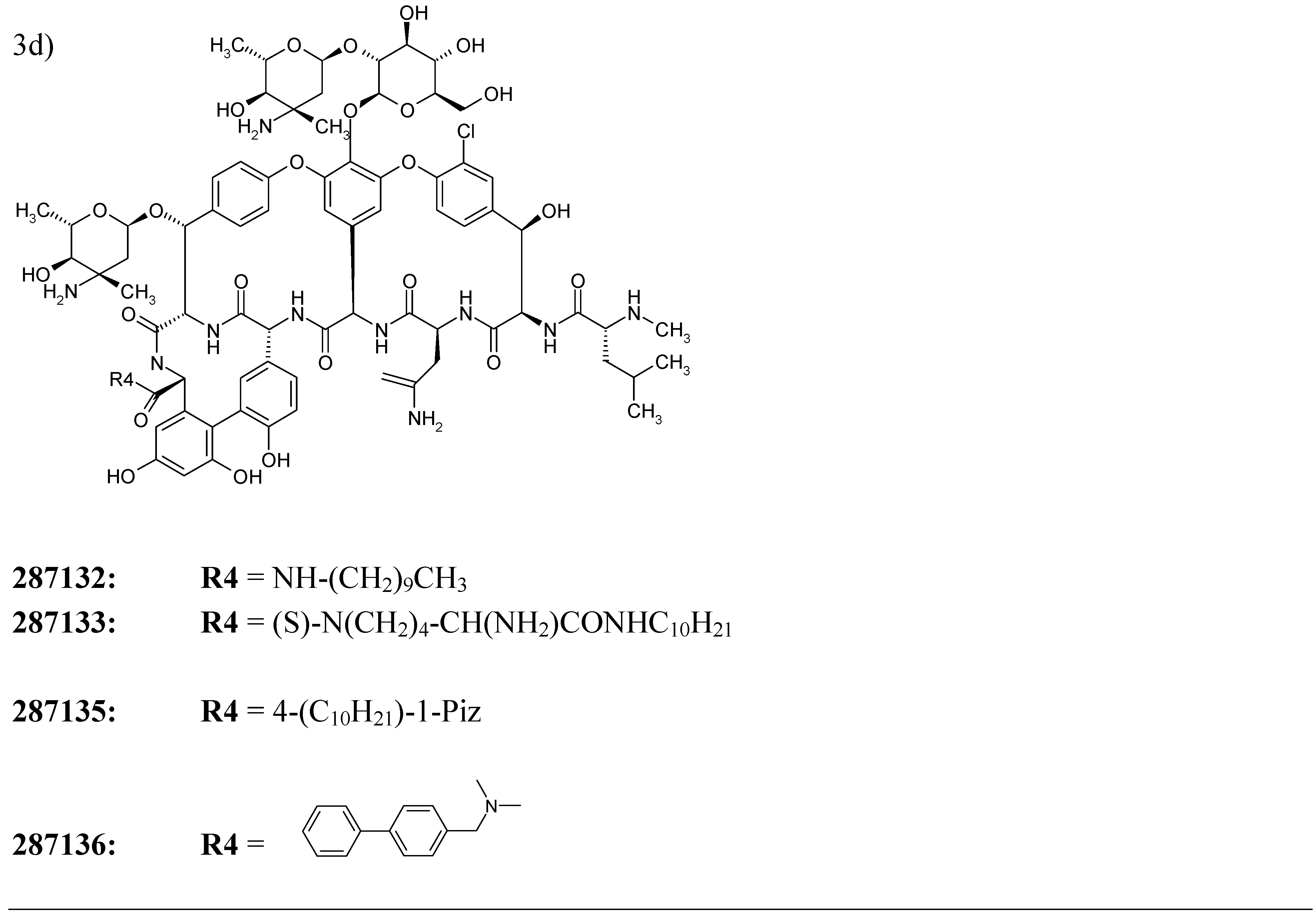
For each of 12 compounds from the validation set we have calculated 34 inductive descriptors used earlier. The normalized patterns of the independent variables have then been passed through 34-3-1 network with its node–associated weights pre-assigned during the training. The ANN has produced the output parameters presented in Table 5. As it can be seen from the data, all of the estimated output values score well above 0.60 threshold what confidently assigns all of the trial molecules to the class of antibiotics.

Table 3. Compounds of the training set and output values from the trained neural network with three hidden nodes.

**Table 3.** Compounds of the training set and output values from the trained neural network with three hidden nodes.
Name	Output	Name	Output
antibiotics		apicycline	0.975
4'-(methylsulfamoyl)sulfanilanilide	0.973	apramycin	0.980
4'-formylsuccinanilic acid thiosemicarbazone		azidocillin	0.979
4'-formylsuccinanilic acid thiosemicarbazone	0.259	arbekacin	0.980
4-sulfanilamidosalicylic acid	0.938	aspoxicillin	0.975
acediasulfone	0.828	azidamfenicol	0.966
acetyl sulfamethoxypyrazine	0.855	azlocillin	0.850
acetyl sulfisoxazole	0.964	aztreonam	0.981
amidinocillin	0.702	bacampicillin	0.982
amidinocillin pivoxil	0.938	benzylpenicillinic acid	0.924
amifloxacin	0.881	benzylsulfamide	0.733
amikacin	0.984	biapenem	0.830
apalcillin	0.981	brodimoprim	0.585
butirosin	0.984	cephalothin	0.977
carbenicillin	0.974	cephapirin sodium	0.984
carfecillin sodium	0.970	cephradine	0.897
carindacillin(a,e,f,i)	0.938	chloramphenicol	0.606
carumonam	0.985	chloramphenicol palmitate	0.604
cefaclor	0.860	chloramphenicol pantothenate	0.983
cefadroxil	0.915	chlortetracycline	0.984
cefamandole	0.964	cinoxacin	0.770
cefatrizine	0.973	clinafloxacin	0.920
cefazedone	0.984	clindamycin	0.926
cefazolin	0.979	clometocillin	0.953
cefbuperazone	0.984	clomocycline	0.982
cefcapene pivoxil	0.983	cloxacillin	0.935
cefclidin(a,i,j)	0.985	cyclacillin	0.960
cefdinir(e,i)	0.984	dibekacin	0.952
cefditoren	0.984	dichloramine	0.253
cefepime	0.982	dicloxacillin	0.983
cefetamet	0.983	difloxacin	0.835
cefixime	0.984	diphenicillin sodium	0.767
cefmenoxime	0.984	doxycycline	0.981
cefmetazole	0.984	enoxacin	0.915
cefminox	0.985	enrofloxacin	0.630
cefodizime	0.985	epicillin	0.963
cefonicid	0.984	fenbenicillin	0.967
ceforanide	0.974	fleroxacin	0.980
cefotiam	0.985	flomoxef	0.985
cefoxitin	0.984	florfenicol	0.955
cefozopran	0.982	floxacillin	0.983
cefpimizole	0.985	fortimicin a	0.978
cefpiramide	0.985	fortimicin b	0.700
cefpirome	0.984	furaltadone	0.901
cefpodoxime proxetil	0.985	gentamicin c1	0.850
cefprozil	0.902	gentamicin c2	0.940
cefroxadine	0.970	gentamicin c3	0.956
cefsulodin	0.982	grepafloxacin	0.862
ceftazidime	0.984	guamecycline	0.977
cefteram	0.979	imipenem	0.577
ceftezole	0.984	isepamicin	0.985
ceftizoxime	0.984	kanamycin a	0.962
cefuroxime	0.980	kanamycin b	0.976
cefuzonam	0.985	kanamycin c	0.971
cephacetrile sodium	0.982	lenampicillin	0.985
cephalexin	0.847	lincomycin	0.907
cephaloglycin	0.951	lomefloxacin	0.946
cephaloridine	0.960	loracarbef	0.862
cephalosporin c	0.976	lymecycline	0.978
meclocycline	0.984	propicillin	0.814
meropenem	0.977	quinacillin	0.984
methacycline	0.983	ribostamycin	0.965
methicillin sodium	0.951	rifamide	0.979
mezlocillin	0.976	rifamycin sv	0.984
micronomicin	0.966	rifaximin	0.984
miloxacin	0.786	ritipenem	0.977
moxalactam	0.984	rolitetracycline	0.979
n2-formylsulfisomidine	0.919	rosoxacin	0.265
n4-sulfanilylsulfanilamide	0.980	rufloxacin	0.975
nadifloxacin	0.658	salazosulfadimidine	0.970
nafcillin sodium	0.919	sancycline	0.980
nalidixic acid	0.268	sisomicin	0.909
neomycin a(c,i,j)	0.983	sparfloxacin	0.975
neomycin b(a,d,h,i)	0.981	spectinomycin	0.628
netilmicin	0.938	succinylsulfathiazole	0.977
nifuradene	0.600	sulbenicillin	0.884
nifuratel	0.980	sulfabenzamide	0.895
nifurfoline	0.963	sulfacetamide	0.955
nifurprazine	0.267	sulfachlorpyridazine	0.915
nifurtoinol	0.694	sulfachrysoidine	0.975
nitrofurantoin	0.291	sulfacytine	0.971
norfloxacin	0.523	sulfadiazine	0.937
N-sulfanilyl-3,4-xylamide	0.956	sulfadicramide	0.933
ofloxacin	0.972	sulfadimethoxine	0.958
oxytetracycline	0.984	sulfadoxine	0.965
panipenem	0.939	sulfaethidole	0.918
paromomycin	0.984	sulfaguanidine	0.904
pasiniazide	0.236	sulfaguanol	0.943
pazufloxacin	0.926	sulfalene	0.938
pefloxacin	0.563	sulfaloxic acid	0.857
penamecillin	0.636	sulfamethazine	0.912
penethamate hydriodide	0.704	sulfamethizole	0.759
penicillin G potassium	0.848	sulfamethomidine	0.940
penicillin N	0.901	sulfamethoxazole	0.908
penicillin O	0.978	sulfamethoxypyridazine	0.912
penicillin V	0.912	sulfamidochrysoidine	0.952
phenethicillin potassium	0.822	sulfamoxole	0.954
phthalylsulfathiazole	0.976	sulfanilamide	0.653
pipacycline	0.921	sulfanilic acid	0.841
pipemidic acid	0.882	sulfanilylurea	0.938
piperacillin	0.982	sulfaphenazole	0.929
piromidic acid	0.696	sulfaproxyline	0.957
pivampicillin	0.916	sulfapyrazine	0.934
pivcefalexin	0.946	sulfathiazole	0.873
p-nitrosulfathiazole	0.893	sulfathiourea	0.849
sulfisomidine	0.909	bamipine	0.036
sulfisoxazole	0.963	biclofibrate	0.247
sultamicillin	0.983	befunolol	0.252
talampicillin	0.911	benfluorex	0.258
temocillin	0.985	benorylate	0.259
tetracycline	0.983	benserazide	0.259
tetroxoprim	0.837	benzitramide	0.259
thiamphenicol	0.942	benzotropine mesylate	0.000
ticarcillin	0.983	benzpiperylon	0.000
tigemonam	0.985	benzydamine	0.000
trimethoprim	0.739	bermoprofen	0.257
trospectomycin	0.850	betaxolol	0.174
trovafloxacin(b)	0.960	bevantolol	0.154
non-antibiotics		bevonium methyl sulfate	0.032
2-amino-4-picoline	0.258	bezafibrate	0.256
5-bromosalicylic acid acetate	0.258	binifibrate	0.319
5-nitro-2propoxyacetanilide	0.280	bisoprolol	0.184
acecarbromal	0.259	bitolterol	0.004
aceclofenac	0.431	bucloxic acid	0.258
acefylline(c,d,e,g)	0.841	bopindolol	0.001
acetaminophen(b,i)	0.258	bromfenac	0.258
acetanilide	0.258	bromisovalum	0.258
acetazolamide	0.023	bromodiphenhydramine	0.057
acetophenazine	0.265	brompheniramine	0.006
acetylsalicylic acid	0.258	bucetin	0.247
acrivastine	0.260	bucolome	0.253
ahistan	0.000	bucumolol	0.256
albuterol	0.258	bufetolol	0.157
alclofenac	0.258	bufexamac	0.258
alminoprofen	0.256	bufuralol	0.008
alphaprodine	0.106	bumadizon	0.205
alprenolol	0.239	bunitrolol	0.258
aminochlorthenoxazin	0.257	butabarbital	0.258
aminopyrine	0.000	butaclamol	0.123
amosulalol	0.078	butallylonal	0.262
amtolmetin guacil	0.001	butanilicaine	0.206
anileridine	0.262	butibufen	0.255
antipyrine	0.017	butidrine hydrochloride	0.183
antrafenine	0.283	butoctamide	0.252
apazone	0.001	butofilolol	0.256
apronalide	0.258	caffeine	0.159
arotinolol	0.293	capuride	0.257
atenolol	0.258	carazolol	0.027
atropine	0.258	carbamazepine	0.015
bambuterol	0.032	carbidopa	0.259
bamifylline	0.290	carbinoxamine	0.066
carbiphene	0.258	diethylbromoacetamide	0.257
carbocloral	0.313	difenamizole	0.006
carbromal	0.257	difenpiramide	0.009
carbuterol	0.258	diflunisal	0.258
carfimate	0.258	dilevalol	0.255
carphenazine	0.263	dioxadrol	0.000
carprofen	0.258	dipyrocetyl	0.315
carsalam	0.258	dipyrone	0.041
carteolol	0.259	disulfiram	0.001
carvedilol	0.000	doxefazepam	0.270
celiprolol	0.211	doxofylline	0.629
cetamolol	0.245	doxylamine(b,f,g,i)	0.000
cetirizine	0.261	droperidol	0.259
chlorhexadol	0.288	droxicam	0.022
chlorobutanol	0.258	dyphylline	0.410
chloropyramine	0.050	ectylurea	0.244
chlorothen	0.070	embramine	0.122
chlorpheniramine	0.095	emorfazone	0.010
chlorprothixene	0.017	enfenamic acid	0.256
chlorthenoxacin		enprofylline	0.246
(chlorthenoxazine)	0.258	epanolol	0.258
chlorcyclizine	0.078	ephedrine	0.229
cinchophen	0.251	epirizole	0.002
cinmetacin	0.248	eprozinol	0.237
cinnarizine	0.388	estazolam	0.000
cinromida	0.197	etafedrine	0.179
ciprofibrate	0.251	etamiphyllin	0.118
clemastine	0.039	etaqualone	0.000
clenbuterol	0.234	eterobarb	0.001
clidanac	0.258	etersalate	0.260
clinofibrate	0.282	ethenzamide	0.243
clofibric acid	0.256	ethinamate	0.258
clometacin	0.292	ethoheptazine	0.000
clometiazol	0.255	ethoxazene	0.248
clonixin	0.254	etodolac	0.259
clopirac	0.257	etofibrate	0.260
cloranolol	0.247	etofylline	0.266
clordesmetildiazepam	0.257	etomidate	0.000
clorprenaline	0.249	etymemazine	0.002
clothiapine	0.003	felbinac	0.258
clozapine	0.051	fenadiazole	0.230
codeine	0.062	fenbufen	0.258
cropropamide	0.002	fenclofenac	0.259
crotethamide	0.035	fenethazine	0.000
deserpidine	0.005	fenofibrate	0.254
diclofenac	0.262	fenoprofen	0.258
fenoterol	0.258	lornoxicam	0.031
fentanyl	0.066	loxapina	0.004
fentiazac	0.259	loxoprofen	0.258
floctafenine	0.266	mazindol(i)	0.162
flufenamic acid	0.259	meclofenamic acid(f)	0.276
fluoresone	0.459	mecloqualone	0.000
fluphenazine	0.260	medibazine	0.004
flupirtine	0.260	medrylamine	0.001
fluproquazone	0.258	meparfynol	0.258
flurazepam	0.010	mepindolol	0.211
flurbiprofen	0.258	meprobamate	0.259
fluspirilene	0.259	mequitazine	0.001
flutropium bromide	0.259	methafurylene	0.000
formoterol	0.259	methaphenilene	0.000
fosazepam	0.258	methotrimeprazine	0.002
fusaric acid	0.258	methoxyphenamine	0.000
gemfibrozil	0.248	methyldopa	0.258
gentisic acid	0.258	methyltyrosine	0.256
glafenine	0.259	methyprylon	0.232
glucametacin	0.335	metiapine	0.002
glutethimide	0.258	metipranolol	0.258
haloperidide	0.259	metofoline	0.094
haloperidol	0.258	metoprolol	0.179
hexapropymate	0.258	metron	0.275
hexobarbital	0.274	mexiletine	0.251
hexoprenaline	0.258	mofezolac	0.340
histapyrrodine	0.004	molindone	0.000
hydroxyethylpromethazine		moperone	0.259
(N-Hydroxyethylpromethazine)	0.261	moprolol	0.213
hydroxyzine	0.261	morazone	0.000
ibufenac	0.258	morphine	0.289
ibuprofen	0.258	moxastine	0.000
ibuproxam	0.258	nadoxolol	0.258
indenolol	0.179	naproxen	0.256
indomethacin	0.323	narcobarbital	0.265
ipratropium bromide	0.259	nefopam	0.000
isoetharine	0.258	niceritrol	0.981
isofezolac	0.183	nicoclonate	0.095
isonixin	0.125	nicofibrate	0.214
isopromethazine	0.000	nifenalol	0.256
isoxicam	0.003	nifenazone	0.000
ketoprofen	0.250	niflumic acid	0.260
ketorolac	0.259	nimetazepam	0.512
labetalol	0.252	nipradilol	0.611
lefetamine	0.068	nitrazepam	0.337
lorazepam	0.268	nordiazepam	0.254
novonal	0.255	propyphenazone	0.000
octopamine	0.258	protokylol	0.260
orphenadrine	0.000	proxibarbital	0.262
oxaceprol	0.259	proxyphylline	0.210
oxametacine	0.284	pyrilamine	0.000
oxanamide	0.254	pyrrobutamine	0.000
oxaprozin	0.259	quazepam	0.331
oxitropium bromide	0.265	ramifenazone	0.000
oxprenolol	0.221	reproterol	0.296
oxypertine	0.000	rimiterol	0.258
paramethadione	0.258	ronifibrate	0.259
parsalmide	0.259	salacetamide	0.258
p-bromoacetanilide	0.258	salicylamide	0.257
pemoline	0.258	salicylamide O-acetic acid	0.258
penbutolol	0.099	salsalate	0.258
penfluridol	0.259	salverine	0.000
perisoxal	0.034	scopolamine	0.278
perphenazine	0.284	secobarbital	0.257
phenacemide	0.258	setastine	0.035
phenacetin	0.247	simetride	0.028
phenoperidine	0.191	simfibrate	0.259
phenopyrazone	0.243	simvastatin	0.355
phenylbutazone	0.000	sotalol	0.013
phenyltoloxamine(a,c,g)	0.000	soterenol	0.099
pindolol	0.055	sulfinalol	0.062
pipebuzone	0.001	sulpiride	0.017
piperacetazine	0.261	suprofen	0.258
piperidione	0.253	talastine	0.000
piperylone	0.000	talinolol	0.245
pirbuterol	0.259	talniflumate	0.399
pirifibrate(g,h)	0.258	temazepam	0.207
piroxicam	0.013	tenoxicam	0.008
pirprofen	0.258	terbutaline	0.258
p-lactophenetide	0.257	tertatolol	0.129
p-methyldiphenhydramine	0.000	tetrabarbital	0.257
pravastatin	0.438	thenaldine	0.000
prazepam	0.008	thenyldiamine	0.000
primidone	0.133	theobromine	0.251
probucol	0.000	theofibrate(b,f,i)	0.435
procaterol	0.260	theophylline(f,h,i,j)	0.224
proglumetacin	0.292	thioridazine	0.003
prolintane	0.024	thiothixene	0.003
promazine	0.000	thonzylamine	0.001
pronethalol	0.237	tiaprofenic acid	0.258
propanolol	0.067	timolol	0.030
toliprolol	0.127	tripelennamine	0.000
tolmetin	0.254	triprolidine	0.000
tolpropamine	0.001	tulobuterol	0.169
tretoquinol	0.418	viminol	0.028
triazolam	0.003	vinylbital	0.258
triclofos	0.276	xenbucin	0.256
trifluoperazine	0.298	xibenolol	0.148
trifluperidol	0.259	zolamine	0.035
trimethadione	0.258	zomepirac	0.263
triparanol	0.248

Table 4. Compounds of the testing set and the corresponding output values from the trained neural network with three hidden nodes.

**Table 4.** Compounds of the testing set and the corresponding output values from the trained neural network with three hidden nodes.
Name	Output	Name	Output
antibiotics		butacetin	0.147
amoxicillin	0.152	chlorpromazine	0.169
ampicillin	0.728	ciramadol	0.150
cefoperazone	0.997	clocinizine	0.125
cefotaxime	0.999	clofibrate	0.142
cefotetan	0.568	diazepam	0.997
cefteram	0.999	diphenhydramine	0.125
ceftriaxone	0.999	diphenylpyraline	0.101
ciprofloxacin	0.999	esmolol	0.151
demeclocycline	0.999	ethclorvinol	0.047
flumequine	0.998	feprazone	0.118
hetacillin	0.992	flunitrazepam	0.069
mafenide	0.999	fosfosal	0.134
metampicillin	0.978	indoprofen	0.287
minocycline	0.984	isoproterenol	0.151
nifurpirinol	0.998	levobunolol	0.150
noprylsulfamide	0.998	lovastatin	0.151
oxacillin	0.999	mabuterol	0.149
oxolinic acid	0.991	mefenamic acid	0.097
sulfamerazine	0.999	mefexamide	0.000
sulfametrole	0.999	meperidine	0.146
sulfanitran	0.998	mephobarbital	0.160
sulfaperine	0.997	methapyrilene	0.000
temafloxacin	0.987	nadolol	0.151
thiazolsulfone	0.994	pheniramine	0.134
tobramycin	0.994	phenocoll	0.000
tosufloxacin	0.995	phenyramidol	0.000
non-antibiotics		pimozide	0.029
acetaminosalol	0.110	practolol	0.152
acetobutolol	0.150	proheptazine	0.149
aminopropylon	0.000	propacetamol	0.166
benoxaprofen	0.150	sulindac	0.975
brotizolam	0.004	talbutal	0.063
bupranolol	0.144

Table 5. Output values from the neural network for the validation set’s antibiotics.

**Table 5.** Output values from the neural network for the validation set’s antibiotics.
Compound	Structural formula	Prediction
286547	3a	0.984
286724	3c	0.985
286725	3c	0.985
286726	3c	0.985
286727	3c	0.985
286728	3c	0.985
286847	3b	0.915
286848	3b	0.914
287132	3d	0.985
287133	3d	0.985
287135	3d	0.985
287136	3d	0.985

These results demonstrate that the developed ANN-based binary classifier of antibacterial activity is adequate and can be considered an effective tool for ‘in silico’ antibiotics discovery. The results also demonstrate that the inductive parameters readily accessible by formulas (1)-(11) from atomic electronegativities, covalent radii and interatomic distances can produce a variety of useful QSAR descriptors to be used ‘in silico’ chemical research.

Conclusions

The results of the present work demonstrate that a variety of atomic, substituent and molecular properties which can be computed within the framework of our previous models for inductive and steric effects, inductive electronegativity and molecular capacitance represent a powerful arsenal of 3D QSAR descriptors for modern ‘in silico’ drug research. Using only 34 inductive descriptors with no additional independent parameters we have achieved 93% correct classification of compounds with- and without antibacterial activity. The introduced inductive descriptors possess a number of important merits: they are 3D- and stereo- sensitive, can be easily computed from fundamental properties of bound atoms and molecules and possess much defined physical meaning. The developed ANN-based model for antibiotic-likeness prediction can be used as a powerful QSAR tool for filtering through the collections of chemical structures to discover novel antibiotic leads.

Methods

The names of the chemical compounds from the dataset from [27] have been translated into SMILES records and MOL files using the ChemIDPlus online service [45] and the MOE package [32]. 50 inductive descriptors have been calculated using by the SVL scripts – a specialized language of the MOE package. The interatomic distances have been calculated by the MOE from the molecular structures optimized with the MMFF94 force-field [46]. The atomic types have been assigned according to the name, valent state and a formal charge of atoms as it is defined within the MOE. The parameters of the corresponding atomic electronegativities and covalent radii have been taken from our works [5,8]. The inductive QSAR descriptors used in the study have been normalized into the range [0.0°1.0] and the non-overlapping training and testing sets have been randomly drawn by the customized Java scripts. The training and testing of the neural networks has been conducted using the Stuttgart Neural Network Simulator [47]. The training was performed through the feed-forward back-propagation algorithm with the weight decay and pattern shuffling. The values of initial rates were randomly assigned in a range [0.0°1.0], the learning rate has been set to 0.8 with the threshold 0.10.

References

Kubinyi, H.; Folkers, G.; Martin, Y.C. (Eds.) 3D QSAR in Drug Design; Kluwer: Dordrecht, 2002.
Truhlar, D.G.; Howe, W.J.; Hopfinger, A.J. (Eds.) Rational Drug Design; Springer: Berlin, 1999.
Karelson, M. Molecular Descriptors in QSAR/QSPR; Wiley: New York, 2000; p. 448. [Google Scholar]
Exner, O. Correlation Analysis of Chemical Data; Kluwer: Dordrecht, 1988. [Google Scholar]
Cherkasov, A.R.; Galkin, V.I.; Cherkasov, R.A. J. Phys. Org. Chem. 1998, 11, 437. [CrossRef]
Cherkasov, A.R.; Galkin, V.I.; Cherkasov, R.A. J. Molec. Struct. (Theochem) 1999, 489, 43. [CrossRef]
Cherkasov, A.R.; Galkin, V.I.; Cherkasov, R.A. J. Molec. Struct. (Theochem) 2000, 497, 115. [CrossRef]
Cherkasov, A. J. Chem. Inf. Comp. Sci. 2003, 43, 2039. [CrossRef]
Babij, C.; Poe, A.J. J. Phys. Org. Chem. 2004, 17, 162.
Galkin, V.I.; Sayakhov, R.D.; Cherkasov, R.A. Russ. Chem. Rev. 1991, 60, 1617.
Cherkasov, A.; Jonsson, M. J. Chem. Inf. Comp. Sci. 1998, 38, 1151. [CrossRef]
Cherkasov, A.; Jonsson, M. J. Chem. Inf. Comp. Sci. 1999, 39, 1057. [CrossRef]
Cherkasov, A.R.; Jonsson, M.; Galkin, V.I. J. Mol. Graph. Model. 1999, 17, 28. [CrossRef]
Cherkasov, A.; Jonsson, M. J. Chem. Inf. Comp. Sci. 2000, 40, 1222. [CrossRef]
Cherkasov, A.; Sprous, D.; Chen, R. J. Phys. Chem. A. 2003, 107, 9695.
Galkin, V.I.; Cherkasov, A.R.; Cherkasov, R.A. Phosphorus, Silicon, Sulphur 1999, 146, 329.
Byvalov, E.; Fechner, U.; Sadowski, J.; Schneider, G. J. Chem. Inf. Comp. Sci. 2003, 43, 1882. [CrossRef]
Zernov, V.; Balakin, K.V.; Ivaschenko, A.A.; Savchuk, N.P.; Pletnev, I.V. J. Chem. Inf. Comp. Sci. 2003, 43, 2048. [CrossRef]
Anzali, S.; Barenickel, G.; Cezanne, B.; Krug, M.; Filimonov, D.; Poroikob, V. J. Med. Chem. 2001, 44, 2432. [CrossRef]
Murcia-Soler, M.; Perez-Gimenez, F.; Garcia-March, F.J.; Salabert-Salvador, M.T.; Diaz-Villanueva, W.; Castro-Bleda, M.J. J. Chem. Inf. Comp. Sci. 2003, 43, 1688. [CrossRef]
Frimurer, T.M.; Bywater, R.; Naerum, L.; Lauritsen, L.N.; Brunak, S. J. Chem. Inf. Comp. Sci. 2000, 40, 1315. [CrossRef]
Sadowski, J.; Kubinyi, H. J. Med. Chem. 1998, 41, 3325. [CrossRef]
Galvez, J.; de Julian-Ortiz, J.V.; Garcia-Domenech, R. J. Mol. Graph. Model. 2001, 20, 84. [CrossRef]
Ajay, A.; Walters, W.P.; Murcko, M.A. J. Med. Chem. 1998, 41, 3314. [CrossRef]
Jaen-Oltra, J.; Salabert-Salvador, M.T.; Garcia-March, F.J.; Perez-Gimenez, F.; Tomas-Vert, F. J. Med. Chem. 2000, 43, 1143. [CrossRef] [PubMed]
Garcia-Domenech, R.; de Julian-Ortiz, J.V. J. Chem. Inf. Comp. Sci. 1998, 38, 445. [CrossRef]
Tomas-Vert, F.; Perez-Gimenez, F.; Salabert-Salvador, M.T.; Garcia-March, F.J.; Jaen-Oltra, J. J. Molec. Struct. (Theochem). 2000, 504, 249. [CrossRef]
Mishra, R.K.; Garcia-Domenech, R.; Galvez, J. J. Chem. Inf. Comp. Sci. 2001, 41, 387. [CrossRef]
Cronin, M.T.D.; Aptula, A.O.; Dearden, J.C.; Duffy, J.C.; Netzeva, T.I.; Patel, H.; Rowe, P.H.; Schultz, T.W.; Worth, A.P.; Voutzoulidis, K.; Schuurmann, G. J. Chem. Inf. Comp. Sci. 2002, 42, 869. [CrossRef]
Molina, E.; Diaz, H.G.; Gonzalez, M.P.; Rodriguez, E.; Uriarte, E. J. Chem. Inf. Comp. Sci. 2004, 44, 515. [CrossRef]
Gozalbez, R.; Galvez, J.; Moreno, A.; Garcia-Domenech, R. J. Pharm. Pharmacol. 1999, 51, 111. [CrossRef]
Molecular Operational Environment; Chemical Computation Group Inc.: Montreal, Canada, 2004.
Zupan, J.; Gasteiger, J. Neural Networks in Chemistry and Drug Design, 2nd Ed. ed; Wiley: New York, 1999. [Google Scholar]
Dastidar, S.D.; Ganguly, K.; Chaudhuri, K.; Chakrabarty, A.N. Int. J. Antimicrob. Agents 2000, 14, 249.
Annadurai, S.; Basu, S.; Ray, S.; Dastidar, S.D.; Chakrabarty, A.N. Indian J. Exp. Biol. 1998, 36, 86.
Dastidar, S.D.; Saha, P.K.; Sanymat, B.; Chakrabarty, A.N. J. Appl. Bact. 1976, 42, 209. [CrossRef]
Dastidar, S.D.; Jairaj, J.; Mookerjee, M.; Chakrabarty, A.N. Acta Microbiol. Immun. Hung. 1997, 44, 241.
Molnar, J.; Mandi, Y.; Kiraly, J. Acta Microbiol. Immun. Hung. 1976, 23, 45.
Kristiansen, J.E. Acta Path. Microbioil. Scand. Sect. B. 1979, 87, 317.
Kristiansen, J.E.; Mortensen, I. Pramocol. Toxicol. 1987, 60, 100.
Dastidar, S.D.; Chaudhuri, K.; Annadurai, S.; Ray, S.; Mookerjee, M.; Chakrabarty, A.N. J. Chemother. 1995, 7, 201. [CrossRef]
Dash, S.K.; Dastidar, S.D.; Chaudhuri, K. Ind. J. Exp. Biol. 1977, 15, 324.
Dastidar, S.D.; Mondal, U.; Niyogi, S.; Chakrabarty, A.N. Ind. J. Med. Res. 1986, 84, 142.
Drug Data Report 2000, 22, 530.
ChemIDPlus database:. http://chem.sis.nlm.nih.gov/chemidplus/.
Halgren, T.A. J. Comp. Chem. 1996, 17, 490. [CrossRef]
SNNS: Stuttgart Neural Network Simulator, Version 4.0; University of Stuttgart: Stuttgart, 1995.

Article Metrics

Citations

Article Access Statistics

Journal Statistics

Multiple requests from the same IP address are counted as one view.