Next Article in Journal
Mesophotic Ecosystems: The Link between Shallow and Deep-Sea Habitats
Previous Article in Journal
Poor Correlation between Diamondback Terrapin Population Estimates Using Two New Estimation Methods
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Diversity
Volume 12
Issue 11
10.3390/d12110410
diversity-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optimizing Costs to Collect Local Infauna through Grabs: Effect of Sampling Size and Replication

by
Lidia N. Álvarez
1,
Sara García-Sanz
1,
Néstor E. Bosch
2,
Rodrigo Riera
3,4 and
Fernando Tuya
4,*
1
elittoral S.L.N.E., Estudios de Ingeniería Costera y Oceanográfica, Edificio Polivalente II e Parque Científico Tecnológico, Oficinas 4 y 19, 35017 Las Palmas, Canary Islands, Spain
2
School of Biological Sciences, UWA Oceans Institute, Crawley (Perth), WA 6009, Australia
3
Departamento de Ecología, Facultad de Ciencias, Universidad Católica de la Santísima Concepción, Concepción 4090541, Chile
4
Grupo en Biodiversidad y Conservación, IU-ECOAQUA, Universidad de Las Palmas de Gran Canaria, 35017 Las Palmas, Canary Islands, Spain
*
Author to whom correspondence should be addressed.
Diversity 2020, 12(11), 410; https://doi.org/10.3390/d12110410
Submission received: 25 September 2020 / Revised: 19 October 2020 / Accepted: 26 October 2020 / Published: 27 October 2020
(This article belongs to the Section Marine Diversity)
Browse Figures
Review Reports Versions Notes

Abstract

:
Most ecological studies require a cost-effective collection of multi-species samples. A literature review unravelled that (1) large-sized grabs to collect infauna have been used at greater depths, despite no consistent relationship between grab size and replication across studies; and (2) the total number of taxa and individuals is largely determined by the replication. Then, infauna from a sedimentary (sandy) seabed at Gran Canaria Island was collected through van Veen grabs of three sizes: 0.018, 0.042 and 0.087 m2 to optimize, on a simple cost-benefit basis, sample size and replication. Specifically, (1) the degree of representativeness in the composition of assemblages, and (2) accuracy of three univariate metrics (species richness, total infaunal abundances and the Shannon-Wiener index), was compared according to replication. Then, by considering mean times (a surrogate of costs) to process a sample by each grab, (3) their cost-efficiency was estimated. Representativeness increased with grab size. Irrespective of the grab size, accuracy of univariate metrics considerably increased when n > 10 replicates. Costs associated with the 0.087 m2 grab were consistently lower than costs by the other grabs. In conclusion, because of high representativeness and low cost, a 6.87 L grab appears to be the optimal sample size to assess infauna at our local site.

Graphical Abstract

1. Introduction

Most ecological studies, particularly in community ecology, require collection of multi-species samples through varying sampling techniques, e.g., quadrats, cores, grabs, transects, traps, etc. At the start of any ecological study, researchers often select the size and replication of their sampling units based on previous studies and, less often, using results from initial pilot studies [1,2,3]. The choice of these sampling properties is, however, a complicated task with direct implications in subsequent costs, in terms of time and money.
The importance of selecting a representative sampling size (e.g., quadrat size) to study ecological patterns, at a particular scale, is well-recognized [2,4]. The size of a sampling unit is primarily determined by the target organism’ size and distribution pattern, i.e., random, uniform or clumped [5]. Small-sized units are successful when an organism is randomly distributed, whereas a clumped distribution require larger sampling sizes [1,6]. When multi-species assemblages are targeted, however, selection of the sampling size is problematic, because the range of species that constitute an assemblage tend to have varying sizes, as well as distribution and abundance patterns [7]. Initial quantitative approaches for optimal determination of sample size [5,8,9,10] have tended to look for precision (or uncertainty) of their population estimates, according to cost constraints. This is particularly the case of (univariate) studies targeting exclusively one species of flora or fauna. Multi-species studies, however, can focus on other attributes, particularly in terms of the level of representativeness of sampling units (the number of species collected relative to the total species richness), as well as accuracy of univariate and multivariate metrics [11,12].
The size and replication of the sampling unit, in the case of multi-species studies, largely conditions further efforts in terms of sorting, taxonomic identification and counting, i.e., costs of time and/or money [13,14]. Often, the larger the size of a sampling unit, the lower the replication is, because of the larger costs/efforts involved [1,10,11]. Large-sized sampling units tend to include a large diversity of floral or faunal species and, therefore, tend to encapsulate a larger representativeness of the target assemblage, which is typically quantified in terms of species richness [12]. This is because a larger area tends to include a larger number of species [1,2,4]. However, collection of large-sized samples may sacrifice a sufficient replication level, which is desirable to avoid a decrease in the power of subsequent statistical analyses and, therefore, severe increases in Type II error rates [15]. Therefore, some researchers tend to select small-sized sampling units to have a large replication, at expenses of sacrificing the representativeness of their samples. In summary, there is often a trade-off between the size of the sampling unit and the replication level of independent samples [1,7].
Infauna, from nearshore to abyssal waters, has been extensively sampled through varying techniques, including cores, dredges, air-pump lifters, and grabs [16,17,18]. When infauna has been collected through grabs, in particular van Veen grabs, a wide range of sizes has been used across a range of geographical locations and depths. The experimental design of studies involving infauna is, at first, important, because the sorting and taxonomic identifications of specimens are very time-consuming and expensive. The distribution of infauna in sediments is often patchy [19], so proper sampling size and replication become critical to avoid low statistical power, increased uncertainty and, importantly, low representativeness [6,10]. Despite a previous study locally compared infaunal assemblages collected by two grab sizes (0.1 vs. 0.25 m2), no cost-efficiency measures were provided to compare both grab sizes [20].
In this study, we initially carried out a literature review to assess whether (1) replication has affected grab size, (2) whether grab size is determined by the depth of collections, and (3) whether larger grab sizes have collected richer and more abundant infaunal assemblages. We then compared the effectiveness of grabs of three sizes (0.018, 0.042 and 0.087 m2, equivalent to 1.95, 3.14 and 6.87 L) to sample infauna at a local, shallow-water (2–3 m depth), sedimentary (sandy) seabed at Gran Canaria island (Canary Islands, NE Atlantic Ocean). The aim was to optimize, on a cost-benefit basis, sample size and replication for the collection of infauna living on nearshore waters. Most specifically, we compared (4) the degree of representativeness in the composition of infaunal assemblages and (5) accuracy of three widely used univariate metrics (species richness, total infaunal abundances and the Shannon-Wiener diversity index), according to replication, between the three grab types. Then, by considering mean working times (a surrogate of costs) to process a sample provided by the three types of grabs, we estimated (6) the cost-efficiency of the three grabs, in terms of costs to reach a certain level in the representativeness of the assemblage. This information is relevant to develop local monitoring programs, taking advantage of the resources and time available. This strategy may help other researchers in the design of their studies to collect infaunal assemblages.

2. Methods

2.1. Literature Review

We searched in the ISI Web of Science for scientific papers collecting infauna through van Veen grabs, which included published peer-reviewed journals from 1965 to 2020. This search was carried out in February 2020, using the keywords: “van Veen” AND “infauna”, “Van Veen” AND “intertidal”, “van Veen” AND “subtidal”, “van Veen” AND “grab size” and “van Veen” AND “depth”. Our analysis, however, focused on marine studies, and we deliberately excluded studies collecting epifauna (suprabenthos) and/or focusing on just one taxonomic group (e.g., polychaetes). For each study (Table S1), we extracted the total number of taxa and the total number of individuals collected by a grab of a particular size and its total replication (N). When data was not directly included in the text, we extracted the total number of taxa and individuals from tables and graphs; if some data was missing, we ignored the study.

2.2. Local Study: Site, Sampling and Taxonomic Identifications

Collection of infaunal samples took place at Taliarte, located on the east coast of Gran Canaria (27°59′23.88″ N, 15°22′8.59″ O, Canary Islands, Spain, NE Atlantic Ocean), on a seabed dominated by fine sands, at 2–3 m depth, in June 2019. Samples were collected through van Veen grabs [16] of three sizes, hereafter G1, G2 and G3, which correspond to internal volumes of ca. 1.95, 3.14 and 6.87 L, and a collection surface of ca. 0.018, 0.042 and 0.087 m2, respectively. Similar grab sizes have been employed previously in studies collecting infaunal assemblages (Table S1). Collection of samples was random on a seabed of ca. 60 m2, for a total of n = 40 samples for the G1, and n = 30 samples for the G2 and G3 grabs, respectively. Adjacent samples were, at least, 50 cm apart from each other. All samples were collected by hand using a rope attached to the grabs. The sediment collected in each grab showed no disturbance on its surface and no sediment suspension occurred before deploying the grabs. We assumed that the depth of grab penetration into the sediment was similar between the three grab types. Once in the laboratory, all samples were carefully sorted through a 1 mm mesh size and preserved in 70% ethanol. Then, each sample was initially allocated in a tray and each organism observed under a stereomicroscope (VisiScope STB250, Visiscope, New Zealand), which displayed high-resolution images into a PC screen. Each individual was then assigned to a species, or the lowest taxonomic entity, following keys provided by [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Unidentified species were given a unique ID code (e.g., Unidentified sp.1) and included in the analyses (Table S2).

2.3. Statistical Analyses: Literature Review

We firstly investigated the influence of the depth of collection and sampling effort (replication) on the size of the grab used across studies. Secondly, we modelled the effect of sampling effort (replication) and grab size on the total number of taxa and individuals reported across studies. In both cases, Generalized Additive Models (GAMs), implemented in the ‘mgcv’ R-package [44], were used to capture non-linear relationships, without making any a priori assumption on its functional form. For all GAMs, the mesh size used by each study (mostly 0.5 and 1 mm) was included as a covariate to account for potential influences of mesh size in tested responses. Predictors were log (x + 1) transformed to improve the spread of data points across the modelling domain. Models were developed with a ‘tweedie’ family error distribution, which is suitable for positive skewed and overdispersed data [45]. The basis dimensions ‘k’ of the cubic regression splines was limited to 4 to ensure monotonic relationships. Violation of model assumptions were visually checked by inspecting residuals against fitted values, and quantile-quantile (Q-Q) plots.

2.4. Statistical Analyses: Local Study

We initially plotted mean-to-variance relationships of infaunal abundances collected by the three grab types to explore if the multi-species data followed theoretical predictions of a Poisson distribution [46]. The representativeness of the sampling effort (replication) by the three types of grabs, to assess infaunal assemblages, was estimated through species accumulation (species-rarefaction) curves, which were computed through the ‘iNEXT’ R-package [12]. We additionally computed the Chao estimator of asymptotic richness for each grab type. Species abundance data was transformed to presence/absence (incidence data) to explore dissimilarities in assemblage composition within each grab type. We calculated Jaccard dissimilarities between all pairs of samples provided by each grab type, using the ‘BiodiversityR’ R-package [47], which were then averaged to obtain a mean similarity (and associated SD) for each grab type. To have balanced comparisons, n = 30 random samples of the G1 were selected. Differences in similarities were then tested through a one-way ANOVA on untransformed data in the R statistical package; the assumption of homogeneity of variances was checked by means of the Cochran’s test.
We used the SE (Standard Error of the mean) of three widely used multi-species ecological metrics: species richness, total infaunal abundance and the Shannon-Wiener (H’) diversity index, to assess accuracy, i.e., uncertainty, of infaunal metrics collected through the three grab types. The SE is a measure of the dispersion of sample means around the population mean. The three metrics were obtained, through the ‘BiodiversityR’ R-package [47], for every sample collected by each grab type. We then calculated the SE of the mean of the three metrics with increasing replication, separately for each grab type. Graphical inspection of changes of the SE of target metrics with increasing number of replicates has been previously implemented as a way to visually analyse the effect of replication levels on accuracy of metrics [1,3].

2.5. Costs

We firstly estimated mean laboratory costs, in terms of time for sorting and taxonomic identifications, for samples (n = 10) processed by each grab type. Then, using the accumulation curves, we estimated how many samples of each of the three grab types were necessary to collect a varying number of taxa. We then plotted the costs, i.e., working time (minutes), to increase the representativeness of the samples, in terms of species richness, for each grab type. For each grab type, costs were obtained by multiplying their mean laboratory costs (per sample) by the number of samples necessary to reach a progressive number of species. A Generalized Linear Model (GLM) then tested whether costs differed between the three grab types. The model incorporated the factor ‘Grab’ and the covariate ‘Richness’, including an interaction term between the factor and the covariate. A ‘Gaussian’ family error structure was selected, with a ‘log’ link function, to reach the requirements of linearity and homogeneous variances, which were checked by visual inspection of residuals and Q-Q plots. The GLM was implemented using the ‘MASS’ R-package [48].

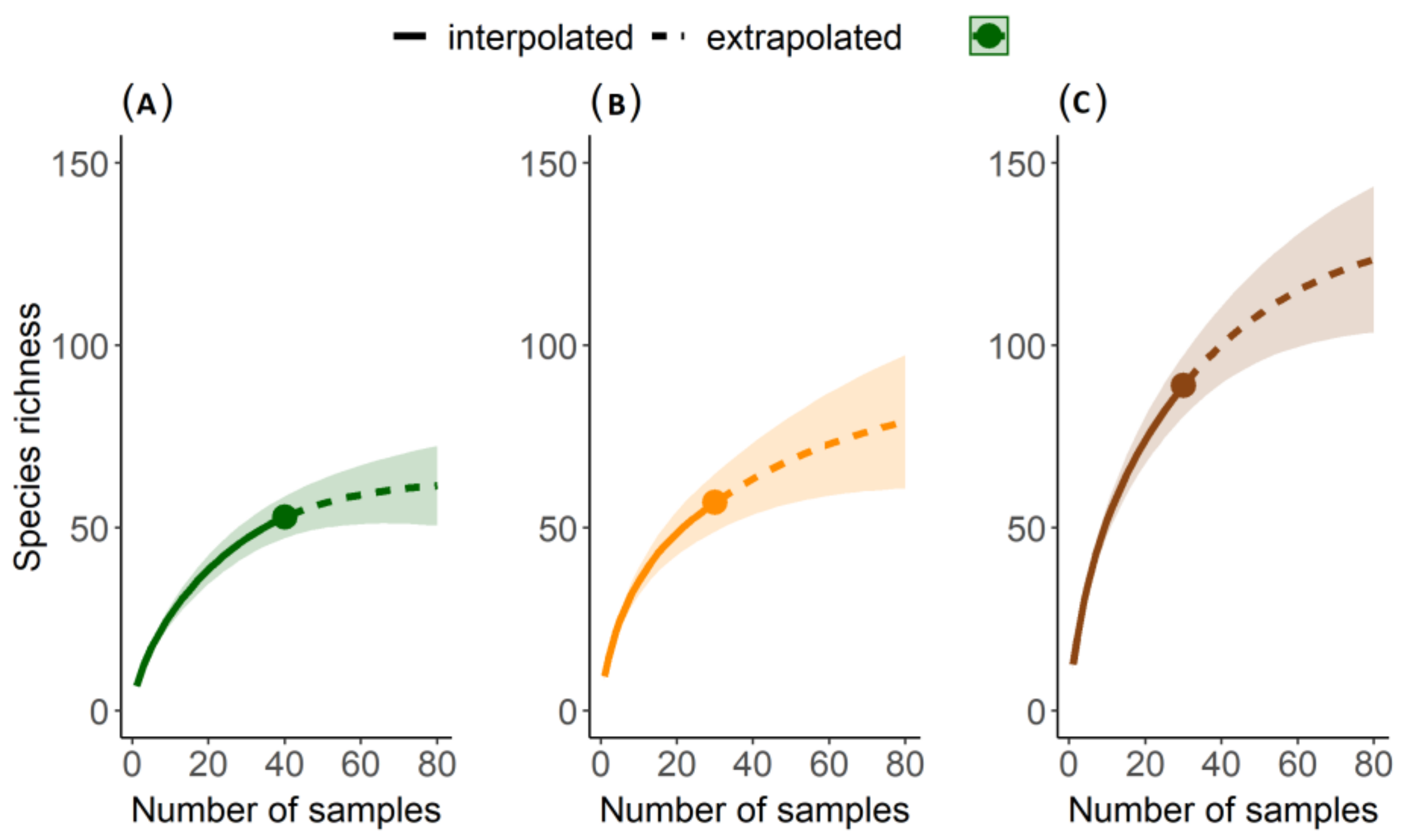
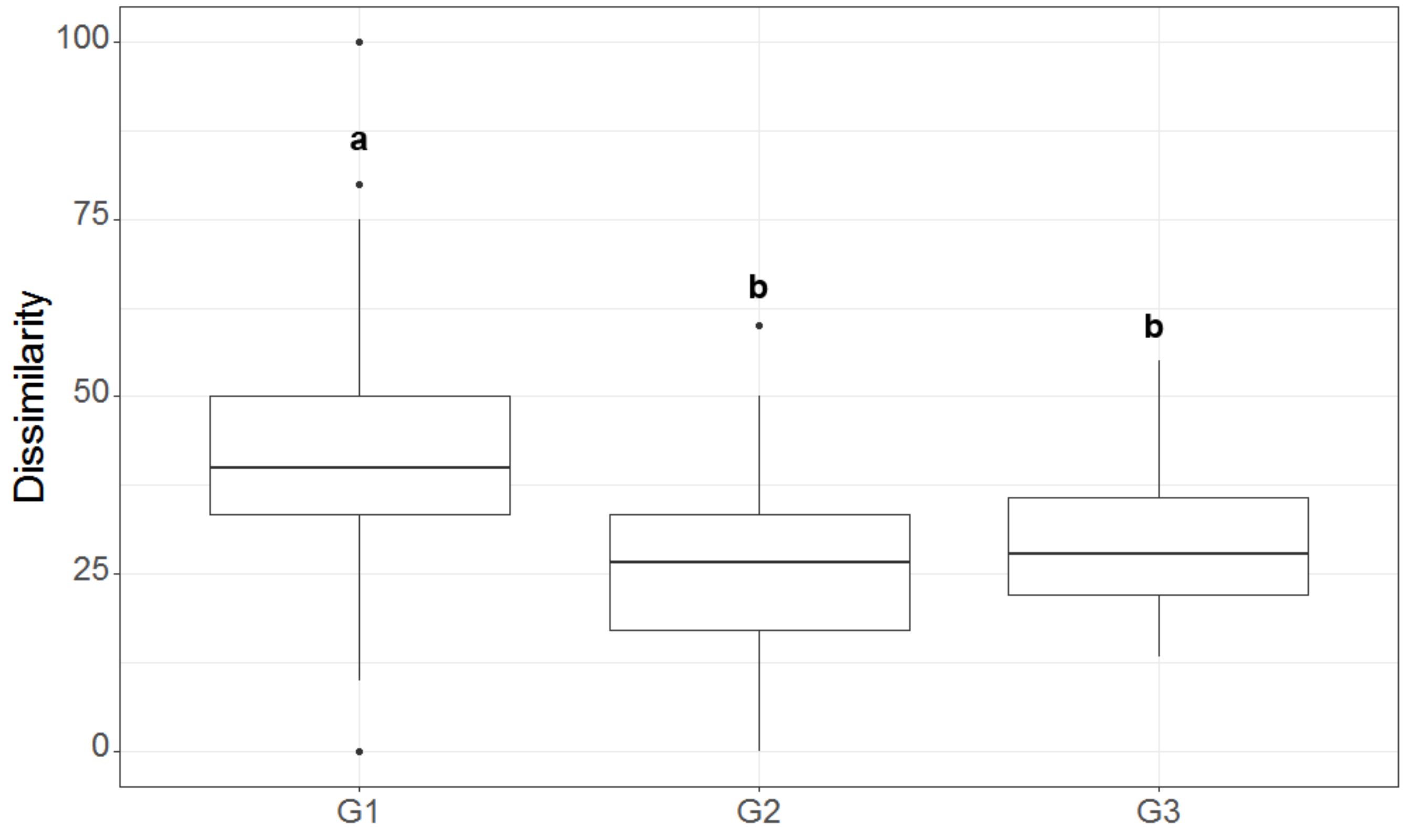
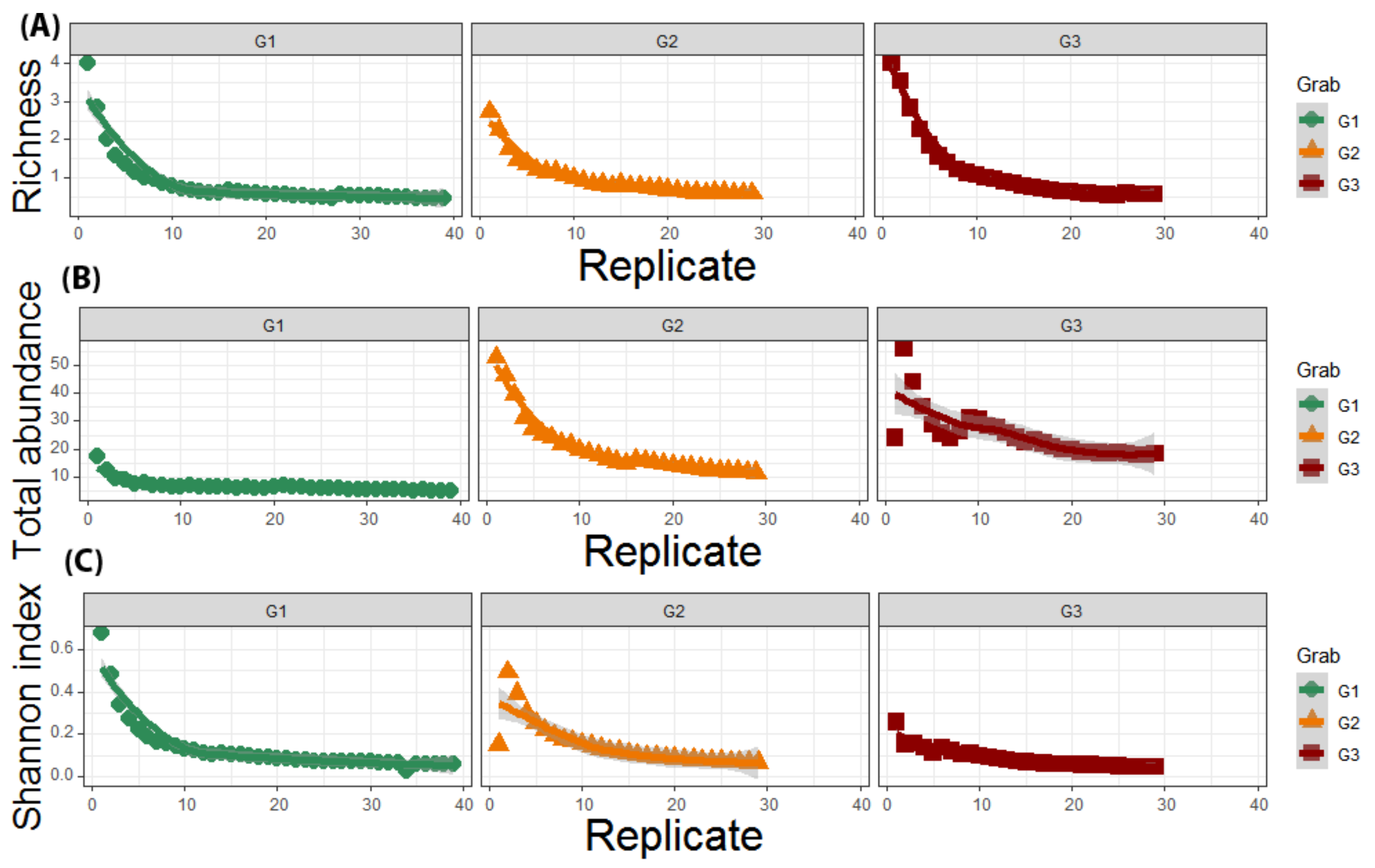
3. Results

3.1. Literature Review

The depth of collection had a significant, positive, effect on the size of the grab used across studies (estimated degrees of freedom, edf = 3.92, F = 12.85, p < 0.001), increasing exponentially with greater depths (Figure 1A). In contrast, the sampling effort (replication) had a negligible effect on the size of the grab used (edf = 1.00, F = 0.742, p = 0.3990; Figure 1B). The sampling effort (replication level) positively influenced both the total number of taxa (edf = 1.00, F = 15.23, p = 0.0011; Figure 1C) and the total number of individuals recorded (edf = 6.69, F = 9.81, p < 0.001; Figure 1E). The replication used across studies was insufficient to reach a plateau for the total number of taxa (Figure 1C), while a plateau beyond ~150 samples was observed for the total infaunal abundance (Figure 1E). After accounting for the effect of the sampling effort, grab size had a negligible (non-significant) effect on both the total number of taxa (edf = 1.00, F = 0.014, p = 0.9070; Figure 1D) and the total number of individuals recorded (edf = 1.00, F = 0.922, p = 0.9251; Figure 1F). For all GAMs, the mesh size used to sort infauna had a non-significant effect on responses (p > 0.1).

3.2. Local Study

A total of 12,916 infaunal individuals were identified, for a total of 53, 57 and 89 infaunal taxa identified by the G1, G2 and G3 grabs, respectively (Table S2). Overall, infaunal abundances collected by the three grab types followed clear mean-to-variance linear relationships, denoting that multivariate abundances follow Poisson distributions (Figure 2). In general, increasing the size of the sampling unit (i.e., grab size) captured a larger representativeness of the assemblage, i.e., a larger total number of taxa (species richness, Figure 3). In turn, the asymptotic richness of samples collected through the three grab sizes increased from an estimate of 63.35 species for the G1 to 90.41 and 134.97 species for the G2 and G3, respectively. Dissimilarities in assemblage composition decreased with increasing grab size (Figure 4). Dissimilarities in faunal composition were larger for samples collected through the G1 grab, relative to G2 and G3 grabs (Figure 4; 1-way ANOVA: F2,402 = 66.2, p < 2 × 10−16). For the three univariate metrics of infaunal assemblages (total infaunal abundance, species richness and the H’ index), the level of uncertainty abruptly decreased with replication up to 10 replicates, beyond which the SE of the three metrics tended to stabilize (Figure 5).
The mean estimated laboratory costs (times of sorting and taxonomic identifications) per sample of each grab increased with grab size (Table 1). The costs, i.e., working minutes, to increase the representativeness of the samples, in terms of species richness, increased linearly for the three grab sizes (Figure 6). Importantly, costs to reach a certain level of faunal representativeness by the G3 were lower than costs by G1 and G2 grabs (Figure 6; GLM: ‘Grab × Richness’, t-value = −2.84, p = 0.009, Table 2).

4. Discussion

Initially, our literature review found a connection between grab size and the depth at which infaunal collections took place. Normally, the larger the depth of a study, the larger the size of the grab. This seems to be logistically determined, as collection of infaunal samples from large depths are only possible onboard large scientific vessels, which are equipped with sophisticated gear to maneuver large-sized grabs [20]. Large samplers (e.g., grabs) often perform better at collecting samples from sediments at large depths, as a result of a more even and forceful hit on the seabed [20]; small grabs are otherwise avoided at large depths due to their low performance [18,22]. On the other hand, grabs collected from nearshore waters are normally small-sized, because such grabs are often manually managed at intertidal bottoms, or from small-sized inflatable boats. Our review, however, has shown no consistent relationship between grab size and the level of replication of analysed studies. This result may be an artefact, however, because most studies have used grabs with a 0.1 m2 collection area, while a low number of studies have employed either small (<0.05 m2) or large-sized grabs (0.4 to 0.6 m2). In turn, it is widely known that trade-offs between a larger sampling size, with greater representativeness but lower replication, or a smaller sampling size with higher replication, are a fundamental consideration in the initial design stage of any ecological study [1,11].
Our literature review also allowed us to assess whether larger grab sizes, under varying replication levels, have captured richer and more abundant infaunal assemblages. Results have shown, however, that replication seems to account for most variation in both the total number of taxa (i.e., species richness) and the total abundance of infauna. Again, the lack of effects of varying grab sizes on species richness and total abundances may result from a large dominance of studies using a 0.1 m2 collection area. Normally, a larger grab captures more species than a small grab [22], despite other studies have detected inconsistent results in this regard [20].
It is important to highlight that our literature review have two limitations. First, the outcomes are limited to studies implemented through collection of infauna by van Veen grabs. In addition, our study has not considered variation in sediment grain size, as a relevant factor affecting the diversity and abundances of infauna.
As expected for multivariate datasets, infaunal abundances collected by the three grab types at our local study site followed clear mean-to-variance (linear on log-scales) relationships, i.e., following predictions of Poisson distributions. This is relevant because any multivariate statistical analyses to test whatever hypothesis should consider this fundamental statistical property [46]. Importantly, this clear pattern reflects that the local infaunal assemblage is constituted by species with very different abundances, i.e., from very conspicuous to very sparse species.
As reported by [20], the species accumulation (rarefaction) curves have indicated that the aggregated species richness detected by each grab is considerably lower than the true asymptotic species richness. Our results have indicated that the representativeness of the assemblage was, as expected, notably conditioned by the grab size. In this sense, the asymptotic richness of samples collected through the three grab sizes increased, from an estimate of 63.35 species for the G1, to 90.41 and 134.97 species for the G2 and G3, respectively. As a result, our data agree with the conclusions by [49] and [20] that the number of replicates must not be based on the target of collecting a larger proportion of the exact number of species [50,51]. Dissimilarities in faunal composition were larger for samples collected through the G1 grab, relative to G2 and G3 grabs. This is most likely the result of the lower number of taxa collected by the G1 grab with respect to G2 and G3 grabs. In this sense, small grabs have shown a higher heterogeneity in infaunal composition, measured as multivariate dispersion, in comparison with large grabs [20]. These authors also showed that small grabs are particularly adequate for patchy infaunal assemblages, whilst large grabs are more suitable to sample homogeneous infaunal communities. Also, grain size is a pivotal factor that may lead to confound factors if sampling is exclusively carried out with a unique grab size, especially in large grain-sized seabeds, such as those dominated by gravels or very coarse sands [20].
As we previously outlined, the representativeness of the assemblage was affected by the grab size. This had relevant implications in the costs (working minutes) to reach a certain degree of representativeness, so costs associated with G3 were lower than costs by the G1 and G2 grabs. This is particularly accentuated if a study targets a large representativeness per sample (>40 species). To some extent, this is expected, as the infaunal assemblage contains a large spectrum of abundances, as our mean-to-variance plots have here shown. Hence, when less abundant, uncommon, species are targeted, the costs of the study dramatically increase. The larger grab size performed better, in terms of associated costs, that the smaller grabs to reach a desirable level in the representativeness of the assemblage. This outcome is reinforced by the fact that, regardless of grab size, accuracy of univariate metrics considerably increased when n > 10 replicates.
Univariate studies, i.e., those that target one response, tend to focus on the accuracy of an estimator to select the level of replication of a study. However, studies focusing on multivariate responses, e.g., multi-species assemblages, must focus on the representativeness of the sampling unit rather than on the level of replication of sampling units [11]. For example, in our study, n = 10 would represent an ideal number of replicates when univariate metrics are considered to describe variation in infaunal assemblages. [10], [52] and [53] pointed out the obvious fact that, for a fixed number of sampling units, smaller units are likely to give more variable estimates of the density of benthic organisms than larger units. In different ecological disciplines, it is often more cost-effective to collect many small, rather than a few larger, sampling units [52,54]. However, other works suggested collection of larger than smaller sampling units [50,55]. It is then clear that the ecological peculiarities of each study system and the target assemblage affect such a decision. For example, [55] pointed out that a 0.2 m2 grab would be ideal to collect macrobenthic assemblages in gravel substrata, where there is a high diversity of species, with ten, or even more, replicates to get a satisfactory assessment of the species composition. In our case-study, we conclude that a 0.087 m2 grab (G1), with 10 replicates, seem to be an ideal combination to sample infaunal assemblages.
As highlight above, grab size and the number of replicates greatly vary depending on the aim of the ecological study. As a general recommendation, we suggest using a small grab size (0.087 m2) in sandy sediments on shallow waters. For exploratory studies to map infaunal assemblages from a small area, a single replicate is adequate, but for studies encompassing broad-scale spatial and/or temporal scales, a higher sampling effort is highly recommended. We here suggest 10 replicates to balance spatial variability among samples. This guarantees accuracy of univariate descriptors of assemblage structure.

Supplementary Materials

The following material is available online at https://www.mdpi.com/1424-2818/12/11/410/s1, Table S1: Studies collecting infaunal assemblages through grabs of varying sizes, including the depth and the total number of replicates (N); Table S2: List of identified taxa.

Author Contributions

F.T. and S.G.-S. conceived the ideas and designed methodology; L.N.Á. and S.G.-S. collected field ecological data; N.E.B. and F.T. performed, analysed and interpreted ecological data; L.N.Á., S.G.S., N.E.B., R.R. and F.T. analysed data and wrote the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

We thank all the staff at elittoral for their support and encouragement at different phases of this study. This paper deals with small-sized invertebrates and, according to our local and national regulations, there is no mandatory ethical considerations.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kingsford, M.; Battershill, C. Studying Temperate Marine Environments: A Handbook for Ecologists; Canterbury University Press: Christchurch, New Zealand, 1998. [Google Scholar]
  2. Quinn, G.P.; Keough, M.J. Experimental Design and Data Analysis for Biologists; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
  3. Fernández-Zabala, J.; Amorim, A.; Tuya, F.; Soler-Onís, E. Benthic dinoflagellates: Testing the reliability of the ‘artificial substrate’ method in the Macaronesian region. Harmful Algae 2019, 87, 101634. [Google Scholar] [CrossRef] [PubMed]
  4. Ludwig, J.A.; Reynolds, J.F. Statistical Ecology: A Primer on Methods and Computing; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
  5. Pringle, J.D. Efficiency estimates for various quadrat sizes used in benthic sampling. Can. J. Fish. Aquat. Sci. 1984, 41, 1485–1489. [Google Scholar] [CrossRef]
  6. Carey, J.M.; Keough, M.J. Compositing and subsampling to reduce costs and improve power in benthic infaunal monitoring programs. Estuaries 2002, 25, 1053–1061. [Google Scholar] [CrossRef]
  7. Carlson, M.; Schmiegelow, F. Cost-effective sampling design applied to large-scale monitoring of boreal birds. Conserv. Ecol. 2002, 6, 11. [Google Scholar] [CrossRef] [Green Version]
  8. Wiegert, R.G. The selection of an optimum quadrat size for sampling the standing crop of grasses and forbs. Ecology 1962, 43, 125–129. [Google Scholar] [CrossRef]
  9. Levy, P.S.; Lemeshow, S. Sampling of Populations: Methods and Applications; Wiley Interscience: New York, NY, USA, 1991. [Google Scholar]
  10. Underwood, A.J.; Chapman, M.G. Design and analysis in benthic surveys. In Methods for the Study of Marine Benthos; Blackwell Publishing: Oxford, UK, 2005. [Google Scholar]
  11. Gotelli, N.J.; Ellison, A.M. A Primer of Ecological Statistics; Sinauer Associates, Inc.: Sunderland, MA, USA, 2004. [Google Scholar]
  12. Hsieh, T.C.; Ma, K.H.; Chao, A. iNEXT: An R package for rarefaction and extrapolation of species diversity (Hill numbers). Methods Ecol. Evol. 2016, 7, 1451–1456. [Google Scholar] [CrossRef]
  13. Langlois, T.J.; Harvey, E.S.; Fitzpatrick, B.; Mclean, D.L. Cost-efficient sampling of fish assemblages: Comparison of baited video stations and diver video transects. Aquat. Biol. 2010, 9, 155–168. [Google Scholar] [CrossRef] [Green Version]
  14. Bosch, N.E.; Gonçalves, J.M.S.; Erzini, K.; Tuya, F. “How” and “what” matters: Sampling method affects biodiversity estimates of reef fishes. Ecol. Evol. 2017, 7, 4891–4906. [Google Scholar] [CrossRef]
  15. Di Stefano, J. How much power is enough? Against the development of an arbitrary convention for statistical power calculations. Funct. Ecol. 2003, 17, 707–709. [Google Scholar] [CrossRef]
  16. Wigley, R.L. Comparative efficiencies of van Veen and Smith-McIntyre grab samplers as revealed by motion pictures. Ecology 1967, 48, 168–169. [Google Scholar] [CrossRef]
  17. Raz-Guzman, A.; Grizzle, R.E. Techniques for quantitative sampling of infauna and small epifauna in seagrass. In Global Seagrass Research Methods; Elsevier: Amsterdam, The Netherland, 2001. [Google Scholar]
  18. Montagna, P.A.; Baguley, J.G.; Hsiang, C.-Y.; Reuscher, M.G. Comparison of sampling methods for deep-sea infauna. Limnol. Oceanogr. Methods 2017, 15, 166–183. [Google Scholar] [CrossRef]
  19. Thrush, S.F. Spatial patterns in soft-bottom communities. Trends Ecol. Evol. 1991, 6, 75–79. [Google Scholar] [CrossRef]
  20. Holte, B.; Buhl-Mortensen, L. Does grab size influence sampled macrofauna composition? A test conducted on deep-sea communities in the northeast Atlantic. Mar. Environ. Res. 2020, 154, 104867. [Google Scholar] [CrossRef] [PubMed]
  21. Dauvin, J.C.; Bellan-Santini, D. Illustrated key to Ampelisca species from the north-eastern Atlantic. J. Mar. Biol. Assoc. UK 1988, 68, 659–676. [Google Scholar] [CrossRef]
  22. Boyd, S.E.; Barry, J.; Nicholson, M. A comparative study of a 0.1 m2 and 0.25 m2 Hamon grab for sampling macrobenthic fauna from offshore marine gravels. J. Mar. Biol. Assoc. UK 2006, 86, 1315–1328. [Google Scholar] [CrossRef]
  23. Hayward, P.J.; Ryland, J.S. The Marine Fauna of the British Isles and North-West Europe. Vol. 1: Introduction and Protozoans to Arthropods; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
  24. Núñez, J.; San Marin, G.; Brito, M.C. Syllinae (Polychaeta. Syllidae) de las Islas Canarias. Rev. Acad. Canar. Cienc. 1992, 3, 109–129. [Google Scholar]
  25. González, J.A. Catálogo de los Crustáceos Decápodos de las Islas Canarias: Gambas, Langostas y Cangrejos; Turquesa: Canary Islands, Spain, 1995. [Google Scholar]
  26. Brito, M.C.; Núñez, J.; Bacallado, J.J.; Ocaña, O. Anélidos Poliquetos de Canarias: Orden Phyllodocida (Chrysopetalidae, Pisionidae, Glyceridae, Sphaerodoridae, Hesionidae y Pilargidae). Monogr. Inst. Canar. Cienc. Mar. 1996, 13, 157–179. [Google Scholar]
  27. Capaccioni-Azzati, R. Prionospio multibranchiata (Polychaeta, Spionidae), Notomastus aberans y N. formianus (Polychaeta, Capitellidae) en el litoral de la Península Ibérica. Mis. Zool. 1988, 12, 47–56. [Google Scholar]
  28. Núñez, J.; Pascual, M.; Delgado, J.D.; Brito, M.C. Polychaetous Annelids from the Canary Islands: Family Eunicidae. Vieraea 1998, 26, 47–75. [Google Scholar]
  29. Corbera, J.; Brito, M.C.; Núñez, J.; Riera, R. Catálogo de los Cumáceos (Crustacea, Malacostraca) de las Islas Canarias. Rev. Acad. Canar. Cienc. 2001, 12, 67–73. [Google Scholar]
  30. Ortiz, M.; Jimeno, A. Guía lustrada para la identificación de las familias y los géneros de los anfípodos del suborden gammaridea de la península ibérica. Graellsia 2001, 57, 3–93. [Google Scholar] [CrossRef]
  31. Pascual, M.; Núñez, J.; Brito, M.C.; Riera, R. Ctenodrilidos y cirratulidos (annelida: Polychaeta) asociados a demosponjas litorales de Canarias y Madeira. Rev. Acad. Canar. Cienc. 2002, 4, 49–59. [Google Scholar]
  32. Moro, L.; Martín, J.L.; Garrido, M.J.; Izquierdo, I. (Eds.) Lista de Especies Marinas de Canarias (Algas, Hongos, Plantas y Animales); Consejería de Política Territorial y Medio Ambiente del Gobierno de Canarias: Canary Islands, Spain, 2003. [Google Scholar]
  33. Riera, R.; Guerra, J.M.; Brito, M.C.; Núñez, J. Estudio de los caprélidos de Lanzarote, Islas Canarias (Crustacea: Amphipoda: Caprellidea). Vieraea 2003, 31, 157–166. [Google Scholar]
  34. Sanz, M.C.; Riera, R.; Brito, M.C.; Núñez, J. Primera aportación al conocimiento de los tanaidáceos (Malacostraca: Tanaidacea) de las Islas Canarias. Rev. Acad. Canar. Cienc. 2003, 15, 69–76. [Google Scholar]
  35. Viéitez, J.M.; Alós, C.; Parapar, J.; Besteiro, C.; Moreira, J.; Núñez, J.; Laborada, J.; San Martín, G. Claves para el reconocimiento de familias de poliquetos. Annelida, Polychaeta I. In Fauna Ibérica; Museo Nacional de Ciencias Naturales: Madrid, Spain, 2004; Volume 25. [Google Scholar]
  36. Núñez, J.; Brito, M.C.; Docoito, J.R. Annelid Polychaetes from Canaries: Catalogue of species, distribution and habitats. Vieraea 2005, 33, 297–321. [Google Scholar]
  37. Rodrigues, A.M.; Pires, A.; Mendo, S.; Quintino, V. Diopatra neapolitana and Diopatra marocensis from the Portuguese coast: Morphological and genetic comparison. Estuar. Coast. Shelf Sci. 2009, 85, 609–617. [Google Scholar] [CrossRef]
  38. Arias, A.; Anadón, N.; Paxton, H. New records of Diopatra marocensis (Annelida: Onuphidae) from northern Spain. Zootaxa 2010, 2691, 67–68. [Google Scholar] [CrossRef] [Green Version]
  39. Moro, L.; Herrera, R.; Ortea, J.; Riera, R.; Bacallado, J.J.; Martín, J. Aportaciones al conocimiento y distribución de los decápodos y estomatópodos (Crustacea: Malacostraca) de las Islas Canarias. Rev. Acad. Canar. Cienc. 2014, 16, 33–82. [Google Scholar]
  40. Borges, J.P.; Martins, A.M.F.; Ávila, S.P. Checklist of the littoral gastropods (Mollusca Gastropoda) from the Archipelago of the Azores (NE Atlantic). Biodivers. J. 2015, 6, 855–900. [Google Scholar]
  41. Herrera-Bachiller, A.; Fernández-Álvarez, F.A.; Junoy, J. A Taxonomic Catalogue of the Nemerteans (Phylum Nemertea) of Spain and Portugal. Zool. Sci. 2015, 32, 507–522. [Google Scholar] [CrossRef] [Green Version]
  42. Esquete, P.; Ramos, E.; Riera, R. New data on the Tanaidacea (Crustacea: Peracarida) from the Canary Islands, with a description of a new species of Apseudopsis. Zootaxa 2016, 4093, 248–260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Paxton, H.; Arias, A. Unveiling a surprising diversity of the genus Diopatra Audouin & Milne Edwards, 1833 (Annelida: Onuphidae) in the Macaronesian region (eastern North Atlantic) with the description of four new species. Zootaxa 2017, 4, 505–535. [Google Scholar]
  44. Wood, S.N. Generalized Additive Models: An Introduction with R; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
  45. Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; CRC Press: Boca-Raton, FL, USA, 1990. [Google Scholar]
  46. Wang, Y.; Neuman, U.; Wright, S.; Warton, D.I. Mvabund: An R package for model-based analysis of multivariate abundance data. Meth. Ecol. Evol. 2012, 3, 471–474. [Google Scholar] [CrossRef]
  47. Kindt, R.; Coe, R. Tree Diversity Analysis: A Manual and Software for Common Statistical Methods for Ecological and Biodiversity Studies; World Agroforestry Centre ICRAF: Nairobi, Kenya, 2005. [Google Scholar]
  48. Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
  49. Rumohr, H.; Karakassis, I.; Jensen, J.N. Estimating species richness, abundance and diversity with 70 macrobenthic replicates in the Western Baltic Sea. Mar. Ecol. Prog. Ser. 2001, 214, 103–110. [Google Scholar] [CrossRef] [Green Version]
  50. Gray, J.S. Okologie Mariner Sedimente; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
  51. Ellingsen, K.E.; Hewitt, J.E.; Thrush, S.F. Rare species, habitat diversity and functional redundancy in marine benthos. J. Sea Res. 2007, 58, 291–301. [Google Scholar] [CrossRef]
  52. Elliott, J.M. Some Statistical Methods for the Statistical Analysis of Samples of Benthic Invertebrates; The Ferry House Ambleside, Westmorland; Freshwater Biological Association, Scientic Publication: Ambleside, UK, 1971. [Google Scholar]
  53. Andrew, N.L.; Mapstone, B.D. Sampling and the description of spatial pattern in marine ecology. Oceanogr. Mar. Biol. 1987, 25, 39–90. [Google Scholar]
  54. Downing, J.A. Aggregation, transformation, and the design of benthos sampling programs. J. Fish. Res. Board Can. 1987, 36, 1454–1463. [Google Scholar] [CrossRef]
  55. Newell, R.C.; Seiderer, L.J.; Robinson, J.E. Animal-sediment relationships in coastal deposits of the eastern English Channel. J. Mar. Biol. Assoc. UK 2001, 81, 1–9. [Google Scholar] [CrossRef]
Diversity 12 00410 g001 550
Figure 1. Model-predicted relationships between the (A) depth and (B) sampling effort on the size of the grab used across studies. Model-predicted relationships between sampling effort (C,E) and grab size (D,F) on the total number of taxa (C,D) and individuals (E,F) recorded across studies are included. Solid lines are mean fitted values from cubic regression splines, and dashed lines are 95% confidence intervals. Dot points are individual studies included in the analysis. Note, predictors variables were log (x + 1) transformed.
Figure 1. Model-predicted relationships between the (A) depth and (B) sampling effort on the size of the grab used across studies. Model-predicted relationships between sampling effort (C,E) and grab size (D,F) on the total number of taxa (C,D) and individuals (E,F) recorded across studies are included. Solid lines are mean fitted values from cubic regression splines, and dashed lines are 95% confidence intervals. Dot points are individual studies included in the analysis. Note, predictors variables were log (x + 1) transformed.
Diversity 12 00410 g001
Diversity 12 00410 g002 550
Figure 2. Mean-variance relationships (on log-transformed axes) of infaunal abundances collected through grabs of varying sizes. Lineal adjustments are for visualization, including 95% confidence intervals.
Figure 2. Mean-variance relationships (on log-transformed axes) of infaunal abundances collected through grabs of varying sizes. Lineal adjustments are for visualization, including 95% confidence intervals.
Diversity 12 00410 g002
Diversity 12 00410 g003 550
Figure 3. Sample-based accumulation (rarefraction) curves of species richness for infauna collected through grabs of varying sizes: (A) G1, (B) G2 and (C) G3.
Figure 3. Sample-based accumulation (rarefraction) curves of species richness for infauna collected through grabs of varying sizes: (A) G1, (B) G2 and (C) G3.
Diversity 12 00410 g003
Diversity 12 00410 g004 550
Figure 4. Compositional dissimilarities (Jaccard dissimilarities) for infaunal assemblages collected through grabs of varying sizes. Different letters above bars denote statistically significant differences.
Figure 4. Compositional dissimilarities (Jaccard dissimilarities) for infaunal assemblages collected through grabs of varying sizes. Different letters above bars denote statistically significant differences.
Diversity 12 00410 g004
Diversity 12 00410 g005 550
Figure 5. Curves of Standard Error of means of (A) species richness, (B) total infaunal abundances and (C) the Shannon-Wiener diversity index, with increasing replication, for grabs of varying sizes. Generalized lineal adjustments, via Poisson models, are for visualization, including 95% confidence intervals.
Figure 5. Curves of Standard Error of means of (A) species richness, (B) total infaunal abundances and (C) the Shannon-Wiener diversity index, with increasing replication, for grabs of varying sizes. Generalized lineal adjustments, via Poisson models, are for visualization, including 95% confidence intervals.
Diversity 12 00410 g005
Diversity 12 00410 g006 550
Figure 6. Costs (working minutes) to achieve increasing representativeness, in terms of species richness, for grabs of varying sizes. Results of lineal adjustments are in Table 2, including 95% confidence intervals.
Figure 6. Costs (working minutes) to achieve increasing representativeness, in terms of species richness, for grabs of varying sizes. Results of lineal adjustments are in Table 2, including 95% confidence intervals.
Diversity 12 00410 g006
Table
Table 1. Summary of the estimated laboratory costs (times in minutes of sorting and taxonomic identifications) per sample of each grab type.
Table 1. Summary of the estimated laboratory costs (times in minutes of sorting and taxonomic identifications) per sample of each grab type.
Sorting (min)Identifications (min)Total (min)
MeanSDMeanSD
G129.858.8414.039.6543.88
G243.4814.5732.7014.8876.18
G375.9832.3433.6821.30109.66
Table
Table 2. Results of the GLM testing for differences in costs (working minutes) between grab types.
Table 2. Results of the GLM testing for differences in costs (working minutes) between grab types.
CoefficientEstimateSEt Valuep
Intercept4.8980.0859.281 × 10−16
Grab (G2)−0.0890.11−0.770.4428
Grab (G3)−0.1110.14−0.750.4538
Richness0.0490.00132.11 × 10−16
Grab (G2) × Richness0.0020.0021.340.1913
Grab (G3) × Richness−0.0070.002−2.840.009
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Álvarez, L.N.; García-Sanz, S.; Bosch, N.E.; Riera, R.; Tuya, F. Optimizing Costs to Collect Local Infauna through Grabs: Effect of Sampling Size and Replication. Diversity 2020, 12, 410. https://doi.org/10.3390/d12110410

AMA Style

Álvarez LN, García-Sanz S, Bosch NE, Riera R, Tuya F. Optimizing Costs to Collect Local Infauna through Grabs: Effect of Sampling Size and Replication. Diversity. 2020; 12(11):410. https://doi.org/10.3390/d12110410

Chicago/Turabian Style

Álvarez, Lidia N., Sara García-Sanz, Néstor E. Bosch, Rodrigo Riera, and Fernando Tuya. 2020. "Optimizing Costs to Collect Local Infauna through Grabs: Effect of Sampling Size and Replication" Diversity 12, no. 11: 410. https://doi.org/10.3390/d12110410

APA Style

Álvarez, L. N., García-Sanz, S., Bosch, N. E., Riera, R., & Tuya, F. (2020). Optimizing Costs to Collect Local Infauna through Grabs: Effect of Sampling Size and Replication. Diversity, 12(11), 410. https://doi.org/10.3390/d12110410

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop