Unimodal Relationships of Understory Alpha and Beta Diversity along Chronosequence in Coppiced and Unmanaged Beech Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites and Field Sampling
2.2. Diversity of Species Combinations and Spatial Scaling
2.3. Other Diversity Indices
2.4. Null Models and Statistical Analyses
3. Results
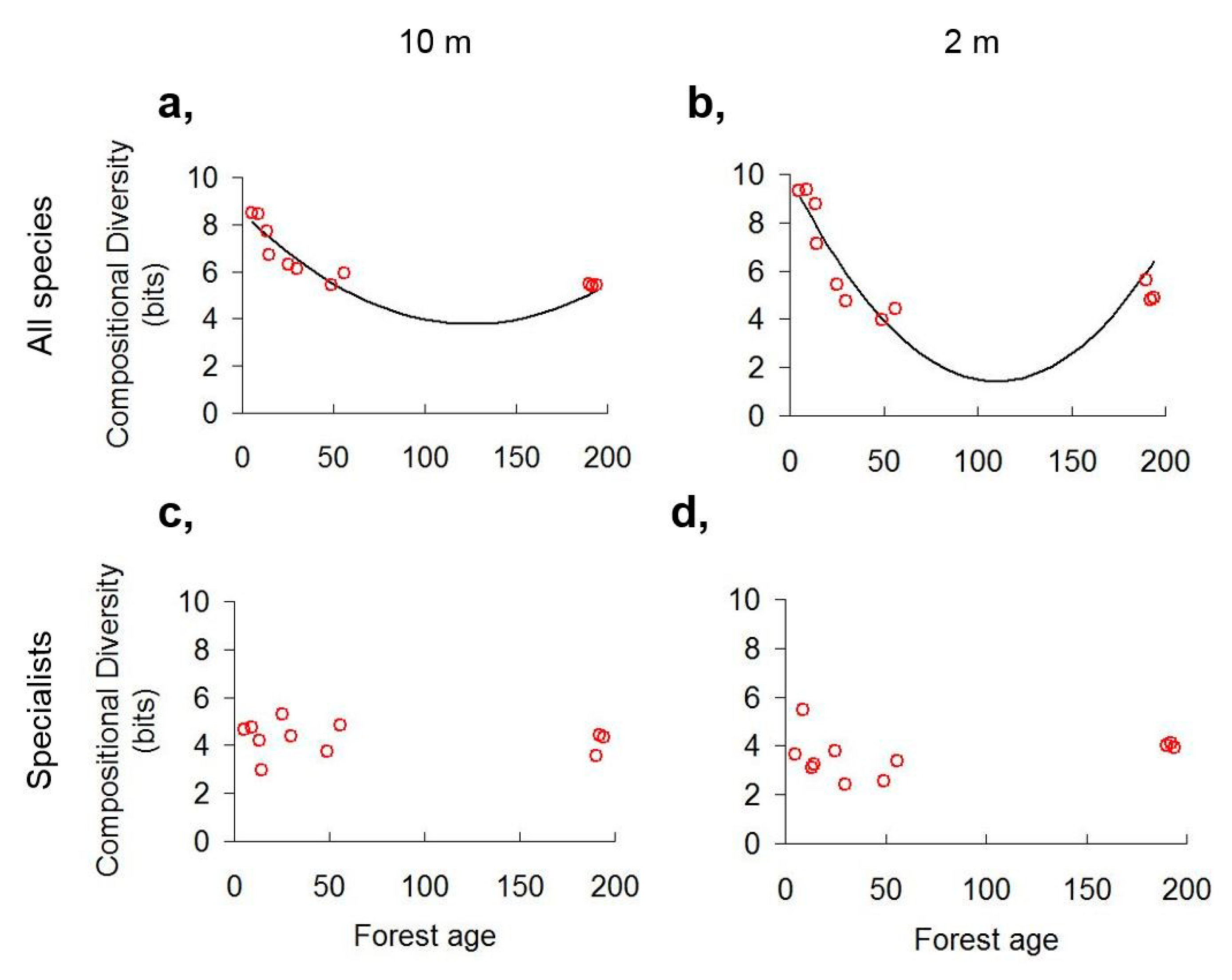
3.1. Scale Dependence of Diversity Patterns
3.2. Diversity Trends along the Chronosequence
3.3. Management Types and the Response of Beech Forest Specialists
4. Discussion
4.1. Scale Dependence of Diversity Patterns
4.2. Diversity Trends in Forest Succession
4.3. Assembly Processes Inferred from Diversity Patterns
4.4. Patterns of Beech Forest Specialists and Management Implications
4.5. Beta Diversity as Indicator of Coexistence Relationships in Forest Understory
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gilliam, F.S. The ecological significance of the herbaceous layer in temperate forest ecosystems. BioScience 2007, 57, 845–857. [Google Scholar] [CrossRef]
- Bartha, S.; Merolli, A.; Campetella, G.; Canullo, R. Changes of vascular plant diversity along a chronosequence of beech coppice stands, central Apennines, Italy. Plant Biosyst. 2008, 142, 572–583. [Google Scholar] [CrossRef]
- Canullo, R.; Simonetti, E.; Cervellini, M.; Chelli, S.; Bartha, S.; Wellstein, C.; Campetella, G. Unravelling mechanisms of short-term vegetation dynamics in complex coppice forest systems. Folia Geobot. 2017, 52, 71–81. [Google Scholar] [CrossRef]
- Horn, H. The ecology of secondary succession. Ann. Rev. Ecol. Syst. 1974, 5, 25–37. [Google Scholar] [CrossRef]
- Christensen, N.L.; Peet, R.K. Convergence during Secondary Forest Succession. J. Ecol. 1984, 72, 25–36. [Google Scholar] [CrossRef]
- Jules, M.J.; Sawyer, J.O.; Jules, E.S. Assessing the relationships between stand development and understory vegetation using a 420-year chronosequence. For. Ecol. Manag. 2008, 155, 2384–2393. [Google Scholar] [CrossRef]
- Kirby, K.J.; Thomas, R.C. Changes in the ground flora in Wytham Woods, southern England from 1974 to 1991—Implications for nature conservation. J. Veg. Sci. 2000, 11, 871–880. [Google Scholar] [CrossRef]
- Müllerová, J.; Hédl, R.; Szabó, P. Coppice abandonment and its implications for species diversity in forest vegetation. For. Ecol. Manag. 2015, 343, 88–100. [Google Scholar] [CrossRef] [Green Version]
- Ujházy, K.; Hederová, L.; Máliš, F.; Ujházyová, M.; Bosela, M.; Čiliak, M. Overstorey dynamics controls plant diversity in age-class temperate forests. For. Ecol. Manag. 2017, 391, 96–105. [Google Scholar] [CrossRef]
- Della Longa, G.; Boscutti, F.; Marini, L.; Alberti, G. Coppicing and plant diversity in a lowland wood remnant in North–East Italy. Plant Biosyst. 2019. [Google Scholar] [CrossRef]
- Balvanera, P.; Lott, E.; Gerardo, S.; Siebe, C.; Islas, A. Patterns of beta-diversity in a Mexican tropical dry forest. J. Veg. Sci. 2002, 13, 145–158. [Google Scholar] [CrossRef]
- Campetella, G.; Botta-Dukát, Z.; Wellstein, C.; Canullo, R.; Gatto, S.; Chelli, S.; Mucina, L.; Bartha, S. Patterns of plant trait–environment relationships along a forest succession chronosequence. Agric. Ecosyst. Environ. 2011, 145, 38–48. [Google Scholar] [CrossRef]
- Sabatini, F.M.; Burrascano, S.; Tuomisto, H.; Blasi, C. Ground Layer Plant Species Turnover and Beta Diversity in Southern-European Old-Growth Forests. PLoS ONE 2014, 9, e95244. [Google Scholar] [CrossRef]
- Ottaviani, G.; Götzenberger, L.; Bacaro, G.; Chiarucci, A.; de Bello, F.; Marcantonio, M. A multifaceted approach for beech forest conservation: Environmental drivers of understory plant diversity. Flora 2019, 256, 85–91. [Google Scholar] [CrossRef]
- Qian, H.; Klinka, K.; Sivak, B. Diversity of the understorey vascular vegetation in 40 year-old and old-growth forest stands on Vancouver Island, British Columbia. J. Veg. Sci. 1997, 8, 773–780. [Google Scholar] [CrossRef]
- Bobiec, A. The mosaic diversity of field layer vegetation in the natural and exploited forests of Bialowieza. Plant Ecol. 1998, 136, 175–187. [Google Scholar] [CrossRef] [Green Version]
- Standovár, T.; Ódor, P.; Aszalós, R.; Gáhidy, L. Sensitivity of ground layer vegetation diversity descriptors in indicating forest naturalness. Commun. Ecol. 2006, 7, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Burrascano, S.; Rosati, L.; Blasi, C. Plant species diversity in Mediterranean old-growth forest: A case study from central Italy. Plant Biosyst. 2009, 143, 190–200. [Google Scholar] [CrossRef]
- Zobel, K.; Zobel, M.; Peet, R.K. Changes in pattern diversity during secondary succession in Estonian forests. J. Veg. Sci. 1993, 4, 489–498. [Google Scholar] [CrossRef]
- Hilmers, T.; Friess, N.; Bassler, C.; Heurich, M.; Brandl, R.; Pretzsh, H.; Seidl, R.; Müller, J. Biodiversity along temperate forest succession. J. Appl. Ecol. 2018, 55, 2756–2766. [Google Scholar] [CrossRef] [Green Version]
- Moola, F.M.; Vasseur, L. Recovery of late-seral vascular plants in a chronosequence of post-clearcut forest stands in coastal Nova Scotia, Canada. Plant Ecol. 2004, 172, 183–197. [Google Scholar] [CrossRef]
- Amici, V.; Santi, E.; Filibeck, G.; Diekmann, M.; Geri, F.; Landi, S.; Scoppola, A.; Chiarucci, A. Influence of secondary forest succession on plant diversity patterns in a Mediterranean landscape. J. Biogeogr. 2013, 40, 2335–2347. [Google Scholar] [CrossRef]
- López-Martinez, J.O.; Hernández-Stefanoni, J.L.; Dupuy, J.M.; Meave, J.A. Partitioning the variation of woody plant β-diversity in a landscape of secondary tropical dry forests across spatial scales. J. Veg. Sci. 2013, 24, 33–45. [Google Scholar] [CrossRef]
- Burrascano, S.; Ripullone, F.; Bernardo, L.; Borghetti, M.; Carli, E.; Colangelo, M.; Gangale, C.; Gargano, D.; Gentilesca, T.; Luzzi, G.; et al. It’s a long way to the top: Plant species diversity in the transition from managed to old-growth forests. J. Veg. Sci. 2018, 29, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Campetella, G.; Canullo, R.; Bartha, S. Coenostate descriptors and spatial dependence in vegetation: Derived variables in monitoring forest dynamics and assembly rules. Commun. Ecol. 2004, 5, 105–114. [Google Scholar] [CrossRef]
- Moora, M.; Daniell, T.; Kalle, H.; Liira, J.; Püssa, K.; Roosaluste, E.; Öpik, M.; Wheatley, R.; Zobel, M. Spatial pattern and species richness of boreonemoral forest understorey and its determinants—A comparison of differently managed forests. For. Ecol. Manag. 2007, 250, 64–70. [Google Scholar] [CrossRef]
- Decocq, G.; Aubert, M.; Dupont, F.; Alard, D.; Saguez, R.; Wattez-Franger, A.; De Fucault, B.; Delelis-Dusollier, A.; Bardat, J. Plant diversity in a managed temperate deciduous forest: Understorey response to two silvicultural systems. J. Appl. Ecol. 2004, 41, 1065–1079. [Google Scholar] [CrossRef]
- Campetella, G.; Canullo, R.; Gimona, A.; Garadnai, J.; Chiarucci, A.; Giorgini, D.; Angelini, E.; Cervellini, M.; Chelli, S.; Bartha, S. Scale-dependent effects of coppicing on the species pool of late successional beech forests in the central Apennines, Italy. Appl. Veg. Sci. 2016, 19, 474–485. [Google Scholar] [CrossRef] [Green Version]
- Cervellini, M.; Fiorini, S.; Cavicchi, A.; Campetella, G.; Simonetti, E.; Chelli, S.; Canullo, R.; Gimona, A. Relationships between understory specialist species and local management practices in coppiced forests—Evidence from the Italian Apennines. For. Ecol. Manag. 2017, 385, 35–45. [Google Scholar] [CrossRef]
- Juhász-Nagy, P.; Podani, J. Information theory methods for the study of spatial processes and succession. Vegetatio 1983, 51, 129–140. [Google Scholar] [CrossRef]
- Podani, J.; Czárán, T.; Bartha, S. Pattern, area and diversity: The importance of spatial scale in species assemblages. Abstr. Bot. 1993, 17, 37–51. [Google Scholar]
- Anderson, M.J.; Crist, T.O.; Chase, J.M.; Vellend, M.; Inouye, B.D.; Freestone, A.L.; Sanders, N.J.; Cornell, H.V.; Comita, L.S.; Davies, K.F.; et al. Navigating the multiple meanings of diversity: A roadmap for the practicing ecologist. Ecol. Lett. 2011, 14, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Swenson, N.G.; Jia, Q.; Rao, M.; Feng, G.; Ren, H.; Daniel, P.; Bebber, D.P.; Ma, K. Stochastic assembly in a subtropical forest chronosequence: Evidence from contrasting changes of species, phylogenetic and functional dissimilarity over succession. Sci. Rep. 2016, 6, 32596. [Google Scholar] [CrossRef]
- Bartha, S.; Campatella, G.; Canullo, R.; Bódis, J.; Mucina, L. On the importance of fine-scale spatial complexity in vegetation restoration. Int. J. Ecol. Environ. Sci. 2004, 30, 101–116. [Google Scholar]
- Chase, J.M.; Kraft, N.J.B.; Smith, K.G.; Vellend, M.; Inouye, B.D. Using null models to disentangle variation in community dissimilarity from variation in alpha-diversity. Ecosphere 2011, 2, 1–11. [Google Scholar] [CrossRef]
- Mori, A.S.; Fujii, S.; Kitagawa, R.; Koide, D. Null model approaches to evaluating the relative role of different assembly processes in shaping ecological communities. Oecologia 2015, 178, 261–273. [Google Scholar] [CrossRef]
- Ódor, P.; Standovár, T. Substrate specificity and community structure of bryophyte vegetation in a near-natural montane beech forest. Commun. Ecol. 2002, 3, 39–49. [Google Scholar] [CrossRef]
- Piovesan, G.; Di Filippo, A.; Alessandrini, A.; Biondi, F.; Schirone, B. Structure, dynamics and dendroecology of an old-growth Fagus forest in the Apennines. J. Veg. Sci. 2004, 16, 13–28. [Google Scholar] [CrossRef]
- Mucina, L.; Bültmann, H.; Dierßen, K.; Theurillat, J.-P.; Raus, T.; Čarni, A.; Šumberová, K.; Willner, W.; Dengler, J.; García, R.G.; et al. Vegetation of Europe: Hierarchical floristic classification system of vascular plant, bryophyte, lichen, and algal communities. Appl. Veg. Sci. 2016, 19, 3–264. [Google Scholar] [CrossRef]
- Canullo, R.; Campetella, G.; Mucina, L.; Chelli, S.; Wellstein, C.; Bartha, S. Patterns of clonal growth modes along a chronosequence of post-coppice forest regeneration in beech forest of Central Italy. Folia Geobot. 2011, 46, 271–288. [Google Scholar] [CrossRef]
- Pickett, S.T.A. Space-for-time substitution as an alternative to long-term studies. In Long-Term Studies in Ecology; Likens, G.E., Ed.; Springer: New York, NY, USA, 1989; pp. 110–135. [Google Scholar]
- Campetella, G.; Canullo, R.; Bartha, S. Fine scale spatial pattern analysis of herb layer of woodland vegetation using information theory. Plant Biosyst. 1999, 133, 277–288. [Google Scholar] [CrossRef]
- Podani, J. Computerized sampling in vegetation studies. Coenoses 1987, 2, 9–18. [Google Scholar]
- Juhász-Nagy, P. On some ‘characteristic area’ of plant community stands. Proc. Colloq. Inf. Theor. 1967, 269–282. [Google Scholar]
- Juhász-Nagy, P. Spatial dependence of plant populations. Part 1. Equivalence analysis (an outline for a new model). Acta Bot. Acad Sci. Hung 1976, 22, 61–78. [Google Scholar]
- Juhász-Nagy, P. Notes on diversity. Part, I. Introduction. Abstr. Bot. 1984, 8, 43–55. [Google Scholar]
- Juhász-Nagy, P. Spatial dependence of plant populations. Part 2. A family of new models. Acta Bot. Acad Sci. Hung 1984, 30, 363–402. [Google Scholar]
- Bartha, S.; Czárán, T.; Podani, J. Exploring plant community dynamics in abstract coenostate spaces. Abstr. Bot. 1998, 22, 49–66. [Google Scholar]
- Podani, J. Analysis of mapped and simulated vegetation patterns by means of computerized sampling techniques. Acta Bot. Hung 1984, 30, 403–425. [Google Scholar]
- Bartha, S.; Campetella, G.; Kertész, M.; Hahn, I.; Kröel-Dulay, G.; Rédei, T.; Kun, A.; Virágh, K.; Fekete, G.; Kovács-Láng, E. Beta diversity and community differentiation in dry perennial sand grasslands. Ann. Bot. 2011, 1, 9–18. [Google Scholar]
- Magurran, A. Measuring Biological Diversity; Blackwell Science Ltd.: Oxford, UK, 2004; p. 256. [Google Scholar]
- Tuomisto, H. A diversity of beta diversities: Straightening up a concept gone awry. Part 2. Quantifying beta diversity and related phenomena. Ecography 2010, 33, 23–45. [Google Scholar] [CrossRef]
- Podani, J. Introduction to the Exploration of Multivariate Biological Data; Backhuys Publishers: Leiden, The Netherlands, 2000; p. 407. [Google Scholar]
- Jost, L. Partitioning diversity into independent alpha and beta components. Ecology 2007, 88, 2427–2439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watkins, A.J.; Wilson, J.B. Fine-scale community structure of lawn. J. Ecol. 1992, 80, 15–24. [Google Scholar] [CrossRef]
- Podani, J. SYN-TAXpc. Version 5.0. User’s Guide; Scientia Publishing: Budapest, Hungary, 1993. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research, 3rd ed.; W.H. Freeman and Co.: New York, NY, USA, 1995. [Google Scholar]
- Campbell, R.C. Statistics for Biologists, 2nd ed.; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological statistics software package for education and data analysis. Palaeontol. Electron. 2001, 4, 9. [Google Scholar]
- Canullo, R.; Campetella, G. Spatial patterns of textural elements in a regenerative phase of a beech coppice (Torricchio Mountain Nature Reserve, Apennines, Italy). Acta Bot. Gall. 2005, 152, 529–543. [Google Scholar] [CrossRef] [Green Version]
- Scheller, R.M.; Mladenoff, D.J. Understory species patterns and diversity in old-growth and managed Northern hardwood forests. Ecol. Appl. 2002, 12, 1329–1343. [Google Scholar] [CrossRef]
- Bartha, S.; Collins, S.L.; Glenn, S.M.; Kertész, M. Fine-scale spatial organization of tallgrass prairie vegetation along a topographic gradient. Folia Geobot. Phytotax. 1995, 30, 169–184. [Google Scholar] [CrossRef]
- Landuyt, D.; Perring, M.P.; Seidl, R.; Taubert, F.; Verbeeck, H.; Verheyen, K. Modelling understorey dynamics in temperate forests under global change–Challenges and perspectives. Perspect. Plant Ecol. 2018, 31, 44–54. [Google Scholar] [CrossRef] [Green Version]
- Tinya, F.; Ódor, P. Congruence of the spatial pattern of light and understory vegetation in an old-growth, temperate mixed forest. For. Ecol. Manag. 2016, 381, 84–92. [Google Scholar] [CrossRef] [Green Version]
- Godefroid, S.; Rucquoij, S.; Koedam, N. To what extent do forest herbs recover after clearcutting in beech forest? For. Ecol. Manag. 2005, 210, 39–53. [Google Scholar] [CrossRef]




| Bedrock | Management | Age Years | n. of Species | Elevation (m, a.s.l.) | Inclination (°) | Exposition | Tree Layer Cover (%) | Shrub Layer Cover (%) | Herb Layer Cover (%) | Light Below Canopy (%) | Variability of Light below Canopy (CV%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Limestone | active coppice | 5 | 121 | 1000 | 32 | N-NE | 40 | 82 | 65 | 21.21 | 18.59 |
| Sandstone | active coppice | 9 | 105 | 1280 | 25 | NE | 45 | 66 | 50 | 13.50 | 12.94 |
| Sandstone | active coppice | 14 | 57 | 1230 | 45 | NW | 85 | 35 | 65 | 4.34 | 6.48 |
| Limestone | active coppice | 14 | 27 | 1020 | 30 | NW | 65 | 25 | 23 | 7.40 | 15.34 |
| Sandstone | active coppice | 25 | 32 | 1430 | 32 | E-NE | 94 | 18 | 20 | 1.60 | 10.92 |
| Limestone | abandoned coppice | 30 | 28 | 1115 | 33 | NW | 90 | 28 | 27 | 3.41 | 7.23 |
| Sandstone | abandoned coppice | 49 | 24 | 1500 | 35 | N | 85 | 6 | 2 | 0.56 | 36.65 |
| Sandstone | abandoned coppice | 56 | 24 | 1490 | 40 | NE | 95 | 1 | 4 | 1.66 | 49.69 |
| Limestone | old growth unmanaged | >400 (190) | 19 | 1700 | 35 | NW | 95 | 50 | 50 | 6.51 | 58.24 |
| Limestone | old growth unmanaged | >400 (190) | 15 | 1700 | 35 | NW | 85 | 20 | 7 | 3.62 | 55.25 |
| Limestone | old growth unmanaged | >400 (190) | 18 | 1700 | 35 | NW | 90 | 7 | 7 | 2.24 | 52.86 |
| Alpha Diversity | Beta Diversity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Species Richness | Shannon Diversity (bits) | Simpson Diversity | Patterns of Realized Species Combinations | Pairwise Spatial Dissimilarity | Spatial Variability Coefficient (CV %) | ||||||
| NRC | CD (bits) | Sorensen | Bray–Curtis | Jaccard | Species Richness | Shannon Diversity | Simpson Diversity | ||||
| (a) Scale: 10 m | |||||||||||
| Active coppice | 18.350 A (27.050) | 3.394 A (2.318) | 0.853 A (0.308) | 306 A (324) | 7.718 A (1.353) | 0.486 A (0.255) | 60.060 A (20.524) | 0.641 A (0.197) | 28.743 A (31.293) | 15.617 A (43.075) | 7.769 A (44.221) |
| Abandoned coppice | 3.950 B (0.950) | 1.472 B (0.333) | 0.533 B (0.086) | 96 B (33) | 5.925 B (0.172) | 0.749 B (0.001) | 82.201 B (2.774) | 0.837 B (0.011) | 68.463 B (13.368) | 61.493 B (17.815) | 53.378 B (21.371) |
| Old-growth | 4.250 AB (1.950) | 1.469 B (0.558) | 0.537 AB (0.170) | 71 B (10) | 5.441 B (0.115) | 0.477 AB (0.141) | 53.958 AB (13.553) | 0.630 AB (0.216) | 41.021 AB (8.514) | 43.556 AB (13.084) | 40.896 C (22.206) |
| (b) Scale: 2 m | |||||||||||
| Active coppice | 6.990 A (12.940) | 2.314 A (2.750) | 0.725 A (0.610) | 545 A (575) | 8.767 A (3.909) | 0.713 A (0.227) | 76.029 A (20.754) | 0.806 A (0.111) | 47.054 A (40.388) | 33.208 A (99.888) | 23.732 A (105.312) |
| Abandoned coppice | 1.250 B (0.270) | 0.380 B (0.130) | 0.157 B (0.044) | 90 B (40) | 4.439 B (0.804) | 0.811 A (0.024) | 83.095 A (2.008) | 0.830 A (0.0279) | 107.422 B (10.076) | 173.172 B (21.696 | 163.104 B (24.413) |
| Old-growth | 2.080 AB (1.490) | 0.737 AB (0.607) | 0.308 AB (0.201) | 81 B (49) | 4.873 AB (0.809) | 0.615 A (0.152) | 66.943 A (13.223) | 0.710 A (0.108) | 62.266 AB (16.242 | 90.226 AB (44.04) | 86.027 AB (47.705) |
| Alpha Diversity | Beta Diversity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Species Richness | Shannon Diversity (Bits) | Simpson Diversity | Patterns of Realized Species Combinations | Pairwise Spatial Dissimilarity | Spatial Variability Coefficient (CV%) | ||||||
| NRC | CD (bits) | Sorensen | Bray–Curtis | Jaccard | Species Richness | Shannon Diversity | Simpson Diversity | ||||
| (a) Scale: 10 m | |||||||||||
| Active coppice | 3.350 A (3.800) | 0.940 A (1.335) | 0.393 A (0.413) | 37 A (58) | 4.667 A (2.361) | 0.459 A (0.372) | 57.777 A (31.86) | 0.596 A (0.359) | 39.164 A (30.835) | 59.914 A (54.178) | 54.333 A (60.752) |
| Abandoned coppice | 1.950 B (0.750) | 0.648 A (0.336) | 0.270 A (0.120) | 36 A (10) | 4.369 A (1.056) | 0.686 B (0.100) | 78.055 B (6.919) | 0.775 B (0.080) | 68.891 B (17.298) | 90.018 A (40.122) | 88.557 A (37.881) |
| Old-growth | 3.400 AB (0.650) | 1.270 A (0.323) | 0.489 A (0.133) | 35 A (18) | 4.354 A (0.858) | 0.382 AB (0.174) | 49.771 AB (16.854) | 0.527 AB (0.187) | 29.879 AB (6.917) | 45.648 A (21.315) | 43.642 A (28.545) |
| (b) Scale: 2 m | |||||||||||
| Active coppice | 1.280 A (2.820) | 0.319 A (1.346) | 0.142 A (0.495) | 40 A (88) | 3.674 A (2.399) | 0.663 A (0.417) | 75.258 A (31.156) | 0.717 A (0.293) | 76.602 A (46.332) | 153.399 A (149.210) | 152.295 A (166.705) |
| Abandoned coppice | 0.700 B (0.440) | 0.148 A (0.130) | 0.066 A (0.056) | 23 A (21) | 2.405 A (0.956) | 0.673 A (0.201) | 70.326 A (22.227) | 0.830 A (0.214) | 120.980 B (46.901) | 272.111 B (119.666) | 269.145 B (126.701) |
| Old-growth | 1.720 AB (0.650) | 0.584 A (0.352) | 0.251 A (0.135) | 37 A (7) | 4.007 A (0.185) | 0.564 A (0.192) | 64.338 A (16.036) | 0.656 A (0.150) | 51.659 AB (23.020) | 97.897 AB (48.175) | 96.050 AB (47.758) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartha, S.; Canullo, R.; Chelli, S.; Campetella, G. Unimodal Relationships of Understory Alpha and Beta Diversity along Chronosequence in Coppiced and Unmanaged Beech Forests. Diversity 2020, 12, 101. https://doi.org/10.3390/d12030101
Bartha S, Canullo R, Chelli S, Campetella G. Unimodal Relationships of Understory Alpha and Beta Diversity along Chronosequence in Coppiced and Unmanaged Beech Forests. Diversity. 2020; 12(3):101. https://doi.org/10.3390/d12030101
Chicago/Turabian StyleBartha, Sándor, Roberto Canullo, Stefano Chelli, and Giandiego Campetella. 2020. "Unimodal Relationships of Understory Alpha and Beta Diversity along Chronosequence in Coppiced and Unmanaged Beech Forests" Diversity 12, no. 3: 101. https://doi.org/10.3390/d12030101
APA StyleBartha, S., Canullo, R., Chelli, S., & Campetella, G. (2020). Unimodal Relationships of Understory Alpha and Beta Diversity along Chronosequence in Coppiced and Unmanaged Beech Forests. Diversity, 12(3), 101. https://doi.org/10.3390/d12030101





