Obtaining Sustainable Population Structures for the Management of Red Deer

Abstract

Cervus elaphus populations are spreading and growing in many parts of Europe. This growth can have detrimental effects on biodiversity and ecosystem function. Successful strategies to manage large herbivores require reliable information on density and population trends. This paper presents a methodology to achieve a sustainable distribution of red deer by age and sex classes over time. Instead of traditional algebraic methods, the method consists of a simple iterative process that uses convergence to obtain the dominant eigenvalue and eigenvector of the biological matrix from an initial population. This eigenvalue represents the annual growth rate of the population, and the eigenvector represents the ideal age and sex class distribution of the population. The method has been applied to a fenced preserve in the province of Toledo, Spain. An annual population growth rate of 1.63 (dominant eigenvalue of the biological matrix) was obtained from an initial population and the biological matrix of the deer on the preserve. The convergence of this rate occurred in year 14, but the carrying capacity allows for a population close to the population in year 17 according to the prediction, which is therefore considered to be the year when the ideal population distribution is achieved. This methodology allows managers to numerically justify how to control population growth to preserve biodiversity and sustainability.

1. Introduction

There is increasing interest in the management of red deer (Cervus elaphus) because populations are spreading and growing in many parts of Europe [1,2,3]. This population growth can vary in terms of the biological attributes of individuals and populations, such as body weight, productivity, antler size, and survival by sex [4,5]. It also can also have detrimental effects on biodiversity and ecosystem function [6,7], resulting in damage to trees due to the bark stripping or browsing effects of large herbivores, crop damage, wildlife–livestock interactions, and transmission of pathogens, with the corresponding economic losses [2,8].

The management of large herbivores is particularly challenging [9,10]. There are a variety of ways to reduce ungulate numbers and mitigate the damage they cause, such as harvesting [11], translocation [12], contraception [13], the introduction of large carnivores [14], fencing to prevent vegetation browsing [15], vaccination to prevent disease transmission [16], management of food and water points to prevent contact between wild and domestic animals [17], etc.

However, while inadequate management leads to unintended situations such as evolutionary impacts on populations due to highly selective harvesting [1], or extinction of the population due to overexploitation [18,19], passive management, combined with the absence of natural predators, countryside abandonment, and large agricultural fields as an unnatural food source, can allow some wild animal populations to increase exponentially, causing the environmental and economic harm [1,20,21,22].

As a result, wildlife managers need to integrate ecological processes, social, cultural, and political values, as well as economic feasibility into their management strategies [23]. Successful strategies to manage these species require reliable information on density and population trends [24]. Management models show how wild populations are developing [18,25,26,27]. These models can also simulate population dynamics over time to compare different management practices [28] and control and guarantee the sustainability and stability of the increasing population.

Red deer (Cervus elaphus) have been a part of the large European mammal fauna since the Middle Pleistocene [29]. These animals have been living in the Iberian Peninsula without interruption since at least the Late Pleistocene [30], with Iberia serving as a refuge during glacial periods [31]. The Iberian red deer (Cervus elaphus hispanicus) is one of the most significant and traditional large game species in the Iberian Peninsula. It has been one of the main game animals from the time of the first hominids until today. Red deer are distributed widely throughout the Iberian Peninsula. The estimated population exceeds 500,000 individuals [32]. The Mediterranean habitat, mixing forest and grassland, is the perfect landscape for the Iberian red deer, providing the animal with both food and protection [33]. When the number of individuals exceeds the carrying capacity, it can cause more vulnerable species to disappear, resulting in a loss of biodiversity for other animals.

Of the different management models that are available, matrix models provide good results to simulate population dynamics over time [34,35,36,37]. A matrix model groups animals into age classes in a vector, and the matrix contains the reproductive and mortality population as a probability, which determines rates for each age class and sex [38]. They are square matrices (A) that involve a linear transformation from a vector space, V, into itself. The vectors (v) of space V are called eigenvectors, and their change in scale due to the transformation is called their eigenvalue (λ). This feature can be written as the equation Av = λv. Eigenvalues and eigenvectors of these matrix models depend on biological rates, but obtaining eigenvalues and eigenvectors from a matrix is an algebra-intensive task [39]. There are online tools that can calculate the Leslie matrix, the first eigenvector, and the first eigenvalue [40], or user-friendly R-packages such as “popbio” [41], but they do not ensure that the stable population distribution will be obtained, and they require wildlife managers who can program in R or other programming languages. These models do not necessarily clarify the link between cause and effect in population dynamics, especially since they pertain to decision-making towards a resource goal. Although these models do have limitations, the influence of spatial–temporal plant and climate variability and the effect of density on mortality, fecundity, and individual growth make it difficult to obtain reliable input data [42].

When an inefficient management situation is detected, it is necessary to quantify when and how to reverse it. This study focuses on the definition of quantitative sustainable management strategies for Iberian red deer populations in Mediterranean habitats based on the Leslie matrix [38]. Governments control red deer populations by the number of hunting licenses they offer, which is determined in the approved management projects. The quantitative method proposed in this work is an affordable management option to achieve a sustainable deer population. It is based on calculating management parameters to structure the population and quantify its growth and productivity, with the goal of sustainable stability.

The main goal of this work is to implement an iterative convergent numeric method based on the projection of a biological matrix that avoids calculating the eigenvector and eigenvalue using the characteristic polynomial and indicators in order to achieve a stabilized sustainable distribution of an Iberian red deer population managed based on age and sex classes and keep the population at this level.

2. Materials and Methods

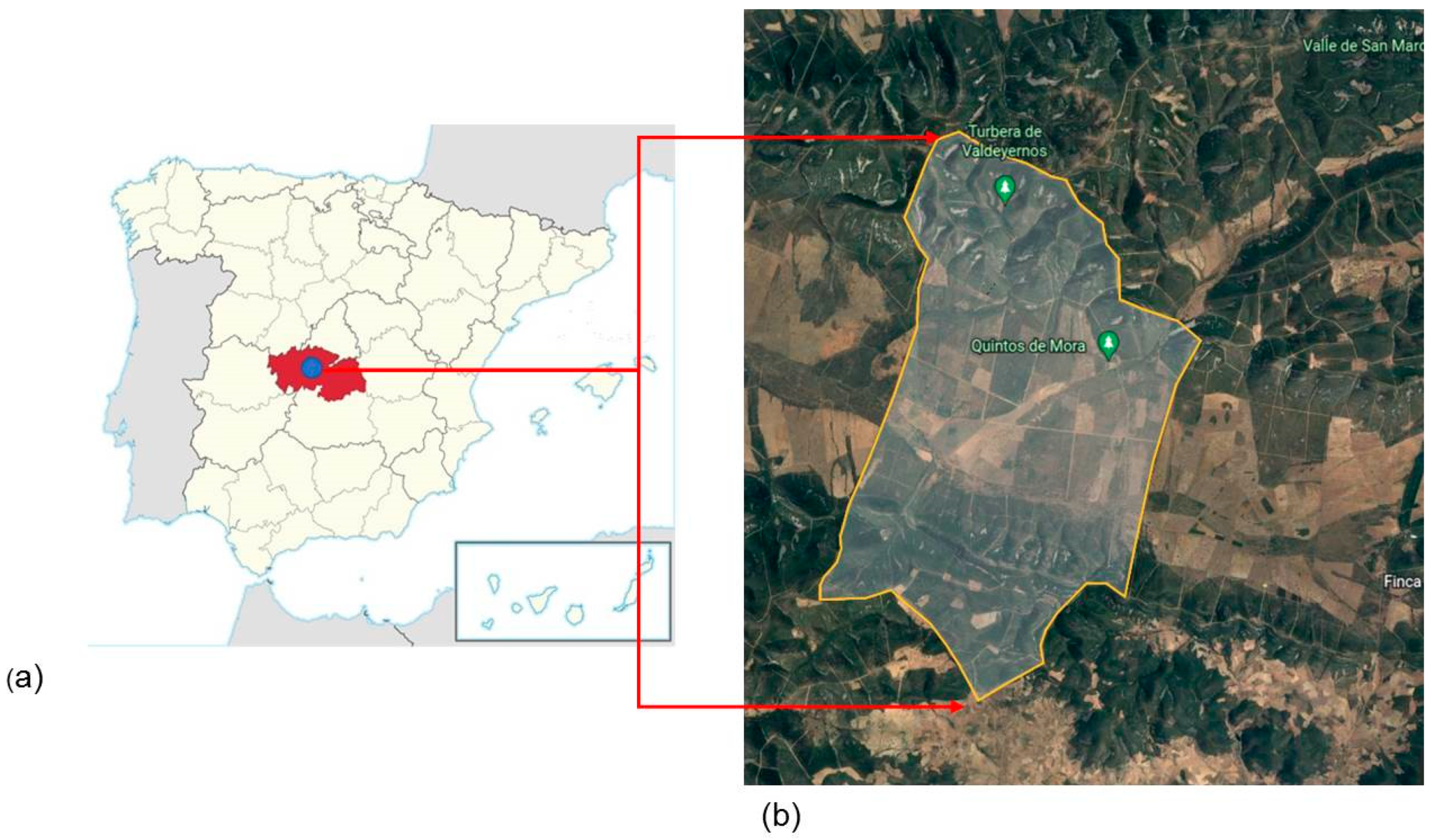
2.1. The Study Area

The study area is located in Quintos de Mora estate in the southwest corner of the province of Toledo, in the municipality of Los Yébenes. It belongs to the National Park Department of the Ministry for Ecological Transition and the Demographic Challenge, and it is categorized as a Natural Space in the province of Toledo [43] (see Figure 1).

It is a fenced preserve with a total area of 6864 ha [32] and an altitude between 735 m.a.s.l. and 1265 m.a.s.l. The climate is the Mediterranean, with an annual rainfall of between 600 and 700 mm. The average monthly maximum and minimum temperatures vary between 34.5 ºC in the warmest month and 1.6 °C in the coldest month. The dry season lasts from mid-June to mid-September.

It has a classic Mediterranean vegetation cover with high biodiversity. The most common species are Quercus ilex ssp. Ballota, Quercus faginea, Quercus pyrenaica, Cistus ladanifer, and Genista hirsuta.

In terms of wildlife, the most important species are red deer (Cervus elaphus), wild boar (Sus scrofa), fallow deer (Dama dama), roe deer (Capreolus capreolus), rabbit (Oryctolagus cuniculus), hare (Lepus granatensis), and fox (Vulpes vulpes). Approximately 1963 deer have been inventoried, which means a density of 28.60 deer/100 ha [43]. In Spain, this density of 0.28 ind/ha is estimated as to be a normal-high value for this type of population [44]. Every year, the autonomous agency of national parks estimates the population by applying the transect sampling method during the rutting season [45]. The principal use of the preserve is deer and wild boar biological control through culling. Interventional studies involving animals or humans, and other studies that require ethical approval, must list the authority that provided approval and the corresponding ethical approval code.

To apply the proposed methodology, the carrying capacity of the study area must first be calculated to determine the maximum number of individuals that can live on the Quintos de Mora preserve. The model that was applied to estimate the carrying capacity considers feeding requirements, water availability, areas of refuge, impacts on the habitat, climate, and landscape (Reglamento de Ordenación de la Caza en Andalucía, Decree 126/2017 of 25 July). The estimated carrying capacity was 1407 individuals (0.2 ind/ha) [43]. The current population exceeds this figure by 556 individuals (see Appendix A).

The current management planning determines the biological values to be entered into matrix A, below the OCC, which avoids undesirable interdependence phenomena. The staff working on the preserve in recent years provided the number of individuals by age and sex classes and their birth and death rates. These figures are needed to complete the model [45] (Reglamento de Ordenación de la Caza en Andalucía, Decree 126/2017 of 25 July). There are ten age classes per sex because individuals older than ten years of age are usually harvested as part of the management planning. These data are supported by specialised references, such as Soriguer [46]; Montoya Oliver [44]; Landete-Castillejos et al. [47]; and Rodriguez-Hidalgo et al. [48].

Table 1. Biological values applied in the model [49].

Rate	Value
Birth rate (Calves birth/reproductive female)	0.564
Birth sex ratio (M:F)	1:1
Females calves death rate (Less than 1 year old)	0.12
Males calves death rate (Less than 1 year old)	0.15
Young females death rate (From 1 to 2 years old)	0.06
Young males death rate (From 1 to 2 years old)	0.1
Adult females death rate (From 2 to 10 years old)	0.03
Adult males death rate (From 2 to 10 years old)	0.05

shows the average statistical biological values for a standard Iberian red deer population with density conditions below optimum capacity applied to the model and maximum growth [49].

2.2. The Model

Leslie introduced the population projection matrix model in 1945 [38]. This model has been widely applied to analyse the evolution, management, harvesting, etc. of wildlife populations since then [34], and it has expanded those results to the male side of the group. These models are defined by the standardized finite difference linear system of equations:

$$X_t=A{X}_{t-1}\mathrm{and}{X}_i\in R^n/n\in N$$

(1)

where X_t and X_t−1 are column vectors containing the number of individuals within each age class and sex at time t and t−1, respectively. A is the square primitive matrix with biological characteristics that express the reproductive and mortality population behaviour. A is known as the Leslie Matrix [38], which is expressed as follows:

$$A=\left(\begin{array}{cc}\begin{array}{ccc}{F}_{11}& F_{12}& F_{13}\\ P_{21}& 0& 0\\ \dots & \dots & \dots \end{array}& \begin{array}{ccc}\dots & F_{1n-1}& F_{1n}\\ \dots & 0& 0\\ \dots & \dots & \dots \end{array}\\ \begin{array}{ccc}0& 0& 0\\ \dots & \dots & \dots \\ 0& 0& 0\end{array}& \begin{array}{ccc}{P}_{ij}& 0& 0\\ \dots & \dots & \dots \\ \dots & P_{n(n-1)}& P_{nn}\end{array}\end{array}\right)$$

(2)

where F_1j is the fecundity of females and age group j, and Pij is the survival probability from age j−1 at time t−1 to age j at time t of the sex group i. Both, F and P integrate the factors that determine population growth, such as birth rates and the probability of an individual reaching the next age class by discretization period.

This means that, for a given period, the vectors containing the number of individuals within each age class and sex are obtained from:

X₂ = AX₁; X₃ = AX₂; …; X_t = AX_(t−1),

(3)

X₂ = AX₁; X₂ = A²X₁; …; X_t = A^(t−1)X₁,

(4)

In general, X_t = A^(t−1) X₁ expresses the projection of the population for t periods of time from the proposed initial situation.

On the other hand, the Leslie Matrix, A, is a square and diagonalizable matrix, so eigenvalues and eigenvectors can be obtained. Its dominant eigenvalue, λ₁, represents the population growth rate.

AV₁ = λ₁ V₁,

(5)

where V₁, is the right eigenvector of A, which corresponds to the dominant eigenvalue, λ₁.

When λ₁ > 1, from a mathematical point of view, the total number of individuals in the population increases exponentially over time. If λ₁ < 1, the individual population decreases and heads towards extinction. Lastly, if the eigenvalue is λ₁ = 1, the population remains constant over time [50]. This means that the right eigenvector of A, V₁, which corresponds to λ₁, represents the distribution of the stable, sustainable population by age and sex classes, with values proportional to λ₁ [50].

The previous applications of this method to population dynamics required the resolution of the characteristic polynomial, by traditional algebraic methods, to obtain the eigenvalues and their corresponding eigenvectors of matrix A. This process requires specific mathematical software, which makes it difficult for ecosystem managers to apply it.

The method proposed in this work simplifies the process through an iterative convergent numeric process that avoids calculating the eigenvector and eigenvalue using the characteristic polynomial. This iterative process gives the stable growing population structure determined by the value of the dominant eigenvalue, λ₁,, that will lead to the sustainability that is sought.

Considering that every vector X_i has its coordinates in a principal base of eigenvectors, (α_i1, α_i2 …, α_in), then the expression of X_i is:

X_i = (α_i1 V₁ + α_i2 V₂ + … + α_in V_n),

(6)

The structure and the behaviour of the model are, therefore, obtained through the convergence of the vector X_t when t→∞, which makes it possible to identify the value of λ that stabilizes the population structure and growth, over time.

Considering the relationship between X_t and X₁, (see Equation (4)) the expression of the limit is:

$$\underset{t\to \infty }{\mathit{lim}}{X}_t=\underset{t\to \infty }{\mathit{lim}}{A^{t-1}X}_1=\underset{t\to \infty }{\mathit{lim}}{({\alpha }_{11}{\lambda }_1^{t-1}V}_1+{{\alpha }_{12}{\lambda }_2^{t-1}V}_2+\cdots +{{\alpha }_{1n}{\lambda }_n^{t-1}V}_n)=\underset{t\to \infty }{\mathit{lim}}{{\lambda }_1^{t-1}({\alpha }_{11}V}_1+{\alpha }_{12}\frac{{\lambda }_2^{t-1}}{{\lambda }_1^{t-1}}{V}_2+\cdots +{\alpha }_{1n}\frac{{\lambda }_n^{t-1}}{{\lambda }_1^{t-1}}{V}_n)$$

(7)

Since λ₁ is the dominant eigenvalue, then λ₁ > λ_i ∀ i ≠ 1 and $\underset{t\to \infty }{\mathit{lim}}\frac{{\lambda }_i^{t-1}}{{\lambda }_1^{t-1}}=0$

When i = 1, the result of the limit is:

$\underset{t\to \infty }{\mathit{lim}}{X}_t=\underset{t\to \infty }{\mathit{lim}{\lambda }_1^{t-1}}{\alpha }_{11}{V}_1$ when the period of time is t.

Considering a sufficiently long period, the vector of the number of individuals by age class and sex, X_t,, converges on a new vector proportional to the dominant eigenvector V₁, λ₁^(t−1) α₁₁ V₁, where λ₁^(t−1) and α₁₁ are numeric constants, and α₁₁ represents the proportionality between the limit of X_t and V₁.

The iterative procedure consists of calculating X₂, X₃, ⋯, X_t−1 until X_t and X_t−1 are proportional and the constant of proportionality is λ₁:

$$X_2=A{X}_1;X_3=A{X}_2=A^2{X}_1;\dots ;X_t=A{X}_{t-1}=A^{t-1}{X}_1={\lambda }_1^{t-1}{V}_1$$

(8)

The iterative process obtains the numerical projection of matrix A, where the value of λ₁ as a dominant eigenvalue is stabilized. λ₁ is the stabilized constant between X_t−1 and X_t. This means that, from time t onwards, the proportionality constant between X_t+i−1 and X_t+i does not change and is λ₁. This convergence on the dominant eigenvalue also means that the initial vector X₁ has converged to the eigenvector V₁. We can represent X_t in the limit as:

$$X_t=A^{t-1}{X}_1={\lambda }_1^{t-1}{V}_1$$

(9)

This mathematical conclusion makes it possible to make a simple reiterative calculation to obtain the stable population composition and the growth ratio during the process. This makes it a quantitative management tool that can be used for ecological control. In summary, the method first needs to describe a mathematical–biological matrix, A, based on knowledge of the biological species. The iterative calculation of projections then obtains the dominant eigenvalue and the corresponding eigenvector over t. At this point, the population structure is proportional to the dominant eigenvector, V, and its total number of individuals is the sum of its components. Based on these results, it is possible to stabilize the growth of a population, and the results are ecologically and mathematically testable [51]. To achieve this objective, populations are considered to naturally maintain their growth with λ₁ > 1, so the management objective will be to control the excessive growth, keeping λ₁ = 1 when the optimal carrying capacity for that medium has been exceeded. Management will focus on quantifying culling to maintain the age structure that stabilizes the mathematical projection system.

The transition matrix is based on linear dependencies through natural and management factors that generate the growth dynamic of the population, which is stabilized using the aforementioned management culling. The result of this approach, considering Verhulst’s theoretical hypothesis, is an S-shaped logistic distribution of the population (see Figure 2) with a horizontal asymptote corresponding to the year when the theoretical carrying capacity is reached.

In this study, we adopted the optimal carrying capacity (OCC), instead of the maximum carrying capacity (MCC). The optimal carrying capacity is the carrying capacity for which the population birth rate does not drop because of density-dependence, overpopulation, diseases, or lack of a correct nutrition. This OCC is the number of individuals that correspond to the mathematical inflection point of the sigmoid “S”. The growth rate decreases from the inflection point (year 17 in Figure 2) because of any of the mentioned phenomena.

The theoretical S-shaped curve has been replaced by the projection’s matrix model, which is based on U-shaped exponential growth (see Figure 3) and is much easier to handle mathematically. This also makes it possible to go from the theoretical models of Verhulst and Pearl to a Malthusian model, simplifying the mathematical integration and parametric adjustments. Applying the described methodology, the population stabilizes at year 17. Figure 3 also shows the number of individuals culled for the stabilized population.

3. Results

In this work, the authors developed a simulation for a hypothetical initial population to explain how the model works, because the model must be tested from values below the OCC to see the increasing evolution of the population. The simulation considered an initial population of 100 deer on this preserve in the past. The range of the projection intervals was one year, and individuals were grouped into twenty age classes, the level of maximum detail, ten for females and ten for males, according to their age in years. The last class (i = 10) includes animals that are ten years of age or older. The model obtains the movement of individuals through age classes over time, with a probabilistic law based on biological survival, making future time projections for annual periods possible. The distribution of the initial population corresponds to vector X₀ (see

Table 2. Distribution of the initial population X₀, the target population X₁₇, and the population in year 18 X₁₈.

	Females										Males										Total
Age	1	2	3	4	5	6	7	8	9	10	1	2	3	4	5	6	7	8	9	10
X0	10	10	8	8	8	6	0	0	0	0	10	10	8	8	8	6	0	0	0	0	100
X17	133	101	81	68	57	47	39	33	28	95	133	97	75	62	50	41	34	27	22	47	1271
X18	155	117	95	79	66	55	46	38	32	119	155	113	88	72	58	48	39	32	26	66	1478

). The next step is to obtain the year when this population reaches the carrying capacity. This is performed by applying matrix A to X₀, which should be very different from V,, to study the convergence process with the iterations of the matrix model. Figure 4 shows that the population peaks at the carrying capacity of 1407 deer by approximately year 17 after the initial situation, for a theoretical unconstrained exponential growth applying Equation (5). Table 2 shows the distribution of the individuals in year 17 by sex and age class.

The model identifies the maximum sustainable harvesting rate to achieve a density similar to the optimum carrying capacity and indicates the justified ecological culling by classes to provide stability based on the calculated carrying capacity. The model therefore provides a stable distribution of each age class and a stabilized growth rate.

The exponential progression that takes the population from 100 individuals to approximately 4500 in just 25 years is remarkable. This value cannot be observed without the application of a prediction model (See Figure 4).

The next step consisted of applying the iterative procedure to calculate the year when lambda, λ₁, converges to a constant value. This convergence value expresses the proportionality between consecutive vectors. At the same time, the population would evolve into a structured stable composition. According to Figure 5, lambda converges at approximately year 14.

This means that, when the initial population (Table 2) is entered into the model and its development over the years is studied, growth becomes stable beginning at t = 14, in this case, with a dominant eigenvalue λ₁ = 1.163, which means a total growth of 16.3% every year, as shown in Figure 5.

When t = 17, there is stable age distribution (see Table 2), which is the goal. The ideal distribution analysis, X₁₇ (Table 2), indicates that the sex ratio is 1.156. This value is acceptable since natural mortality is higher in males.

Table 3. Ideal distribution by age classes, in percentage.

Stable Distribution (%)										TOTAL
F1	F2	F3	F4	F5	F6	F7	F8	F9	F10
10.5	7.9	6.4	5.3	4.5	3.7	3.1	2.6	2.2	7.5
M1	M2	M3	M4	M5	M6	M7	M8	M9	M10
10.5	7.7	5.9	4.8	4.0	3.2	2.6	2.2	1.8	3.7	100

shows the percentage of individuals for each class in X₁₇ that determines the desired stability.

From year 17 onwards, managers will remove some individuals from the population to maintain the optimum carrying capacity value. This means that the ecosystem can maintain its population equilibrium, and the managers can justify the profits from the culling. In addition, there is a healthy population. The application of the model to obtain the population for t = 18 shows that the total population is higher than the population that corresponds to the optimum carrying capacity, and the distribution per age and sex classes does not follow the ideal (Table 2).

This means that, starting in year 17, managers would need to start selective culling to keep this density below the carrying capacity. The proposal would therefore be to cull the difference between X₁₇ and X₁₈ (Figure 6). This means that sustainable management would require managers to cull 207 individuals annually to preserve biodiversity, taking the values proportional to the vector V. These values make it possible to plan management and justify profits from this natural resource, while controlling and ensuring theoretical, numerical, and biological sustainability at this point.

In summary, the steps of the process would be as follows (See Figure 7 and Appendix A to see how an iteration works).

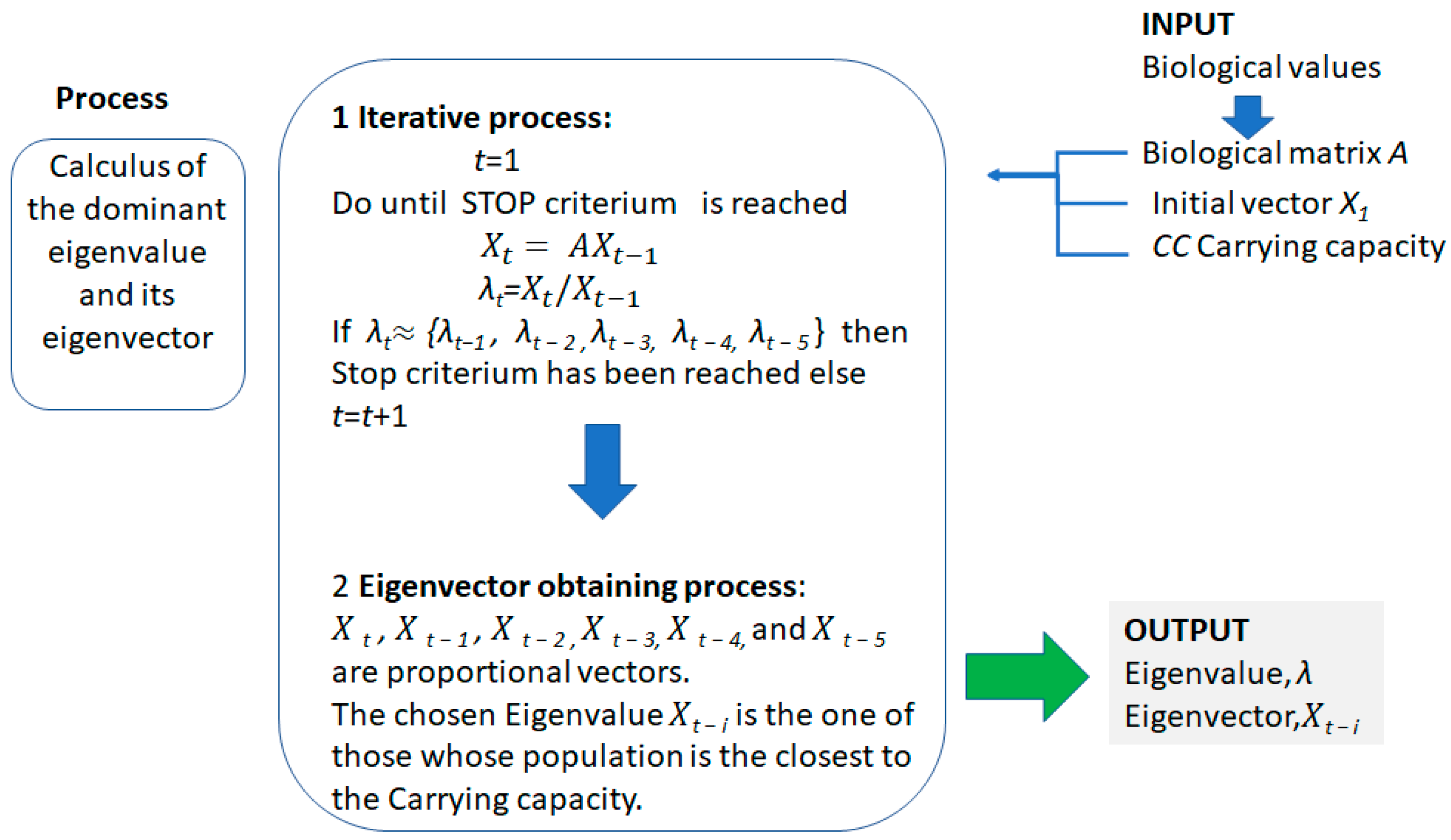
• The manager must obtain the birth and death rates by age and sex classes to obtain the matrix A, the initial population distribution by age and sex classes X₁, and the optimum carrying capacity of the preserve.
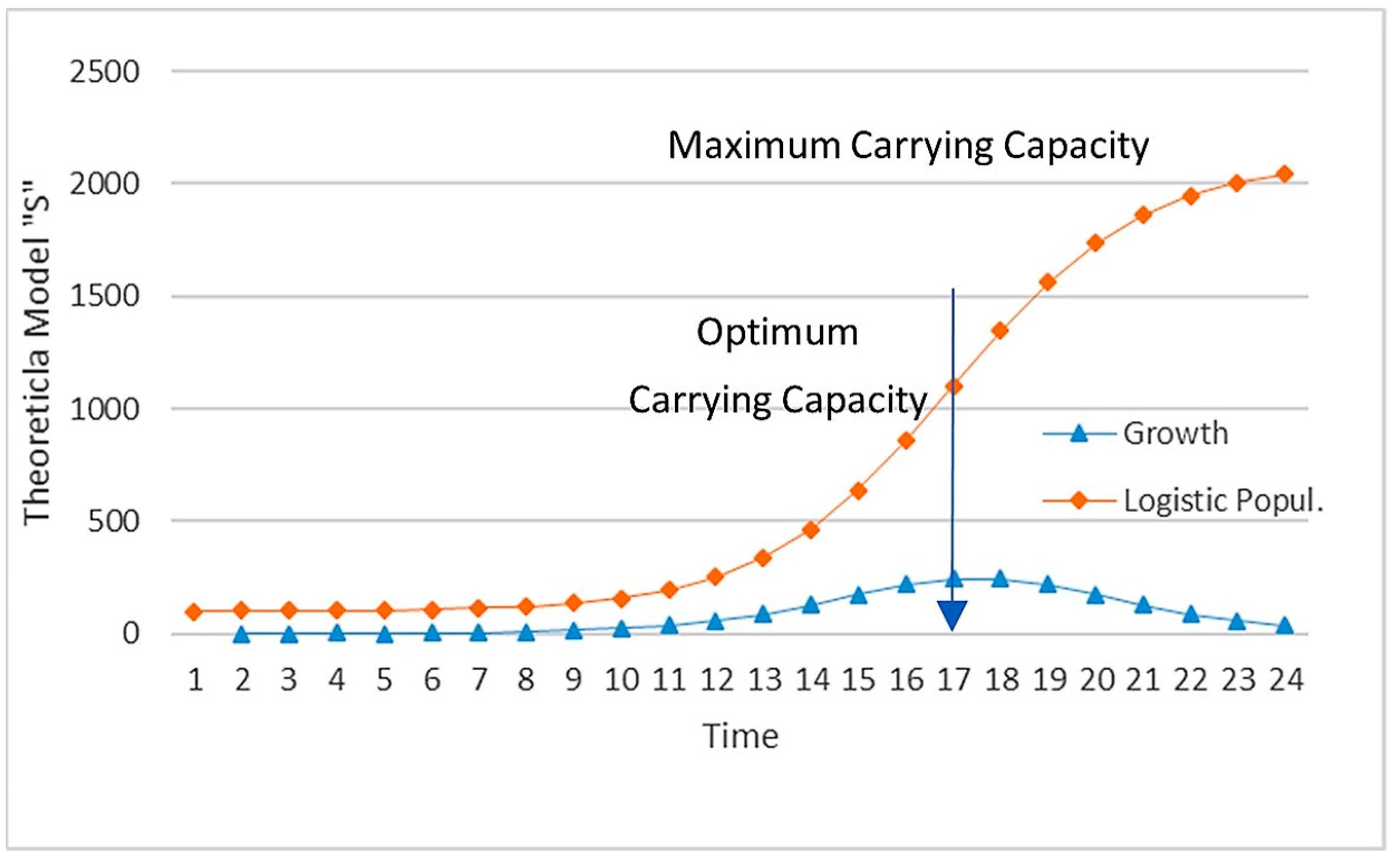
• The eigenvalue can be obtained in a fast iterative process, (software such as Excel can be used) that ends when this value is the same as the ones obtained in the previous five iterations (see Figure 7).
• The chosen eigenvector X_t−i is the one from X_t, X_t−1, X_t−2, X_t−3, X_t−4, and X_t−5 whose total population is the closest to the optimum carrying capacity.
• From year t−i onwards, managers will remove some individuals from the population to maintain the optimum carrying capacity value.

After the biological behaviour has been studied, along with the factors involved in the evolution of the population, if the manager identifies population levels above the OCC, it indicates a dependency phenomenon in the state that favours diseases and the need to decrease the population by culling in the following iterative phases:

• The management culling to lower the population structure should be proportional to the eigenvector that was calculated in the stabilization process. The sum of the components of this vector must be lower than and close to the OCC value.
• For the following periods, the culling quotas by age classes should stabilize the population according to the dominant lambda value.
• Stabilize the population structure and quantity and make them sustainable, with a management plan that will be updated periodically and with statistical sampling of abundance by the age classes in matrix A.

4. Discussion

This paper proposes a quantitative method for managing wild species that provides maximum growth but avoids dependency phenomena because it keeps populations below the OCC of the area. The results show that the method determines not only the exact numerical values of population increase, but also the ideal distribution of the population by age and sex, considering the carrying capacity of the study area, to ensure sustainability (Table 2).

The dominant eigenvalue (λ₁) of matrix A gives information about the total annual growth without harvesting (Figure 5) as an indicator of a population’s fate. This result contributes to the knowledge of how eigenvalues, as vital rates, help obtain the dynamic behaviour of a population [39]. The proposed method shows an efficient and available approach to calculating the eigenvalue and determining the year after which the eigenvalue converges to a constant value. This procedure avoids the challenging task of obtaining the dominant eigenvalue and its associate eigenvector [39]. Previous Leslie matrix models simulated and studied the evolution of wild ungulates [52,53,54,55]. However, these models focus on the historical and long-term evolution from a demographic perspective and normally simulate only the female part [55,56] or focus on harvesting rates. These models make no assumptions about the underlying form of the age-specific natural mortality and fertility rates, which is a relevant simplification from the wildlife management point of view [57]. These classical approaches to solving Leslie matrices give the dominant eigenvalue and the associate eigenvector but do not provide the evolution of the population composition from the initial situation to the population distribution of the eigenvector. The method proposed in this paper shows this evolution, year by year, from the initial situation to the eigenvalue. The authors did not find any models in the literature that had been obtained from the convergence of the projection of the Leslie matrix to quantify the evolution of the population structure, while incorporating sexes and age classes into the same matrix, that considers different kinds of male and female interactions in this evolution.

In this study, the value of the dominant eigenvalue is 1.16, very close to the theoretical value λ₁ = 1, which indicates that its associated eigenvector contains a stable distribution [50,51]. The total population therefore grows 16% annually, which is in line with Martínez and Martín’s [51] results for the red deer in the same area but grouping the population into different classes. It also indicates that the size of the total population should be 1407 when the OCC is reached and stabilization occurs, lowering the lambda from 1.16 to a lambda equal to 1 through culling. This use of the eigenvalue leverages the achievement of conservation goals [58]. Since hunting is supposed to keep the population sustainable, the harvest rate must be equal to the reproductive output [8]. In our study, the harvest rate is 16%.

The eigenvalue converged at year 14. However, the total population was lower than the optimum carrying capacity (Figure 4). This means that the ideal distribution for every age class and sex to guarantee the sustainability and stability of the population and to minimise the impact on animal communities and biodiversity corresponds to the distribution at year 17 [59].

The estimated annual culling (see Figure 3) maintains the density after the reproductive season according to the carrying capacity of the preserve. This result helps managers to make decisions regarding culling for the coming years if the vital rates remain the same, and it gives managers strict control over the population dynamics [60]. This type of management also reduces the impact of hunting on population dynamics [23] when the selection of individuals by sex or age class improves the population structure of ages and sexes [61,62]. It also helps minimise both the economic damage to forestry and collisions with vehicles [63]. The dominant eigenvalue, like the finite population growth rate, is a helpful tool for developing endangered species management policies [64]. In addition to using density-dependent phenomena to determine the OCC, it could also be established based on problematic social phenomena, such as traffic accidents, damage to crops, or interactions that are harmful to biodiversity.

The development of matrix A requires the knowledge of the biological parameters by the manager for the mathematical purpose of quantifying the population status for each period and population composition because the dominant eigenvalue, λ₁, depends on the parameters that are selected for matrix A. This matrix lets managers simulate different production rates and estimate the economic benefits of the exploitation. This means that the proposed methodology cannot be applied in open preserves with different management strategies, due to the interactions with neighbouring preserves that share the same red deer populations, which causes the population composition to vary constantly. In addition, the ecological characteristics of the preserves may vary between preserves, which also changes the carrying capacity.

Classifying the deer population into one-year age classes with the least possible bias and the highest precision is only possible by capturing the individuals, but even the methods based on tooth wear that have achieved the best results depend on the eye of the practitioner, and on environmental conditions that can change spatially and across time [65]. Some authors propose grouping by age classes, such as Martinez and Martin [51], who describe a deer management model that groups the population into three age classes for females and five for males in order to facilitate management, or Forsyth et al., who, in their study on population dynamics, group the population into three age classes per sex [66]. However, any simplification to obtain management classes by grouping age classes into quality classes would facilitate the mathematical calculation system. Nevertheless, the new parameters of fecundity and the probability of moving to the next group, F and P, are obtained by statistically integrating the age and sex class parameters P_ij, and F_1j, which makes them less accurate.

The main limitations of the method are that the parameters of matrix A should be checked every year. It is very difficult to practically determine birth and mortality rates by age class (i.e., in the field), but they are critical for applying these models. Managers often take this data from studies in other areas. Another limitation of the study is that it is only applicable to fenced preserves where hunting and management are independent from neighbouring preserves [67]. Lastly, it is a deterministic method, so the error of λ and of other parameters depend on the precision of the data and the factors of the model considered [68,69]. Stochastic models can estimate these errors, but the survey intensity and the frequency are higher [69,70].

5. Conclusions

This paper describes a simple method based on the convergence of the Leslie matrix that models how a deer population, in this case, a theoretical population of 100 individuals, can be managed to achieve a stable population size and to determine the annual cull rate, 16% in this case, needed to maintain this population in these conditions. The input data was taken from the Quintos de Mora reserve in the province of Toledo. Because the optimum carrying capacity (1407 individuals) was considered rather than the maximum carrying capacity, the parameters of the Leslie matrix do not need to be revised annually to detect changes due to density dependence problems. However, practical application in actual populations requires periodic reviews of management plans to update the input data of the model. It is also important to note that this model can only be applied to fenced estates, where variables are more controlled than in open estates.