Conservation Genetic Analysis of Blanding’s Turtles across Ohio, Indiana, and Michigan
Abstract
:1. Introduction
2. Materials and Methods
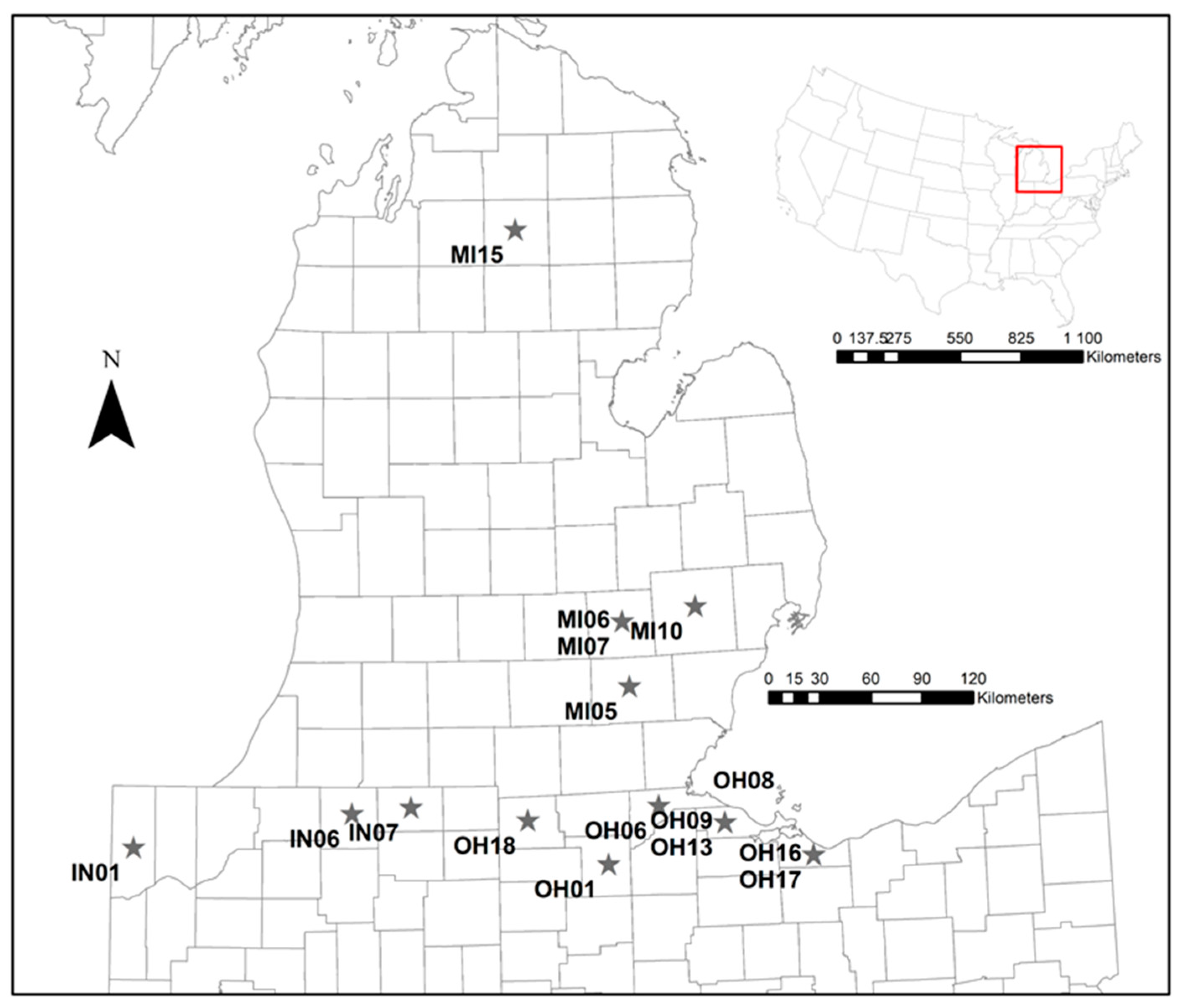
2.1. Samples and Genotyping
2.2. Analysis within Localities
2.3. Population Structure
3. Results
3.1. Tests of Equilibrium
3.2. Analyses within Localities
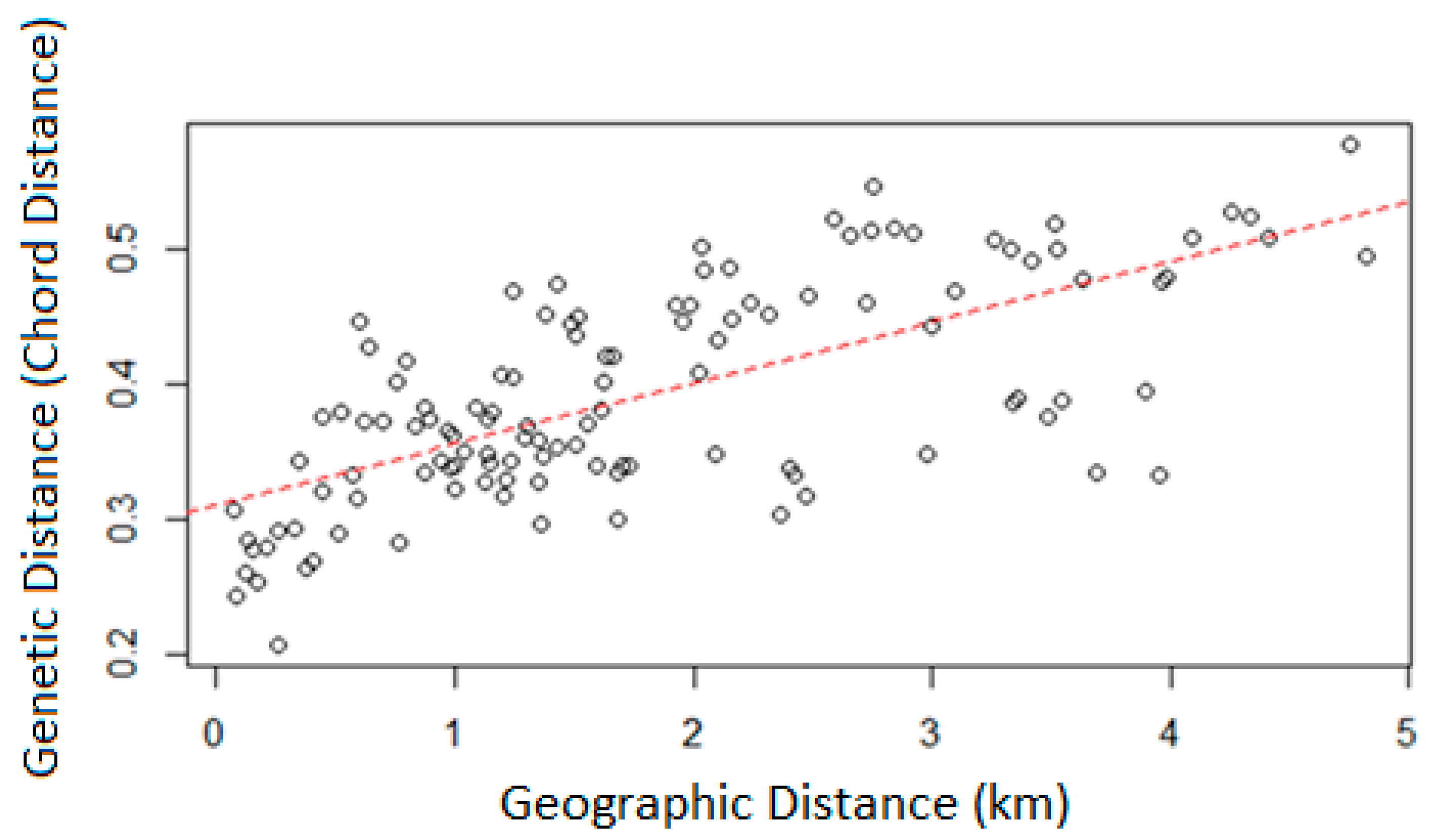
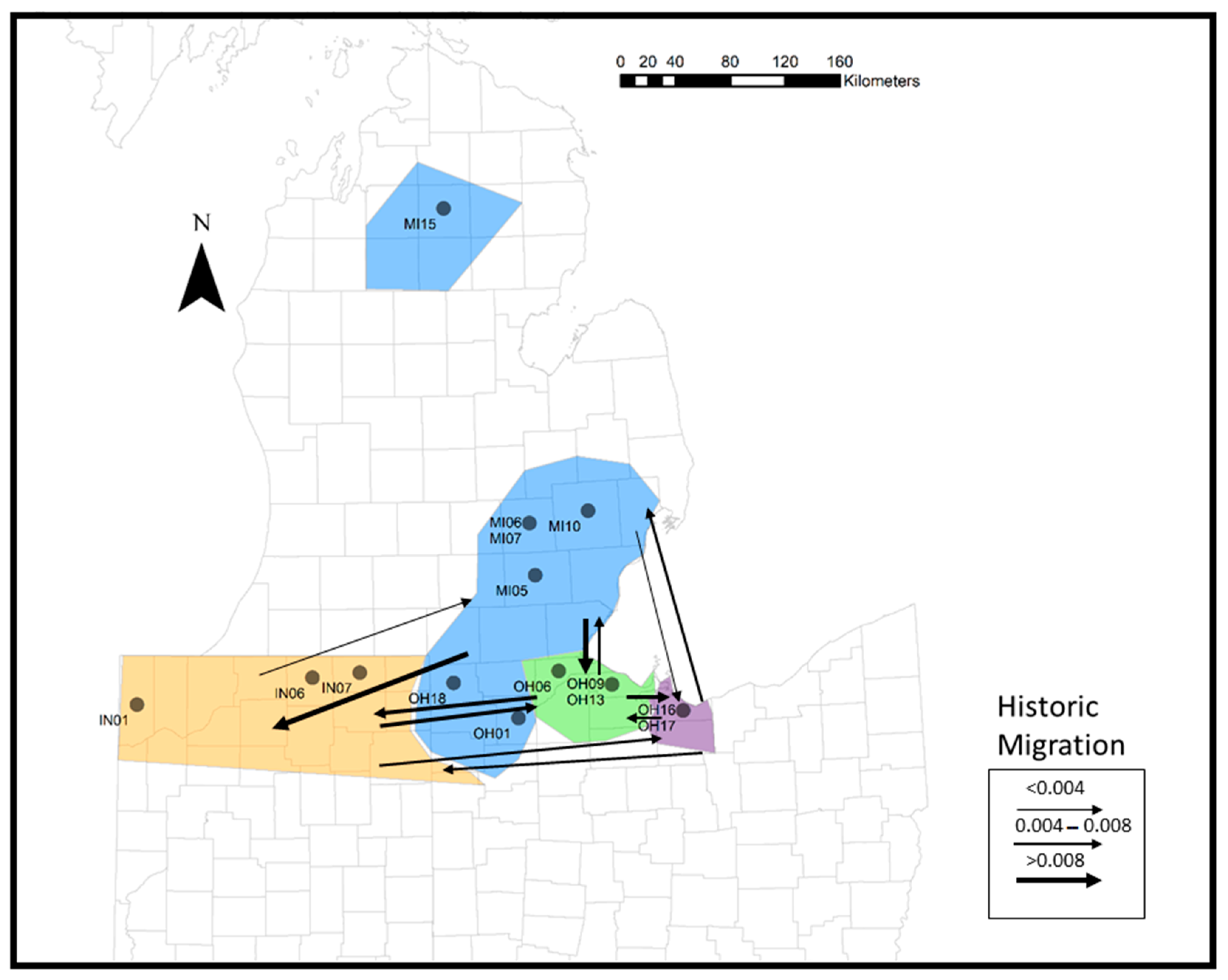
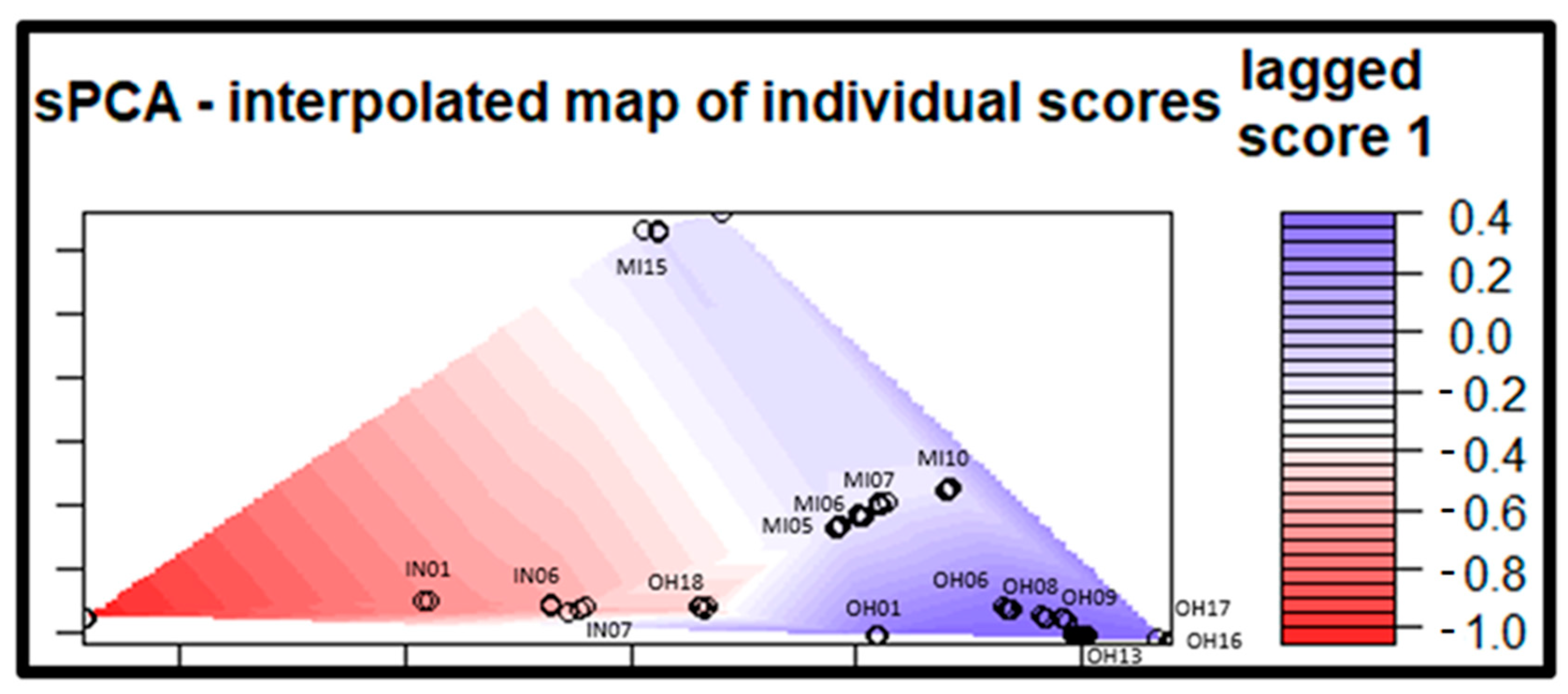
3.3. Population Structure
4. Discussion
4.1. Analyses within Localities
4.2. Population Structure
4.3. Conservation Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lovich, J.E.; Ennen, J.R.; Agha, M.; Gibbons, J.W. Where have all the turtles gone, and why does it matter? BioScience 2018, 68, 771–781. [Google Scholar] [CrossRef]
- Congdon, J.D.; Dunham, A.; van Loben Sels, R. Delayed sexual maturity and demographics of Blanding’s turtles (Emydoidea blandingii): Implications for conservation and management of long-lived organisms. Conserv. Biol. 1993, 7, 826–833. [Google Scholar] [CrossRef]
- Kinney, O.M. Movements and Habitat Use of Blanding’s Turtles in Southeast Michigan: Implications for Conservation and Management; University of Georgia: Athens, GA, USA, 1999. [Google Scholar]
- Shaffer, H.B.; Minx, P.; Warren, D.E.; Shedlock, A.M.; Thomson, R.C.; Valenzuela, N.; Abramyan, J.; Amemiya, C.T.; Badenhorst, D.; Biggar, K.K. The western painted turtle genome, a model for the evolution of extreme physiological adaptations in a slowly evolving lineage. Genome Biol. 2013, 14, R28. [Google Scholar] [CrossRef] [PubMed]
- Joyal, L.A.; McCollough, M.; Hunter, M.L., Jr. Landscape ecology approaches to wetland species conservation: A case study of two turtle species in southern Maine. Conserv. Biol. 2001, 15, 1755–1762. [Google Scholar] [CrossRef]
- Congdon, J.; Graham, T.; Herman, T.; Lang, J.; Pappas, M.; Brecke, B. Emydoidea blandingii (Holbrook 1838)—Blanding’s turtle. Conserv. Biol. Freshw. Turt. Tortoises Chelonian Res. Monogr. 2008, 5, 015.011–015.012. [Google Scholar]
- Jordan, M.A.; Mumaw, V.; Millspaw, N.; Mockford, S.W.; Janzen, F.J. Range-wide phylogeography of Blanding’s Turtle [Emys (=Emydoidea) blandingii]. Conserv. Genet. 2019, 20, 419–430. [Google Scholar] [CrossRef]
- Avise, J.C.; Bowen, B.W.; Lamb, T.; Meylan, A.B.; Bermingham, E. Mitochondrial DNA evolution at a turtle’s pace: Evidence for low genetic variability and reduced microevolutionary rate in the Testudines. Mol. Biol. Evol. 1992, 9, 457–473. [Google Scholar]
- Alacs, E.A.; Janzen, F.J.; Scribner, K.T. Genetic issues in freshwater turtle and tortoise conservation. Chelonian Res. Monogr. 2007, 4, 107. [Google Scholar]
- Mockford, S.; Herman, T.; Snyder, M.; Wright, J.M. Conservation genetics of Blanding’s turtle and its application in the identification of evolutionarily significant units. Conserv. Genet. 2007, 8, 209–219. [Google Scholar] [CrossRef]
- Rödder, D.; Lawing, A.M.; Flecks, M.; Ahmadzadeh, F.; Dambach, J.; Engler, J.O.; Habel, J.C.; Hartmann, T.; Hörnes, D.; Ihlow, F. Evaluating the significance of paleophylogeographic species distribution models in reconstructing Quaternary range-shifts of Nearctic chelonians. PLoS ONE 2013, 8, e72855. [Google Scholar] [CrossRef]
- Parmley, D. Turtles from the late Hemphillian (latest Miocene) of Knox County, Nebraska. Tex. J. Sci. 1992, 44, 339–348. [Google Scholar]
- Holman, J.; Parmley, D. Noteworthy turtle remains from the Late Miocene (Late Hemphillian) of northeastern Nebraska. Tex. J. Sci. 2005, 57, 307–316. [Google Scholar]
- Spinks, P.Q.; Thomson, R.C.; McCartney-Melstad, E.; Shaffer, H.B. Phylogeny and temporal diversification of the New World pond turtles (Emydidae). Mol. Phylogenetics Evol. 2016, 103, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Congdon, J.; Keinath, D. Blanding’s Turtle (Emydoidea blandingii): A Technical Conservation Assessment; USDA Forest Service, Rocky Mountain Region: Lakewood, CO, USA, 2006. [Google Scholar]
- Dahl, T.E. Wetlands Losses in the United States, 1780’s to 1980’s; US Department of the Interior, Fish and Wildlife Service: Washington, DC, USA, 1990.
- Ross, D.A.; Anderson, R.K. Habitat use, movements, and nesting of Emydoidea blandingii in central Wisconsin. J. Herpetol. 1990, 24, 6–12. [Google Scholar] [CrossRef]
- Grgurovic, M.; Sievert, P.R. Movement patterns of Blanding’s turtles (Emydoidea blandingii) in the suburban landscape of eastern Massachusetts. Urban Ecosyst. 2005, 8, 203–213. [Google Scholar] [CrossRef]
- Congdon, J.D.; Tinkle, D.W.; Breitenbach, G.L.; van Loben Sels, R.C. Nesting ecology and hatching success in the turtle Emydoidea blandingii. Herpetologica 1983, 39, 417–429. [Google Scholar]
- Prange, S.; Gehrt, S.D.; Wiggers, E.P. Demographic factors contributing to high raccoon densities in urban landscapes. J. Wildl. Manag. 2003, 67, 324–333. [Google Scholar] [CrossRef]
- Riley, S.P.; Hadidian, J.; Manski, D.A. Population density, survival, and rabies in raccoons in an urban national park. Can. J. Zool. 1998, 76, 1153–1164. [Google Scholar] [CrossRef]
- Ashley, E.P.; Robinson, J.T. Road mortality of amphibians, reptiles and other wildlife on the Long Point Causeway, Lake Erie, Ontario. Can. Field Nat. 1996, 110, 403–412. [Google Scholar]
- Congdon, J.D.; van Loben Sels, R.C. Growth and body size in Blanding’s turtles (Emydoidea blandingii): Relationships to reproduction. Can. J. Zool. 1991, 69, 239–245. [Google Scholar] [CrossRef]
- Frazer, N.B.; Gibbons, J.W.; Greene, J.L. Life tables of a slider turtle population. In Life History and Ecology of the Slider Turtle; Gibbons, J.W., Ed.; Smithsonian Institution Press: Washington, DC, USA, 1990. [Google Scholar]
- Kuo, C.-H.; Janzen, F.J. Genetic effects of a persistent bottleneck on a natural population of ornate box turtles (Terrapene ornata). Conserv. Genet. 2004, 5, 425–437. [Google Scholar] [CrossRef]
- Mockford, S.; McEachern, L.; Herman, T.; Snyder, M.; Wright, J.M. Population genetic structure of a disjunct population of Blanding’s turtle (Emydoidea blandingii) in Nova Scotia, Canada. Biol. Conserv. 2005, 123, 373–380. [Google Scholar] [CrossRef]
- Davy, C.M.; Bernardo, P.H.; Murphy, R.W. A Bayesian approach to conservation genetics of Blanding’s turtle (Emys blandingii) in Ontario, Canada. Conserv. Genet. 2014, 15, 319–330. [Google Scholar] [CrossRef]
- Sethuraman, A.; McGaugh, S.E.; Becker, M.L.; Chandler, C.H.; Christiansen, J.L.; Hayden, S.; LeClere, A.; Monson-Miller, J.; Myers, E.M.; Paitz, R.T. Population genetics of Blanding’s turtle (Emys blandingii) in the midwestern United States. Conserv. Genet. 2014, 15, 61–73. [Google Scholar] [CrossRef]
- McCluskey, E.M.; Mockford, S.W.; Sands, K.; Herman, T.B.; Johnson, G.; Gonser, R.A. Population Genetic Structure of Blanding’s Turtles (Emydoidea blandingii) in New York. J. Herpetol. 2016, 50, 70–76. [Google Scholar] [CrossRef]
- Anthonysamy, W.; Dreslik, M.; Douglas, M.; Thompson, D.; Klut, G.; Kuhns, A.; Mauger, D.; Kirk, D.; Glowacki, G.; Douglas, M. Population genetic evaluations within a co-distributed taxonomic group: A multi-species approach to conservation planning. Anim. Conserv. 2018, 21, 137–147. [Google Scholar] [CrossRef]
- Smith, P.W. An analysis of post-Wisconsin biogeography of the Prairie Peninsula region based on distributional phenomena among terrestrial vertebrate populations. Ecology 1957, 38, 205–218. [Google Scholar] [CrossRef]
- Howes, B.J.; Brown, J.W.; Gibbs, H.L.; Herman, T.B.; Mockford, S.W.; Prior, K.A.; Weatherhead, P.J. Directional gene flow patterns in disjunct populations of the black ratsnake (Pantheropis obsoletus) and the Blanding’s turtle (Emydoidea blandingii). Conserv. Genet. 2009, 10, 407–417. [Google Scholar] [CrossRef]
- Osentoski, M.F. Population Genetic Structure and Male Reproductive Success of a Blanding’s Turtle (Emydoidea blandingii) Population in Southeastern Michigan; University of Miami: Coral Gables, FL, USA, 2001. [Google Scholar]
- McGuire, J.M.; Scribner, K.T.; Congdon, J.D. Spatial aspects of movements, mating patterns, and nest distributions influence gene flow among population subunits of Blanding’s turtles (Emydoidea blandingii). Conserv. Genet. 2013, 14, 1029–1042. [Google Scholar] [CrossRef]
- Willey, L.L.; Jones, M.T. Conservation Plan for the Blanding’s Turtle and associated Species of Conservation Need in the Northeastern United States. Unpublished management plan, NE Blanding’s Turtle Working Group 2014.
- Blacket, M.; Robin, C.; Good, R.; Lee, S.; Miller, A. Universal primers for fluorescent labelling of PCR fragments—An efficient and cost-effective approach to genotyping by fluorescence. Mol. Ecol. Resour. 2012, 12, 456–463. [Google Scholar] [CrossRef]
- Reid, B.N.; Mladenoff, D.J.; Peery, M.Z. Genetic effects of landscape, habitat preference and demography on three co-occurring turtle species. Mol. Ecol. 2017, 26, 781–798. [Google Scholar] [CrossRef] [PubMed]
- Pearse, D.E.; Janzen, F.J.; Avise, J.C. Genetic markers substantiate long-term storage and utilization of sperm by female painted turtles. Heredity 2001, 86, 378–384. [Google Scholar] [CrossRef] [PubMed]
- Osentoski, M.; Mockford, S.; Wright, J.M.; Snyder, M.; Herman, T.; Hughes, C. Isolation and characterization of microsatellite loci from the Blanding’s turtle, Emydoidea blandingii. Mol. Ecol. Notes 2002, 2, 147–149. [Google Scholar] [CrossRef]
- King, T.L.; Julian, S. Conservation of microsatellite DNA flanking sequence across 13 Emydid genera assayed with novel bog turtle (Glyptemys muhlenbergii) loci. Conserv. Genet. 2004, 5, 719–725. [Google Scholar] [CrossRef]
- Libants, S.; Kamarainen, A.; Scribner, K.; Congdon, J. Isolation and cross-species amplification of seven microsatellite loci from Emydoidea blandingii. Mol. Ecol. Notes 2004, 4, 300–302. [Google Scholar] [CrossRef]
- Reid, B.N.; Peery, M.Z. Land use patterns skew sex ratios, decrease genetic diversity and trump the effects of recent climate change in an endangered turtle. Divers. Distrib. 2014, 20, 1425–1437. [Google Scholar] [CrossRef]
- Peakall, R.; Smouse, P.E. GENALEX 6: Genetic analysis in Excel. Population genetic software for teaching and research. Mol. Ecol. Notes 2006, 6, 288–295. [Google Scholar] [CrossRef]
- Adamack, A.T.; Gruber, B. PopGenReport: Simplifying basic population genetic analyses in R. Methods Ecol. Evol. 2014, 5, 384–387. [Google Scholar] [CrossRef]
- Rousset, F. Genepop’007: A complete re-implementation of the genepop software for Windows and Linux. Mol. Ecol. Resour. 2008, 8, 103–106. [Google Scholar] [CrossRef]
- Hale, M.L.; Burg, T.M.; Steeves, T.E. Sampling for microsatellite-based population genetic studies: 25 to 30 individuals per population is enough to accurately estimate allele frequencies. PLoS ONE 2012, 7, e45170. [Google Scholar] [CrossRef]
- Keenan, K.; McGinnity, P.; Cross, T.F.; Crozier, W.W.; Prodöhl, P.A. diveRsity: An R package for the estimation and exploration of population genetics parameters and their associated errors. Methods Ecol. Evol. 2013, 4, 782–788. [Google Scholar] [CrossRef]
- Piry, S.; Luikart, G.; Cornuet, J.M. Computer note. BOTTLENECK: A computer program for detecting recent reductions in the effective size using allele frequency data. J. Hered. 1999, 90, 502–503. [Google Scholar] [CrossRef]
- Cornuet, J.M.; Luikart, G. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics 1996, 144, 2001–2014. [Google Scholar] [CrossRef] [PubMed]
- Luikart, G.; Cornuet, J.-M. Empirical evaluation of a test for identifying recently bottlenecked populations from allele frequency data. Conserv. Biol. 1998, 12, 228–237. [Google Scholar] [CrossRef]
- Davy, C.M.; Murphy, R.W. Conservation genetics of the endangered Spotted Turtle (Clemmys guttata) illustrate the risks of “bottleneck tests”. Can. J. Zool. 2014, 92, 149–162. [Google Scholar] [CrossRef]
- Congdon, J.; Nagle, R.; Kinney, O.; van Loben Sels, R. Hypotheses of aging in a long-lived vertebrate, Blanding’s turtle (Emydoidea blandingii). Exp. Gerontol. 2001, 36, 813–827. [Google Scholar] [CrossRef] [PubMed]
- Cosentino, B.J.; Phillips, C.A.; Schooley, R.L. Wetland Occupancy and Landscape Connectivity for Blanding’s and Western Painted Turtles in the Green River Valley; Illinois Natural History Survey: Champaign, IL, USA, 2008. [Google Scholar]
- Frankham, R. Effective population size/adult population size ratios in wildlife: A review. Genet. Res. 1995, 66, 95–107. [Google Scholar] [CrossRef]
- Nomura, T. Estimation of effective number of breeders from molecular coancestry of single cohort sample. Evol. Appl. 2008, 1, 462–474. [Google Scholar] [CrossRef] [PubMed]
- Do, C.; Waples, R.S.; Peel, D.; Macbeth, G.; Tillett, B.J.; Ovenden, J.R. NeEstimator v2: Re-implementation of software for the estimation of contemporary effective population size (Ne) from genetic data. Mol. Ecol. Resour. 2014, 14, 209–214. [Google Scholar] [CrossRef]
- Kuo, C.H.; Janzen, F. bottlesim: A bottleneck simulation program for long-lived species with overlapping generations. Mol. Ecol. Notes 2003, 3, 669–673. [Google Scholar] [CrossRef]
- Jombart, T. adegenet: A R package for the multivariate analysis of genetic markers. Bioinformatics 2008, 24, 1403–1405. [Google Scholar] [CrossRef] [PubMed]
- Cavalli-Sforza, L.L.; Edwards, A.W. Phylogenetic analysis. Models and estimation procedures. Am. J. Hum. Genet. 1967, 19, 233. [Google Scholar] [PubMed]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef]
- Caye, K.; Deist, T.M.; Martins, H.; Michel, O.; François, O. TESS3: Fast inference of spatial population structure and genome scans for selection. Mol. Ecol. Resour. 2016, 16, 540–548. [Google Scholar] [CrossRef]
- François, O.; Durand, E. Spatially explicit Bayesian clustering models in population genetics. Mol. Ecol. Resour. 2010, 10, 773–784. [Google Scholar] [CrossRef]
- Hubisz, M.J.; Falush, D.; Stephens, M.; Pritchard, J.K. Inferring weak population structure with the assistance of sample group information. Mol. Ecol. Resour. 2009, 9, 1322–1332. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.L.; Liu, J.X. StructureSelector: A web-based software to select and visualize the optimal number of clusters using multiple methods. Mol. Ecol. Resour. 2018, 18, 176–177. [Google Scholar] [CrossRef]
- Puechmaille, S.J. The program structure does not reliably recover the correct population structure when sampling is uneven: Subsampling and new estimators alleviate the problem. Mol. Ecol. Resour. 2016, 16, 608–627. [Google Scholar] [CrossRef]
- Jombart, T.; Devillard, S.; Dufour, A.-B.; Pontier, D. Revealing cryptic spatial patterns in genetic variability by a new multivariate method. Heredity 2008, 101, 92–103. [Google Scholar] [CrossRef]
- Moran, P.A. The interpretation of statistical maps. J. R. Stat. Society. Ser. B (Methodol.) 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Jombart, T. A Tutorial for the Spatial Analysis of Principal Components (sPCA) Using Adegenet 2.1.0; Imperial Collger London: London, UK, 2017. [Google Scholar]
- Lipps, G.J. The use of automated GPS dataloggers for locating Blanding’s Turtle nesting sites. Unpublished report to the Ohio Department of Natural Resources, Division of Wildlife, Columbus, OH, USA. 2011. [Google Scholar]
- Thioulouse, J.; Chessel, D.; Champely, S. Multivariate analysis of spatial patterns: A unified approach to local and global structures. Environ. Ecol. Stat. 1995, 2, 1–14. [Google Scholar] [CrossRef]
- Beerli, P. How to use MIGRATE or why are Markov chain Monte Carlo programs difficult to use. Popul. Genet. Anim. Conserv. 2009, 17, 42–79. [Google Scholar]
- Goldstein, D.B.; Ruiz Linares, A.; Cavalli-Sforza, L.L.; Feldman, M.W. Genetic absolute dating based on microsatellites and the origin of modern humans. Proc. Natl. Acad. Sci. USA 1995, 92, 6723–6727. [Google Scholar] [CrossRef] [PubMed]
- Wilson, G.A.; Rannala, B. Bayesian inference of recent migration rates using multilocus genotypes. Genetics 2003, 163, 1177–1191. [Google Scholar] [CrossRef] [PubMed]
- Manoukis, N.C. FORMATOMATIC: A program for converting diploid allelic data between common formats for population genetic analysis. Mol. Ecol. Notes 2007, 7, 592–593. [Google Scholar] [CrossRef]
- Rambaut, A.; Drummond, A.J.; Xie, D.; Baele, G.; Suchard, M.A. Posterior summarization in Bayesian phylogenetics using Tracer 1.7. Syst. Biol. 2018, 67, 901. [Google Scholar] [CrossRef]
- Allendorf, F.W.; Funk, W.C.; Aitken, S.N.; Byrne, M.; Luikart, G.; Antunes, A. Conservation and the Genomics of Populations; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Willoughby, J.R.; Sundaram, M.; Lewis, T.L.; Swanson, B.J. Population decline in a long-lived species: The wood turtle in Michigan. Herpetologica 2013, 69, 186–198. [Google Scholar] [CrossRef]
- Charbonnel, E.; Daguin-Thiébaut, C.; Caradec, L.; Moittié, E.; Gilg, O.; Gavrilo, M.V.; Strøm, H.; Mallory, M.L.; Morrison, R.G.; Gilchrist, H.G. Searching for genetic evidence of demographic decline in an arctic seabird: Beware of overlapping generations. Heredity 2022, 128, 364–376. [Google Scholar] [CrossRef]
- King, R.B.; Golba, C.K.; Glowacki, G.A.; Kuhns, A.R. Blanding’s turtle demography and population viability. J. Fish Wildl. Manag. 2021, 12, 112–138. [Google Scholar] [CrossRef]
- Compton, B.W. Ecology and Conservation of the Wood Turtle (Clemmys Insculpta) in Maine; University of Maine: Orono, ME, USA, 1999. [Google Scholar]
- Jamieson, I.G.; Allendorf, F.W. How does the 50/500 rule apply to MVPs? Trends Ecol. Evol. 2012, 27, 578–584. [Google Scholar] [CrossRef]
- Frankham, R.; Ballou, J.D.; Ralls, K.; Eldridge, M.; Dudash, M.R.; Fenster, C.B.; Lacy, R.C.; Sunnucks, P. A Practical Guide for Genetic Management of Fragmented Animal and Plant Populations; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Wang, J. A comparison of single-sample estimators of effective population sizes from genetic marker data. Mol. Ecol. 2016, 25, 4692–4711. [Google Scholar] [CrossRef]
- Waples, R.S.; Antao, T.; Luikart, G. Effects of overlapping generations on linkage disequilibrium estimates of effective population size. Genetics 2014, 197, 769–780. [Google Scholar] [CrossRef] [PubMed]
- Luikart, G.; Antao, T.; Hand, B.K.; Muhlfeld, C.C.; Boyer, M.C.; Cosart, T.; Trethewey, B.; Al-Chockhachy, R.; Waples, R.S. Detecting population declines via monitoring the effective number of breeders (Nb). Mol. Ecol. Resour. 2021, 21, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, C. Population Genomics of Blandings Turtle on a Regional Scale in the Midwest. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2021. [Google Scholar]
- Frankham, R.; Bradshaw, C.J.; Brook, B.W. Genetics in conservation management: Revised recommendations for the 50/500 rules, Red List criteria and population viability analyses. Biol. Conserv. 2014, 170, 56–63. [Google Scholar] [CrossRef]
- Franklin, I.R. Evolutionary change in small populations. In Conservation Biology—An Evolutionary-Ecological Perspective; Soule, M.E., Wilcox, B.A., Eds.; Sinauer Associates, U.S.A: Sunderland, MA, USA, 1980; pp. 135–149. [Google Scholar]
- Cross, M.D.; Mayer, J.; Breymaier, T.; Chiotti, J.A.; Bekker, K. Estimating Population Size of a Threatened Turtle Using Community and Citizen Science. Chelonian Conserv. Biol. 2021, 20, 43–49. [Google Scholar] [CrossRef]
- Waples, R.S.; Luikart, G.; Faulkner, J.R.; Tallmon, D.A. Simple life-history traits explain key effective population size ratios across diverse taxa. Proc. R. Soc. B Biol. Sci. 2013, 280, 20131339. [Google Scholar] [CrossRef]
- Allendorf, F.W.; Ryman, N. The role of genetics in population viability analysis. In Population Viability Analysis; Beissinger, S.R., McCullough, D.R., Eds.; The University of Chicago Press: Chicago, IL, USA; London, UK, 2002; pp. 50–85. [Google Scholar]
- King, R.B. PVA-based Assessment of Resiliency, Redundancy, and Representation in an Imperiled Freshwater Turtle. Glob. Ecol. Conserv. 2023, 43, e02419. [Google Scholar] [CrossRef]
- Gutzke, W.H.; Packard, G.C. The influence of temperature on eggs and hatchlings of Blanding’s Turtles, Emydoidea blandingii. J. Herpetol. 1987, 21, 161–163. [Google Scholar] [CrossRef]
- Thompson, D.; Glowacki, G.; Ludwig, D.; Reklau, R.; Kuhns, A.R.; Golba, C.K.; King, R. Benefits of Head-starting for Blanding’s Turtle Size Distributions and Recruitment. Wildl. Soc. Bull. 2020, 44, 57–67. [Google Scholar] [CrossRef]
- Golba, C.K.; Glowacki, G.A.; King, R.B. Growth and Survival of Wild and Head-Started Blanding’s Turtles (Emydoidea blandingii). Ichthyol. Herpetol. 2022, 110, 378–387. [Google Scholar] [CrossRef]
- Byer, N.W.; Fountain, E.D.; Reid, B.N.; Miller, K.; Kulzer, P.J.; Peery, M.Z. Land use and life history constrain adaptive genetic variation and reduce the capacity for climate change adaptation in turtles. BMC Genom. 2021, 22, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Whiteley, A.R.; Fitzpatrick, S.W.; Funk, W.C.; Tallmon, D.A. Genetic rescue to the rescue. Trends Ecol. Evol. 2015, 30, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Jensen, E.L.; Edwards, D.L.; Garrick, R.C.; Miller, J.M.; Gibbs, J.P.; Cayot, L.J.; Tapia, W.; Caccone, A.; Russello, M.A. Population genomics through time provides insights into the consequences of decline and rapid demographic recovery through head-starting in a Galapagos giant tortoise. Evol. Appl. 2018, 11, 1811–1821. [Google Scholar] [CrossRef]
- Hedrick, P.W.; Fredrickson, R. Genetic rescue guidelines with examples from Mexican wolves and Florida panthers. Conserv. Genet. 2010, 11, 615–626. [Google Scholar] [CrossRef]
- Dodd, C.K., Jr.; Seigel, R.A. Relocation, repatriation, and translocation of amphibians and reptiles: Are they conservation strategies that work? Herpetologica 1991, 47, 336–350. [Google Scholar]
- Mullin, D.I.; White, R.C.; Lentini, A.M.; Brooks, R.J.; Bériault, K.R.; Litzgus, J.D. Predation and disease limit population recovery following 15 years of headstarting an endangered freshwater turtle. Biol. Conserv. 2020, 245, 108496. [Google Scholar] [CrossRef]
- DeVore, S. Endangered Blanding’s Turtles in Illinois Face New Threat from Fungal Disease. 21 June 2022. Available online: https://www.chicagotribune.com/news/environment/ct-blandings-turtles-illinois-fungus-20220621-cxopkjtkc5gk5e5sk3nmvqhx44-story.html (accessed on 3 April 2023).
- Starking-Szymanski, M.D.; Yoder-Nowak, T.; Rybarczyk, G.; Dawson, H.A. Movement and habitat use of headstarted Blanding’s turtles in Michigan. J. Wildl. Manag. 2018, 82, 1516–1527. [Google Scholar] [CrossRef]
- Frankel, O.H.; Frankel, O.; Soulé, M.E. Conservation and Evolution; Cambridge University Press: London, UK; New York, NY, USA; New Rochelle, NY, USA; Melbourne, Australia; Sydney, Australia, 1981. [Google Scholar]


| Site | State | County | N | A | PA | AR | HO | HE | FIS |
|---|---|---|---|---|---|---|---|---|---|
| IN-01 | IN | Lake | 12 | 70 | 4 | 4.08 (0.66) | 0.59 (0.09) | 0.56 (0.08) | −0.06 (−0.16–0.02) |
| IN-06 | IN | Elkhart | 15 | 75 | 3 | 4.27 (0.52) | 0.63 (0.07) | 0.60 (0.07) | −0.05 (−0.13–0.03) |
| IN-07 | IN | LaGrange | 22 | 92 | 7 | 4.77 (0.39) | 0.64 (0.05) | 0.64 (0.04) | 0.00 (−0.07–0.06) |
| MI-05 | MI | Washtenaw | 20 | 84 | 1 | 4.42 (0.43) | 0.61 (0.05) | 0.61 (0.05) | −0.01 (−0.08–0.05) |
| MI-06 | MI | Livingston | 16 | 86 | 3 | 4.60 (0.47) | 0.65 (0.06) | 0.63 (0.06) | −0.03 (−0.09–−0.02) |
| MI-07 | MI | Livingston | 30 | 97 | 1 | 4.84 (0.29) | 0.64 (0.03) | 0.66 (0.03) | 0.03 (−0.01–0.08) |
| MI-10 | MI | Oakland | 11 | 74 | 0 | 4.40 (0.83) | 0.62 (0.10) | 0.61 (0.10) | −0.01 (−0.11–−0.06) |
| MI-15 | MI | Crawford | 10 | 71 | 1 | 4.32 (0.82) | 0.59 (0.10) | 0.60 (0.09) | 0.03 (−0.08–0.12) |
| OH-01 | OH | Henry | 11 | 81 | 6 | 4.75 (0.71) | 0.58 (0.09) | 0.62 (0.09) | 0.06 (−0.16–0.25) |
| OH-06 | OH | Lucas | 30 | 87 | 1 | 4.44 (0.26) | 0.61 (0.03) | 0.62 (0.03) | 0.03 (−0.02–0.08) |
| OH-08 | OH | Ottawa | 30 | 81 | 2 | 4.22 (0.25) | 0.61 (0.03) | 0.61 (0.03) | −0.01 (−0.07–0.06) |
| OH-09 | OH | Ottawa | 14 | 68 | 0 | 4.06 (0.53) | 0.64 (0.07) | 0.62 (0.06) | −0.04 (−0.14–0.03) |
| OH-13 | OH | Ottawa | 21 | 88 | 0 | 4.58 (0.40) | 0.62 (0.05) | 0.63 (0.05) | 0.01 (−0.07–0.09) |
| OH-16 | OH | Erie | 30 | 79 | 1 | 4.12 (0.21) | 0.63 (0.03) | 0.61 (0.03) | −0.04 (−0.10–0.03) |
| OH-17 | OH | Erie | 29 | 76 | 2 | 4.01 (0.18) | 0.65 (0.03) | 0.62 (0.03) | −0.04 (−0.11–0.02) |
| OH-18 | OH | Williams | 12 | 68 | 2 | 4.07 (0.59) | 0.58 (0.09) | 0.58 (0.09) | −0.00 (−0.11–0.09) |
| BOTTLENECK | Effective Population Size | ||||
|---|---|---|---|---|---|
| Site | Wilcoxon Test | Sign Test | Mode Shift | Ne 0.05 95% CI | Ne 0.02 95% CI |
| IN-1 | p = 0.892 | p = 0.049 | none | 53.3 (15.3–∞) | 97.5 (23.8–∞) |
| IN-6 | p = 0.812 | p = 0.271 | none | 450.0 (33.1–∞) | ∞ (69.0–∞) |
| IN-7 | p = 0.729 | p = 0.473 | none | 323.9 (55.5–∞) | 632.7 (83.4–∞) |
| MI-5 | p = 0.945 | p = 0.069 | none | 71.6 (31.4–∞) | 730.4 (77.3–∞) |
| MI-6 | p = 0.996 | p = 0.002 | none | ∞ (53.5–∞) | ∞ (68.4–∞) |
| MI-7 | p = 0.596 | p = 0.157 | none | ∞ (448.0–∞) | ∞ (242.3–∞) |
| MI-10 | p = 0.607 | p = 0.452 | none | ∞ (44.3–∞) | ∞ (70.9–∞) |
| MI-15 | p = 0.793 | p = 0.224 | none | 1770.8 (27.4–∞) | 1770.8 (27.4–∞) |
| OH-1 | p = 0.996 | p = 0.034 | none | 7.9 (4.4–13.8) | 8.5 (5.6–13.3) |
| OH-6 | p = 0.446 | p = 0.498 | none | ∞ (132.9–∞) | 350.4 (84.6–∞) |
| OH-8 | p = 0.607 | p = 0.477 | none | 195.5 (68.1–∞) | 262.4 (80.3–∞) |
| OH-9 | p = 0.040 | p = 0.339 | none | 106.2 (25.0–∞) | ∞ (41.6–∞) |
| OH-13 | p = 0.473 | p = 0.521 | none | 54.2 (27.9–270.7) | 202.8 (59.0–∞) |
| OH-16 | p = 0.905 | p = 0.042 | none | 14.6 (11.1–19.8) | 22.1 (16.8–30.5) |
| OH-17 | p = 0.729 | p = 0.259 | none | 10.9 (8.4–14.1) | 14.0 (10.9–18.4) |
| OH-18 | p = 0.661 | p = 0.156 | none | 42.1 (14.5–∞) | 50.1 (18.2–∞) |
| Site | N | Ne 0.05 (95% CI) | Ne 0.02 95% CI |
|---|---|---|---|
| OH-8 | 10 | 772.0 (22.7–∞) | 772.0 (22.7–∞) |
| OH-8 | 30 | 195.5 (68.1–∞) | 262.4 (80.3–∞) |
| OH-8 | 77 | 137.1 (87.5–271.8) | 189.1 (121.4–380.9) |
| Location | Pairwise FST | AR | HE | Localities | Loci | N | Reference |
|---|---|---|---|---|---|---|---|
| Nova Scotia | 0.04–0.12 | - | 0.45–0.54 | 3 | 5 | 110 | Mockford et al. (2005) [26] |
| Rangewide | 0.00–0.47 | - | 0.45–0.71 | 12 | 5 | 200 | Mockford et al. (2007) [10] |
| NE, IA, MN, IL | 0.01–0.47 | - | 0.49–0.79 | 12 | 8 | 202 | Sethuraman et al. (2014) [28] |
| Ontario | 0.04–0.10 | 4.8–5.3 | 0.59–0.66 | 12 | 4 | 97 | Davy et al. (2014) [27] |
| NY and southeast Ontario | 0.01–0.38 | 0.31–0.63 | 5 | 7 | 115 | McCluskey et al. (2016) [29] | |
| WI | 0.00–0.18 | 0.59–0.70 | 18 | 14 | 389 | Reid et al. (2017) [37] | |
| northeast IL | 0.02–0.10 | 3.6–3.9 | 0.51–0.64 * | 6 | 14 | 186 | Anthonysamy et al. (2018) [30] |
| IN, OH, MI | 0.00–0.15 | 4.01–4.84 | 0.56–0.66 | 16 | 14 | 313 | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guinto, D.; Cross, M.; Lipps, G., Jr.; Lee, Y.; Kingsbury, B.; Earl, D.; Dempsey, C.; Hinson, J.; Jordan, M. Conservation Genetic Analysis of Blanding’s Turtles across Ohio, Indiana, and Michigan. Diversity 2023, 15, 668. https://doi.org/10.3390/d15050668
Guinto D, Cross M, Lipps G Jr., Lee Y, Kingsbury B, Earl D, Dempsey C, Hinson J, Jordan M. Conservation Genetic Analysis of Blanding’s Turtles across Ohio, Indiana, and Michigan. Diversity. 2023; 15(5):668. https://doi.org/10.3390/d15050668
Chicago/Turabian StyleGuinto, Daniel, Matthew Cross, Gregory Lipps, Jr., Yuman Lee, Bruce Kingsbury, Daniel Earl, Connor Dempsey, Jessica Hinson, and Mark Jordan. 2023. "Conservation Genetic Analysis of Blanding’s Turtles across Ohio, Indiana, and Michigan" Diversity 15, no. 5: 668. https://doi.org/10.3390/d15050668
APA StyleGuinto, D., Cross, M., Lipps, G., Jr., Lee, Y., Kingsbury, B., Earl, D., Dempsey, C., Hinson, J., & Jordan, M. (2023). Conservation Genetic Analysis of Blanding’s Turtles across Ohio, Indiana, and Michigan. Diversity, 15(5), 668. https://doi.org/10.3390/d15050668







