Decoupled Six-Axis Force–Moment Sensor with a Novel Strain Gauge Arrangement and Error Reduction Techniques
Abstract
:1. Introduction
2. Structural Design and Strain Gauge Arrangement
2.1. Structural Design
2.2. Strain Gauge Arrangement
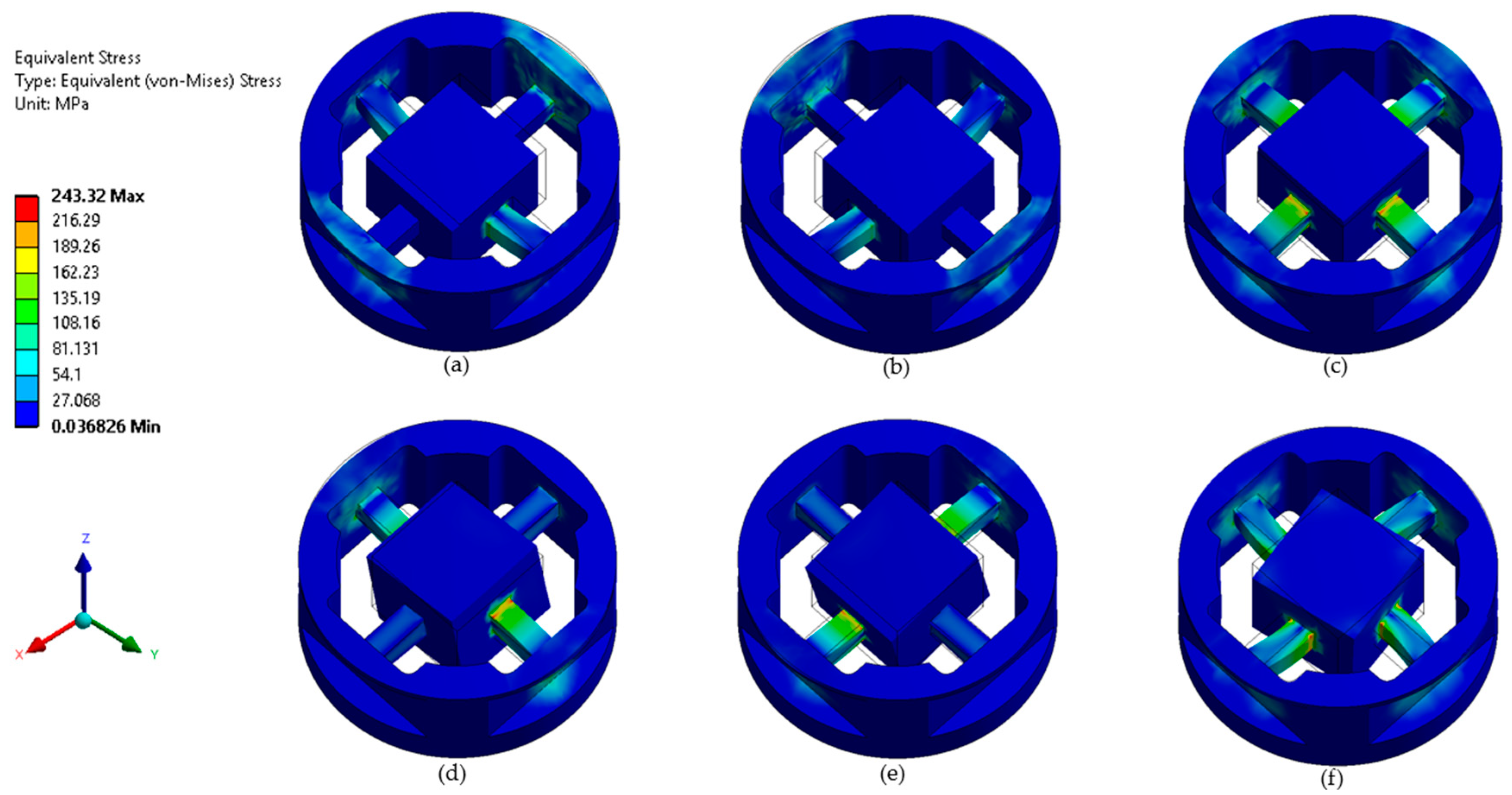
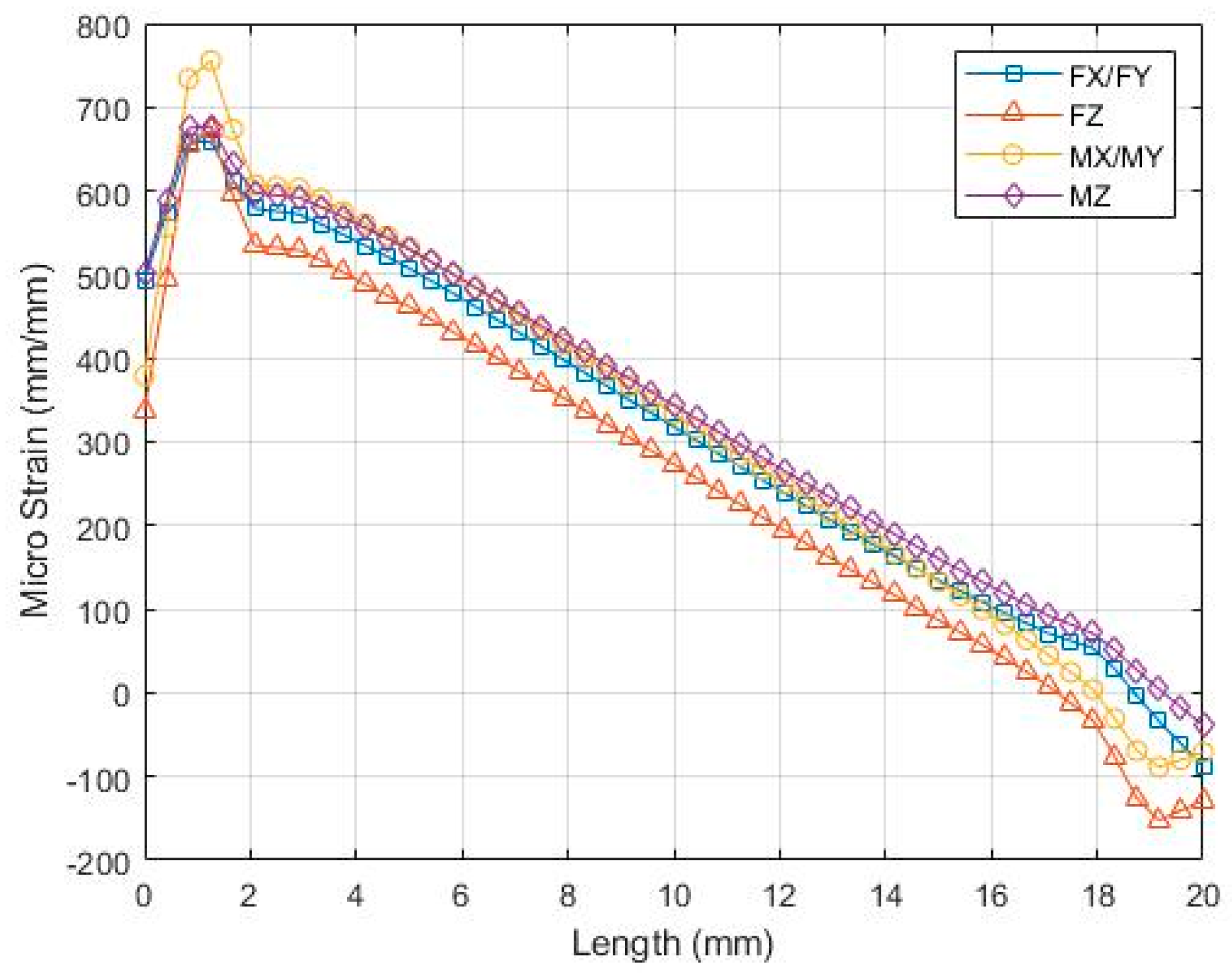
2.3. Finite Element Analysis
2.4. Measurement Principle
3. Sensor Calibration
3.1. Decoupling Matrix
3.2. Calibration Setup
- The zero point of the output signal of six filtered channels is adjusted using the error reduction technique.
- Pure forces and moments are applied to the mounted six-axis F/M sensor on the calibration jig through hanging weights with a 2.5 kg increment from +10 kg to −10 kg.
- The output voltage signal response is measured and counted for each data point corresponding to the applied load of the six-channel force sensor, and each axis of the measured force and moment is generated.
- The load is applied for 100 s, and the output voltages in each component are collected by taking the calculated average value.
- After completing the applied load, the decoupling matrix [D] is obtained using the pseudoinverse method. The output signals of the sensor and decoupling matrix are used to calculate the measured forces and moments.
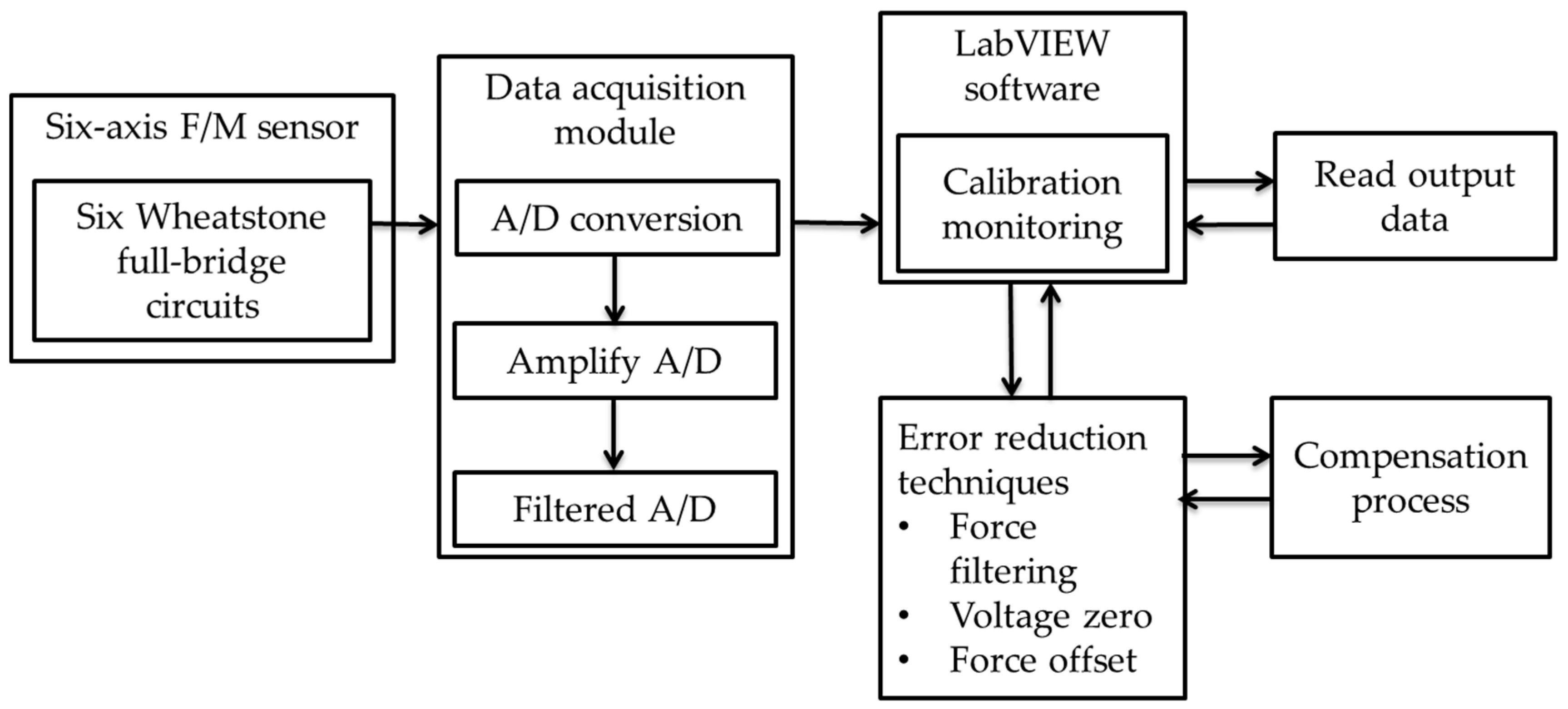
4. Error Reduction Techniques
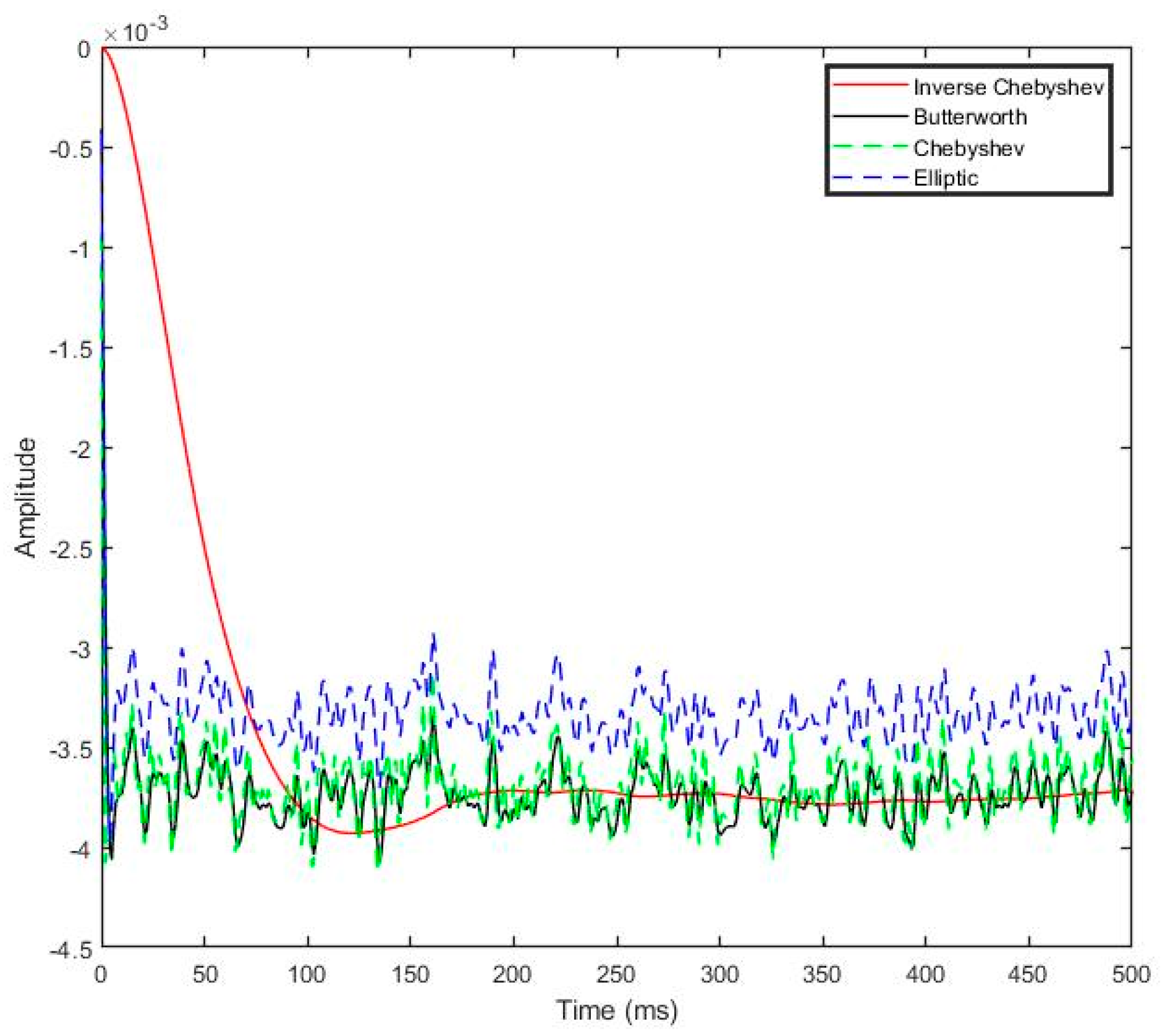
4.1. Force Filtering
4.2. Moving Average Filter
4.2.1. Voltage Zero
4.2.2. Force Offset
4.3. Error Reduction Techniques Process
4.3.1. Calibration Process
- First step: the signals from the F/M sensors should be filtered using “force filtering” techniques.
- Second step: after installing F/M into the calibration jig, before loading, “voltage zero” technique should be used to set six readings to zeros.
4.3.2. Measurement Process
- First step: to get the filtered output signal from F/M sensors using “force filtering” techniques.
- Second step: after installing F/M into the end effector and installing the tool on it, before the start of robot applications, the “force offset” process should be conducted to set six undesirably existing readings to zero.
5. Experimental Results and Discussion
5.1. Software Configuration
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kang, M.-K.; Lee, S.; Kim, J.-H. Shape optimization of a mechanically decoupled six-axis force/torque sensor. Sens. Actuators Phys. 2014, 209, 41–51. [Google Scholar] [CrossRef]
- Park, J.-J.; Kim, G.-S. Development of the 6-axis force/moment sensor for an intelligent robot’s gripper. Sens. Actuators Phys. 2005, 118, 127–134. [Google Scholar] [CrossRef]
- Song, A.; Wu, J.; Qin, G.; Huang, W. A novel self-decoupled four degree-of-freedom wrist force/torque sensor. Measurement 2007, 40, 883–891. [Google Scholar] [CrossRef]
- Joo, J.; Na, K.; Kang, D. Design and evaluation of a six-component load cell. Measurement 2002, 32, 125–133. [Google Scholar] [CrossRef]
- Krouglicof, N.; Alonso, L.M.; Keat, W.D. Development of a mechanically coupled, six degree-of-freedom load platform for biomechanics and sports medicine. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics, Hague, The Netherlands, 10–13 October 2004; pp. 4426–4431. [Google Scholar]
- Bicchi, A. A criterion for optimal design of multi-axis force sensors. Robot. Auton. Syst. 1992, 10, 269–286. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Song, A. A novel three degree-of-freedom force sensor. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation: ICMTMA’09, Zhangjiajie, China, 11–12 April 2009; pp. 77–80. [Google Scholar]
- Weiyi, H.; Hongming, J.; Hanqing, Z. Mechanical analysis of a novel six-degree-of-freedom wrist force sensor. Sens. Actuators Phys. 1993, 35, 203–208. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiao, L.; Weng, D.; Zhang, D.; Zheng, R. Decoupling principle analysis and development of a parallel three-dimensional force sensor. Sensors 2016, 16, 1506. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.-S. Design of a six-axis wrist force/moment sensor using FEM and its fabrication for an intelligent robot. Sens. Actuators Phys. 2007, 133, 27–34. [Google Scholar] [CrossRef]
- Liu, S.A.; Tzo, H.L. A novel six-component force sensor of good measurement isotropy and sensitivities. Sens. Actuators Phys. 2002, 100, 223–230. [Google Scholar] [CrossRef]
- Zhang, W.; Lua, K.B.; Senthil, K.A.; Lim, T.T.; Yeo, K.S.; Zhou, G. Design and characterization of a novel T-shaped multi-axis piezoresistive force/moment sensor. IEEE Sens. J. 2016, 16, 4198–4210. [Google Scholar] [CrossRef]
- Kang, C. Performance improvement of a 6-axis force-torque sensor via novel electronics and cross-shaped double-hole structure. Int. J. Control Autom. Syst. 2005, 3, 469. [Google Scholar]
- Kang, C.-G. Maximum structural error propagation of multi-axis force sensors. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2001, 44, 676–681. [Google Scholar] [CrossRef]
- Beyeler, F.; Muntwyler, S.; Nelson, B.J. Design and calibration of a microfabricated 6-axis force-torque sensor for microrobotic applications. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation: ICRA’09, Kobe, Japan, 12–17 May 2009; pp. 520–525. [Google Scholar]
- Kim, K.; Sun, Y.; Voyles, R.M.; Nelson, B.J. Calibration of multi-axis MEMS force sensors using the shape-from-motion method. IEEE Sens. J. 2007, 7, 344–351. [Google Scholar] [CrossRef]
- Oddo, C.; Valdastri, P.; Beccai, L.; Roccella, S.; Carrozza, M.; Dario, P. Investigation on calibration methods for multi-axis, linear and redundant force sensors. Meas. Sci. Technol. 2007, 18, 623. [Google Scholar] [CrossRef]
- Voyles, R.M.; Morrow, J.D.; Khosla, P.K. The shape from motion approach to rapid and precise force/torque sensor calibration. J. Dyn. Syst. Meas. Control 1997, 119, 229–235. [Google Scholar] [CrossRef]
- Liang, Q.; Wu, W.; Coppola, G.; Zhang, D.; Sun, W.; Ge, Y.; Wang, Y. Calibration and decoupling of multi-axis robotic Force/Moment sensors. Robot. Comput. Integr. Manuf. 2018, 49, 301–308. [Google Scholar] [CrossRef]
- Shimano, B.; Roth, B. On force sensing information and its use in controlling manipulators. IFAC Proc. Vol. 1977, 10, 119–126. [Google Scholar] [CrossRef]
- Sedra, A.S.; Smith, K.C. Microelectronic Circuits; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Chen, D.; Song, A.; Li, A. Design and calibration of a six-axis force/torque sensor with large measurement range used for the space manipulator. Procedia Eng. 2015, 99, 1164–1170. [Google Scholar] [CrossRef]



| Crosstalk Reading (%) | Axis of Reading | ||||||
|---|---|---|---|---|---|---|---|
| Fx | Fy | Fz | Mx | My | Mz | ||
| Applied load | Fx | - | 0% | 0% | 1% | −10% | 0% |
| Fy | −1% | - | 0% | 11% | 1% | 0% | |
| Fz | 0% | 0% | - | −1% | 0% | -6% | |
| Mx | 0% | 7% | 0% | - | 0% | 0% | |
| My | −8% | 2% | 1% | 0% | - | 0% | |
| Mz | 0% | 0% | −1% | −1% | 0% | - | |
| Input Signal Components | Impulse Signals Response Range (V) | Filtered Output Signal (V) | |
|---|---|---|---|
| Fx | upper | −0.0037 | −0.00445 |
| lower | −0.0052 | ||
| Fy | upper | 0.00125 | 0.00028 |
| lower | −0.0007 | ||
| Fz | upper | −0.0086 | −0.00935 |
| lower | −0.0101 | ||
| Mx | upper | 0.00075 | −0.00058 |
| lower | −0.0019 | ||
| My | upper | 0 | −0.00095 |
| lower | −0.0019 | ||
| Mz | upper | 0.0028 | 0.00175 |
| lower | 0.0007 | ||
| Sensor Components | LS Best Fit Value (V/V) | Experimental Value (V/V) | Error (%) |
|---|---|---|---|
| Fx = 98.1 N | 0.077 | 0.075 | 2.40 |
| Fy = 98.1 N | 0.089 | 0.090 | 0.80 |
| Fz = 98.1 N | 0.055 | 0.056 | 1.00 |
| Mx = 13.322 Nm | 0.336 | 0.323 | 3.91 |
| My = 13.322 Nm | 0.433 | 0.432 | 0.28 |
| Mz = 9.81 Nm | 0.153 | 0.154 | 0.45 |
| Sensor Components | LS Best Fit Value (V/V) | Experimental Value (V/V) | Error (%) |
|---|---|---|---|
| Fx = −98.1 N | −0.077 | −0.079 | −3.10 |
| Fy = −98.1 N | −0.094 | −0.093 | −0.55 |
| Fz = −98.1 N | −0.060 | −0.060 | −0.19 |
| Mx = −13.322 Nm | −0.340 | −0.343 | −0.84 |
| My = −13.322 Nm | −0.421 | −0.413 | −1.95 |
| Mz = −9.81 Nm | −0.151 | −0.147 | −2.71 |
| F/M Measurement Error and Crosstalk Reading (%) | Axis of Reading | ||||||
|---|---|---|---|---|---|---|---|
| Fx | Fy | Fz | Mx | My | Mz | ||
| Applied load | Fx | 0.61 | 0.53 | 1.01 | 0.57 | 0.33 | 1.03 |
| Fy | 0.77 | 0.37 | 0.81 | 0.45 | 0.32 | 1.44 | |
| Fz | 1.77 | 1.78 | 0.58 | 3.36 | 0.40 | 3.31 | |
| Mx | 1.71 | 0.98 | 1.86 | 1.78 | 0.31 | 4.78 | |
| My | 1.17 | 1.47 | 1.39 | 0.79 | 1.74 | 3.48 | |
| Mz | 1.23 | 1.24 | 1.28 | 0.68 | 0.12 | 1.45 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kebede, G.A.; Ahmad, A.R.; Lee, S.-C.; Lin, C.-Y. Decoupled Six-Axis Force–Moment Sensor with a Novel Strain Gauge Arrangement and Error Reduction Techniques. Sensors 2019, 19, 3012. https://doi.org/10.3390/s19133012
Kebede GA, Ahmad AR, Lee S-C, Lin C-Y. Decoupled Six-Axis Force–Moment Sensor with a Novel Strain Gauge Arrangement and Error Reduction Techniques. Sensors. 2019; 19(13):3012. https://doi.org/10.3390/s19133012
Chicago/Turabian StyleKebede, Getnet Ayele, Anton Royanto Ahmad, Shao-Chun Lee, and Chyi-Yeu Lin. 2019. "Decoupled Six-Axis Force–Moment Sensor with a Novel Strain Gauge Arrangement and Error Reduction Techniques" Sensors 19, no. 13: 3012. https://doi.org/10.3390/s19133012
APA StyleKebede, G. A., Ahmad, A. R., Lee, S.-C., & Lin, C.-Y. (2019). Decoupled Six-Axis Force–Moment Sensor with a Novel Strain Gauge Arrangement and Error Reduction Techniques. Sensors, 19(13), 3012. https://doi.org/10.3390/s19133012






