A SAFT Method for the Detection of Void Defect inside a Ballastless Track Structure Using Ultrasonic Array Sensors
Abstract
:1. Introduction
2. Ballastless Track Structure Multilayer Synthetic Aperture Focusing Technique Method
2.1. SAFT Imaging Method
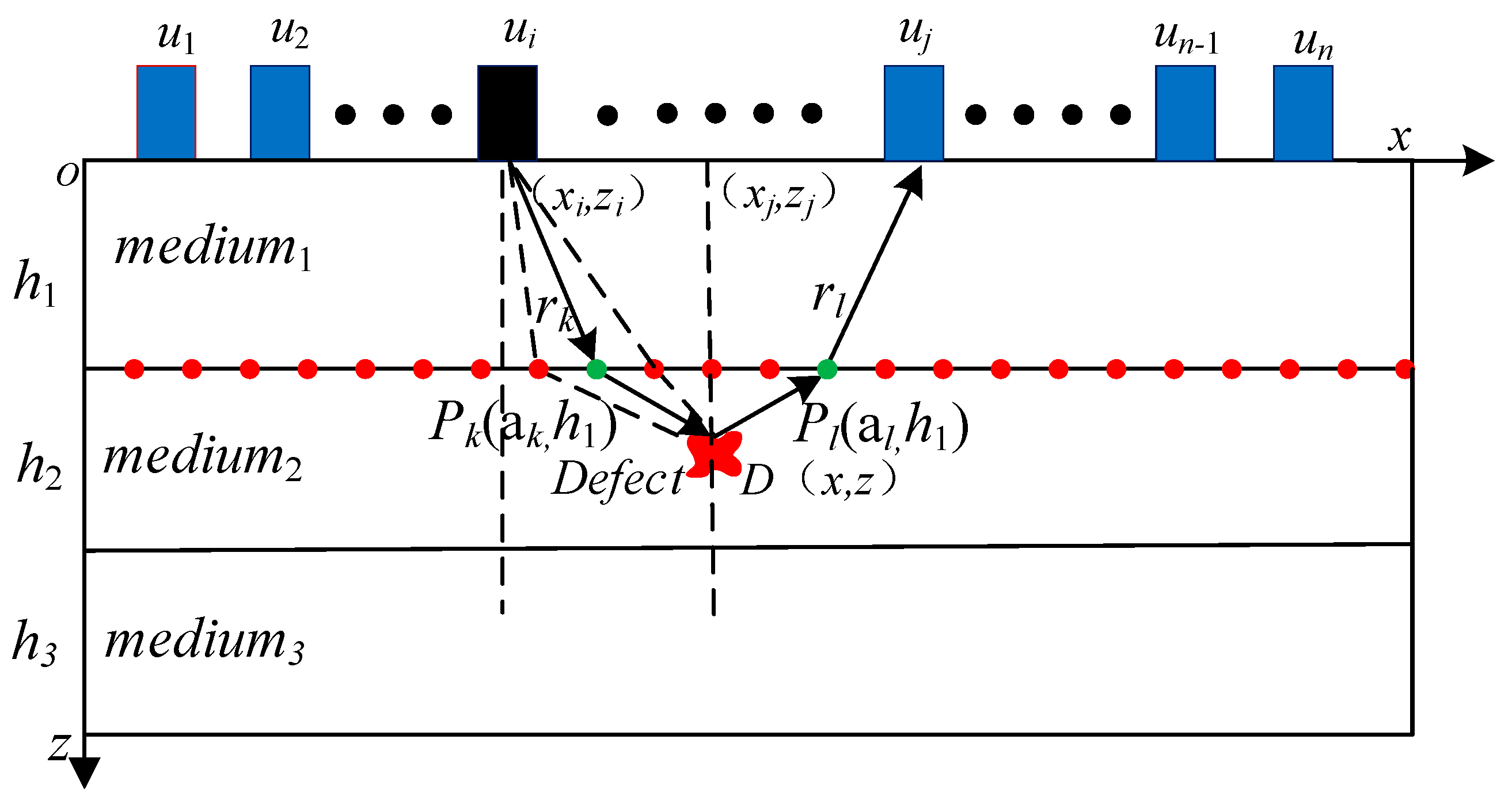
2.2. Multilayer SAFT Imaging Method Based on Ray Tracing Technique
3. Finite Element Simulation
3.1. Finite Element Model
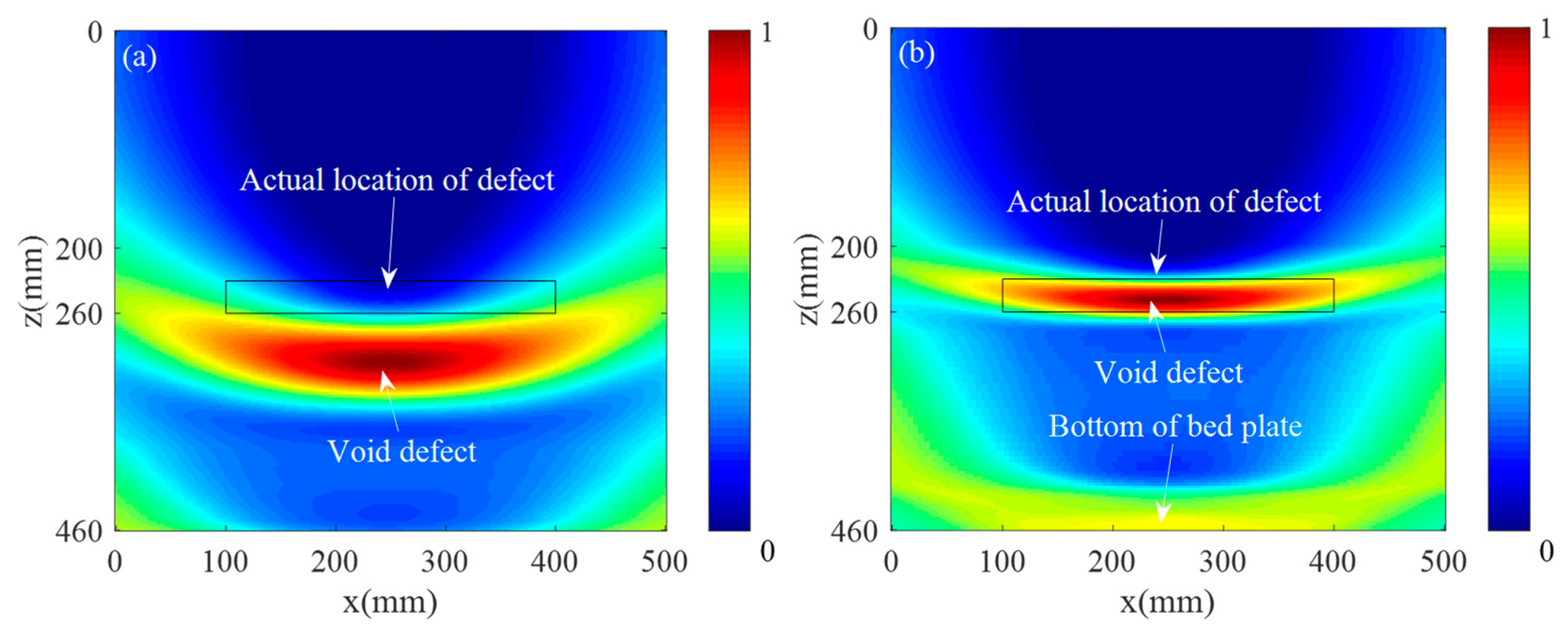
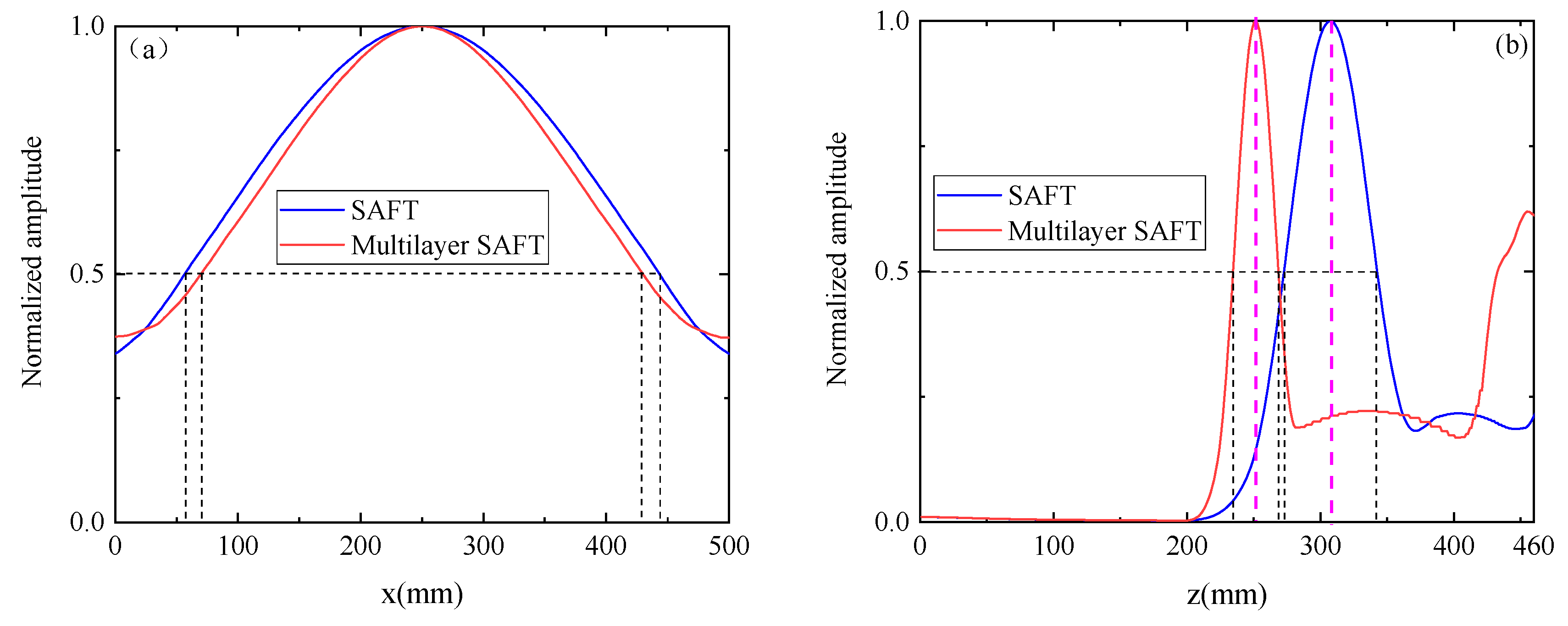
3.2. Analysis of Finite Element Simulation Results
4. Experimental Verification
4.1. Experimental System
4.2. Method of Suppressing Surface Wave
4.3. Analysis of Experimental Results
5. Conclusions
- (1)
- Based on the shortest path principle of Fermat, the function of the position of the refraction point and the propagation path of the forward tracking ultrasonic wave were obtained. Thereby, the tracking of the propagation path of the acoustic wave in the ballastless track structure was realized, and the propagation delay of the ultrasonic wave in the ballastless track structure could be accurately calculated.
- (2)
- A two-dimensional finite element model of ultrasonic wave propagation in a ballastless track structure was established. The ultrasonic signal matrix was captured in the finite element model. The acquired signal was ultrasonically imaged by conventional SAFT imaging and the multilayer SAFT imaging method, separately. Compared with traditional SAFT imaging, this method improved the length characterization accuracy by 32.9%, the height characterization accuracy by 93.2%, and the positioning accuracy in the z-direction center position by 93.2%.
- (3)
- A model of a ballastless track structure with a 1:1 ratio was constructed in the laboratory. Ultrasonic echo signals were acquired by a MIRA-A1040 concrete ultrasonic tomography scanner. The data were exported and processed in MATLAB software. The experimental results showed that, according to the characteristics of the time domain of the experimental signal, selecting a reasonable window function can effectively remove the influence of surface waves. The Multilayer SAFT imaging method provided better accuracy determination in the two directions (the length and height) of the void defect. These results were significantly improved compared with those achieved by the traditional SAFT algorithm. The length characterization accuracy was improved by 27%, the height characterization accuracy was improved by 62.6%, and the positioning accuracy in the z-direction center position was improved by 90.8%.
Author Contributions
Funding
Conflicts of Interest
References
- Tang, J.L. China Railway (CR): Chinese High-Speed Rail Operating Mileage Reached More Than 29,000 Kilometers [EB/OL]. 2019. Available online: http://news.china.com.cn/txt/2019-01/02/content_74333468.htm (accessed on 2 January 2019).
- Zhao, G.T. Research and application of general constructions technologies for high-speed railway in China. J. China Railw. Soc. 2019, 41, 87–98. [Google Scholar]
- Fan, G.P.; Zhang, H.Y.; Zhu, W.F.; Zhang, H.; Chai, X.D. Numerical and experimental research on identifying a delamination in ballastless slab track. Materials 2019, 12, 1788. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.M.; Wang, P.; An, B.Y. Damage detection of ballastless railway tracks by the impact-echo method. Proc. Inst. Civ. Eng. Transp. 2018, 171, 106–114. [Google Scholar] [CrossRef]
- Cosmes-Lopez, M.F.; Castellanos, F.; Cano-Barrita, P.F.D. Ultrasound frequency analysis for identification of aggregates and cement paste in concrete. Ultrasonics 2017, 73, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Chen, H.B.; Song, X. Numerical study on the mechanism of active interfacial debonding detection for rectangular CFSTs based on wavelet packet analysis with piezoceramics. Mech. Syst. Signal Process. 2017, 86, 108–121. [Google Scholar] [CrossRef]
- Luo, M.Z.; Li, W.J.; Hei, C. Concrete infill monitoring in concrete-filled FRP tubes using a PZT-based ultrasonic time-of-flight method. Sensors 2016, 16, 2083. [Google Scholar] [CrossRef]
- Xu, B.; Li, B.; Song, G.B. Active debonding detection for large rectangular CFSTs based on wavelet packet energy spectrum with piezoceramics. J. Struct. Eng. 2013, 139, 1435–1443. [Google Scholar] [CrossRef]
- Zhu, W.; Xiang, Y.; Liu, C.J.; Deng, M.; Xuan, F.Z. A feasibility study on fatigue damage evaluation using nonlinear Lamb waves with group-velocity mismatching. Ultrasonics 2018, 90, 18–22. [Google Scholar] [CrossRef]
- Zhu, W.F.; Zhang, H.Y.; Liu, F.J. Lamb waves topological imaging of multiple blind defects in an isotropic plate. Int. J. Acoust. Vib. 2019, 24, 320–326. [Google Scholar] [CrossRef]
- Liu, H.; Xia, H.Y.; Zhuang, M.W. Reverse time migration of acoustic waves for imaging based defects detection for concrete and CFST structures. Mech. Syst. Signal Process. 2019, 117, 210–220. [Google Scholar] [CrossRef]
- Freeseman, K.; Khazanovich, L.; Hoegh, K. Nondestructive monitoring of subsurface damage progression in concrete columns damaged by earthquake loading. Eng. Struct. 2016, 114, 148–157. [Google Scholar] [CrossRef] [Green Version]
- Khazanovich, L.; Hoegh, K. Quantitative ultrasonic evaluation of concrete structures using one-sided access. In American Institute of Physics Conference Series; AIP Publishing LLC: Melville, NY, USA, 2016. [Google Scholar]
- White, J.; Hurlebaus, S.; Shokouhi, P.; Wimsatt, A. Use of ultrasonic tomography to detect structural impairment in tunnel linings. Transp. Res. Rec. 2014, 2407, 20–31. [Google Scholar] [CrossRef]
- Sherwin, C.W.; Ruina, J.P.; Rawcliffe, R.D. Some early developments in synthetic aperture radar systems. Mil. Electron. IRE Trans. 1962, 2, 111–115. [Google Scholar] [CrossRef]
- Frederick, J.R.; Vanden Broek, C.; Ganapathy, S.; Elzinga, M.B.; de Vries, W.; Papworth, D.; Hamano, N. Improved Ultrasonic Nondestructive Testing of Pressure Vessels; Michigan University: Ann Arbor, MI, USA, 1979. [Google Scholar]
- Sternini, S.; Liang, A.Y.; Di, S. Rail defect imaging by improved ultrasonic synthetic aperture focus techniques. Mater. Eval. 2019, 7, 931–940. [Google Scholar]
- Wu, H.T.; Chen, J.; Yang, K.J. Ultrasonic array imaging of multilayer structures using full matrix capture and extended phase shift migration. Meas. Sci. Technol. 2016, 27, 045401. [Google Scholar] [CrossRef]
- Lin, S.B.; Shams, S.; Choi, H.J. Ultrasonic imaging of multi-layer concrete structures. NDT E Int. 2018, 9, 101–109. [Google Scholar] [CrossRef]
- He, Y.L.; Shen, J.K.; Li, Z.W. Fractal characteristics of transverse crack propagation on CRTSII type track slab. Math. Probl. Eng. 2019, 2019, 6587343. [Google Scholar] [CrossRef]
- Wu, S.W.; Skjelvareid, M.H.; Yang, K.; Chen, J. Synthetic aperture imaging for multilayer cylindrical object using an exterior rotating transducer. Rev. Sci. Instrum. 2015, 86, 083703. [Google Scholar] [CrossRef]
- Zheng, S.B.; Zhong, Q.W.; Chai, X.D. A novel prediction model for car body vibration acceleration based on correlation analysis and neural networks. J. Adv. Transp. 2018, 2018, 1752070. [Google Scholar] [CrossRef]
- Zhu, W.J.; Deng, M.X.; Xiang, Y.X.; Xuan, F.Z.; Liu, C.J.; Wang, Y.N. Modeling of ultrasonic nonlinearities for dislocation evolution in plastically deformed materials: Simulation and experimental validation. Ultrasonics 2016, 68, 134–141. [Google Scholar] [CrossRef]
- Skjelvareid, M.H.; Birkelund, Y.; Larsen, Y. Internal pipeline inspection using virtual source synthetic aperture ultrasound imaging. NDT E Int. 2013, 54, 151–158. [Google Scholar] [CrossRef]
- Fredrik, L.; Tomas, O.; Tadeusz, S. Synthetic aperture imaging using sources with finite aperture: Deconvolution of the spatial impulse response. J. Acoust. Soc. Am. 2003, 114, 225–234. [Google Scholar]
- Skjelvareid, M.H.; Olofsson, T.; Birkelund, Y. Synthetic aperture focusing of ultrasonic data from multilayered media using an omega-k algorithm. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1037–1048. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.A.; Barna, B.A. The effects of surface mapping corrections with synthetic-aperture focusing techniques on ultrasonic-imaging. IEEE Trans. Sonics Ultrason. 1983, 30, 283–294. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.Y.; Zhang, J.Y.; Liu, J.Q.; Zhu, W.F.; Fan, G.P.; Zhu, Q. Wavenumber imaging of near-surface defects in rails using green’s function reconstruction of ultrasonic diffuse fields. Sensors 2019, 19, 3744. [Google Scholar] [CrossRef]


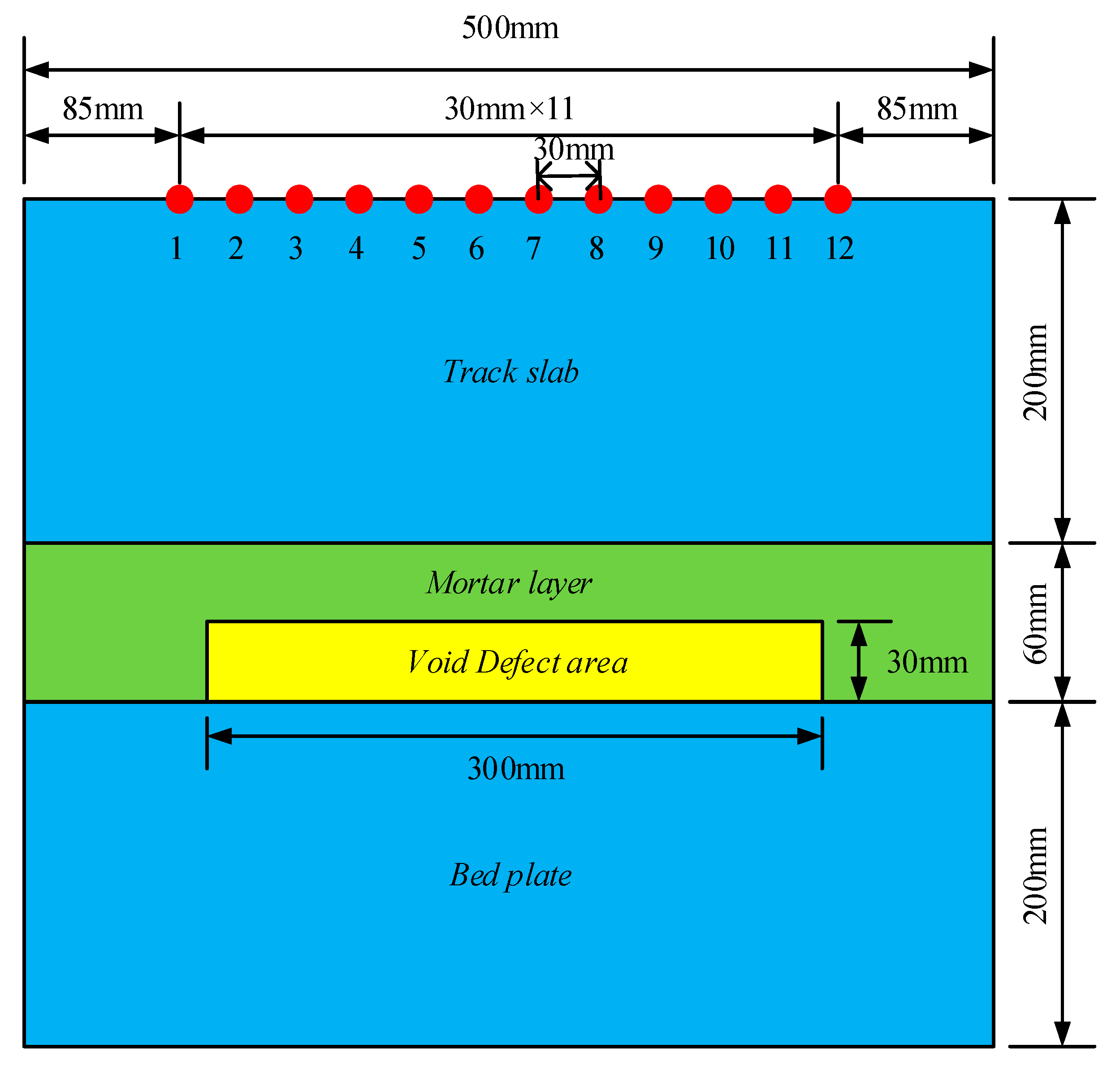











| Property | Track Slab | Mortar Layer | Bed Plate | Void Area |
|---|---|---|---|---|
| Density (kg/m3) | 2500 | 1800 | 2500 | 1.29 (air density) |
| Width (mm) | 500 | 500 | 500 | 300 |
| Thick (mm) | 200 | 60 | 200 | 30 |
| Shear wave velocity (m/s) | 2466 | 1521 | 2466 | 0 |
| Model Size | 500 × 460 mm |
|---|---|
| Transducer spacing | 30 mm |
| Exciting frequency | 50 kHz |
| Grid size | 0.425 × 0.425 mm |
| Sampling frequency | 10 MHz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.-F.; Chen, X.-J.; Li, Z.-W.; Meng, X.-Z.; Fan, G.-P.; Shao, W.; Zhang, H.-Y. A SAFT Method for the Detection of Void Defect inside a Ballastless Track Structure Using Ultrasonic Array Sensors. Sensors 2019, 19, 4677. https://doi.org/10.3390/s19214677
Zhu W-F, Chen X-J, Li Z-W, Meng X-Z, Fan G-P, Shao W, Zhang H-Y. A SAFT Method for the Detection of Void Defect inside a Ballastless Track Structure Using Ultrasonic Array Sensors. Sensors. 2019; 19(21):4677. https://doi.org/10.3390/s19214677
Chicago/Turabian StyleZhu, Wen-Fa, Xing-Jie Chen, Zai-Wei Li, Xiang-Zhen Meng, Guo-Peng Fan, Wei Shao, and Hai-Yan Zhang. 2019. "A SAFT Method for the Detection of Void Defect inside a Ballastless Track Structure Using Ultrasonic Array Sensors" Sensors 19, no. 21: 4677. https://doi.org/10.3390/s19214677
APA StyleZhu, W.-F., Chen, X.-J., Li, Z.-W., Meng, X.-Z., Fan, G.-P., Shao, W., & Zhang, H.-Y. (2019). A SAFT Method for the Detection of Void Defect inside a Ballastless Track Structure Using Ultrasonic Array Sensors. Sensors, 19(21), 4677. https://doi.org/10.3390/s19214677





