Mono-Component Feature Extraction for Condition Assessment in Civil Structures Using Empirical Wavelet Transform
Abstract
1. Introduction
2. Empirical Wavelet Transform
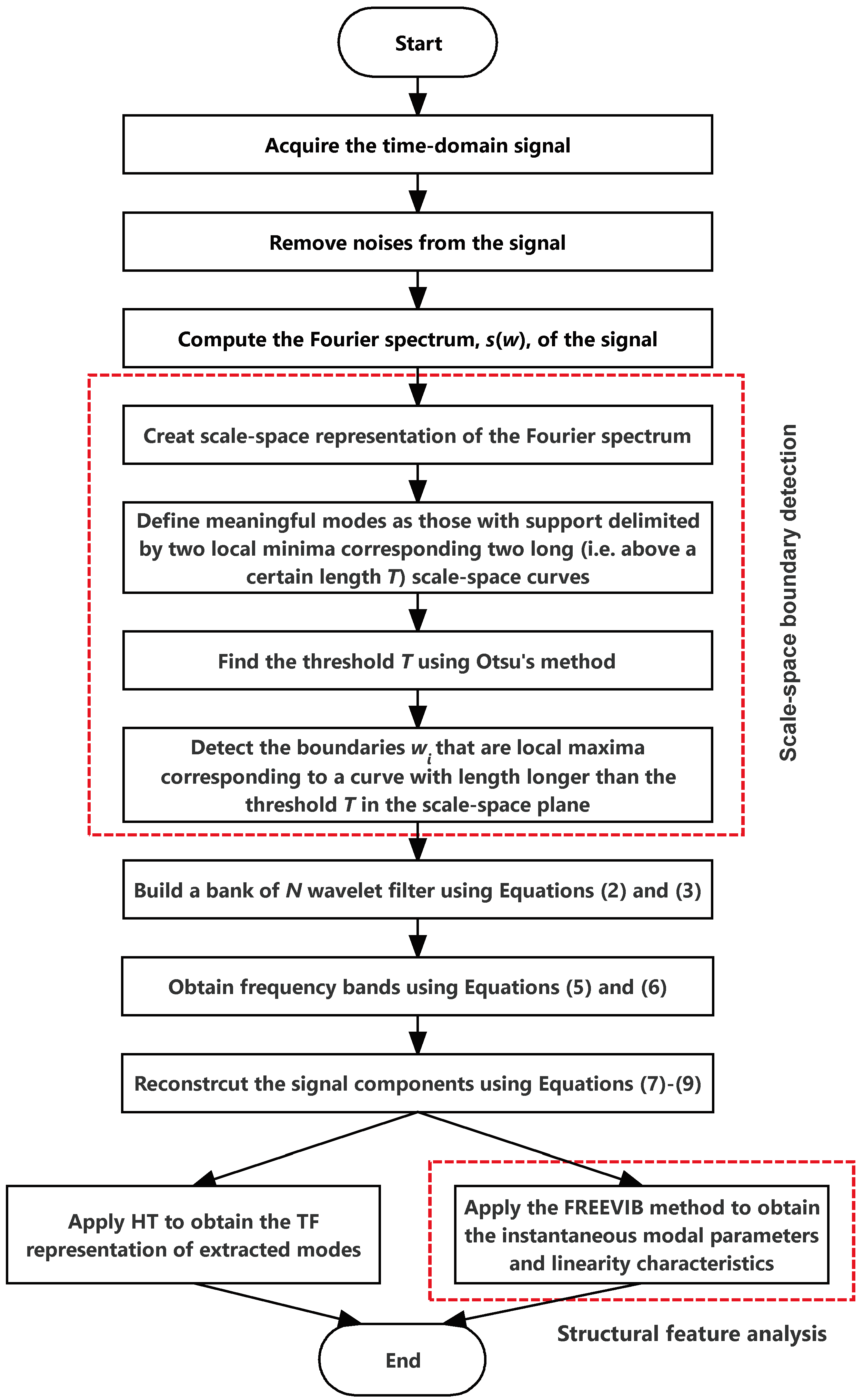
3. Methodology
3.1. Scale-Space Boundary Detection
3.1.1. Scale-Space Representation of a Spectrum
3.1.2. Definition of Meaningful Modes
3.1.3. Determination of Threshold
3.2. Time-Frequency Representation of Extracted Modes
3.3. Structural Feature Analysis using Mono-Component
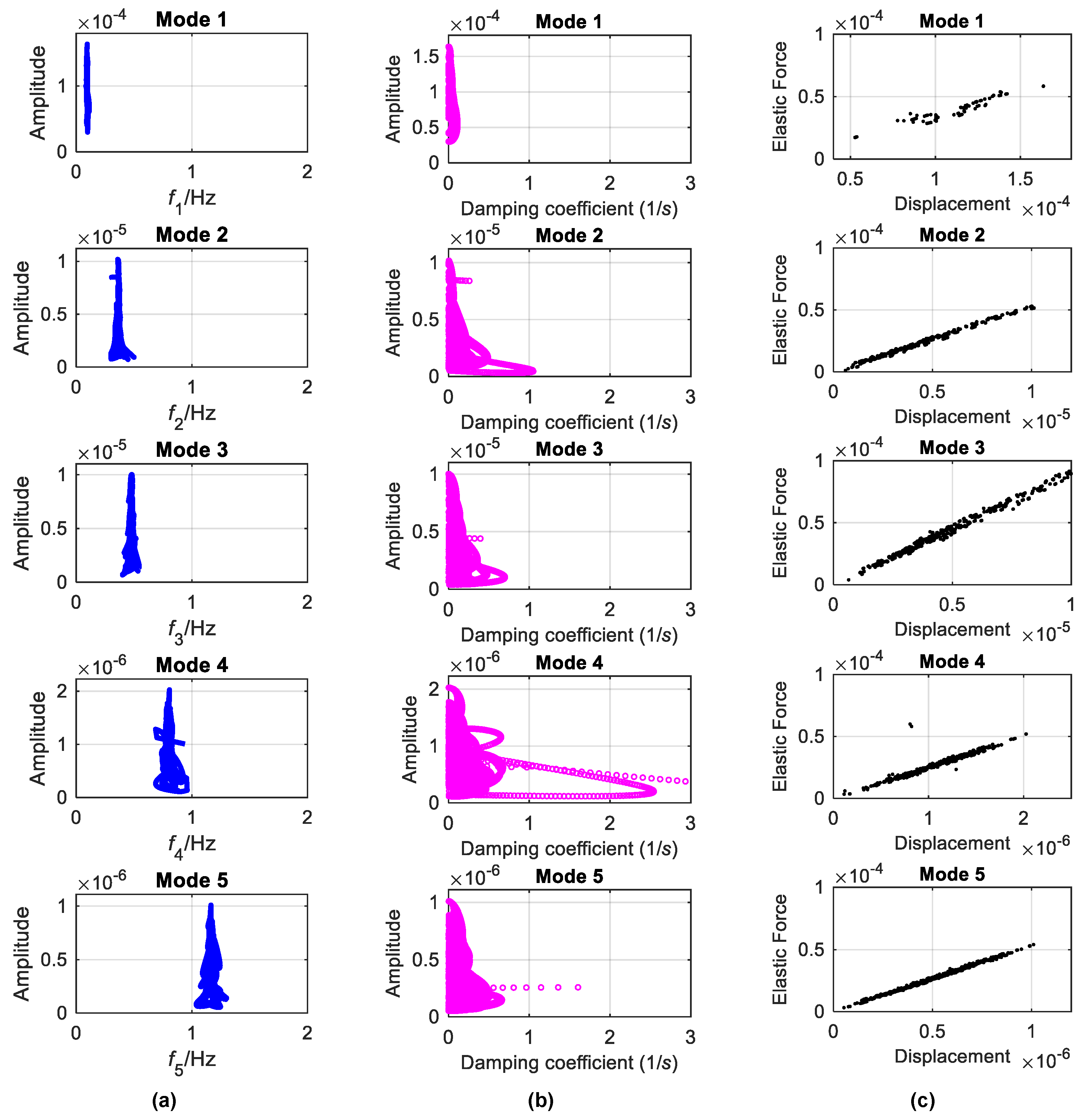
3.3.1. Modal Characteristics
3.3.2. Backbone and Damping Curve
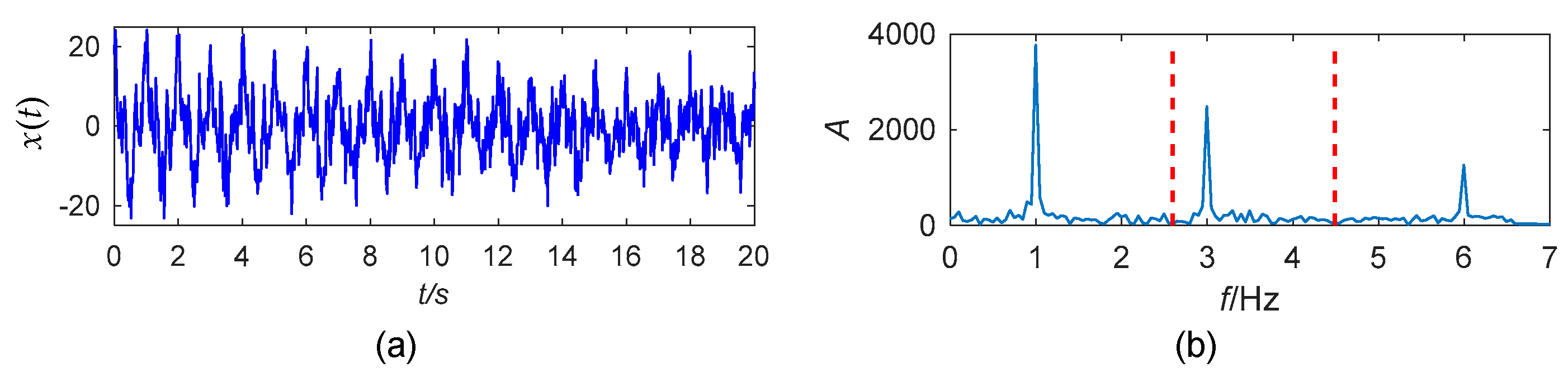
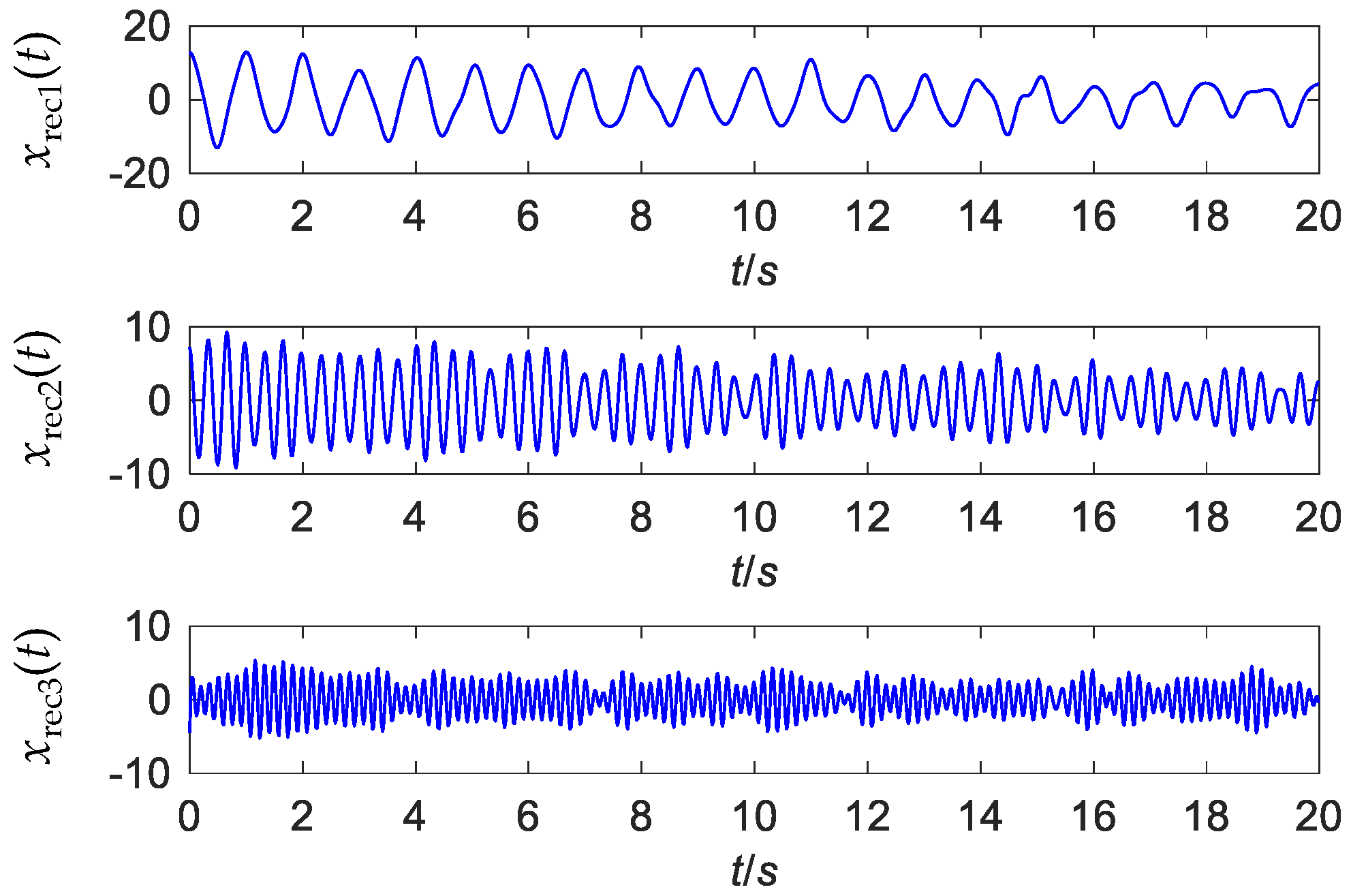
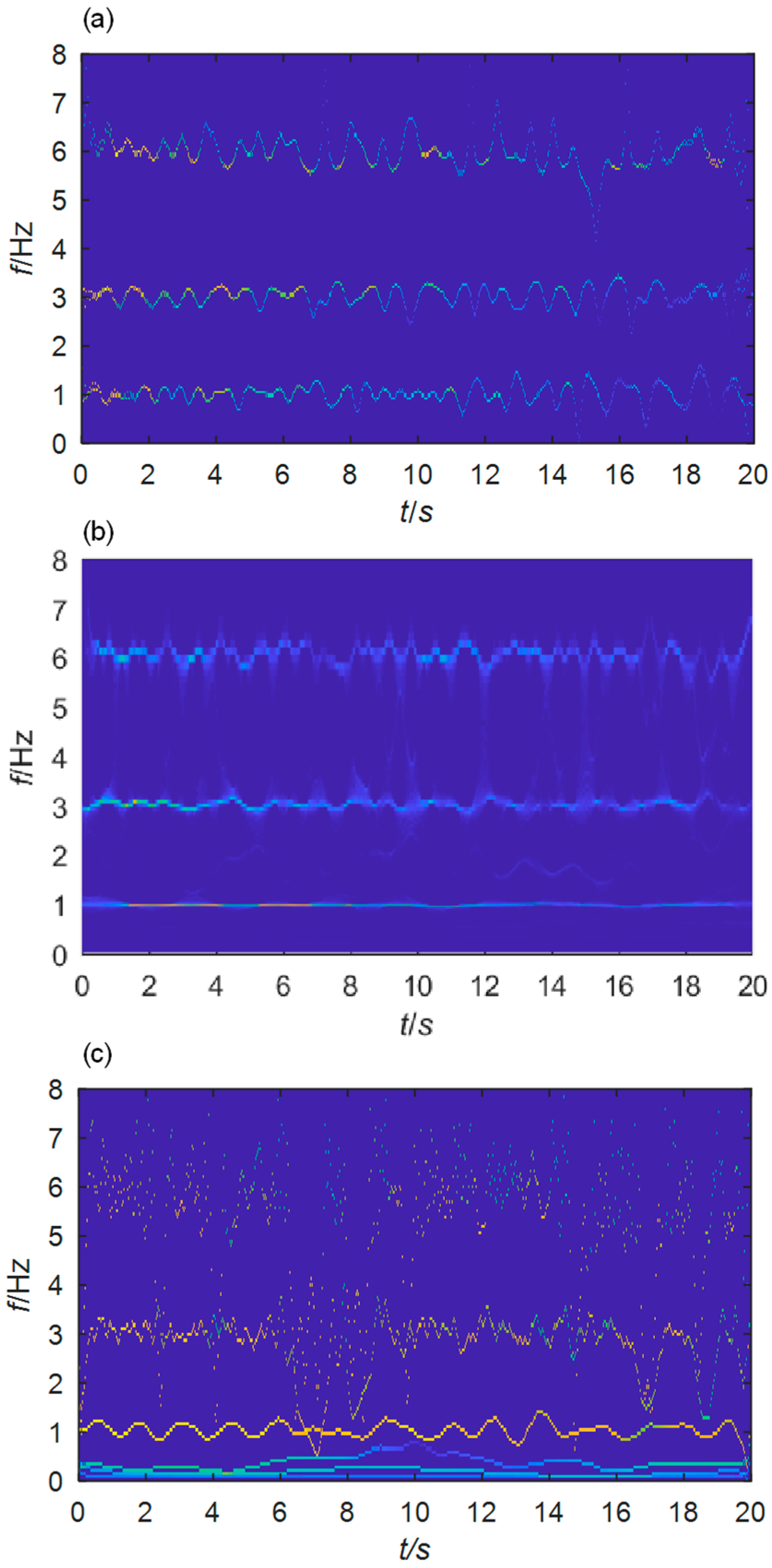
4. Numerical Study
5. Case Study
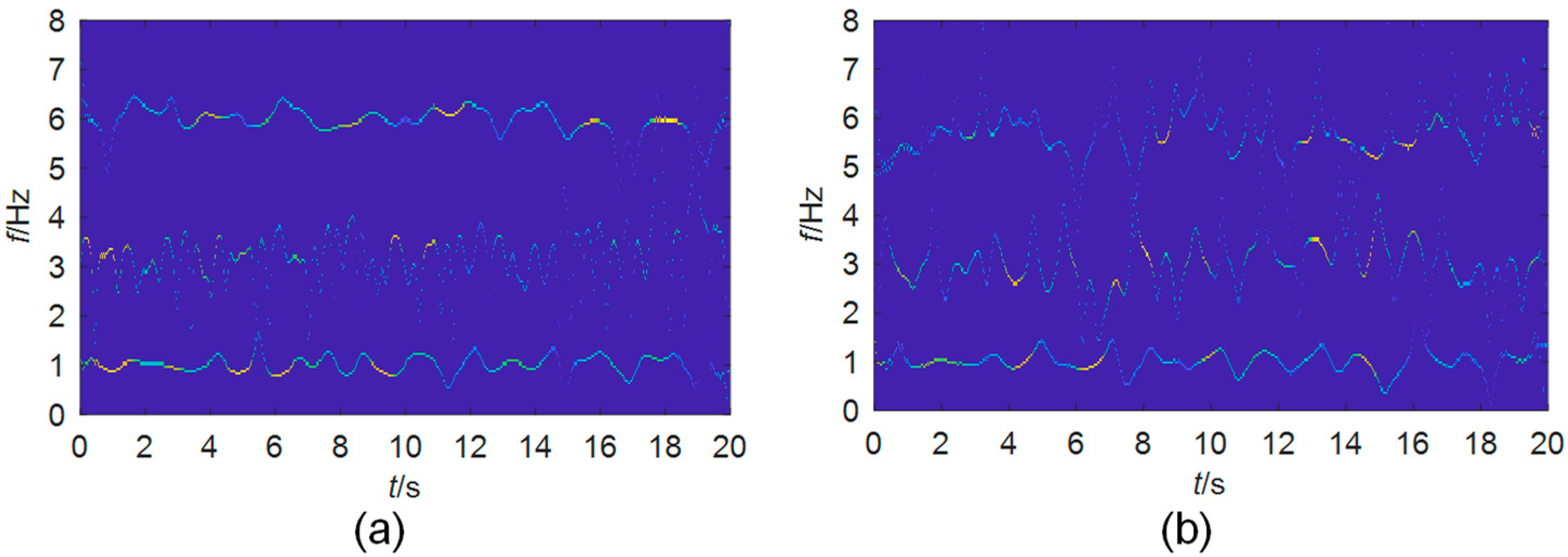
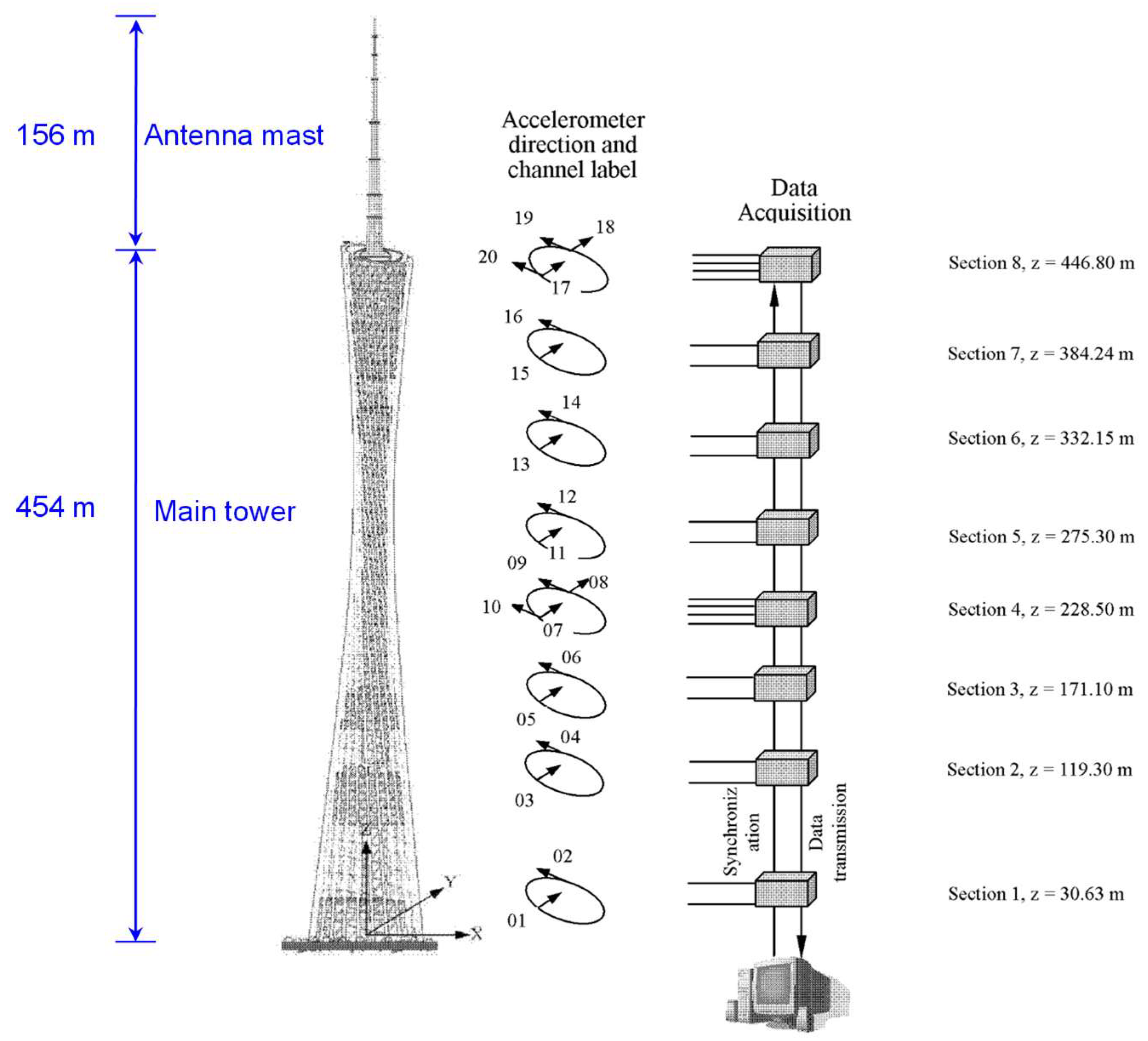
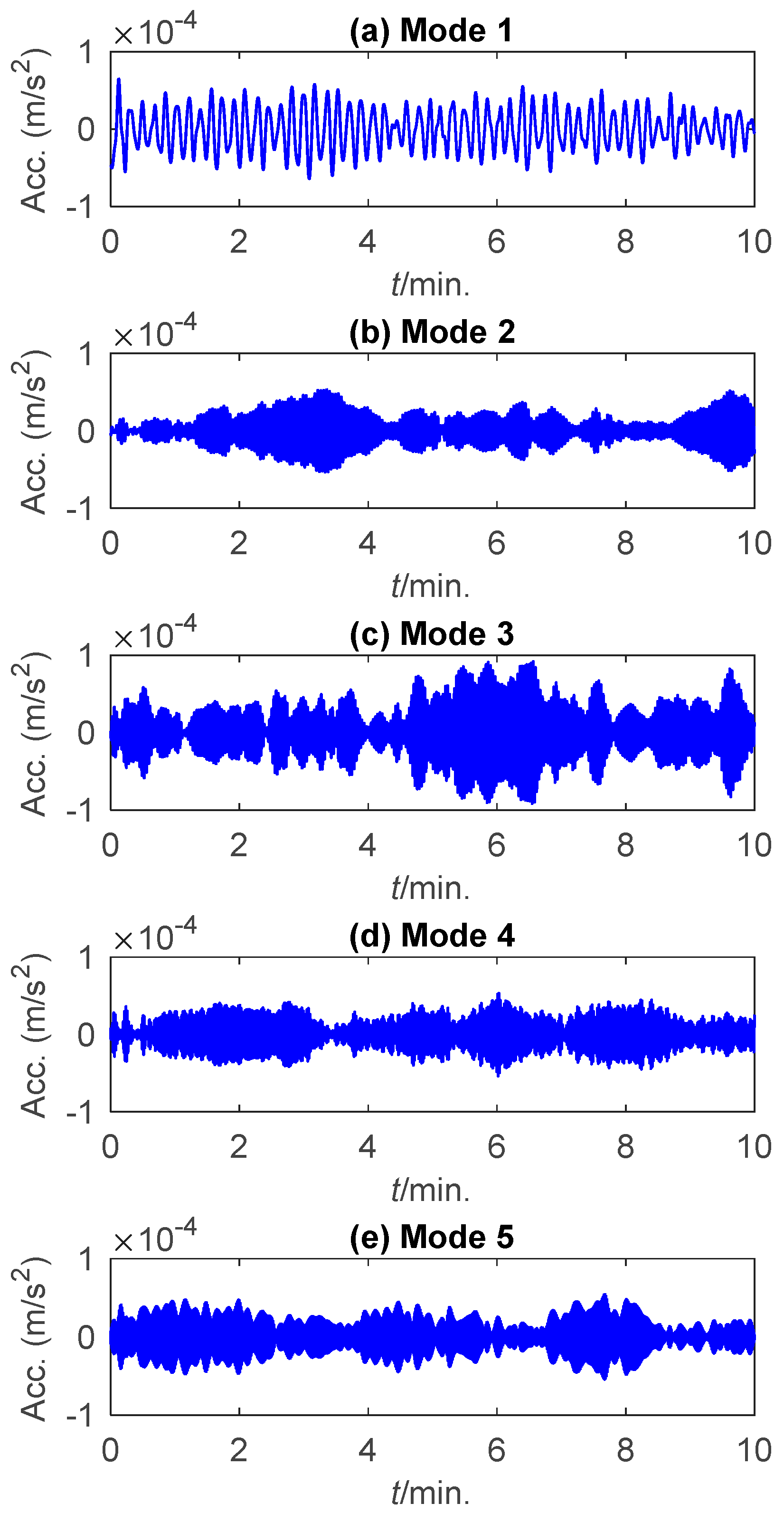
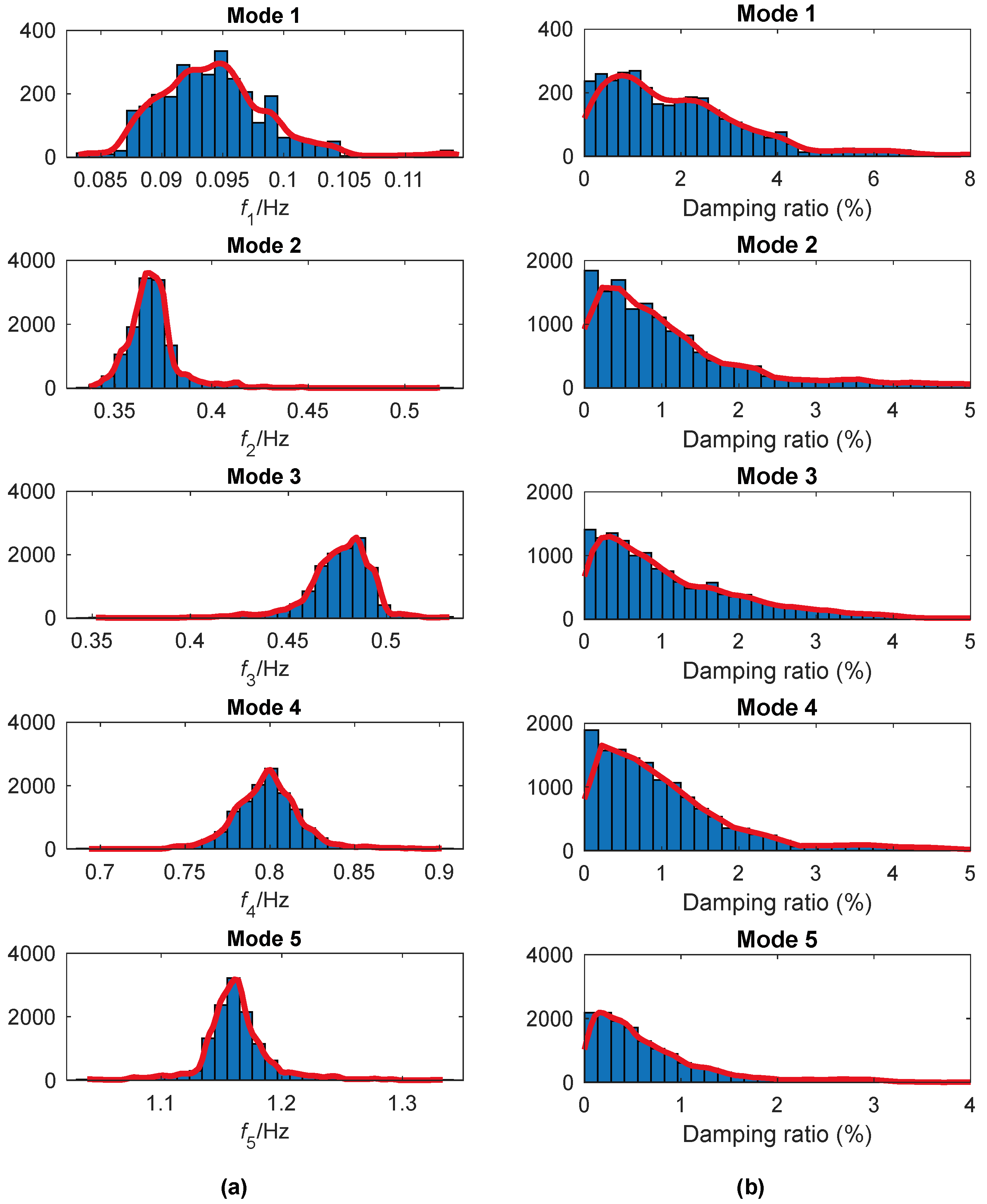
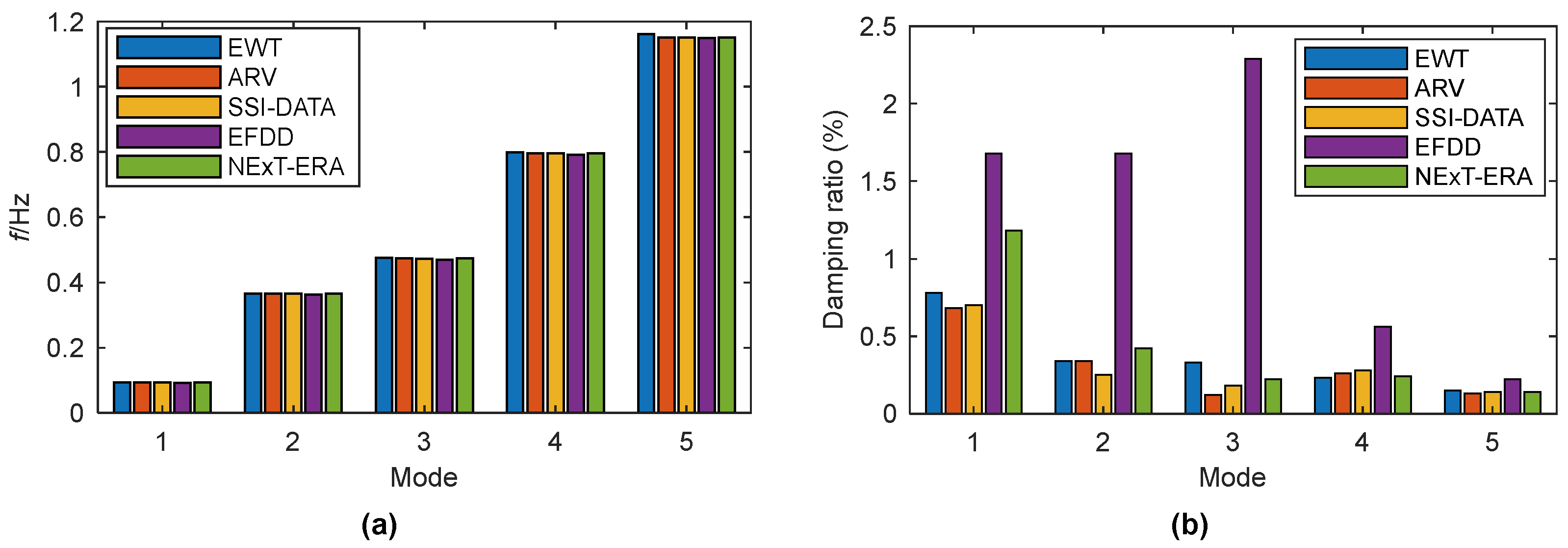
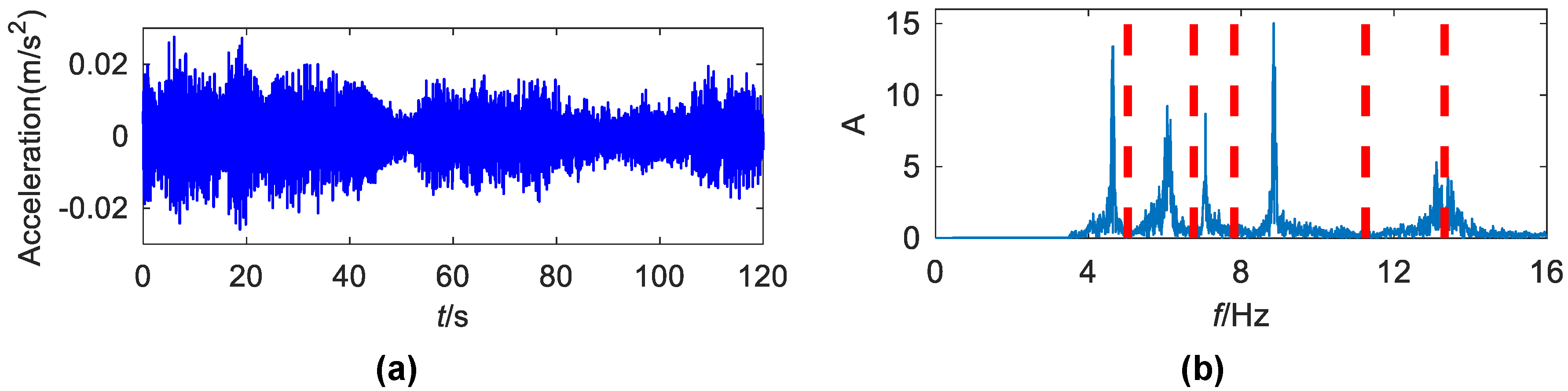
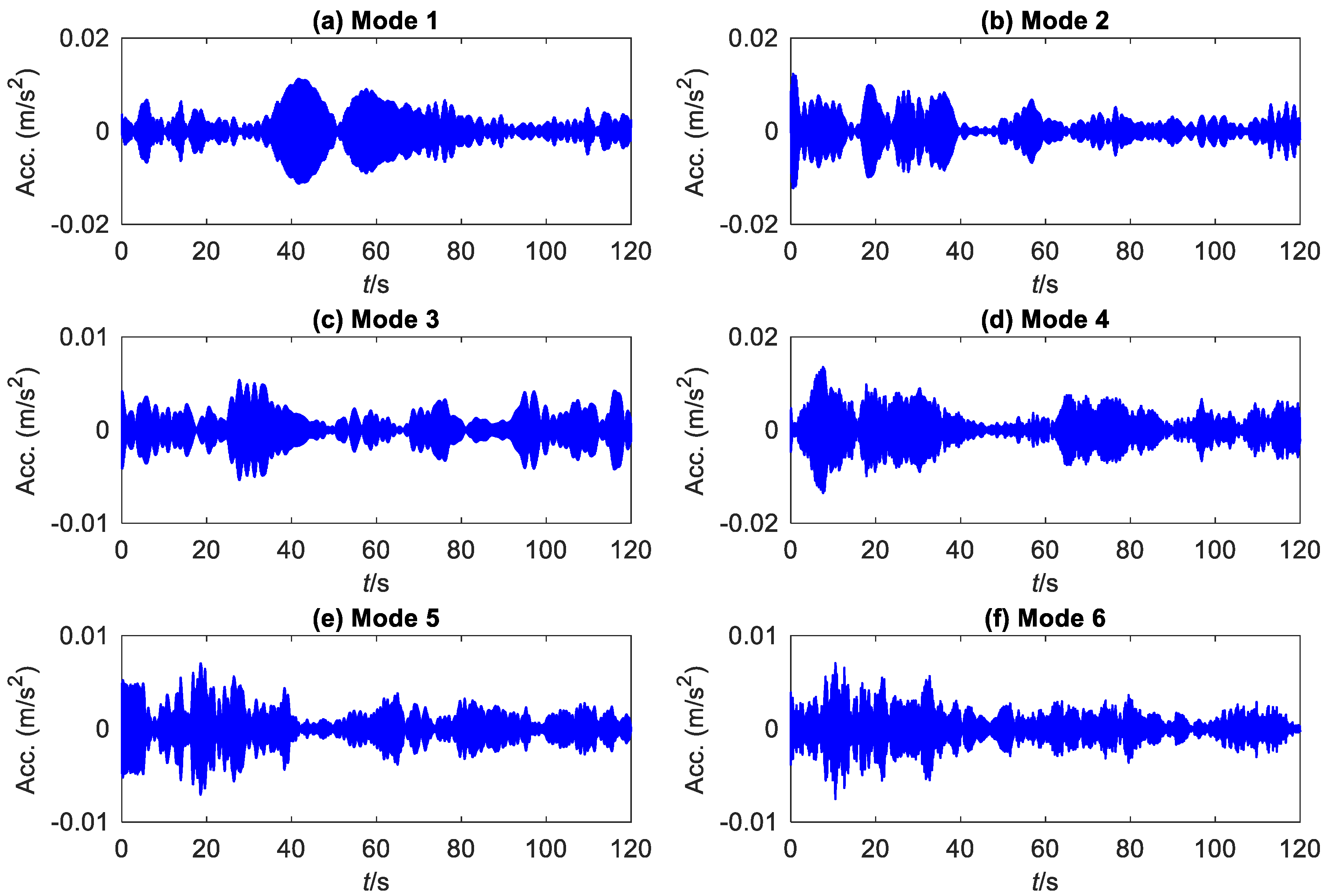
5.1. A High-Rise Building
5.2. A Footbridge
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Allen, J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Trans. Signal Process. 1977, 25, 235–238. [Google Scholar] [CrossRef]
- O’Neill, J.C.; Flandrin, P.; Williams, W.J. On the existence of discrete Wigner distributions. IEEE Signal Process. Lett. 1999, 6, 304–306. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; SIAM(Society for Industrial and Applied Mathematics): Philadelphia, PA, USA, 1992. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Gu, M. Wavelet based multi-step filtering method for bridge health monitoring using GPS and accelerometer. Smart Struct. Syst. 2013, 11, 331–348. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Zhao, X.-Y. Noise smoothing for structural vibration test signals using an improved wavelet thresholding technique. Sensors 2012, 12, 11205–11220. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.X.; Ni, Y.Q. Wavelet-based signal processing of large SHM data. In Proceedings of the 7th Asia-Pacific Workshop on Structural Health Monitoring (APWSHM), Hong Kong, China, 12–15 November 2018; pp. 35–46. [Google Scholar]
- Pakrashi, V.; O’Connor, A.; Basu, B. A study on the effects of damage models and wavelet bases for damage identification and calibration in beams. Comput. Aided Civ. Infrastruct. 2007, 22, 555–569. [Google Scholar] [CrossRef]
- Ren, W.-X.; Sun, Z.-S. Structural damage identification by using wavelet entropy. Eng. Struct. 2008, 30, 2840–2849. [Google Scholar] [CrossRef]
- Yan, G.; Duan, Z.; Ou, J.; De Stefano, A. Structural damage detection using residual forces based on wavelet transform. Comput. Aided Civ. Infrastruct. 2010, 24, 224–239. [Google Scholar] [CrossRef]
- Xia, Y.-X.; Ni, Y.-Q. A wavelet-based despiking algorithm for large data of structural health monitoring. Int. J. Distrib. Sens. Netw. 2018, 14. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Pines, D.; Salvino, L. Structural health monitoring using empirical mode decomposition and the Hilbert phase. J. Sound Vib. 2006, 294, 97–124. [Google Scholar] [CrossRef]
- Rezaei, D.; Taheri, F. Damage identification in beams using empirical mode decomposition. Struct. Health Monit. 2011, 10, 261–274. [Google Scholar] [CrossRef]
- Tang, J.-P.; Chiou, D.-J.; Chen, C.-W.; Chiang, W.-L.; Hsu, W.-K.; Chen, C.-Y.; Liu, T.-Y. A case study of damage detection in benchmark buildings using a Hilbert-Huang Transform-based method. J. Vib. Control 2011, 17, 623–636. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Kumar, R.; Saini, I. Empirical wavelet transform based ECG signal compression. IETE J. Res. 2014, 60, 423–431. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Short-term wind speed prediction using empirical wavelet transform and Gaussian process regression. Energy 2015, 93, 1456–1466. [Google Scholar] [CrossRef]
- Merainani, B.; Benazzouz, D.; Rahmoune, C. Early detection of tooth crack damage in gearbox using empirical wavelet transform combined by Hilbert transform. J. Vib. Control 2015, 23, 1623–1634. [Google Scholar] [CrossRef]
- Cao, H.; Fan, F.; Zhou, K.; He, Z. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Chen, J.; Pan, J.; Li, Z.; Zi, Y.; Chen, X. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Chen, Y. Seismic time-frequency analysis via empirical wavelet transform. IEEE Geosci. Remote Sens. Lett. 2016, 13, 28–32. [Google Scholar] [CrossRef]
- Xu, X.; Liang, Y.; He, P.; Yang, J. Adaptive motion artifact reduction based on empirical wavelet transform and wavelet thresholding for the non-contact ECG monitoring systems. Sensors 2019, 19, 2916. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zuo, S.; Hou, M.; Liu, W.; Yu, L.; Yang, X.; Deng, W. Novel adaptive signal processing method based on enhanced empirical wavelet transform technology. Sensors 2018, 18, 3323. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Yuan, M.; Wang, Q.; Liang, Z. A modified empirical wavelet transform for acoustic emission signal decomposition in structural health monitoring. Sensors 2018, 18, 1645. [Google Scholar] [CrossRef]
- Wang, Q.; Li, H.; Lin, J.; Zhang, C. Future trend forecast by empirical wavelet transform and autoregressive moving average. Sensors 2018, 18, 2621. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A comparative study between empirical wavelet transforms and empirical mode decomposition methods: Application to bearing defect diagnosis. Comput. Aided Civ. Infrastruct. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Xin, Y.; Hao, H.; Li, J. Operational modal identification of structures based on improved empirical wavelet transform. Struct. Control Health Monit. 2019, 26, e2323. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. A new music-empirical wavelet transform methodology for time—Frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Process. 2015, 45, 55–68. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Park, H.S.; Adeli, H. A novel methodology for modal parameters identification of large smart structures using MUSIC, empirical wavelet transform, and Hilbert transform. Eng. Struct. 2017, 147, 148–159. [Google Scholar] [CrossRef]
- Gilles, J.; Heal, K. A parameterless scale-space approach to find meaningful modes in histograms—Application to image and spectrum segmentation. Int. J. Wavelets Multiresolut. Inf. Process. 2014, 12, 1450044. [Google Scholar] [CrossRef]
- Feldman, M. Non-linear system vibration analysis using Hilbert transform—I. Free vibration analysis method ’Freevib’. Comput. Aided Civ. Infrastruct. 1994, 8, 119–127. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Wang, Z.-C.; Ren, W.-X.; Chen, G. Time-frequency analysis and applications in time-varying/nonlinear structural systems: A state-of-the-art review. Adv. Struct. Eng. 2018, 21, 1562–1584. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert Transform Applications in Mechanical Vibration; John Wiley & Sons: West Sussex, UK, 2011. [Google Scholar]
- Ni, Y.Q.; Xia, Y.; Liao, W.; Ko, J. Technology innovation in developing the structural health monitoring system for Guangzhou New TV Tower. Struct. Control Health Monit. 2009, 16, 73–98. [Google Scholar] [CrossRef]
- Ni, Y.; Xia, Y.; Lin, W.; Chen, W.; Ko, J. SHM benchmark for high-rise structures: A reduced-order finite element model and field measurement data. Smart Struct. Syst. 2012, 10, 411–426. [Google Scholar] [CrossRef]
- Niu, Y.; Kraemer, P.; Fritzen, C.-P. Operational modal analysis for Canton Tower. Smart Struct. Syst. 2012, 10, 393–410. [Google Scholar] [CrossRef]
- Faravelli, L.; Ubertini, F.; Fuggini, C. System identification of a super high-rise building via a stochastic subspace approach. Smart Struct. Syst. 2011, 7, 133–152. [Google Scholar] [CrossRef]
- Ye, X.; Yan, Q.; Wang, W.; Yu, X. Modal identification of Canton Tower under uncertain environmental conditions. Smart Struct. Syst. 2012, 10, 353–373. [Google Scholar] [CrossRef]
- Moser, P.; Moaveni, B. Design and deployment of a continuous monitoring system for the Dowling Hall Footbridges. Exp. Tech. 2013, 37, 15–26. [Google Scholar] [CrossRef]
- Moser, P.; Moaveni, B. Environmental effects on the identified natural frequencies of the Dowling Hall Footbridge. Mech. Syst. Signal Process. 2011, 25, 2336–2357. [Google Scholar] [CrossRef]
- Moaveni, B.; Behmanesh, I. Effects of changing ambient temperature on finite element model updating of the Dowling Hall Footbridge. Eng. Struct. 2012, 43, 58–68. [Google Scholar] [CrossRef]




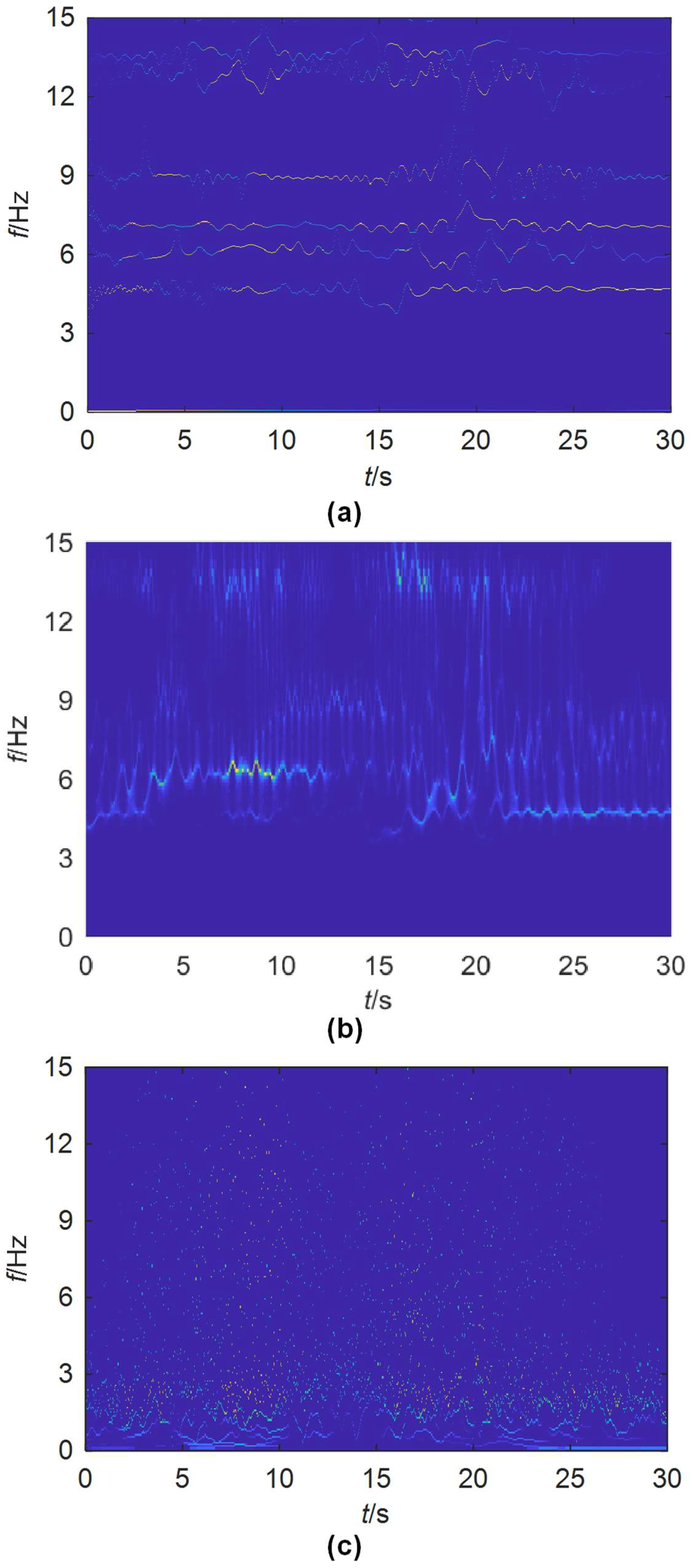
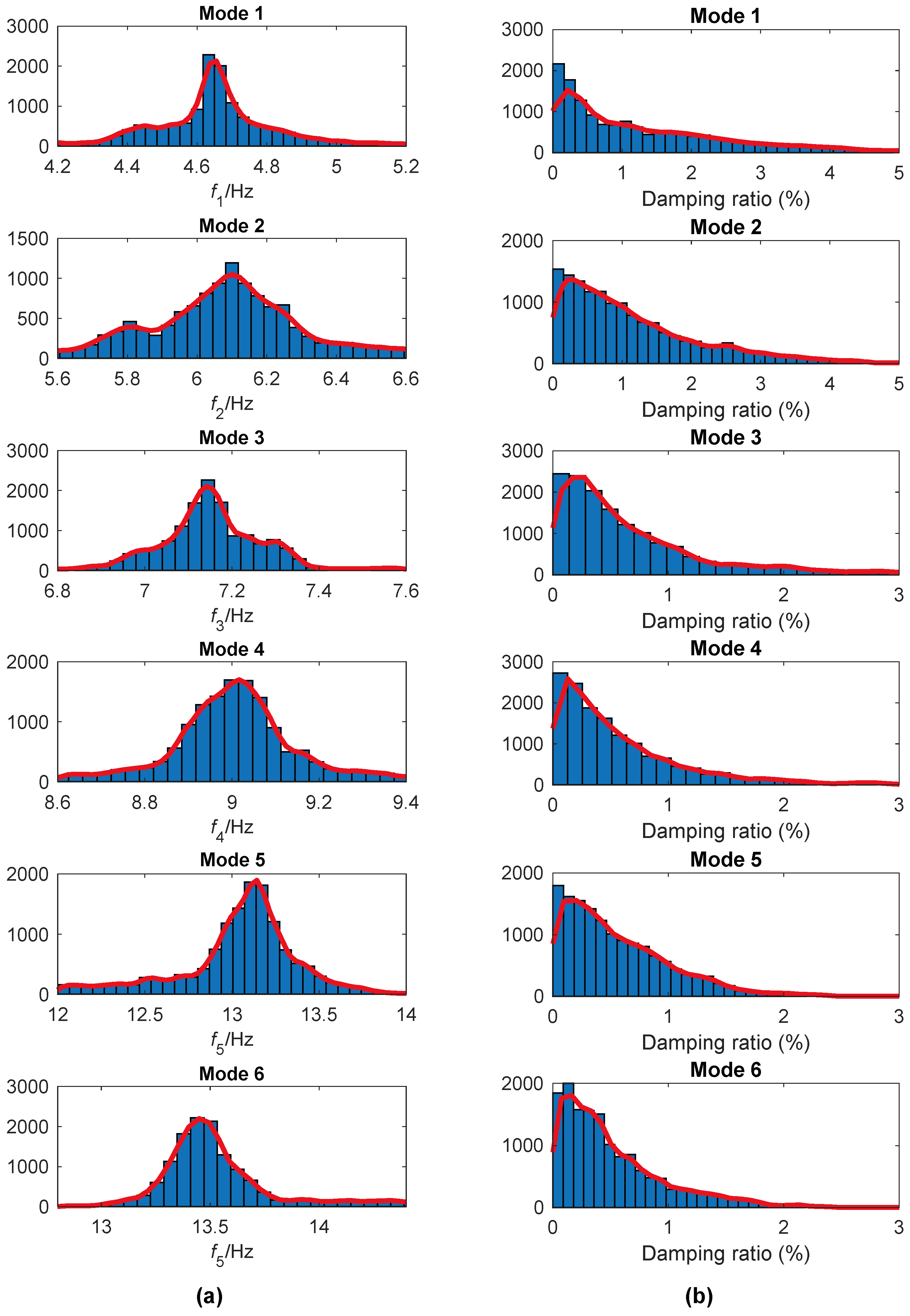

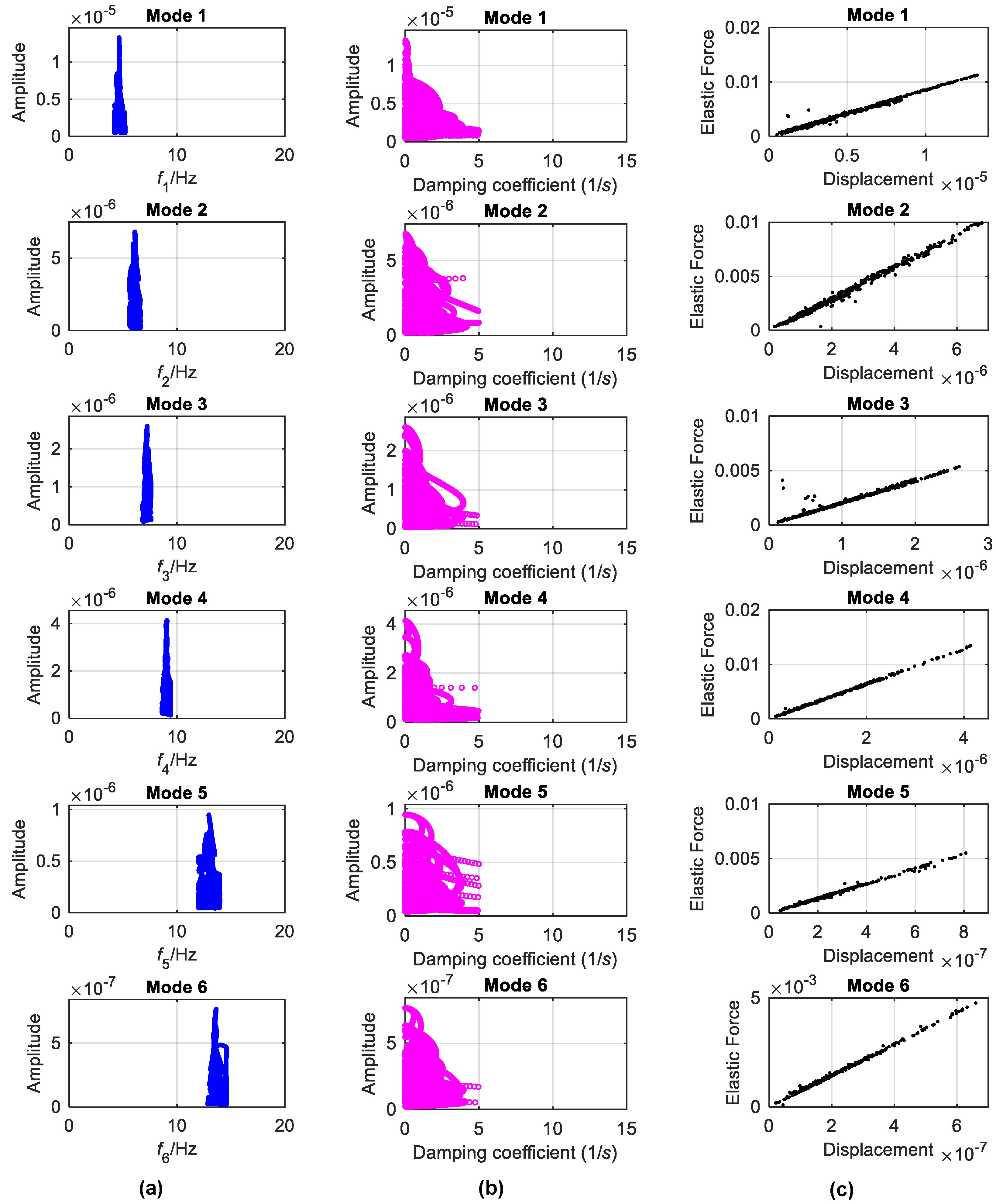
| Modes | Methods | Frequency (Hz) | CV | Damping Ratio (%) | CV | ||
|---|---|---|---|---|---|---|---|
| Analyzed | Theoretical | Analyzed | Theoretical | ||||
| 1 | EWT | 1.01 | 1 | 0.03 | 0.41 | 0.80 | 1.37 |
| SWT | 1.01 | 0.02 | 0.35 | 0.82 | |||
| EMD | 1.00 | 0.02 | 0.33 | 0.76 | |||
| 2 | EWT | 3.06 | 3 | 0.01 | 0.26 | 0.27 | 0.64 |
| SWT | 3.09 | 0.01 | 0.28 | 1.51 | |||
| EMD | 3.08 | 0.27 | 0.70 | 1.79 | |||
| 3 | EWT | 6.00 | 6 | 0.05 | 0.28 | 0.13 | 1.90 |
| SWT | 6.00 | 0.32 | 2.44 | 1.45 | |||
| EMD | 6.09 | 0.52 | 1.89 | 0.98 | |||
| Mode | Frequency (Hz) | CV | Damping Ratio (%) | CV |
|---|---|---|---|---|
| 1 | 0.0948 | 0.05 | 0.78 | 0.84 |
| 2 | 0.3659 | 0.06 | 0.34 | 1.04 |
| 3 | 0.4847 | 0.04 | 0.33 | 1.03 |
| 4 | 0.7983 | 0.02 | 0.23 | 1.24 |
| 5 | 1.1610 | 0.08 | 0.15 | 1.41 |
| Mode | Frequency (Hz) | CV | Damping Ratio (%) | CV |
|---|---|---|---|---|
| 1 | 4.66 | 0.05 | 0.21 | 1.24 |
| 2 | 6.10 | 0.09 | 0.29 | 0.90 |
| 3 | 7.16 | 0.02 | 0.27 | 1.22 |
| 4 | 9.02 | 0.04 | 0.13 | 1.44 |
| 5 | 13.14 | 0.40 | 0.20 | 1.34 |
| 6 | 13.45 | 0.49 | 0.16 | 1.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.-X.; Zhou, Y.-L. Mono-Component Feature Extraction for Condition Assessment in Civil Structures Using Empirical Wavelet Transform. Sensors 2019, 19, 4280. https://doi.org/10.3390/s19194280
Xia Y-X, Zhou Y-L. Mono-Component Feature Extraction for Condition Assessment in Civil Structures Using Empirical Wavelet Transform. Sensors. 2019; 19(19):4280. https://doi.org/10.3390/s19194280
Chicago/Turabian StyleXia, Yun-Xia, and Yun-Lai Zhou. 2019. "Mono-Component Feature Extraction for Condition Assessment in Civil Structures Using Empirical Wavelet Transform" Sensors 19, no. 19: 4280. https://doi.org/10.3390/s19194280
APA StyleXia, Y.-X., & Zhou, Y.-L. (2019). Mono-Component Feature Extraction for Condition Assessment in Civil Structures Using Empirical Wavelet Transform. Sensors, 19(19), 4280. https://doi.org/10.3390/s19194280






