Characterizing Dielectric Permittivity of Nanoscale Dielectric Films by Electrostatic Micro-Probe Technology: Finite Element Simulations
Abstract
:1. Introduction
2. Numerical Simulation and Analysis Scheme
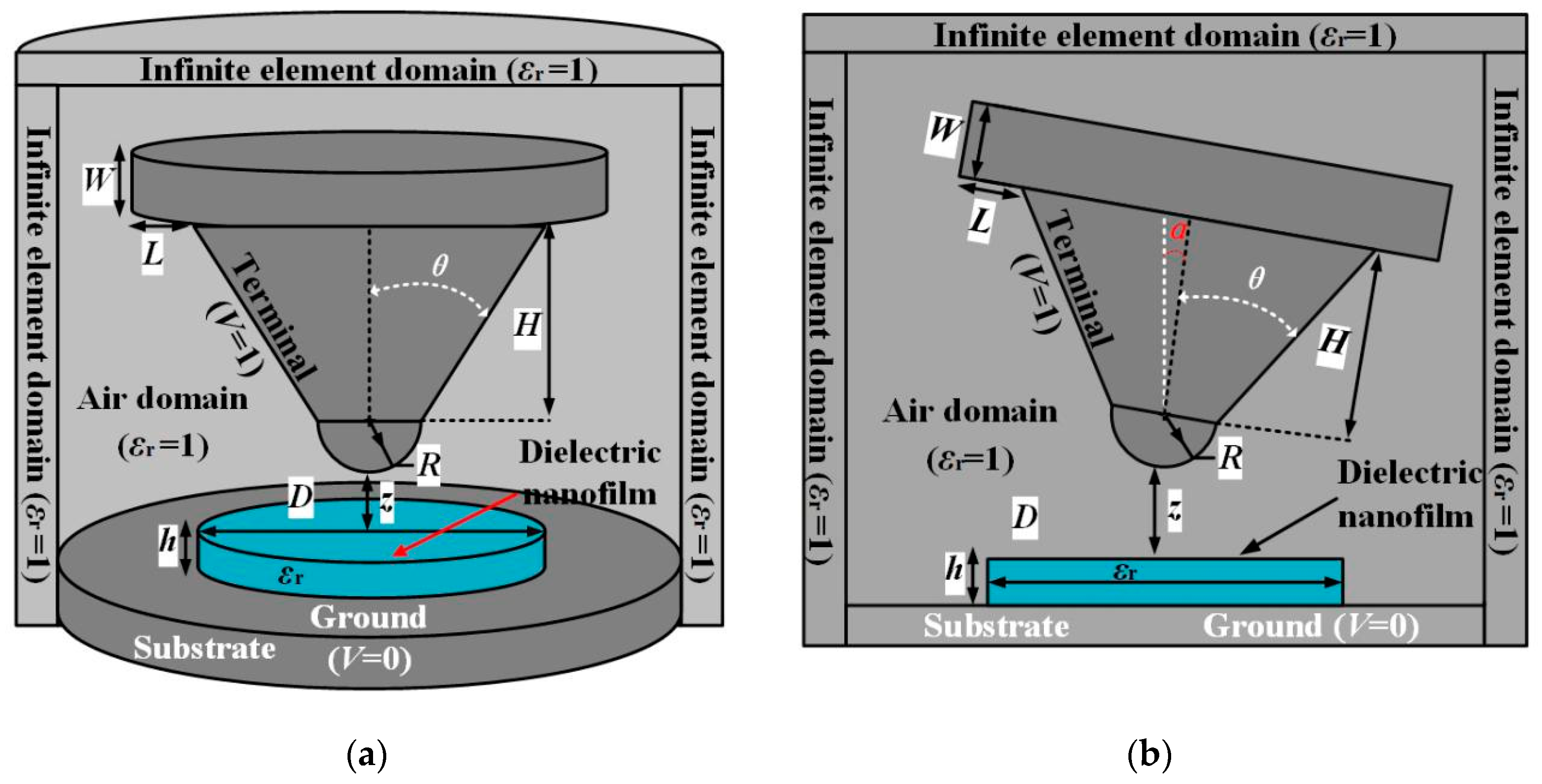
2.1. Finite Element Simulation
2.2. Electrostatic Force Analysis Scheme
3. Results and Discussion
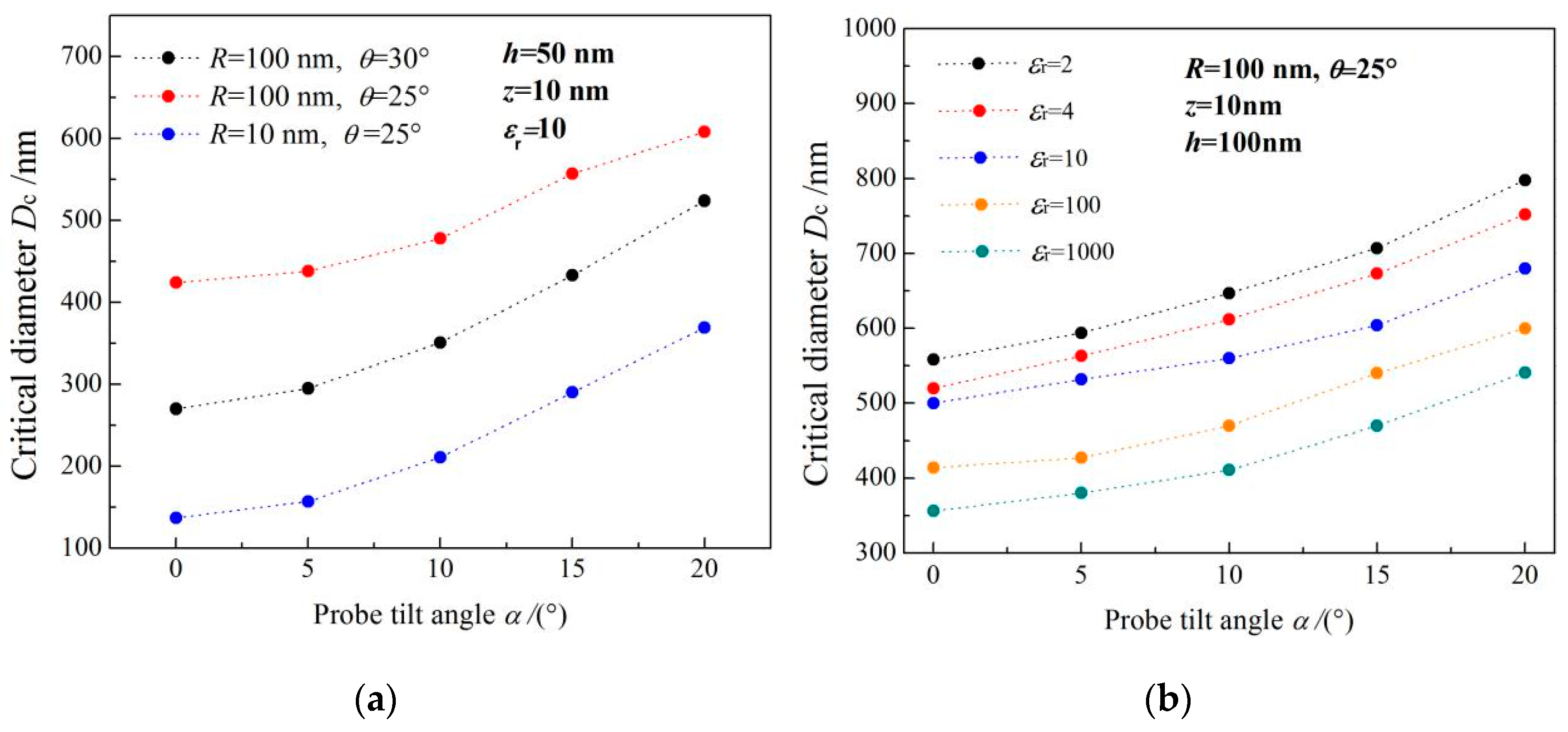
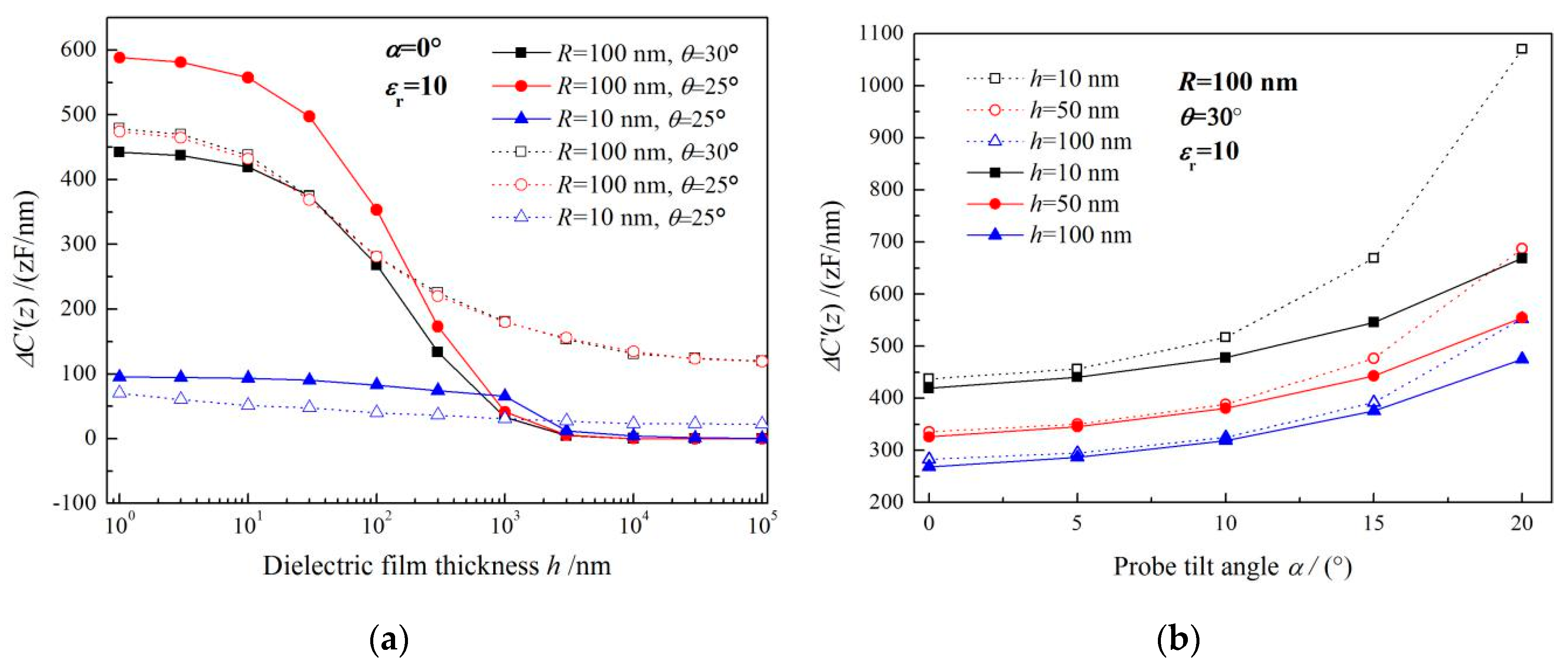
3.1. Film Lateral Dimension and Probe Tilt Angle
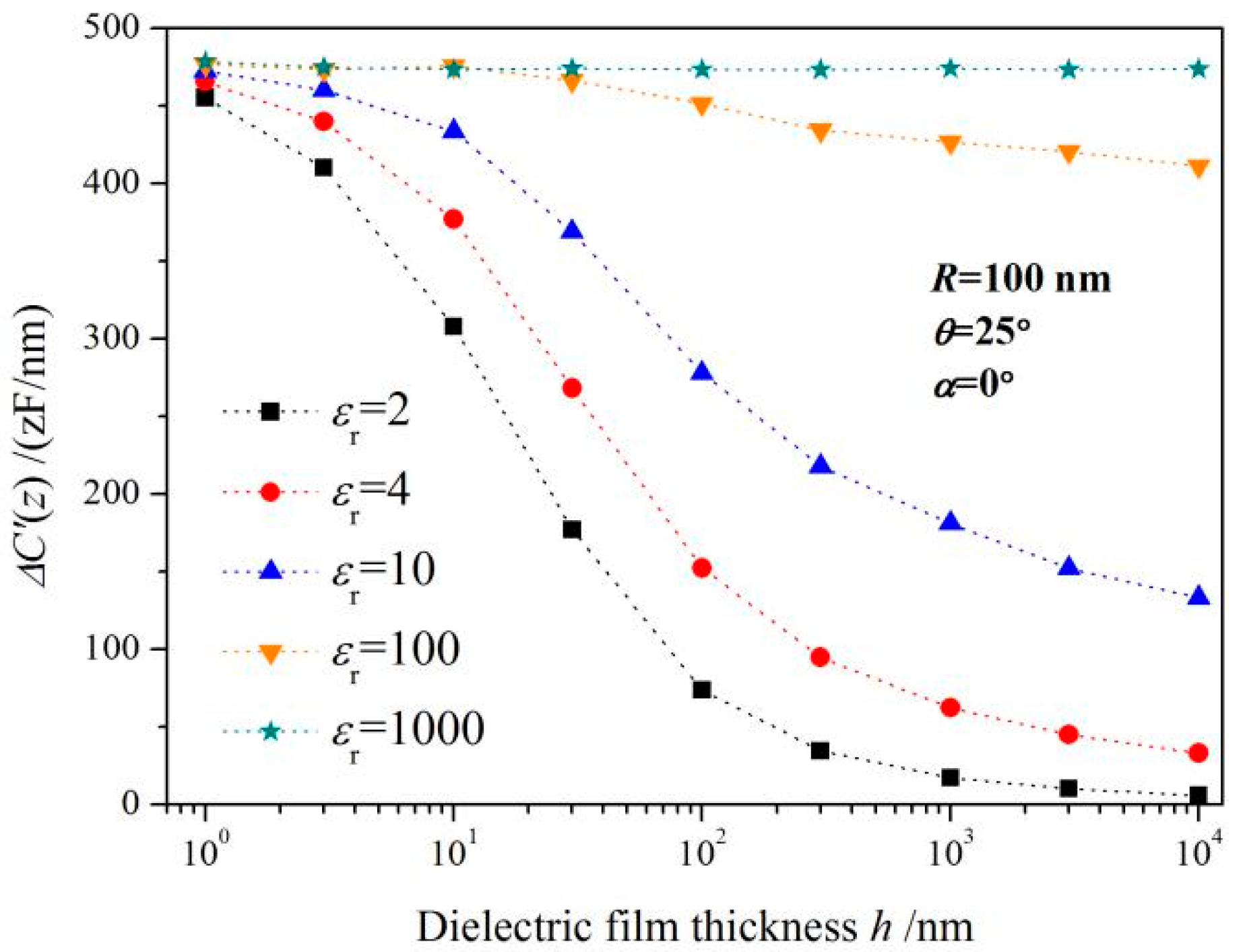
3.2. Electric Potential Distribution Analysis
3.3. Establishment and Verification of Analytical Equations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lai, K.; Ji, M.B.; Leindecker, N.; Kelly, M.A.; Shen, Z.X. AFM-compatible near-field scanning microwave microscope with separated excitation and sensing probes. Rev. Sci. Instrum. 2007, 78, 063702. [Google Scholar] [CrossRef] [PubMed]
- Shao, R.; Kalinin, S.V.; Bonnell, D.A. Local impedance imaging and spectroscopy of polycrystalline ZnO using contact atomic force microscopy. Appl. Phys. Lett. 2003, 82, 1869–1871. [Google Scholar] [CrossRef]
- Lu, W.; Wang, D.; Chen, L. Near-static dielectric polarization of individual carbon nanotubes. Nano Lett. 2007, 7, 2729–2733. [Google Scholar] [CrossRef] [PubMed]
- Gomila, G.; Toset, J.; Fumagalli, L. Nanoscale capacitance microscopy of thin dielectric films. J. Appl. Phys. 2008, 104, 024315. [Google Scholar] [CrossRef] [Green Version]
- Pu, H.B.; Lin, L.; Sun, D.W. Principles of hyperspectral microscope imaging techniques and their applications in food quality and safety detection: A review. Compr. Rev. Food Sci. Food Saf. 2019, 18, 853–866. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Gu, X.; Lowther, S.E.; Park, C.; Jean, Y.C.; Nguyen, T. Subsurface characterization of carbon nanotubes in polymer composites via quantitative electric force microscopy. Nanotechnology 2010, 21, 225702. [Google Scholar] [CrossRef]
- Fumagalli, L.; Ferrari, G.; Sampietro, M.; Gomila, G. Dielectric-constant measurement of thin insulating films at low frequency by nanoscale capacitance microscopy. Appl. Phys. Lett. 2007, 91, 243110. [Google Scholar] [CrossRef]
- Fumagalli, L.; Ferrari, G.; Sampietro, M.; Gomila, G. Quantitative nanoscale dielectric microscopy of single-layer supported biomembranes. Nano Lett. 2009, 9, 1604–1608. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esteban-Ferrer, D.; Cuervo, A.; Gomila, G.; Carrascosa, J.L. Label-free identification of single dielectric nanoparticles and viruses with ultraweak polarization forces. Nature Mater. 2012, 11, 808–816. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esfandiar, A.; Fabregas, R.; Ares, P.; Janardanan, A.; Radha, B.; Taniguchi, T.; Watanabe, K.; Gomila, G.; Novoselov, K.S.; et al. Anomalously low dielectric constant of confined water. Science 2018, 360, 1339–1342. [Google Scholar] [CrossRef] [Green Version]
- Lozano, H.; Fabregas, R.; Blanco-Cabra, N.; Millan-Solsona, R.; Torrents, E.; Fumagalli, L.; Gomila, G. Dielectric constant of flagellin proteins measured by scanning dielectric microscopy. Nanoscale 2018, 10, 19188–19194. [Google Scholar] [CrossRef] [Green Version]
- Crider, P.S.; Majewski, M.R.; Zhang, J.; Oukris, H.; Israeloff, N.E. Local dielectric spectroscopy of near-surface glassy polymer dynamics. J. Chem. Phys. 2008, 128, 044908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crider, P.S.; Majewski, M.R.; Zhang, J.; Israeloff, N.E. Local dielectric spectroscopy of polymer films. Appl. Phys. Lett. 2007, 91, 13102. [Google Scholar] [CrossRef]
- Riedel, C.; Schwartz, G.A.; Arinero, R.; Tordjeman, P.; Leveque, G.; Alegria, A.; Colmenero, J. Nanoscale dielectric properties of insulating thin films: From single point measurements to quantitative images. Ultramicroscopy 2010, 110, 634–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riedel, C.; Arinero, R.; Tordjeman, P.; Ramonda, M.; Leveque, G.; Schwartz, G.A.; Oteyza, D.G.; Alegria, A.; Colmenero, J. Determination of the nanoscale dielectric constant by means of a double pass method using electrostatic force microscopy. J. Appl. Phys. 2009, 106, 024315. [Google Scholar] [CrossRef] [Green Version]
- Riedel, C.; Alegria, A.; Schwartz, G.A.; Colmenero, J.; Saenz, J.J. Numerical study of the lateral resolution in electrostatic force microscopy for dielectric samples. Nanotechnology 2011, 22, 285705. [Google Scholar] [CrossRef] [PubMed]
- Mottaghizadeh, A.; Lang, P.L.; Cui, L.M.; Lesueur, J.; Li, J. Nanoparticles charge response from electrostatic force microscopy. Appl. Phys. Lett. 2013, 102, 053118. [Google Scholar] [CrossRef]
- Labardi, M.; Barsotti, J.; Prevosto, D.; Capaccioli, S.; Roland, C.M.; Casalini, R. Extended model for the interaction of dielectric thin films with an electrostatic force microscope probe. J. Appl. Phys. 2015, 118, 224104. [Google Scholar] [CrossRef]
- Cadena, M.J.; Sung, S.H.; Boudouris, B.W.; Reifenberger, R.; Raman, A. Nanoscale Mapping of Dielectric Properties of Nanomaterials from kHz to MHz Using Ultra Small Cantilevers. ACS Nano 2016, 10, 4062–4071. [Google Scholar] [CrossRef]
- Hudlet, S.; Jean, M.S.; Guthmann, C.; Berger, J. Evaluation of the capacitive force between an atomic force microscopy tip and a metallic surface. Eur. Phys. J. B 1998, 2, 5–10. [Google Scholar] [CrossRef]
- Riedel, C.; Alegria, A.; Schwartz, G.A.; Arinero, R.; Colmenero, J.; Saenz, J.J. On the use of electrostatic force microscopy as a quantitative subsurface characterization technique: A numerical study. Appl. Phys. Lett. 2011, 99, 023101. [Google Scholar] [CrossRef] [Green Version]
- Riedel, C.; Alegría, A.; Arinero, R.; Colmenero, J.; Saenz, J.J. Contrast inversion in electrostatic force microscopy imaging of trapped charges: Tip–sample distance and dielectric constant dependence. Nanotechnology 2011, 22, 345702. [Google Scholar] [CrossRef] [PubMed]
- Arinero, R.; Riedel, C.; Guasch, C. Numerical simulations of electrostatic interactions between an atomic force microscopy tip and a dielectric sample in presence of buried nano-particles. J. Appl. Phys. 2012, 112, 114313. [Google Scholar] [CrossRef]
- Boularas, A.; Baudoin, F.; Teyssedre, G.; Villeneuve-Faure, C.; Clain, S. 3D modeling of electrostatic interaction between atomic force microscopy probe and dielectric surface: Impact of tip shape and cantilever contribution. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 705–712. [Google Scholar] [CrossRef]
- Gramse, G.; Gomila, G.; Fumagalli, L. Quantifying the dielectric constant of thick insulators by electrostatic force microscopy: Effects of the microscopic parts of the probe. Nanotechnology 2012, 23, 205703. [Google Scholar] [CrossRef] [PubMed]
- Fumagalli, L.; Edwards, M.A.; Gomila, G. Quantitative electrostatic force microscopy with sharp silicon tips. Nanotechnology 2014, 25, 495701. [Google Scholar] [CrossRef]
- Gomila, G.; Esteban-Ferrer, D.; Fumagalli, L. Quantification of the dielectric constant of single non-spherical nanoparticles from polarization forces: Eccentricity effects. Nanotechnology 2013, 24, 505713. [Google Scholar] [CrossRef]
- Law-Bruce, M.; Rieutord, F. Electrostatic forces in atomic force microscopy. Phys. Rev. B 2002, 66, 035402. [Google Scholar]
- Sahagún, E.; Sáenz, J.J.; Sacha, G.M. A method for calculating capacitances and electrostatic forces in atomic force microscopy. J. Appl. Phys. 2007, 101, 024310. [Google Scholar]
- Gomila, G.; Gramse, G.; Fumagalli, L. Finite-size effects and analytical modeling of electrostatic force microscopy applied to dielectric films. Nanotechnology 2014, 25, 255702. [Google Scholar] [CrossRef]
- Gomez-Monivas, S.; Froufe-Pérez, L.S.; Caamano, A.; Sáenz, J.J. Electrostatic forces between sharp tips and metallic and dielectric samples. Appl. Phys. Lett. 2001, 79, 4048. [Google Scholar] [CrossRef] [Green Version]
- Jespersen, T.S.; Nygård, J. Mapping of individual carbon nanotubes in polymer/nanotube composites using electrostatic force microscopy. Appl. Phys. Lett. 2007, 90, 183108. [Google Scholar] [CrossRef]
- Castaneda-Uribe, O.A.; Reifenberger, R.; Raman, A.; Avila, A. Depth-sensitive subsurface imaging of polymer nanocomposites using second harmonic kelvin probe force microscopy. ACS Nano 2015, 9, 2938–2947. [Google Scholar] [CrossRef] [PubMed]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Sun, W.-F. Characterizing Dielectric Permittivity of Nanoscale Dielectric Films by Electrostatic Micro-Probe Technology: Finite Element Simulations. Sensors 2019, 19, 5405. https://doi.org/10.3390/s19245405
Ren H, Sun W-F. Characterizing Dielectric Permittivity of Nanoscale Dielectric Films by Electrostatic Micro-Probe Technology: Finite Element Simulations. Sensors. 2019; 19(24):5405. https://doi.org/10.3390/s19245405
Chicago/Turabian StyleRen, He, and Wei-Feng Sun. 2019. "Characterizing Dielectric Permittivity of Nanoscale Dielectric Films by Electrostatic Micro-Probe Technology: Finite Element Simulations" Sensors 19, no. 24: 5405. https://doi.org/10.3390/s19245405
APA StyleRen, H., & Sun, W.-F. (2019). Characterizing Dielectric Permittivity of Nanoscale Dielectric Films by Electrostatic Micro-Probe Technology: Finite Element Simulations. Sensors, 19(24), 5405. https://doi.org/10.3390/s19245405




