A Novel PZT Pump with Built-in Compliant Structures
Abstract
:1. Introduction
2. Working Principle and Theoretical Analysis
2.1. Working Principle
2.2. Theoretical Analysis
3. Fabrication
4. Experimental Setups
4.1. Measurement of the Flow-Resistance Differences
4.2. Measurement of the Amplitude Characteristics
4.3. Measurement of the Flow Rate
5. Results and Discussion
5.1. Results of the Flow-Resistance Differences
5.2. Results of the Amplitude Characteristics
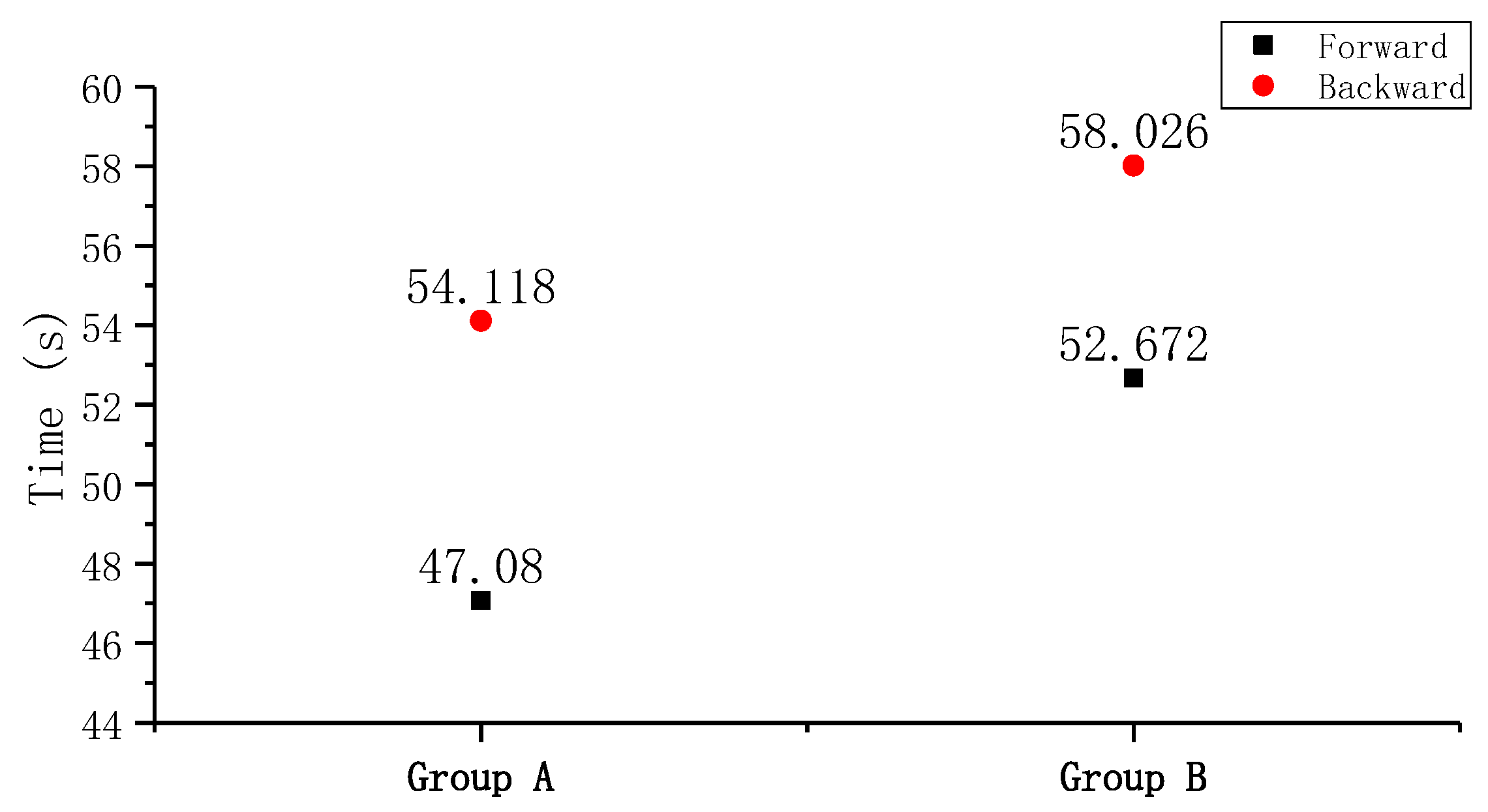
5.3. Results of the Flow Rate Measurements
5.4. Research on the Siphon- Caused Flow Rate
5.5. Future Investigations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iverson, B.D.; Garimella, S.V. Recent advances in microscale pumping technologies: A review and evaluation. Microfluid. Nanofluid. 2008, 5, 145–174. [Google Scholar] [CrossRef]
- Tsai, N.C.; Sue, C.Y. Review of MEMS-based drug delivery and dosing systems. Sens. Actuators A Phys. 2007, 134, 555–564. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35. [Google Scholar] [CrossRef]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Hao, S.; Wang, H.; Zhong, C.; Wang, L.; Zhang, H. Research and Fabrication of High-Frequency Broadband and Omnidirectional Transmitting Transducer. Sensors 2018, 18, 2347. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Li, W.; Hei, C.; Song, G. Concrete infill monitoring in concrete-filled FRP tubes using a PZT-based ultrasonic time-of-flight method. Sensors 2016, 16, 2083. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ren, W.; Liu, Y.; Wu, X.; Fei, C.; Quan, Y.; Zhou, Q. Fabrication and Characterization of High-Frequency Ultrasound Transducers Based on Lead-Free BNT-BT Tape-Casting Thick Film. Sensors 2018, 18, 3166. [Google Scholar] [CrossRef] [PubMed]
- Patra, S.; Ahmed, H.; Banerjee, S. Peri-Elastodynamic Simulations of Guided Ultrasonic Waves in Plate-Like Structure with Surface Mounted PZT. Sensors 2018, 18, 274. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Li, H.; Gajic, B.; Zhou, W.; Chen, P.; Gu, H. Wind turbine blade health monitoring with piezoceramic-based wireless sensor network. Int. J. Smart Nano Mater. 2013, 4, 150–166. [Google Scholar] [CrossRef]
- Kim, N.; Jang, K.; An, Y.K. Self-Sensing Nonlinear Ultrasonic Fatigue Crack Detection under Temperature Variation. Sensors 2018, 18, 2527. [Google Scholar] [CrossRef]
- Ma, G.; Xu, M.; Zhang, S.; Zhang, Y.; Liu, X. Active Vibration Control of an Axially Moving Cantilever Structure Using PZT Actuator. J. Aerosp. Eng. 2018, 31, 04018049. [Google Scholar] [CrossRef]
- Agrawal, B.N.; Elshafei, M.A.; Song, G. Adaptive antenna shape control using piezoelectric actuators. Acta Astronaut. 1997, 40, 821–826. [Google Scholar] [CrossRef]
- Song, G.; Zhou, X.; Binienda, W. Thermal deformation compensation of a composite beam using piezoelectric actuators. Smart Mater. Struct. 2003, 13, 30. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mater. Struct. 2017, 27, 015023. [Google Scholar] [CrossRef] [Green Version]
- Huo, L.; Wang, F.; Li, H.; Song, G. A fractal contact theory based model for bolted connection looseness monitoring using piezoceramic transducers. Smart Mater. Struct. 2017, 26, 104010. [Google Scholar] [CrossRef]
- Ma, Y.; Ji, Q.; Chen, S.; Song, G. An experimental study of ultra-low power wireless sensor-based autonomous energy harvesting system. J. Renew. Sustain. Ener. 2017, 9, 054702. [Google Scholar] [CrossRef]
- Vyas, A.; Staaf, H.; Rusu, C.; Ebefors, T.; Liljeholm, J.; Smith, A.D.; Lundgren, P.; Enoksson, P. A Micromachined Coupled-Cantilever for Piezoelectric Energy Harvesters. Micromachines 2018, 9, 252. [Google Scholar] [CrossRef] [PubMed]
- Ewere, F.; Wang, G.; Frendi, A. Experimental Investigation of a Bioinspired Bluff-Body Effect on Galloping Piezoelectric Energy-Harvester Performance. AIAA J. 2017, 56, 1284–1287. [Google Scholar] [CrossRef]
- Dziendzikowski, M.; Niedbala, P.; Kurnyta, A.; Kowalczyk, K.; Dragan, K. Structural Health Monitoring of a Composite Panel Based on PZT Sensors and a Transfer Impedance Framework. Sensors 2018, 18, 1521. [Google Scholar] [CrossRef]
- Jiang, T.; Kong, Q.; Wang, W.; Huo, L.; Song, G. Monitoring of Grouting Compactness in a Post-Tensioning Tendon Duct Using Piezoceramic Transducers. Sensors 2016, 16, 1343. [Google Scholar] [CrossRef]
- Fan, S.; Zhao, S.; Qi, B.; Kong, Q. Damage Evaluation of Concrete Column under Impact Load Using a Piezoelectric-Based EMI Technique. Sensors 2018, 18, 1591. [Google Scholar] [CrossRef]
- Huo, L.; Li, C.; Jiang, T.; Li, H. Feasibility Study of Steel Bar Corrosion Monitoring Using a Piezoceramic Transducer Enabled Time Reversal Method. Appl. Sci. 2018, 8, 2304. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Shen, Y.; Chen, S.; Yang, Z. A Resonant Piezoelectric Diaphragm Pump Transferring Gas with Compact Structure. Micromachines 2016, 7, 219. [Google Scholar] [CrossRef] [PubMed]
- Fan, B.; Song, G.; Hussain, F. Simulation of a piezoelectrically actuated valveless micropump. Smart Mater. Struct. 2005, 14, 400. [Google Scholar] [CrossRef]
- Jenke, C.; Pallejà Rubio, J.; Kibler, S.; Häfner, J.; Richter, M.; Kutter, C. The combination of micro diaphragm pumps and flow sensors for single stroke based liquid flow control. Sensors 2017, 17, 755. [Google Scholar] [CrossRef]
- Connacher, W.; Zhang, N.; Huang, A.; Mei, J.; Zhang, S.; Gopesh, T.; Friend, J. Micro/nano acoustofluidics: Materials, phenomena, design, devices, and applications. Lab Chip 2018, 18, 1952–1996. [Google Scholar] [CrossRef]
- Ehrenberg, O.; Kosa, G. Analysis of a Novel Piezoelectric Micro-Pump for Drug Delivery in a Medical Integrated Micro System. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 467–472. [Google Scholar]
- Leu, T.S.; Gong, D.C.; Pan, D. Numerical and experimental studies of phase difference effects on flow rate of peristaltic micro-pumps with pumping chambers in series configurations. Microsyst. Technol. 2017, 23, 329–341. [Google Scholar] [CrossRef]
- Tanaka, Y. A Peristaltic Pump Integrated on a 100% Glass Microchip Using Computer Controlled Piezoelectric Actuators. Micromachines 2014, 5, 289–299. [Google Scholar] [CrossRef] [Green Version]
- Pecar, B.; Krizaj, D.; Vrtacnik, D.; Resnik, D.; Dolzan, T.; Mozek, M. Piezoelectric peristaltic micropump with a single actuator. J. Micromech. Microeng. 2014, 24, 105010. [Google Scholar] [CrossRef]
- Zhang, W.; Eitel, R.E. An integrated multilayer ceramic piezoelectric micropump for microfluidic systems. J. Intell. Mater. Syst. Struct. 2013, 24, 1637–1646. [Google Scholar] [CrossRef]
- Graf, N.J.; Bowser, M.T. A soft-polymer piezoelectric bimorph cantilever-actuated peristaltic micropump. Lab Chip 2008, 8, 1664–1670. [Google Scholar] [CrossRef] [PubMed]
- Husband, B.; Bu, M.; Evans, A.G.R.; Melvin, T. Investigation for the operation of an integrated peristaltic micropump. J. Micromech. Microeng. 2004, 14, S64. [Google Scholar] [CrossRef]
- Jang, L.; Shu, K.; Yu, Y.; Li, Y.; Chen, C. Effect of actuation sequence on flow rates of peristaltic micropumps with PZT actuators. Biomed. Microdevices 2009, 11, 173–181. [Google Scholar] [CrossRef]
- Lee, D.S.; Ko, J.S.; Kim, Y.T. Bidirectional pumping properties of a peristaltic piezoelectric micropump with simple design and chemical resistance. Thin Solid Films 2004, 468, 285–290. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Huang, X.; Chuan, T.K. MEMS-micropumps: A review. J. Fluids Eng. 2002, 124, 384–392. [Google Scholar] [CrossRef]
- Zhang, C.; Xing, D.; Li, Y. Micropumps, microvalves, and micromixers within PCR microfluidic chips: Advances and trends. Biotechnol. Adv. 2007, 25, 483–514. [Google Scholar] [CrossRef]
- Nisar, A.; AftuIpurkar, N.; Mahaisavariya, B.; Tuantranont, A. MEMS-based micropumps in drug delivery and biomedical applications. Sens. Actuators B Chem. 2008, 130, 917–942. [Google Scholar] [CrossRef]
- Li, S.; Ren, W.; Chen, X.; Wang, Z.; Shi, P.; Wu, X.; Yao, X. Preparation of Diffuser-Type Micropumps Using PZT Thin Films Prepared by Metallo-Organic Compound Decomposition Process. Ferroelectrics 2009, 383, 144–150. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Fu, J.; Yan, K.; Li, Z.; Zhao, C. Advances in Technologies of Piezoelectric Pumping with Valves. Trans. Nanjing Univ Aeronaut. Astronaut. 2016, 33, 260–273. [Google Scholar]
- Stemme, E.; Stemme, G. A valveless diffuser/nozzle-based fluid pump. Sens. Actuators A Phys. 1993, 39, 159–167. [Google Scholar] [CrossRef]
- Munas, F.R.; Melroy, G.; Amarasinghe, R. Development of PZT Actuated Valveless Micropump. Sensors 2018, 18, 1302. [Google Scholar] [CrossRef]
- Leng, X.; Zhang, J.; Jiang, Y.; Zhang, J.Y.; Sun, X.; Lin, X. Theory and experimental verification of spiral flow tube-type valveless piezoelectric pump with gyroscopic effect. Sens. Actuators A Phys. 2013, 195, 1–6. [Google Scholar] [CrossRef]
- Yang, S.; He, X.; Yuan, S.; Zhu, J.; Deng, Z. A valveless piezoelectric micropump with a Coanda jet element. Sens. Actuators A Phys. 2015, 230, 74–82. [Google Scholar] [CrossRef]
- Ma, Y.; Pei, Z.; Chen, Z. Multi-Field Analysis and Experimental Verification on Piezoelectric Valve-Less Pumps Actuated by Centrifugal Force. Chin. J. Mech. Eng. 2017, 30, 1032–1043. [Google Scholar] [CrossRef]
- Forster, F.K.; Bardell, R.L.; Afromowitz, M.A.; Sharma, N.R.; Blanchard, A.J. Design, fabrication and testing of fixed-valve micro-pumps. In Proceedings of the 1995 Asme International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 234, pp. 39–44. [Google Scholar]
- Bardell, R.L.; Sharma, N.R.; Forster, F.K.; Afromowitz, M.A.; Penney, R.J. Designing high-performance micro-pumps based on no-moving-parts valves. In Proceedings of the 1997 Asme International Mechanical Engineering Congress and Exposition, Dallas, TX, USA, 16–21 November 1997; Volume 354, pp. 47–54. [Google Scholar]
- Huang, J.; Zhang, J.; Wang, S.; Liu, W. Analysis of the Flow Rate Characteristics of Valveless Piezoelectric Pump with Fractal-like Y-shape Branching Tubes. Chin. J. Mech. Eng. 2014, 27, 628–634. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Huang, J. Equivalent Circuit Modeling for a Valveless Piezoelectric Pump. Sensors 2018, 18, 2881. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zhang, J.; Hu, X.; Chen, X. Experimental Study on Flow Characteristics of Valve-Less Piezoelectric Pump with Triangular Prism Bluff Bpdies. J. Vib. Meas. Diagn. 2016, 36, 580–585. [Google Scholar]
- Huang, Y.; Wei, C.; Zhang, J.; Xia, Q.; Hu, X. Analysis of Disc Brake Judder Using Multipoint Contact Dynamic Model. J. Vib. Meas. Diagn. 2010, 30, 295–299. [Google Scholar]
- Zhang, J.; Wang, Y.; Huang, J. Advances in Valveless Piezoelectric Pump with Cone-shaped Tubes. Chin. J. Mech. Eng. 2017, 30, 766–781. [Google Scholar] [CrossRef] [Green Version]
- Sutera, S.P.; Skalak, R. The history of Poiseuille’s law. Ann. Rev. Fluid Mech. 1993, 25, 1–20. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, Q.; Huang, J.; Wu, C. Experimental Verification of the Pumping Effect Caused by the Micro-Tapered Hole in a Piezoelectric Atomizer. Sensors 2018, 18, 2311. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Xia, Q. Research on vibration and pump flow rate of valveless piezoelectric pump with Y-shape tubes. Opt. Precis. Eng. 2007, 15, 922–929. [Google Scholar]
- Zhang, R.; You, F.; Lv, Z.; He, Z.; Wang, H.; Huang, L. Development and Characterization a Single-Active-Chamber Piezoelectric Membrane Pump with Multiple Passive Check Valves. Sensors 2016, 16, 2108. [Google Scholar] [CrossRef]
- Kan, J.; Tang, K.; Liu, G.; Zhu, G.; Shao, C. Development of serial-connection piezoelectric pumps. Sens. Actuators A Phys. 2008, 144, 321–327. [Google Scholar] [CrossRef]
- Huang, F.; Kan, J.; Zhang, Z.; Ma, Z.; Wang, S.; Cheng, G. Fabrication and Performance of a Double-Chamber Serial Piezoelectric Micropump. Adv. Mater. Res. 2012, 424–425, 1164–1168. [Google Scholar] [CrossRef]
- Muralidhara, S.N.; Rao, R. Design and Simulation of High Pressure Piezohydraulic Pump with Active valves. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 1608–1613. [Google Scholar]
- Kan, J.; Xuan, M.; Yang, Z.; Wu, Y.; Wu, B.; Cheng, G. Analysis and test of piezoelectric micropump for drug delivery. J. Biomed. Eng. 2005, 22, 809–813. [Google Scholar]











| Parameter | Diameter of Brass Substrate | Thickness of Brass Substrate | Diameter of PZT Ceramic | Thickness of PZT Ceramic |
|---|---|---|---|---|
| Value | 15 mm | 0.1 mm | 11 mm | 0.1 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Q.; Zhang, J.; Tang, M.; Huang, Z.; Lai, L.; Huang, J.; Wu, C. A Novel PZT Pump with Built-in Compliant Structures. Sensors 2019, 19, 1301. https://doi.org/10.3390/s19061301
Bao Q, Zhang J, Tang M, Huang Z, Lai L, Huang J, Wu C. A Novel PZT Pump with Built-in Compliant Structures. Sensors. 2019; 19(6):1301. https://doi.org/10.3390/s19061301
Chicago/Turabian StyleBao, Qibo, Jianhui Zhang, Ming Tang, Zhi Huang, Liyi Lai, Jun Huang, and Chuanyu Wu. 2019. "A Novel PZT Pump with Built-in Compliant Structures" Sensors 19, no. 6: 1301. https://doi.org/10.3390/s19061301
APA StyleBao, Q., Zhang, J., Tang, M., Huang, Z., Lai, L., Huang, J., & Wu, C. (2019). A Novel PZT Pump with Built-in Compliant Structures. Sensors, 19(6), 1301. https://doi.org/10.3390/s19061301






