New Proposal for Inverse Algorithm Enhancing Noise Robust Eddy-Current Non-Destructive Evaluation
Abstract
:1. Introduction
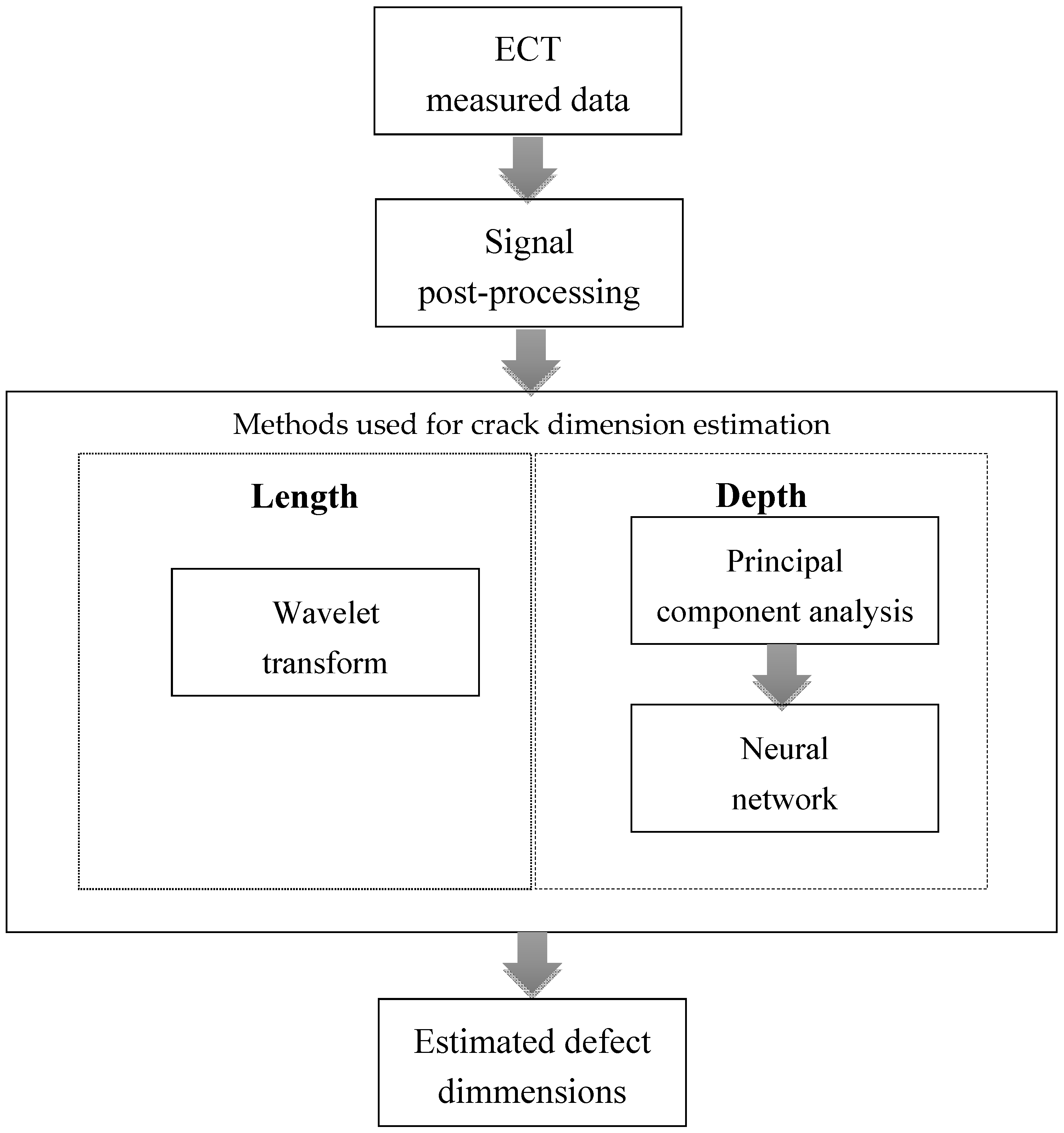
2. New Inverse Algorithm
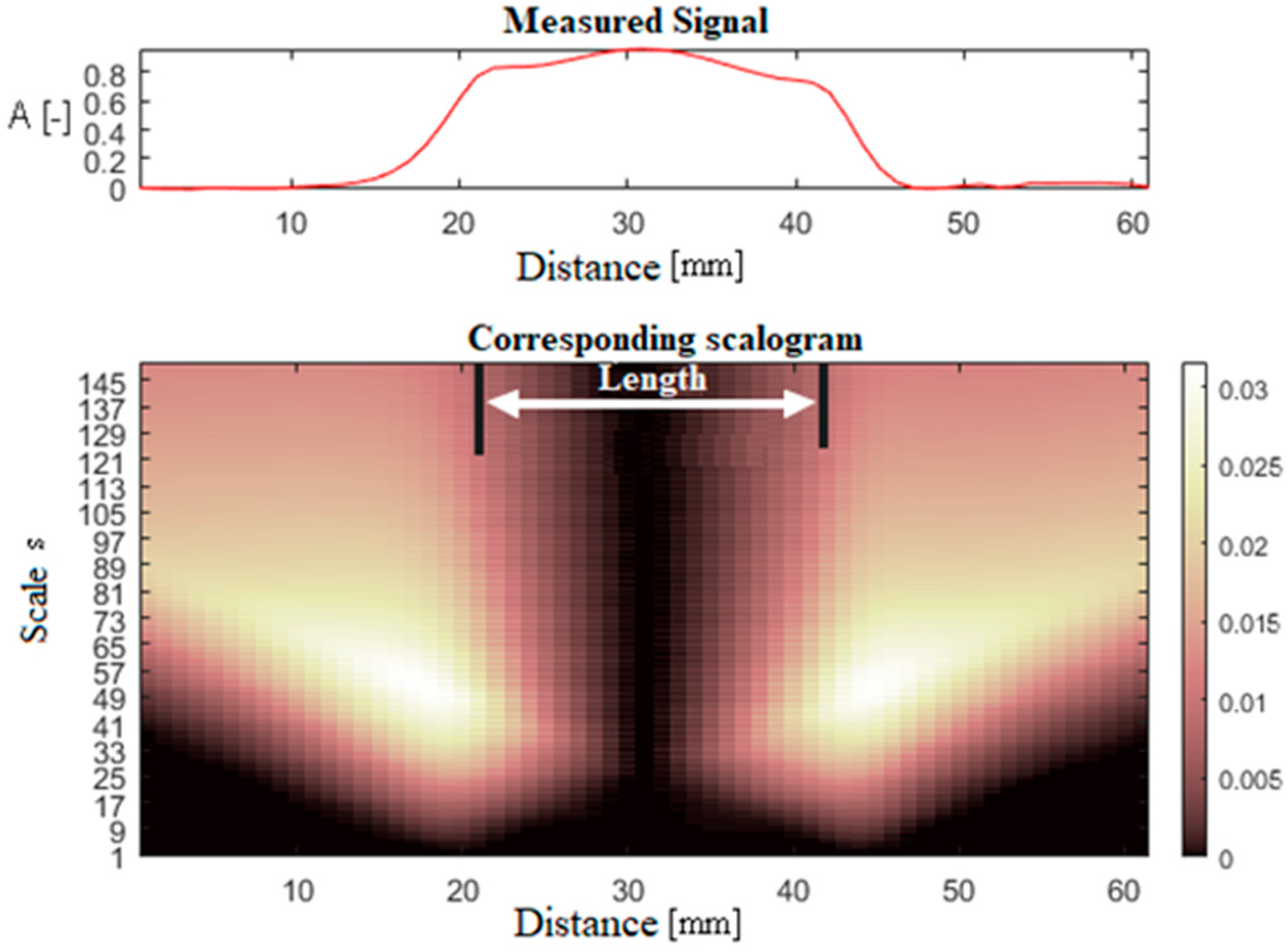
2.1. Wavelet Transform
2.2. Principal Component Analysis
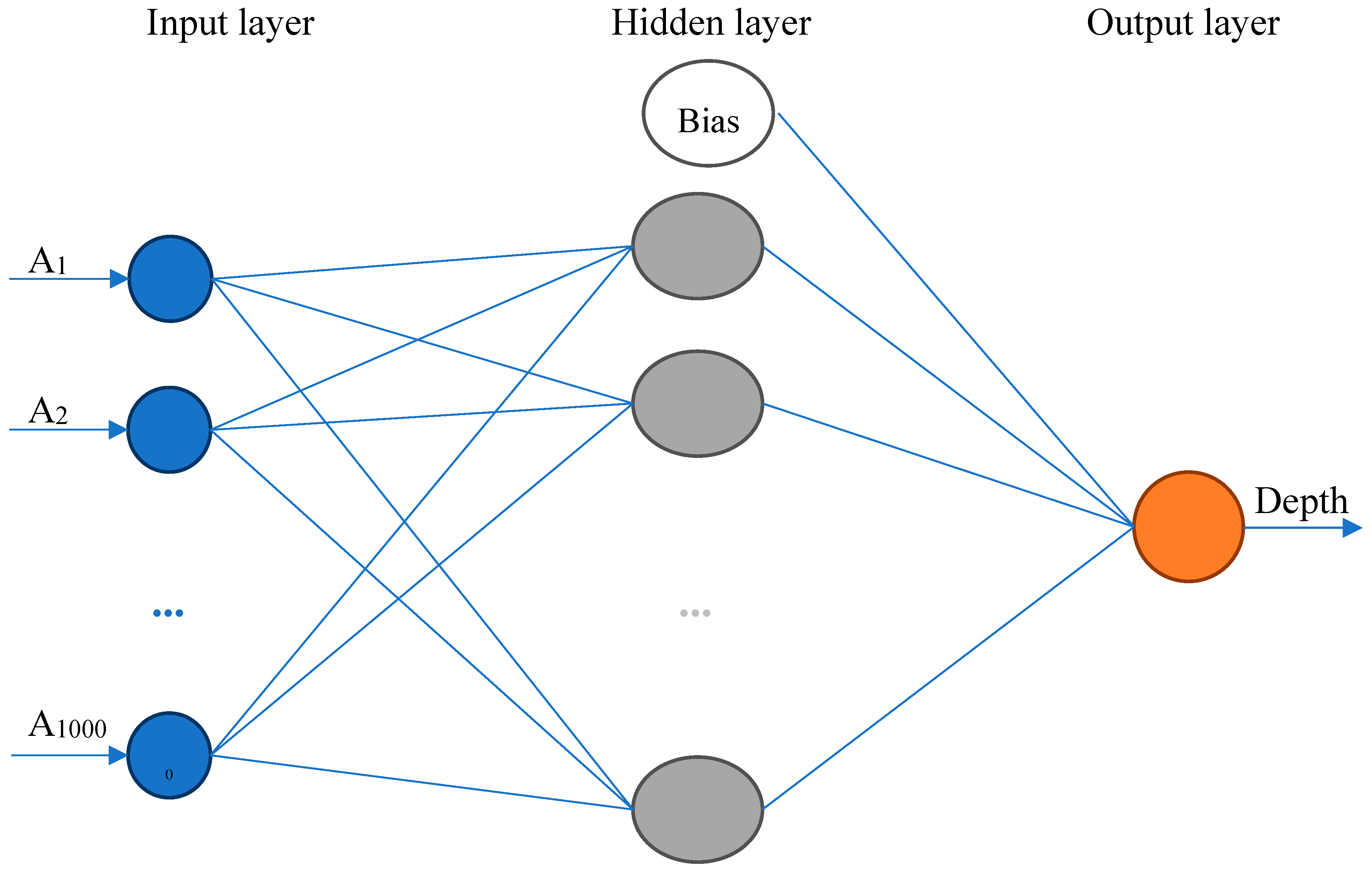
2.3. Neural Network
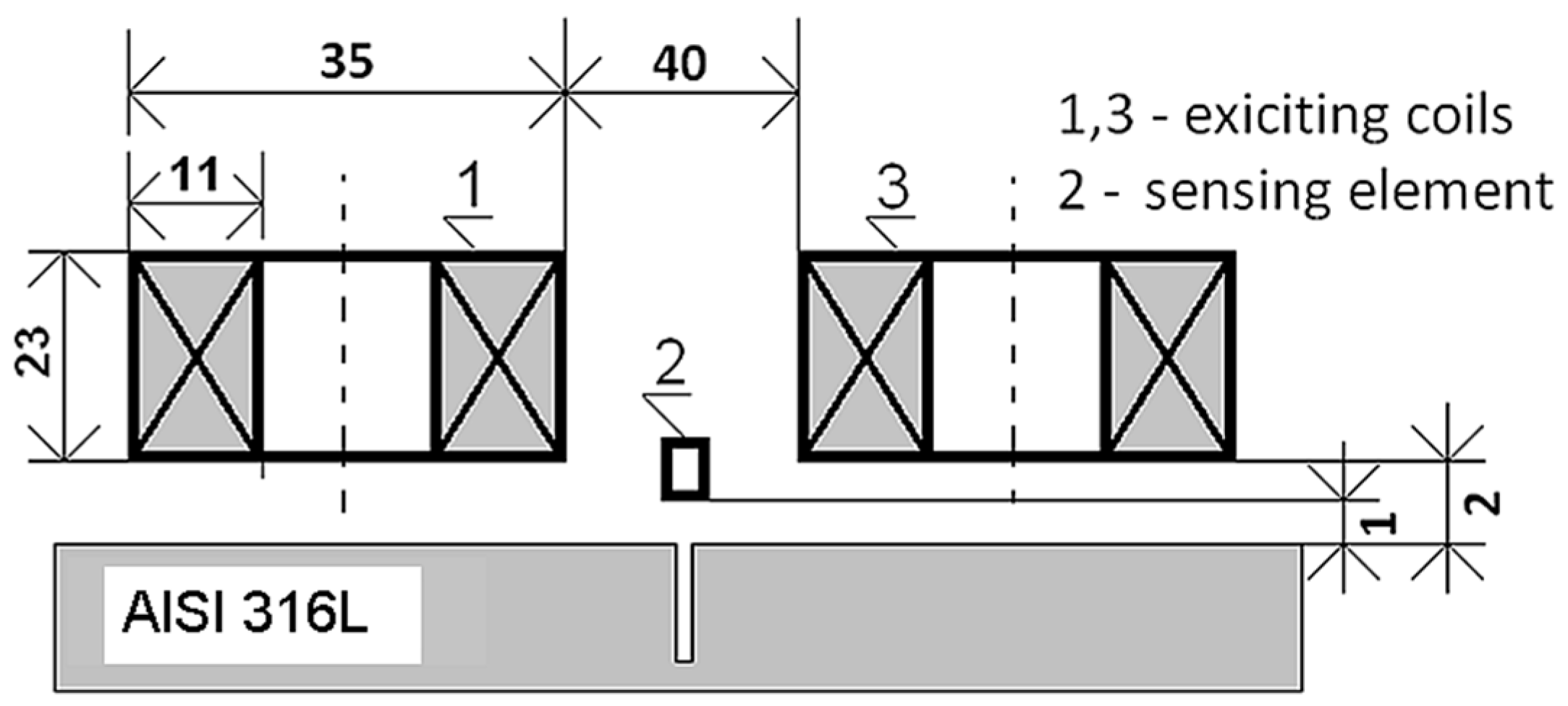
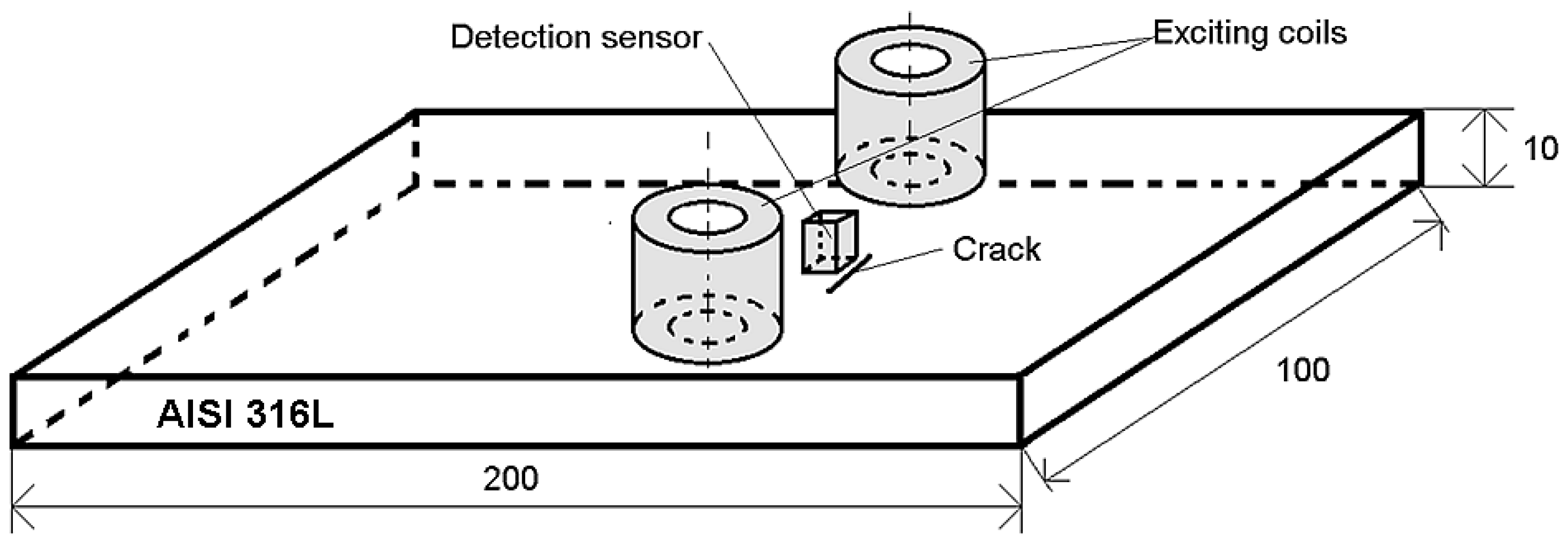
3. Experimental Setup
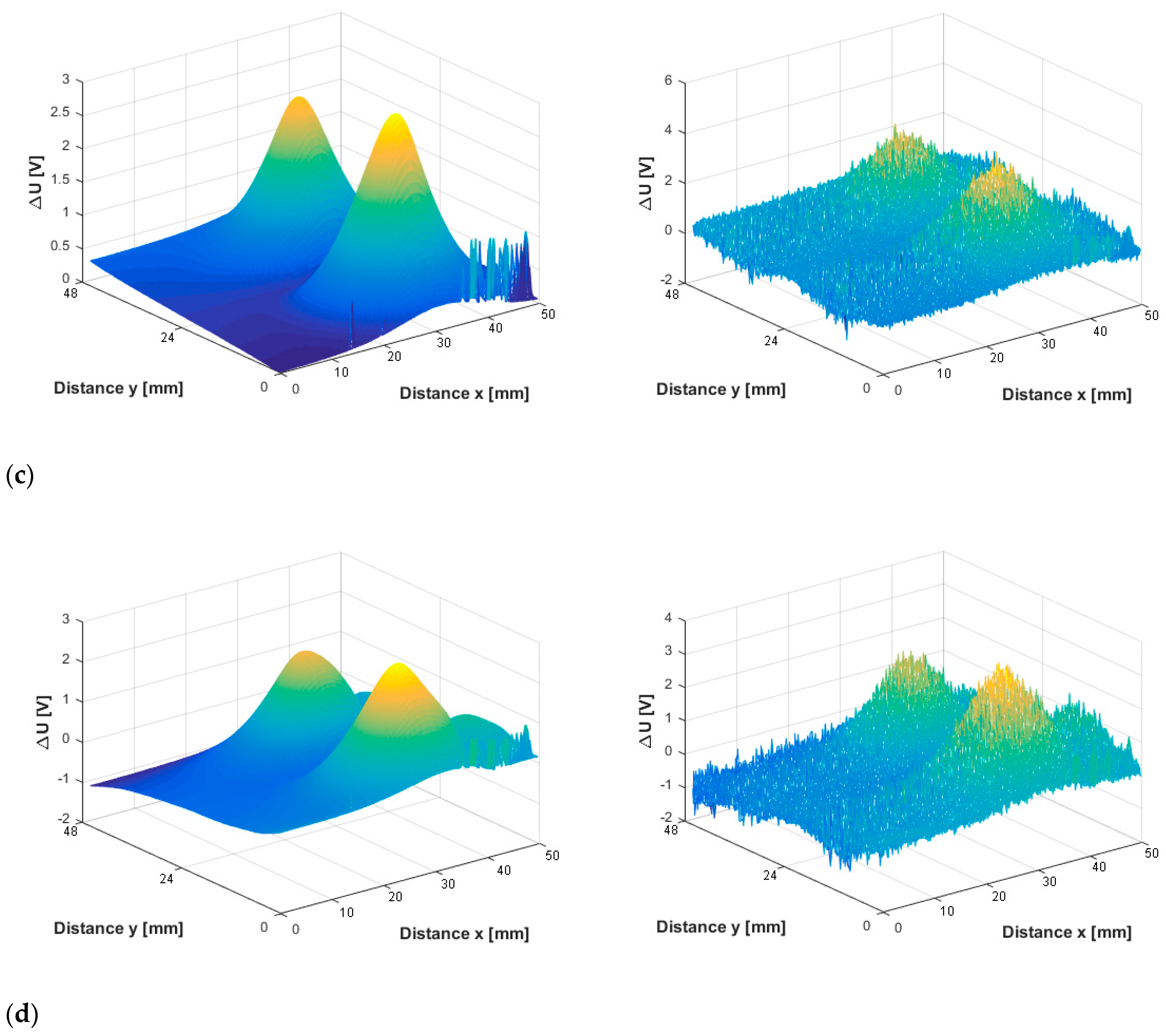
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yusa, N.; Huang, H.; Miya, K. Numerical evaluation of the ill-posedness of eddy current problems to size real cracks. NDT E Int. 2006, 40, 185–191. [Google Scholar] [CrossRef]
- Fan, M.; Wu, G.; Cao, B.; Gyan, T.S.; Li, Z.; Tian, G. Uncertainty metric in model-based eddy current inversion using the adaptive Monte Carlo method. Measurement 2019, 137, 323–331. [Google Scholar] [CrossRef]
- Cai, C.; Miorelli, R.; Lambert, M.; Rodet, T.; Lesselier, D.; Lhuillier, P.E. Metamodel-based Markov-Chain-Monte-Carlo parameter inversion applied in eddy current flaw characterization. NDT E Int. 2018, 99, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Biju, N.; Ganesan, N.; Krishnamurthy, C.V.; Balasubramaniam, K. Defect sizing simulation studies for the tone-burst eddy current thermography using genetic algorithm based inversion. J. Nondestruct. Eval. 2012, 31, 342–348. [Google Scholar] [CrossRef]
- Zhu, P.; Cheng, Y.; Banerjee, P.; Tamburrino, A.; Deng, Y. A novel machine learning model for eddy current testing with uncertainty. NDT E Int. 2019, 101, 104–112. [Google Scholar] [CrossRef]
- Duca, A.; Rebican, M.; Duca, L.; Janousek, L.; Altinoz, T. Advanced PSO algorithms and local search strategies for NDT-ECT inverse problems. In Proceedings of the 2014 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 28–29 November 2014; p. 5, ISBN 978-1-4799-6821-3. [Google Scholar]
- Grimberg, R. Electromagnetic non-destructive evaluation: Present and future. J. Mech. Eng. 2011, 57, 204–217. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, X. Electromagnetic imaging methods for nondestructive evaluation applications. Sensors 2011, 11, 11774–11808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haddar, H.; Jiang, Z.; Riahi, M.K. A robust inversion method for quantitative 3D shape reconstruction from coaxial eddy current measurements. J. Sci. Comput. 2017, 70, 29–59. [Google Scholar] [CrossRef] [Green Version]
- Ramos, H.G.; Ribeiro, A.L. Image post-processing and inversion for eddy current crack detection problems. In Proceedings of the 2016 IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016; p. 6, ISBN 978-1-4673-8292-2. [Google Scholar]
- Ribeiro, L.A.; Pasadas, D.; Ramos, H.G.; Rocha, T. Regularization of the inversion process in eddy current characterization of superficial defects. In Proceedings of the 20th International Workshop on Electromagnetic Non-destructive Evaluation, Sendai, Japan, 21–23 September 2015; Yusa, N., Uchimoto, T., Kikichi, H., Eds.; IOS Press: Amsterdam, The Netherlands, 2016; pp. 48–54, ISBN 978-1-61499-638-5. [Google Scholar]
- Ahmed, S.; Miorelli, R.; Salucci, M.; Massa, A. Real-time flaw characterization through learning-by-examples techniques: A comparative study applied to ECT. In Proceedings of the 21st International Workshop on Electromagnetic Non-destructive Evaluation, Lisbon, Portugal, 25–28 September 2016; Ramos, H.G., Ribeiro, A.L., Eds.; IOS Press: Amsterdam, The Netherlands, 2017; pp. 228–235, ISBN 978-1-61499-766-5. [Google Scholar]
- Behun, L.; Smetana, M. Decreasing uncertainty in width estimation of EDM cracking from eddy-current Signals. In Proceedings of the 11th International Conference ELEKTRO 2016, Strbske Pleso, Slovakia, 16–18 May 2016; pp. 474–477, ISBN 978-1-4673-8698-2. [Google Scholar]
- Behun, L.; Smetana, M.; Capova, K. Estimation of defect geometry in eddy current non-destructive evaluation of conductive biomaterials. Acta Tech. CSAV 2018, 63, 43–52. [Google Scholar]



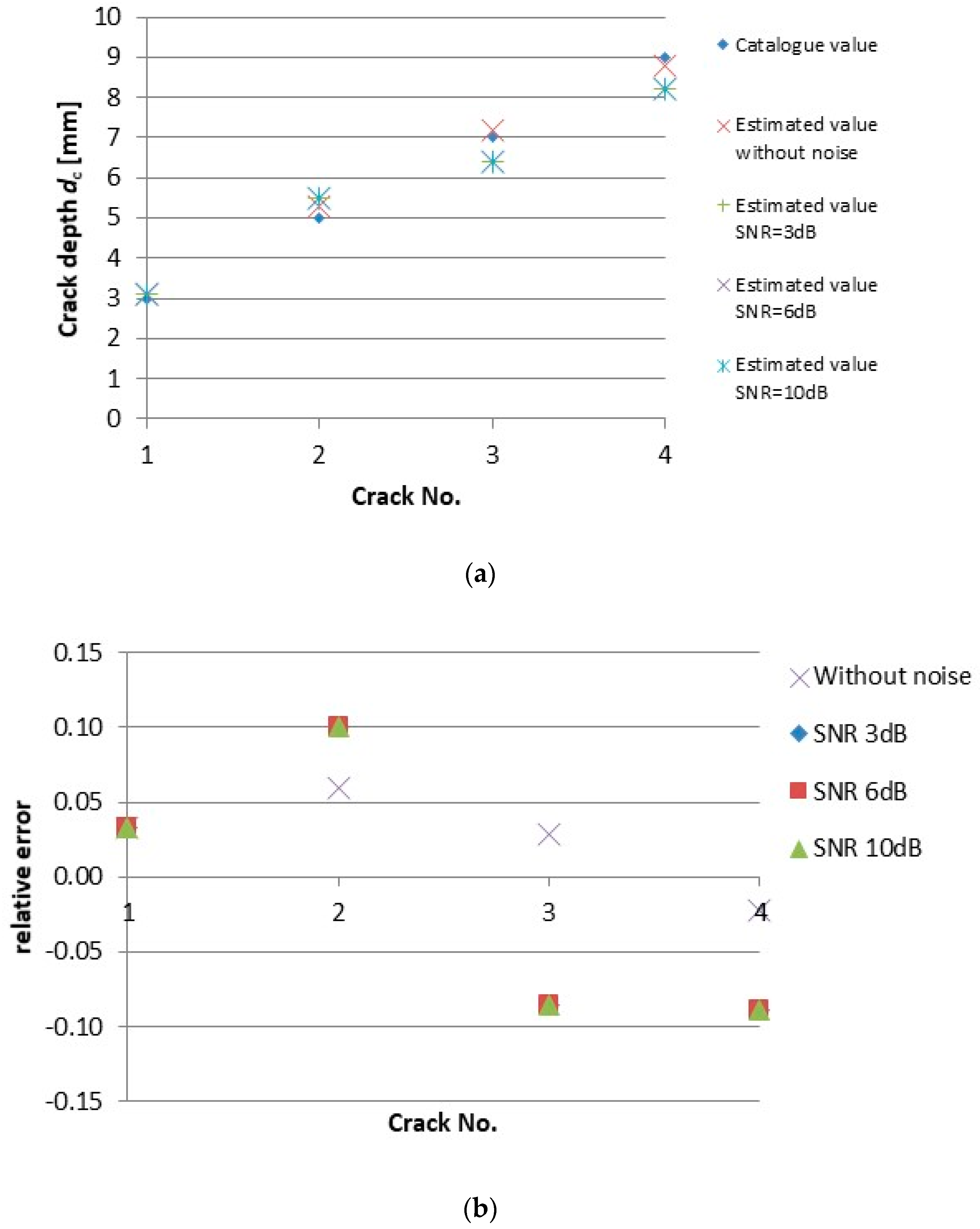
| Crack No. | lc [mm] | wc [mm] | dc [mm] |
|---|---|---|---|
| 1 | 9 | 0.20 | 3 |
| 2 | 15 | 0.25 | 5 |
| 3 | 21 | 0.25 | 7 |
| 4 | 27 | 0.25 | 9 |
| Crack No. | Real Crack Length | SNR [dB] | |||
|---|---|---|---|---|---|
| 0 | 3 | 6 | 10 | ||
| 1 | 9.0 | 10.0 | 11.5 | 11.0 | 9.5 |
| 2 | 15.0 | 16.0 | 17.0 | 16.0 | 16.0 |
| 3 | 21.0 | 21.5 | 24.0 | 23.5 | 23.0 |
| 4 | 27.0 | 25.5 | 28.5 | 28.0 | 27.5 |
| Crack No. | Real Crack Depth | SNR [dB] | |||
|---|---|---|---|---|---|
| 0 | 3 | 6 | 10 | ||
| 1 | 3.0 | 3.1 | 3.1 | 3.1 | 3.1 |
| 2 | 5.0 | 5.3 | 5.5 | 5.5 | 5.5 |
| 3 | 7.0 | 7.2 | 6.4 | 6.4 | 6.4 |
| 4 | 9.0 | 8.8 | 8.2 | 8.2 | 8.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smetana, M.; Behun, L.; Gombarska, D.; Janousek, L. New Proposal for Inverse Algorithm Enhancing Noise Robust Eddy-Current Non-Destructive Evaluation. Sensors 2020, 20, 5548. https://doi.org/10.3390/s20195548
Smetana M, Behun L, Gombarska D, Janousek L. New Proposal for Inverse Algorithm Enhancing Noise Robust Eddy-Current Non-Destructive Evaluation. Sensors. 2020; 20(19):5548. https://doi.org/10.3390/s20195548
Chicago/Turabian StyleSmetana, Milan, Lukas Behun, Daniela Gombarska, and Ladislav Janousek. 2020. "New Proposal for Inverse Algorithm Enhancing Noise Robust Eddy-Current Non-Destructive Evaluation" Sensors 20, no. 19: 5548. https://doi.org/10.3390/s20195548
APA StyleSmetana, M., Behun, L., Gombarska, D., & Janousek, L. (2020). New Proposal for Inverse Algorithm Enhancing Noise Robust Eddy-Current Non-Destructive Evaluation. Sensors, 20(19), 5548. https://doi.org/10.3390/s20195548





