Displacement Study of a Large-Scale Freeform Timber Plate Structure Using a Total Station and a Terrestrial Laser Scanner
Abstract
:1. Introduction
2. Experimental Tests
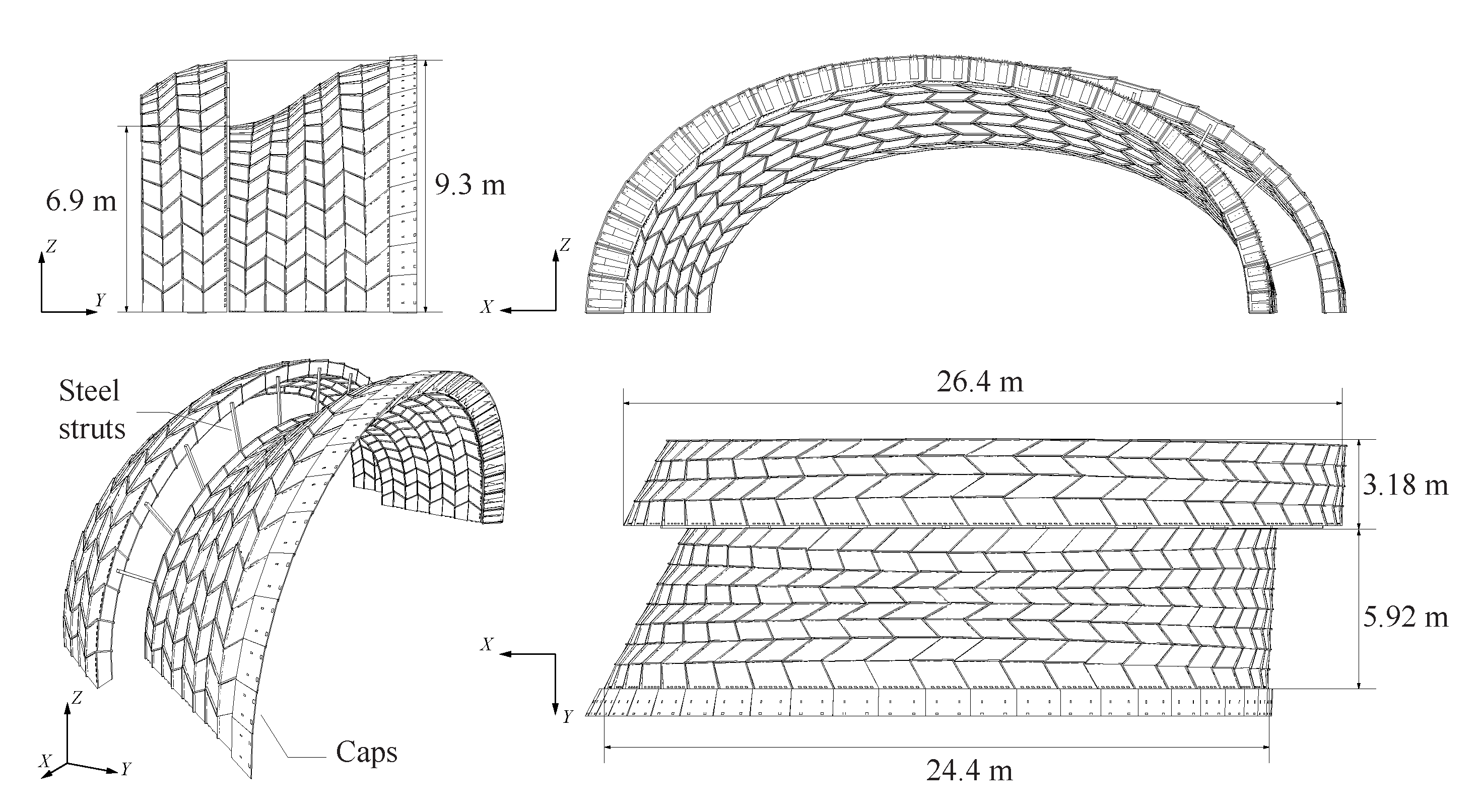
2.1. Structural Design
2.2. Fabrication and Assembly
2.3. Supports
2.4. Loading Procedure
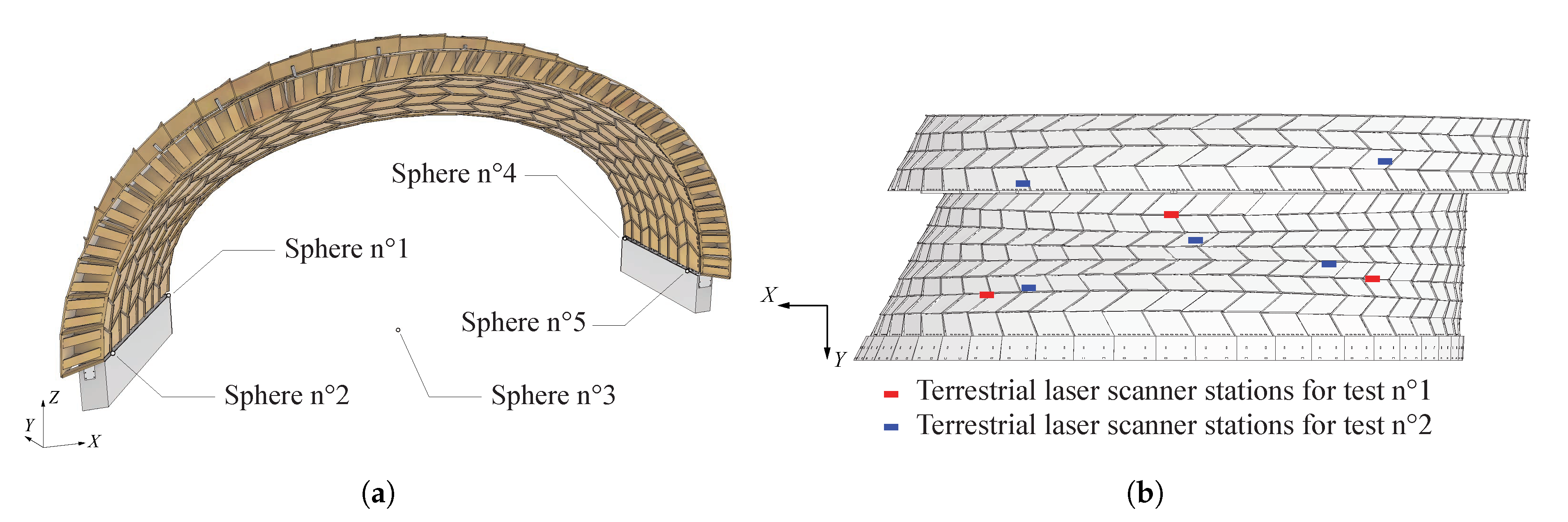
- Test n° 1: arch n° 22 not connected to half of arch n° 21, which was therefore not considered in the test measurements, on 22 May 2018 and;
- Test n° 2: arch n° 22 fixed to half of arch n° 21 by steel struts, as illustrated in Figure 2, on 23 May 2018.
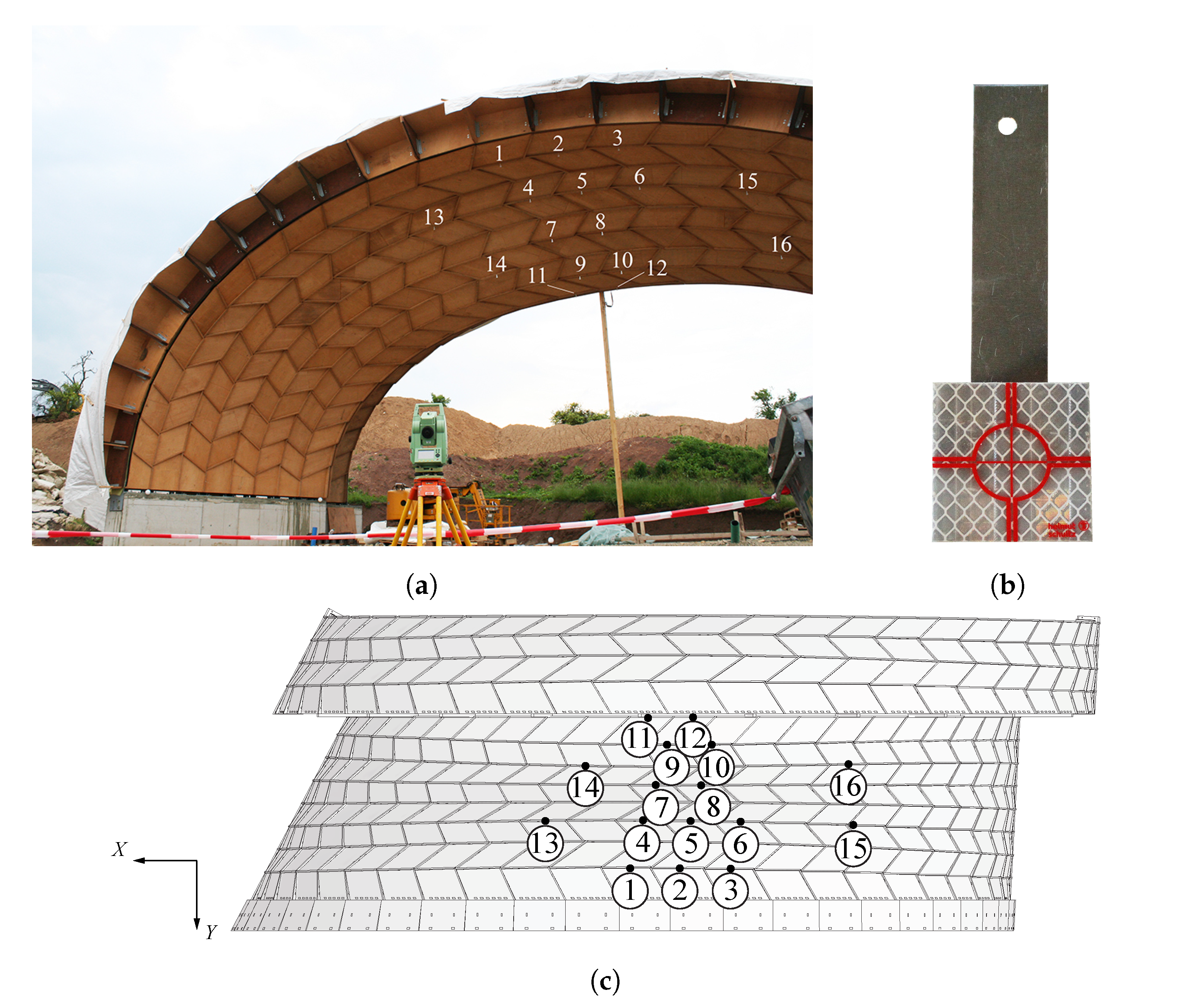
3. Instrumentation
- Load case n° 1: test n° 1 before loading
- Load case n° 2: test n° 1 under final loading
- Load case n° 3: test n° 2 before loading
- Load case n° 4: test n° 2 under final loading
3.1. Total Station
3.2. Terrestrial Laser Scanner
3.2.1. Survey Procedure
3.2.2. Registration and Pre-Processing
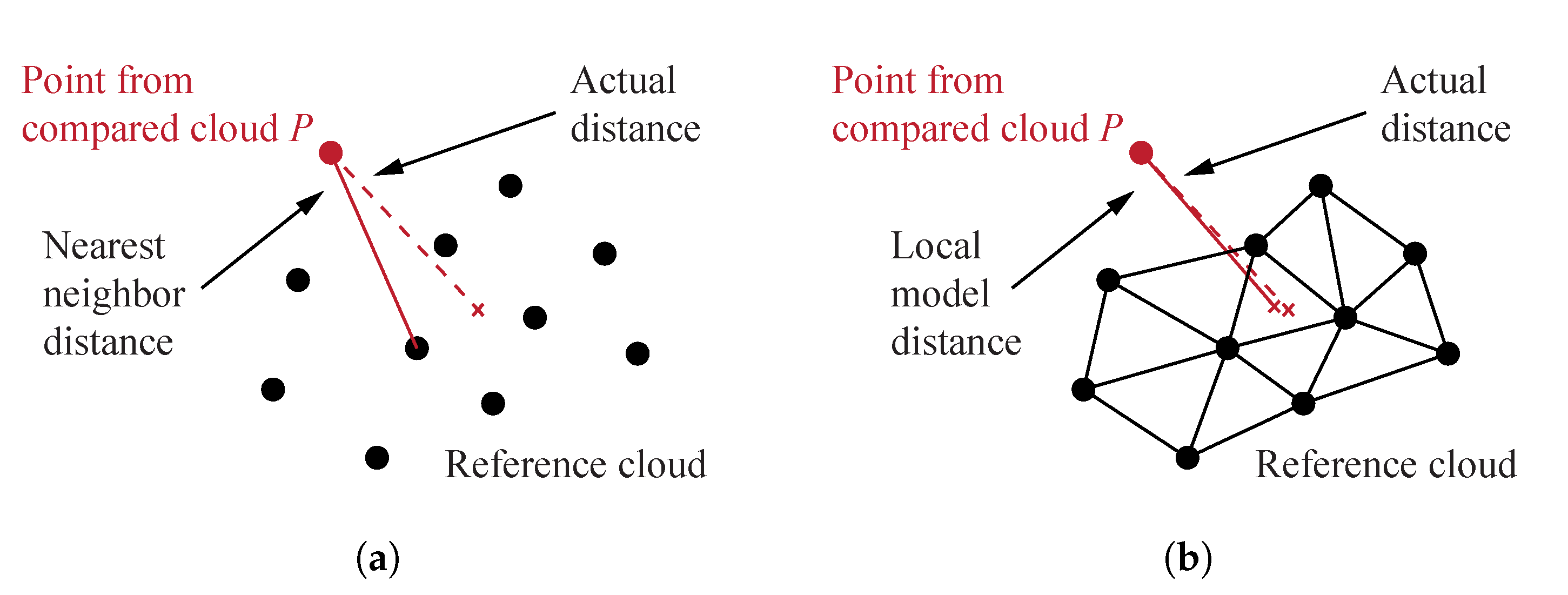
3.2.3. Distances Computation
4. Numerical Model
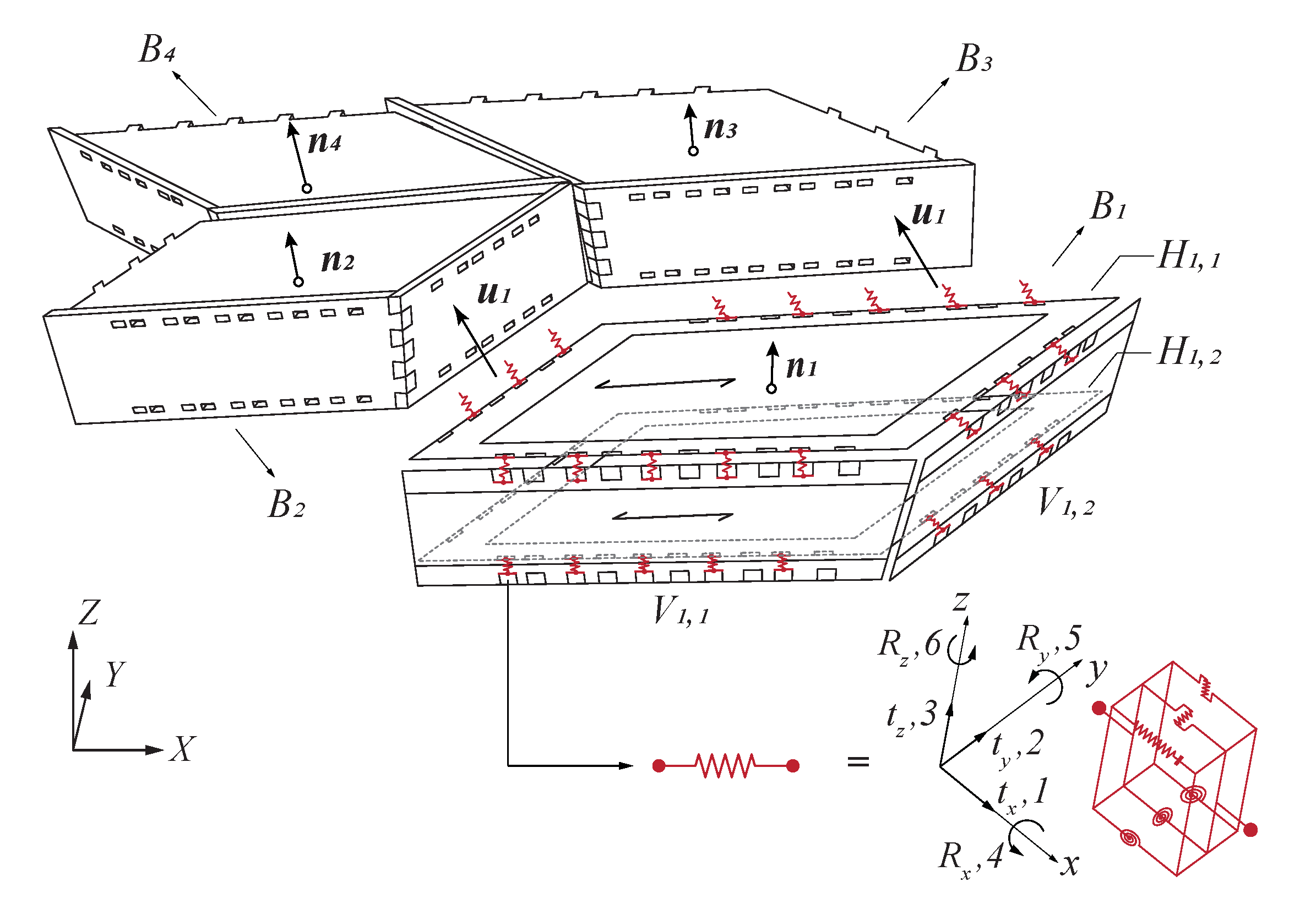
4.1. Semi-Rigid Spring Model
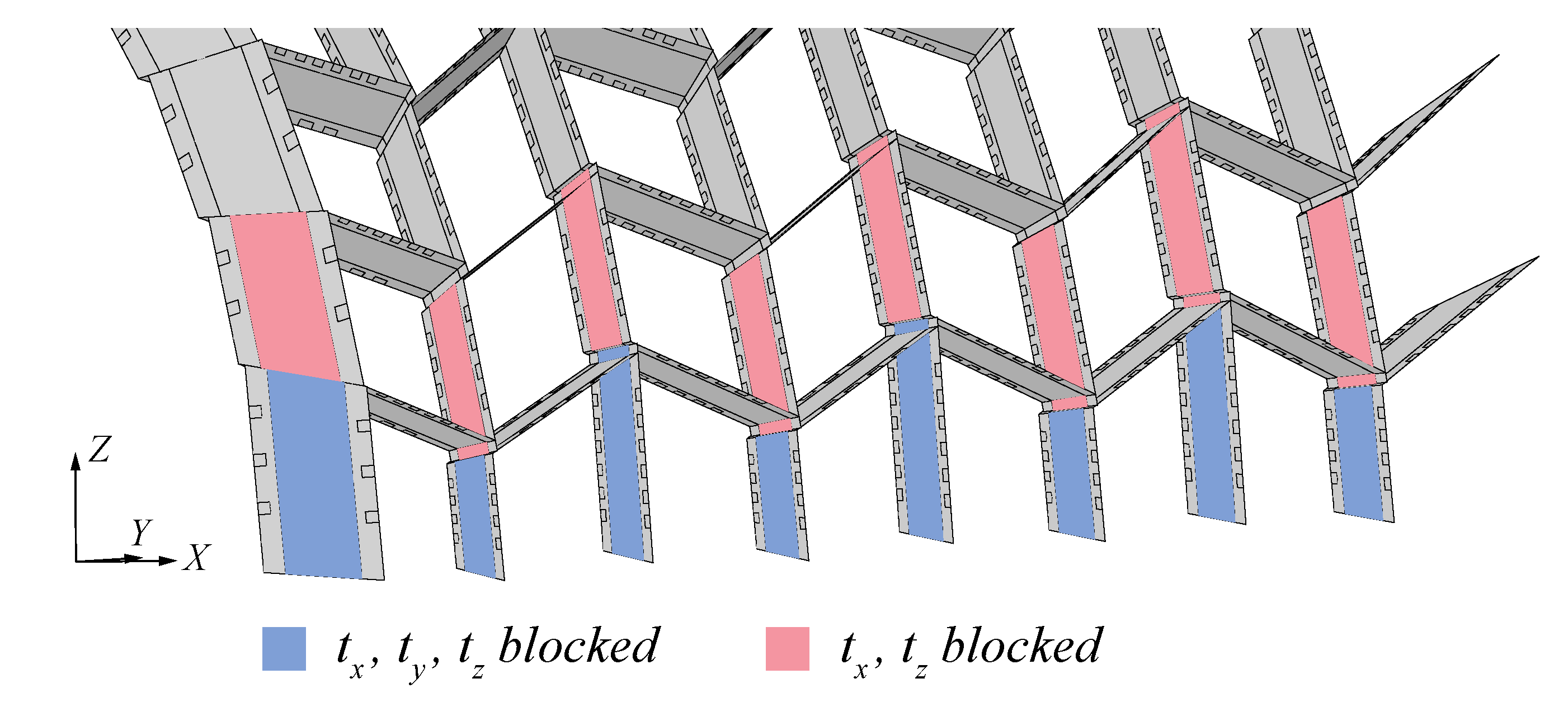
4.2. Loads and Boundary Conditions
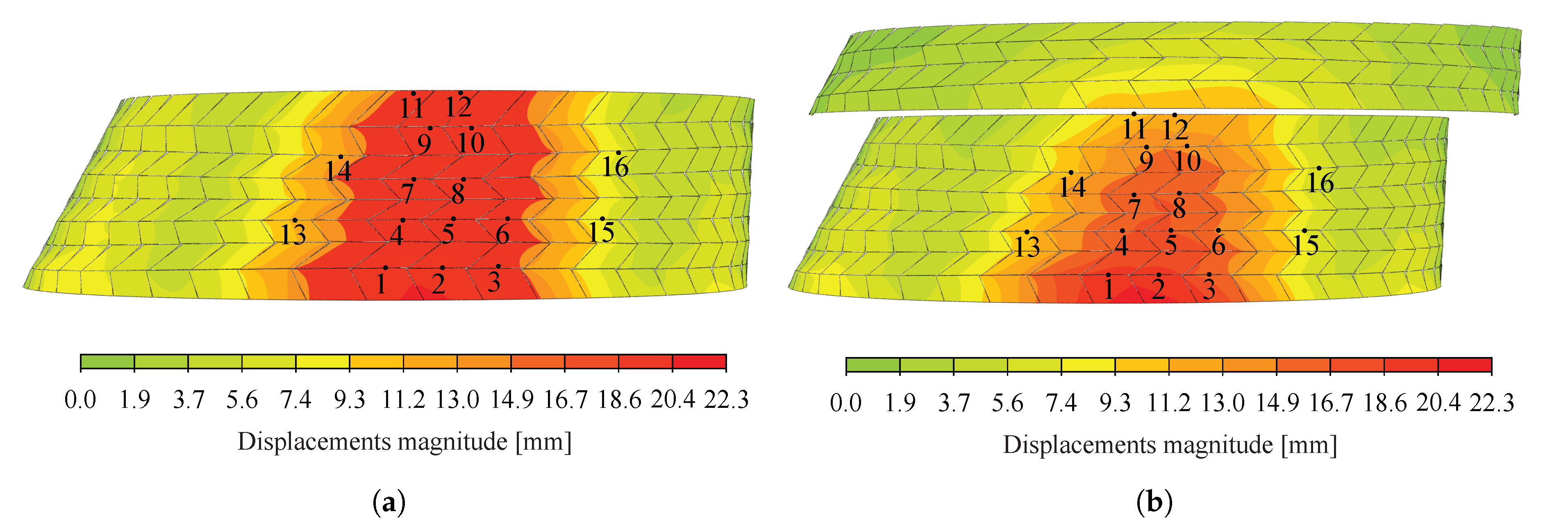
5. Results and Discussion
5.1. Discrete Target Positions
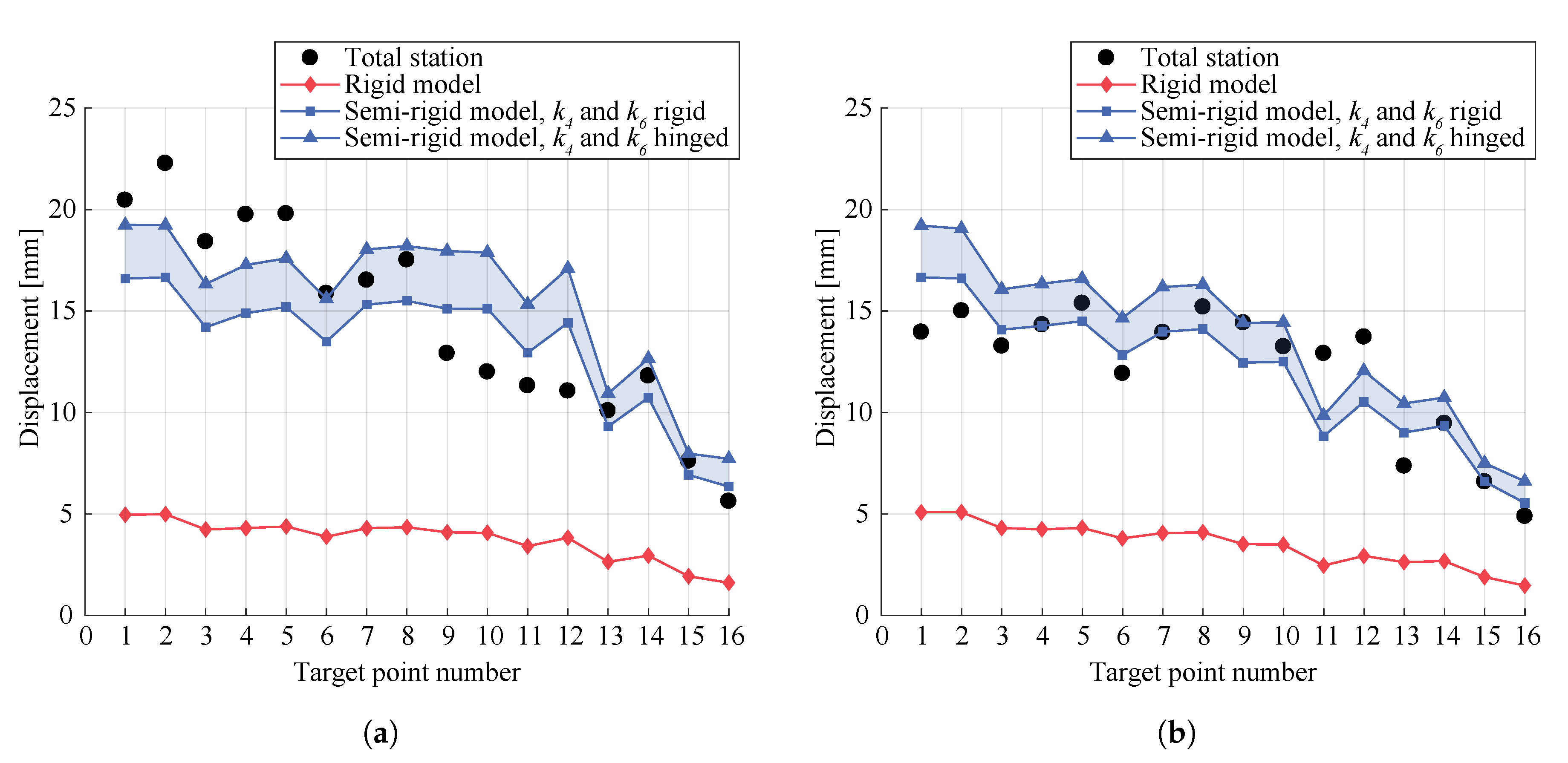
5.1.1. Total Station Measurements
5.1.2. Validation of the Numerical Model
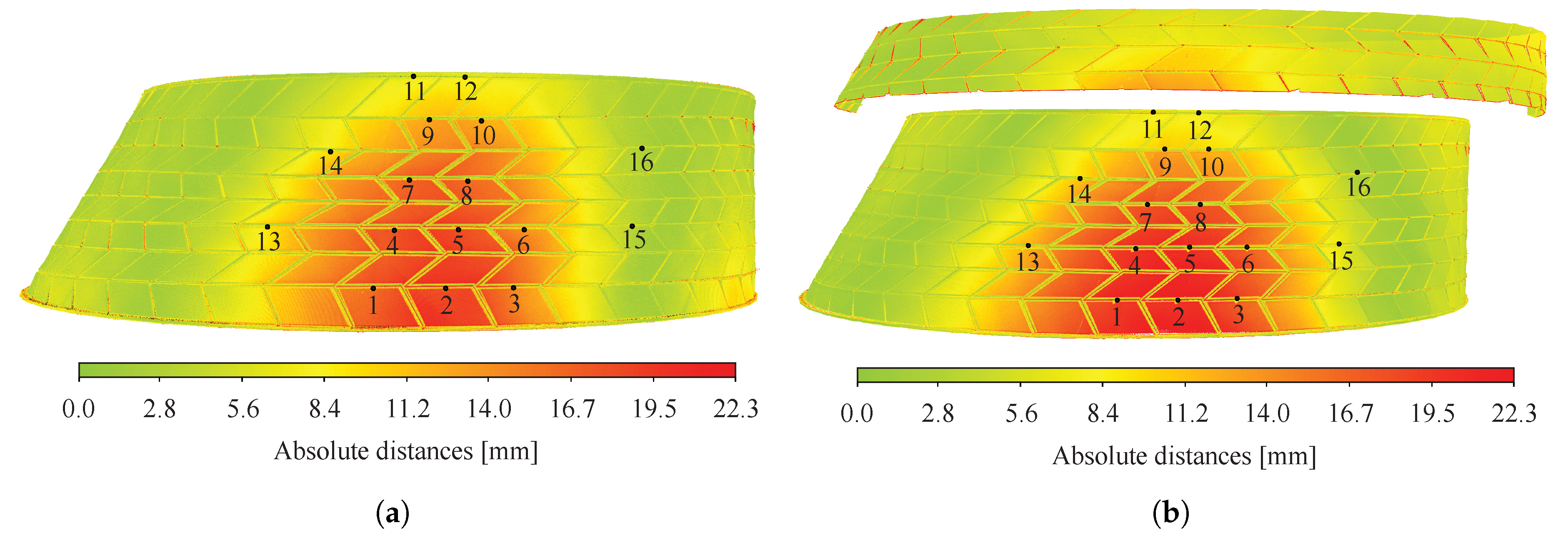
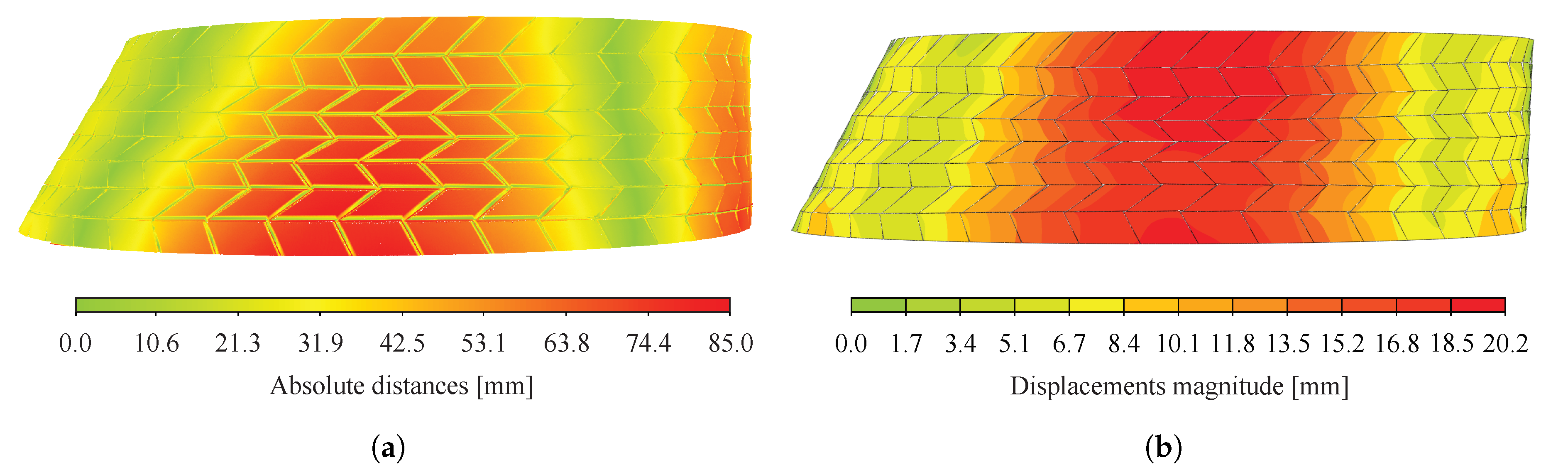
5.2. Displacement Fields
5.2.1. Cloud-Cloud Distances Computation
5.2.2. Total Station Measurements vs. Point Clouds
5.2.3. Validation of the Numerical Model
5.2.4. Evaluation of the Built Geometry
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Assembly System

References
- La Magna, R.; Gabler, M.; Reichert, S.; Schwinn, T.; Waimer, F.; Menges, A.; Knippers, J. From Nature to Fabrication: Biomimetic Design Principles for the Production of Complex Spatial Structures. Int. J. Space Struct. 2013, 28, 27–39. [Google Scholar] [CrossRef]
- Li, J.M.; Knippers, J. Segmental Timber Plate Shell for the Landesgartenschau Exhibition Hall in Schwäbisch Gmünd—The Application of Finger Joints in Plate Structures. Int. J. Space Struct. 2015, 30, 123–140. [Google Scholar] [CrossRef]
- Robeller, C. Integral Mechanical Attachment for Timber Folded Plate Structures. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2015. [Google Scholar] [CrossRef]
- Gamerro, J.; Robeller, C.; Weinand, Y. Rotational mechanical behaviour of wood-wood connections with application to double-layered folded timber-plate structure. Constr. Build. Mater. 2018, 165, 434–442. [Google Scholar] [CrossRef]
- Stitic, A.; Nguyen, A.C.; Rad, A.R.; Weinand, Y. Numerical Simulation of the Semi-Rigid Behaviour of Integrally Attached Timber Folded Surface Structures. Buildings 2019, 9, 55. [Google Scholar] [CrossRef] [Green Version]
- Menges, A. BUGA Wood Pavilion 2019. 2019. Available online: http://www.achimmenges.net/?p=20987 (accessed on 13 December 2019).
- Negro, P. Do We Still Need Full-Scale Testing of Complete Structures? In Proceedings of the 5th International Conference on Advances in Experimental Structural Engineering, Taipei, Taiwan, 8–9 November 2013. [Google Scholar]
- Tuomi, R.L. Full-Scale Testing of Wood Structures. In Full-Scale Load Testing of Structures; Schriever, W.R., Ed.; American Society for Testing and Materials: West Conshohocken, PA, USA, 1980; pp. 45–62. [Google Scholar] [CrossRef]
- Wong, H.; Teng, J.; Wang, Z. A pulley-based system for the simulation of distributed loading on shell roof structures. Exp. Tech. 2006, 27, 21–27. [Google Scholar] [CrossRef]
- Harris, H.G.; Sabnis, G. Structural Modeling and Experimental Techniques, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1999; p. 808. [Google Scholar] [CrossRef]
- Stitic, A.; Robeller, C.; Weinand, Y. Experimental investigation of the influence of integral mechanical attachments on structural behaviour of timber folded surface structures. Thin-Walled Struct. 2018, 122, 314–328. [Google Scholar] [CrossRef]
- Doudak, G.; McClure, G.; Smith, I. Experimental Evaluation of Load Paths in Light-Frame Wood Structure. J. Struct. Eng. 2012, 138, 258–265. [Google Scholar] [CrossRef]
- Liddell, I. Frei Otto and the development of gridshells. Case Stud. Struct. Eng. 2015, 4, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.P.; Ni, Y.Q. Structural Health Monitoring of Large Civil Engineering Structures, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; p. 306. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Recent research and applications of GPS-based monitoring technology for high-rise structures. Struct. Control Health Monit. 2013, 20, 649–670. [Google Scholar] [CrossRef]
- Nassif, H.H.; Gindy, M.; Davis, J. Comparison of laser Doppler vibrometer with contact sensors for monitoring bridge deflection and vibration. NDTE Int. 2005, 38, 213–218. [Google Scholar] [CrossRef]
- Castellini, P.; Martarelli, M.; Tomasini, E. Laser Doppler Vibrometry: Development of advanced solutions answering to technology’s needs. Mech. Syst. Signal Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
- Hill, C.D.; Sippel, K.D. Modern Deformation Monitoring: A Multi Sensor Approach. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002; p. 12. [Google Scholar]
- Kuhlmann, H.; Gläser, A. Investigation of New Measurement Techniques for Bridge Monitoring. In Proceedings of the 2nd Symposium on Geodesy for Geotechnical and Structural Engineering, Berlin, Germany, 21–24 May 2002; pp. 123–132. [Google Scholar]
- Cosser, E.; Roberts, G.; Meng, X.; Dodson, A. Measuring the dynamic deformation of bridges using a total station. In Proceedings of the 11th Fédération Internationale des Géomètres (FIG) Symposium on Deformation Measurements, Santorini, Greece, 5–28 May 2003; p. 9. [Google Scholar]
- Barham, W.; Oncul, F.; Meadati, P.; Oguzmert, M. Three Dimensional Displacement Response Study of a Rubble-House Using a 3D Laser Scanner. Comput. Civ. Eng. 2012, 477–484. [Google Scholar] [CrossRef]
- Lee, M.C.; Tsai, Y.L.; Wang, R.Z.; Lin, M.L. Finding the displacement of wood structure in heritage building by 3D laser scanner. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015, II-5/W3, 165–169. [Google Scholar] [CrossRef] [Green Version]
- Ziolkowski, P.; Szulwic, J.; Miskiewicz, M. Deformation Analysis of a Composite Bridge during Proof Loading Using Point Cloud Processing. Sensors 2018, 18, 4332. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gawronek, P.; Makuch, M.; Mitka, B.; Gargula, T. Measurements of the Vertical Displacements of a Railway Bridge Using TLS Technology in the Context of the Upgrade of the Polish Railway Transport. Sensors 2019, 19, 4275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robeller, C.; Konakovic, M.; Dedijer, M.; Pauly, M.; Weinand, Y. A Double-layered Timber Plate Shell—Computational Methods for Assembly, Prefabrication and Structural Design, Zurich, Switzerland, 12–13 September 2016. In Advances in Architectural Geometry 2016; Adriaenssens, S., Gramazio, F., Kohler, M., Menges, A., Pauly, M., Eds.; vdf Hochschulverlag AG: Zurich, Switzerland, 2016; pp. 104–122. [Google Scholar] [CrossRef]
- Nguyen, A.C.; Vestartas, P.; Weinand, Y. Design framework for the structural analysis of free-form timber plate structures using wood-wood connections. Autom. Constr. 2019, 107, 102948. [Google Scholar] [CrossRef]
- Blaß, H.J.; Streib, J. BauBuche Beech Laminated Veneer Lumber—Design Assistance for Drafting and Calculation in Accordance with Eurocode 5, 2017. Available online: http://pollmeier.com/en/downloads/design-manual.html (accessed on 13 December 2019).
- Leica Geosystems. User Manual TC(R)303/305/307, Version 3.5.; Leica Geosystems: Sen Gallen, Switzerland, 1998. [Google Scholar]
- FARO Technologies Inc. FARO® Laser Scanner User Manual; FARO Technologies Inc.: Lake Mary, FL, USA, 2018. [Google Scholar]
- Theiler, P.; Schindler, K. Automatic registration of terrestrial laser scanner point clouds using natural planar surfaces. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, I-3, 173–178. [Google Scholar] [CrossRef] [Green Version]
- Girardeau-Montaut, D. Détection de changement sur des données géométriques tridimensionnelles. Ph.D. Thesis, Télécom ParisTech, Paris, France, 2006. [Google Scholar]
- CloudCompare. User manual - Version 2.6.1. 2015. Available online: http://www.cloudcompare.org/doc/qCC/CloudCompare%20v2.6.1%20-%20User%20manual.pdf (accessed on 13 December 2019).
- Dassault Systèmes Simulia. Abaqus 6.12 Online Documentation, 2012. Available online: http://abaqus.software.polimi.it/v6.12/index.html (accessed on 13 December 2019).
- Rad, A.R.; Burton, H.; Weinand, Y. Performance assessment of through-tenon timber joints under tension loads. Constr. Build. Mater. 2019, 207, 706–721. [Google Scholar] [CrossRef]
- Rad, A.R.; Weinand, Y.; Burton, H. Experimental push-out investigation on the in-plane force-deformation behavior of integrally-attached timber Through-Tenon joints. Constr. Build. Mater. 2019, 215, 925–940. [Google Scholar] [CrossRef]
- Time and Date AS. Weather in Manternach, 2018. Available online: https://www.timeanddate.com/weather/@2960296/historic?month=5&year=2018 (accessed on 13 December 2019).
- Block, P.; Rippmann, M.; Van Mele, T.; Escobedo, D. The Armadillo Vault: Balancing computation and traditional craft. In FABRICATE 2017, Stuttgart, Germany, 6–8 April 2017; Menges, A.B., Sheil, R.G., Skavara, M., Eds.; UCL Press: London, UK, 2017; pp. 286–293. [Google Scholar]
- Wang, L.L.; Chang, Y.Z. Effects of Initial Geometric Imperfections on the Stability of Steel-Concrete Composite Ribbed Shell. In Advances in Civil Engineering and Architecture; Trans Tech Publications Ltd.: Durnten-Zurich, Switzerland, 2011; Volume 243, pp. 7001–7004. [Google Scholar] [CrossRef]
- Liew, A.; Stürz, Y.; Guillaume, S.; Mele, T.V.; Smith, R.; Block, P. Active control of a rod-net formwork system prototype. Autom. Constr. 2018, 96, 128–140. [Google Scholar] [CrossRef]
- Roche, S.; Gamerro, J.; Weinand, Y. Multiple Tab-and-Slot Joint: Improvement of the Rotational Stiffness for the Connection of Thin Structural Wood Panels. In Proceedings of the WCTE 2016 World Conference on Timber Engineering e-book, Vienna, Austria, 22–25 August 2016; pp. 1556–1564. [Google Scholar] [CrossRef]







| Property | Symbol | Value | Unit |
|---|---|---|---|
| Elastic modulus 11 | 13,200 | N/mm | |
| Elastic modulus 22 | 2200 | N/mm | |
| Elastic modulus 33 | 2200 | N/mm | |
| Shear modulus 12 | 820 | N/mm | |
| Shear modulus 13 | 430 | N/mm | |
| Shear modulus 23 | 430 | N/mm | |
| Poisson’s ratio 12 | 0.365 | – | |
| Poisson’s ratio 13 | 0.464 | – | |
| Poisson’s ratio 23 | 0.726 | – | |
| Density | 800 | kg/m |
| Symbol | Component | Value | Units |
|---|---|---|---|
| translation x | 416.81 | N/mm | |
| translation y | 15,009.24 | N/mm | |
| translation z | 9489.04 | N/mm | |
| rotation around x | 10/0.1 | N·mm/° | |
| rotation around y | 170,190.41 | N·mm/° | |
| rotation around z | 10/0.1 | N·mm/° |
| Displacements [mm] | |||
|---|---|---|---|
| Target n° | Test n° 1 | Test n° 2 | Difference [%] |
| 1 | 20.5 | 14.0 | −31.8 |
| 2 | 22.3 | 15.0 | −32.6 |
| 3 | 18.4 | 13.3 | −27.9 |
| 4 | 19.8 | 14.3 | −27.5 |
| 5 | 19.8 | 15.4 | −22.3 |
| 6 | 15.9 | 11.9 | −24.8 |
| 7 | 16.5 | 13.9 | −15.6 |
| 8 | 17.5 | 15.2 | −13.2 |
| 9 | 12.9 | 14.4 | +11.7 |
| 10 | 12.0 | 13.2 | +10.4 |
| 11 | 11.3 | 12.9 | +14.1 |
| 12 | 11.1 | 13.7 | +24.1 |
| 13 | 10.1 | 7.4 | −27.0 |
| 14 | 11.8 | 9.5 | −19.8 |
| 15 | 7.6 | 6.6 | −13.4 |
| 16 | 5.6 | 4.9 | −13.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, A.C.; Weinand, Y. Displacement Study of a Large-Scale Freeform Timber Plate Structure Using a Total Station and a Terrestrial Laser Scanner. Sensors 2020, 20, 413. https://doi.org/10.3390/s20020413
Nguyen AC, Weinand Y. Displacement Study of a Large-Scale Freeform Timber Plate Structure Using a Total Station and a Terrestrial Laser Scanner. Sensors. 2020; 20(2):413. https://doi.org/10.3390/s20020413
Chicago/Turabian StyleNguyen, Anh Chi, and Yves Weinand. 2020. "Displacement Study of a Large-Scale Freeform Timber Plate Structure Using a Total Station and a Terrestrial Laser Scanner" Sensors 20, no. 2: 413. https://doi.org/10.3390/s20020413
APA StyleNguyen, A. C., & Weinand, Y. (2020). Displacement Study of a Large-Scale Freeform Timber Plate Structure Using a Total Station and a Terrestrial Laser Scanner. Sensors, 20(2), 413. https://doi.org/10.3390/s20020413





