Strong Wind Characteristics and Buffeting Response of a Cable-Stayed Bridge under Construction
Abstract
:1. Introduction
2. Full-Scale Measurement Set-Ups
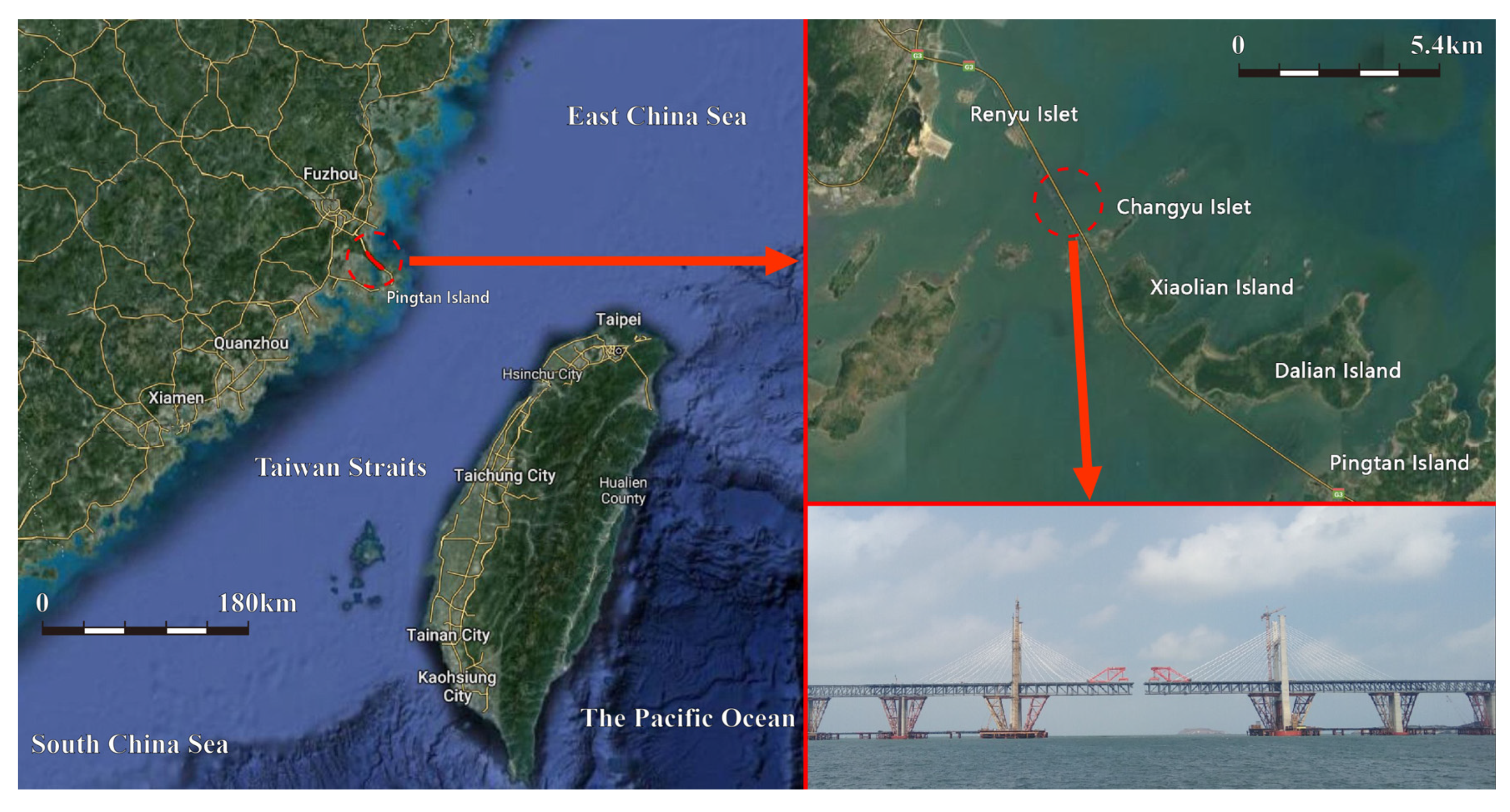
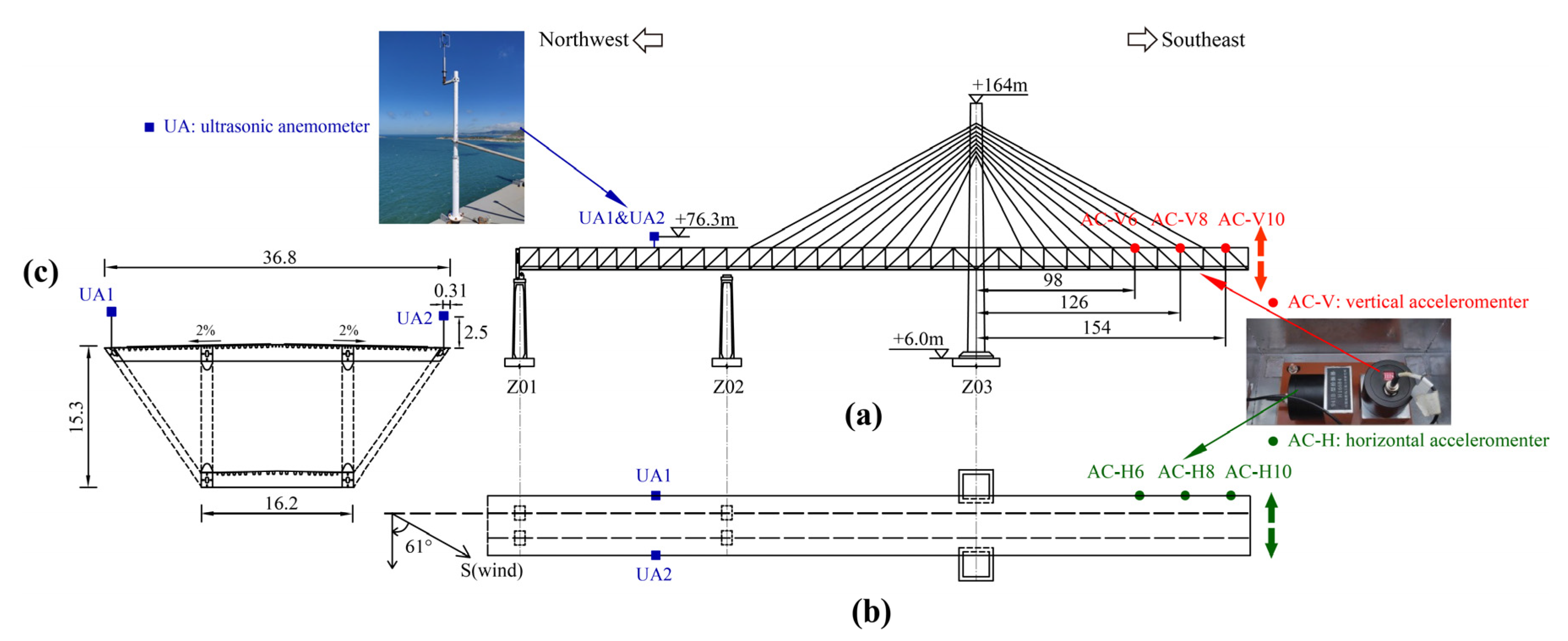
2.1. Cable-Stayed Bridge and Its Surrounding Topography
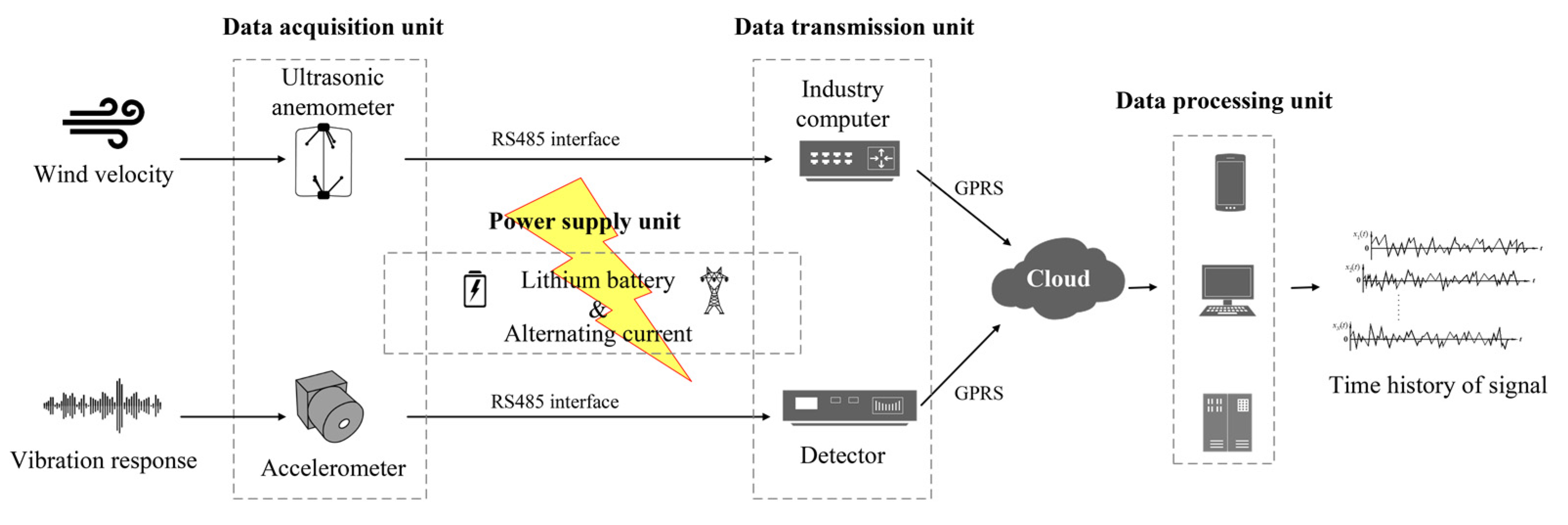
2.2. Wireless Monitoring System
3. Strong Wind Characteristics
3.1. Mean Wind Velocity and Direction
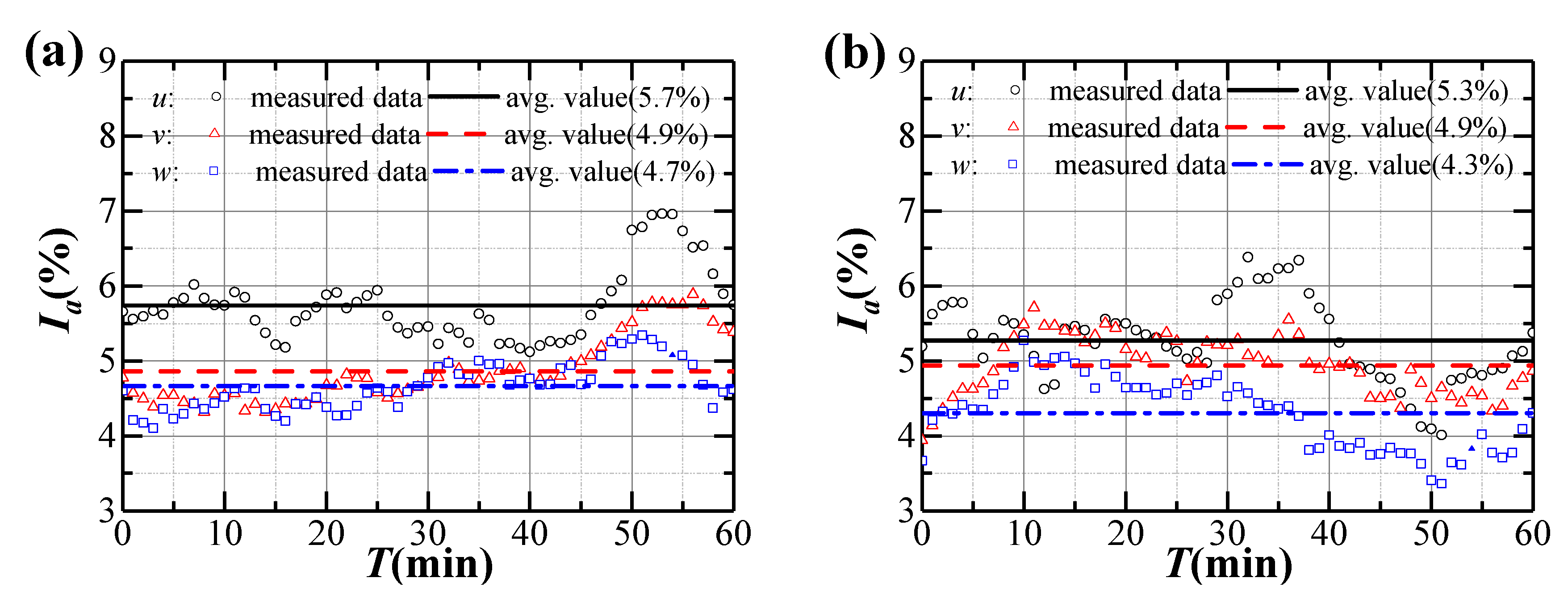
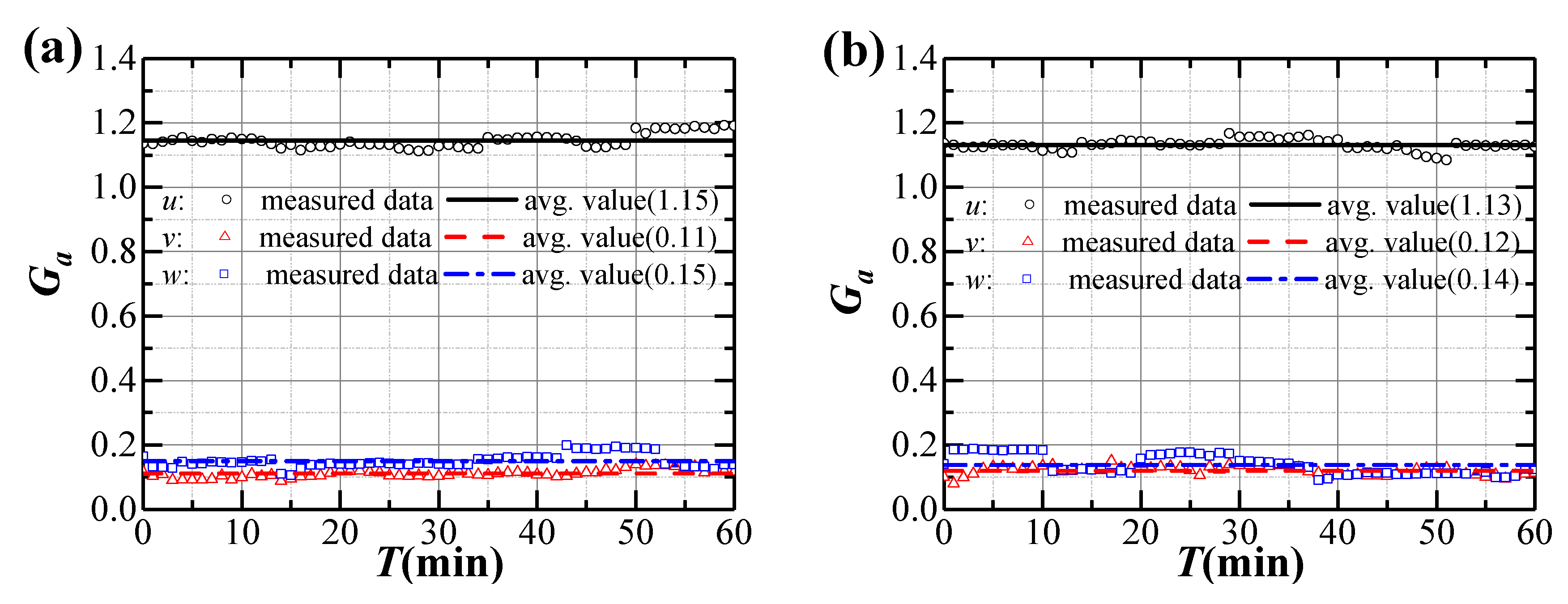
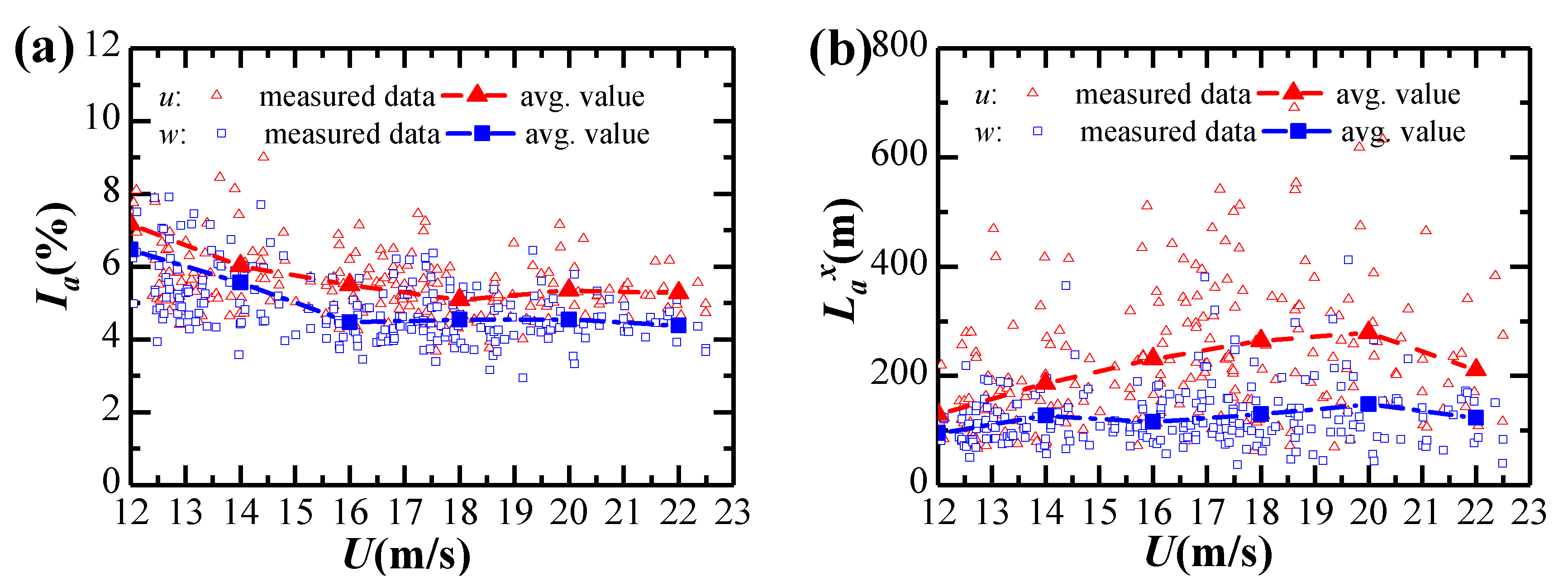
3.2. Turbulence Intensity and Gust Factor
3.3. Turbulence Integral Scale
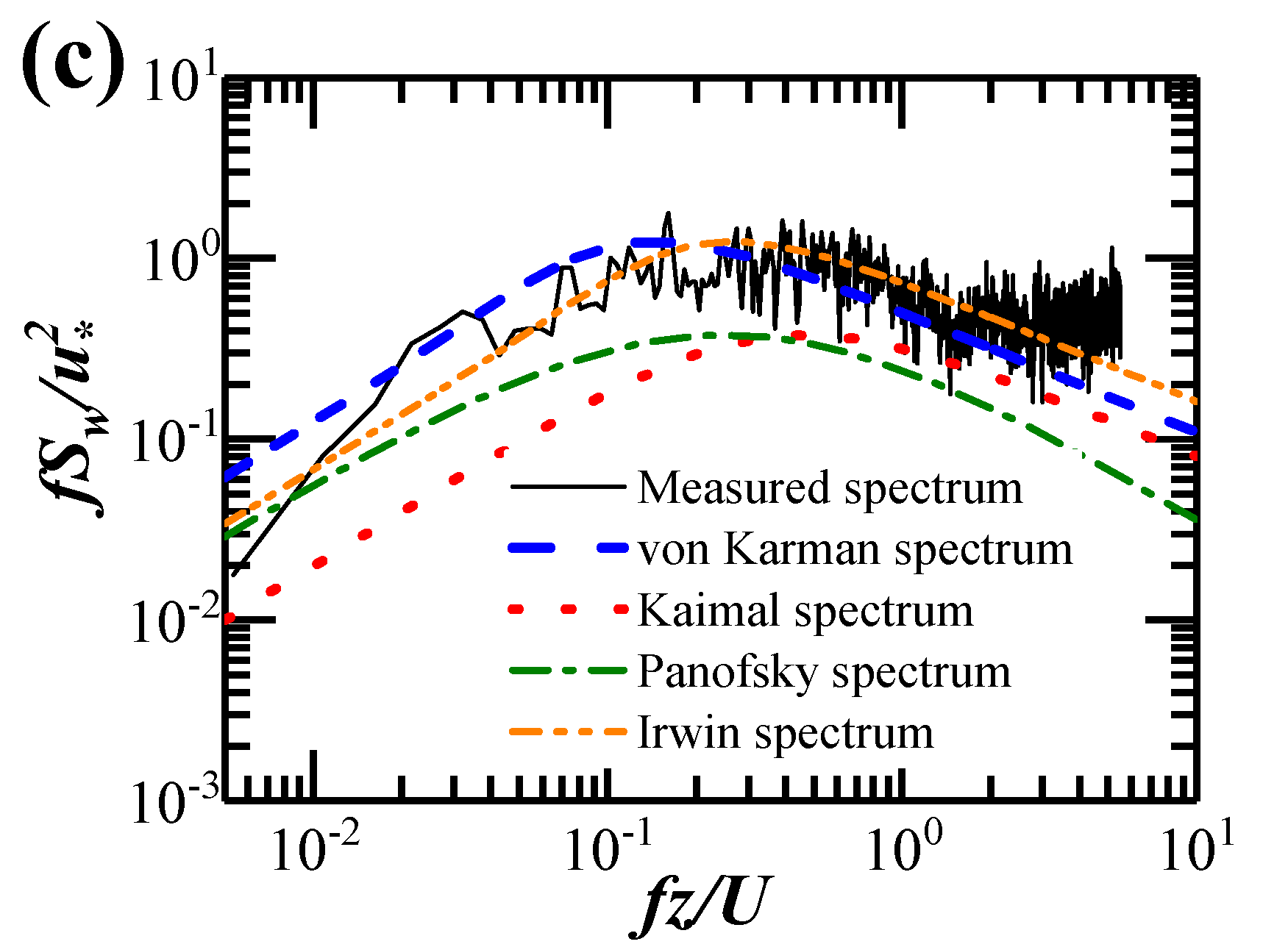
3.4. Wind Velocity Power Spectrum
4. Buffeting Response of the Bridge during the Extreme Single-Cantilever State
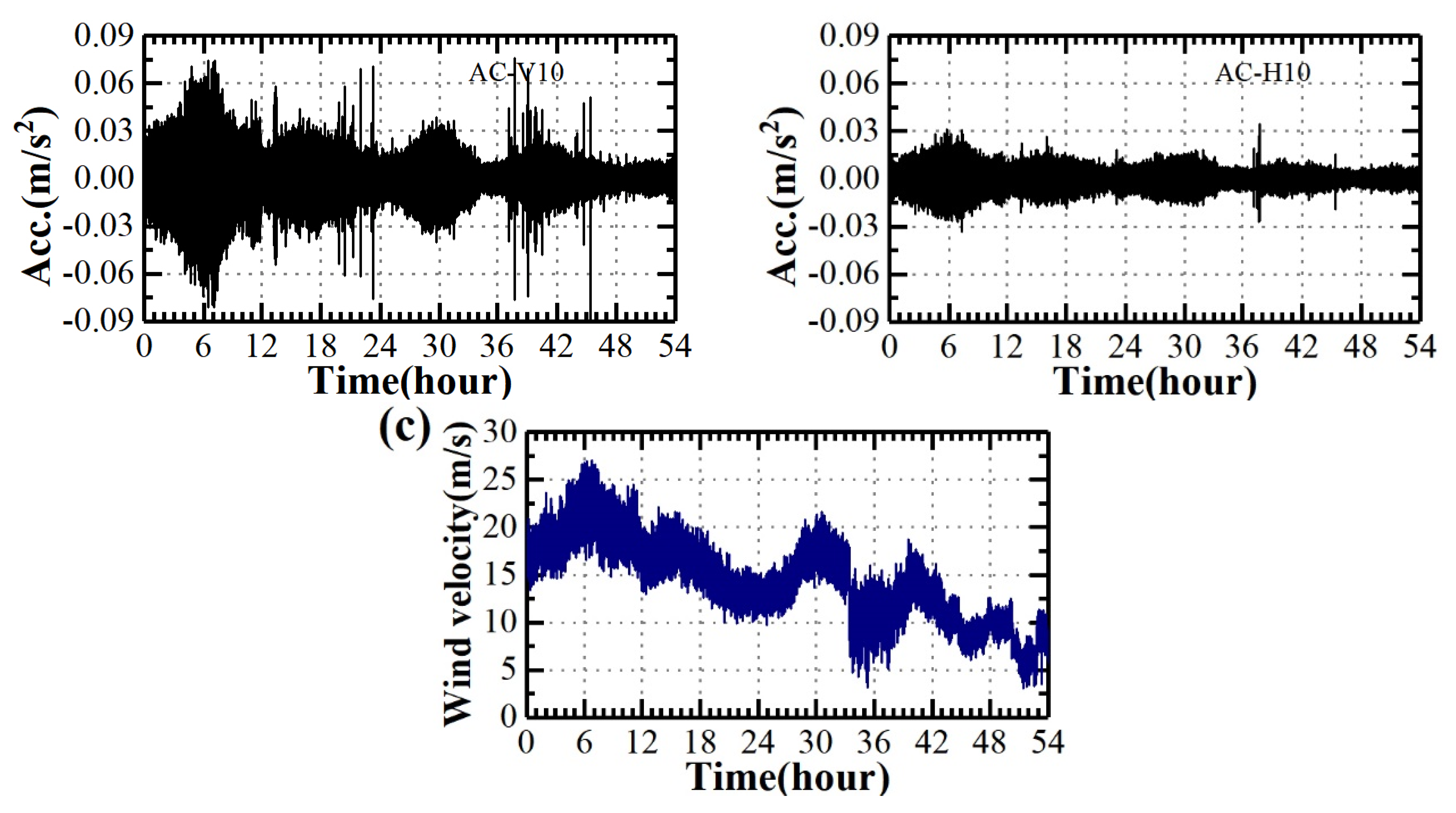
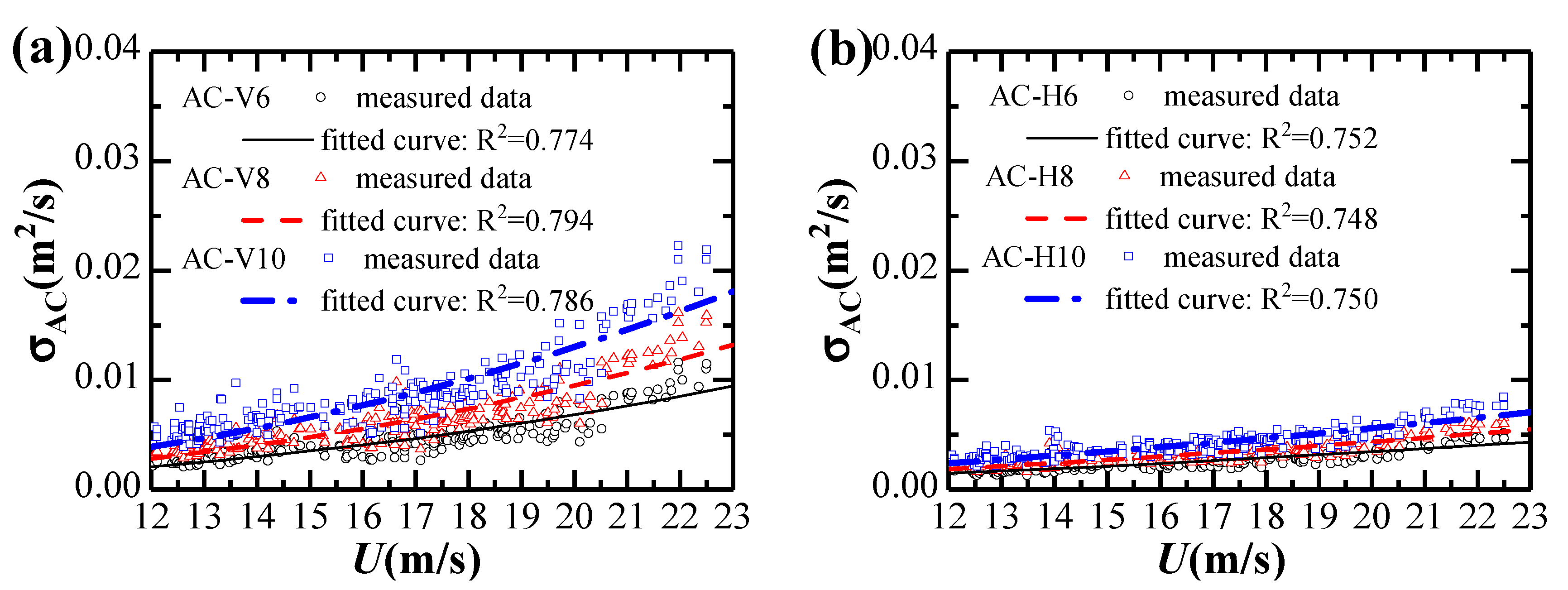
4.1. Acceleration Responses
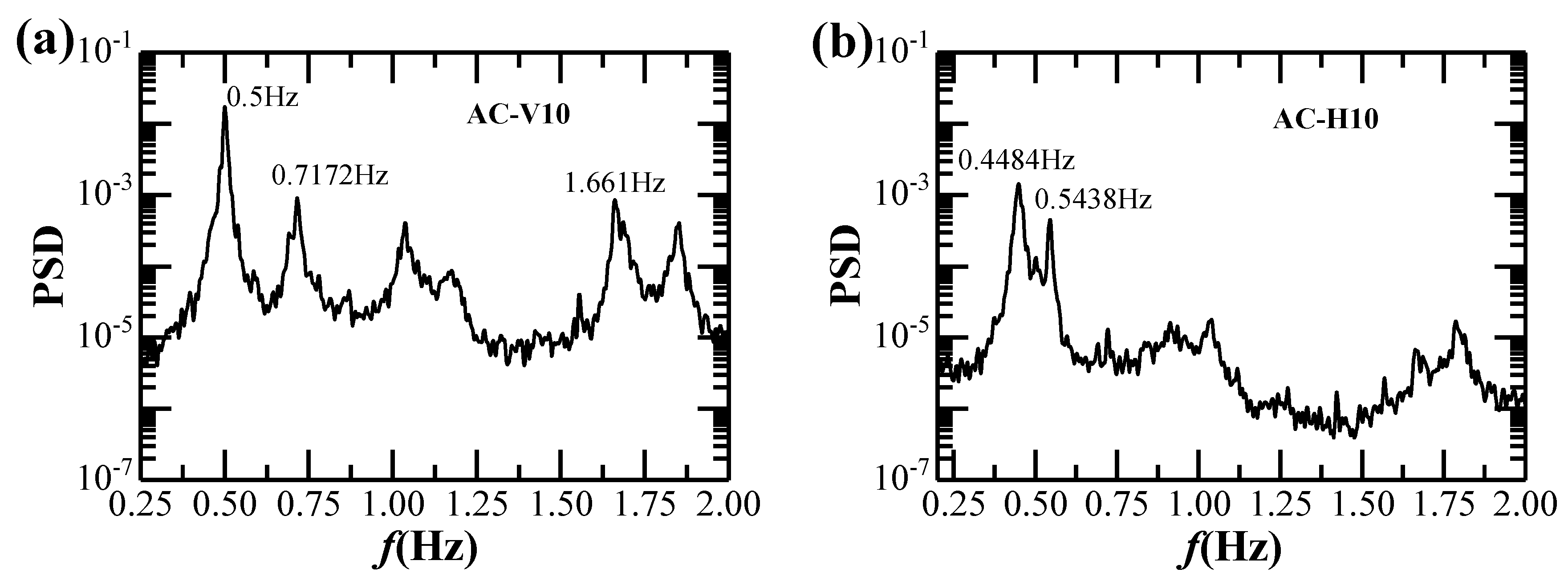
4.2. Spectra and Natural Frequencies
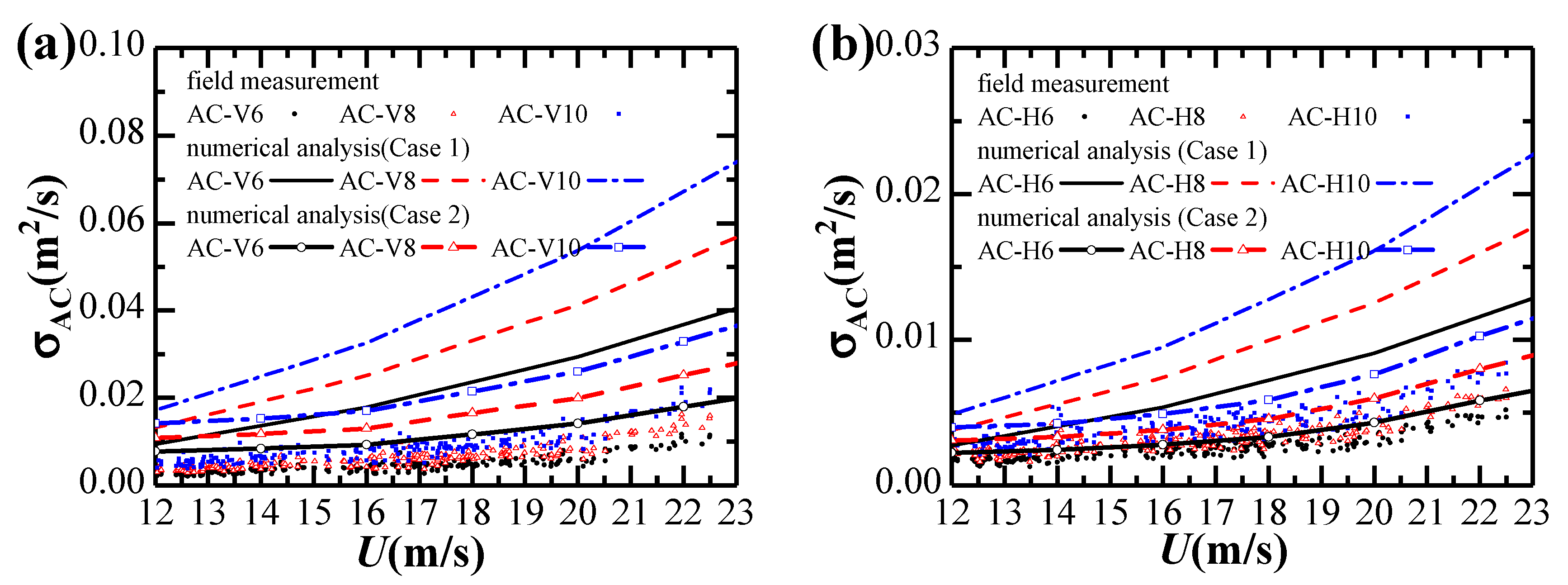
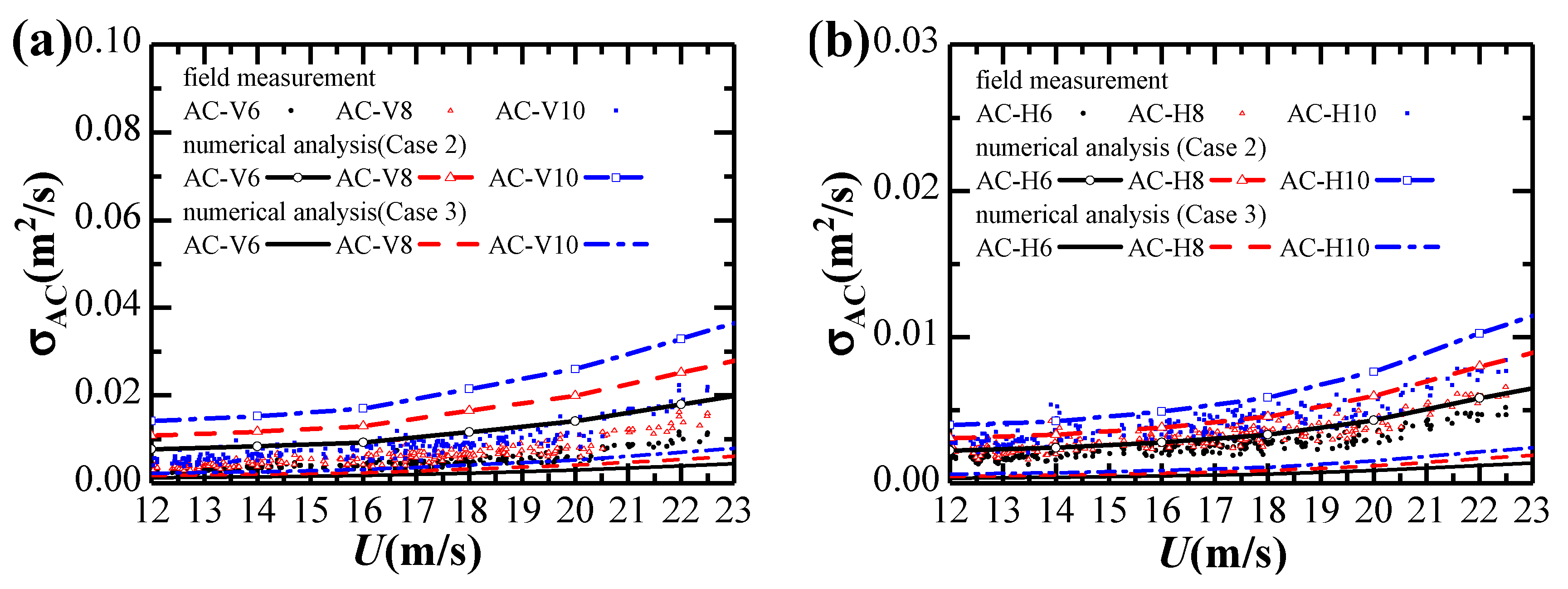
4.3. Comparison of Buffeting Analysis between Field-Measurements and Numerical Analysis
5. Conclusions
- Wind characteristics during typhoon and monsoon events share a considerable amount of similarity, and can be described as the input turbulence parameters for the current wind-induced vibration theory.
- The longitudinal turbulence integral scales are consistent with those in regional structural codes, while the turbulence intensities and gust factors are less than the recommended values. The wind spectra obtained via the field measurements can be well approximated by the von Karman spectra.
- The vertical acceleration responses of the bridge girder at the extreme single-cantilever state are larger than those in the horizontal direction, and the increasing tendencies with mean wind speeds are also different from each other.
- The buffeting analysis results using wind turbulence parameters proposed in the design code and the unity aerodynamic admittance of the bridge girder are on the conservative side, and they can be used in the preliminary phase of the design of cable-stayed bridges.
- The buffeting analysis results using measured wind turbulence parameters provide a good estimate of buffeting response, especially for the horizontal response. Accordingly, it is important to measure wind velocities at the bridge site for reasonable design and construction of cable-stayed bridges.
- The discrepancies between the field-measurements and numerical results may mainly be attributed to the bridge girder aerodynamic admittance, and hence more attention should be given to accurately and reliably identify its values using wind tunnel experiments or computational fluid dynamics simulations in the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hui, M.C.H.; Larsen, A.; Xiang, H.F. Wind turbulence characteristics study at the Stonecutters Bridge site: Part I-Mean wind and turbulence intensities. J. Wind Eng. Ind. Aerodyn. 2009, 97, 22–36. [Google Scholar] [CrossRef]
- Huang, G.Q.; Peng, L.L.; Su, Y.W.; Liao, H.L.; Li, M.S. A wireless high-frequency anemometer instrumentation system for field measurements. Wind Struct. 2015, 20, 739–749. [Google Scholar] [CrossRef]
- Lystad, T.M.; Fenerci, A.; Øiseth, O. Evaluation of mast measurements and wind tunnel terrain models to describe spatially variable wind field characteristics for long-span bridge design. J. Wind Eng. Ind. Aerodyn. 2018, 179, 558–573. [Google Scholar] [CrossRef]
- Lin, L.; Chen, K.; Xia, D.D.; Wang, H.F.; Hu, H.T.; He, F.Q. Analysis on the wind characteristics under typhoon climate at the southeast coast of China. J. Wind Eng. Ind. Aerodyn. 2018, 182, 37–48. [Google Scholar] [CrossRef]
- Solari, G.; Piccardo, G. Probabilistic 3-D turbulence modeling for gust buffeting of structures. Probabilist. Eng. Mech. 2001, 16, 73–86. [Google Scholar] [CrossRef]
- Li, L.; Zhou, Y.; Wang, H.; Zhou, H.; He, X.; Wu, T. An analytical framework for the investigation of tropical cyclone wind characteristics over different measurement conditions. Appl. Sci. 2019, 9, 5385. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.L.; Zhu, L.D.; Wong, K.Y.; Chan, K.W.Y. Field measurement results of Tsing Ma suspension Bridge during Typhoon Victor. Struct. Eng. Mech. 2000, 10, 545–559. [Google Scholar] [CrossRef]
- Yoshizumi, F.; Inoue, H. An experimental approach on aerodynamic stability of a cable-stayed cantilever bridge. J. Wind Eng. Ind. Aerodyn. 2002, 90, 2099–2111. [Google Scholar] [CrossRef]
- Macdonald, J.H.G. Evaluation of buffeting predictions of a cable-stayed bridge from full-scale measurements. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1465–1483. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.B.; Snæbjörnsson, J. Buffeting response of a suspension bridge in complex terrain. Eng. Struct. 2016, 128, 474–487. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhou, X.; Wang, X.; Dong, L.L.; Qian, Y.H. Deployment of a smart structural health monitoring system for long-span arch bridges: A review and a case study. Sensors 2017, 17, 2151. [Google Scholar] [CrossRef] [PubMed]
- He, X.H.; Qin, H.X.; Tao, T.Y.; Liu, W.S.; Wang, H. Measurement of non-stationary characteristics of a landfall typhoon at the Jiangyin bridge site. Sensors 2017, 17, 2186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Z.D.; Wang, H.; Wu, T.; Tao, T.Y.; Mao, J.X. Wind characteristics at Sutong Bridge site using 8-year field measurement data. Wind Struct. 2017, 25, 195–214. [Google Scholar]
- Bastos, F.; Caetano, E.; Cunha, Á.; Cespedes, X.; Flamand, O. Characterisation of the wind properties in the Grande Ravine viaduct. J. Wind Eng. Ind. Aerodyn. 2018, 173, 112–131. [Google Scholar] [CrossRef]
- Fenerci, A.; Øiseth, O. Strong wind characteristics and dynamic response of a long-span suspension bridge during a storm. J. Wind Eng. Ind. Aerodyn. 2018, 172, 116–138. [Google Scholar] [CrossRef]
- Thalla, O.; Stiros, S. Wind-induced fatigue and asymmetric damage in a timber bridge. Sensors 2018, 18, 3867. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Jung, H.; Kong, M.J.; Lee, D.K.; An, Y.K. In-situ data-driven buffeting response analysis of a cable-stayed bridge. Sensors 2019, 19, 3048. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.M.; Duan, Q.S.; Li, Q.S.; Liao, H.L.; Tao, Q.Y. Aerodynamic characteristics of a long-span cable-stayed bridge under construction. Eng. Struct. 2019, 184, 232–246. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Jones, N.P. Aeroelastic analysis of cable-stayed bridges. J. Struct. Eng. 1990, 116, 279–297. [Google Scholar] [CrossRef]
- Conti, E.; Grillaud, G.; Jacob, J.; Cohen, N. Wind effects on the Normandie cable-stayed bridge: Comparison between full aeroelastic model tests and quasi-steady analytical approach. J. Wind Eng. Ind. Aerodyn. 1996, 65, 189–201. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, K.T.; Lee, H.; Kim, S. Performance of unpretensioned wind stabilizing cables in the construction of a cable-stayed bridge. J. Bridge Eng. 2013, 18, 722–734. [Google Scholar] [CrossRef]
- Ito, Y.; Nakashima, Y.; Kobayashi, H.; Sakai, Y. Gust response evaluation of cable-stayed bridges under erection using gust response analysis and elastic model. In Proceedings of the 9th Asia-Pacific Conference on Wind Engineering, Auckland, New Zealand, 3–7 December 2017. [Google Scholar]
- Yan, L.; Ren, L.; He, X.H.; Li, Y.; Du, B.; Zhong, R.L. Experimental study of buffeting control of Pingtang Bridge during construction. J. Bridge Eng. 2020, in press. [Google Scholar] [CrossRef]
- Xu, F.Y.; Ying, X.Y.; Zhang, Z. Three-degree-of-freedom coupled numerical technique for extracting 18 aerodynamic derivatives of bridge decks. J. Struct. Eng. 2014, 140, 04014085. [Google Scholar] [CrossRef]
- Yang, Y.X.; Wu, T.; Ge, Y.J.; Kareem, A. Aerodynamic stabilization mechanism of a twin box girder with various slot widths. J. Bridge Eng. 2015, 20, 04014067. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, L.D.; Flay, R.G.J. Identification of aerodynamic admittance functions of a flat closed-box deck in different grid-generated turbulent wind fields. Adv. Struct. Eng. 2018, 21, 380–395. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, L.D.; He, X.H.; Flay, R.G.J. Experimental determination of aerodynamic admittance functions of a bridge deck considering oscillation effect. J. Wind Eng. Ind. Aerodyn. 2019, 190, 83–97. [Google Scholar] [CrossRef]
- Ministry of Transportation and Communication of PRC. JTG/T 3360–01-2018 Wind-Resistant Design Specification for Highway Bridges; China Communications Press Co., Ltd.: Beijing, China, 2018. [Google Scholar]
- Zou, Y.F.; Lei, X.; Yan, L.; He, X.H.; Nie, M.; Xie, W.P.; Luo, X.Y. Full-scale measurements of wind structure and dynamic behaviour of a transmission tower during a typhoon. Struct. Infrastruct. Eng. 2019, 1–11. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Simiu, E.; Yeo, D.H. Wind Effects on Structures: Modern Structural Design for Winds, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2019. [Google Scholar]
- Masters, F.J.; Tieleman, H.W.; Balderrama, J.A. Surface wind measurements in three Gulf Coast hurricanes of 2005. J. Wind Eng. Ind. Aerodyn. 2010, 98, 533–547. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1991–1-4:2005 Eurocode 1: Actions on Structures—Part 1–4: General Actions—Wind actions; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Architectural Institute of Japan. Recommendations for Loads on Buildings; AIJ: Tokyo, Japan, 2004. [Google Scholar]
- Flay, R.G.J.; Stevenson, D.C. Integral length scales in strong winds below 20 m. J. Wind Eng. Ind. Aerodyn. 1988, 28, 21–30. [Google Scholar] [CrossRef]
- Von Karman, T. Progress in the statistical theory of turbulence. P. NATL. ACAD. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [Green Version]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Cote, O.R. Spectral characteristics of surface-layer turbulence. Q. J. Roy. Meteor. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Harris, R.I. The nature of the wind. In Seminar on Modern Design of Wind-Sensitive Structures, Construction Industry Research & Information; CIRIA: London, UK, 1971; pp. 29–55. [Google Scholar]
- Bietry, J.; Simiu, E.; Sacre, C. Mean wind profiles and change of terrain roughness. J. Struct. Div. 1978, 104, 1585–1593. [Google Scholar]
- Panofsky, H.A.; McCormick, R.A. The spectrum of vertical velocity near the surface. J. Roy. Meteor. Soc. 1960, 86, 495–503. [Google Scholar] [CrossRef]
- Irwin, H.P.A.H. Wind Tunnel and Analytical Investigations of the Response of Lions’ Gate Bridge to a Turbulent Wind; N.A.E. Report, LTR-LA-210; National Research Council of Canada: Ottawa, ON, Canada, 1997. [Google Scholar]
- Li, Q.S.; Xiao, Y.Q.; Wong, C.K.; Jeary, A.P. Field measurements of typhoon effects on a super tall building. Eng. Struct. 2004, 26, 233–244. [Google Scholar] [CrossRef]
- Ding, Q.S.; Chen, A.R.; Xiang, H.F. Coupled buffeting response analysis of long-span bridges by the CQC approach. Struct. Eng. Mech. 2002, 14, 505–520. [Google Scholar] [CrossRef]
- Strømmen, E.; Hjorth-Hansen, E.; Hansen, S.O.; Bogunovic Jakobsen, J. Aerodynamic investigations for the tender design concepts of the Øresund cable-stayed bridge. J. Wind Eng. Ind. Aerodyn. 1999, 80, 351–372. [Google Scholar] [CrossRef]
- Liepmann, H.W. On the application of statistical concepts to the buffeting problem. J. Aeronaut. Sci. 1952, 19, 793–800. [Google Scholar] [CrossRef]




| Wind Field | Iu (%) | Iv (%) | Iw (%) | Iu:Iv:Iw | Gu | Gv | Gw |
|---|---|---|---|---|---|---|---|
| Typhoon Bailu | 5.7 | 4.9 | 4.7 | 1:0.85:0.81 | 1.15 | 0.11 | 0.15 |
| Strong monsoon | 5.3 | 4.9 | 4.3 | 1:0.94:0.82 | 1.13 | 0.12 | 0.14 |
| Average values | 5.5 | 4.9 | 4.5 | 1:0.89:0.81 | 1.14 | 0.12 | 0.14 |
| JTG/T 3360-01-2018 [28] | 11.0 | 9.6 | 5.5 | 1:0.88:0.5 | 1.24 | ||
| EN 1991-1-4:2005 [33] | 9.8 | 1.30 | |||||
| AIJ 2004 [34] | 11.9 | 1.35 |
| Fitting Parameters | AC-V6 | AC-V8 | AC-V10 | AC-H6 | AC-H8 | AC-H10 |
|---|---|---|---|---|---|---|
| p | −5.19 | −5.12 | −4.97 | −4.63 | −4.53 | −4.43 |
| q | 2.32 | 2.38 | 2.37 | 1.66 | 1.66 | 1.67 |
| Case | Conditions | |
|---|---|---|
| Wind Turbulence Parameters | Bridge Girder Aerodynamic Admittance | |
| Case 1 | Wind spectrum, turbulence intensity and turbulence integral scale proposed by design code | Unity function |
| Case 2 | von Karman spectrum, measured turbulence intensity and turbulence integral scale with mean wind velocity | Unity function |
| Case 3 | von Karman spectrum, measured turbulence intensity and turbulence integral scale with mean wind velocity | Sears function |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Ren, L.; He, X.; Lu, S.; Guo, H.; Wu, T. Strong Wind Characteristics and Buffeting Response of a Cable-Stayed Bridge under Construction. Sensors 2020, 20, 1228. https://doi.org/10.3390/s20041228
Yan L, Ren L, He X, Lu S, Guo H, Wu T. Strong Wind Characteristics and Buffeting Response of a Cable-Stayed Bridge under Construction. Sensors. 2020; 20(4):1228. https://doi.org/10.3390/s20041228
Chicago/Turabian StyleYan, Lei, Lei Ren, Xuhui He, Siying Lu, Hui Guo, and Teng Wu. 2020. "Strong Wind Characteristics and Buffeting Response of a Cable-Stayed Bridge under Construction" Sensors 20, no. 4: 1228. https://doi.org/10.3390/s20041228
APA StyleYan, L., Ren, L., He, X., Lu, S., Guo, H., & Wu, T. (2020). Strong Wind Characteristics and Buffeting Response of a Cable-Stayed Bridge under Construction. Sensors, 20(4), 1228. https://doi.org/10.3390/s20041228







