Pose Estimation of Excavator Manipulator Based on Monocular Vision Marker System
Abstract
:1. Introduction
2. Related Work
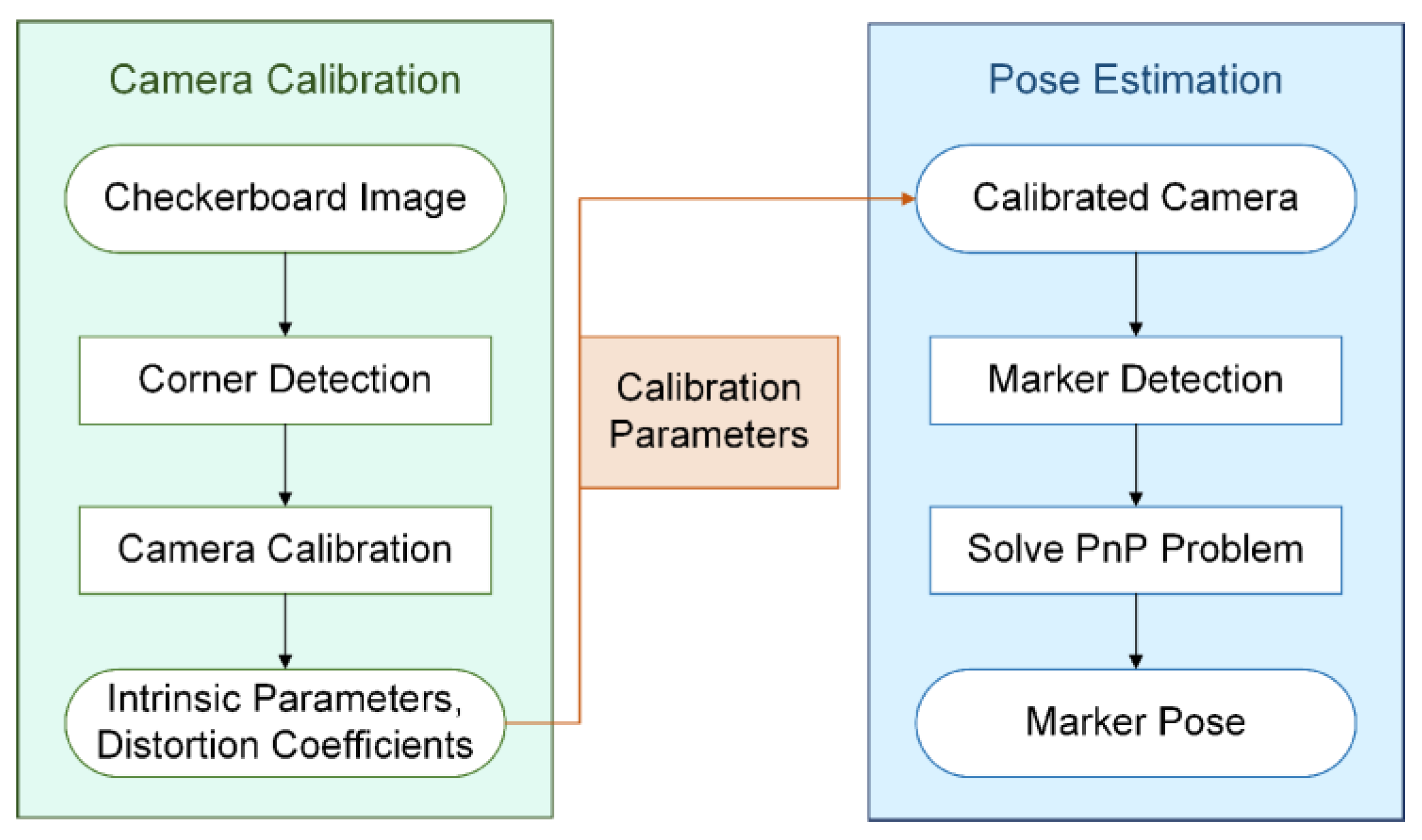
3. Pose Estimation Approach
3.1. Camera Calibration
3.2. Pose Estimation
3.3. Error Analysis
4. Design of the Measurement System
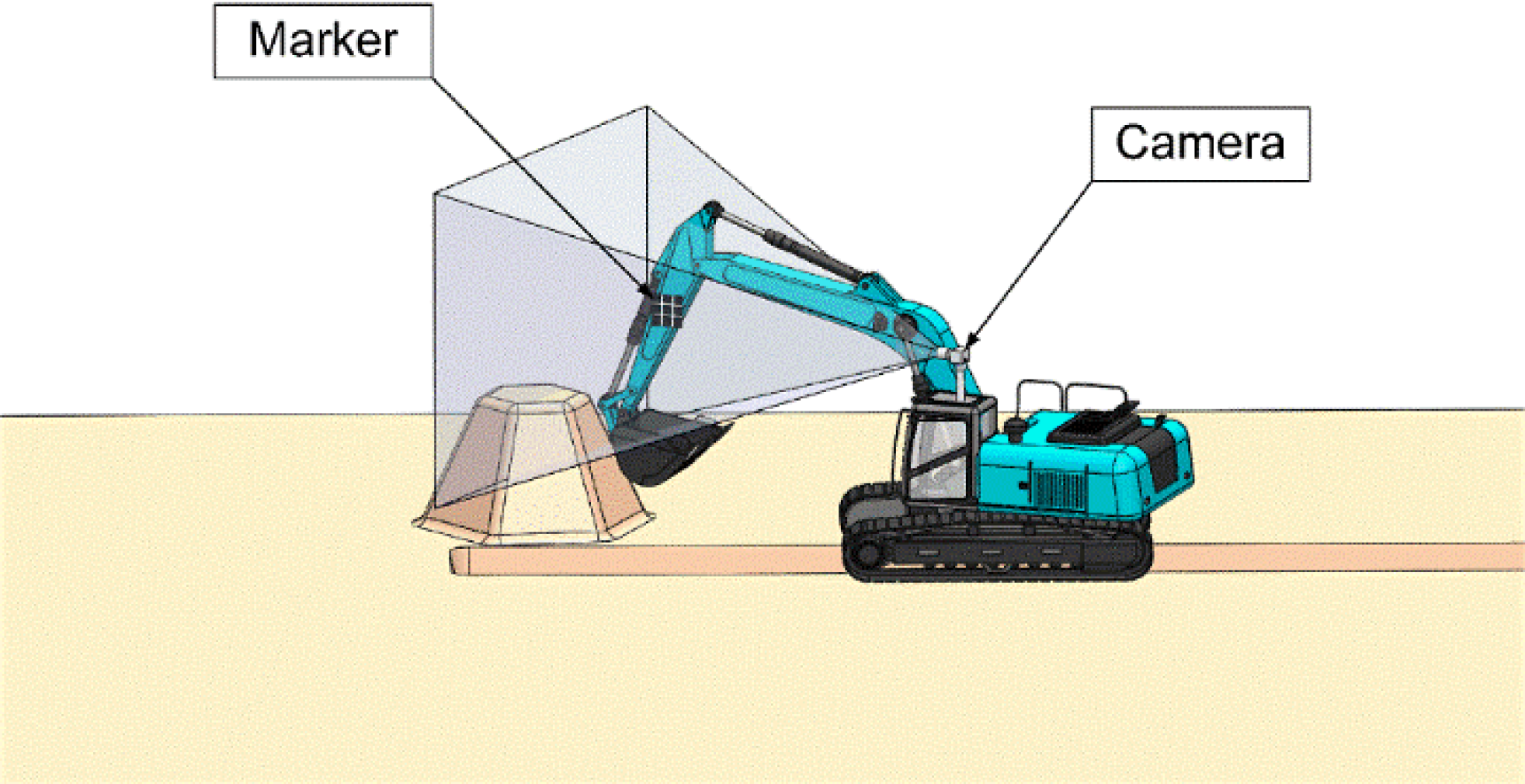
4.1. Marker Layout
4.2. Monocular Vision Marker System Design
4.3. System Prototype
5. Results and Discussion
5.1. Results
5.1.1. Effectiveness Experiments of Measurement System
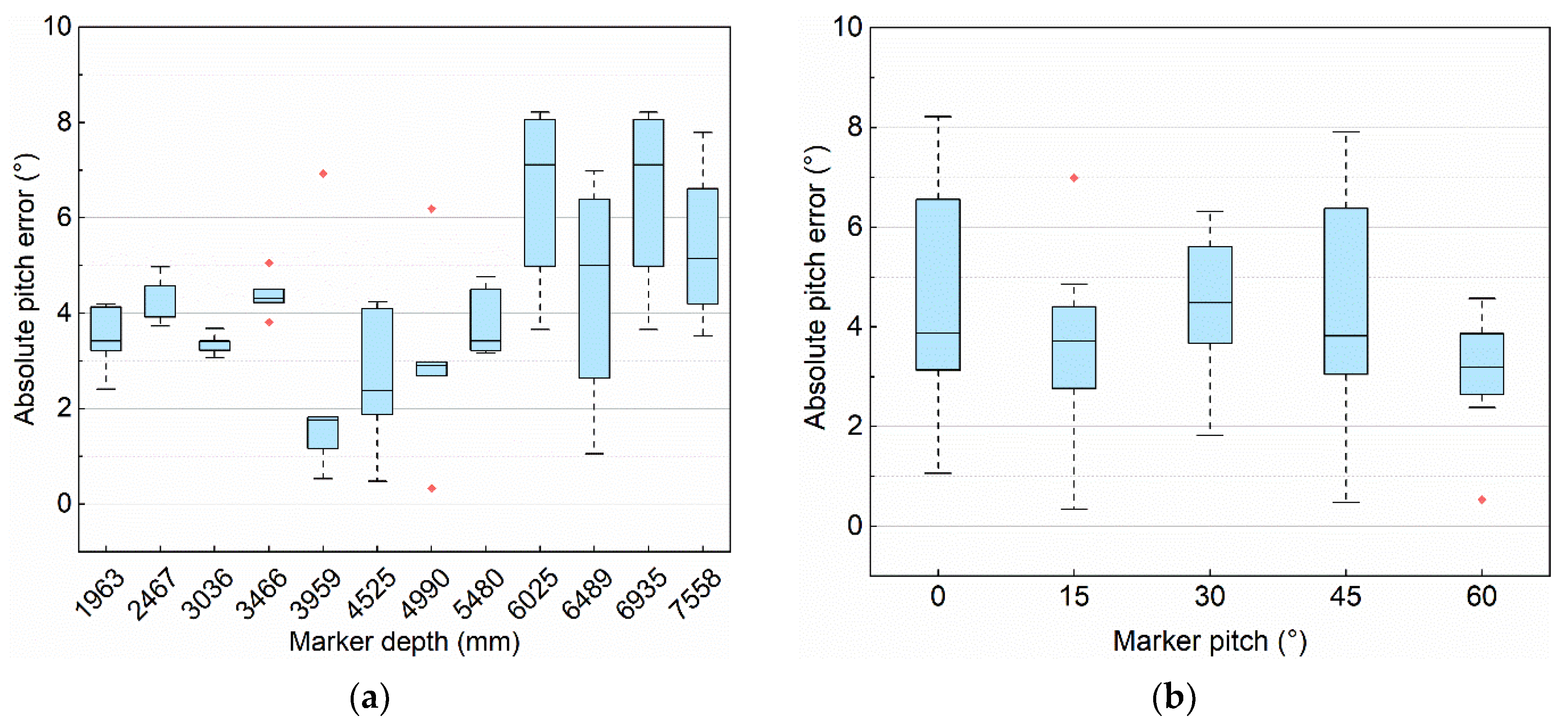
5.1.2. Orientation Accuracy Experiments
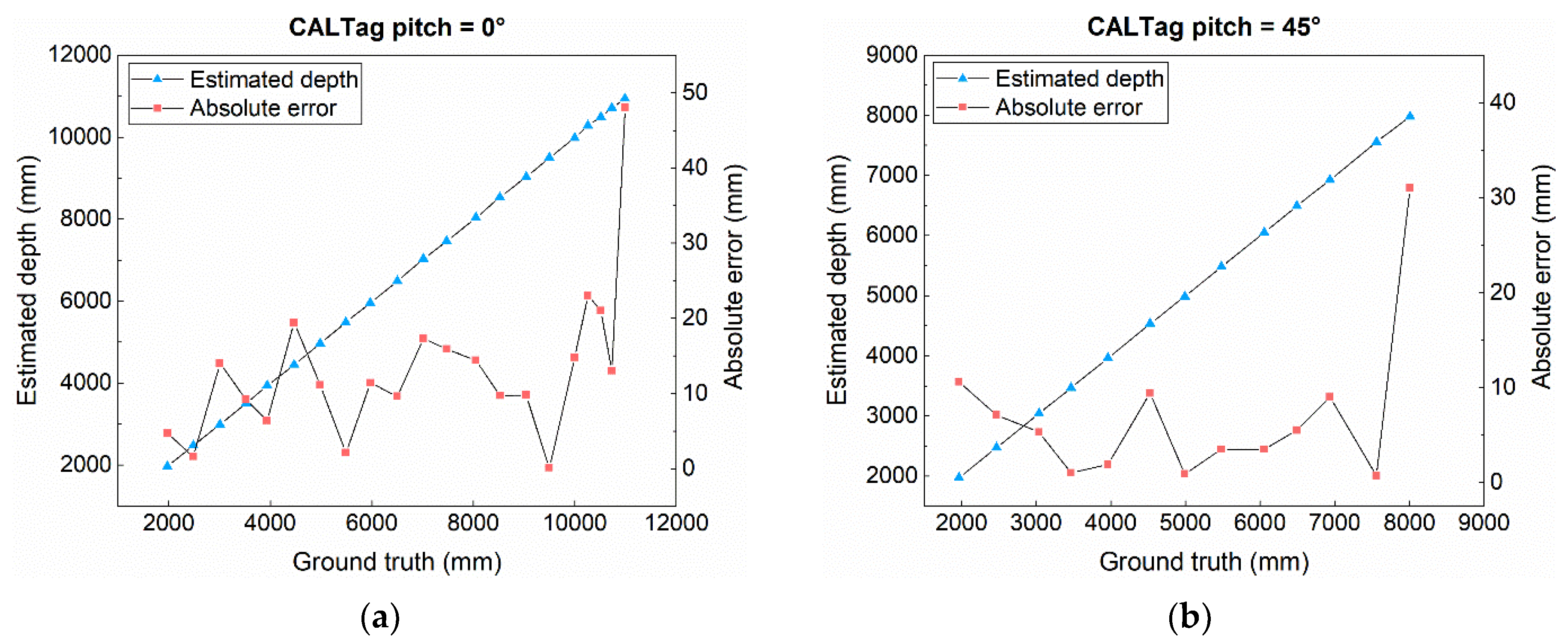
5.1.3. Position Accuracy Experiments
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BLS. Labor Productivity and Costs. Available online: https://www.bls.gov/lpc/construction.htm (accessed on 11 January 2021).
- MOHURD. Announcement of the General Office of the Ministry of Housing and Urban-Rural Development on the Production Safety Accidents of Housing and Municipal Engineering in 2019. Available online: http://www.mohurd.gov.cn/wjfb/202006/t20200624_246031.html (accessed on 21 November 2020).
- Bock, T. The future of construction automation: Technological disruption and the upcoming ubiquity of robotics. Autom. Constr. 2015, 59, 113–121. [Google Scholar] [CrossRef]
- Seo, J.; Han, S.; Lee, S.; Kim, H. Computer vision techniques for construction safety and health monitoring. Adv. Eng. Inform. 2015, 29, 239–251. [Google Scholar] [CrossRef]
- Liang, C.-J.; Kamat, V.R.; Menassa, C.M. Real-time construction site layout and equipment monitoring. In Proceedings of the Construction Research Congress 2018, New Orleans, LA, USA, 2–4 April 2018; pp. 64–74. [Google Scholar]
- Cheng, T.; Mantripragada, U.; Teizer, J.; Vela, P.A. Automated trajectory and path planning analysis based on ultra wideband data. J. Comput. Civ. Eng. 2012, 26, 151–160. [Google Scholar] [CrossRef]
- Pradhananga, N.; Teizer, J. Automatic spatio-temporal analysis of construction site equipment operations using GPS data. Autom. Constr. 2013, 29, 107–122. [Google Scholar] [CrossRef]
- Mathur, N.; Aria, S.S.; Adams, T.; Ahn, C.R.; Lee, S. Automated cycle time measurement and analysis of excavator’s loading operation using smart phone-embedded IMU sensors. In Proceedings of the Computing in Civil Engineering 2015, Austin, TX, USA, 21–23 June 2015; pp. 215–222. [Google Scholar]
- Zou, J.; Kim, H. Using hue, saturation, and value color space for hydraulic excavator idle time analysis. J. Comput. Civ. Eng. 2007, 21, 238–246. [Google Scholar] [CrossRef]
- Rezazadeh Azar, E.; McCabe, B. Part based model and spatial–temporal reasoning to recognize hydraulic excavators in construction images and videos. Autom. Constr. 2012, 24, 194–202. [Google Scholar] [CrossRef]
- Rezazadeh Azar, E.; Dickinson, S.; McCabe, B. Server-customer interaction tracker: Computer vision–based system to estimate dirt-loading cycles. J. Constr. Eng. Manag. 2013, 139, 785–794. [Google Scholar] [CrossRef]
- Yuan, C.; Cai, H. Key nodes modeling for object detection and location on construction site using color-depth cameras. In Proceedings of the Computing in Civil and Building Engineering, Orlando, FL, USA, 23–25 June 2014; pp. 729–736. [Google Scholar]
- Yuan, C.; Li, S.; Cai, H. Vision-based excavator detection and tracking using hybrid kinematic shapes and key nodes. J. Comput. Civ. Eng. 2017, 31, 04016038. [Google Scholar] [CrossRef]
- Soltani, M.M.; Zhu, Z.; Hammad, A. Skeleton estimation of excavator by detecting its parts. Autom. Constr. 2017, 82, 1–15. [Google Scholar] [CrossRef]
- Soltani, M.M.; Zhu, Z.; Hammad, A. Automated annotation for visual recognition of construction resources using synthetic images. Autom. Constr. 2016, 62, 14–23. [Google Scholar] [CrossRef]
- Xu, J.; Yoon, H.-S.; Lee, J.Y.; Kim, S. Estimation of excavator manipulator position using neural network-based vision system. SAE Tech. Pap. 2016. [Google Scholar] [CrossRef]
- Xu, J.; Yoon, H.-S. Vision-based estimation of excavator manipulator pose for automated grading control. Autom. Constr. 2019, 98, 122–131. [Google Scholar] [CrossRef]
- Liang, C.-J.; Lundeen, K.M.; McGee, W.; Menassa, C.C.; Lee, S.; Kamat, V.R. A vision-based marker-less pose estimation system for articulated construction robots. Autom. Constr. 2019, 104, 80–94. [Google Scholar] [CrossRef]
- Liang, C.-J.; Lundeen, K.M.; McGee, W.; Menassa, C.C.; Lee, S.; Kamat, V.R. Stacked Hourglass Networks for Markerless Pose Estimation of Articulated Construction Robots. In Proceedings of the 35th International Symposium on Automation and Robotics in Construction (ISARC), Berlin, Germany, 20–25 July 2018; pp. 859–865. [Google Scholar]
- Liang, C.-J.; Lundeen, K.M.; McGee, W.; Menassa, C.C.; Lee, S.; Kamat, V.R. Fast dataset collection approach for articulated equipment pose estimation. In Proceedings of the Computing in Civil Engineering 2019, Atlanta, GA, USA, 17–19 June 2019; pp. 146–152. [Google Scholar]
- Calderon, W.T.; Roberts, D.; Golparvar-Fard, M. Synthesizing Pose Sequences from 3D Assets for Vision-Based Activity Analysis. J. Comput. Civ. Eng. 2021, 35, 04020052. [Google Scholar] [CrossRef]
- Fang, Q.; Li, H.; Luo, X.; Li, C.; An, W. A sematic and prior-knowledge-aided monocular localization method for construction-related entities. Comput. Aided Civ. Infrastruct. Eng. 2020, 35, 979–996. [Google Scholar] [CrossRef]
- Luo, H.; Wang, M.; Wong, P.K.-Y.; Tang, J.; Cheng, J.C.P. Vision-Based Pose Forecasting of Construction Equipment for Monitoring Construction Site Safety. In Proceedings of the 18th International Conference on Computing in Civil and Building Engineering (ICCCBE 2020), São Paulo, Brazil, 18–20 August 2020; pp. 1127–1138. [Google Scholar]
- Luo, H.; Wang, M.; Wong, P.K.-Y.; Cheng, J.C.P. Full body pose estimation of construction equipment using computer vision and deep learning techniques. Autom. Constr. 2020, 110, 103016. [Google Scholar] [CrossRef]
- Luo, H.; Wang, M.; Wong, P.K.-Y.; Tang, J.; Cheng, J.C.P. Construction machine pose prediction considering historical motions and activity attributes using gated recurrent unit (GRU). Autom. Constr. 2021, 121, 103444. [Google Scholar] [CrossRef]
- Rezazadeh Azar, E.; Feng, C.; Kamat, V.R. Feasibility of in-plane articulation monitoring of excavator arm using planar marker tracking. J. Inf. Technol. Constr. 2015, 20, 213–229. [Google Scholar]
- Olson, E. AprilTag: A robust and flexible visual fiducial system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3400–3407. [Google Scholar]
- Lundeen, K.M.; Dong, S.; Fredricks, N.; Akula, M.; Kamat, V.R. Electromechanical development of a low cost end effector pose estimation system for articulated excavators. In Proceedings of the 32nd International Symposium on Automation and Robotics in Construction and Mining (ISARC 2015), Oulu, Finland, 15–18 June 2015; pp. 1–8. [Google Scholar]
- Lundeen, K.M.; Dong, S.; Fredricks, N.; Akula, M.; Seo, J.; Kamat, V.R. Optical marker-based end effector pose estimation for articulated excavators. Autom. Constr. 2016, 65, 51–64. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.; Dong, S.; Lundeen, K.M.; Xiao, Y.; Kamat, V.R. Vision-based articulated machine pose estimation for excavation monitoring and guidance. In Proceedings of the 32nd International Symposium on Automation and Robotics in Construction and Mining (ISARC 2015), Oulu, Finland, 15–18 June 2015; pp. 1–9. [Google Scholar]
- Feng, C.; Kamat, V.R.; Cai, H. Camera marker networks for articulated machine pose estimation. Autom. Constr. 2018, 96, 148–160. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Fiala, M. ARTag, a fiducial marker system using digital techniques. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 590–596. [Google Scholar]
- Atcheson, B.; Heide, F.; Heidrich, W. Caltag: High precision fiducial markers for camera calibration. In Proceedings of the 15th International Workshop on Vision, Modeling and Visualization (VMV 2010), Siegen, Germany, 15–17 November 2010; pp. 41–48. [Google Scholar]
- Sagitov, A.; Shabalina, K.; Sabirova, L.; Li, H.; Magid, E. ARTag, AprilTag and CALTag fiducial marker systems: Comparison in a presence of partial marker occlusion and rotation. In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017), Madrid, Spain, 26–28 July 2017; pp. 182–191. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.S.; Hou, X.R.; Tang, J.; Cheng, H.F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar] [CrossRef]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An accurate O(n) solution to the pnp problem. Int. J. Comput. Vis. 2009, 81, 155. [Google Scholar] [CrossRef] [Green Version]
- Penate-Sanchez, A.; Andrade-Cetto, J.; Moreno-Noguer, F. Exhaustive linearization for robust camera pose and focal length estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2387–2400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle adjustment—A modern synthesis. In Proceedings of the International Workshop on Vision Algorithms (IWVA 1999), Corfu, Greece, 21–22 September 1999; pp. 298–372. [Google Scholar]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar]






| Calibration Parameters | Calibration Results | |
|---|---|---|
| Intrinsic parameters (pixels) | (fx, fy) | (3172.2, 3144.8) |
| (u0, v0) | (590.0959, 485.6238) | |
| Distortion coefficients | (k1, k2, k3) | (0.0353, −0.7045, −0.7541) |
| (p1, p2) | (−0.0015, −0.0043) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Hu, Y.; Tian, M. Pose Estimation of Excavator Manipulator Based on Monocular Vision Marker System. Sensors 2021, 21, 4478. https://doi.org/10.3390/s21134478
Zhao J, Hu Y, Tian M. Pose Estimation of Excavator Manipulator Based on Monocular Vision Marker System. Sensors. 2021; 21(13):4478. https://doi.org/10.3390/s21134478
Chicago/Turabian StyleZhao, Jiangying, Yongbiao Hu, and Mingrui Tian. 2021. "Pose Estimation of Excavator Manipulator Based on Monocular Vision Marker System" Sensors 21, no. 13: 4478. https://doi.org/10.3390/s21134478
APA StyleZhao, J., Hu, Y., & Tian, M. (2021). Pose Estimation of Excavator Manipulator Based on Monocular Vision Marker System. Sensors, 21(13), 4478. https://doi.org/10.3390/s21134478





