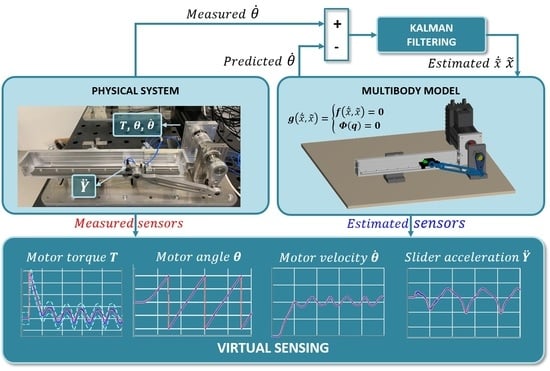
A Discrete-Time Extended Kalman Filter Approach Tailored for Multibody Models: State-Input Estimation
Abstract
:1. Introduction
2. Multi-Body Model and Time-Disretization
2.1. The Multibody Equations of Motion
2.2. The Differential-Algebraic form of the EOMs
2.3. EOMs: The Discrete Index-3 Form
3. An Explicit Linearized Approximation for Use of the Multibody Model in State-Estimation
4. State-Input Estimation for MB Models
4.1. Model and Measurement Equations with Uncertainty
4.2. The Augmented Constraint Measurement Equations
4.3. An Efficient Strategy for the Measurement Sensitivities Computation
4.4. Augmented Discrete Extended Kalman Filter
4.5. The Adopted Extended Kalman Filter Scheme
- A-priori step: Assuming that the augmented states at the previous filter step and the input are known, the a-priori state prediction and generalized accelerations can be computed solving the ID-DAEs of Equation (17):Knowing the estimated state covariance matrix for the previous timestep, the a-priori covariance at the current time () step can be approximated from Equation (47) aswhere is the process noise matrix of the augmented state-space model.The predicted measurement can then be evaluated from Equation (30) as:The Kalman filter gain allows achieving a desireable trade-off between the confidence in the model and the available measurements, and can be evaluated as:where is obtained from Equation (48) and is the measurement covariance matrix of the augmented measurement equations.
- A-posteriori step: When the real measurement becomes available together with the predicted measurement , the a posteriori state vector is obtained as:The inclusion of the actual measurements also affects the posterior covariance matrix and can be evaluated as:
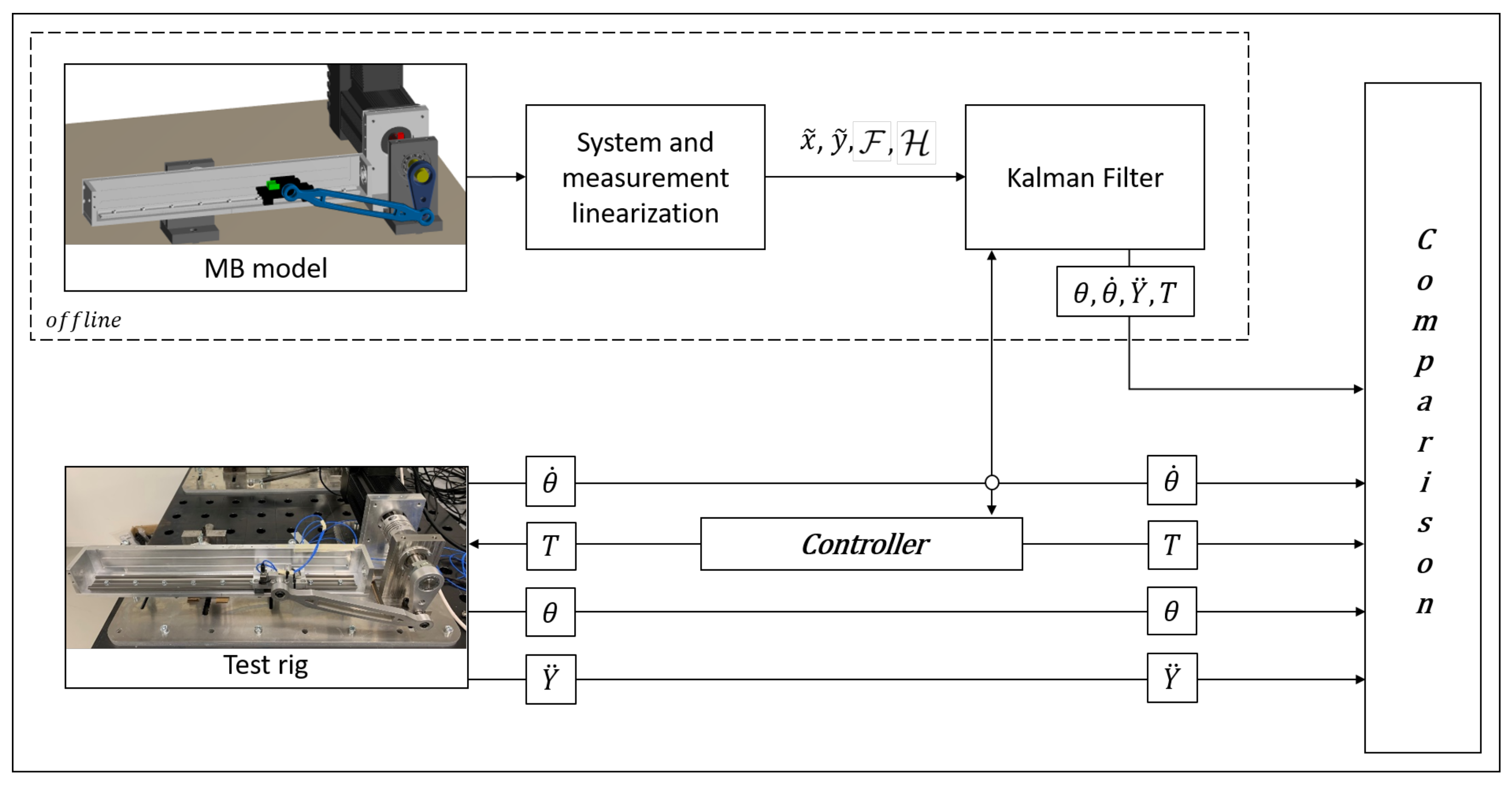
5. Validation: Joint State-Input Estimation
5.1. The Slider-Crank System
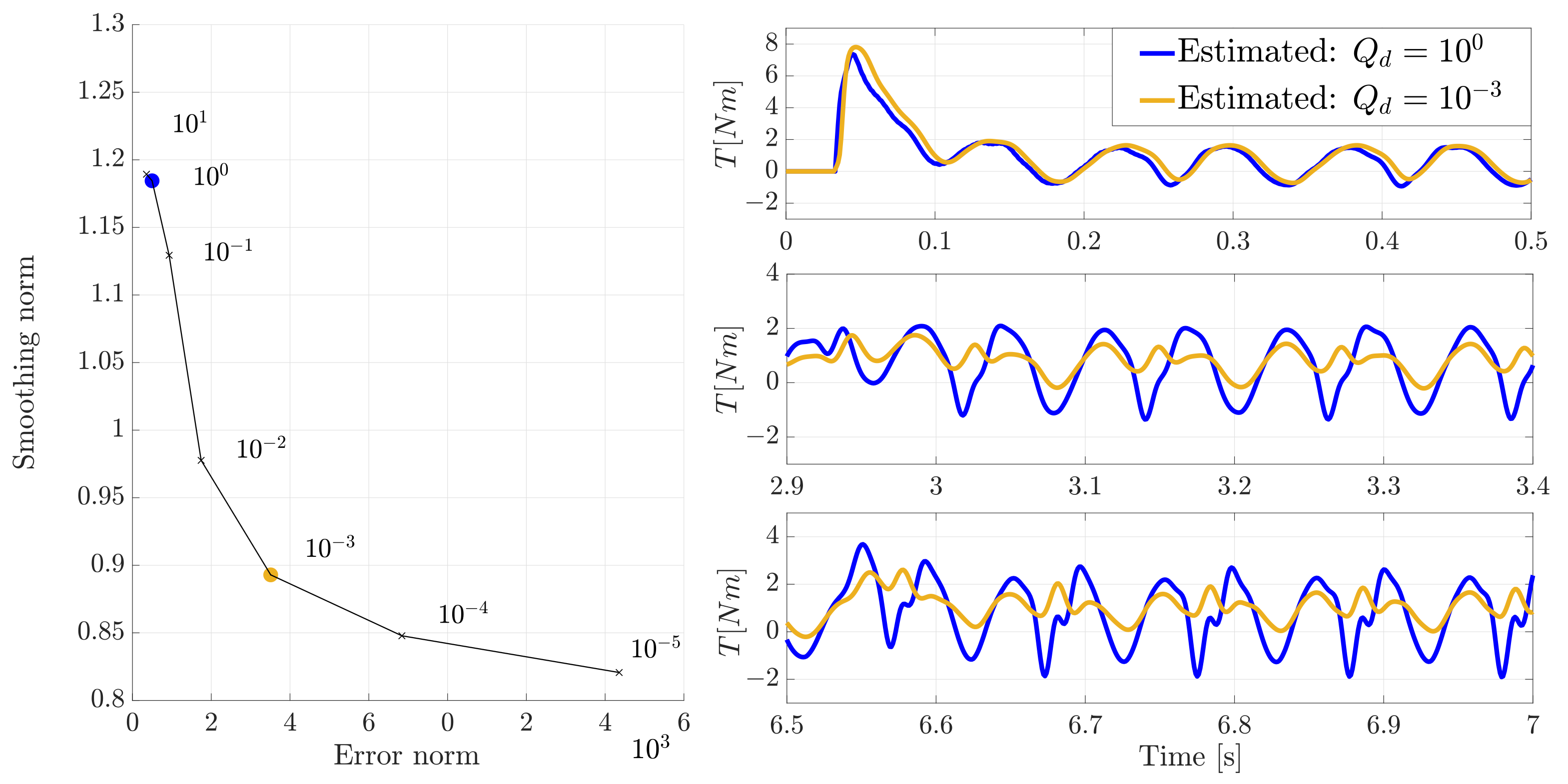
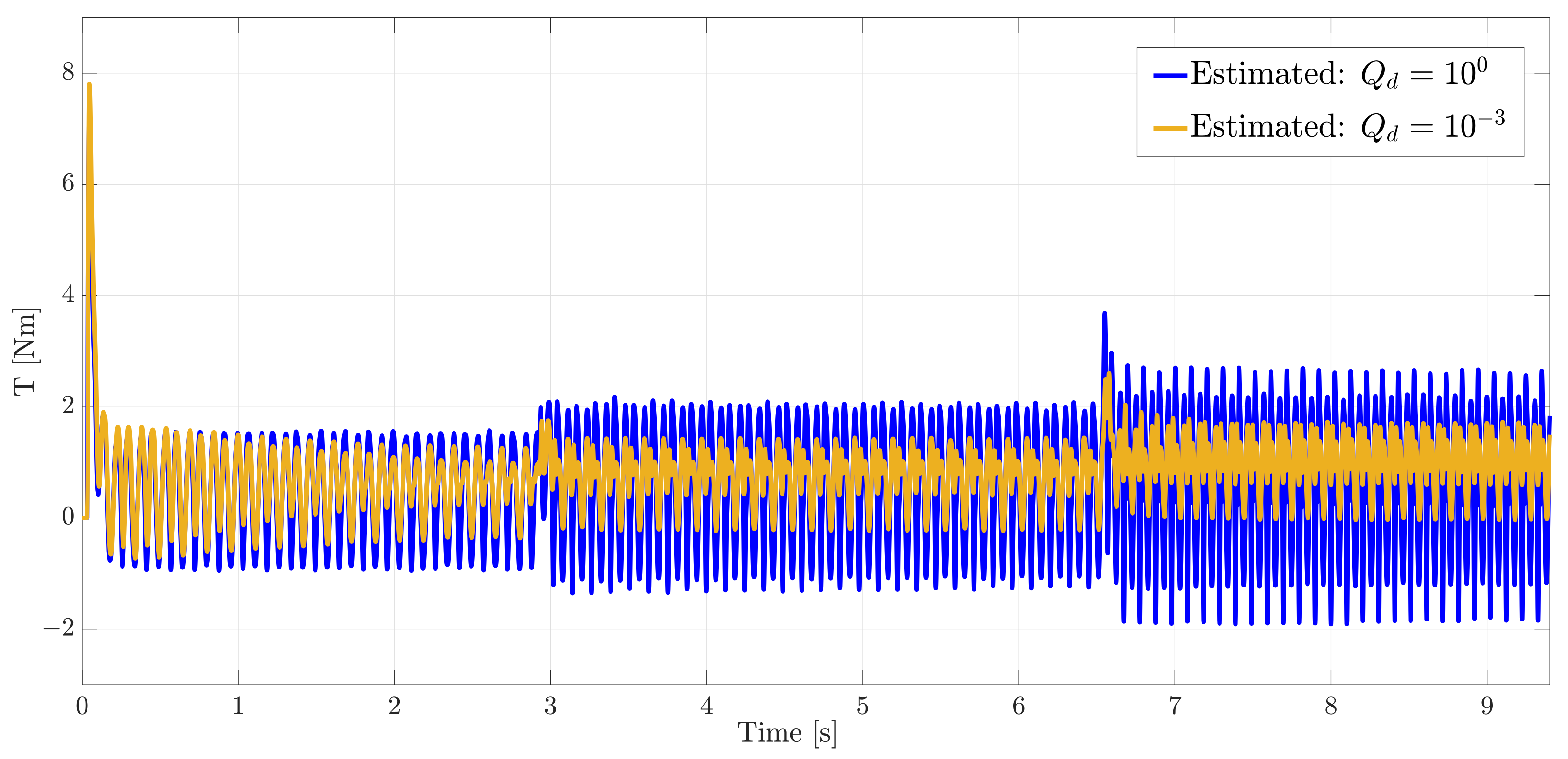
5.2. Results
5.3. Kalman Filter Tuning
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPA | Transfer Path Analysis |
| KF | Kalman Filter |
| ADE-KF | Augmented Discrete Extended Kalman Filter |
| MB | MultiBody |
| FE | Finite Element |
| EOM | Equation Of Motion |
| (I-), (E-) DAE | (Implicit), (Explicit) Differential Algebraic Equation |
| (I-), (E-) ODE | (Implicit), (Explicit) Ordinary Differential Equation |
| MBRC | MultiBody Research Code |
| FNCF | Flexible Natural Coordinates Formulation |
| BDF | Backward Differentiation Formula |
| VS | Virtual Sensor |
| MEMS | Micro Electro-Mechanical Systems |
| PID | Proportional Integrative Derivative |
| integer numbers set | |
| real numbers set | |
| scalar | |
| column vector | |
| vertical vector concatenation | |
| matrix | |
| identity matrix | |
| zero vector | |
| zero matrix | |
| transpose operator | |
| inverse matrix operator | |
| a priori prediction | |
| a posteriori prediction | |
| th time step | |
| natural coordinates | |
| , | time derivatives |
| total derivative | |
| partial derivative | |
| second partial derivative | |
| 2-norm operator |
Appendix A. Influence of the Forward Differentiation Scheme to the Linearization of the EOMs

References
- Forrier, B.; Naets, F.; Desmet, W. Broadband Load Torque Estimation in Mechatronic Powertrains Using Nonlinear Kalman Filtering. IEEE Trans. Ind. Electron. 2018, 65, 2378–2387. [Google Scholar] [CrossRef]
- Van der Seijs, M.V.; De Klerk, D.; Rixen, D.J. General framework for transfer path analysis: History, theory and classification of techniques. Mech. Syst. Signal Process. 2016, 68–69, 217–244. [Google Scholar] [CrossRef]
- Naets, F.; Croes, J.; Desmet, W. An online coupled state/input/parameter estimation approach for structural dynamics. Comput. Methods Appl. Mech. Eng. 2015, 283, 1167–1188. [Google Scholar] [CrossRef]
- Naets, F.; Cuadrado, J.; Desmet, W. Stable force identification in structural dynamics using Kalman filtering and dummy-measurements. Mech. Syst. Signal Process. 2015, 50–51, 235–248. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Géradin, M.; Cardona, A. Flexible Multibody Dynamics: A Finite Element Approach; John Wiley & Sons: New York, NY, USA, 2001; Volume 4. [Google Scholar]
- Bauchau, O.A. Flexible Multibody Dynamics; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2011; Volume 176. [Google Scholar] [CrossRef]
- Hiller, M.; Kecskeméthy, A. Dynamics of Multibody Systems with Minimal Coordinates. In Computer-Aided Analysis of Rigid and Flexible Mechanical Systems; Seabra Pereira, M.F.O., Ambrósio, J.A.C., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 61–100. [Google Scholar] [CrossRef]
- Cuadrado, J.; Dopico Dopico, D.; Perez, J.; Pastorino, R. Automotive observers based on multibody models and the extended Kalman filter. Multibody Syst. Dyn. 2012, 27, 3–19. [Google Scholar] [CrossRef] [Green Version]
- Pastorino, R.; Richiedei, D.; Cuadrado, J.; Trevisani, A. State estimation using multibody models and non-linear Kalman filters. Int. J. Non-Linear Mech. 2013, 53, 83–90. [Google Scholar] [CrossRef]
- Sanjurjo, E.; Dopico, D.; Luaces, A.; Naya, M.Á. State and force observers based on multibody models and the indirect Kalman filter. Mech. Syst. Signal Process. 2018, 106, 210–228. [Google Scholar] [CrossRef]
- Sanjurjo, E.; Naya, M.; Blanco, J.L.; Moreno, J.L.; Gimenez, A. Accuracy and efficiency comparison of various nonlinear Kalman filters applied to multibody models. Nonlinear Dyn. 2017, 88. [Google Scholar] [CrossRef]
- Palomba, I.; Richiedei, D.; Trevisani, A. Kinematic state estimation for rigid-link multibody systems by means of nonlinear constraint equations. Multibody Syst. Dyn. 2017, 40, 1–22. [Google Scholar] [CrossRef]
- Angeli, A.; Desmet, W.; Naets, F. Deep learning for model order reduction of multibody systems to minimal coordinates. Comput. Methods Appl. Mech. Eng. 2021, 373, 113517. [Google Scholar] [CrossRef]
- Angeli, A.; Desmet, W.; Naets, F. Deep learning of multibody minimal coordinates for state and input estimation with Kalman filtering. Multibody Syst. Dyn. 2021, 1–19. [Google Scholar] [CrossRef]
- Risaliti, E.; Tamarozzi, T.; Vermaut, M.; Cornelis, B.; Desmet, W. Multibody model based estimation of multiple loads and strain field on a vehicle suspension system. Mech. Syst. Signal Process. 2019, 123, 1–25. [Google Scholar] [CrossRef]
- Vermaut, M.; Tamarozzi, T.; Naets, F.; Desmet, W. Development of a flexible multibody simulation package for in-house benchmarking. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Barcelona, Spain, 29 June–2 July 2015; pp. 1560–1571. [Google Scholar]
- De Jalon, J.G.; Bayo, E. Kinematic and Dynamic Simulation of Multibody Systems: The Real-Time Challenge; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Vermaut, M.; Naets, F.; Desmet, W. A flexible natural coordinates formulation (FNCF) for the efficient simulation of small-deformation multibody systems. Int. J. Numer. Methods Eng. 2018, 115, 1353–1370. [Google Scholar] [CrossRef]
- Pechstein, A.; Reischl, D.; Gerstmayr, J. A Generalized Component Mode Synthesis Approach for Flexible Multibody Systems With a Constant Mass Matrix. J. Comput. Nonlinear Dyn. 2012, 8, 011019. [Google Scholar] [CrossRef]
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations; Siam: Philadelphia, PA, USA, 1996; Volume 14. [Google Scholar] [CrossRef]
- Blockmans, B. Model Reduction of Contact Problems in Flexible Multibody Dynamics. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2018. [Google Scholar]
- Simon, D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef] [Green Version]
- Kirchner, M.; Croes, J.; Cosco, F.; Desmet, W. Exploiting input sparsity for joint state/input moving horizon estimation. Mech. Syst. Signal Process. 2018, 101, 237–253. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tamarozzi, T.; Risaliti, E.; Rottiers, W.; Desmet, W. Noise, ill-conditioning and sensor placement analysis for force estimation through virtual sensing. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA2016), Leuven, Belgium, 19–21 September 2016; KU Leuven: Leuven, Belgium, 2016; pp. 1741–1756. [Google Scholar]
- Pacejka, H. The Wheel Shimmy Phenomenom: A Theoretical and Experimental Investigation with Particular Reference to the Nonlinear Problem (Analysis of Shimmy in Pneumatic Tires due to Lateral Flexibility for Stationary and Nonstationary Conditions). Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1966. [Google Scholar]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]







| Body | m [kg] | [kg · m] | [kg · m] | [kg · m] | |
|---|---|---|---|---|---|
| C | |||||
| - | - | - | |||
| - | - | - | |||
| S | |||||
| - | - | - | |||
| [N/m] | [Ns/m] | b [s/m] | |||
|---|---|---|---|---|---|
| [rad] | [rad/s] | [m/s] | T [Nm] | |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adduci, R.; Vermaut, M.; Naets, F.; Croes, J.; Desmet, W. A Discrete-Time Extended Kalman Filter Approach Tailored for Multibody Models: State-Input Estimation. Sensors 2021, 21, 4495. https://doi.org/10.3390/s21134495
Adduci R, Vermaut M, Naets F, Croes J, Desmet W. A Discrete-Time Extended Kalman Filter Approach Tailored for Multibody Models: State-Input Estimation. Sensors. 2021; 21(13):4495. https://doi.org/10.3390/s21134495
Chicago/Turabian StyleAdduci, Rocco, Martijn Vermaut, Frank Naets, Jan Croes, and Wim Desmet. 2021. "A Discrete-Time Extended Kalman Filter Approach Tailored for Multibody Models: State-Input Estimation" Sensors 21, no. 13: 4495. https://doi.org/10.3390/s21134495
APA StyleAdduci, R., Vermaut, M., Naets, F., Croes, J., & Desmet, W. (2021). A Discrete-Time Extended Kalman Filter Approach Tailored for Multibody Models: State-Input Estimation. Sensors, 21(13), 4495. https://doi.org/10.3390/s21134495