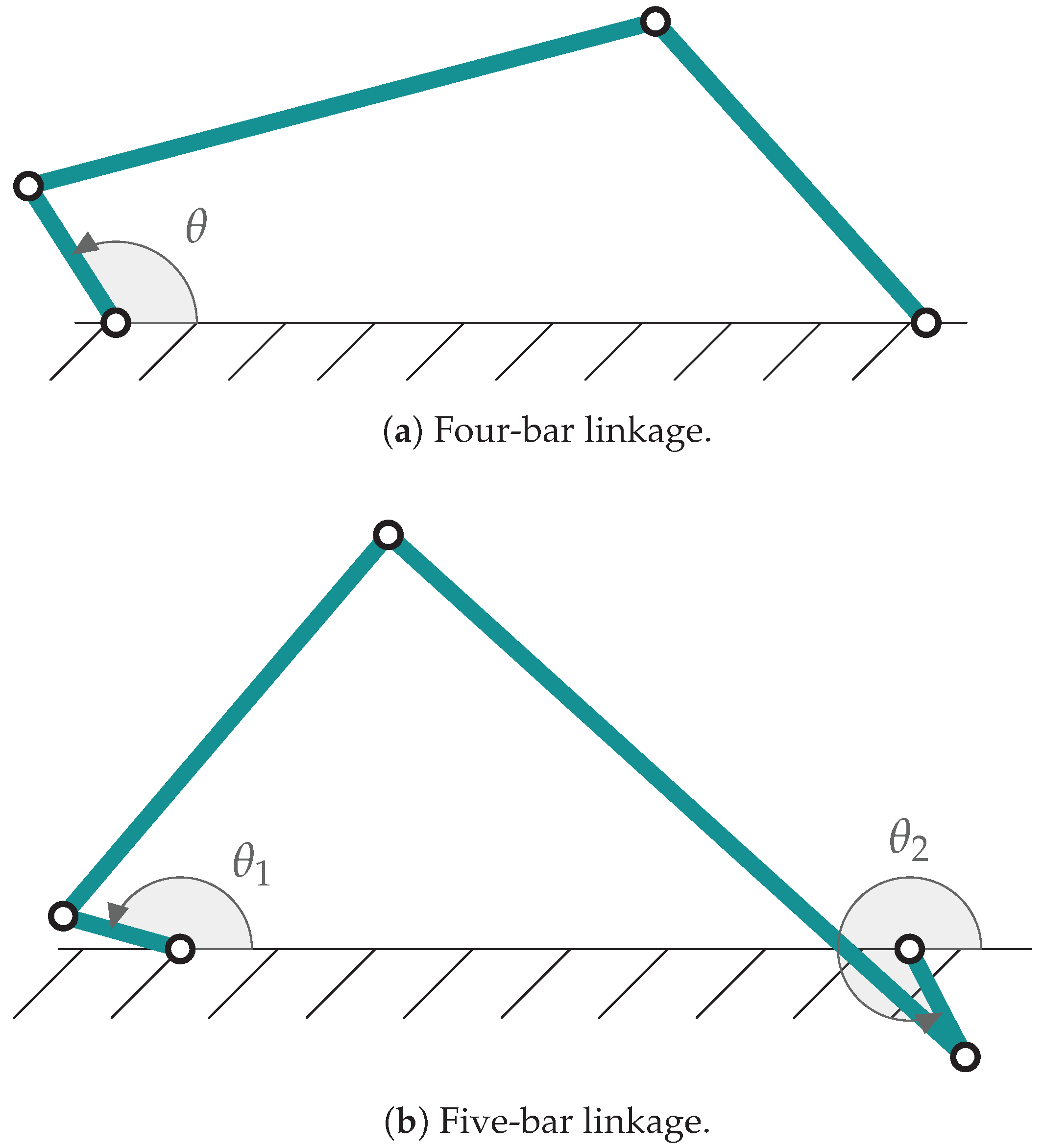
1. Introduction
In many applications, it is required to acquire data in order to analyze the performance of a particular machine, to make decisions through control strategies or to gather data for durability purposes. Most of the time, it is possible to get all the data through sensors. However, there are particular cases where a sensor cannot be installed due to economical or technical issues. In these situations, data acquisition relies on estimations.
Kalman filter [
1] stands out as one of the most used estimation techniques. It combines a model describing the system with sensor measurements. The estimations are based on the statistical properties of the desired variables conditioned on the sensors measurements [
2]. Although the Kalman filter was designed for linear systems, several approaches have been developed in the literature extending its use to non-linear models. Such is the case of the extended Kalman filter (EKF) or unscented Kalman filter (UKF) [
2]. These approaches introduced the Kalman filter to real problems, which are predominantly non-linear.
Similarly, the interest for mulibody models has grown in the recent years in several fields of the industry, such as automotive, biomechanics or machinery. Through multibody dynamics, a system can be modeled with high accuracy [
3], at expenses of a moderate computational cost. Recently, multibody models have started to be used in combination with Kalman filters for estimation. Such is the case of virtual sensing in automotive applications [
4]. However, the assembly between a multibody model and a Kalman filter is not trivial due to the high non-linearities of multibody models.
The first approach presented in the literature is [
5], where an EKF was combined with a simple mechanism. However, the complexity of the implementation and the computational cost limits its application. Several approaches have been presented later on [
6,
7,
8,
9]. In [
7], an UKF based on a multibody model is proposed, reducing the complexity of the implementation. However, it entails high computational cost: the estimations are based on a set of sample points propagated through the model. Hence, it requires to simulate as many multibody models as sample points each time step. From the work presented in [
8], a new Kalman filter known as error-state extended Kalman filter (errorEKF) shows accurate results while reducing the computational cost. In addition, the filter entails low coupling with the model. Thus, the implementation of any model becomes simpler. The errorEKF has been improved in more recent works, extending its estimations to inputs [
9] and parameters [
10].
The Kalman filter, besides being developed for linear systems, assumes that the noise of the measurements and the process (or system) are zero-mean white Gaussian with known covariance matrices [
1]. These assumptions are hard to satisfy in real scenarios. The use of wrong statistics in the design of the filter can lead to large estimation errors or even a divergence in the filter [
11]. In practice, these matrices are estimated through a tedious trial-and-error procedure. This is especially critical for the process noise covariance matrix (PNCM), since it is not possible to determine the accuracy of the model. Regarding the measurement noise covariance matrix (MNCM), each sensor is characterized and, hence, an initial value can be approximated.
However, even though a proper value of the noise covariance matrices is found, they remain constant reducing the robustness of the filter [
10,
12]. In some scenarios, the system can experiment a noticeable change during a particular maneuver. This change can affect the model accuracy and, thus, invalidate the initial noise covariances. This explains the increasing interest on developing methods for noise covariance matrices estimation [
13]. These methods are usually known as Adaptive Kalman filters (AKF).
Adaptive Kalman filters can be divided in two major approaches: multiple-model based adaptive estimation (MMAE) and innovation-based adaptive estimation (IAE). Both approaches share the same concept of using the new information of the innovation sequence of the filter (difference between real and estimated measurements) [
14]. MMAE methods implement a bank of several different models and compute the probability for each model to be the true system model given the measurement sequence and under the assumption that one of the models in the bank is the correct one. IAE performs the adaptation based directly on the innovation sequence, using the fact that the innovation sequence is white noise if the filter has the right values of the covariance matrices [
15].
Multibody models can be computationally expensive and achieving real-time performance in practical applications is a challenge [
16]. Hence, executing several models in parallel following the MMAE approach would compromise real-time performance and, thus, the viability of the solution.
Focusing on the IAE, there are many alternatives presented in the literature. In [
14], an approach based on the maximum likelihood criteria (ML) is proposed to estimate both the PNCM and MNCM for inertial navigation, where Kalman filters are employed to overcome the lack of GPS signals in certain areas. The proposed approach is also compared against conventional Kalman filters. The ML aims to maximize the probability that a set of data (i.e., innovation) is observed for a given a parameter (i.e., noise covariance matrices). The ML depends on a window of past innovation data. If the sample data grows without bound, the estimate converges to the true value of the covariance matrices. As a counterpart, the ML could be biased for small sample sizes (over-trained). This issue is addressed in [
17] by combining the ML with a fuzzy control in order to select only the viable satellites for the estimation, removing outlier data from the innovation sequence.
In [
18], an IAE adaptive Kalman filter is also proposed for sensor fusion in INS/GPS navigation. The algorithm is equivalent to the maximum likelihood criteria. Combining the GPS with an IMU, the position can be accurately tracked, even in environments without GPS signal.
For spacecraft navigation, in [
12], an AKF based on ML combined with fuzzy logic is proposed. The fuzzy logic is based on the discrepancy between the estimated covariance and the theoretical covariance bounds. The use of fuzzy logic helped to reduce the computational cost. However, the use of fuzzy logic incremented the estimation errors.
In [
19], a Sage-Husa (SH) filter is combined with a Kalman filter to obtain the angular velocities of a vehicle from an inertial navigation system which uses only accelerometers. The SH algorithm is equivalent to those resulting from maximum likelihood estimation [
20]. It is based on the maximum a posterior probability (MAP), which maximizes the probability of a parameter for a given set of data. It means that the likelihood is weighted by the prior information. In practice, it can be seen as applying weights in the ML estimates, giving more relevance to the most recent estimations. Sage-Husa algorithm is an alternative to the ML when there are not enough data available. However, it cannot estimate the PNCM and MNCM simultaneously without causing divergence in the estimations [
21].
The SH algorithm is also used with modifications in [
22] to estimate the MNCM of an UKF for state estimation in a vehicle. A similar approach is followed in [
21], where a robust UKF is complemented with the SH algorithm for estimating the PNCM for autonomous underwater vehicle acoustic navigation.
Another approach for adaptive Kalman filtering is known as Variational Bayesian (VB). While ML and MAP give a fixed value for the noise covariance matrices (point estimators), the VB gives a probability density function. The advantage of this method is that it mitigates the effect of over-trained filters [
23]. As an example, the VB is applied in [
24] in order to improve the measurements of inertial navigation systems. It shows robustness against anomalous measurements. As a counterpart, the VB assumes that the PNCM is accurately known. Thus, it can be only used for estimating the states and the MNCM [
25]. This is an important drawback since, as reflected in [
26,
27], the filter performance will decrease with the uncertainties of the PNCM. The VB approach is extended in [
26,
28] including the calculation of the predicted error covariance matrix instead of the process covariance matrix seeking for higher accuracy. In the same way, in [
29], the VB approach is enhanced by its combination with a Sage-Husa algorithm for the PNCM estimation achieving satisfactory results.
The aim of this work is to explore the use of adaptive algorithms with multibody based Kalman filters, solving the actual limitation of the unknown statistics of the noise covariance matrices. For that purpose, a Kalman filter based on multibody models has to be combined with an adaptive method. This implies to study how to combine the different equations involved, performing the required modifications. Most of the research made in adaptive Kalman filtering is related to navigation applications. However, multibody models present strong non-linearities that can affect the performance of the adaptive filters. To the authors’ knowledge, adaptive Kalman filtering is a technique that has never been applied to multibody-based estimation and, at the state of the art of Kalman filtering in this field, it is the next natural step to be taken.
As novelty, this work presents a state and input estimator for multibody models, which includes an adaptive methodology in order to estimate the noise covariance matrices. The lack of knowledge on the statistics of the system is an actual limitation for industrial applications of multibody-based estimation. That is the case, for example, of automotive applications, where the maneuvers are continuously changing and adjusting the noise covariance matrices following a trial-and-error procedure is not viable. Following the presented approach, this limitation can be overcome, and the use of estimation based on multibody models can be increased in real industrial applications.
3. Results
To asses the performance of the proposed adaptive Kalman filter, different tests are launched. During the first test, the mechanisms are in the vertical plane and they are only affected by the gravity force. A batch of tests is executed under these conditions for different initial values of the PNCM. The results of each simulation are compared against the results obtained from the conventional errorEKF with force estimation. In a second test, the mechanisms are modified with the addition of a torsional spring in the crank. During the simulation, the spring is removed from the real mechanism, simulating a failure on a real machine. The AerrorEKF-FE is expected to overcome this new modeling error (together with the error in the gravity acceleration and initial position) in the observer and adapt the covariance matrices to the new situation.
The simulations are executed with a time step of 5 milliseconds, that is a frequency of 200 Hz. The measurements are gathered at 200 Hz. Hence, there is one measurement available at each time step. The errors introduced in the model for each test are of in gravity acceleration and of an offset in the initial value of the crank angle . In addition, for testing the robustness, a torsional spring is introduced in the crank. During the simulation, this spring is removed only from the real mechanism. The observer should detect this event through the sensor measurements and perform the required corrections.
3.1. Accuracy Test
For testing the convergence of the adaptive filter, different initial values of the PNCM are selected. While the MNCM can be approximated by testing the sensors, an initial value for the process noise is more difficult to obtain. Due to this inconvenience, it is of interest to test the robustness of the proposed filter under different initial values of the PNCM. The results are compared with the ones obtained from the errorEKF-FE. This would show the error reduction when using the AerrorEKF-FE if the initial PNCM is not close to the true value.
Following Equation (
36), for the four-bar linkage, only one value is required. For the five-bar linkage, since it has two degrees of freedom, two elements of the PNCM matrix should be instantiated. For simplicity, both elements are set to the same value. The different initial values are summarized in
Table 4.
Note that the initial values of both noise covariance matrices are used for the errorEKF-FE and AerrorEKF-FE. For the errorEKF-FE, these values are constant during the simulation, since it assumes that the PNCM is constant. Meanwhile, for the AerrorEKF-FE, these are the initial values of the PNCM, which are modified by the adaptive method. Hence, a total of six simulations for each sensor configuration are launched for each filter in order to compare their performance.
From the initial tests, an undesired behavior is detected. If both the PNCM and MNCM are estimated at the same time, the filter shows a trend to diverge. In
Figure 4, the evolution of the estimated PNCM in the four-bar linkage is represented and compared with its evolution when the MNCM is not included in the estimation. Except for the case of the accelerometers, there is a trend to a continuous growth of the PNCM. This implies that the filter is reducing its trust on the model in exchange of the measurements.
The different behavior within configuration relies on the nature of the sensors. In the scenarios without accelerometers, there is a trend of divergence in the acceleration error. In addition, when using only an encoder, both the velocity and acceleration error diverge. Once that the estimator detects that the error is increasing through the innovation sequence, it starts to reduce the confidence in the model and trusting more in the sensors. However, correcting the acceleration error from measurements in position or velocity is not accurate. Hence, the error keeps growing causing the filter to diverge. At some point, this issue will lead to a failure of the filter. This, together with the non-linearities of the mechanisms, can result in unpredictable behaviors as the case of the gyroscope in the crank. Hence, for the rest of the experiments, only the PNCM is estimated.
Regarding the size of the sliding window for the innovation sequence, it should be noted that a large window leads to low mean errors in smooth maneuvers. However, a large window also implies slow corrections to the covariance matrix. Hence, in some tests, the delay in the correction can result in an error which is not corrected. This is the case shown in
Figure 5. It corresponds to a simulation of the four-bar linkage with a gyroscope on the coupler and an initial process covariance noise of
, and a window length of 100 time steps. The same maneuver is performed with a window length of 50 samples. The innovation sequences are shown in
Figure 5a. The value of the crank angle for each slide window size is shown in
Figure 5b.
As can be seen in
Figure 5a, with a window length of 100 samples, there are a notable difference between the estimated and measured angular rate of the coupler at particular moments of the maneuvers. In these points of the maneuver, the mechanism reaches a position where the crank and the rocker are parallel. In this situation, the possible velocities of the coupler are limited. Thus, for an error in position, the error in velocity can be incorrigible. This is a consequence of the non-linearity of the system.
Comparing the results between different window sizes, it is possible to appreciate the effects of the samples considered for the estimation. With a large window, the filter cannot correct with immediacy the error. Although it is able to correct the error in terms of crank angular rate, as is shown in the innovation sequence, a permanent offset appears in the position of the crank angle. Meanwhile, with a short window length, the influence of previous values is reduced and the filter can perform the correction properly. Hence, the tests of this work are executed with a window of 50 samples for the innovation sequence.
There is no a general criteria for selecting the length of this window. It should be adjusted depending on the nature of the maneuver aiming to include only the relevant information of past events. The main idea is to avoid the effect of past events which do not have relation with the actual state of the mechanism. If a maneuver is close to steady state, a large window can be selected. On the other hand, a short window length is adequate in cases where the system changes.
In order to analyze the performance of the proposed adaptive filter, the RMSE for the position, velocity, acceleration and force acting in the degree of freedom of each mechanism is evaluated. From
Figure 6,
Figure 7,
Figure 8 and
Figure 9, the RMSE between the AerrorEKF-FE and errorEKF-FE are compared for the four-bar mechanism. Results show that the adaptive version of the errorEKF-FE leads in most of the test to a lower error in all the measured magnitudes. In fact, in some configurations, the RMSE is almost constant. This behavior is what could be initially expected: despite the different initial PNCM, the AerrorEKF-FE is capable of finding an optimal covariance that minimizes the errors in all tests.
The confidence intervals of the error in position, velocity and acceleration are shown in
Figure 10 for one of the simulations. It can be seen how the errors converge to the true value and that the confidence intervals are consistent with the evolution of the error. Considering that the confidence interval is of 95%, it can be asserted that only the 5% of the estimations will have an error higher than 1.96 times the standard deviation of the variable (i.e., the square root of the diagonal elements of the covariance matrix,
, of Equation (21)). These plots also provide useful information about the observability of the system. Since the confidence interval is based on the PNCM elements, if the system were not observable, it could be expected an unlimited growth of the covariance of the states.
With respect to the five-bar linkage, a similar trend can be appreciated from
Figure 11,
Figure 12,
Figure 13 and
Figure 14. Except for the crank angle and angular rate when using gyroscopes in couplers, the rest of the experiments show that the AerrorEFK-FE converges to accurate solutions in every tested case. Thus, it is able to estimate the value of the PNCM which minimizes the error.
3.2. Robustness Test
For evaluating the robustness of the filter, the four-bar linkage is equipped with a torsional spring actuating over the crank angle. In order to replicate a failure, at 5 s, the spring breaks. In this new scenario, the real mechanism continues the maneuver without the spring, while the observer is still considering its existence for the dynamics. This test is useful to analyze the response of the filter to unexpected changes. The observer is also under the errors of previous tests: in gravity acceleration. In addition, the initial value of the crank angle has an offset of .
The results in terms of force estimation are shown in
Figure 15. The estimated force can be understood as the torque, which would have to be applied to the crank to compensate the errors. It is equivalent to the difference between the force applied in the
real mechanism and the
model. It can be seen how, at the time of 5 s, the
observer has to subtract the force in the crank. Since there is no spring in the
real mechanism, the
observer needs to apply a torque equal in magnitude but different in sign to the torque applied by its spring.
It can be seen how, except for the encoder configuration, the
observer tracks the reference values. In addition, the filter responses with immediacy to the spring failure. This time response can be achieved by adjusting the innovation window length, seeking for a compromise between accuracy and time response. For this case, the window length is of 50 samples. Regarding the encoder configuration, the behavior is similar to what could be appreciated in [
9]. There is a delay in the estimation and the noise is noticeable. It can be explained by the fact that obtaining acceleration from position information.
With respect to the other three configurations, the estimations present a reduced noise, being the use of accelerometers the most accurate solution. The use of gyroscopes shows a good behavior before the spring breaks. Once this event takes place, both tests show a remarkable overshooting which is quickly corrected at expenses of higher noise. However, in both cases, it can be appreciated how the noise is being reduced with time. This is in line with what is shown in
Figure 16.
It can be seen how the confidence interval becomes wider when the spring breaks. In terms of the PNCM, it means that the AerrorEKF-FE has detected the change in the real mechanism. To address this new modeling error, the filter increases the values of the PNCM giving more relevance to the sensor measurements. Once that the observer tracks the new scenario of the real mechanism, the covariances are reduced together with the noise of the estimations.
3.3. Computational Cost
For most of the industrial applications, it is required to achieve real-time performance. In previous works, the errorEKF-FE has proven to be capable of running in real time with complex multibody models [
10]. Hence, it is of interest to analyze the increment in computational cost derived by the presented adaptive procedure.
It is important to remark that this work is developed in MATLAB
, which is not oriented to real-time applications. Hence, measuring the computation time of the algorithm is not a fair test. However, since the errorEKF-FE and AerrorEKF-FE are executed under the same conditions, a reference in the increment in computational cost can be derived. It can be seen in
Table 5. From the results, it can be concluded that the AerrorEKF requires about the double of time than the error errorEKF-FE for computing the same simulation.
4. Discussion
From the presented results, it can be seen that the adaptive version of the errorEKF-FE solves one of the main drawbacks of the filter: setting the values of the process noise covariance matrix. The tests performed during this work show that, with independence of the initial assumptions on the PNCM, the AerrorEKF-FE converge to an accurate solution. As shown during the accuracy test, the AerrorEKF-FE is able to achieve a similar level of error in the estimations despite of the initial values of the PNCM. This allows to reduce the development time of multibody-based Kalman filters, where the determination of the statistics of the system is a tedious process. In addition, even though the maximum likelihood method depends on a sliding window of the past innovation, the filter has shown an acceptable response to sudden changes in the system. Through the simulation of a sudden failure in the real mechanism, the robustness of the filter is tested. The results show that the estimator is able to track the new situation and correct the new error with accuracy, without compromising the convergence of the simulation.
It can also be concluded that, although the measurement noise covariance matrix can also be estimated through the ML method, in this particular case it led to a filter divergence in the absence of accelerometers. When the estimator detects an error, it starts to rely on the corrections in the measurements instead of the model. However, through sensors in position or velocity, the acceleration cannot be obtained with accuracy and hence, the error cannot be corrected. This, together with the non-linearities of the model, leads to a divergence of the filter. In addition, the estimation of the MNCM did not offer an improvement of the estimations. However, as opposite from the PNCM, it is possible to obtain an acceptable initial value for the MNCM after characterizing the sensors or through the information provided by the manufacturer of each sensor.
The length of the sliding window for the innovation sequence is also an important factor and one of the main limitations of the approach. A large window size can result into wrong estimations in maneuvers with high variability. This is one of the known disadvantages of the ML method, since there does not exist a general rule in order to select the most suitable innovation window length. Algorithms such as Sage-Husa are focused on minimizing the impact of the window length by giving different weights to the elements of past events, giving higher weights to the more recent events.
Regarding the computational cost, the AerrorEKF-FE has lower efficiency than the errorEKF-FE due to the adaptive procedure. Estimating the process noise covariance matrix each time step entails an increment of the computations per time step, which is turned into a noticeable increment of computational cost. This limitation can be critical in real-time applications. It is necessary to test the computational cost of the method in each particular application. The efficiency of the estimator not only depends on the algorithm, but on the platform where it is going to be executed. This also implies to explore the possibility of increasing the efficiency of the solution. Since the estimation of the noise covariance matrices is independent from the state estimation each time step, the code execution can be parallelized, increasing the algorithm efficiency and reducing the computational cost of the approach.
5. Conclusions
This work presents an adaptive Kalman filter for state and input estimation based on multibody models (AerrorEKF-FE). The aim is to accurately estimate the noise covariance matrix of the estimator, which has shown to be a critical factor for accurate and robust observer performance. The method is tested on two different planar mechanisms: a four-bar linkage and a five-bar linkage. In addition, four different sensor configurations are considered, increasing the general application of the proposed solution. Several tests are presented in order to analyze the behavior of the filter in terms of accuracy and robustness.
The AerrorEKF-FE combines an error-state Kalman filter with an adaptive method based on the maximum likelihood criteria. This adaptive technique, commonly used for navigation estimation, has several assumptions which are not fulfilled in multibody dynamics. Even though adaptive algorithms have the capacity of overcoming some of the main difficulties of multibody based Kalman filtering, its application has never been explored. In this work, the selected adaptive method is adjusted to fit with multibody particularities, such as time-variant transition and observation matrices. Furthermore, the estimated matrix should be adapted to the shape of the covariance matrix (if known), increasing the accuracy of the observer.
The first test evaluates the accuracy of the filter under different initial values of the noise covariance matrix. The results are compared against the estimations obtained with a non-adaptive version of the filter (errorEKF-FE). The results show an improvement in accuracy with the use of adaptive techniques. In addition, it can be seen how the adaptive method allows to achieve similar results in terms of accuracy in spite of the initial assumption of the covariance noises.
In a second test, the robustness of the filter is studied through a simulation in which an unexpected event changes the system. The filter shows a quick reaction and corrects with accuracy the new error, without loosing the stability of the estimator.
The tests executed in this work and their results show the potential of adaptive Kalman filtering for multibody based estimation. Determining the noise covariance matrix (specially the noise of the process) in multibody based estimators is an actual limitation for the general use of this techniques in multibody applications. Through adaptive estimation, the uncertainties on the process noise covariance matrix can be solved and the robustness and accuracy of the estimators can be increased and guaranteed during different scenarios. However, this method also implies a reduction of the computational efficiency that should be considered in real-time applications.
In future works, the proposed adaptive filter should be applied in systems of more complexity, such as vehicle dynamics, where the state and input estimation is of high interest. In addition, techniques for reducing the associated increment in computational cost can be studied.