Self-Excited Acoustical Measurement System for Rock Mass Stress Mapping
Abstract
:1. Introduction
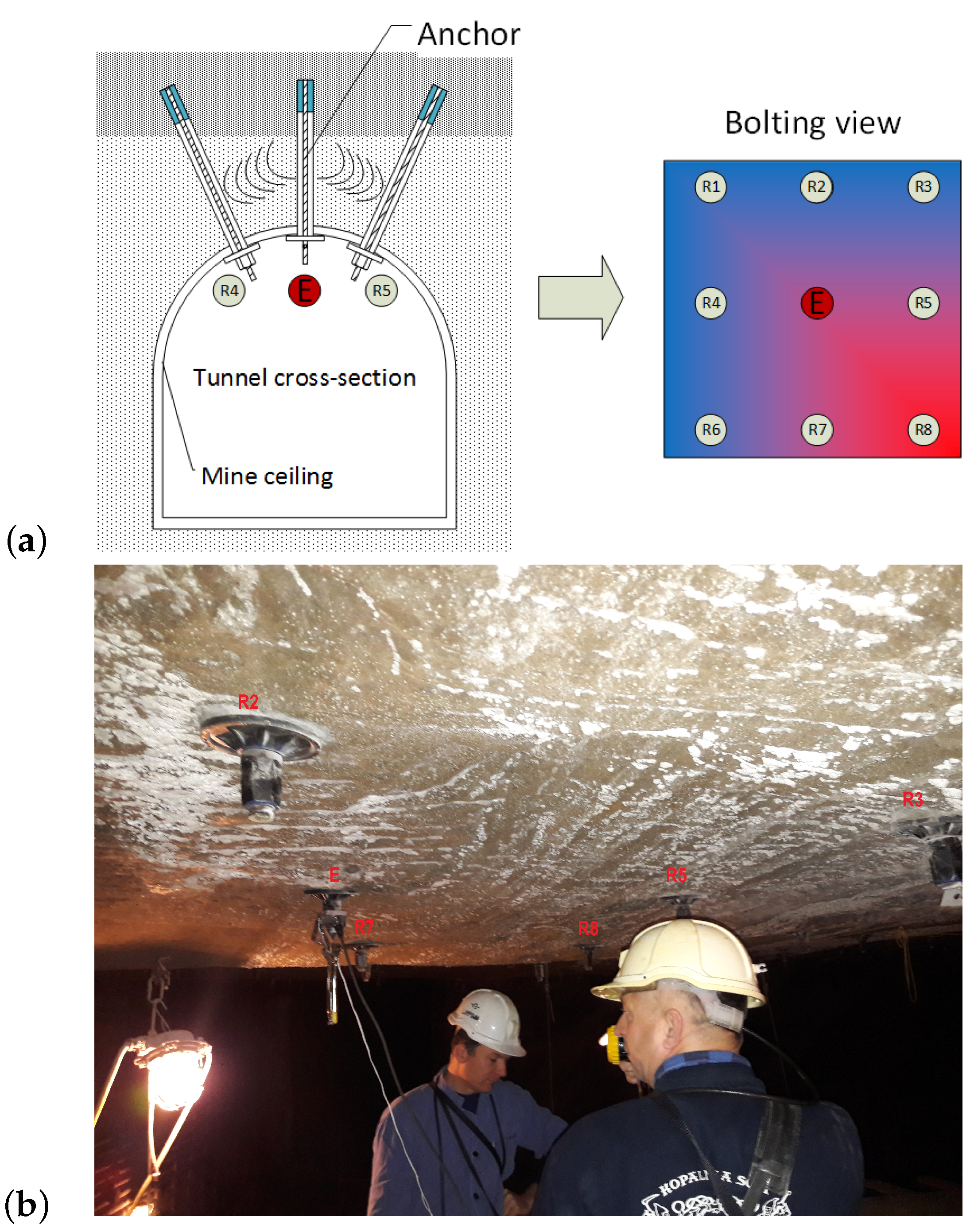
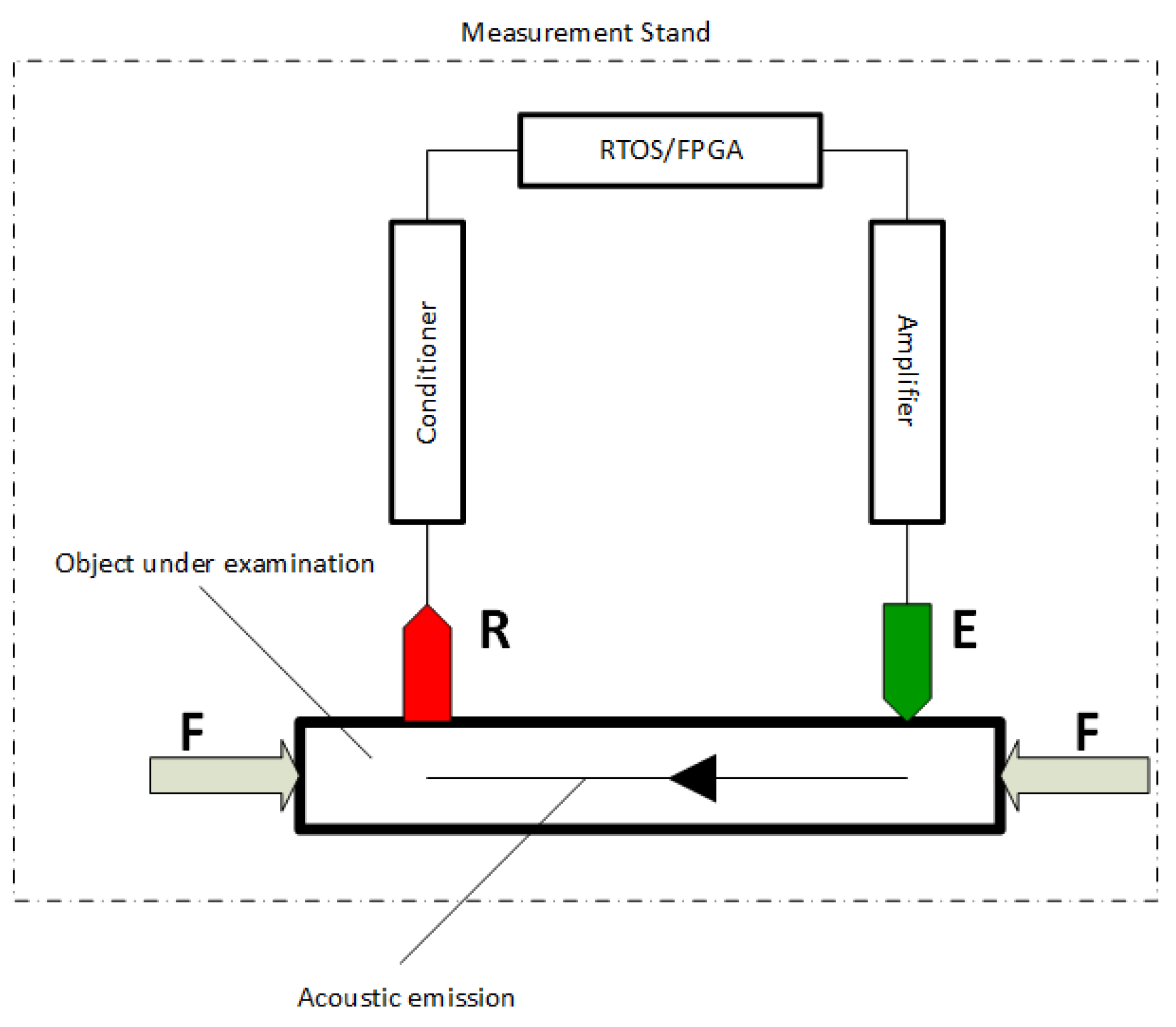
2. Methodology
3. System Modelling
- —Gain,
- —Signal delay.
- ,—Amplitudes of vibration for corresponding bolting,
- —SAS frequency.
- —Elastoacoustic coefficient,
- —Stress,
- E—Young modulus,
- —Time of acoustic wave propagation in no-stress state.
4. Stress Modeling in a Mine Roof
- , —Effective maximum and minimum stress at failure,
- —The limit strength of the rock material in uniaxial compression,
- —Value of the Hoek–Brown constant for the rock mass,
- s, a—Empirical constants determined on the basis of rock mass properties tests.
- —constant for unruptured rock, depending on the type of rock, determined using a triaxial compression test or from tabular data,
- —Geological Strength Index,
- D —the factor of weakening of the rock mass resulting from the mining method.
- ,—Normal and shear stresses on the slipping surface,
- —Maximum normal stress,
- —Minimum normal stress,
- —Horizontal coordinate of the center of Mohr’s circle,
- —Radius of Mohr’s circle,
- —Internal friction angle,
- c—Material cohesion.
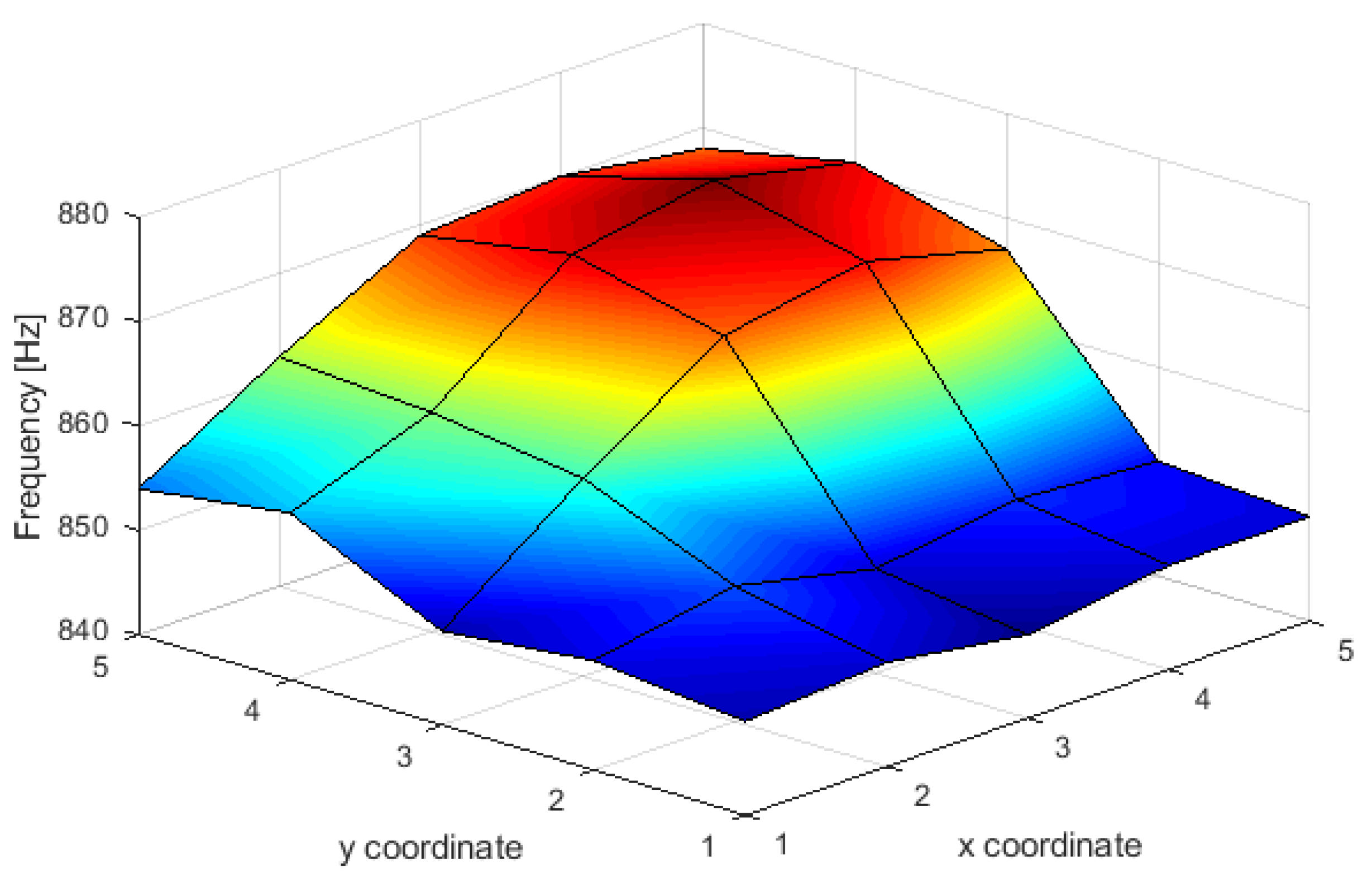
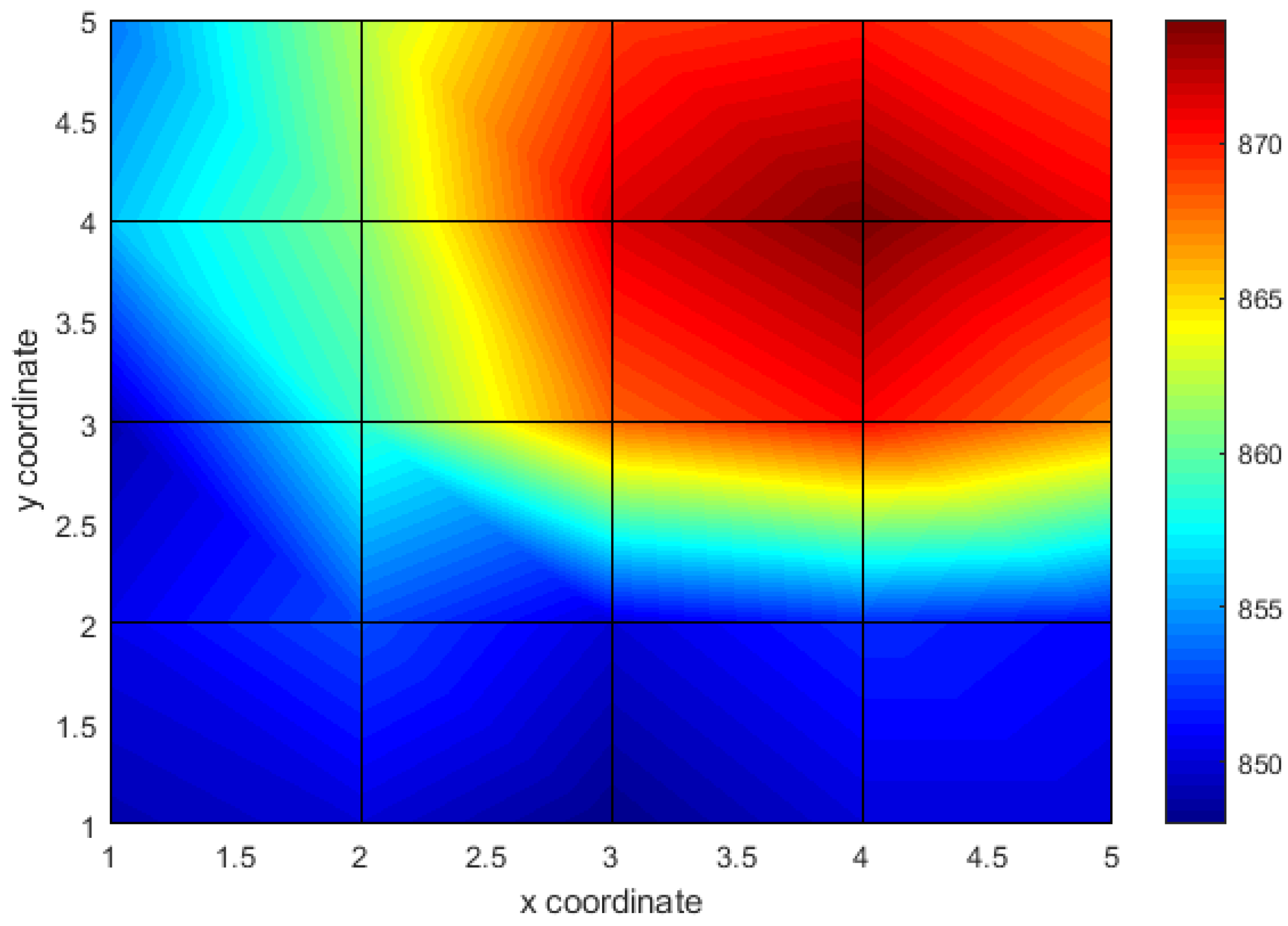
5. Results
6. Conclusions
- The proposed reduced model can be used in the future to determine the absolute value of stress between anchors based on the measured frequency of the SAS system.
- It is possible to quantify the stress increase in the tested anchored specimen with the SAS system. As a general rule, the SAS system indicates higher frequencies for a head application direction consistent with the predominant stress direction.
- The presented results of preliminary tests at the Wieliczka Salt Mine allowed confirming the applicability of the measurement system in the conditions of a real mine.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAS | Self-excited Acoustical System |
| NDT | Non-Destructive Testing |
| DOF | Degrees of Freedom |
| SF | Strength Factor |
| GSI | Geological Strength Index |
| FPGA | Field Programmable Gate Array |
| RTOS | Real Time Operating System |
References
- Mark, C.; Gadde, M. Global Trends in Coal Mine Horizontal Stress Measurements. In Proceedings of the 2010 Coal Operators’ Conference, Wollongong, Australia, 18–20 February 2019. [Google Scholar]
- Zhang, W.; Goh, A.T. Reliability assessment on ultimate and serviceability limit states and determination of critical factor of safety for underground rock caverns. Tunn. Undergr. Space Technol. 2012, 32, 221–230. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Wang, X.; Yu, H.; Bai, L.; Sun, Q. Exploring the impacts of factors contributing to unsafe behavior of coal miners. Saf. Sci. 2019, 115, 339–348. [Google Scholar] [CrossRef]
- Tong, R.; Zhang, Y.; Cui, P.; Zhai, C.; Shi, M.; Xu, S. Characteristic analysis of unsafe behavior by coal miners: Multi-dimensional description of the pan-Scene data. Int. J. Environ. Res. Public Health 2018, 15, 1608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Q.L.; Qiao, S.F.; Liu, B.C. The movement and deformation of soil and rock mass resulted from mining activity. J. Min. Saf. Eng. 2011, 28, 109–114. [Google Scholar]
- Mufundirwa, A.; Fujii, Y.; Kodama, N.; Kodama, J.I. Analysis of natural rock slope deformations under temperature variation: A case from a cool temperate region in Japan. Cold Reg. Sci. Technol. 2011, 65, 488–500. [Google Scholar] [CrossRef] [Green Version]
- Skrzypkowski, K. Case studies of rock bolt support loads and rock mass monitoring for the room and pillar method in the legnica-głogów copper district in Poland. Energies 2020, 13, 2998. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Pan, R.; Li, S.C.; He, M.C.; Sun, H.B.; Qin, Q.; Yu, H.C.; Luan, Y.C. Failure mechanism of surrounding rock with high stress and confined concrete support system. Int. J. Rock Mech. Min. Sci. 2018, 102, 89–100. [Google Scholar] [CrossRef]
- Lozynskyi, V.; Saik, P.; Petlovanyi, M.; Sai, K.; Malanchuk, Y. Analytical research of the stress-deformed state in the rock massif around faulting. Int. J. Eng. Res. Afr. 2018, 35, 77–88. [Google Scholar] [CrossRef]
- Fan, X.; Li, K.; Lai, H.; Xie, Y.; Cao, R.; Zheng, J. Internal stress distribution and cracking around flaws and openings of rock block under uniaxial compression: A particle mechanics approach. Comput. Geotech. 2018, 102, 28–38. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.; Zhu, J. Correlational fractal characterisation of stress and acoustic emission during coal and rock failure under multilevel dynamic loading. Int. J. Rock Mech. Min. Sci. 2019, 117, 1–10. [Google Scholar] [CrossRef]
- Kapur, A.; Graedel, T.E. Copper Mines above and below the Ground. Environ. Sci. Technol. 2006, 40, 3135–3141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, J.; Jiang, D.; Liu, W.; Wu, F.; Chen, J.; Daemen, J. Discontinuous fatigue of salt rock with low-stress intervals. Int. J. Rock Mech. Min. Sci. 2019, 115, 77–86. [Google Scholar] [CrossRef]
- Chen, G.Z.; Zhu, Z.C.; Zhou, G.B.; Shen, C.F.; Sun, Y.J. Sensor deployment strategy for chain-type wireless underground mine sensor network. J. China Univ. Min. Technol. 2008, 18, 561–566. [Google Scholar] [CrossRef]
- Li, W.; Wang, S.; Liu, L.; Meng, Q.; Liu, X.; Mei, S. Measurement analyses of rock mass movement and deformation due to underground mining of deep fractured orebody in Guanzhuang iron mine. Chin. J. Rock Mech. Eng. 2010, 29, 681–688. [Google Scholar]
- Danjo, T.; Yokoyama, T.; Ogawa, K.; Takagi, S.; Tanaka, H.; Arima, Y.; Ishida, T. Rock stress measurement by using hydraulic fracturing technique in Oga, Akita, Japan. In Proceedings of the 5th ISRM Young Scholars’ Symposium on Rock Mechanics and International Symposium on Rock Engineering for Innovative Future, Japan, Okinawa, 1–4 December 2019. [Google Scholar]
- Ishida, T.; Mizuta, Y.; Nakayama, Y. Investigation on a new dry single fracture method of in situ stress measurement. In Rock Stress; CRC Press: Boca Raton, FL, USA, 2020; pp. 301–306. [Google Scholar]
- Wang, H.; Lee, M.; Doe, T.; Haimson, B.; Oldenburg, C.; Dobson, P. In-situ stress measurement at 1550-meters depth at the kISMET test site in Lead, SD. In Proceedings of the 51st US Rock Mechanics Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Li, G.; Hu, Y.; Li, Q.B.; Yin, T.; Miao, J.X.; Yao, M. Inversion method of in situ stress and rock damage characteristics in dam site using neural network and numerical simulation—A case study. IEEE Access 2020, 8, 46701–46712. [Google Scholar] [CrossRef]
- Qiu, L.; Wang, E.; Song, D.; Liu, Z.; Shen, R.; Lv, G.; Xu, Z. Measurement of the stress field of a tunnel through its rock EMR. J. Geophys. Eng. 2017, 14, 949–959. [Google Scholar] [CrossRef]
- Kwaśniewki, J.; Dominik, I.; Lalik, K.; Holewa, K. Influence of acoustoelastic coefficient on wave time of flight in stress measurement in piezoelectric self-excited system. Mech. Syst. Signal Process. 2016, 78, 143–155. [Google Scholar] [CrossRef]
- Lalik, K.; Dominik, I.; Cwiakala, P.; Kwasniewski, J. Integrated stress measurement system in tower crane mast. Measurement 2017, 102, 47–56. [Google Scholar] [CrossRef]
- Lalik, K.; Kozek, M.; Dominik, I. Autonomous Machine Learning Algorithm for Stress Monitoring in Concrete Using Elastoacoustical Effect. Materials 2021, 14, 4116. [Google Scholar] [CrossRef]
- Skrzypkowski, K.; Korzeniowski, W.; Zagorski, K.; Dominik, I.; Lalik, K. Fast, non-destructive measurement of roof-bolt loads. Stud. Geotech. Mech. 2019, 41, 93–101. [Google Scholar] [CrossRef] [Green Version]
- Dominik, I. Advanced controlling of the prototype of SMA linear actuator. In Control Engineering in Materials Processing; Kot, A., Ed.; Trans Tech Publications Ltd.: Zurich, Switzerland, 2011; Volume 177, pp. 93–101. [Google Scholar] [CrossRef]







| Sensitivity: | (±5%) 100 mV/g (10.2 mV/(m/s)) |
| Frequency Range: | (±3 dB) 48 to 900,000 cpm (0.8 to 15,000 Hz) |
| Sensing Element: | Ceramic |
| Measurement Range: | ±50 g (±490 m/s) |
| Parameter | Piezo: PS-X-03-6/500 | |
| 1 | Weight | 40 g |
| 2 | Flat frequency range | 50 kHz |
| 3 | Capacity | <250 nF |
| 4 | Stroke | 2.4 m |
| 5 | Preload on piezo | 400 N |
| 6 | Blocking force | 5 kN |
| 7 | Piezoelectric modulus (d33) | 1.22 × 10 m/V |
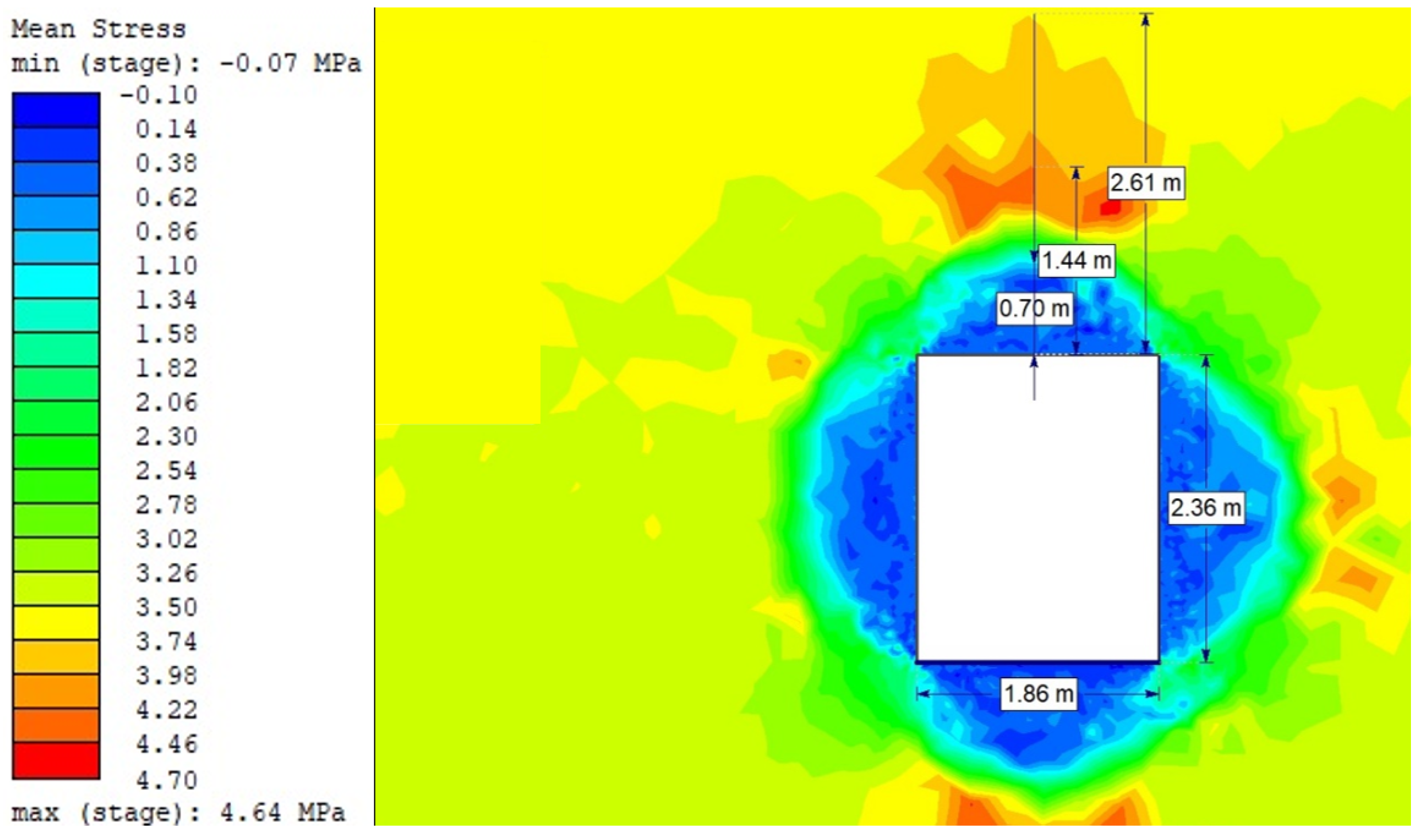
| Type of Bolting | The Hoek–Brown Criterion | |||
|---|---|---|---|---|
| Mean Stress | Total Strain | Strength Factor | Maximum Axial Force in the Anchorages [MN] | |
| [MPa] | [m] | [-] | ||
| [Coverage, [m]] | ||||
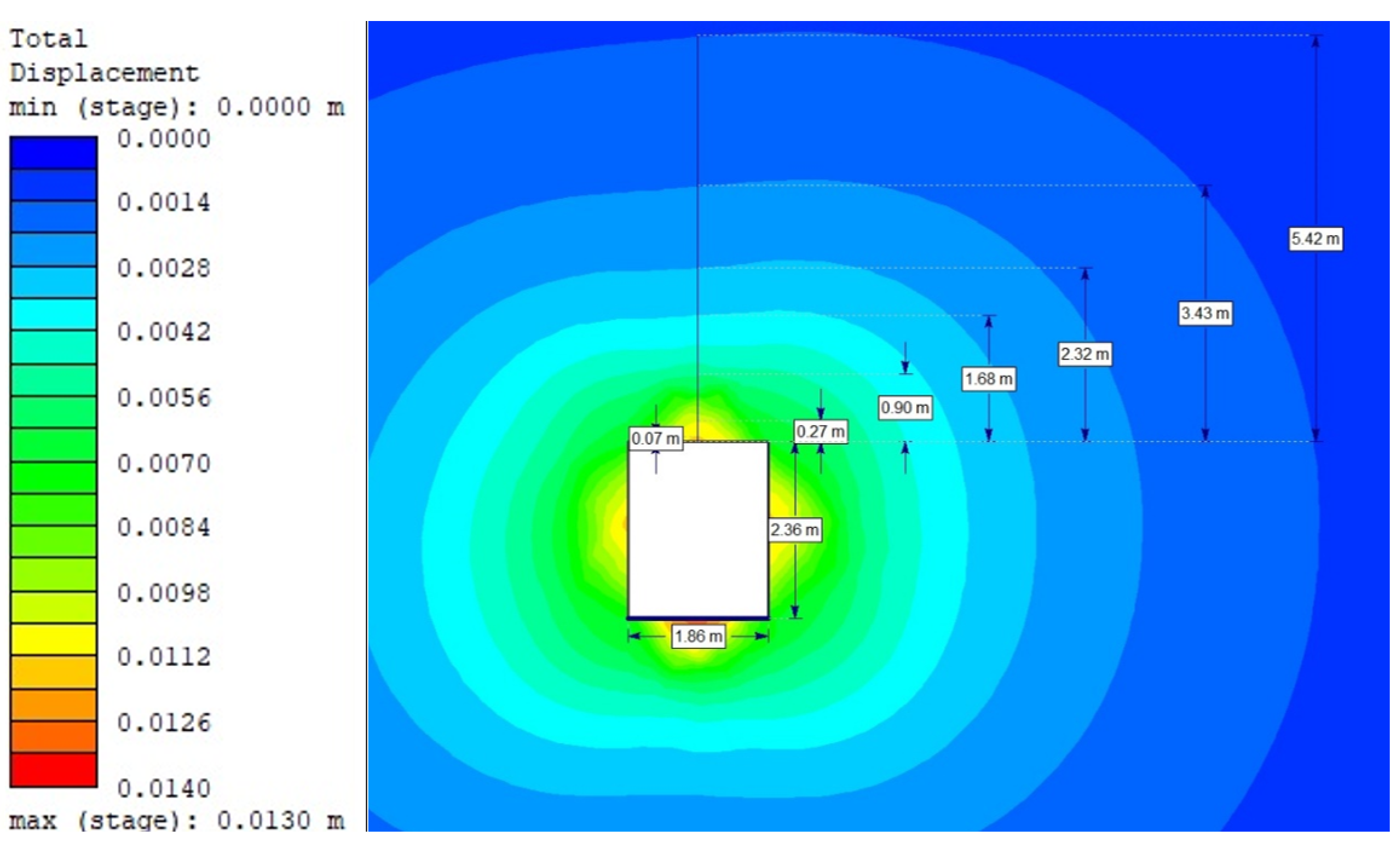
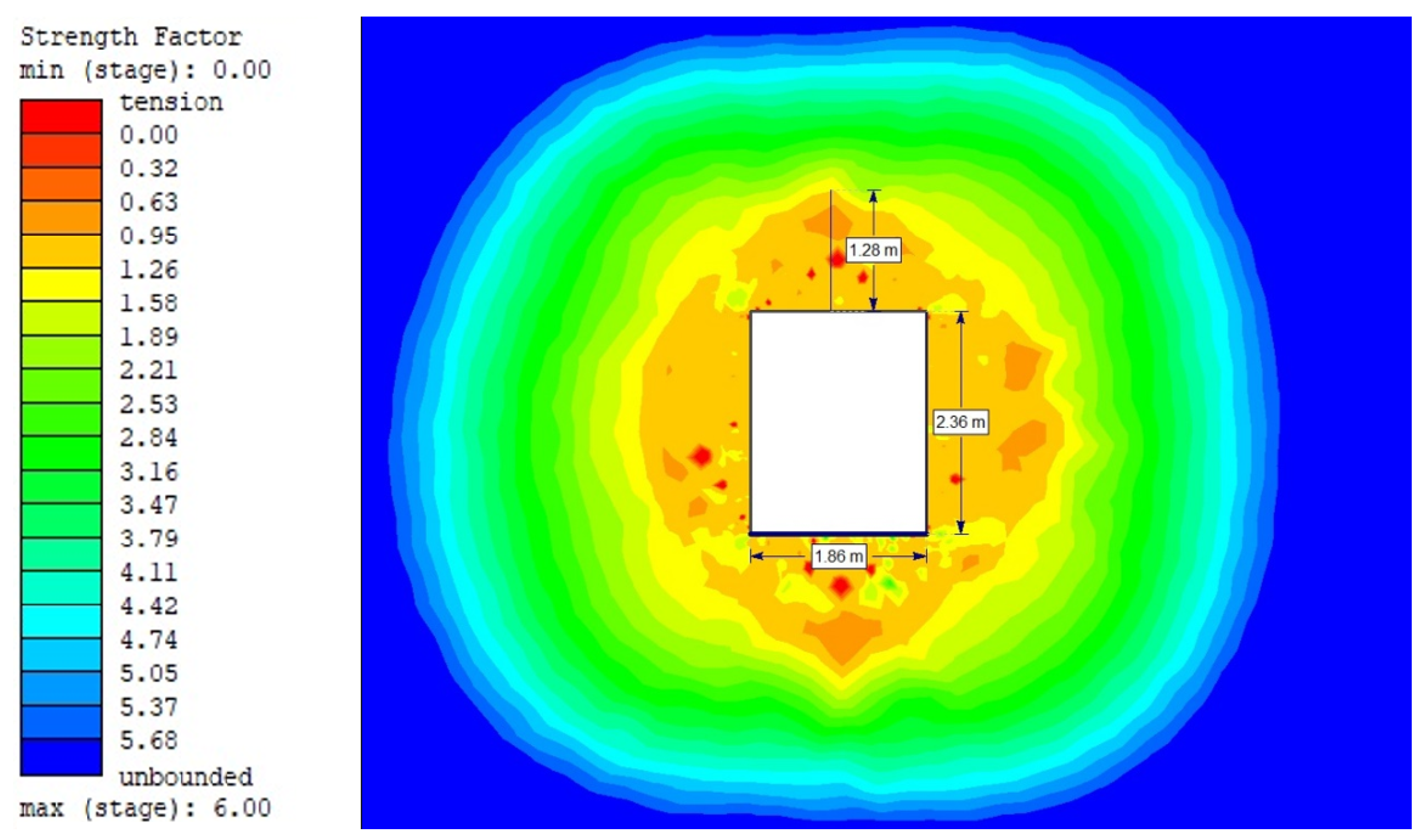
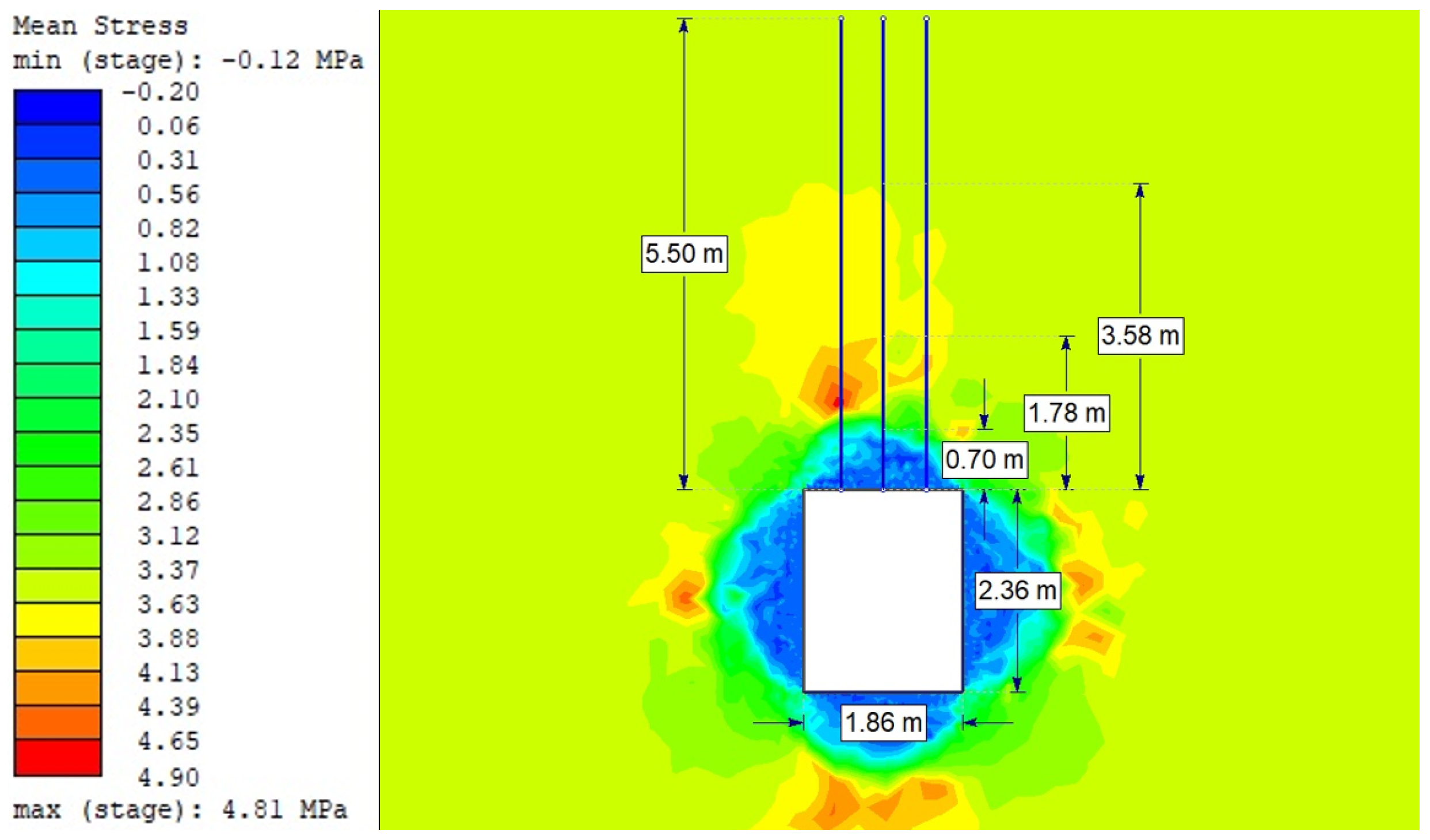
| Without bolting | 4.7/[1.44] | 0.014/[0.07] | [1.28] | - |
| Full-length bolting | 4.9/[1.78] | 0.012/ [0.11] | [1.21] | 0.0179 |
| The Coulomb–Mohr Criterion | ||||
| Mean Stress | Total Strain | Strength Factor | Maximum Axial Force in the Anchorages [MN] | |
| [MPa] | [m] | [-] | ||
| [Coverage, [m]] | ||||
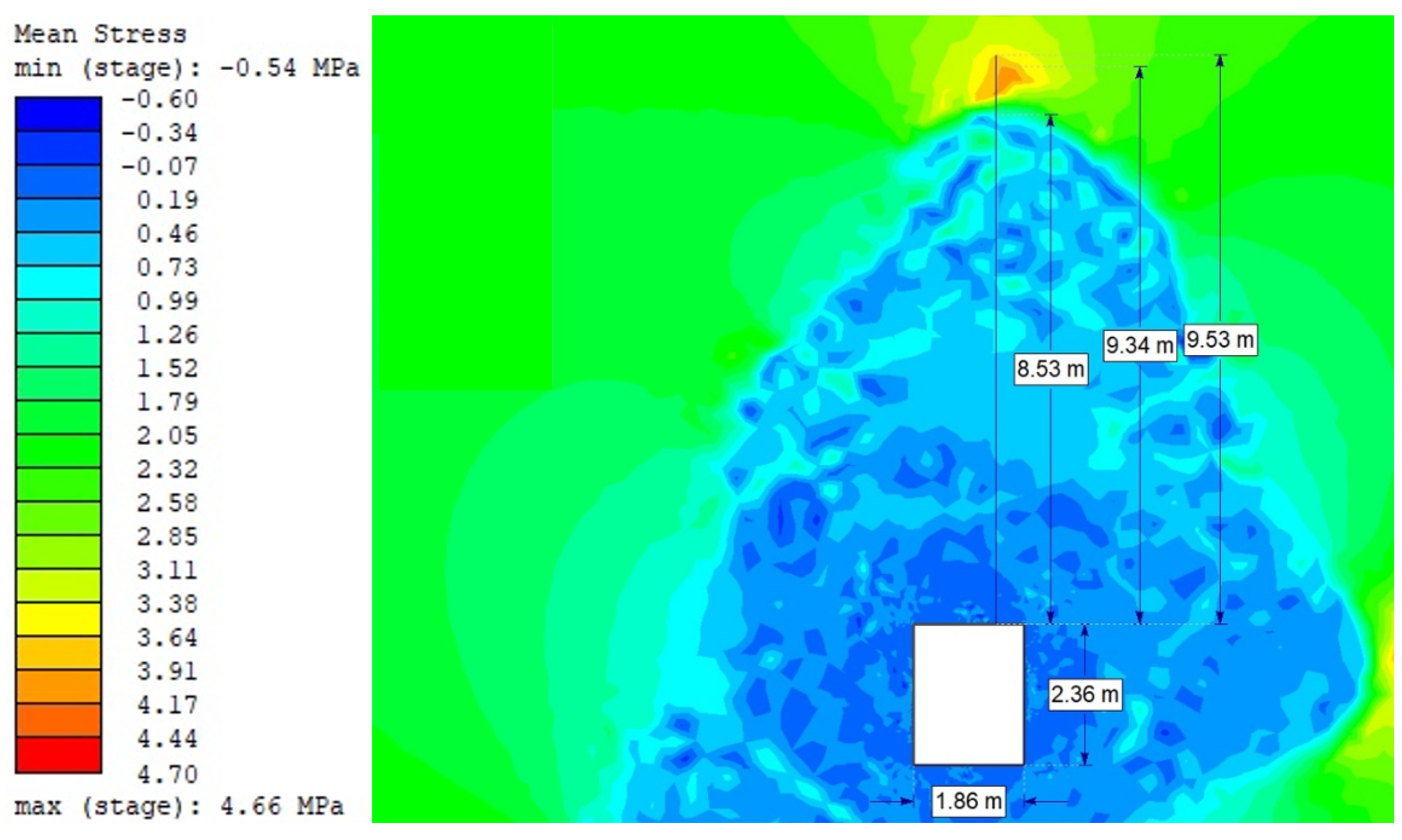
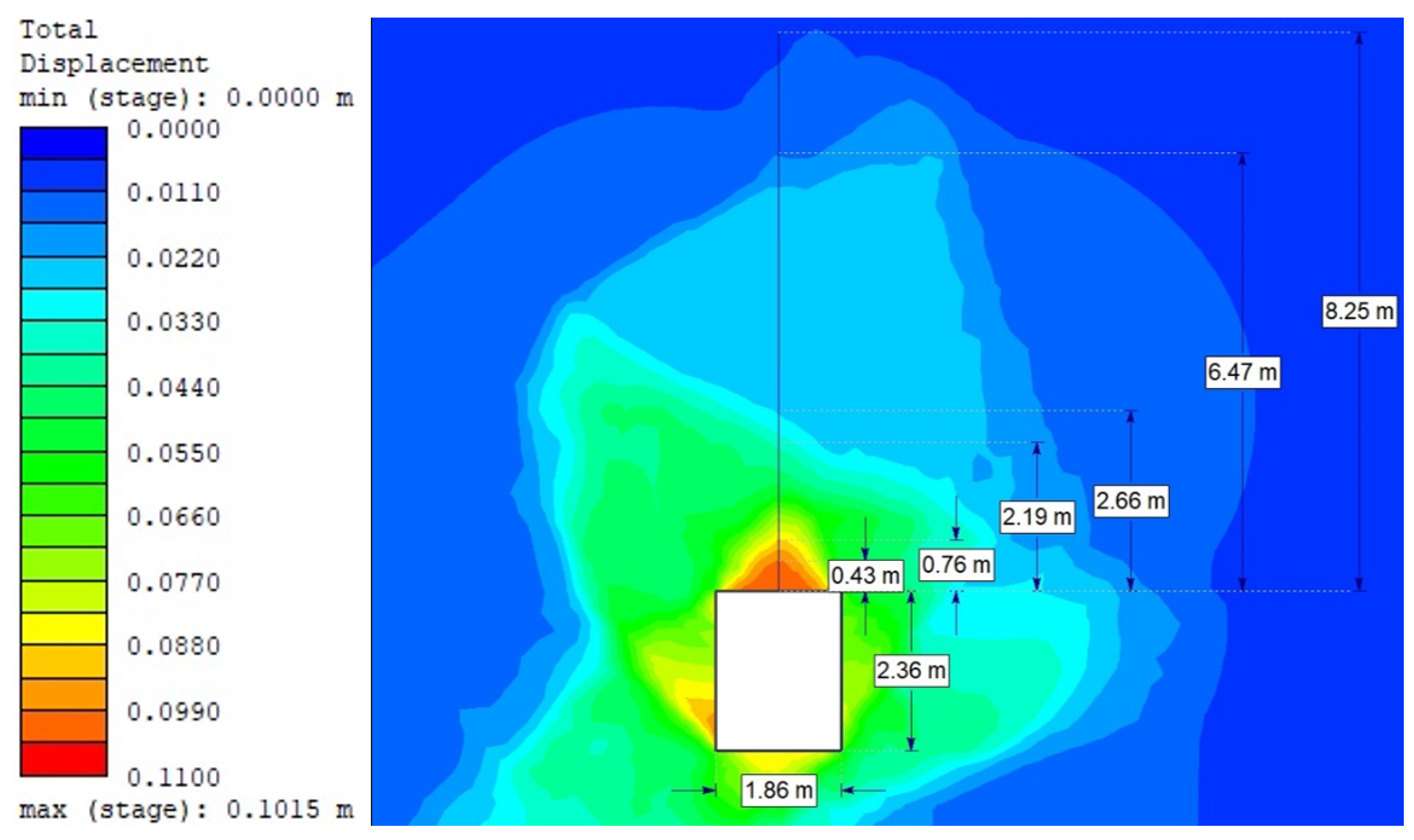
| Without bolting | 4.7 [9.34] | 0.11 [0.43] | 9.06 | - |
| Full-length bolting | 4.8 [5.41] | 0.10 [0.19] | 5.49 | 0.088 |
| Load Direction | Frequency Difference [Hz] between the Heads Applied in the Direction Consistent with the Load and the Heads on the Other Two Anchors | Frequency Difference [Hz] between Heads Applied in a Different Direction to the Load and Diagonal Heads (Emitter on K5 Anchor) |
|---|---|---|
| K1–K2 | 51.2 ± 0.1 | 16.7 ± 0.3 (K5–K1/2) |
| K3–K4 | 49.2 ± 0.3 | 15.1 ± 0.7 (K5–K3/4) |
| K1–K3 | 42.5 ± 0.6 | 11.6 ± 0.3 (K5–K1/3) |
| K2–K4 | 43.7 ± 0.3 | 10.2 ± 0.4 (K5–K2/4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lalik, K.; Dominik, I.; Skrzypkowski, K.; Korzeniowski, W.; Zagórski, K. Self-Excited Acoustical Measurement System for Rock Mass Stress Mapping. Sensors 2021, 21, 6749. https://doi.org/10.3390/s21206749
Lalik K, Dominik I, Skrzypkowski K, Korzeniowski W, Zagórski K. Self-Excited Acoustical Measurement System for Rock Mass Stress Mapping. Sensors. 2021; 21(20):6749. https://doi.org/10.3390/s21206749
Chicago/Turabian StyleLalik, Krzysztof, Ireneusz Dominik, Krzysztof Skrzypkowski, Waldemar Korzeniowski, and Krzysztof Zagórski. 2021. "Self-Excited Acoustical Measurement System for Rock Mass Stress Mapping" Sensors 21, no. 20: 6749. https://doi.org/10.3390/s21206749
APA StyleLalik, K., Dominik, I., Skrzypkowski, K., Korzeniowski, W., & Zagórski, K. (2021). Self-Excited Acoustical Measurement System for Rock Mass Stress Mapping. Sensors, 21(20), 6749. https://doi.org/10.3390/s21206749









