Assessment of SMA Electrical Resistance Change during Cyclic Stretching with Small Elongation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methodology
2.2. Control Algorithm
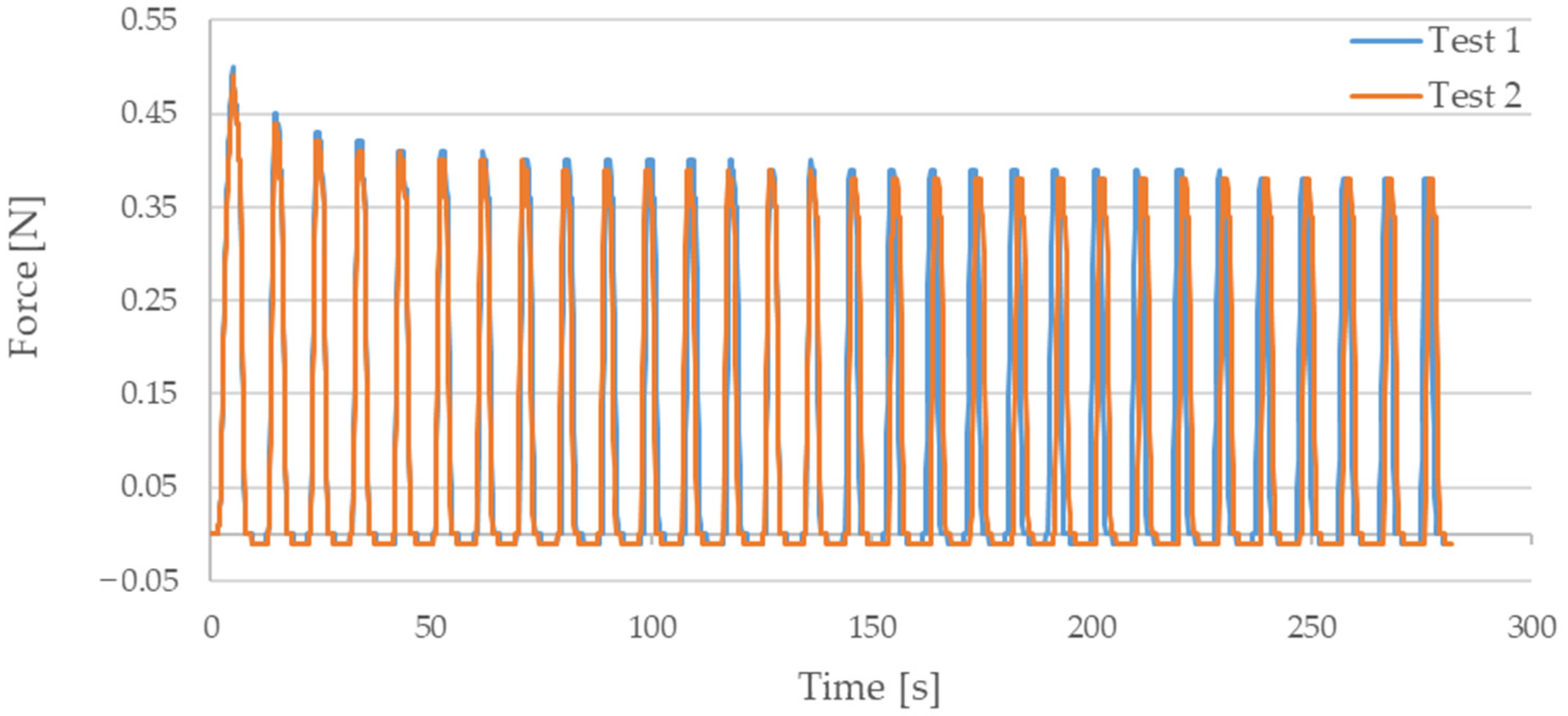
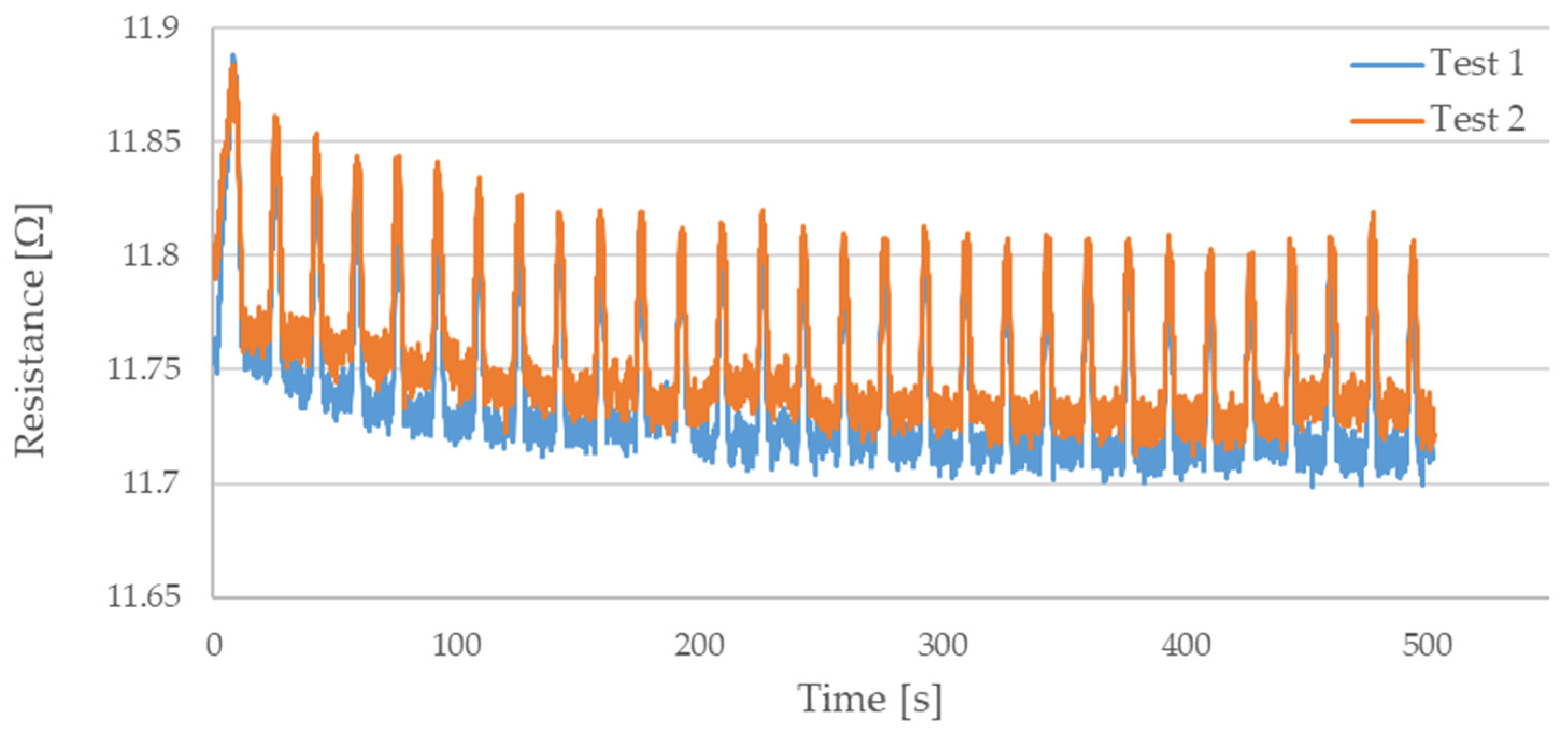
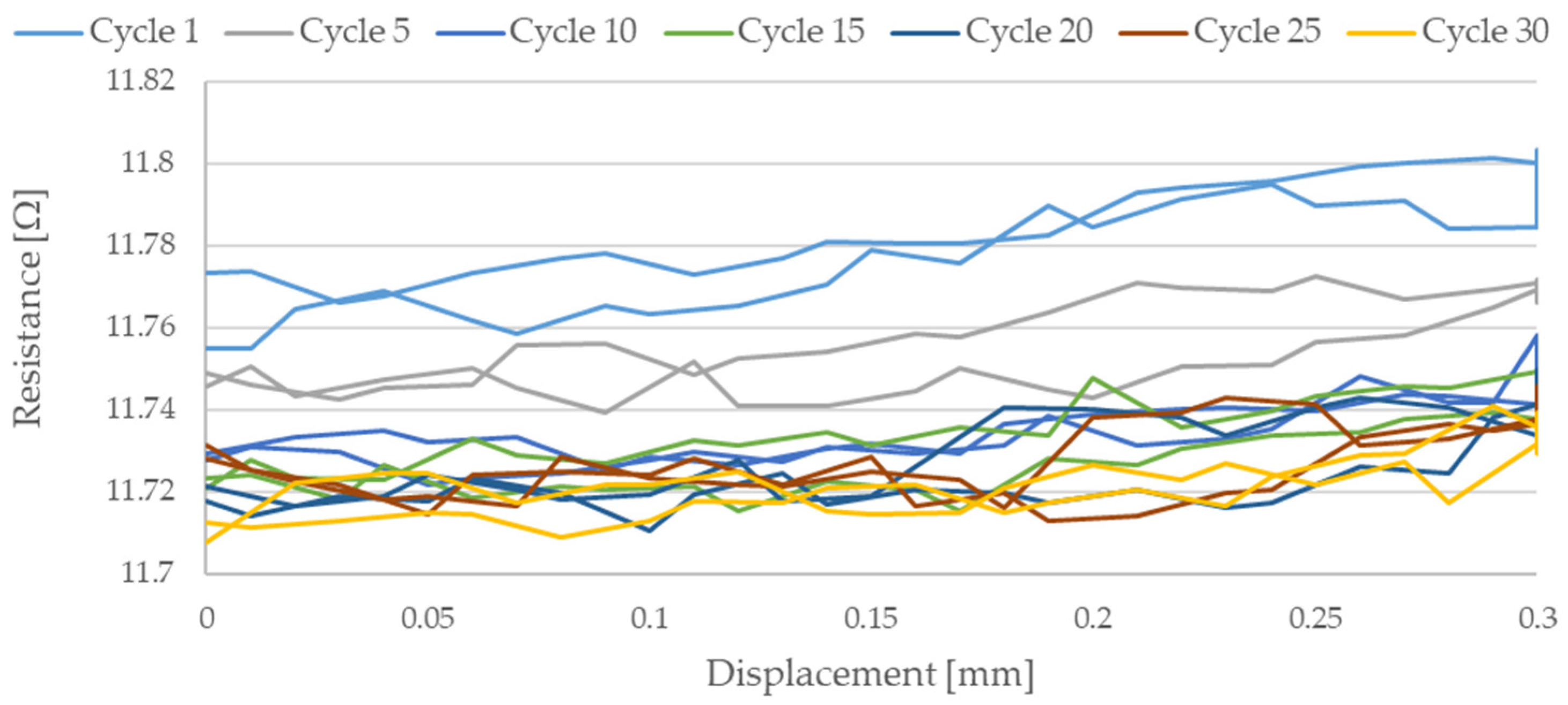
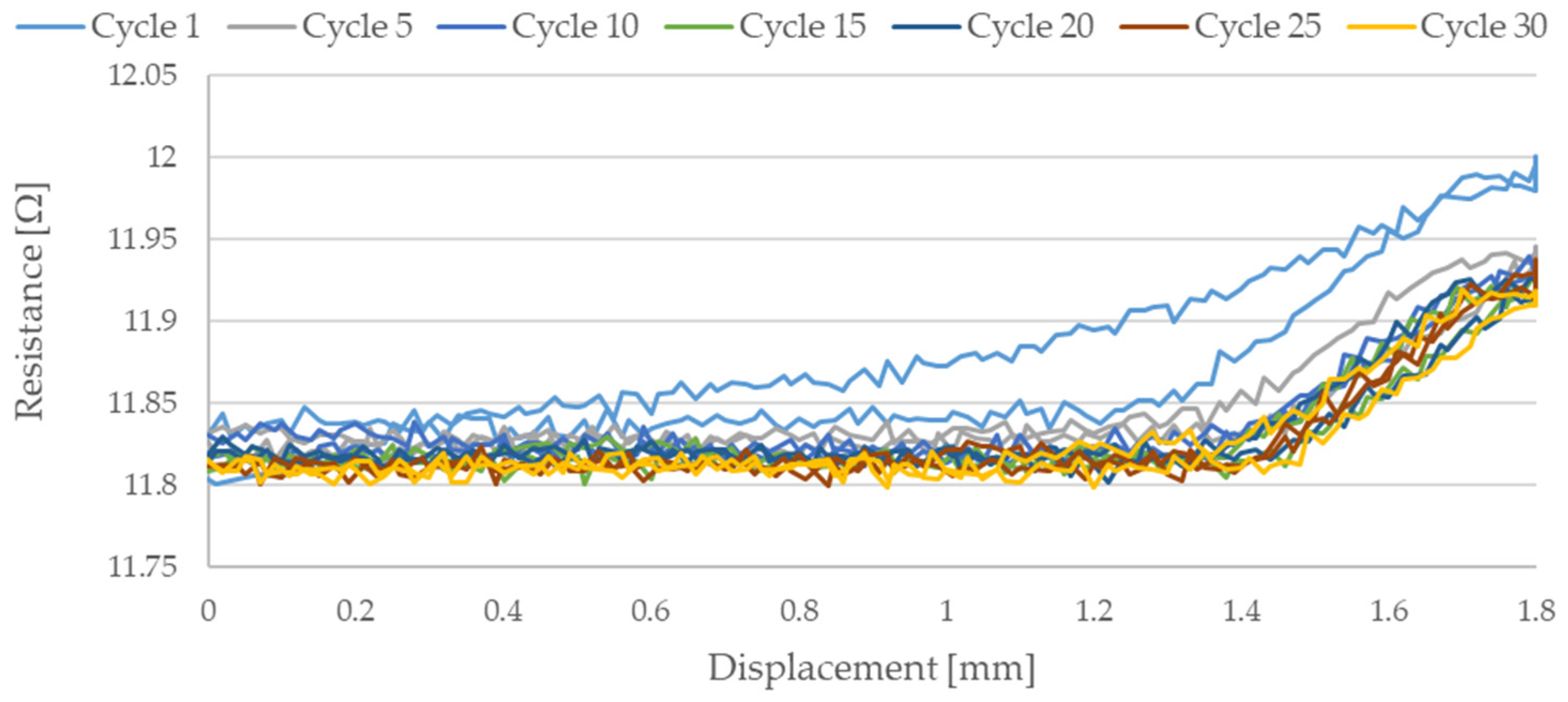
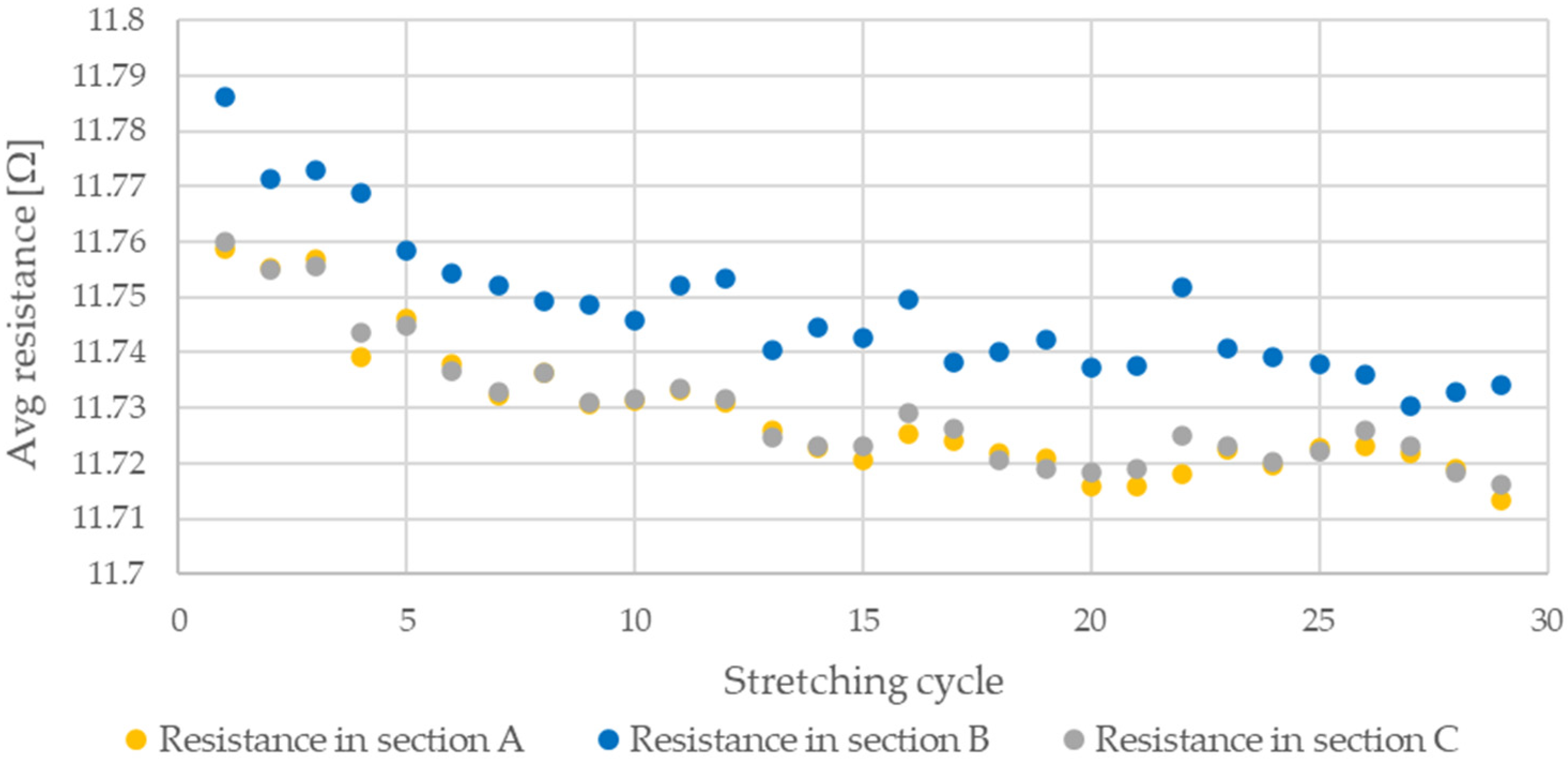
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A




References
- Mohd Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, S.W. Self-sensing-based deflection control of carbon fibre-reinforced polymer (CFRP)-based shape memory alloy hybrid composite beams. Compos. Struct. 2020, 251, 112544. [Google Scholar] [CrossRef]
- Abavisani, I.; Rezaifar, O.; Kheyroddin, A. Multifunctional properties of shape memory materials in civil engineering applications: A state-of-the-art review. J. Build. Eng. 2021, 44, 102657. [Google Scholar] [CrossRef]
- Ferčec, J.; Anžel, I.; Rudolf, R. Stress dependent electrical resistivity of orthodontic wire from the shape memory alloy NiTi. Mater. Des. 2014, 55, 699–706. [Google Scholar] [CrossRef]
- Prasad, M.H. Development of shape memory alloy (SMA)-based actuator for remotely piloted vehicles (RPVs). Smart Mater. Struct. Syst. 2003, 5062, 906–913. [Google Scholar] [CrossRef]
- Amari, M.D.; Che Abdullah, S. A Model for Hypersensitive Airflow Sensor Concept. J. Mech. Eng. 2017, 4, 163–174. [Google Scholar]
- Lan, C.C.; Lin, C.M.; Fan, C.H. A self-sensing microgripper module with wide handling ranges. IEEE/ASME Trans. Mechatron. 2011, 16, 141–150. [Google Scholar] [CrossRef]
- Mao, C.; Li, H. SMA-based smart damper/displacement transducer. In Proceedings of the Smart Structures and Materials 2005: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 7–10 March 2005; Volume 5765, pp. 442–452. [Google Scholar] [CrossRef]
- Pittaccio, S.; Garavaglia, L.; Ceriotti, C.; Passaretti, F. Applications of Shape Memory Alloys for Neurology and Neuromuscular Rehabilitation. J. Funct. Biomater. 2015, 6, 328–344. [Google Scholar] [CrossRef] [Green Version]
- Madill, D.R.; Wang, D. Modeling and L2-stability of a shape memory alloy position control system. IEEE Trans. Control Syst. Technol. 1998, 6, 473–481. [Google Scholar] [CrossRef]
- Velázquez, R.; Pissaloux, E.; Szewczyk, J.; Hafez, M. Miniature shape memory alloy actuator for tactile binary information display. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; Volume 2005, pp. 1344–1349. [Google Scholar] [CrossRef]
- Kciuk, M.; Chwastek, K.; Kluszczyński, K.; Szczygłowski, J. A study on hysteresis behaviour of SMA linear actuators based on unipolar sigmoid and hyperbolic tangent functions. Sens. Actuators A Phys. 2016, 243, 52–58. [Google Scholar] [CrossRef]
- Laudani, A.; Lozito, G.M.; Fulginei, F.R. Dynamic hysteresis modelling of magnetic materials by using a neural network approach. In Proceedings of the 2014 AEIT Annual Conference—From Research to Industry: The Need for a More Effective Technology Transfer (AEIT), Trieste, Italy, 18–19 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Mohsenian, A.; Zakerzadeh, M.; Shariat Panahi, M.; Fakhrzade, A. Modeling SMA actuated systems based on Bouc-Wen hysteresis model and feed-forward neural network. J. Comput. Appl. Mech. 2018, 49, 9–17. [Google Scholar] [CrossRef]
- Ikuta, K.; Tsukamoto, M.; Hirose, S. Shape memory alloy servo actuator system with electric resistance feedback and application for active endoscope. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; Volume 1, pp. 427–430. [Google Scholar] [CrossRef]
- Sreekanth, M.; Mathew, A.T.; Vijayakumar, R. A novel model-based approach for resistance estimation using rise time and sensorless position control of sub-millimetre shape memory alloy helical spring actuator. J. Intell. Mater. Syst. Struct. 2018, 29, 1050–1064. [Google Scholar] [CrossRef]
- Kciuk, M.; Kuchcik, W.; Pilch, Z.; Klein, W. A novel SMA drive based on the Graham Clock escapement and resistance feedback. Sens. Actuators A Phys. 2019, 285, 406–413. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S. Seismic assessment of bridge structures isolated by a shape memory alloy/rubber-based isolation system. Smart Mater. Struct. 2011, 20, 015003. [Google Scholar] [CrossRef]
- Liu, Z.-Q.; Li, H.; Chen, W.-L.; Ou, J.-P. Study on Strain-Sense Property of TiNi and TiNiCu Shape Memory Alloys. Adv. Struct. Eng. 2005, 8, 637–643. [Google Scholar] [CrossRef]
- Rączka, W.; Konieczny, J.; Sibielak, M. Laboratory Tests of Shape Memory Alloy Wires. Solid State Phenom. 2013, 199, 365–370. [Google Scholar] [CrossRef]
- Zhang, J.-J.; Yin, Y.-H.; Zhu, J.-Y. Electrical Resistivity-Based Study of Self-Sensing Properties for Shape Memory Alloy-Actuated Artificial Muscle. Sensors 2013, 13, 12958–12974. [Google Scholar] [CrossRef] [PubMed]
- Šittner, P.; Landa, M.; Lukáš, P.; Novák, V. R-phase transformation phenomena in thermomechanically loaded NiTi polycrystals. Mech. Mater. 2006, 38, 475–492. [Google Scholar] [CrossRef]
- Wang, X.; Kustov, S.; Verlinden, B.; Van Humbeeck, J. Fundamental Development on Utilizing the R-phase Transformation in NiTi Shape Memory Alloys. Shape Mem. Superelasticity 2015, 1, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Šittner, P.; Sedlák, P.; Landa, M.; Novák, V.; Lukáš, P. In situ experimental evidence on R-phase related deformation processes in activated NiTi wires. Mater. Sci. Eng. A 2006, 438–440, 579–584. [Google Scholar] [CrossRef]
- Uchil, J.; Mahesh, K.K.; Kumara, K.G. Electrical resistivity and strain recovery studies on the effect of thermal cycling under constant stress on R-phase in NiTi shape memory alloy. Phys. B Condens. Matter 2002, 324, 419–428. [Google Scholar] [CrossRef]
- Kyzioł, L.; Panasiuk, K.; Hajdukiewicz, G.; Dudzik, K. Acoustic Emission and K-S Metric Entropy as Methods for Determining Mechanical Properties of Composite Materials. Sensors 2021, 21, 145. [Google Scholar] [CrossRef]
- Palacz, M. Spectral Methods for Modelling of Wave Propagation in Structures in Terms of Damage Detection—A Review. Appl. Sci. 2018, 8, 1124. [Google Scholar] [CrossRef] [Green Version]
- Duda, S.; Gembalczyk, G.; Jurkojc, J.; Kciuk, S.; Michnik, R. Mechatronic solution of components cooperation in the device for gait reeducation. In Proceedings of the Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics 2015, Barcelona, Spain, 29 June–2 July 2015; pp. 799–805. [Google Scholar]
- Garcia, C.; Trendafilova, I. Triboelectric sensor as a dual system for impact monitoring and prediction of the damage in composite structures. NANO Energy 2019, 60, 527–535. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.D.; Fan, Y.Z.; Wu, J.S. A study on the variations of the electrical resistance for NiTi shape memory alloy wires during the thermo-mechanical loading. Mater. Des. 2000, 21, 511–515. [Google Scholar] [CrossRef]
- Antonucci, V.; Faiella, G.; Giordano, M.; Mennella, F.; Nicolais, L. Electrical resistivity study and characterization during NiTi phase transformations. Thermochim. Acta 2007, 462, 64–69. [Google Scholar] [CrossRef]
- Novák, V.; Šittner, P.; Dayananda, G.N.; Braz-Fernandes, F.M.; Mahesh, K.K. Electric resistance variation of NiTi shape memory alloy wires in thermomechanical tests: Experiments and simulation. Mater. Sci. Eng. A 2008, 481–482, 127–133. [Google Scholar] [CrossRef]
- Urbina, C.; la Flor, S.D.; Gispert-Guirado, F.; Ferrando, F. New Understanding of the Influence of the Pre-Training Phase Transformation Behaviour on the TWSME in NiTi SMA Wires. Exp. Mech. 2013, 53, 1415–1436. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Ou, J. Experimental study of a simple reinforced concrete beam temporarily strengthened by SMA wires followed by permanent strengthening with CFRP plates. Eng. Struct. 2008, 30, 716–723. [Google Scholar] [CrossRef]
- Furst, S.J.; Seelecke, S. Modeling and experimental characterization of the stress, strain, and resistance of shape memory alloy actuator wires with controlled power input. J. Intell. Mater. Syst. Struct. 2012, 23, 1233–1247. [Google Scholar] [CrossRef]
- Furst, S.J.; Crews, J.H.; Seelecke, S. Stress, strain, and resistance behavior of two opposing shape memory alloy actuator wires for resistance-based self-sensing applications. J. Intell. Mater. Syst. Struct. 2013, 24, 1951–1968. [Google Scholar] [CrossRef]
- Kciuk, M.; Kłapyta, G.; Świątek, K. Investigations of the Shape Memory Alloy actuator applied in a current sensitive switch. Meas. Autom. Monit. 2016, 62, 221–226. [Google Scholar]
- Hasegawa, T.; Majima, S. A control system to compensate the hysteresis by Preisach model on SMA actuator. In Proceedings of the 1998 International Symposium on Micromechatronics and Human Science (MHA’98), Nagoya, Japan, 25–28 November 1998; pp. 171–176. [Google Scholar] [CrossRef]
- Technical Characteristics of Flexinol® Actuator Wires. Available online: https://www.dynalloy.com/pdfs/TCF1140.pdf (accessed on 24 June 2021).
- Sławski, S.; Szymiczek, M.; Kaczmarczyk, J.; Domin, J.; Świtoński, E. Low Velocity Impact Response and Tensile Strength of Epoxy Composites with Different Reinforcing Materials. Materials 2020, 13, 3059. [Google Scholar] [CrossRef]
- Sławski, S.; Kaczmarczyk, J.; Szymiczek, M.; Pakieła, W. Numerical Studies on the Influence of a Reinforcing Material on the Energy Absorption in a Multilayered Composite during Impacts. Mech. Compos. Mater. 2021, 57, 309–320. [Google Scholar] [CrossRef]
- Setlak, L.; Kowalik, R.; Lusiak, T. Practical Use of Composite Materials Used in Military Aircraft. Materials 2021, 14, 4812. [Google Scholar] [CrossRef] [PubMed]
- Krzyzak, A.; Kosicka, E.; Borowiec, M.; Szczepaniak, R. Selected Tribological Properties and Vibrations in the Base Resonance Zone of the Polymer Composite Used in the Aviation Industry. Materials 2020, 13, 1364. [Google Scholar] [CrossRef] [PubMed] [Green Version]

















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sławski, S.; Kciuk, M.; Klein, W. Assessment of SMA Electrical Resistance Change during Cyclic Stretching with Small Elongation. Sensors 2021, 21, 6804. https://doi.org/10.3390/s21206804
Sławski S, Kciuk M, Klein W. Assessment of SMA Electrical Resistance Change during Cyclic Stretching with Small Elongation. Sensors. 2021; 21(20):6804. https://doi.org/10.3390/s21206804
Chicago/Turabian StyleSławski, Sebastian, Marek Kciuk, and Wojciech Klein. 2021. "Assessment of SMA Electrical Resistance Change during Cyclic Stretching with Small Elongation" Sensors 21, no. 20: 6804. https://doi.org/10.3390/s21206804
APA StyleSławski, S., Kciuk, M., & Klein, W. (2021). Assessment of SMA Electrical Resistance Change during Cyclic Stretching with Small Elongation. Sensors, 21(20), 6804. https://doi.org/10.3390/s21206804






