NrtNet: An Unsupervised Method for 3D Non-Rigid Point Cloud Registration Based on Transformer
Abstract
:1. Introduction
- We propose a transformer-based point cloud correspondence learning framework for learning dense correspondences between point clouds, and we are the first to introduce a transformer into the field of non-rigid point cloud registration.
- Our network eliminates the reliance on ground truth and achieves unsupervised learning of non-rigid point cloud registration in an end-to-end manner, and has a better registration effect for different objects.
- Experiments demonstrate that NrtNet has significant advantages in non-rigid point cloud registration. In particular, it is superior to methods that directly compute the drift of coherent points between point clouds and methods that use a grid as input.
2. Related Work
2.1. Deep Learning on Point Cloud
2.2. Non-Rigid Point Cloud Registration
2.3. Deep Learning Based on Transformer
3. Framework
3.1. Overview
3.2. Feature Extraction Module
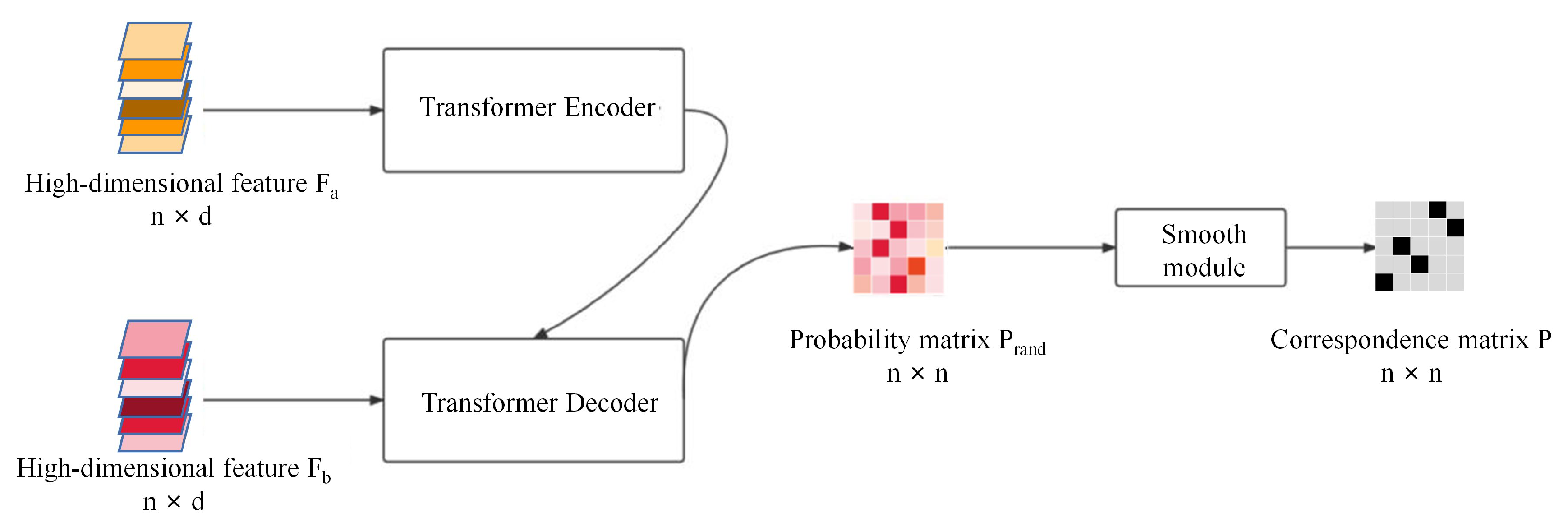
3.3. Transformer Module
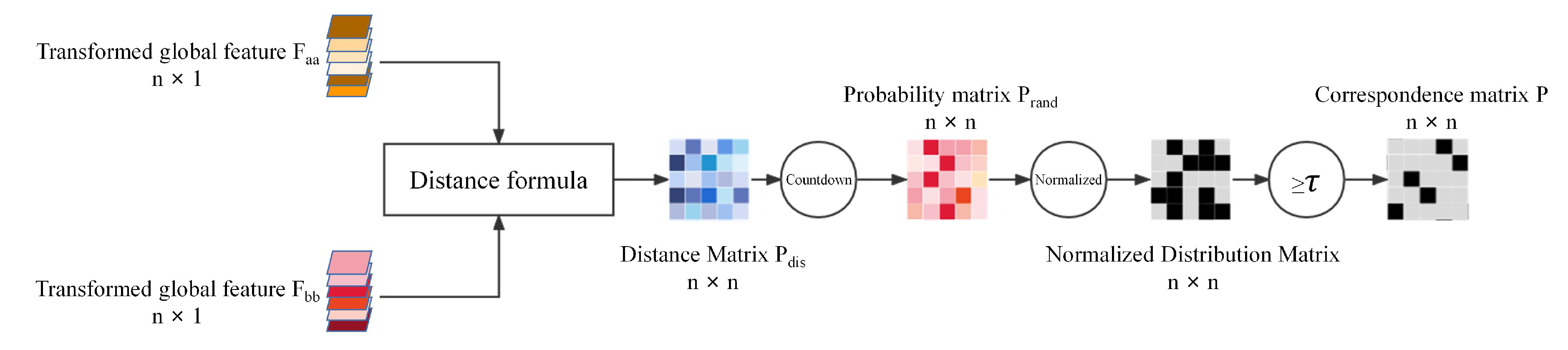
3.4. The Reconstruction Module
3.5. Unsupervised Loss Function
4. Experiment
4.1. Experimental Setup
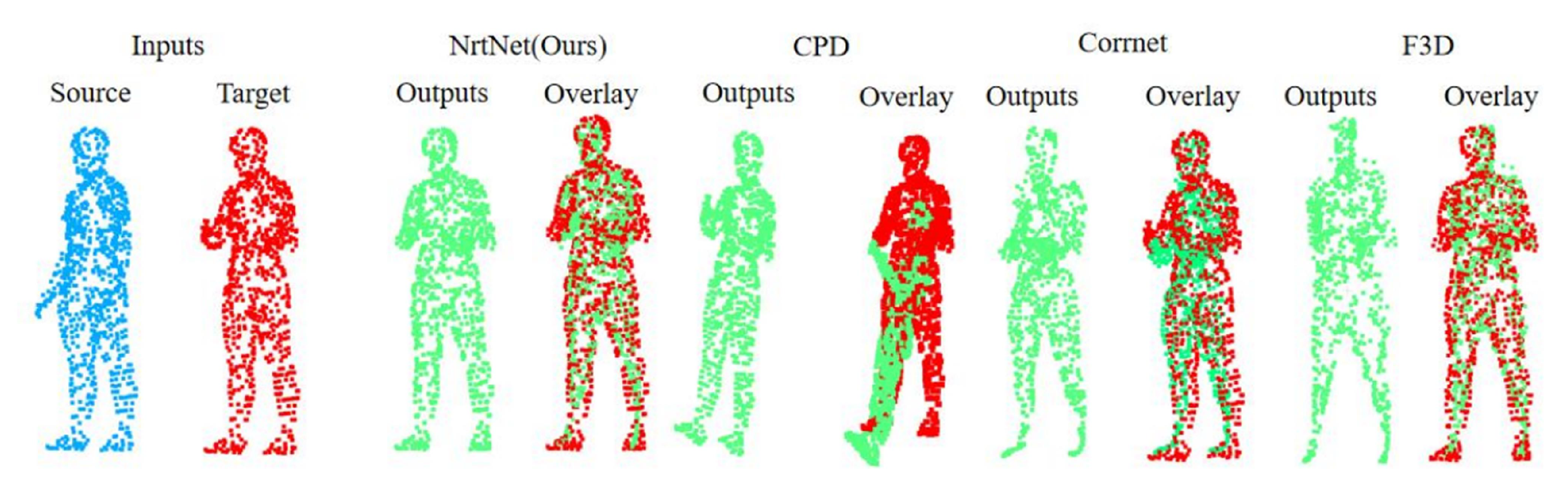
4.2. Experimental Evaluation of Non-Rigid Point Cloud Registration
4.3. Experimental Evaluation of Rigid Point Cloud Registration
4.4. Comparison between Different Datasets
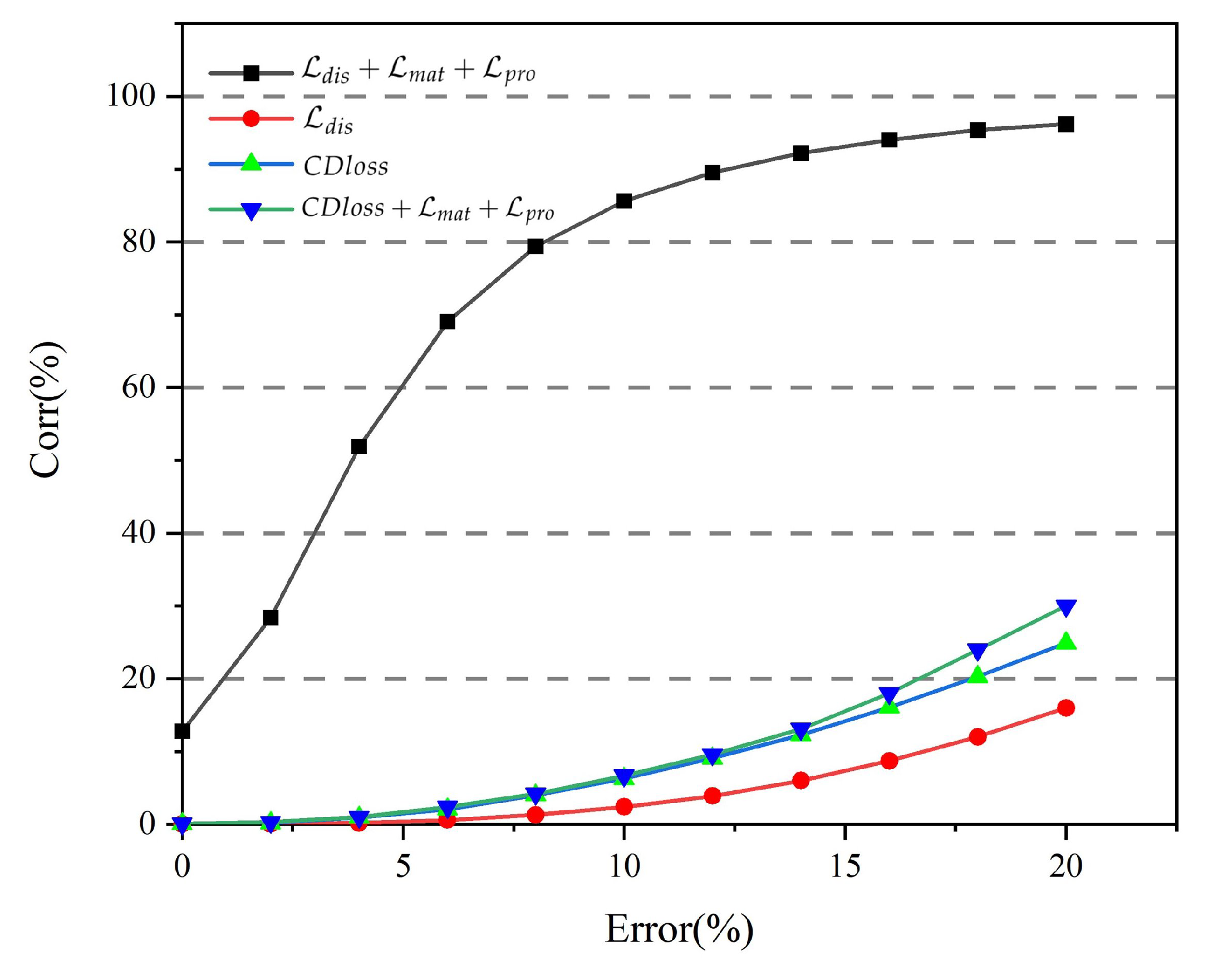
4.5. Comparison of Different Losses
4.6. Real Scan Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Apostolopoulos, J.G.; Chou, P.A.; Culbertson, B.; Kalker, T.; Trott, M.D.; Wee, S. The road to immersive communication. Proc. IEEE 2012, 100, 974–990. [Google Scholar] [CrossRef]
- Raviteja, T.; Vedaraj, I.R. An introduction of autonomous vehicles and a brief survey. J. Crit. Rev 2020, 7, 196–202. [Google Scholar]
- Silva, R.; Oliveira, J.C.; Giraldi, G.A. Introduction to augmented reality. Natl. Lab. Sci. Comput. 2003, 11, 1–11. [Google Scholar]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3d. net: A new large-scale point cloud classification benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar]
- Reisi, A.R.; Moradi, M.H.; Jamasb, S. Classification and comparison of maximum power point tracking techniques for photovoltaic system: A review. Renew. Sustain. Energy Rev. 2013, 19, 433–443. [Google Scholar] [CrossRef]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Brox, T.; Malik, J. Object segmentation by long term analysis of point trajectories. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 282–295. [Google Scholar]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [Green Version]
- Pomerleau, F.; Colas, F.; Siegwart, R. A review of point cloud registration algorithms for mobile robotics. Found. Trends Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef] [Green Version]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 37–44. [Google Scholar]
- Zha, H.; Ikuta, M.; Hasegawa, T. Registration of range images with different scanning resolutions. In Proceedings of the SMC 2000 Conference Proceedings, 2000 IEEE International Conference on Systems, Man and Cybernetics.’Cybernetics Evolving to Systems, Humans, Organizations, and Their Complex Interactions’, Nashville, TN, USA, 8–11 October 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 1495–1500, cat. no. 0. [Google Scholar]
- Zinßer, T.; Schmidt, J.; Niemann, H. Point set registration with integrated scale estimation. In Proceedings of the International Conference on Pattern Recognition and Image Processing, Estoril, Portugal, 7–9 June 2005; pp. 116–119. [Google Scholar]
- Amberg, B.; Romdhani, S.; Vetter, T. Optimal step nonrigid ICP algorithms for surface registration. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, Minnesota, 17–22 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Wang, C.; Shu, Q.; Yang, Y.; Yuan, F. Point cloud registration in multidirectional affine transformation. IEEE Photonics J. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Zeng, Y.; Qian, Y.; Zhu, Z.; Hou, J.; Yuan, H.; He, Y. CorrNet3D: Unsupervised end-to-end learning of dense correspondence for 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6052–6061. [Google Scholar]
- Vyas, A.; Katharopoulos, A.; Fleuret, F. Fast transformers with clustered attention. Adv. Neural Inf. Process. Syst. 2020, 33, 21665–21674. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. Scannet: Richly-annotated 3d reconstructions of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5828–5839. [Google Scholar]
- Huang, J.; You, S. Point cloud labeling using 3d convolutional neural network. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2670–2675. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 922–928. [Google Scholar]
- Engelcke, M.; Rao, D.; Wang, D.Z.; Tong, C.H.; Posner, I. Vote3deep: Fast object detection in 3d point clouds using efficient convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1355–1361. [Google Scholar]
- Graham, B. Spatially-sparse convolutional neural networks. arXiv 2014, arXiv:1409.6070. [Google Scholar]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and multi-view cnns for object classification on 3d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Phan, A.V.; Le Nguyen, M.; Nguyen, Y.L.H.; Bui, L.T. Dgcnn: A convolutional neural network over large-scale labeled graphs. Neural Netw. 2018, 108, 533–543. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, W.; Neumann, U. Recurrent slice networks for 3d segmentation of point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2626–2635. [Google Scholar]
- Ye, X.; Li, J.; Huang, H.; Du, L.; Zhang, X. 3d recurrent neural networks with context fusion for point cloud semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 403–417. [Google Scholar]
- Thabet, A.; Alwassel, H.; Ghanem, B. Mortonnet: Self-supervised learning of local features in 3d point clouds. arXiv 2019, arXiv:1904.00230. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 206–215. [Google Scholar]
- Vakalopoulou, M.; Chassagnon, G.; Bus, N.; Marini, R.; Zacharaki, E.I.; Revel, M.P.; Paragios, N. Atlasnet: Multi-atlas non-linear deep networks for medical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 658–666. [Google Scholar]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. 3d-coded: 3d correspondences by deep deformation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 230–246. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; SPIE: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Chui, H.; Rangarajan, A. A new algorithm for non-rigid point matching. In Proceedings of the Proceedings IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2000 (Cat. No. PR00662), Hilton Head Island, SC, USA, 13–15 June 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 44–51. [Google Scholar]
- Myronenko, A.; Song, X.; Carreira-Perpinan, M. Non-rigid point set registration: Coherent point drift. Adv. Neural Inf. Process. Syst. 2006, 19, 1–8. [Google Scholar]
- Ma, J.; Zhao, J.; Yuille, A.L. Non-rigid point set registration by preserving global and local structures. IEEE Trans. Image Process. 2015, 25, 53–64. [Google Scholar]
- Wang, L.; Li, X.; Chen, J.; Fang, Y. Coherent point drift networks: Unsupervised learning of non-rigid point set registration. arXiv 2019, arXiv:1906.03039. [Google Scholar]
- Shimada, S.; Golyanik, V.; Tretschk, E.; Stricker, D.; Theobalt, C. Dispvoxnets: Non-rigid point set alignment with supervised learning proxies. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 27–36. [Google Scholar]
- Wang, L.; Chen, J.; Li, X.; Fang, Y. Non-rigid point set registration networks. arXiv 2019, arXiv:1904.01428. [Google Scholar]
- Ma, J.; Wu, J.; Zhao, J.; Jiang, J.; Zhou, H.; Sheng, Q.Z. Nonrigid point set registration with robust transformation learning under manifold regularization. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3584–3597. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Wu, F.; Fan, A.; Baevski, A.; Dauphin, Y.N.; Auli, M. Pay less attention with lightweight and dynamic convolutions. arXiv 2019, arXiv:1901.10430. [Google Scholar]
- Tchapmi, L.; Choy, C.; Armeni, I.; Gwak, J.; Savarese, S. Segcloud: Semantic segmentation of 3d point clouds. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 537–547. [Google Scholar]
- Dovrat, O.; Lang, I.; Avidan, S. Learning to sample. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2760–2769. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Wang, Z.; Delingette, H. Attention for Image Registration (AiR): An unsupervised Transformer approach. arXiv 2021, arXiv:2105.02282. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. Pct: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Donati, N.; Sharma, A.; Ovsjanikov, M. Deep geometric functional maps: Robust feature learning for shape correspondence. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8592–8601. [Google Scholar]
- Bednarik, J.; Fua, P.; Salzmann, M. Learning to reconstruct texture-less deformable surfaces from a single view. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 606–615. [Google Scholar]
- Liu, X.; Qi, C.R.; Guibas, L.J. Flownet3d: Learning scene flow in 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 529–537. [Google Scholar]




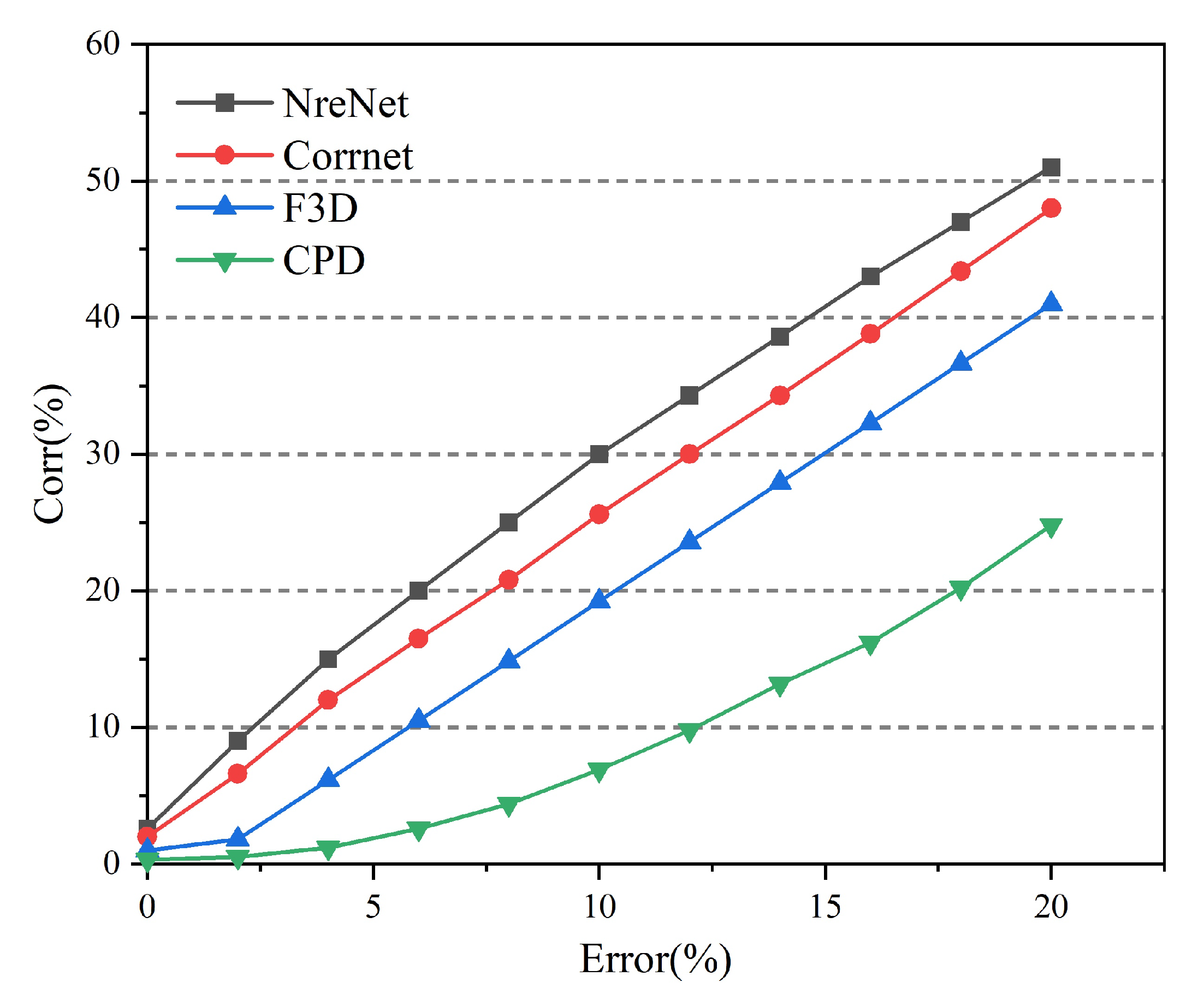



| Method | 0% Error Tolerance | 10% Error Tolerance | 20% Error Tolerance |
|---|---|---|---|
| CPD-Net | 0.3311 | 6.8212 | 24.8963 |
| FlowNet3D | 1.2133 | 19.7614 | 41.3494 |
| Corrnet3D | 2.0494 | 25.68 | 48.8636 |
| NrtNet | 2.6889 | 30.0429 | 51.8758 |
| Method | 0% Error Tolerance | 10% Error Tolerance | 20% Error Tolerance |
|---|---|---|---|
| CPD-Net | 0.1769 | 9.6191 | 24.286 |
| FlowNet3D | 10.8945 | 71.5576 | 90.368 |
| Corrnet3D | 12.4062 | 80.895 | 95.61 |
| NrtNet | 12.7793 | 85.6191 | 96.247 |
| Loss | 0% Error Tolerance | 10% Error Tolerance | 20% Error Tolerance |
|---|---|---|---|
| 0.0214 | 2.4287 | 16.081 | |
| 0.0879 | 6.3662 | 24.9873 | |
| 0.1045 | 6.7686 | 30.7441 | |
| 12.7793 | 85.6191 | 96.247 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Zhang, D.; Chen, J.; Wu, Y.; Chen, Y. NrtNet: An Unsupervised Method for 3D Non-Rigid Point Cloud Registration Based on Transformer. Sensors 2022, 22, 5128. https://doi.org/10.3390/s22145128
Hu X, Zhang D, Chen J, Wu Y, Chen Y. NrtNet: An Unsupervised Method for 3D Non-Rigid Point Cloud Registration Based on Transformer. Sensors. 2022; 22(14):5128. https://doi.org/10.3390/s22145128
Chicago/Turabian StyleHu, Xiaobo, Dejun Zhang, Jinzhi Chen, Yiqi Wu, and Yilin Chen. 2022. "NrtNet: An Unsupervised Method for 3D Non-Rigid Point Cloud Registration Based on Transformer" Sensors 22, no. 14: 5128. https://doi.org/10.3390/s22145128
APA StyleHu, X., Zhang, D., Chen, J., Wu, Y., & Chen, Y. (2022). NrtNet: An Unsupervised Method for 3D Non-Rigid Point Cloud Registration Based on Transformer. Sensors, 22(14), 5128. https://doi.org/10.3390/s22145128









