Development of a Soil Organic Matter Content Prediction Model Based on Supervised Learning Using Vis-NIR/SWIR Spectroscopy
Abstract
:1. Introduction
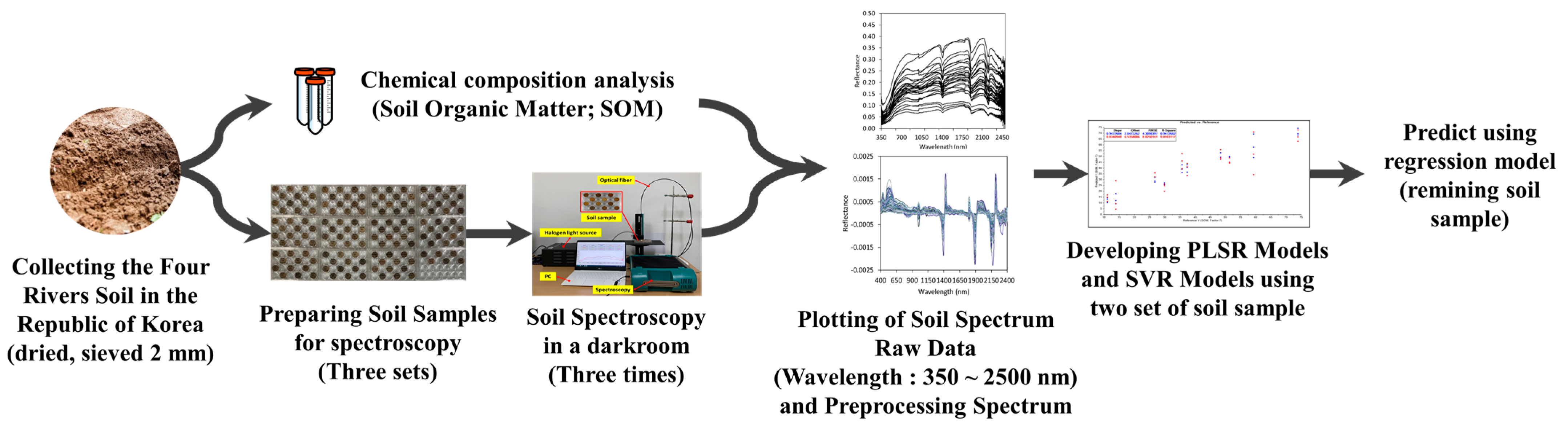
2. Materials and Methods
2.1. Study Region and Soil Samples
2.2. Spectral Measurements
2.3. Spectral Pre-Processing
2.4. Multivariate Data Methods
2.5. Model Validation
3. Results and Discussion
3.1. SOM Content of Topsoil Samples
3.2. Spectral Soil Properties
3.3. PLSR and SVR Model Development in Calibration-Validation Approaches
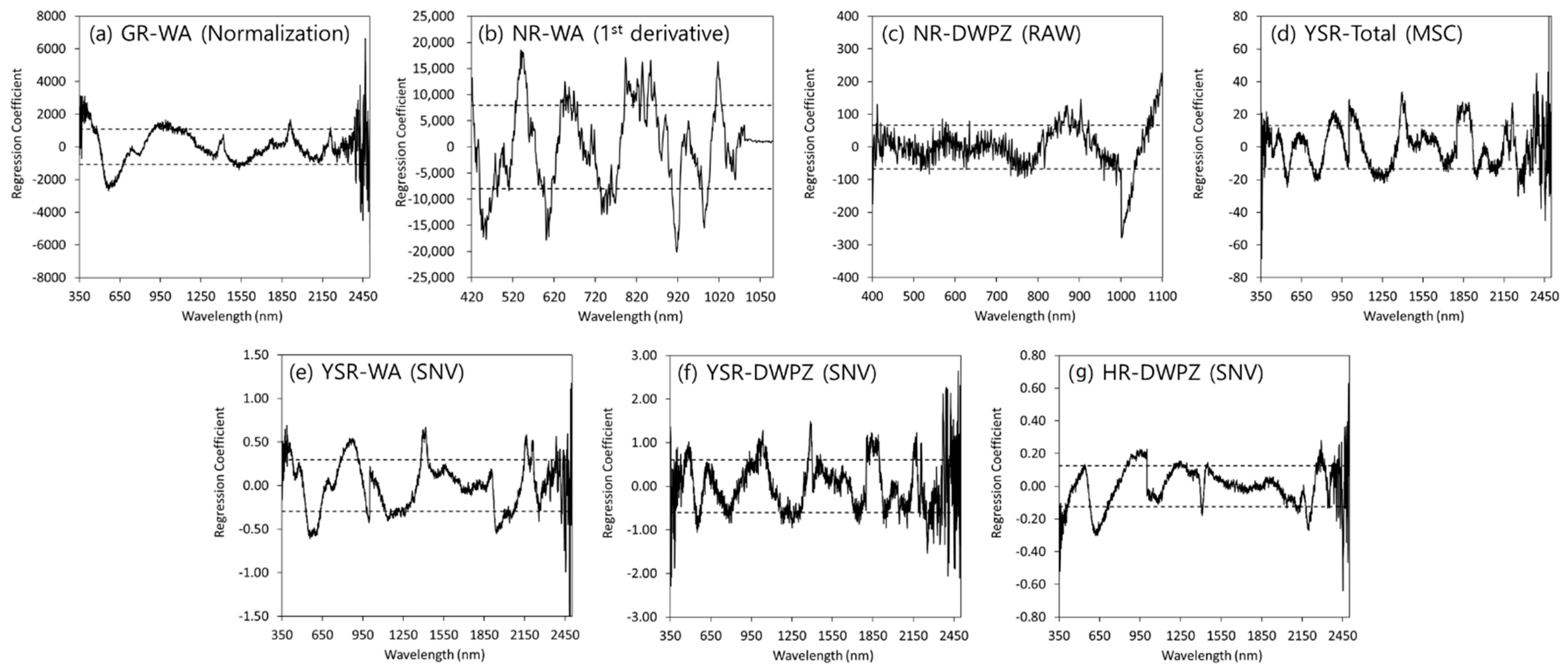
3.4. Selection of Effective Wavelengths in the PLSR Model
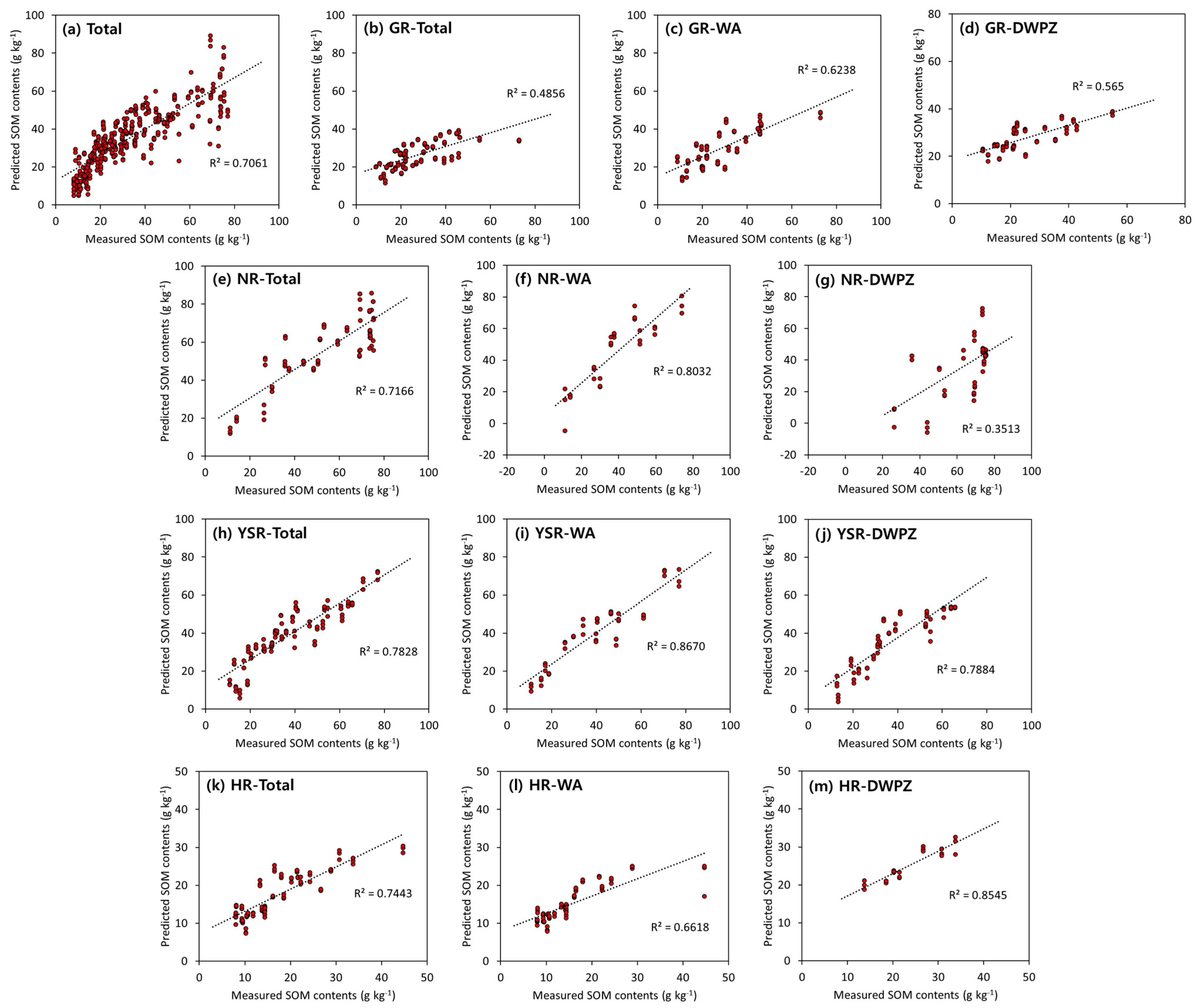
3.5. Evaluation of Optimal Models’ Performance for Predictive SOM Contents
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lim, Y.; Kim, S.; Nam, S.; Chun, K.; Kim, M. A Comparison of Current Trends in Soil Erosion Research Using Keyword Co-occurrence Analysis. Korean J. Environ. Ecol. 2020, 34, 413–424. [Google Scholar] [CrossRef]
- Lee, J.-H. Derivation of regional annual mean rainfall erosivity for predicting topsoil erosion in Korea. J. Korea Water Resour. Assoc. 2018, 51, 783–793. [Google Scholar] [CrossRef]
- Lee, J.Y.; Raza, M.; Kwon, K.D. Land use and land cover changes in the Haean Basin of Korea: Impacts on soil erosion. Episodes 2019, 42, 17–32. [Google Scholar] [CrossRef]
- Song, J.M.; Yang, J.E.; Lim, K.J.; Park, Y.S. Application of KORSLE to Estimate Soil Erosion at Field Scale. J. Soil Groundw. Environ. 2019, 24, 31–41. [Google Scholar] [CrossRef]
- Morellos, A.; Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.; Tziotzios, G.; Wiebensohn, J.; Bill, R.; Mouazen, A.M. Machine learning based prediction of soil total nitrogen, organic carbon and moisture content by using VIS-NIR spectroscopy. Biosyst. Eng. 2016, 152, 104–116. [Google Scholar] [CrossRef] [Green Version]
- Jeong, G. Evaluating Spectral Preprocessing Methods for Visible and Near Infrared Reflectance Spectroscopy to Predict Soil Carbon and Nitrogen in Mountainous Areas. Korean Geogr. Soc. 2016, 51, 509–523. [Google Scholar]
- Seo, Y.; Mo, Y.; Cho, B.; Kang, A.; Jeong, B.-C.; Jung, Y.-S. Feasibility of a simple determination of soil organic matter content using spectrophotometric method in Korean soils. Korean J. Soil Sci. Fertil. 2010, 43, 1008–1011. [Google Scholar]
- Conforti, M.; Buttafuoco, G.; Leone, A.P.; Aucelli, P.P.C.; Robustelli, G.; Scarciglia, F. Studying the relationship between water-induced soil erosion and soil organic matter using Vis-NIR spectroscopy and geomorphological analysis: A case study in southern Italy. Catena 2013, 110, 44–58. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, X.; Guo, X.; Guo, J. Deep Learning Application for Predicting Soil Organic Matter Content by VIS-NIR Spectroscopy. Comput. Intell. Neurosci. 2019, 2019, 3563761. [Google Scholar] [CrossRef]
- Conforti, M.; Matteucci, G.; Buttafuoco, G. Using laboratory Vis-NIR spectroscopy for monitoring some forest soil properties. J. Soils Sediments 2018, 18, 1009–1019. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; MacDonald, L.M.; McLaughlin, M.J. The performance of visible, near-, and mid-infrared reflectance spectroscopy for prediction of soil physical, chemical, and biological properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- Choe, E.; Hong, S.Y.; Kim, Y.; Song, K.; Zhang, Y. Quantification of Soil Properties using Visible-NearInfrared Reflectance Spectroscopy. Korean J. Soil Sci. Fertil. 2009, 42, 522–528. [Google Scholar]
- Kim, W.-K.; Hong, S.-J.; Cui, J.; Kim, H.-J.; Park, J.; Yang, S.-H.; Kim, G. Application of NIR Spectroscopy and Artificial Neural Network Techniques for Real-Time Discrimination of Soil Categories. J. Korean Soc. Nondestruct. Test. 2017, 37, 148–157. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; Noon, C.; Van Wesemael, B. Prediction of soil organic carbon for different levels of soil moisture using Vis-NIR spectroscopy. Geoderma 2013, 199, 37–42. [Google Scholar] [CrossRef]
- Pudełko, A.; Chodak, M.; Roemer, J.; Uhl, T. Application of FT-NIR spectroscopy and NIR hyperspectral imaging to predict nitrogen and organic carbon contents in mine soils. Meas. J. Int. Meas. Confed. 2020, 164, 108117. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Fründ, H.C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Alomar, S.; Mireei, S.A.; Hemmat, A.; Masoumi, A.A.; Khademi, H. Comparison of Vis/SWNIR and NIR spectrometers combined with different multivariate techniques for estimating soil fertility parameters of calcareous topsoil in an arid climate. Biosyst. Eng. 2021, 201, 50–66. [Google Scholar] [CrossRef]
- Angelopoulou, T.; Balafoutis, A.; Zalidis, G.; Bochtis, D. From laboratory to proximal sensing spectroscopy for soil organic carbon estimation—A review. Sustainability 2020, 12, 443. [Google Scholar] [CrossRef] [Green Version]
- Vohland, M.; Ludwig, B.; Seidel, M.; Hutengs, C. Quantification of soil organic carbon at regional scale: Benefits of fusing vis-NIR and MIR diffuse reflectance data are greater for in situ than for laboratory-based modelling approaches. Geoderma 2022, 405, 115426. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.Z.; Zheng, L.H.; Zhao, Y.; Pei, X. Soil nitrogen content forecasting based on real-time NIR spectroscopy. Comput. Electron. Agric. 2016, 124, 29–36. [Google Scholar] [CrossRef]
- Broge, N.H.; Thomsen, A.G.; Greve, M.H. Prediction of topsoil organic matter and clay content from measurements of spectral reflectance and electrical conductivity. Acta Agric. Scand. Sect. B Soil Plant Sci. 2004, 54, 232–240. [Google Scholar] [CrossRef]
- Selige, T.; Böhner, J.; Schmidhalter, U. High resolution topsoil mapping using hyperspectral image and field data in multivariate regression modeling procedures. Geoderma 2006, 136, 235–244. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by Vis–NIR spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Vestergaard, R.J.; Vasava, H.B.; Aspinall, D.; Chen, S.; Gillespie, A.; Adamchuk, V.; Biswas, A. Evaluation of Optimized Preprocessing and Modeling Algorithms for Prediction of Soil Properties Using VIS-NIR Spectroscopy. Sensors 2021, 21, 6745. [Google Scholar] [CrossRef] [PubMed]
- Sikora, L.J.; Moore-Kucera, J. Soil Test Methods From the Southeastern United States. South. Coop. Ser. Bull. 2014, 419, 54–58. [Google Scholar]
- Tiecher, T.; Moura-Bueno, J.M.; Caner, L.; Minella, J.P.G.; Evrard, O.; Ramon, R.; Naibo, G.; Barros, C.A.P.; Silva, Y.J.A.B.; Amorim, F.F.; et al. Improving the quantification of sediment source contributions using different mathematical models and spectral preprocessing techniques for individual or combined spectra of ultraviolet–visible, near- and middle-infrared spectroscopy. Geoderma 2021, 384, 114815. [Google Scholar] [CrossRef]
- Barra, I.; Haefele, S.M.; Sakrabani, R.; Kebede, F. Soil spectroscopy with the use of chemometrics, machine learning and pre-processing techniques in soil diagnosis: Recent advances—A review. TrAC Trends Anal. Chem. 2021, 135, 116166. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Brodský, L.; Vašát, R.; Klement, A.; Zádorová, T.; Jakšík, O. Uncertainty propagation in VNIR reflectance spectroscopy soil organic carbon mapping. Geoderma 2013, 199, 54–63. [Google Scholar] [CrossRef]
- Kiala, Z.; Odindi, J.; Mutanga, O.; Peerbhay, K. Comparison of partial least squares and support vector regressions for predicting leaf area index on a tropical grassland using hyperspectral data. J. Appl. Remote Sens. 2016, 10, 036015. [Google Scholar] [CrossRef]
- Shi, T.; Cui, L.; Wang, J.; Fei, T.; Chen, Y.; Wu, G. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy. Plant Soil 2013, 366, 363–375. [Google Scholar] [CrossRef]
- Šestak, I.; Mihaljevski Boltek, L.; Mesić, M.; Zgorelec, Ž.; Perčin, A. Hyperspectral sensing of soil ph, total carbon and total nitrogen content based on linear and non-linear calibration methods. J. Cent. Eur. Agric. 2019, 20, 504–523. [Google Scholar] [CrossRef]
- Lee, M.S.; Kim, K.S.; Min, G.; Son, D.H.; Kim, J.E.; Kim, S.C. Recent Trends of Hyperspectral Imaging Technology. Electron. Telecommun. Trends 2019, 34, 86–97. [Google Scholar] [CrossRef]
- Kang, D.; Sung, K.; Yeo, U.; Chung, Y.; Lee, S.-M. Riparian Area Characteristics of the Middle and Lower Reaches of the Nakdong River, Korea Riparian Area Characteristics of the Middle and Lower Reaches of the Nakdong River, Korea. J. Environ. Impact Assess. 2008, 17, 189–200. [Google Scholar]
- Tahmasbian, I.; Xu, Z.; Boyd, S.; Zhou, J.; Esmaeilani, R.; Che, R.; Hosseini Bai, S. Laboratory-based hyperspectral image analysis for predicting soil carbon, nitrogen and their isotopic compositions. Geoderma 2018, 330, 254–263. [Google Scholar] [CrossRef]
- Fidêncio, P.H.; Poppi, R.J.; De Andrade, J.C. Determination of organic matter in soils using radial basis function networks and near infrared spectroscopy. Anal. Chim. Acta 2002, 453, 125–134. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Banin, A. Near infrared analysis(NIRA) as a method to simultaneously evaluate spectral featureless constituents in soils. Soil Sci. 1995, 159, 259–270. [Google Scholar] [CrossRef]
- Morra, M.J.; Hall, M.H.; Freeborn, L.L. Carbon and Nitrogen Analysis of Soil Fractions Using Near-Infrared Reflectance Spectroscopy. Soil Sci. Soc. Am. J. 1991, 55, 288–291. [Google Scholar] [CrossRef]



| Total | GR (a) | NR (b) | YSR (c) | HR (d) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total | WA (e) | DWPZ (f) | Total | WA | DWPZ | Total | WA | DWPZ | Total | WA | DWPZ | ||
| Calibration dataset | 828 | 288 | 150 | 138 | 150 | 60 | 90 | 210 | 90 | 120 | 180 | 138 | 42 |
| Prediction dataset | 414 | 144 | 75 | 69 | 75 | 30 | 45 | 105 | 45 | 60 | 90 | 69 | 21 |
| Soil Sample | Count | SOM (g kg−1) | ||||
|---|---|---|---|---|---|---|
| Min. | Max. | Ave. | Std. | |||
| Total | 138 | 8.00 | 77.03 | 32.44 | 19.23 | |
| GR (a) | Total | 48 | 8.85 | 72.80 | 27.39 | 13.09 |
| WA (e) | 25 | 8.85 | 72.80 | 28.74 | 14.31 | |
| DWPZ (f) | 23 | 10.40 | 55.08 | 25.91 | 11.12 | |
| NR (b) | Total | 25 | 11.14 | 75.46 | 52.61 | 20.70 |
| WA | 10 | 11.14 | 73.91 | 38.82 | 18.77 | |
| DWPZ | 15 | 26.23 | 75.46 | 61.80 | 15.47 | |
| YSR (c) | Total | 35 | 10.82 | 77.03 | 37.83 | 17.93 |
| WA | 15 | 10.82 | 77.03 | 39.06 | 19.56 | |
| DWPZ | 20 | 12.75 | 65.71 | 36.91 | 16.06 | |
| HR (d) | Total | 30 | 8.00 | 44.71 | 17.44 | 8.77 |
| WA | 23 | 8.00 | 44.71 | 15.57 | 8.30 | |
| DWPZ | 7 | 13.71 | 33.76 | 23.58 | 6.58 | |
| Soil Sample | Model | Wavelength Range (nm) | Pre-Processing | Rc2 | RMSEc (g kg−1) | Rv2 | RMSEv (g kg−1) | Factor | |
|---|---|---|---|---|---|---|---|---|---|
| Total | PLSR | 400–1100 | Normalization | 0.657 | 11.23 | 0.630 | 11.66 | 8 | |
| SVR | 350–2500 | 1st derivative (20 nm) | 0.716 | 10.55 | 0.678 | 11.12 | - | ||
| GR | Total | PLSR | 400–1100 | Normalization | 0.668 | 7.47 | 0.526 | 8.93 | 8 |
| SVR | 350–2500 | SNV | 0.627 | 8.54 | 0.544 | 9.17 | - | ||
| WA | PLSR | 350–2500 | Normalization | 0.680 | 8.10 | 0.556 | 9.60 | 5 | |
| SVR | 350–2500 | 1st derivative (20 nm) | 0.649 | 9.56 | 0.531 | 10.38 | - | ||
| DWPZ | PLSR | 350–2500 | SNV | 0.713 | 5.95 | 0.629 | 6.83 | 4 | |
| SVR | 350–2500 | Normalization | 0.794 | 5.33 | 0.735 | 5.97 | - | ||
| NR | Total | PLSR | 350–2500 | - | 0.766 | 9.81 | 0.659 | 11.96 | 7 |
| SVR | 350–2500 | 1st derivative (20 nm) | 0.735 | 10.54 | 0.662 | 11.84 | - | ||
| WA | PLSR | 400–1100 | 1st derivative (20 nm) | 0.912 | 5.57 | 0.746 | 9.55 | 9 | |
| SVR | 1100–2500 | 1st derivative (20 nm) | 0.706 | 10.89 | 0.470 | 13.80 | - | ||
| DWPZ | PLSR | 400–1100 | - | 0.806 | 8.28 | 0.703 | 10.29 | 7 | |
| SVR | 350–2500 | 2nd derivative (20 nm) | 0.858 | 7.35 | 0.644 | 10.29 | - | ||
| YSR | Total | PLSR | 350–2500 | MSC | 0.829 | 7.31 | 0.678 | 10.21 | 8 |
| SVR | 400–1100 | 1st derivative (15 nm) | 0.708 | 9.96 | 0.675 | 10.42 | - | ||
| WA | PLSR | 350–2500 | SNV | 0.912 | 5.79 | 0.826 | 8.17 | 7 | |
| SVR | 350–2500 | 1st derivative (15 nm) | 0.838 | 9.03 | 0.682 | 11.76 | - | ||
| DWPZ | PLSR | 350–2500 | SNV | 0.911 | 4.80 | 0.729 | 8.42 | 11 | |
| SVR | 350–2500 | SNV | 0.710 | 9.78 | 0.596 | 11.22 | - | ||
| HR | Total | PLSR | 350–2500 | SNV | 0.704 | 4.69 | 0.615 | 5.38 | 5 |
| SVR | 350–2500 | SNV | 0.755 | 4.55 | 0.691 | 4.96 | - | ||
| WA | PLSR | 350–2500 | SNV | 0.810 | 3.62 | 0.657 | 4.92 | 5 | |
| SVR | 350–2500 | SNV | 0.731 | 4.90 | 0.675 | 5.20 | - | ||
| DWPZ | PLSR | 350–2500 | SNV | 0.877 | 2.31 | 0.694 | 3.72 | 6 | |
| SVR | 400–1100 | SNV | 0.689 | 3.82 | 0.559 | 5.76 | - | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-J.; Lee, H.-I.; Choi, J.-H.; Lim, K.J.; Mo, C. Development of a Soil Organic Matter Content Prediction Model Based on Supervised Learning Using Vis-NIR/SWIR Spectroscopy. Sensors 2022, 22, 5129. https://doi.org/10.3390/s22145129
Kim M-J, Lee H-I, Choi J-H, Lim KJ, Mo C. Development of a Soil Organic Matter Content Prediction Model Based on Supervised Learning Using Vis-NIR/SWIR Spectroscopy. Sensors. 2022; 22(14):5129. https://doi.org/10.3390/s22145129
Chicago/Turabian StyleKim, Min-Jee, Hye-In Lee, Jae-Hyun Choi, Kyoung Jae Lim, and Changyeun Mo. 2022. "Development of a Soil Organic Matter Content Prediction Model Based on Supervised Learning Using Vis-NIR/SWIR Spectroscopy" Sensors 22, no. 14: 5129. https://doi.org/10.3390/s22145129
APA StyleKim, M.-J., Lee, H.-I., Choi, J.-H., Lim, K. J., & Mo, C. (2022). Development of a Soil Organic Matter Content Prediction Model Based on Supervised Learning Using Vis-NIR/SWIR Spectroscopy. Sensors, 22(14), 5129. https://doi.org/10.3390/s22145129







