Sensitivity Optimization and Experimental Study of the Long-Range Metal Detector Based on Chaotic Duffing Oscillator
Abstract
:1. Introduction
- We propose a quantitative estimation of the chaotic oscillator’s sensitivity and based on it, present an algorithm for searching for their most sensitive regimes. This information is of vital importance when constructing chaotic sensors.
- Using the developed approach, we study the sensitivity of the electronic circuit implementing the Duffing oscillator. Numerically, we find a parameter set at which the circuit most rapidly switches from periodic to chaotic mode and verify our findings experimentally.
- We apply the Duffing circuit in the metal detector proposed by W. Hu et al. This detector consists of three coils, a differential amplifier, the Duffing oscillator and a detector. We propose our own designs of differential amplifier and detector circuits, as well as the numerical detection algorithm by analyzing the Duffing oscillator state variables by counting the switching rate between attractor scrolls. This method of oscillations’ quantification has never previously been applied to constructing the sensor based on the Duffing oscillator.
- In a well-controlled experiment, we study the sensitivity and accuracy of the developed metal detector by finding limit distances at which the detector is capable of sensing the metal plates of different materials and sizes. Such tests had not yet been performed for the metal detector of the proposed design. Then, we compare the obtained results with available data on inductive sensors and metal detectors.
2. Materials and Methods
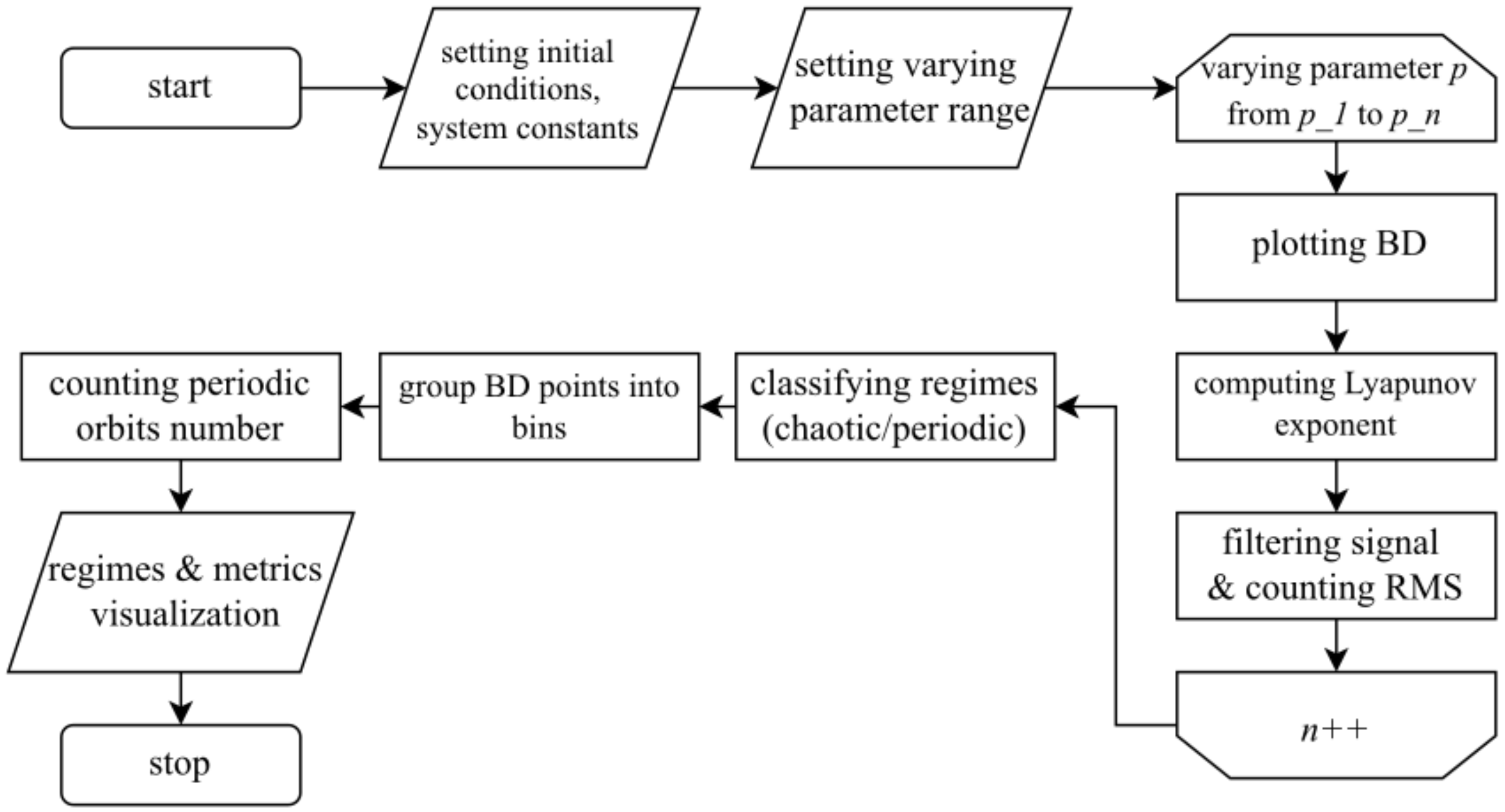
2.1. Sensitivity Optimization Algorithm
- Calculation of the largest Lyapunov exponent (LLE) using a method presented in [16]. In the study of chaotic systems, it is the most frequently used indicator of chaos presence, which allows for accurately distinguishing the chaotic mode from the periodic.
- Plotting a bifurcation diagram (BD) with respect to the varying parameter. Bifurcation diagram analysis allows for visually presenting the system dynamics, including sharp mode transitions, as well as counting the number of periodic orbits.
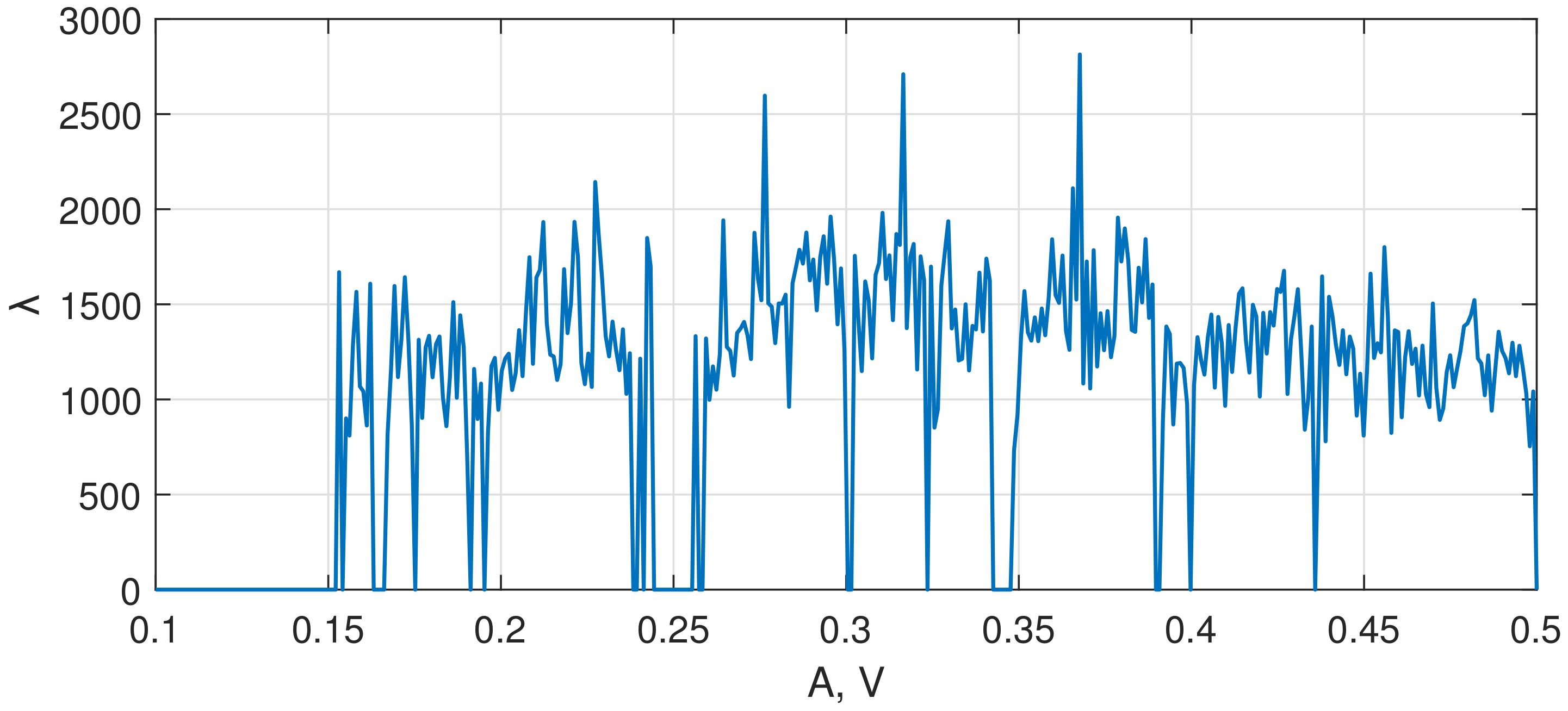
- Searching for bifurcation diagram areas with higher sensitivity. This requires tracking the rapid changes in the chaotic system dynamics. In this stage, we apply a low-frequency bandpass filter to decrease the non-chaotic signal amplitude compared to the chaotic signal. Then we calculate the difference between adjacent average signal values and find the derivative with respect to the varying system parameter. After applying the algorithm, we obtain a plot of the system sensitivity with bursts at the points of oscillations mode changing.
- For segments with a zero Lyapunov exponent, i.e., periodic oscillations, the number of periodic orbits is counted. The field of the bifurcation diagram is divided into a matrix of bins of size M × N, where M is the specified number of bins and N is the number of parameter values. For each value of the bifurcation parameter, we check whether a point of the bifurcation diagram belongs to the bin corresponding to a certain range of state variable amplitude values. Each appearance of a bifurcation diagram point in the bin is counted. Then, the periodic orbits are calculated according to the following algorithm:
- If the first (upper) bin contains points and the second (lower) bin is empty, then consider it as a separate orbit;
- If the bin in the middle is full, and the next (lower) bin is an empty one, then consider it as a separate orbit (in the case of several filled bins located next to each other, consider them all belonging to the same orbit);
- If the last bin is full, and the bin before it (upper bin) is empty, then consider it a separate orbit.
2.2. Metal Detector Based on the Duffing Oscillator
2.2.1. The Duffing Oscillator
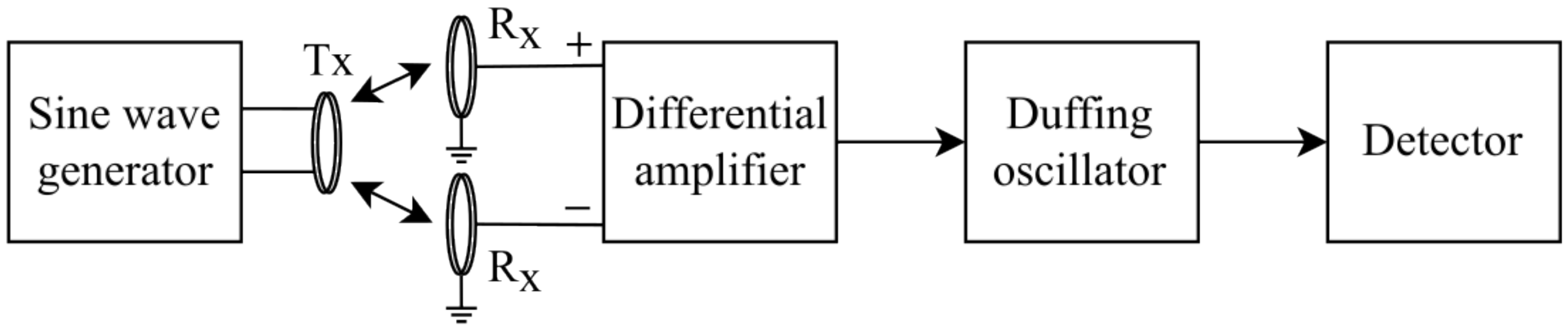
2.2.2. Conceptual Design
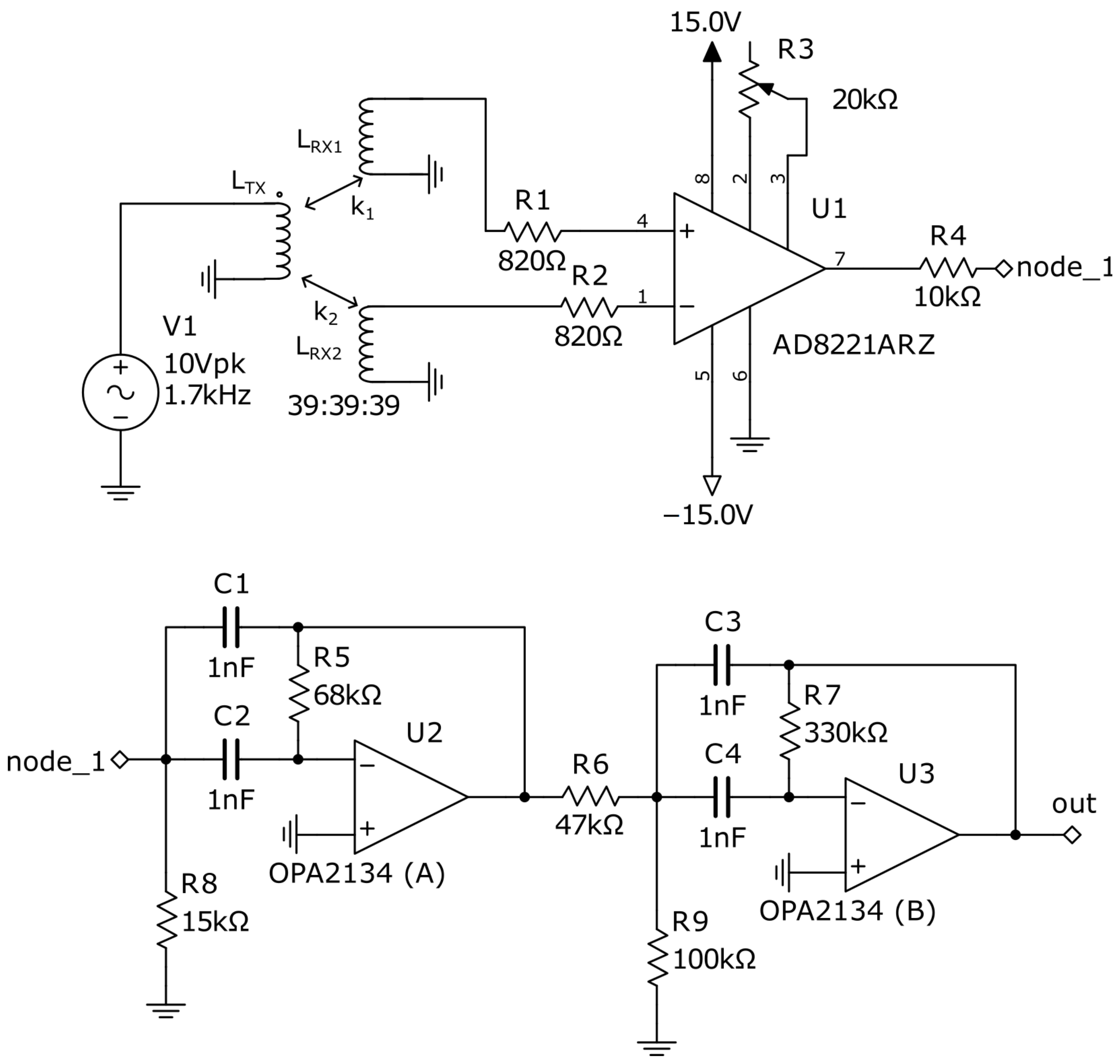
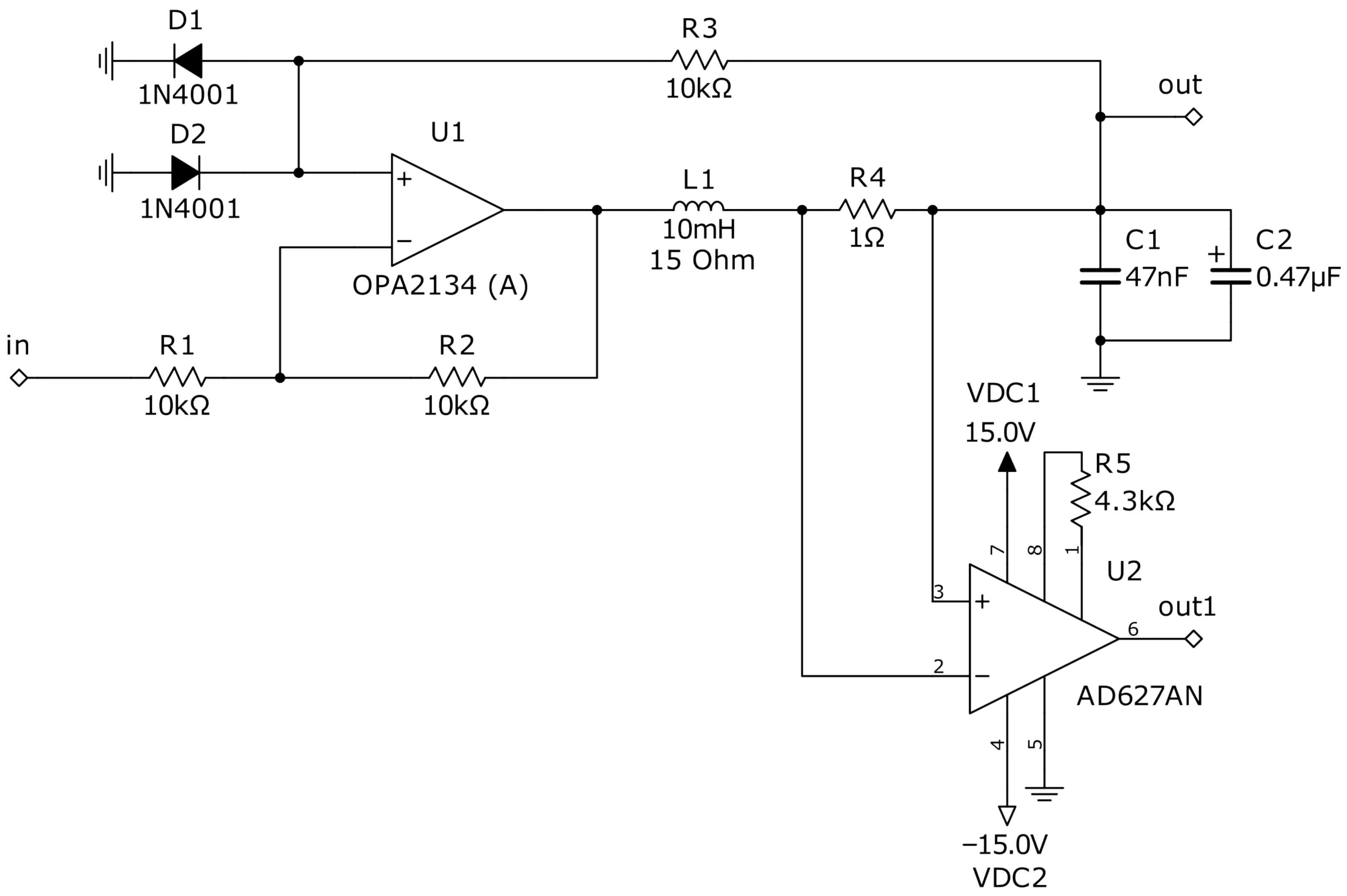
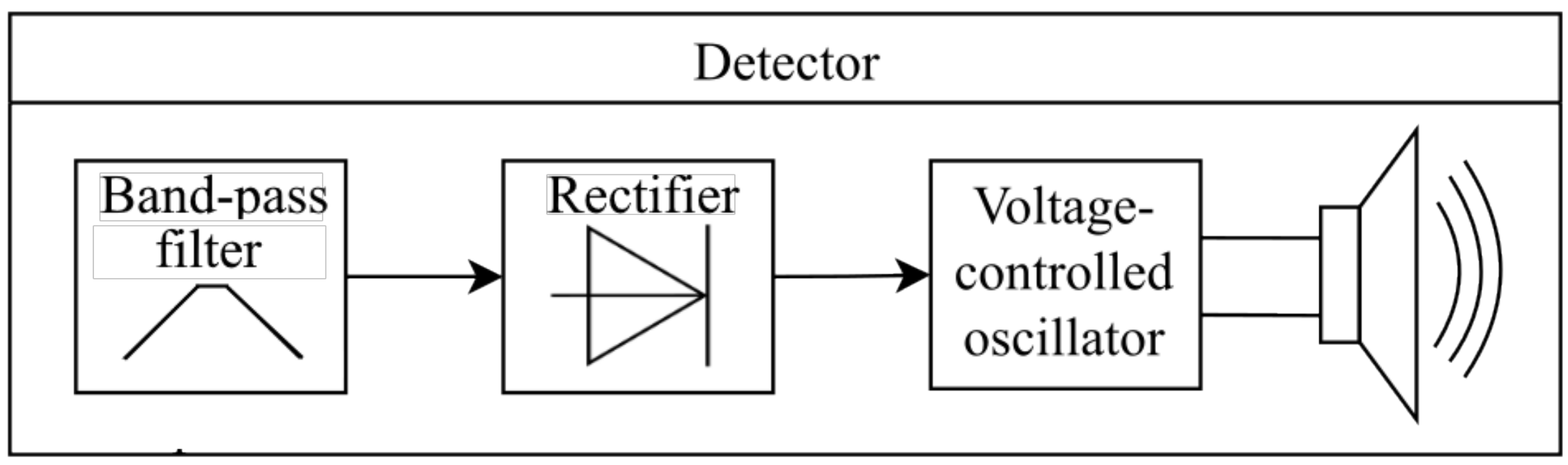
2.2.3. Circuit Design
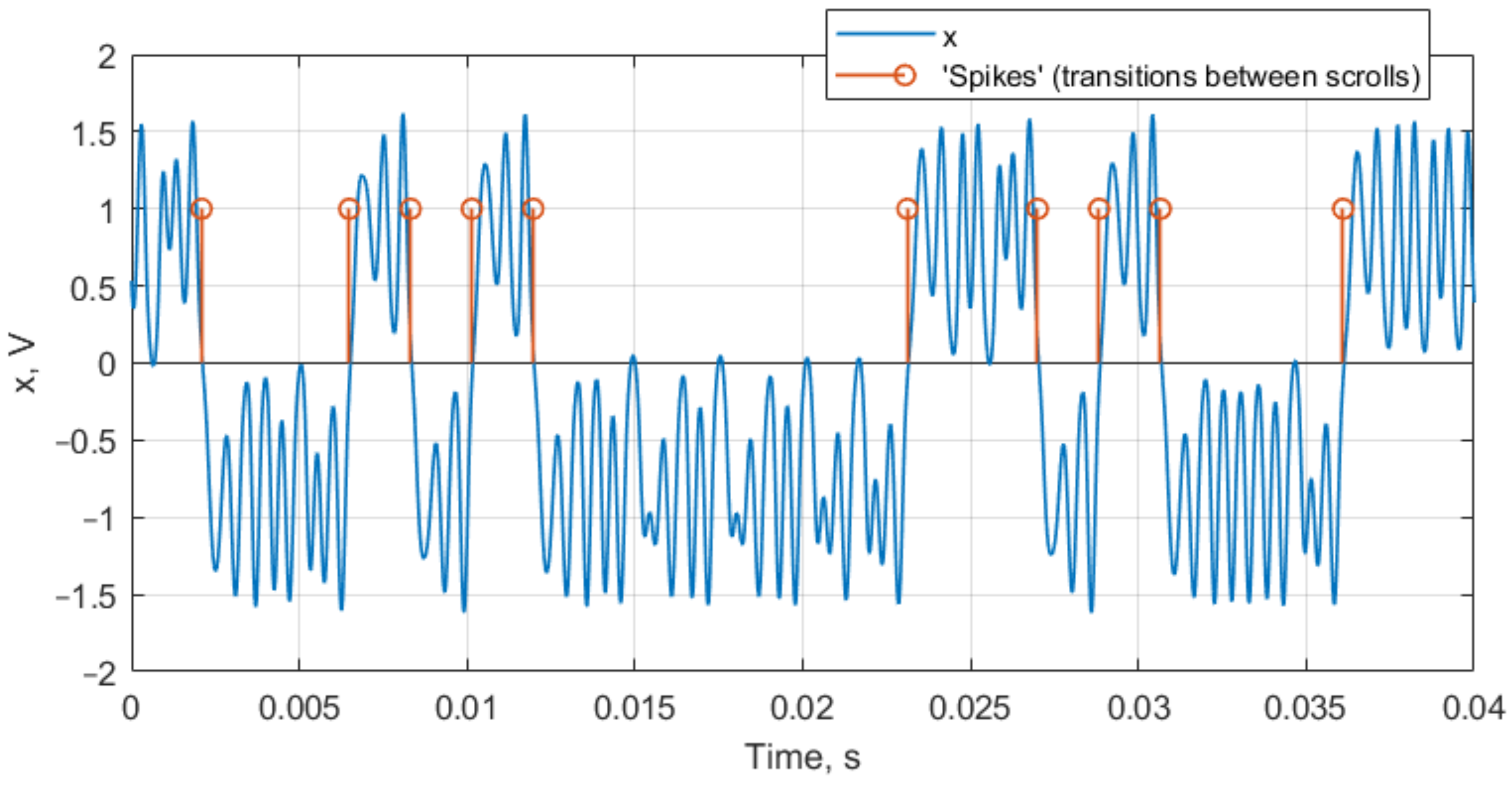
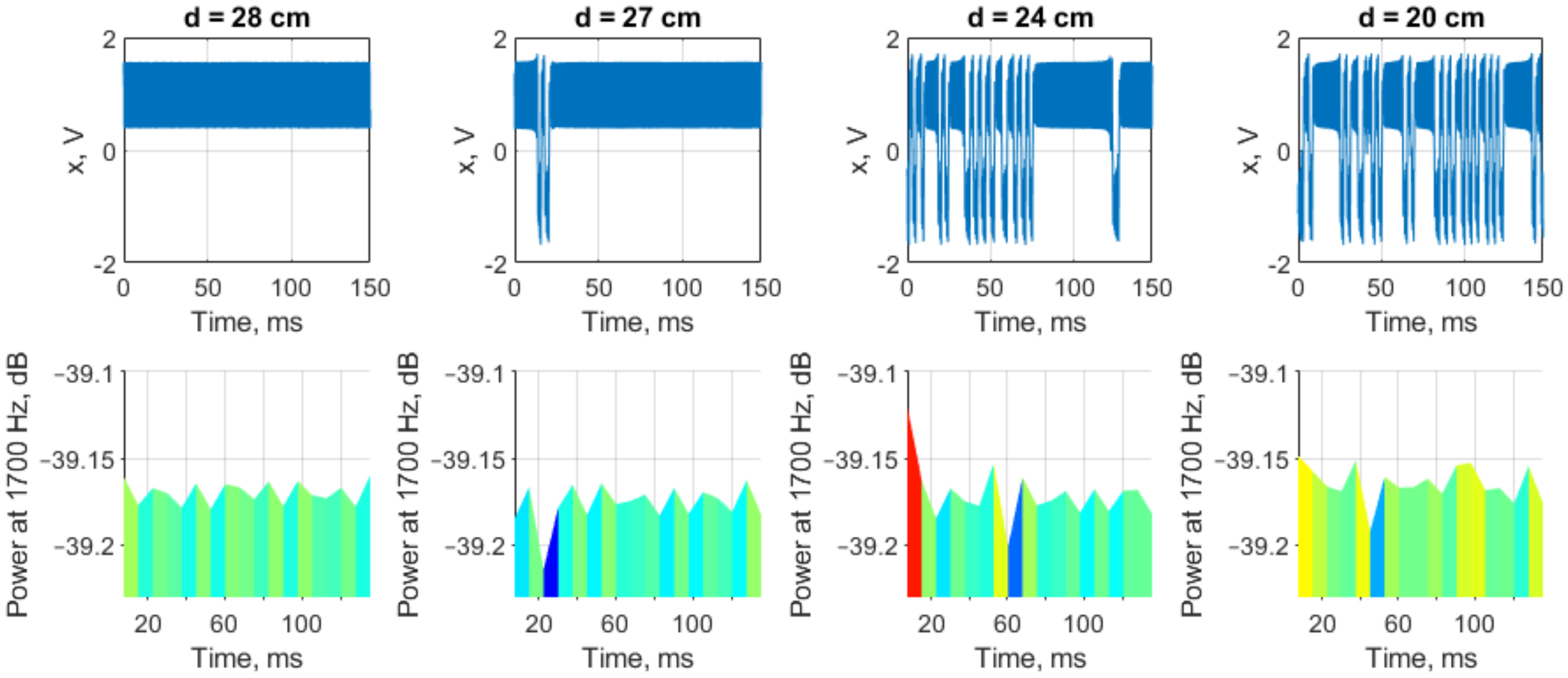
2.2.4. Recognition of the Duffing Oscillator Operation Mode
- When there are no spikes, the oscillator is in a periodic mode.
- When there are very few interspike intervals present, the oscillator is also in a periodic mode.
- The chaotic mode is characterized by a variety of interspike intervals with the presence of rare ones.
3. Results
- (a)
- Tuning of the mathematical model parameters to better match the real circuit.
- (b)
- Using the tuned model, search for the most sensitive regime with the developed algorithm.
- Verification of the regime experimentally.
- Investigation of the developed detector sensitivity on a set of test targets.
- Comparison of the differential amplifier signal analysis by the Duffing oscillator and conventional signal-processing methods.

3.1. Numerical Optimization of the Duffing Oscillator-Based Metal Detector System Parameters
3.2. Metal Detector Performance Study
3.3. Investigation of the Developed Detector Sensitivity on a Set of Test Targets
3.4. Comparison of the Differential Amplifier Signal Analysis by the Duffing Oscillator and Conventional Numerical Analysis
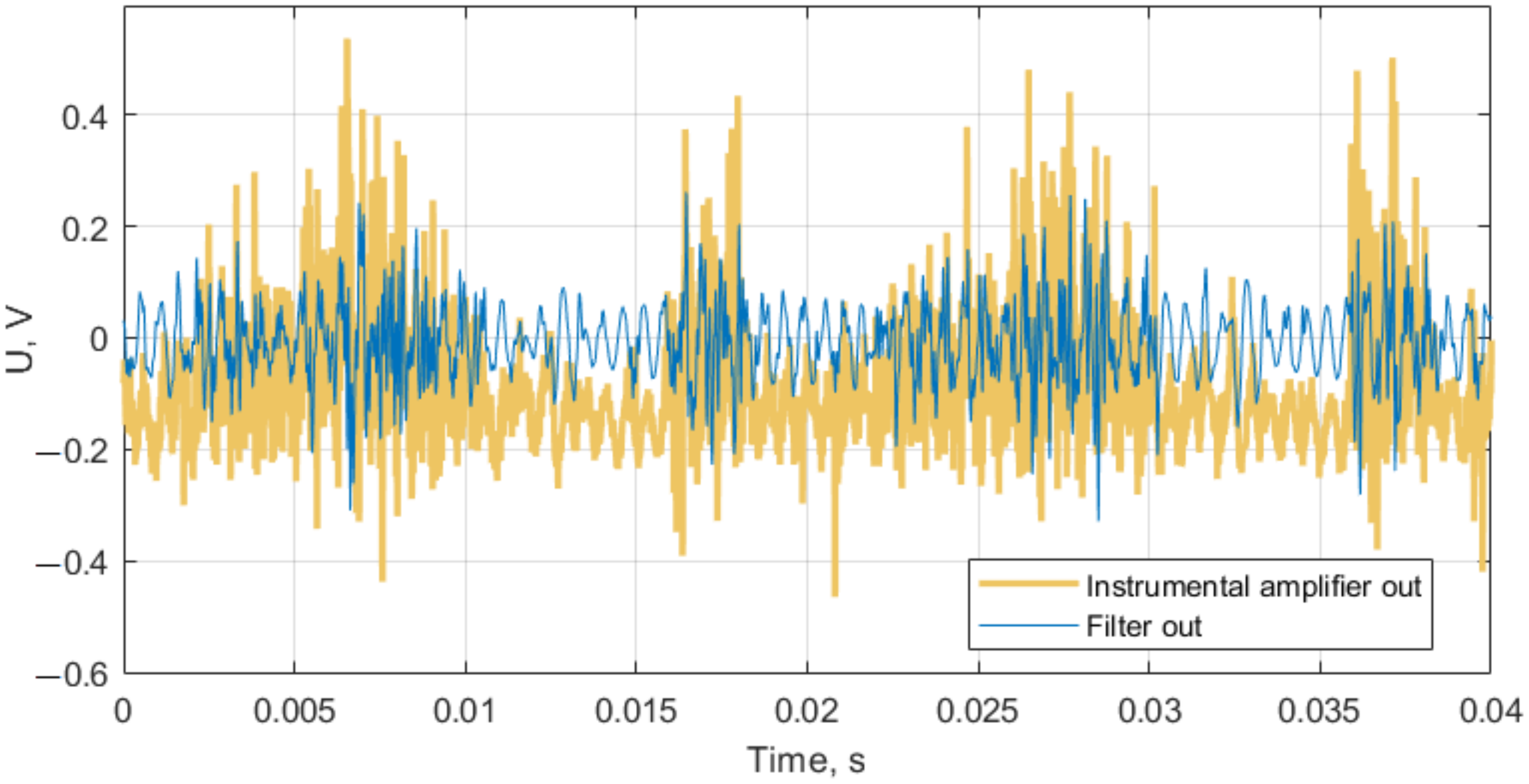
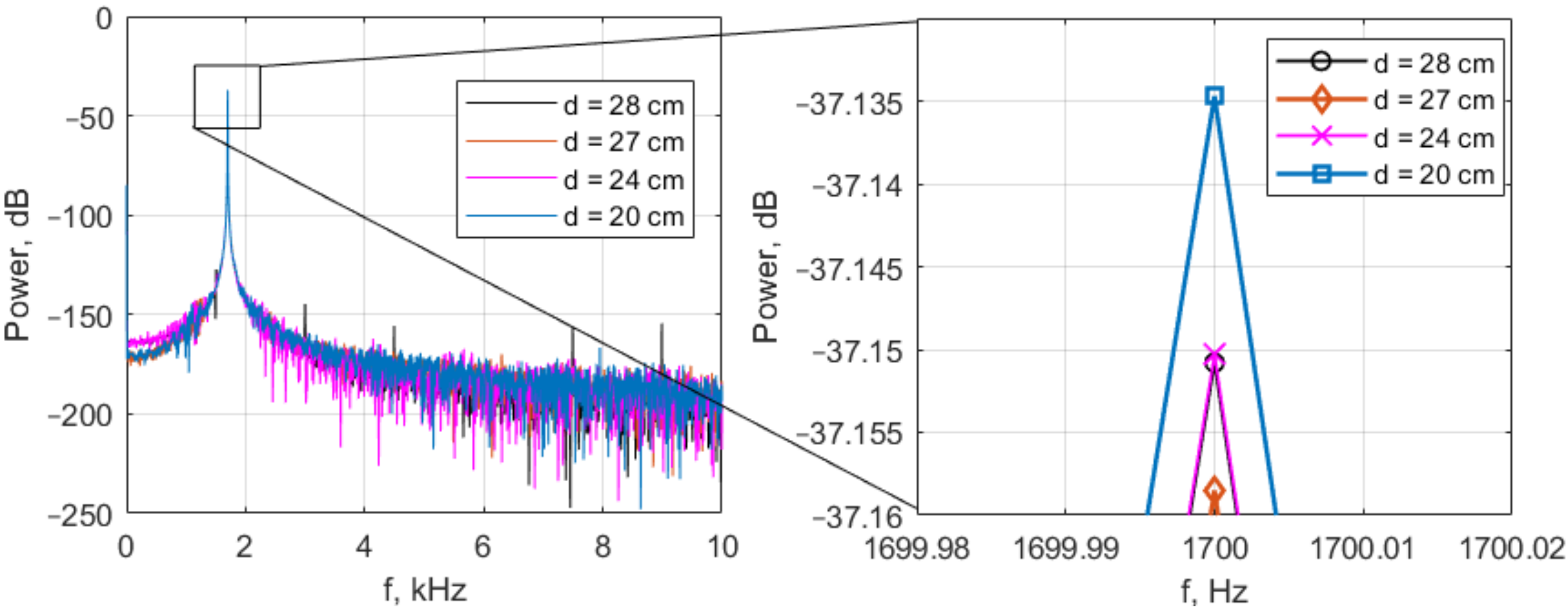
3.4.1. Frequency–Domain Analysis
3.4.2. Time-Domain Analysis
4. Discussion
4.1. Practical Applicability of the Developed Metal Detector
4.1.1. Stability of the Sensor Behavior
4.1.2. Possible Sensitive Coil Setups
4.2. Sensitivity Comparison of the Developed Detector with Other Sensor Designs
5. Conclusions
- We proposed a definition and an algorithm for calculating the sensitivity of chaotic oscillators in the context of their application for sensor systems.
- We have assembled a metal detector consisting of a transmitting coil, two similar receiving coils connected to a differential amplifier, the circuit implementing Duffing oscillator, and a sound indicator. Using the proposed algorithm, we investigated the developed electronic circuit sensitivity and found that its highest value can be achieved at the point of rapid switching from the periodic mode to the chaotic mode at the Duffing oscillator input sine wave amplitude mV at frequency Hz.
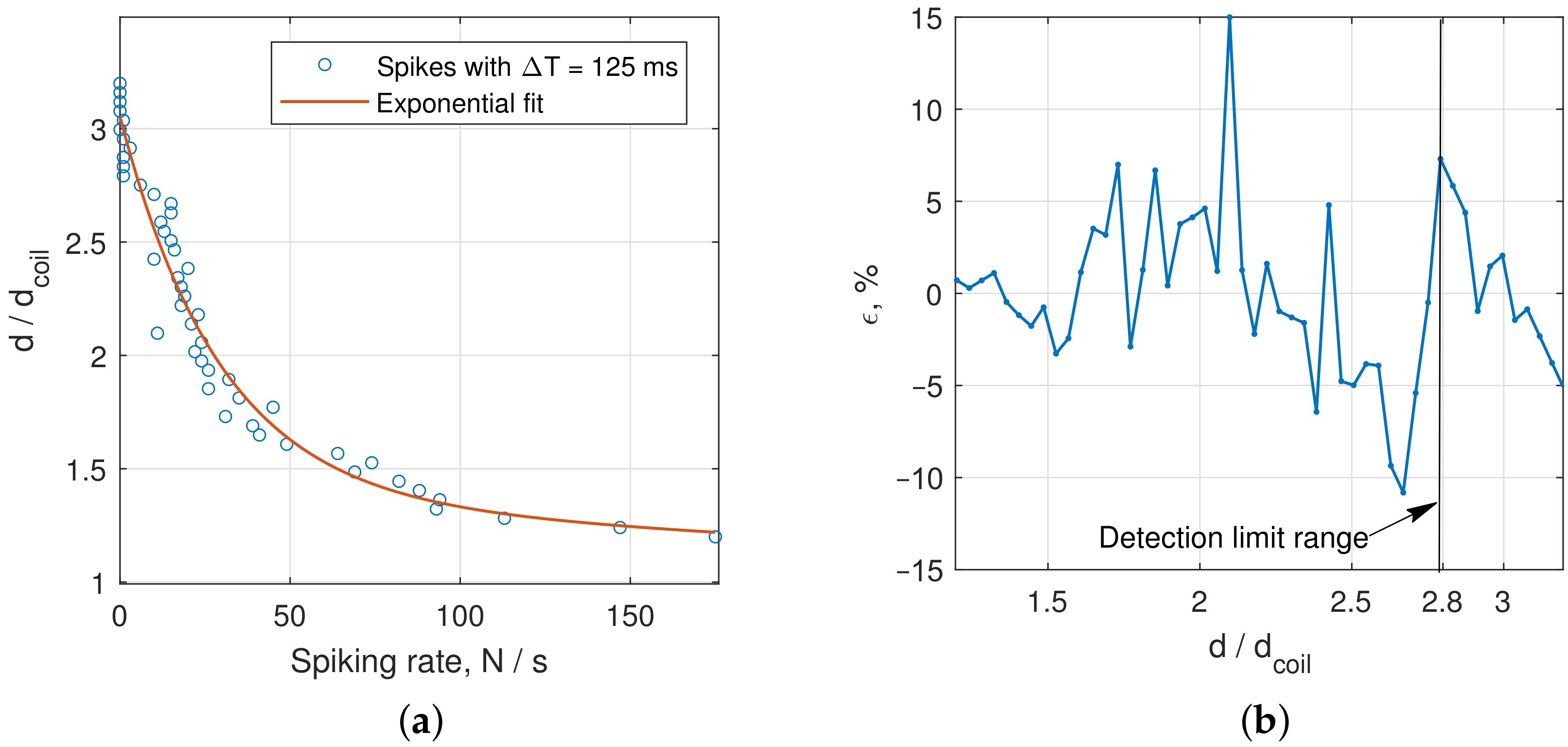
- To numerically estimate the distances between sensitive coils and target from the waveform of the Duffing oscillator, we counted the number N of switching between the scrolls of the double-scroll Duffing attractor. We found that at distances to the target from 1.2 to 1.5 of coil diameter, the error of the exponential approximation of N did not exceed , which is sufficient for many demanding applications, and at distances up to maximum detection range, it averaged about .
- We managed to detect metal plates at distances up to 2.8 times coils diameter, depending on the material. We have compared the obtained results with available data on inductive sensors and metal detectors and found that this is the state-of-the-art result.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BD | Bifurcation diagram |
| DA | Differential amplifier |
| DC | Direct current |
| LLE | Largest Lyapunov exponent |
| LTCC | Low temperature co-fired ceramics |
| LUT | Look-up table |
| NI | National Instruments (Austin, TX, US) |
| PCB | Printed circuit board |
| RMS | Root-mean-square |
| RQA | Recurrence quantification analysis |
| STFT | Short-time Fourier transform |
| TI | Texas Instruments (Austin, TX, US) |
Appendix A


References
- Wu, J.; Wang, Y.; Zhang, W.; Nie, Z.; Lin, R.; Ma, H. Defect detection of pipes using Lyapunov dimension of Duffing oscillator based on ultrasonic guided waves. Mech. Syst. Signal Process. 2017, 82, 130–147. [Google Scholar] [CrossRef]
- Korneta, W.; Garcia-Moreno, E.; Sena, A. Noise activated dc signal sensor based on chaotic Chua circuit. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 145–152. [Google Scholar] [CrossRef]
- Karimov, T.; Druzhina, O.; Karimov, A.; Butusov, D. Axial movement sensor based on chaotic oscillator and planar coil. In Proceedings of the 2020 26th Conference of Open Innovations Association (FRUCT), Yaroslavl, Russia, 20–24 April 2020; pp. 130–135. [Google Scholar]
- Hu, W.; Liu, Z.; Li, Z. The Design of Improved Duffing Chaotic Circuit Used for High-Frequency Weak Signal Detection. In Electronics and Signal Processing; Hu, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 831–838. [Google Scholar]
- Wang, G.; Chen, D.; Lin, J.; Chen, X. The application of chaotic oscillators to weak signal detection. IEEE Trans. Ind. Electron. 1999, 46, 440–444. [Google Scholar] [CrossRef]
- Wu, J.; Hao, H.; Li, J.; Wang, Y.; Wu, Z.; Ma, H. Defect detection in pipe structures using stochastic resonance of the Duffing oscillator and ultrasonic guided waves. Int. J. Press. Vessel. Pip. 2020, 187, 104168. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Wang, X.; Liu, C.; Li, Z.; Hao, Y. Weak infrared radiation intensity measurement based on extended Duffing oscillator. AOPC 2021: Infrared Device and Infrared Technology. Proc. SPIE 2021, 12061, 425–432. [Google Scholar]
- Hu, W.; Liu, Z. Study of metal detection based on chaotic theory. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 6–9 July 2010; pp. 2309–2314. [Google Scholar]
- Hu, W. A new kind of metal detector based on chaotic oscillator. IOP Conf. Ser. Earth Environ. Sci. 2017, 100, 012186. [Google Scholar] [CrossRef]
- Hu, W.J.; Liu, Z. A New Metal Detection Method Based on Duffing Chaotic System. Destech Trans. Eng. Technol. Res. 2017. [Google Scholar] [CrossRef] [Green Version]
- Karimov, T.I.; Druzhina, O.S.; Ostrovskii, V.Y.; Karimov, A.I.; Butusov, D.N. The Study on Multiparametric Sensitivity of Chaotic Oscillators. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 27–30 January 2020; pp. 134–137. [Google Scholar] [CrossRef]
- He, B.; Yang, C.-Y.; Zhou, Y.-S.; Chen, Y. Using chaos to improve measurement precision. J. Zhejiang Univ.-Sci. A 2002, 3, 47–51. [Google Scholar] [CrossRef]
- Teodorescu, H.N.L. Sensors based on nonlinear dynamic systems—A survey. In Proceedings of the 2017 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 5–6 September 2017; pp. 1–10. [Google Scholar]
- Korneta, W.; Gomes, I.; Picos, R.; Zábovský, M. Biomimetic Chaotic Sensor for Moderate Static Magnetic Field. Sensors 2021, 21, 6964. [Google Scholar] [CrossRef] [PubMed]
- Karimov, T.; Druzhina, O.; Karimov, A.; Tutueva, A.; Ostrovskii, V.; Rybin, V.; Butusov, D. Single-coil metal detector based on spiking chaotic oscillator. Nonlinear Dyn. 2021, 107, 1295–1312. [Google Scholar] [CrossRef]
- Mendes, E.M.; Nepomuceno, E.G. A very simple method to calculate the (positive) largest Lyapunov exponent using interval extensions. Int. J. Bifurc. Chaos 2016, 26, 1650226. [Google Scholar] [CrossRef]
- Tamaševičiūtė, E.; Tamaševičius, A.V.; Mykolaitis, G.; Bumelienė, S.; Lindberg, E. Analogue electrical circuit for simulation of the Duffing–Holmes equation. Nonlinear Anal. Model. Control 2008, 13, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Karimov, T.; Nepomuceno, E.G.; Druzhina, O.; Karimov, A.; Butusov, D. Chaotic oscillators as inductive sensors: Theory and practice. Sensors 2019, 19, 4314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karimov, T.; Butusov, D.; Andreev, V.; Karimov, A.; Tutueva, A. Accurate synchronization of digital and analog chaotic systems by parameters re-identification. Electronics 2018, 7, 123. [Google Scholar] [CrossRef] [Green Version]
- Karimov, T.I.; Druzhina, O.S.; Karimov, A.I.; Kolev, G.Y.; Butusov, D.N. Comparison of Bifurcation Diagrams for Numerical and Analog Chaotic Systems. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Moscow and St. Petersburg, Russia, 26–29 January 2021; pp. 124–128. [Google Scholar]
- Pérez, G.; Cerdeira, H.A. Extracting messages masked by chaos. Phys. Rev. Lett. 1995, 74, 1970. [Google Scholar] [CrossRef] [PubMed]
- Tsukamoto, N.; Fujisaka, H. Return map analysis of chaotic phase synchronization. Phys. D Nonlinear Phenom. 2007, 233, 32–38. [Google Scholar] [CrossRef]
- Ostrovskii, V.Y.; Tutueva, A.V.; Rybin, V.G.; Karimov, A.I.; Butusov, D.N. Continuation Analysis of Memristor-Based Modified Chua’s Circuit. In Proceedings of the 2020 International Conference Nonlinearity, Information and Robotics (NIR), Innopolis, Russia, 3–6 December 2020; pp. 1–5. [Google Scholar]
- Ostrovskii, V.Y.; Tutueva, A.V.; Andreev, V.S.; Rybin, V.G. Phase Bifurcation Analysis of Nonlinear Dynamical Systems. In Proceedings of the 2020 XXIII International Conference on Soft Computing and Measurements (SCM), St. Petersburg, Russia, 27–29 May 2020; pp. 88–91. [Google Scholar]
- Guo, Y.X.; Shao, Z.B.; Li, T. An analog-digital mixed measurement method of inductive proximity sensor. Sensors 2015, 16, 30. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Wang, Y.; Liu, F.; Zhang, F.; Liu, Z.; Li, Y. Passive wireless LC proximity sensor based on LTCC technology. Sensors 2019, 19, 1110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sosnicki, O.; Michaud, G.; Claeyssen, F. Eddy current sensors on Printed Circuit Board for compact mechatronic application. In Proceedings of the Sensoren und Messsysteme, Meylan, France, 18–19 May 2010; pp. 244–251. [Google Scholar]
- Mizuno, T.; Mizuguchi, T.; Isono, Y.; Fujii, T.; Kishi, Y.; Nakaya, K.; Kasai, M.; Shimizu, A. Extending the operating distance of inductive proximity sensor using magnetoplated wire. IEEE Trans. Magn. 2009, 45, 4463–4466. [Google Scholar] [CrossRef] [Green Version]
- Zuk, S.; Pietrikova, A.; Vehec, I. LTCC based planar inductive proximity sensor design. Period. Polytech. Electr. Eng. Comput. Sci. 2016, 60, 200–205. [Google Scholar] [CrossRef] [Green Version]













| Plate Size | Steel | Brass | Aluminum |
|---|---|---|---|
| 25 × 25 | 22 | 28 | 25 |
| 12 × 12 | 10 | 15 | 14 |
| 5 × 5 | 1 | 7 | 7 |
| Plate Size | Steel | Brass | Aluminum |
|---|---|---|---|
| 2.5 × 2.5 | 2.2 | 2.8 | 2.5 |
| 1.2 × 1.2 | 1.0 | 1.5 | 1.4 |
| 0.5 × 0.5 | 0.1 | 0.7 | 0.7 |
| Sensor | Max. Range/Coil Width |
|---|---|
| Cylinder coil and mixed analog-digital unit [25] | 0.66 |
| Passive Wireless LC Sensor Based on LTCC [26] | 0.75 |
| Multilayer PCB coil and ECS75 conditioner [27] | 1 |
| Inductive Proximity Magnetoplated Wire Sensor [28] | 1 |
| LTCC planar coil and TI LDC1000 chip [29] | 1.26 |
| Single-coil chaotic metal detector [15] | 1.4 |
| Current study | 2.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimov, T.; Druzhina, O.; Vatnik, V.; Ivanova, E.; Kulagin, M.; Ponomareva, V.; Voroshilova, A.; Rybin, V. Sensitivity Optimization and Experimental Study of the Long-Range Metal Detector Based on Chaotic Duffing Oscillator. Sensors 2022, 22, 5212. https://doi.org/10.3390/s22145212
Karimov T, Druzhina O, Vatnik V, Ivanova E, Kulagin M, Ponomareva V, Voroshilova A, Rybin V. Sensitivity Optimization and Experimental Study of the Long-Range Metal Detector Based on Chaotic Duffing Oscillator. Sensors. 2022; 22(14):5212. https://doi.org/10.3390/s22145212
Chicago/Turabian StyleKarimov, Timur, Olga Druzhina, Valerii Vatnik, Ekaterina Ivanova, Maksim Kulagin, Veronika Ponomareva, Anzhelika Voroshilova, and Vyacheslav Rybin. 2022. "Sensitivity Optimization and Experimental Study of the Long-Range Metal Detector Based on Chaotic Duffing Oscillator" Sensors 22, no. 14: 5212. https://doi.org/10.3390/s22145212
APA StyleKarimov, T., Druzhina, O., Vatnik, V., Ivanova, E., Kulagin, M., Ponomareva, V., Voroshilova, A., & Rybin, V. (2022). Sensitivity Optimization and Experimental Study of the Long-Range Metal Detector Based on Chaotic Duffing Oscillator. Sensors, 22(14), 5212. https://doi.org/10.3390/s22145212






