Development of the Measurement of Lateral Electron Density (MOLE) Probe Applicable to Low-Pressure Plasma Diagnostics
Abstract
:1. Introduction
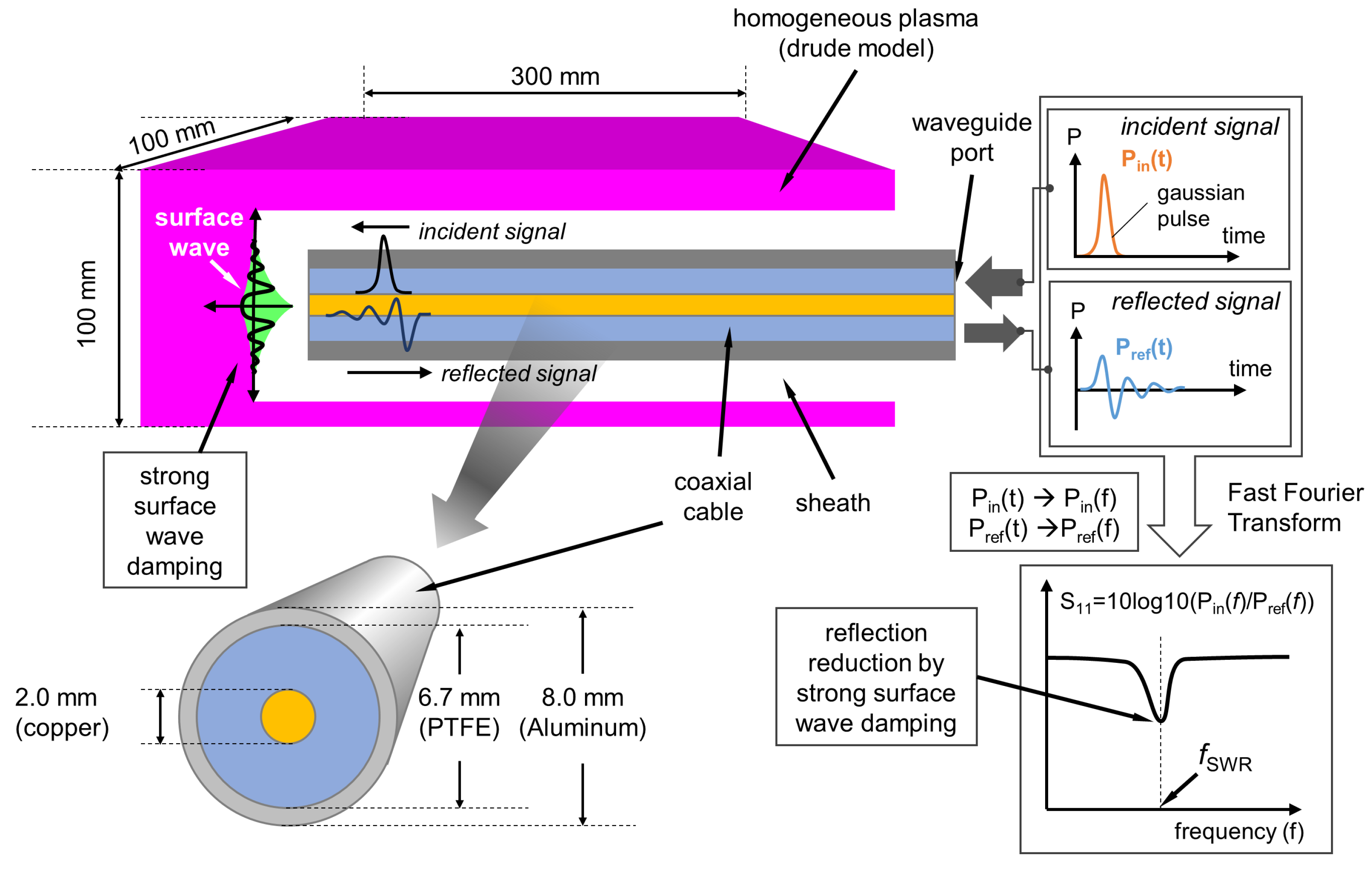
2. Three-Dimensional Electromagnetic Wave Simulation Analysis
2.1. Simulation Details
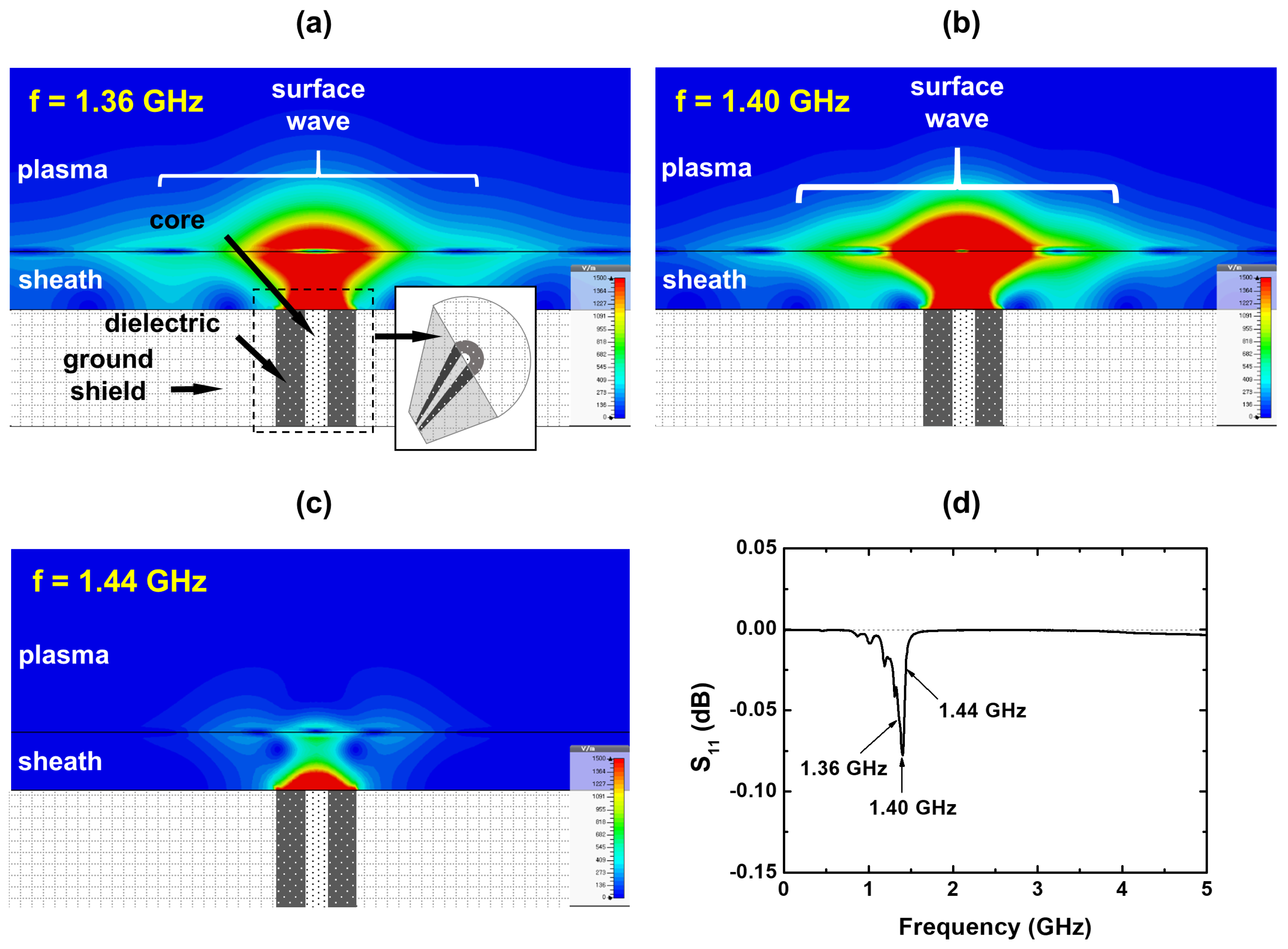
2.2. Validation of Surface Wave Resonance
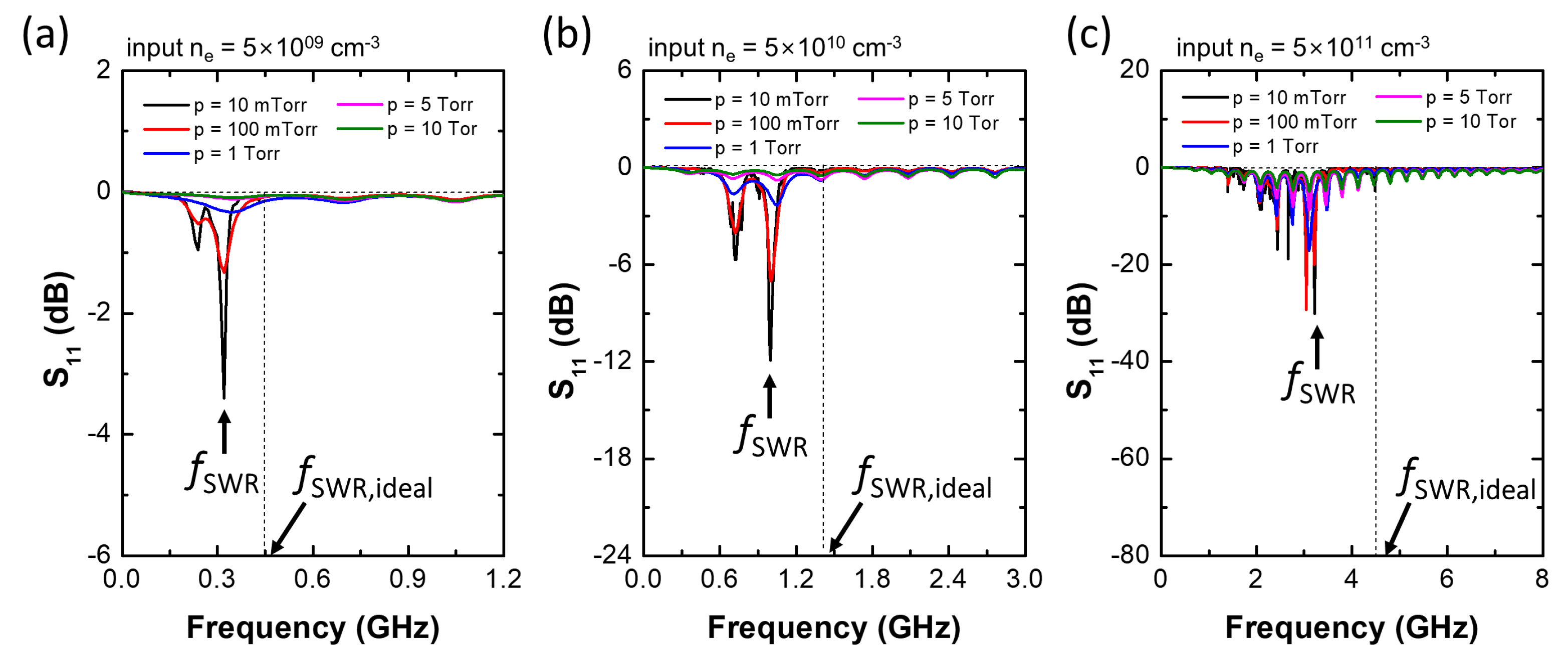
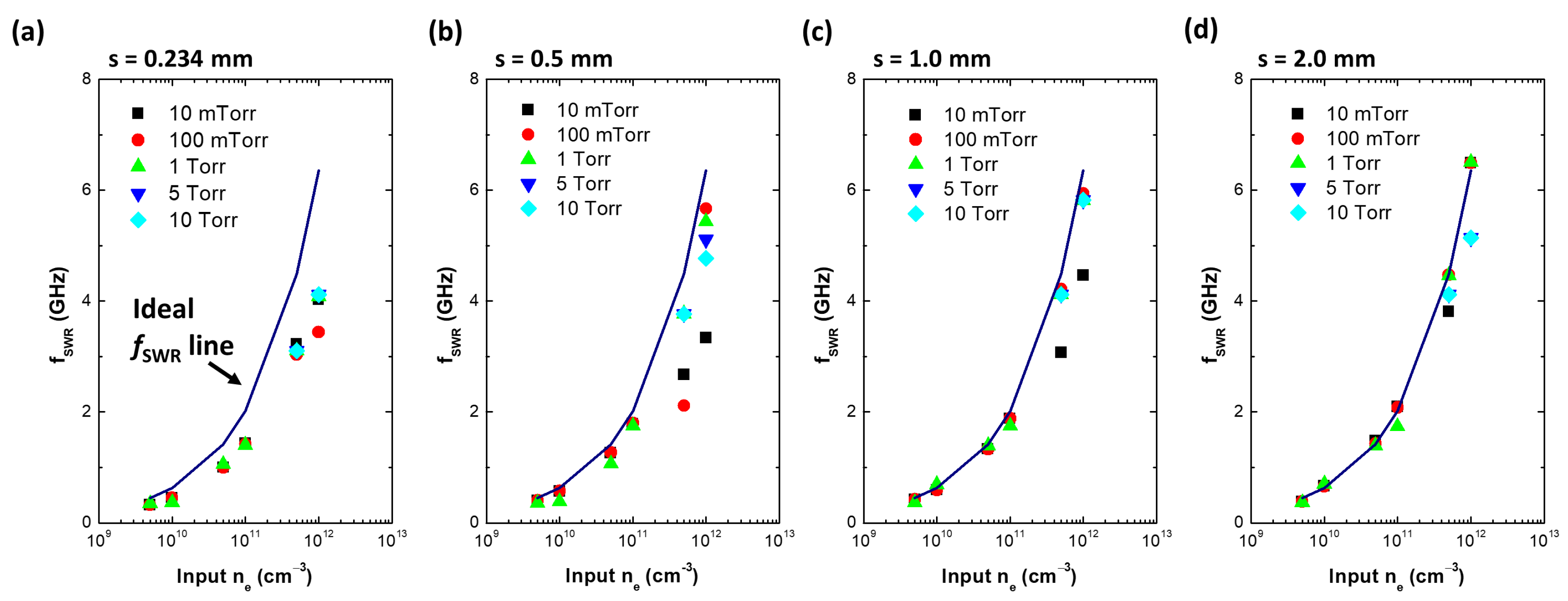
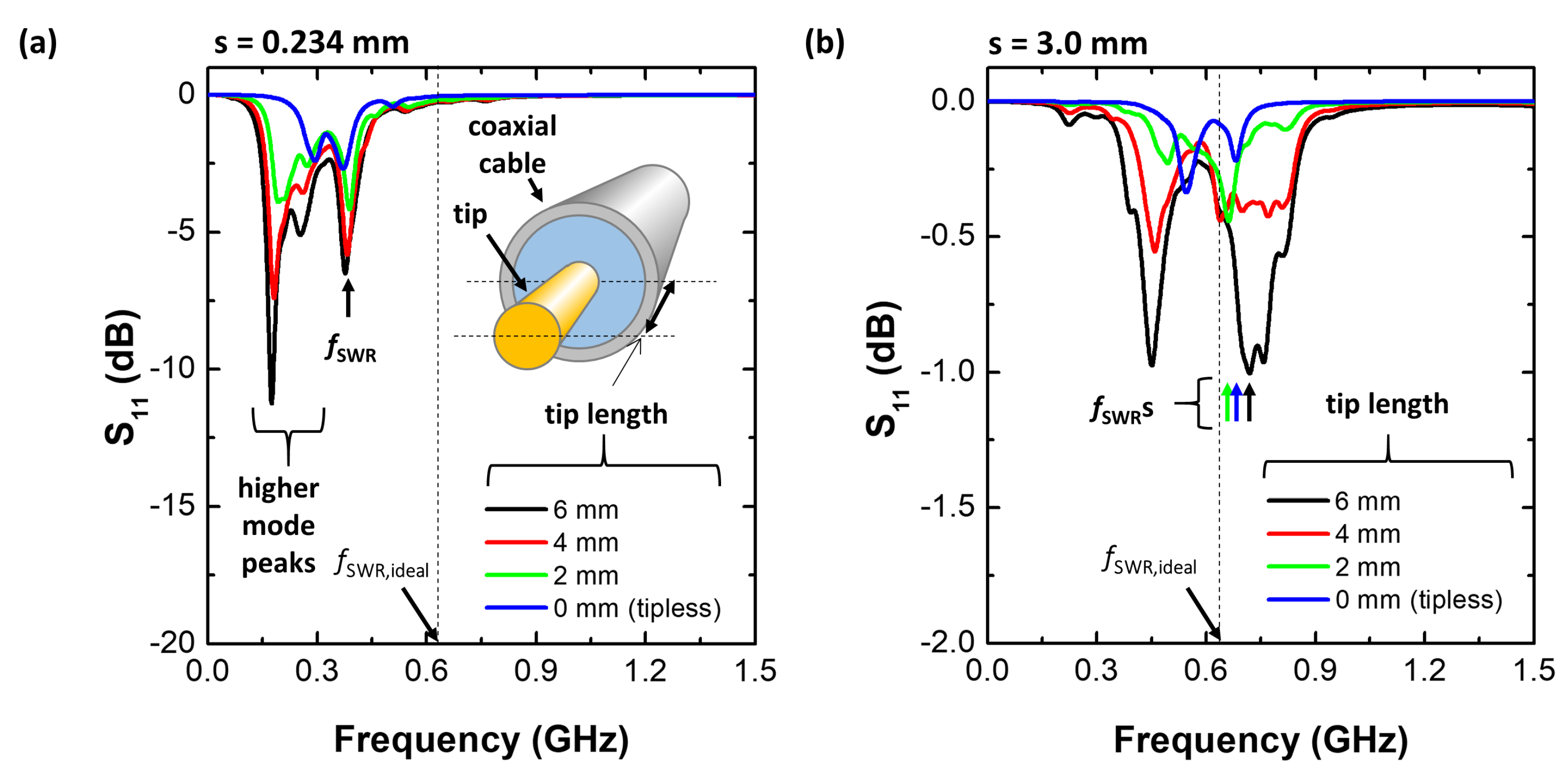
2.3. Simulation Results and Discussion
2.4. Difference between the MOLE Probe and the PAP
3. Experimental Demonstration
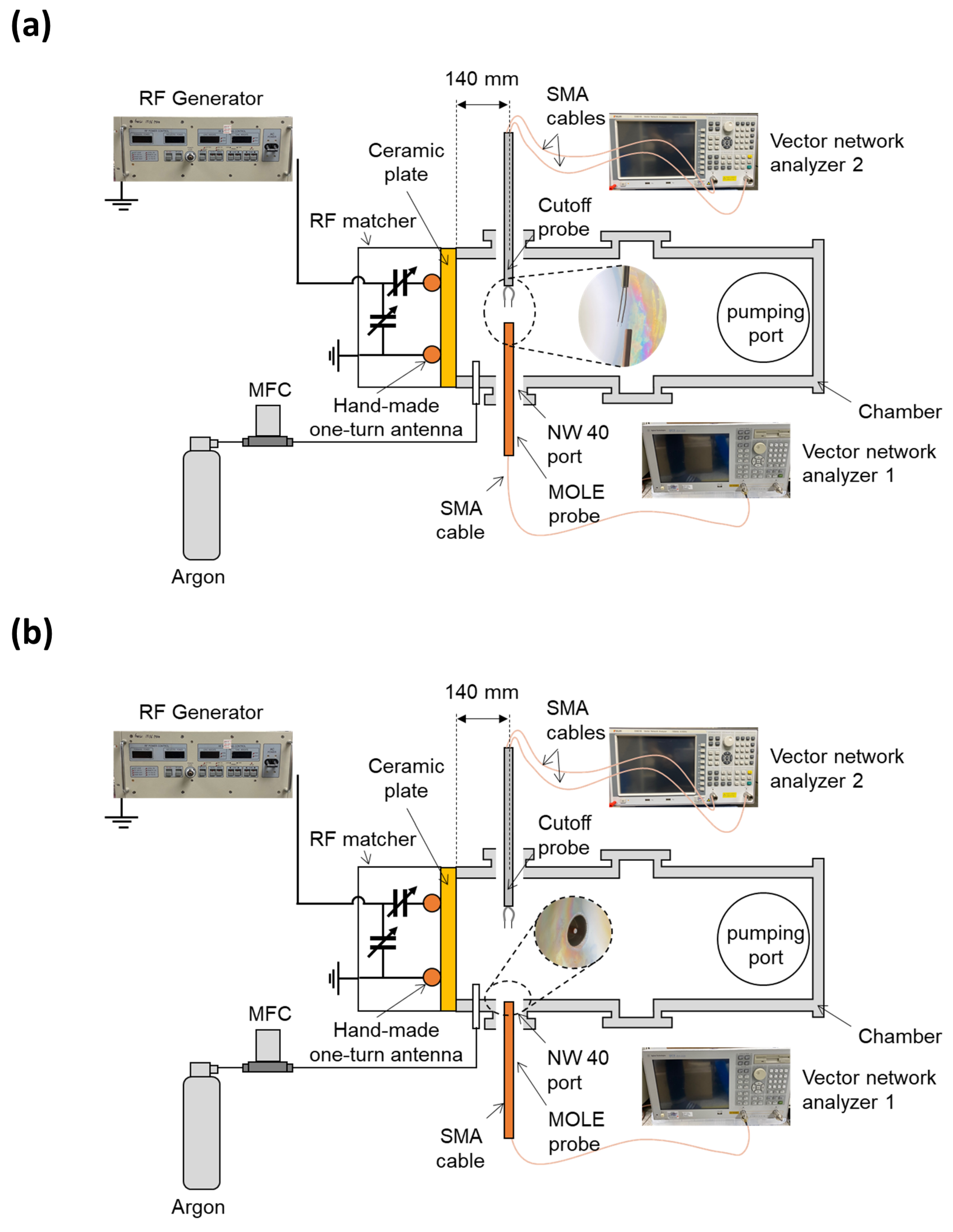
3.1. Experimental Setup
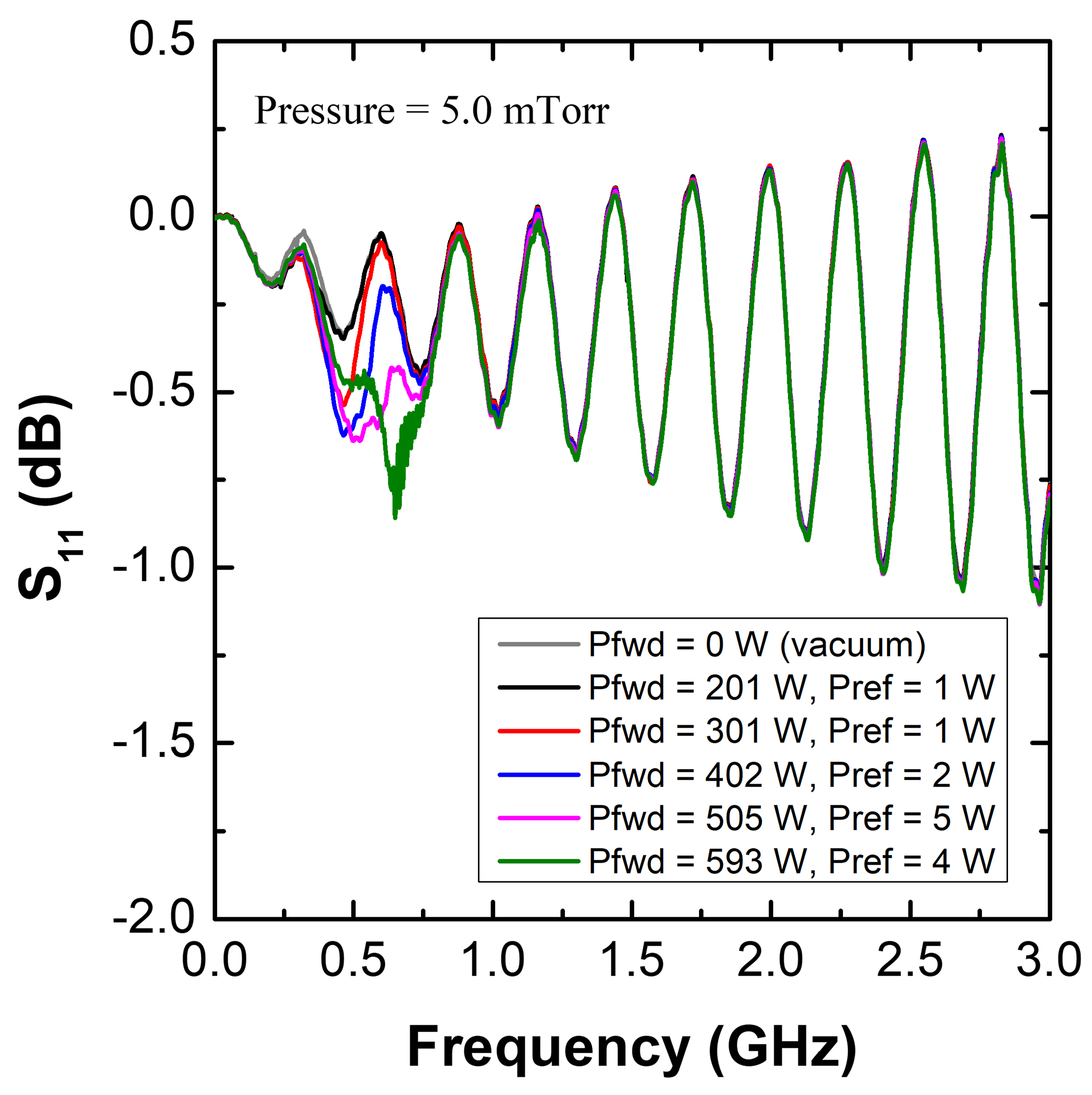
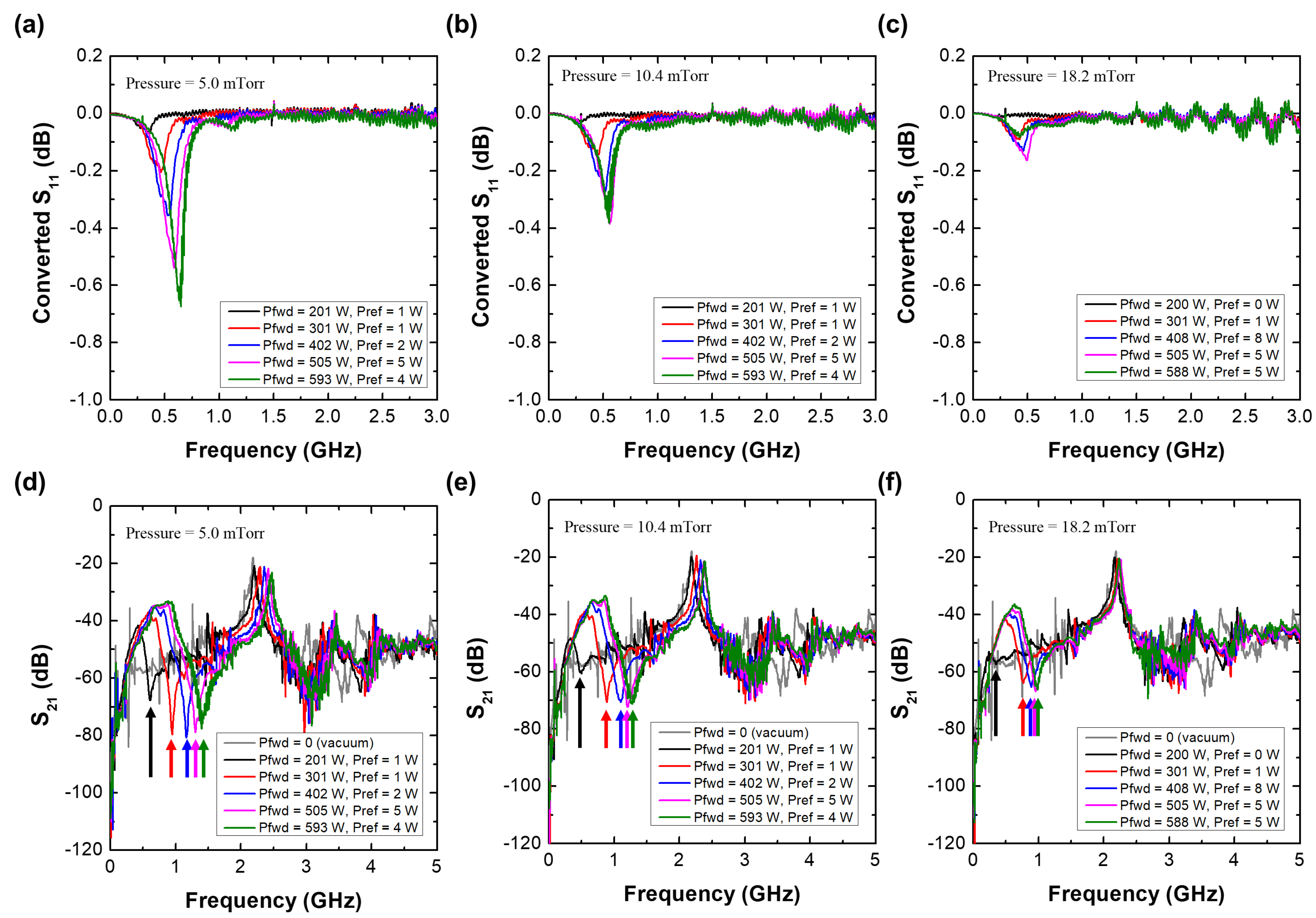
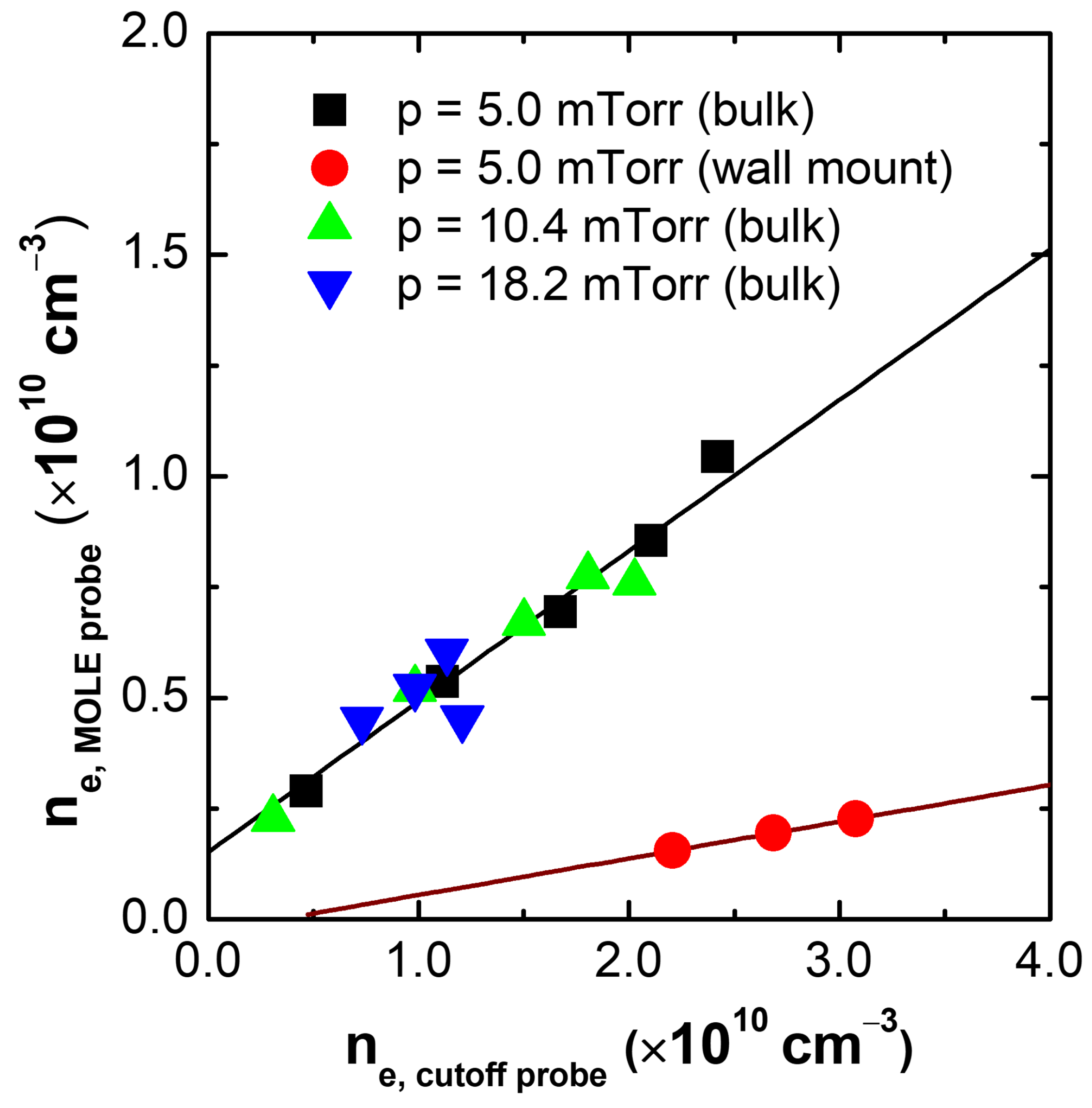
3.2. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bogaerts, A.; Tu, X.; Whitehead, J.C.; Centi, G.; Lefferts, L.; Guaitella, O.; Azzolina-Jury, F.; Kim, H.H.; Murphy, A.B.; Schneider, W.F.; et al. The 2020 plasma catalysis roadmap. J. Phys. Appl. Phys. 2020, 53, 443001. [Google Scholar] [CrossRef]
- Adamovich, I.; Baalrud, S.; Bogaerts, A.; Bruggeman, P.; Cappelli, M.; Colombo, V.; Czarnetzki, U.; Ebert, U.; Eden, J.; Favia, P.; et al. The 2017 Plasma Roadmap: Low temperature plasma science and technology. J. Phys. Appl. Phys. 2017, 50, 323001. [Google Scholar] [CrossRef]
- Laroussi, M.; Bekeschus, S.; Keidar, M.; Bogaerts, A.; Fridman, A.; Lu, X.; Ostrikov, K.; Hori, M.; Stapelmann, K.; Miller, V.; et al. Low-temperature plasma for biology, hygiene, and medicine: Perspective and roadmap. IEEE Trans. Radiat. Plasma Med. Sci. 2022, 6, 127–157. [Google Scholar] [CrossRef]
- Attri, P.; Ishikawa, K.; Okumura, T.; Koga, K.; Shiratani, M. Plasma agriculture from laboratory to farm: A review. Processes 2020, 8, 1002. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 1–22. [Google Scholar]
- Yang, R.; Chen, R. Real-time plasma process condition sensing and abnormal process detection. Sensors 2010, 10, 5703–5723. [Google Scholar] [CrossRef] [Green Version]
- Abbas, M.A.; Dijk, L.V.; Jahromi, K.E.; Nematollahi, M.; Harren, F.J.; Khodabakhsh, A. Broadband time-resolved absorption and dispersion spectroscopy of methane and ethane in a plasma using a mid-infrared dual-comb spectrometer. Sensors 2020, 20, 6831. [Google Scholar] [CrossRef]
- Wang, J.; Ji, W.; Du, Q.; Xing, Z.; Xie, X.; Zhang, Q. A Long Short-Term Memory Network for Plasma Diagnosis from Langmuir Probe Data. Sensors 2022, 22, 4281. [Google Scholar] [CrossRef]
- Kim, S.J.; Lee, J.J.; Lee, Y.S.; Cho, C.H.; You, S.J. Crossing Frequency Method Applicable to Intermediate Pressure Plasma Diagnostics Using the Cutoff Probe. Sensors 2022, 22, 1291. [Google Scholar] [CrossRef]
- Kim, S.J.; Lee, J.J.; Lee, Y.S.; Yeom, H.J.; Lee, H.C.; Kim, J.H.; You, S.J. Computational Characterization of Microwave Planar Cutoff Probes for Non-Invasive Electron Density Measurement in Low-Temperature Plasma: Ring-and Bar-Type Cutoff Probes. Appl. Sci. 2020, 10, 7066. [Google Scholar] [CrossRef]
- Kim, D.; You, S.; Kim, S.; Kim, J.; Lee, J.; Kang, W.; Hur, M. Planar cutoff probe for measuring the electron density of low-pressure plasmas. Plasma Sources Sci. Technol. 2019, 28, 015004. [Google Scholar] [CrossRef]
- Lynn, S.; Ringwood, J.; Ragnoli, E.; McLoone, S.; MacGearailty, N. Virtual metrology for plasma etch using tool variables. In Proceedings of the 2009 IEEE/SEMI Advanced Semiconductor Manufacturing Conference, Berlin, Germany, 10–12 May 2009; pp. 143–148. [Google Scholar]
- Jang, Y.C.; Park, S.H.; Jeong, S.M.; Ryu, S.W.; Kim, G.H. Role of features in plasma information based virtual metrology (PI-VM) for SiO2 etching depth. J. Semicond. Disp. Technol. 2019, 18, 30–34. [Google Scholar]
- Kim, B.; Bae, J.K.; Hong, W.S. Plasma control using neural network and optical emission spectroscopy. J. Vac. Sci. Technol. A 2005, 23, 355–358. [Google Scholar] [CrossRef]
- Kwon, J.W.; Ryu, S.; Park, J.; Lee, H.; Jang, Y.; Park, S.; Kim, G.H. Development of virtual metrology using plasma information variables to predict Si etch profile processed by SF6/O2/Ar capacitively coupled plasma. Materials 2021, 14, 3005. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.K.; Baek, K.H.; Shin, K. Resolving critical dimension drift over time in plasma etching through virtual metrology based wafer-to-wafer control. Jpn. J. Appl. Phys. 2017, 56, 066502. [Google Scholar] [CrossRef]
- Yeom, H.; Kim, J.; Choi, D.; Choi, E.; Yoon, M.; Seong, D.; You, S.J.; Lee, H.C. Flat cutoff probe for real-time electron density measurement in industrial plasma processing. Plasma Sources Sci. Technol. 2020, 29, 035016. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Lee, Y.; Kim, D.; You, S. Finding the optimum design of the planar cutoff probe through a computational study. AIP Adv. 2021, 11, 025241. [Google Scholar] [CrossRef]
- Fantz, U. Basics of plasma spectroscopy. Plasma Sources Sci. Technol. 2006, 15, S137. [Google Scholar] [CrossRef] [Green Version]
- Engeln, R.; Klarenaar, B.; Guaitella, O. Foundations of optical diagnostics in low-temperature plasmas. Plasma Sources Sci. Technol. 2020, 29, 063001. [Google Scholar] [CrossRef]
- Seo, B.; Kim, D.W.; Kim, J.H.; You, S. Investigation of reliability of the cutoff probe by a comparison with Thomson scattering in high density processing plasmas. Phys. Plasmas 2017, 24, 123502. [Google Scholar] [CrossRef] [Green Version]
- Ogawa, D.; Nakamura, K.; Sugai, H. Experimental validity of double-curling probe method in film-depositing plasma. Plasma Sources Sci. Technol. 2021, 30, 085009. [Google Scholar] [CrossRef]
- Friedrichs, M.; Oberrath, J. The planar Multipole Resonance Probe: A functional analytic approach. EPJ Tech. Instrum. 2018, 5, 7. [Google Scholar] [CrossRef]
- Kim, J.; Lee, K.I.; Jeong, H.Y.; Lee, J.H.; Choi, Y.S. Anti-contamination SMART (Spectrum Monitoring Apparatus with Roll-to-roll Transparent film) window for optical diagnostics of plasma systems. Rev. Sci. Instrum. 2021, 92, 013507. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Choi, S.C.; Shin, Y.H.; Chung, K.H. Wave cutoff method to measure absolute electron density in cold plasma. Rev. Sci. Instrum. 2004, 75, 2706–2710. [Google Scholar] [CrossRef]
- You, K.; You, S.; Kim, D.W.; Na, B.; Seo, B.; Kim, J.; Seong, D.; Chang, H. Measurement of electron density using reactance cutoff probe. Phys. Plasmas 2016, 23, 053515. [Google Scholar] [CrossRef]
- Tudisco, O.; Lucca Fabris, A.; Falcetta, C.; Accatino, L.; De Angelis, R.; Manente, M.; Ferri, F.; Florean, M.; Neri, C.; Mazzotta, C.; et al. A microwave interferometer for small and tenuous plasma density measurements. Rev. Sci. Instrum. 2013, 84, 033505. [Google Scholar] [CrossRef]
- Neumann, G.; Bänziger, U.; Kammeyer, M.; Lange, M. Plasma-density measurements by microwave interferometry and Langmuir probes in an rf discharge. Rev. Sci. Instrum. 1993, 64, 19–25. [Google Scholar] [CrossRef]
- Arshadi, A.; Brinkmann, R.P.; Hotta, M.; Nakamura, K. A simple and straightforward expression for curling probe electron density diagnosis in reactive plasmas. Plasma Sources Sci. Technol. 2017, 26, 045013. [Google Scholar] [CrossRef]
- Arshadi, A.; Brinkmann, R.P. Analytical investigation of microwave resonances of a curling probe for low and high-pressure plasma diagnostics. Plasma Sources Sci. Technol. 2016, 26, 015011. [Google Scholar] [CrossRef]
- Liang, I.; Nakamura, K.; Sugai, H. Modeling microwave resonance of curling probe for density measurements in reactive plasmas. Appl. Phys. Express 2011, 4, 066101. [Google Scholar] [CrossRef]
- van Ninhuijs, M.A.; Daamen, K.; Beckers, J.; Luiten, O. Design and characterization of a resonant microwave cavity as a diagnostic for ultracold plasmas. Rev. Sci. Instrum. 2021, 92, 013506. [Google Scholar] [CrossRef]
- Staps, T.; Platier, B.; Mihailova, D.; Meijaard, P.; Beckers, J. Numerical profile correction of microwave cavity resonance spectroscopy measurements of the electron density in low-pressure discharges. Rev. Sci. Instrum. 2021, 92, 093504. [Google Scholar] [CrossRef] [PubMed]
- Beckers, J.; Van De Wetering, F.; Platier, B.; Van Ninhuijs, M.; Brussaard, G.; Banine, V.; Luiten, O. Mapping electron dynamics in highly transient EUV photon-induced plasmas: A novel diagnostic approach using multi-mode microwave cavity resonance spectroscopy. J. Phys. D Appl. Phys. 2018, 52, 034004. [Google Scholar] [CrossRef] [Green Version]
- Lapke, M.; Oberrath, J.; Schulz, C.; Storch, R.; Styrnoll, T.; Zietz, C.; Awakowicz, P.; Brinkmann, R.P.; Musch, T.; Mussenbrock, T.; et al. The multipole resonance probe: Characterization of a prototype. Plasma Sources Sci. Technol. 2011, 20, 042001. [Google Scholar] [CrossRef]
- Schulz, C.; Styrnoll, T.; Awakowicz, P.; Rolfes, I. The planar multipole resonance probe: Challenges and prospects of a planar plasma sensor. IEEE Trans. Instrum. Meas. 2014, 64, 857–864. [Google Scholar] [CrossRef]
- Pohle, D.; Schulz, C.; Oberberg, M.; Awakowicz, P.; Rolfes, I. The planar multipole resonance probe: A minimally invasive monitoring concept for plasma-assisted dielectric deposition processes. IEEE Trans. Microw. Theory Tech. 2020, 68, 2067–2079. [Google Scholar] [CrossRef]
- Wang, C.; Friedrichs, M.; Oberrath, J.; Brinkmann, R.P. Kinetic investigation of the planar multipole resonance probe in the low-pressure plasma. Plasma Sources Sci. Technol. 2021, 30, 105011. [Google Scholar] [CrossRef]
- Huang, S.; Huard, C.; Shim, S.; Nam, S.K.; Song, I.C.; Lu, S.; Kushner, M.J. Plasma etching of high aspect ratio features in SiO2 using Ar/C4F8/O2 mixtures: A computational investigation. J. Vac. Sci. Technol. A 2019, 37, 031304. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, K.; Karahashi, K.; Ishijima, T.; Cho, S.I.; Elliott, S.; Hausmann, D.; Mocuta, D.; Wilson, A.; Kinoshita, K. Progress in nanoscale dry processes for fabrication of high-aspect-ratio features: How can we control critical dimension uniformity at the bottom? Jpn. J. Appl. Phys. 2018, 57, 06JA01. [Google Scholar] [CrossRef]
- Kokura, H.; Nakamura, K.; Ghanashev, I.P.; Sugai, H. Plasma absorption probe for measuring electron density in an environment soiled with processing plasmas. Jpn. J. Appl. Phys. 1999, 38, 5262. [Google Scholar] [CrossRef]
- Dine, S.; Booth, J.P.; Curley, G.A.; Corr, C.; Jolly, J.; Guillon, J. A novel technique for plasma density measurement using surface-wave transmission spectra. Plasma Sources Sci. Technol. 2005, 14, 777. [Google Scholar] [CrossRef]
- Anwar, R.S.; Ning, H.; Mao, L. Recent advancements in surface plasmon polaritons-plasmonics in subwavelength structures in microwave and terahertz regimes. Digit. Commun. Netw. 2018, 4, 244–257. [Google Scholar] [CrossRef]
- Nakamura, K.; Ohata, M.; Sugai, H. Highly sensitive plasma absorption probe for measuring low-density high-pressure plasmas. J. Vac. Sci. Technol. A 2003, 21, 325–331. [Google Scholar] [CrossRef]
- Lapke, M.; Mussenbrock, T.; Brinkmann, R.; Scharwitz, C.; Böke, M.; Winter, J. Modeling and simulation of the plasma absorption probe. Appl. Phys. Lett. 2007, 90, 121502. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Kim, D.; Kim, J.; You, S. A transmission line model of the cutoff probe. Plasma Sources Sci. Technol. 2019, 28, 055014. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Lee, Y.; Kim, D.; You, S. Effect of an inhomogeneous electron density profile on the transmission microwave frequency spectrum of the cutoff probe. Plasma Sources Sci. Technol. 2020, 29, 125014. [Google Scholar] [CrossRef]
- Kim, D.W.; You, S.; Kwon, J.; You, K.; Seo, B.; Kim, J.; Yoon, J.S.; Oh, W.Y. Reproducibility of the cutoff probe for the measurement of electron density. Phys. Plasmas 2016, 23, 063501. [Google Scholar] [CrossRef]
- Kim, D.W.; You, S.; Kim, J.; Chang, H.; Oh, W.Y. Computational comparative study of microwave probes for plasma density measurement. Plasma Sources Sci. Technol. 2016, 25, 035026. [Google Scholar] [CrossRef]
- Kim, Y.-C.; Lee, H.-C.; Chung, C.-W. Study on Plasma Uniformity Using 2-D Measurement Method in Argon Inductively Coupled Plasmas. IEEE Trans. Plasma Sci. 2014, 42, 2858–2859. [Google Scholar]
- Kim, D.W.; You, S.J.; Kim, J.H.; Seong, D.J.; Chang, H.Y.; Oh, W.Y. Computational study on reliability of sheath width measurement by the cutoff probe in low pressure plasmas. J. Instrum. 2015, 10, T11001. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-j.; Lee, S.-h.; You, Y.-b.; Lee, Y.-s.; Seong, I.-h.; Cho, C.-h.; Lee, J.-j.; You, S.-j. Development of the Measurement of Lateral Electron Density (MOLE) Probe Applicable to Low-Pressure Plasma Diagnostics. Sensors 2022, 22, 5487. https://doi.org/10.3390/s22155487
Kim S-j, Lee S-h, You Y-b, Lee Y-s, Seong I-h, Cho C-h, Lee J-j, You S-j. Development of the Measurement of Lateral Electron Density (MOLE) Probe Applicable to Low-Pressure Plasma Diagnostics. Sensors. 2022; 22(15):5487. https://doi.org/10.3390/s22155487
Chicago/Turabian StyleKim, Si-jun, Sang-ho Lee, Ye-bin You, Young-seok Lee, In-ho Seong, Chul-hee Cho, Jang-jae Lee, and Shin-jae You. 2022. "Development of the Measurement of Lateral Electron Density (MOLE) Probe Applicable to Low-Pressure Plasma Diagnostics" Sensors 22, no. 15: 5487. https://doi.org/10.3390/s22155487
APA StyleKim, S.-j., Lee, S.-h., You, Y.-b., Lee, Y.-s., Seong, I.-h., Cho, C.-h., Lee, J.-j., & You, S.-j. (2022). Development of the Measurement of Lateral Electron Density (MOLE) Probe Applicable to Low-Pressure Plasma Diagnostics. Sensors, 22(15), 5487. https://doi.org/10.3390/s22155487







