Multi Spherical Wave Imaging Method Based on Ultrasonic Array
Abstract
:1. Introduction
2. Theoretical Analysis of Traditional Imaging
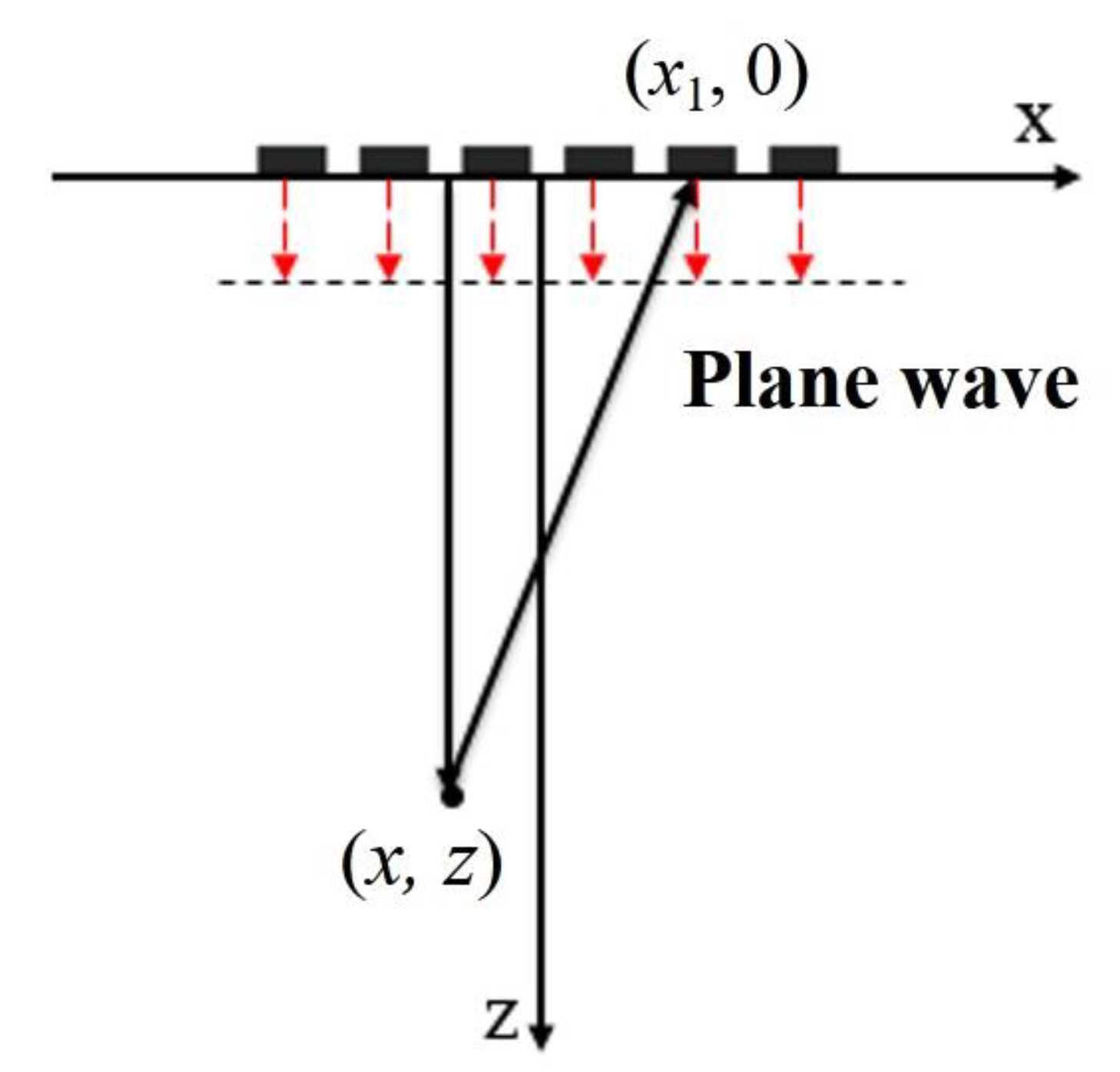
2.1. Principle of Single Plane Wave Imaging
2.2. Principle of Coherent Plane Wave Compounding
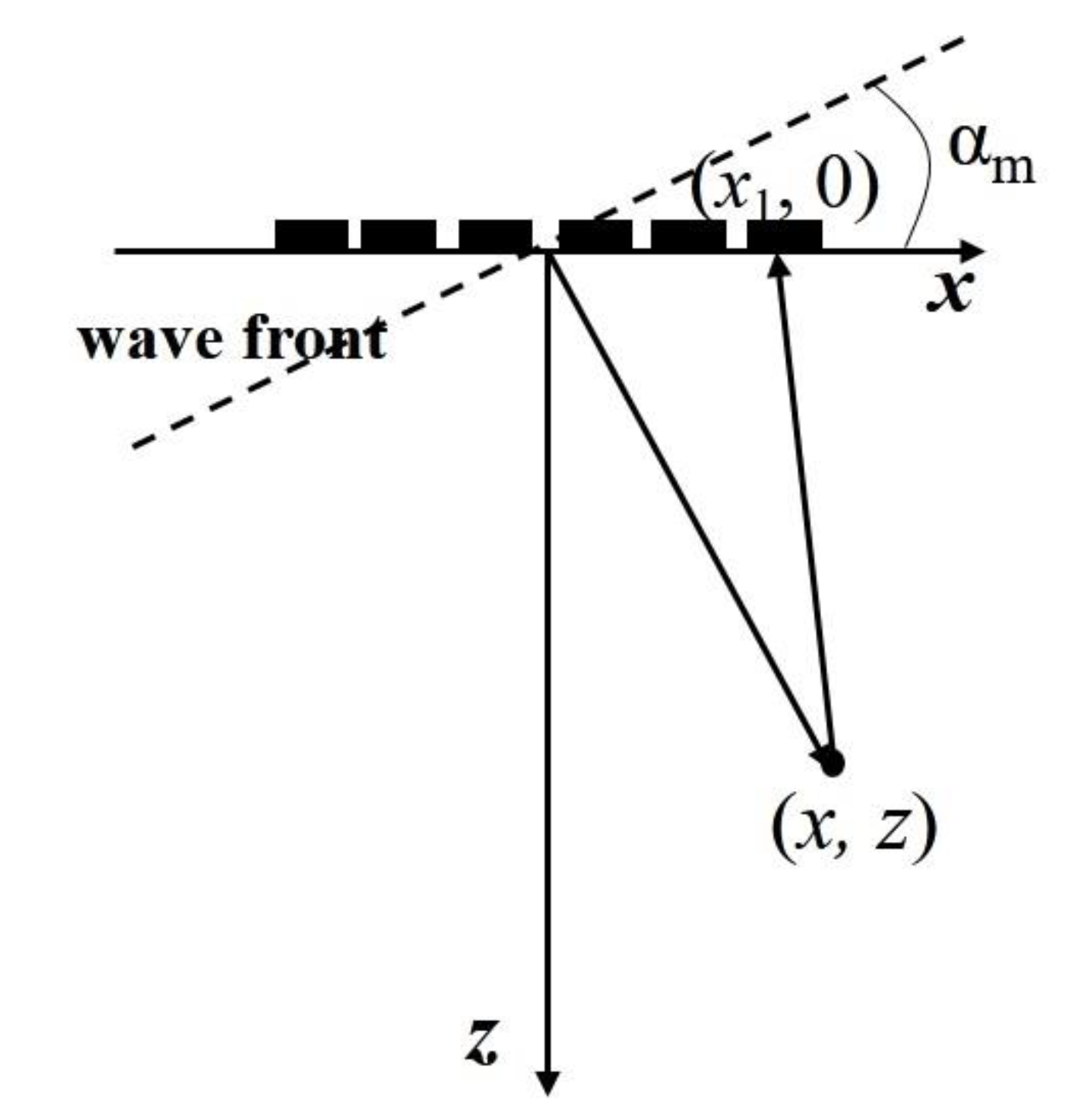
2.3. Principle of Spherical Wave Imaging
2.3.1. Single Spherical Wave Imaging
2.3.2. Coherent Spherical Wave Compounding
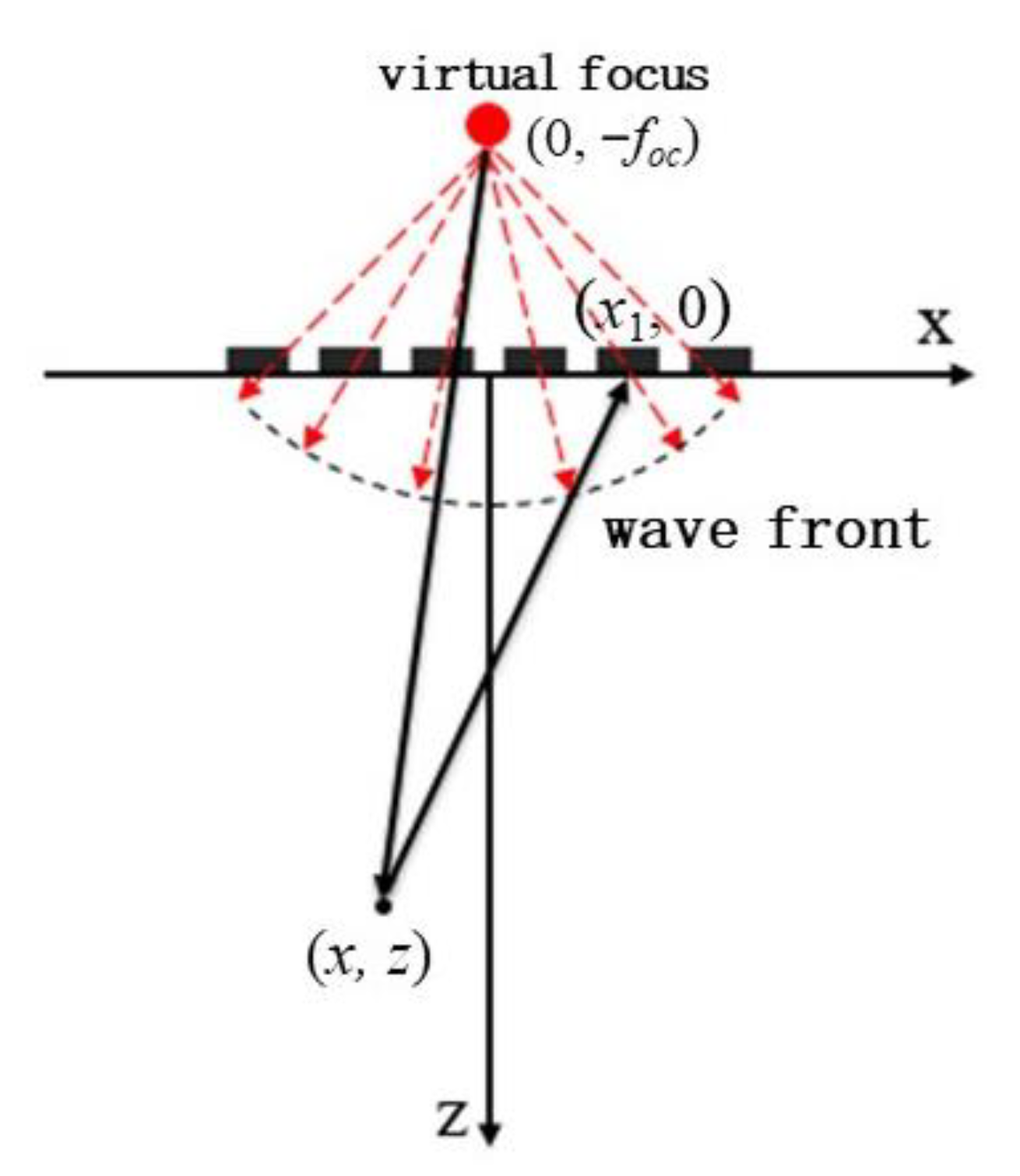
3. Multi Spherical Wave Imaging Method
3.1. Multi Spherical Wave Emission
3.2. Coherent Multi Spherical Wave Compounding
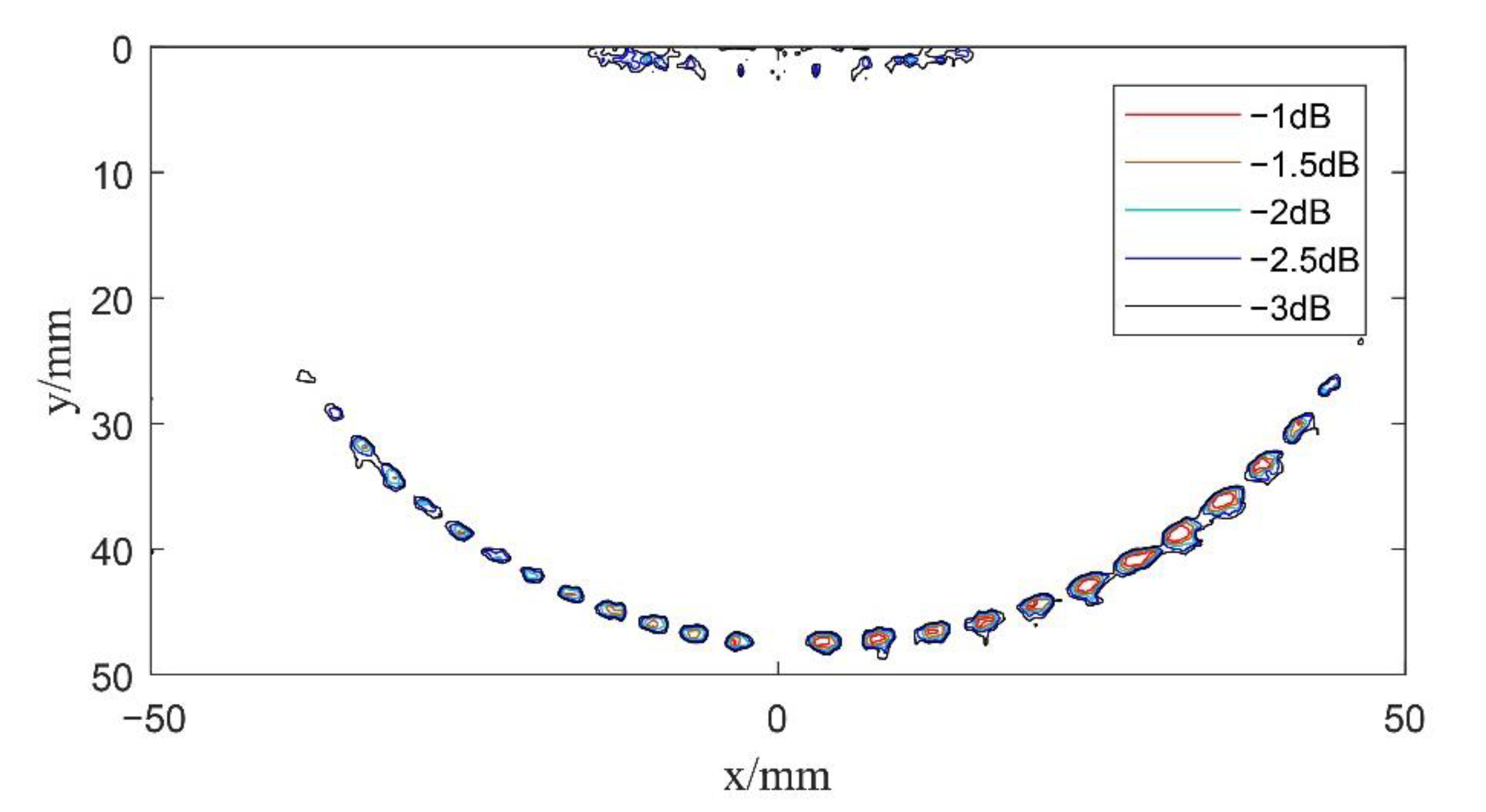
4. Imaging Results and Discussion
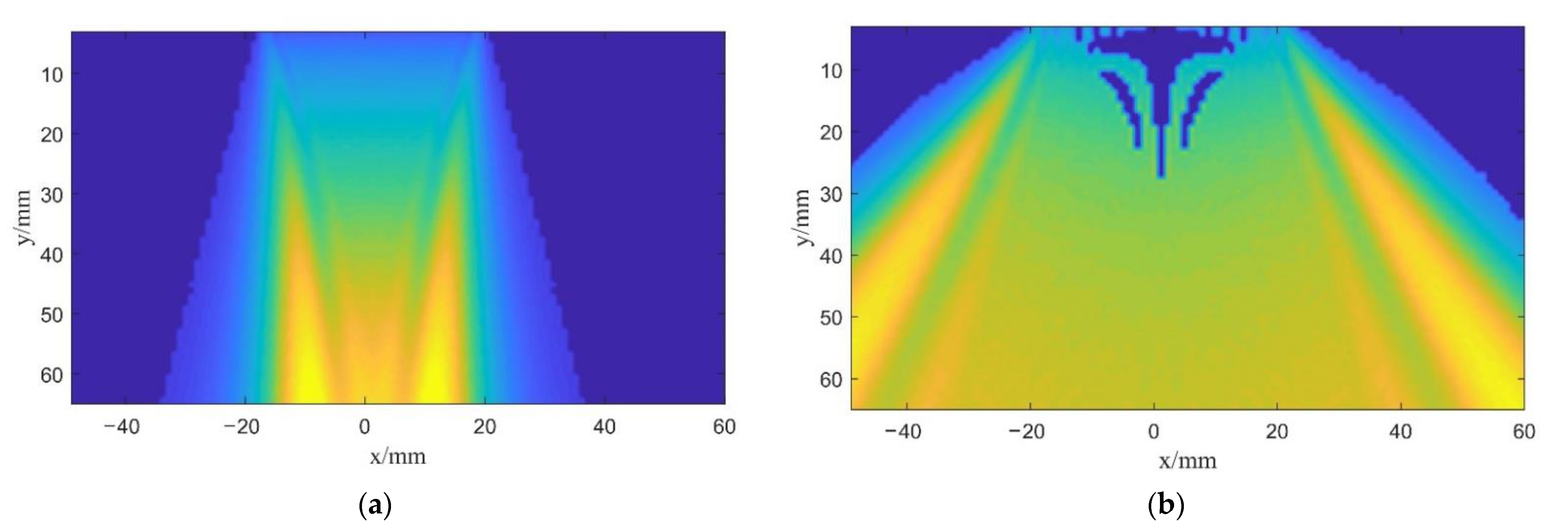
4.1. Undeflected Plane and Spherical Wave Imaging
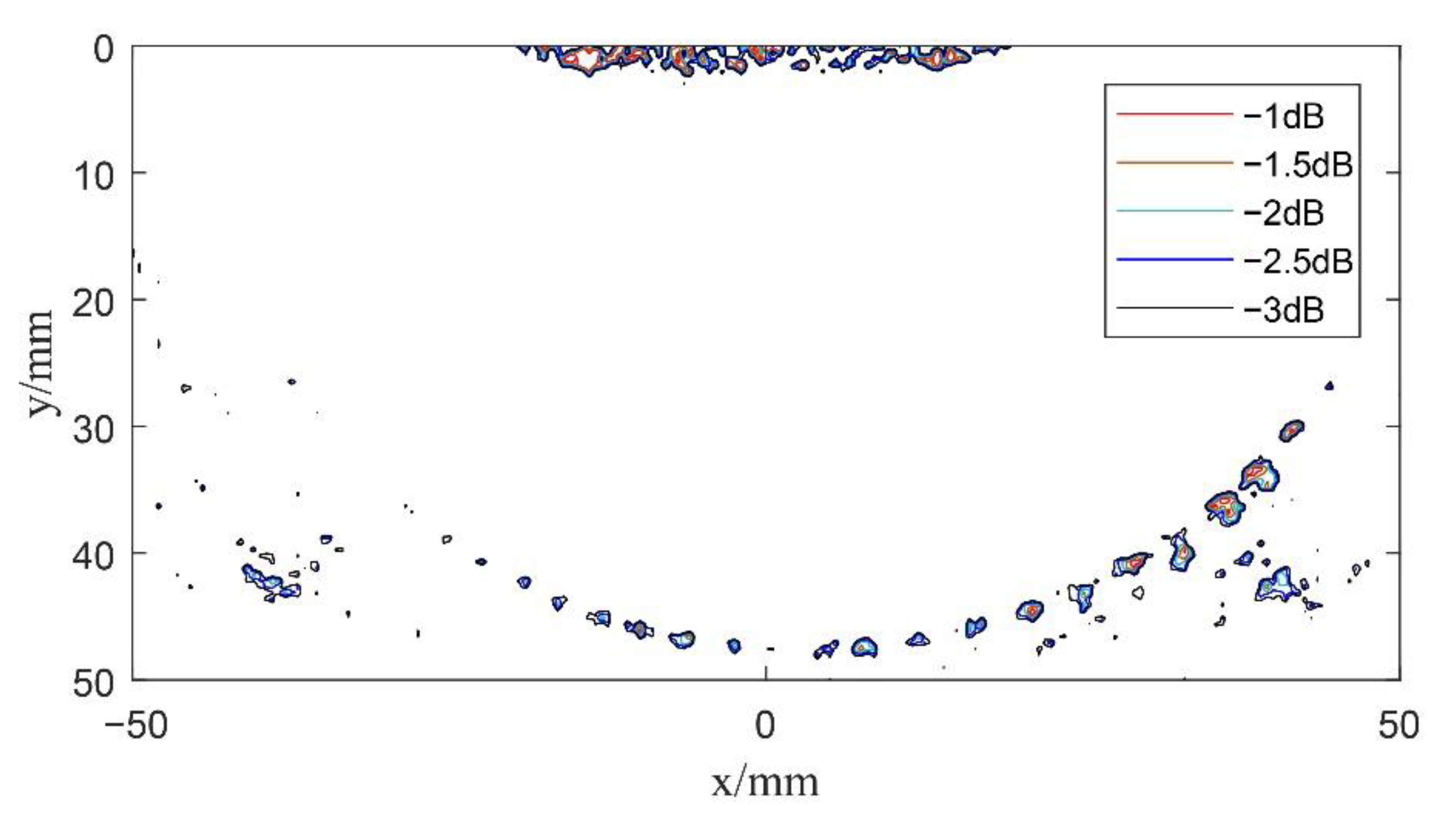
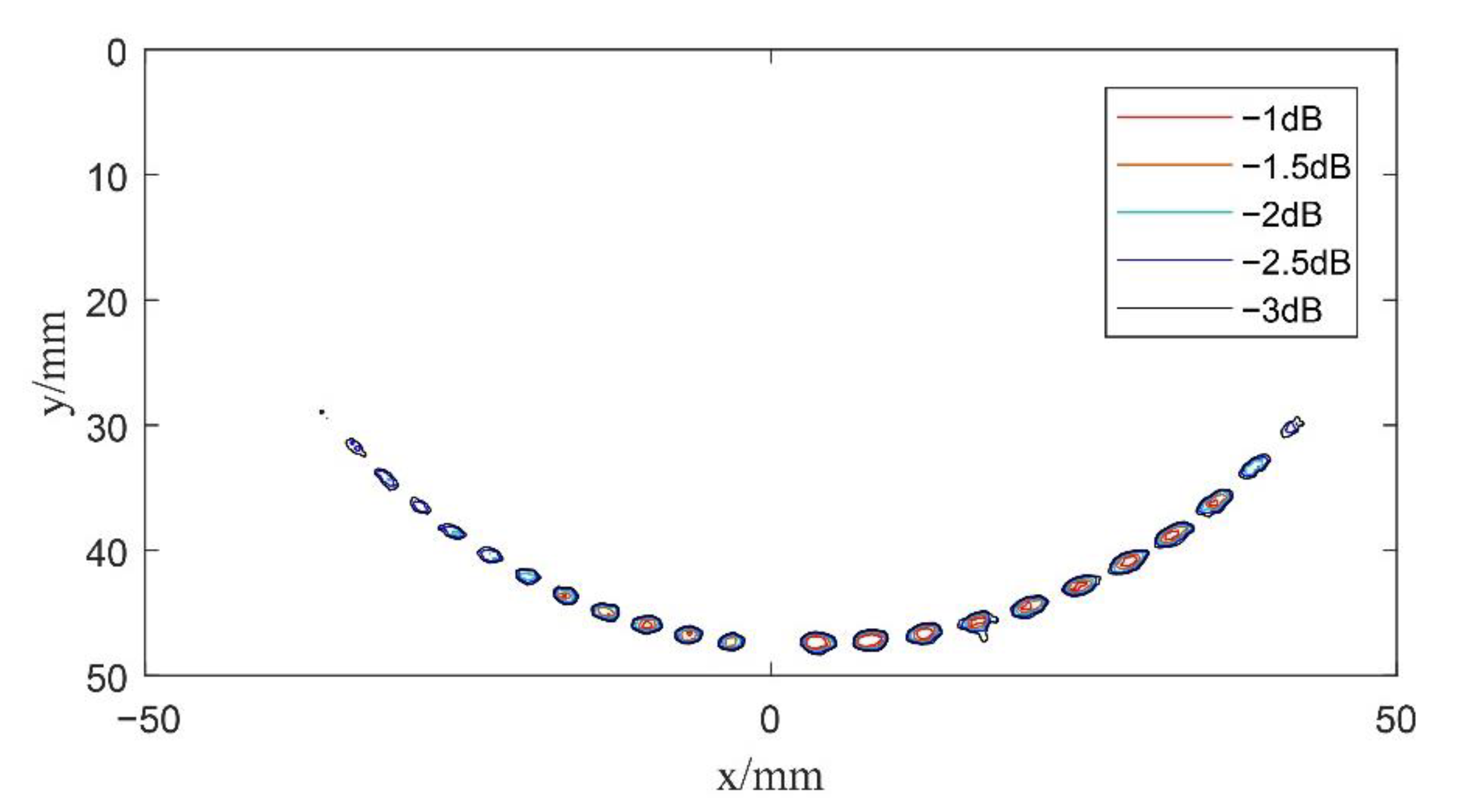
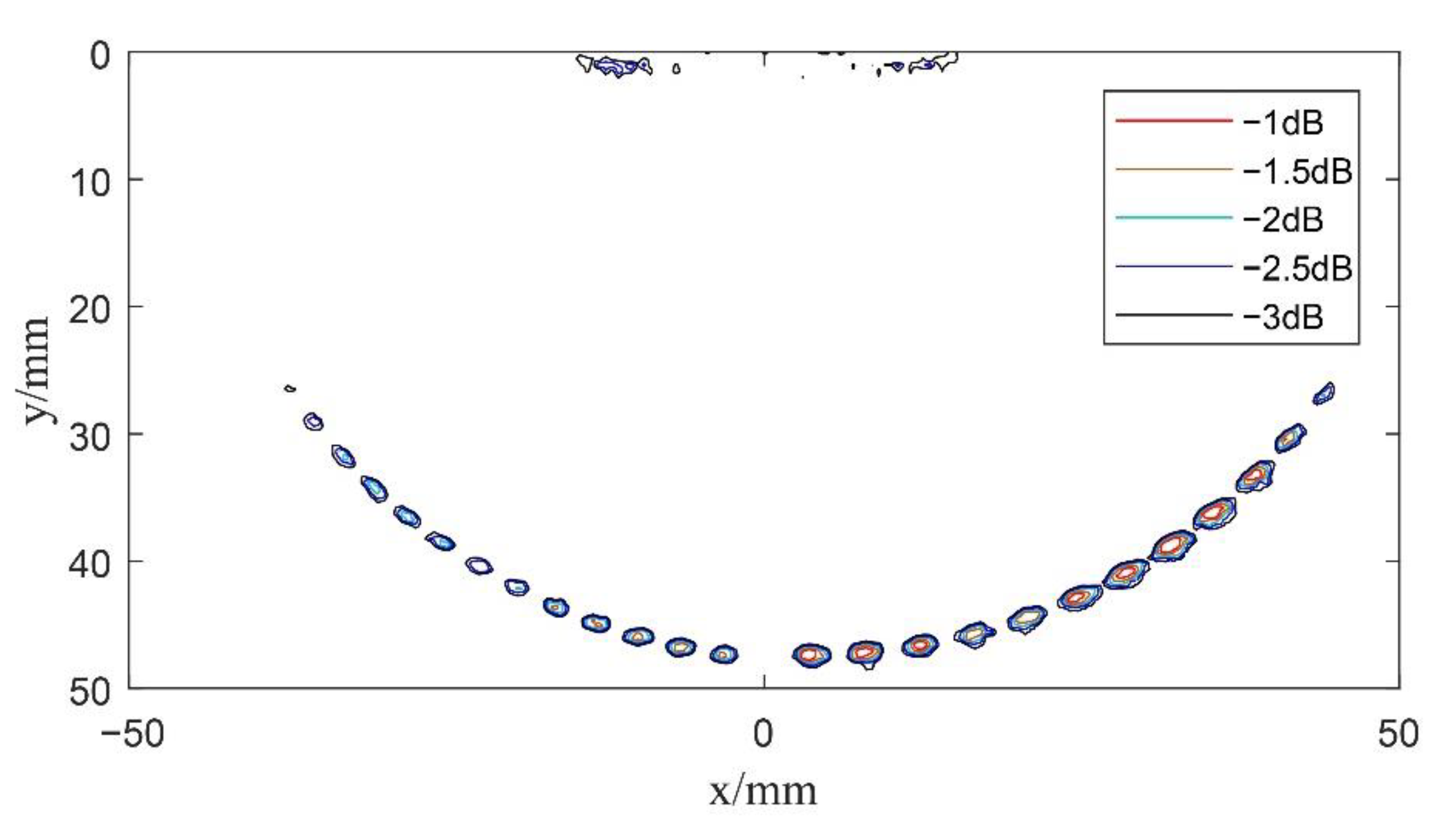
4.2. Composite Multi Spherical Wave Imaging
5. Conclusions
- The imaging region of the undeflected plane wave has been seriously affected by the size of the transducer. Plane wave imaging without deflection can only detect the corresponding defects below the transducer array. However, undeflected spherical wave imaging can detect the defects beyond the vertical range of the transducer array.
- Compared with spherical wave imaging without deflection, the detection sensitivity of the composite multi spherical wave is slightly improved in the sensitivity of the large angle. However, there is no focusing emission, and the overall imaging effect is relatively poor.
- Compared with undeflected plane wave and spherical wave imaging, the resolution and SNR of composite spherical wave imaging and composite multi spherical wave imaging are greatly improved. Since the properties of both compressional and shear waves are utilized, multi spherical wave imaging can obtain better images over a larger deflection region.
- Composite multi spherical wave imaging can improve the speed of echo processing by appropriately reducing the number of transmission deflections, and the imaging effect is better than that of composite spherical wave ultrasonic imaging.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, K.; Choi, H. High-efficiency high-voltage class F amplifier for high-frequency wireless ultrasound systems. PLoS ONE 2021, 16, e0249034. [Google Scholar] [CrossRef] [PubMed]
- Delannoy, B.; Torguet, R.; Bruneel, C.; Bridoux, E. Ultrafast Electronical Image Reconstruction Device. In Echocardiology; Springer: Dordrecht, The Netherlands, 1979; pp. 447–450. [Google Scholar]
- Delannoy, B.; Torguet, R.; Bruneel, C.; Bridoux, E.; Rouvaen, J.M.; Lasota, H. Acoustical image reconstruction in parallel-processing analog electronic systems. J. Appl. Phys. 1979, 50, 3153–3159. [Google Scholar] [CrossRef]
- Shattuck, D.P.; Weinshenker, M.D. Explososcan: A parallel processing technique for high speed ultrasound imaging with linear phased arrays. J. Acoust. Soc. Am. 1984, 75, 1273–1282. [Google Scholar] [PubMed]
- Sandrin, L.; Tanter, M.; Catheline, S.; Fink, M. Elasticity imaging with time-resolved pulsed elastography. J. Acoust. Soc. Am. 2001, 109, 2361. [Google Scholar] [CrossRef]
- Sandrin, L.; Catheline, S.; Tanter, M.; Fink, M. 2D Transient Elastography. In Proceedings of the 25th International Symposium on Acoustical Imaging, Bristol, UK, 19–22 March 2000; pp. 485–492. [Google Scholar]
- Sandrin, L.; Tanter, M.; Catheline, S.; Fink, M. Shear Modulus Imaging with 2-D Transient Elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 426–435. [Google Scholar] [CrossRef] [PubMed]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Denarie, B.; Tangen, T.A.; Ekroll, I.K.; Rolim, N.; Torp, H.; Bjastad, T.; Lovstakken, L. Coherent plane wave compounding for very high frame rate ultrasonography of rapidly moving targets. IEEE Trans. Med. Imaging 2013, 32, 1265–1276. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D.; Hunter, A.J. Defect detection using ultrasonic arrays: The multi-mode total focusing method. NDT E Int. 2010, 43, 123–133. [Google Scholar] [CrossRef]
- Zhang, B.X.; Liu, D.D.; Shi, F.F.; Dong, H.F. Ultrasonic focusing and scanning with multiple waves. Chin. Phys. B 2013, 22, 014302. [Google Scholar] [CrossRef]
- Wang, G.J.; Chen, D.; Zhao, A.H.; Chen, Y. Multi-component seismic exploration. Prog. Geophys. 2000, 15, 54–60. [Google Scholar]
- Holfort, I.K.; Gran, F.; Jensen, J.A. Plane wave medical ultrasound imaging using adaptive beamforming. In Proceedings of the 2008 Fifth IEEE Sensor Array and Multichannel Signal Processing Workshop, Darmstadt, Germany, 21–23 July 2008. [Google Scholar]
- You, B.Y.; Tsang, I.K.; Yu, A.C. GPU-based beamformer: Fast realization of plane wave compounding and synthetic aperture imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1698–1705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, X.J. Ultrasonic plane wave imaging based on multi-angle coherent compositing. Fash. Baby 2017, 210–211. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, S. A Novel Method of Coherent Plane-Wave Compounding Imaging Based as on Compressive Sensing Algorithm. Master’s Thesis, Northeastern University, Shenyang, China, 2016. [Google Scholar]
- Zhang, P.; Yan, S.G.; Dai, Y.X.; Huang, J.; Kong, C.; Shi, F.F.; Zhang, B.X. The Multi-wave total focusing method for full-matrix imaging using an ultrasonic phased array. Mater. Eval. 2021, 79, 1179–1188. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.-Y.; Zhang, P.; Zhang, B.-X.; Wang, W. Multi Spherical Wave Imaging Method Based on Ultrasonic Array. Sensors 2022, 22, 6800. https://doi.org/10.3390/s22186800
Liu Z-Y, Zhang P, Zhang B-X, Wang W. Multi Spherical Wave Imaging Method Based on Ultrasonic Array. Sensors. 2022; 22(18):6800. https://doi.org/10.3390/s22186800
Chicago/Turabian StyleLiu, Zhi-Ying, Ping Zhang, Bi-Xing Zhang, and Wen Wang. 2022. "Multi Spherical Wave Imaging Method Based on Ultrasonic Array" Sensors 22, no. 18: 6800. https://doi.org/10.3390/s22186800
APA StyleLiu, Z.-Y., Zhang, P., Zhang, B.-X., & Wang, W. (2022). Multi Spherical Wave Imaging Method Based on Ultrasonic Array. Sensors, 22(18), 6800. https://doi.org/10.3390/s22186800





