Azimuth Full-Aperture Processing of Spaceborne Squint SAR Data with Block Varying PRF
Abstract
:1. Introduction
2. Range Cell Migration Analysis for Squint SAR
3. PRF Design and Signal Analysis
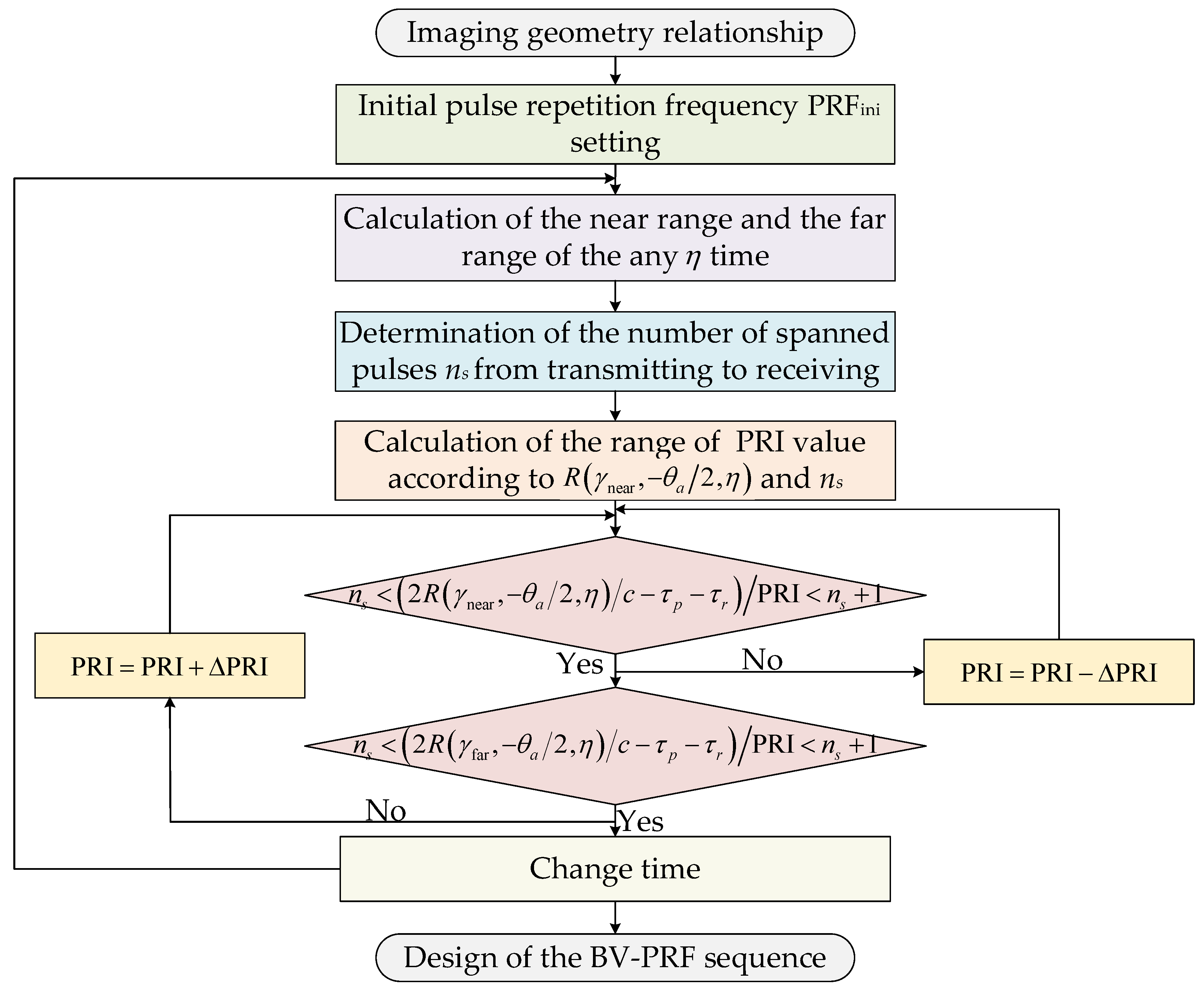
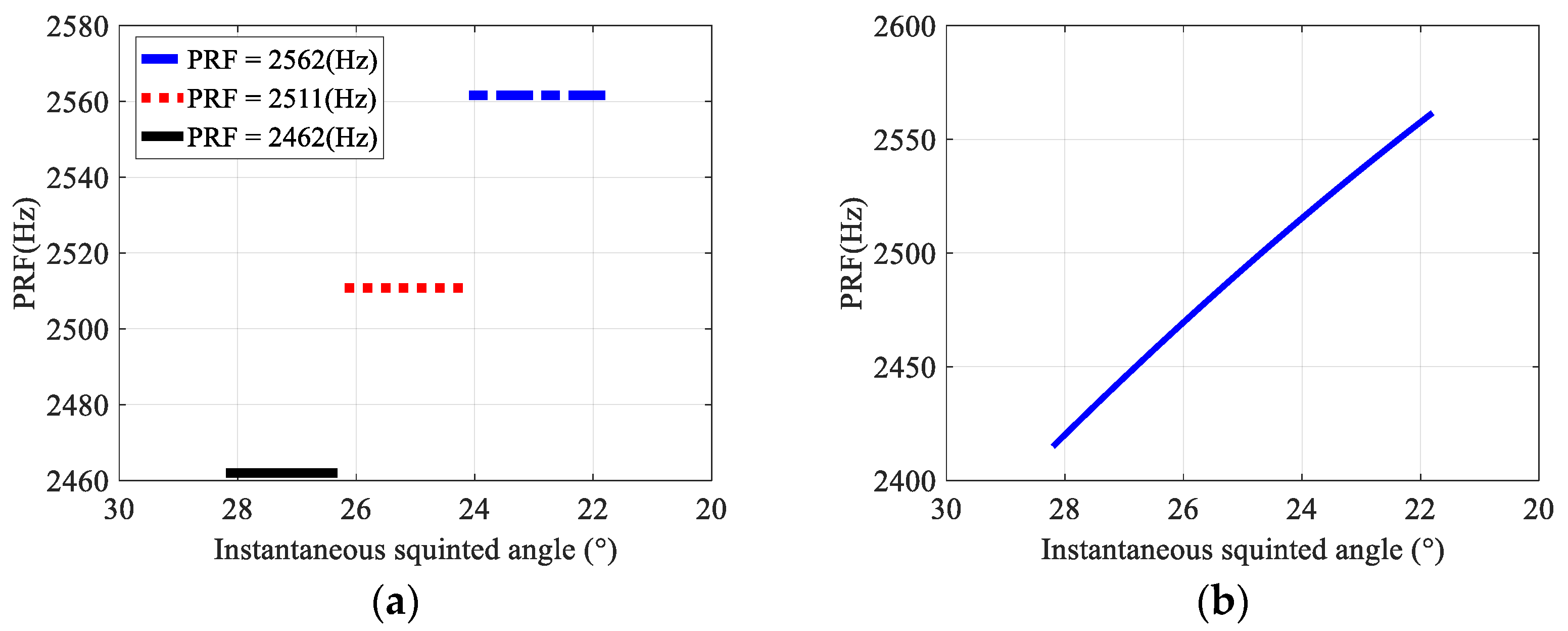
3.1. Design of the BV-PRF Scheme
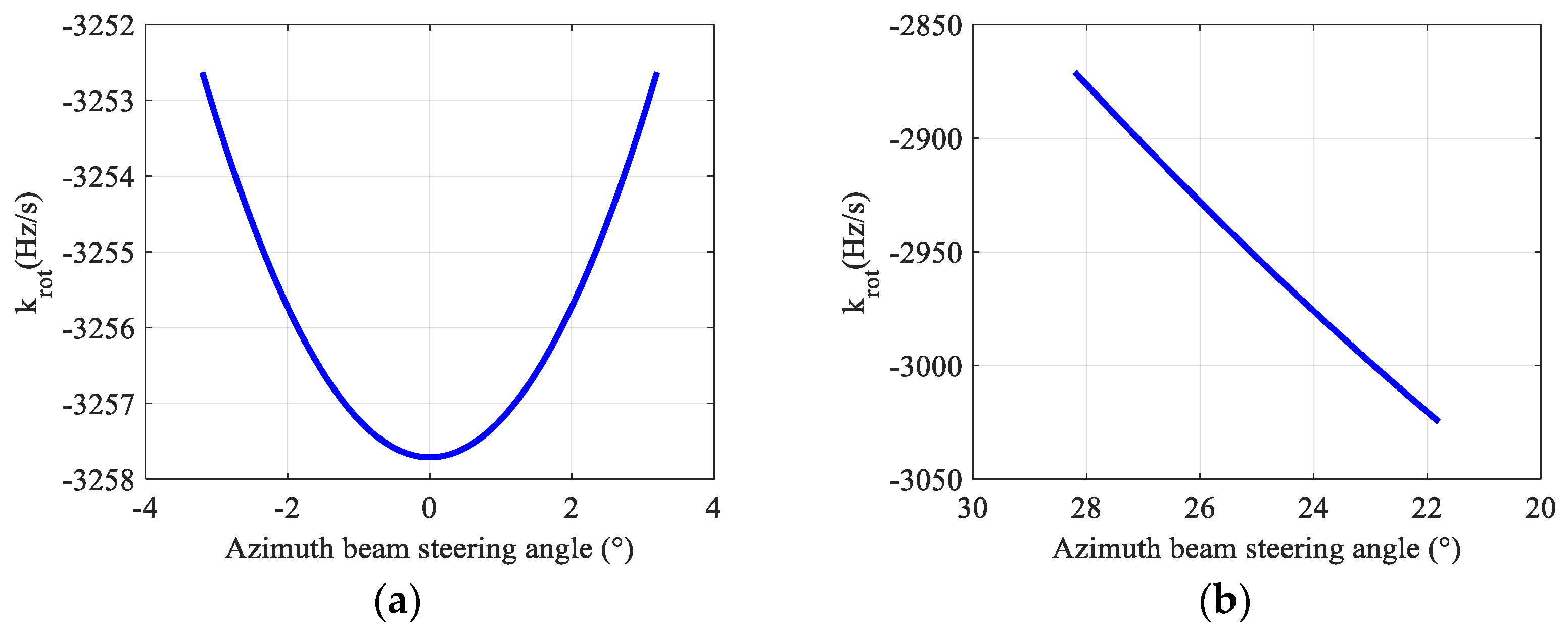
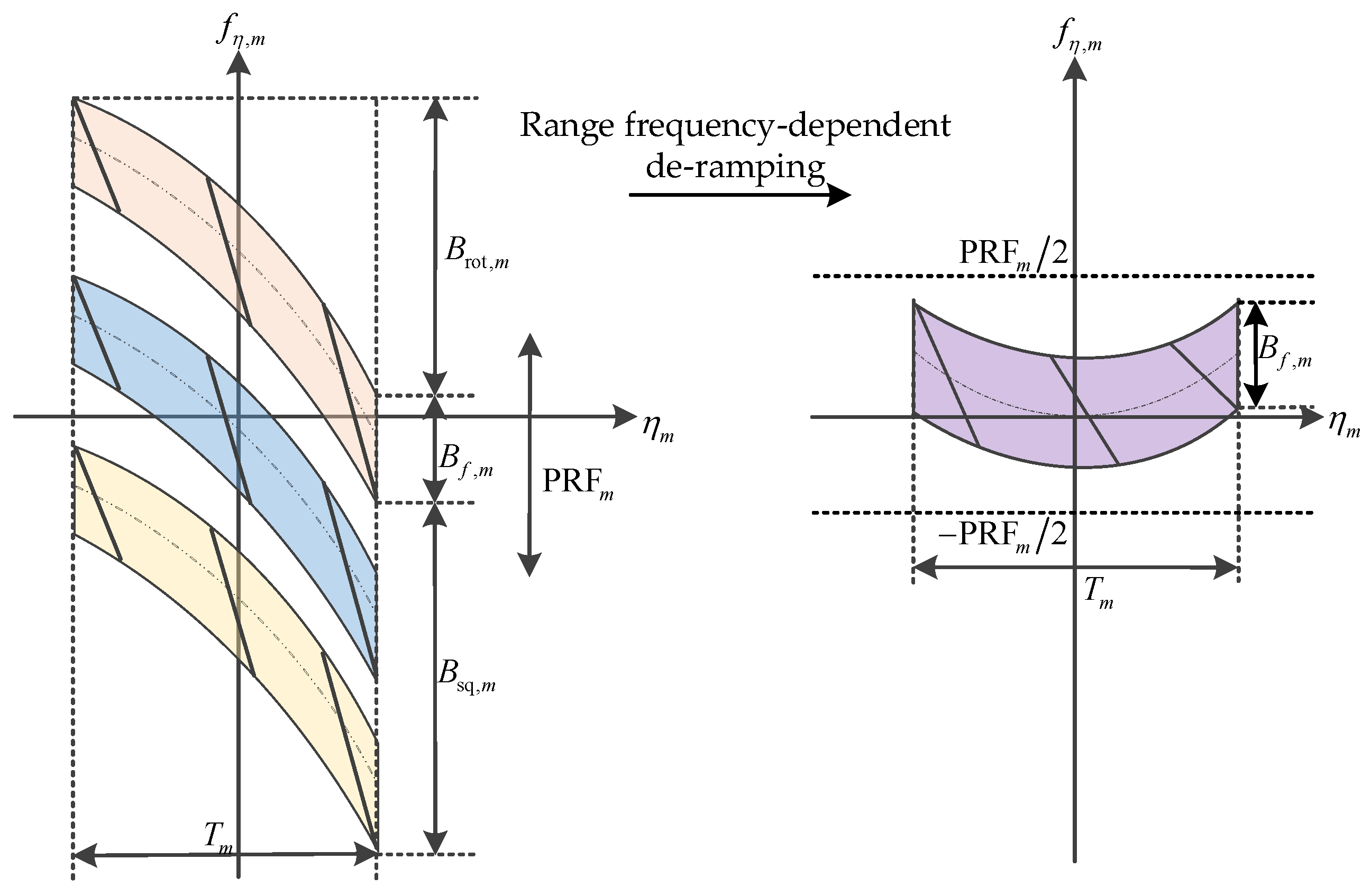
3.2. Properties of Echo Signal with BV-PRF
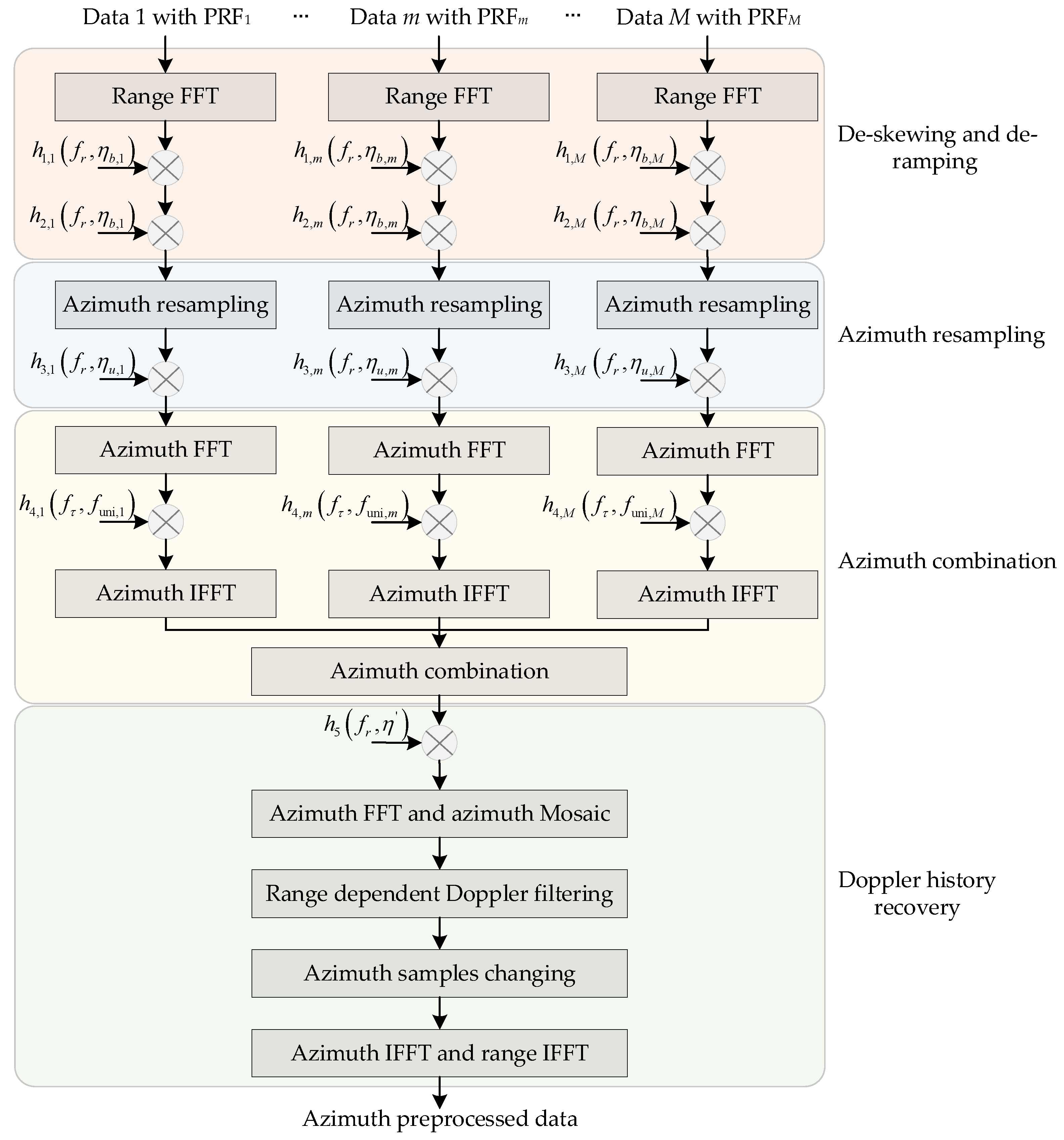
4. Azimuth Pre-Processing
4.1. Azimuth Pre-Processing in the 1-D Domain
4.2. Azimuth Pre-Processing in the 2-D Domain
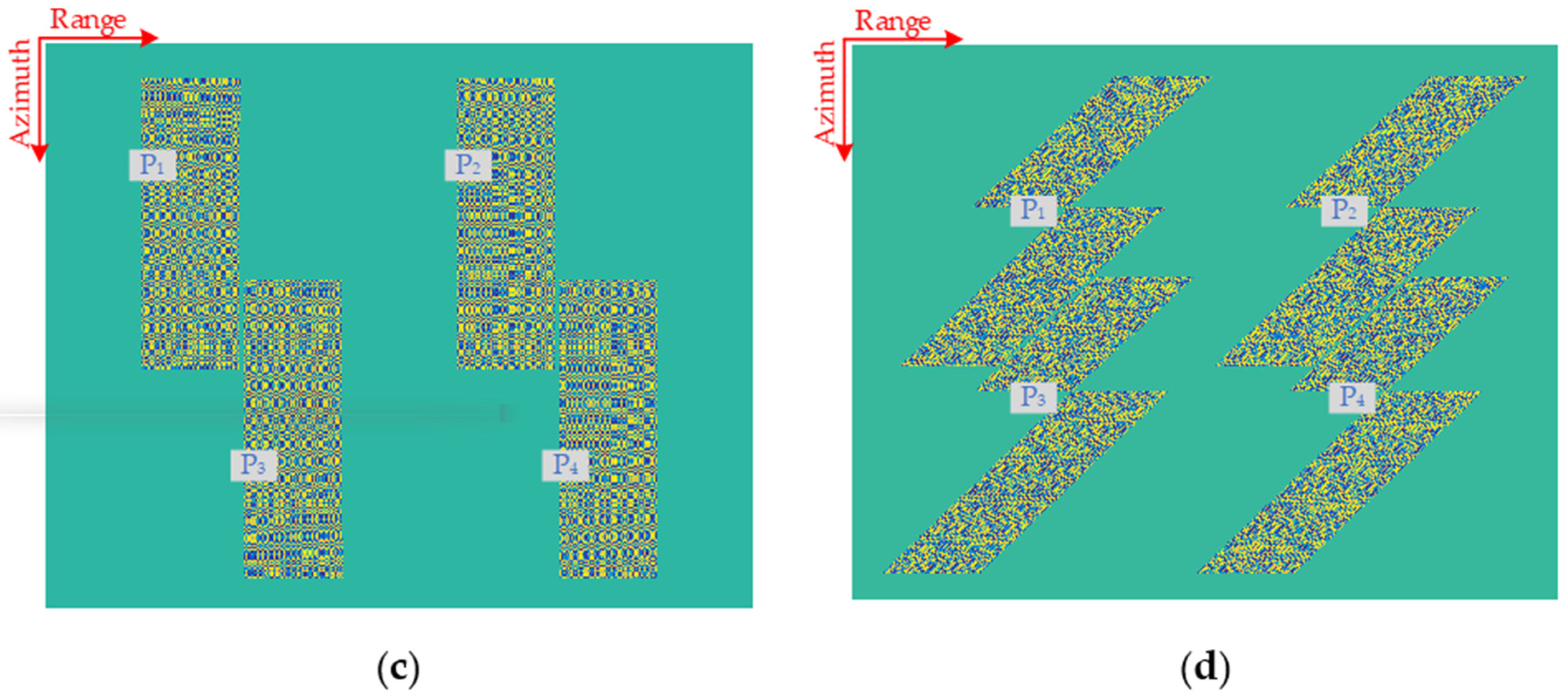
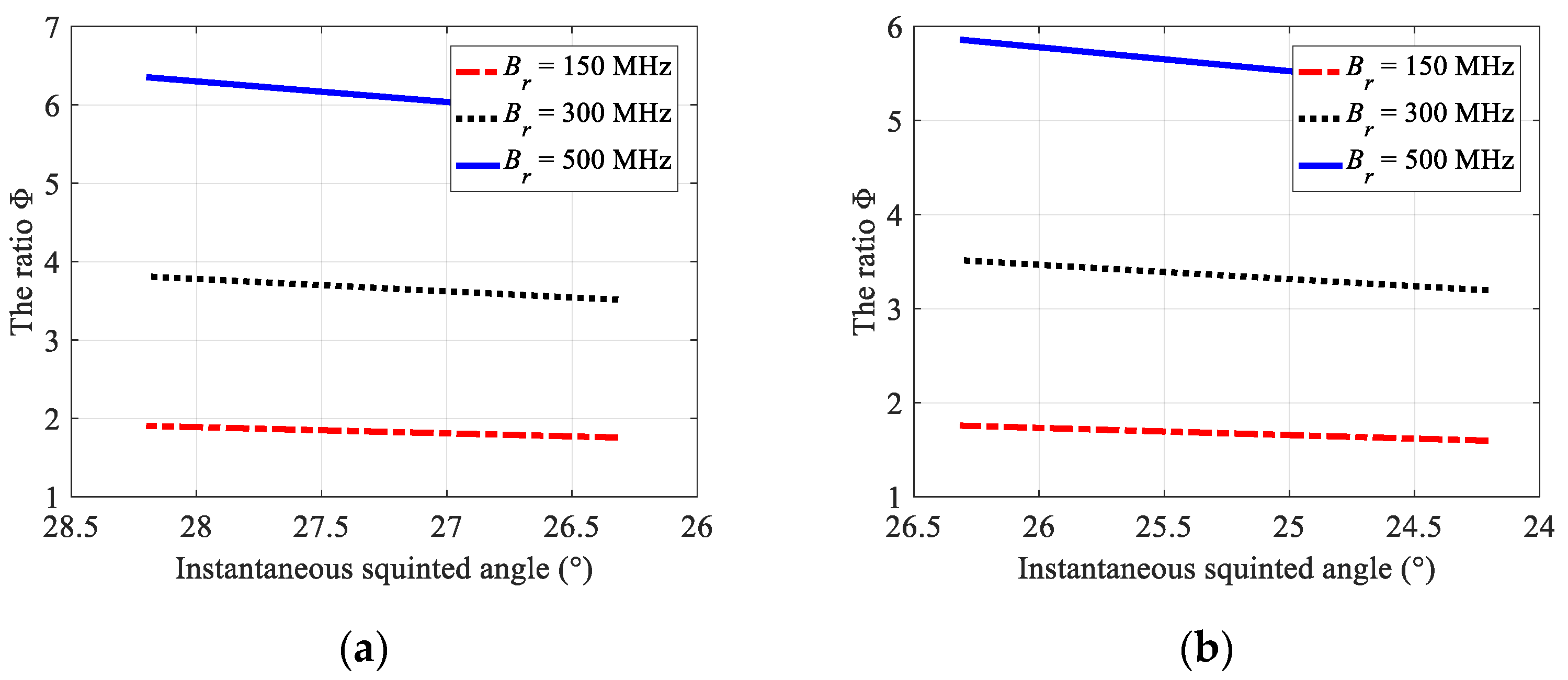
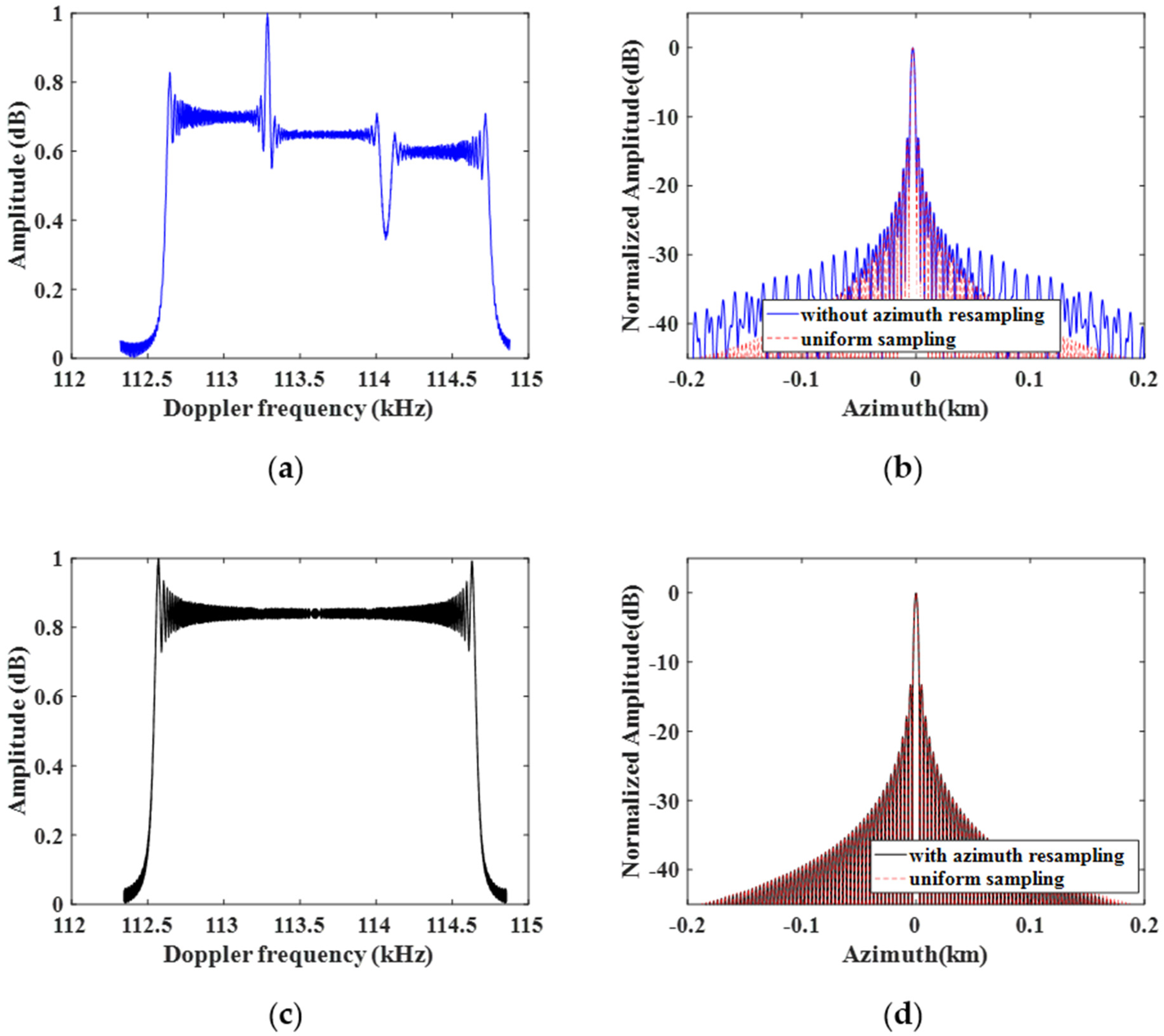
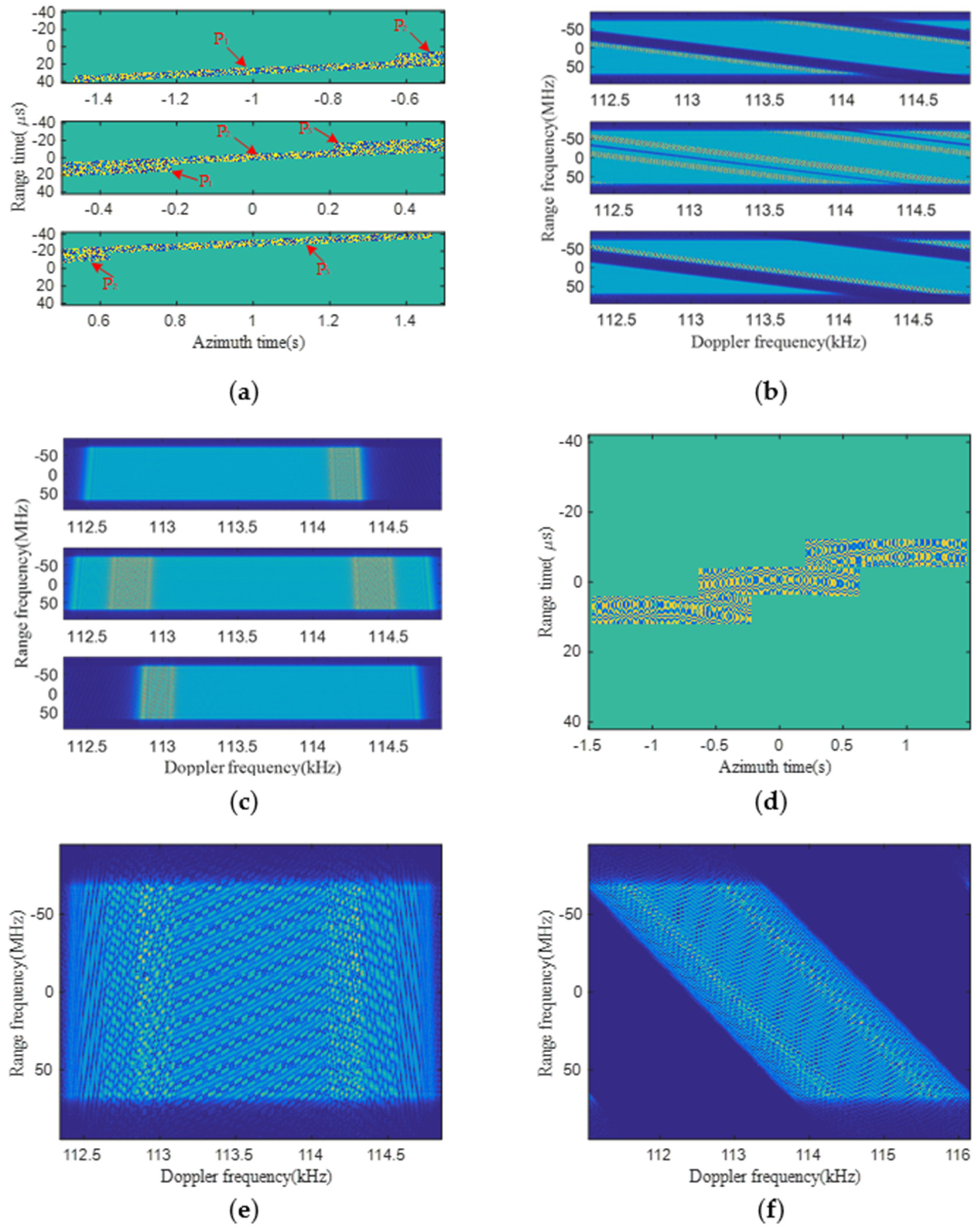
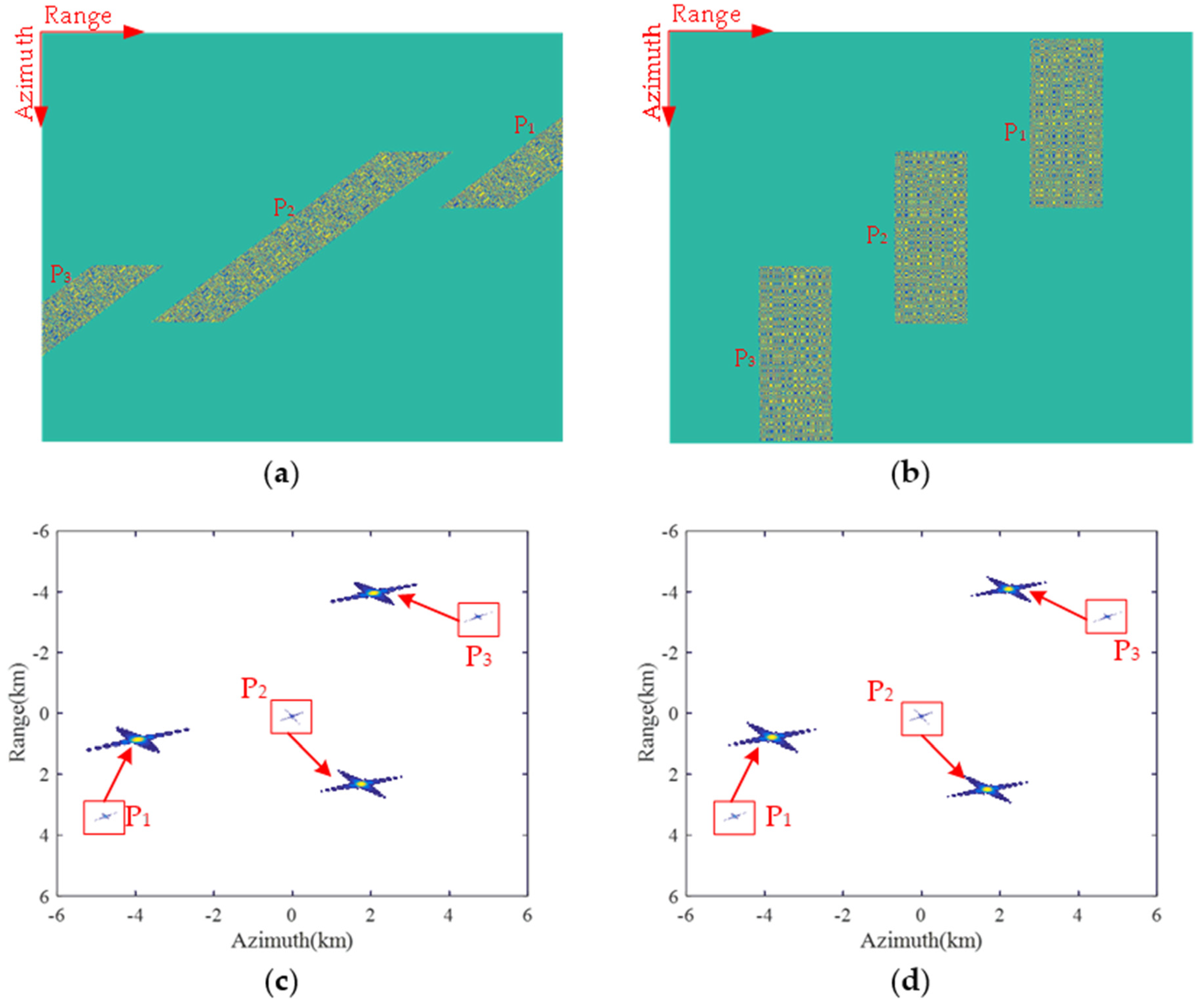
5. Simulation Experiments
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, S.; Nie, X.; Zhang, X. Research on Synthetic Aperture Radar Processing for the Spaceborne Sliding Spotlight Mode. Sensors 2018, 18, 455. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Zhang, X.; Jun, S.H.I.; Wei, S. HyperLi-Net: A hyper-light deep learning network for high-accurate and high-speed ship detection from synthetic aperture radar imagery. ISPRS J. Photogramm. Remote Sens. 2020, 167, 123–153. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. A polarization fusion network with geometric feature embedding for SAR ship classification. Pattern Recognit. 2022, 123, 108365. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Zhang, T. Lite-YOLOv5: A Lightweight Deep Learning Detector for On-Board Ship Detection in Large-Scene Sentinel-1 SAR Images. Remote Sens. 2022, 14, 1018. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Shao, Z.; Shi, J.; Wei, S.; Zhang, T.; Zeng, T. A Group-Wise Feature Enhancement-and-Fusion Network with Dual-Polarization Feature Enrichment for SAR Ship Detection. Remote Sens. 2022, 14, 5276. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. HTC+ for SAR Ship Instance Segmentation. Remote Sens. 2022, 14, 2395. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Shi, J.; Wei, S. Depthwise Separable Convolution Neural Network for High-Speed SAR Ship Detection. Remote Sens. 2019, 11, 2483. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Zhang, X.; Liu, C.; Shi, J.; Wei, S.; Ahmad, I.; Zhan, X.; Zhou, Y.; Pan, D.; Li, J.; et al. Balance learning for ship detection from synthetic aperture radar remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2021, 182, 190–207. [Google Scholar] [CrossRef]
- Hu, X.; Wang, P.; Zeng, H.; Guo, Y. An Improved Equivalent Squint Range Model and Imaging Approach for Sliding Spotlight SAR Based on Highly Elliptical Orbit. Remote Sens. 2021, 13, 4883. [Google Scholar] [CrossRef]
- Tian, F.; Suo, Z.; Wang, Y.; Lu, Z.; Wang, Z.; Li, Z. A Unified Algorithm for the Sliding Spotlight and TOPS Modes Data Processing in Bistatic Configuration of the Geostationary Transmitter with LEO Receivers. Remote Sens. 2022, 14, 2006. [Google Scholar] [CrossRef]
- Kuang, H.; Wang, Z.; Lu, Z.; Zhu, Y.; Liu, Y.; Xu, M. An Improved Imaging Algorithm for High Resolution Spaceborne Squinted Sliding Spotlight SAR. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar]
- Sun, G.C.; Wu, Y.; Yang, J.; Xing, M.; Bao, Z. Full-Aperture Focusing of Very High Resolution Spaceborne-Squinted Sliding Spotlight SAR Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3309–3321. [Google Scholar] [CrossRef]
- Li, N.; Niu, S.; Guo, Z.; Liu, Y.; Chen, J. Raw Data-Based Motion Compensation for High-Resolution Sliding Spotlight Synthetic Aperture Radar. Sensors 2018, 18, 842. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Hu, J.; Huang, P.; Tan, W.; Dong, Y. Processing of Multichannel Sliding Spotlight SAR Data with Large Pulse Bandwidth and Azimuth Steering Angle. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5202414. [Google Scholar] [CrossRef]
- Hu, L.; Wang, G.; Hou, L. Spatial-Variant SAR Range Cell Migration Correction Using Subaperture Strategy. Sensors 2021, 21, 2444. [Google Scholar] [CrossRef]
- Xu, W.; Li, R.; Fang, C.; Huang, P.; Tan, W.; Qi, Y. Azimuth Multichannel Reconstruction Based on Advanced Hyperbolic Range Equation. Remote Sens. 2021, 13, 4705. [Google Scholar] [CrossRef]
- Zeng, H.-C.; Chen, J.; Liu, W.; Yang, W. Modified Omega-k Algorithm for High-Speed Platform Highly-Squint Staggered SAR Based on Azimuth Non-Uniform Interpolation. Sensors 2015, 15, 3750–3765. [Google Scholar] [CrossRef] [Green Version]
- Xia, Z.; Jin, S.; Yue, F.; Yang, J.; Zhang, Q.; Zhao, Z.; Zhang, C.; Gao, W.; Zhang, T.; Zhang, Y.; et al. A Novel Space-Borne High-Resolution SAR System with the Non-Uniform Hybrid Sampling Technology for Space Targets Imaging. Appl. Sci. 2022, 12, 4848. [Google Scholar] [CrossRef]
- Yang, W.; Zeng, H.-C.; Chen, J.; Wang, P.-B. Errata: Fast image-formation algorithm for ultrahigh-resolution airborne squint spotlight synthetic aperture radar based on adaptive sliding receive-window technique. J. Appl. Remote Sens. 2014, 8, 089998. [Google Scholar] [CrossRef] [Green Version]
- Villano, M.; Krieger, G.; Moreira, A. Staggered SAR: High-Resolution Wide-Swath Imaging by Continuous PRI Variation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4462–4479. [Google Scholar] [CrossRef]
- Xu, H.; Gao, J.; Li, J. A variable PRF imaging method for high squint diving SAR. Prog. Electromagn. Res. 2013, 135, 215–229. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, P.; Xu, W.; Tan, W.; Wu, Z.; Li, Y. Block Varying PRI Design for High Squint Sliding-spotlight Synthetic Aperture Radar. In Proceedings of the 2019 Photonics & Electromagnetics Research Symposium—Fall (PIERS—Fall), Xiamen, China, 17–20 December 2019; pp. 1316–1321. [Google Scholar]
- Luo, X.; Xu, W.; Deng, Y.-K.; Guo, L. Modification of Multichannel Reconstruction Algorithm on the SAR With Linear Variation of PRI. Sel. Top. Appl. Earth Obs. Remote Sens. IEEE J. 2014, 7, 3050–3059. [Google Scholar] [CrossRef]
- Men, Z.; Wang, P.; Li, C.; Chen, J.; Liu, W.; Fang, Y. High-Temporal-Resolution High-Spatial-Resolution Spaceborne SAR Based on Continuously Varying PRF. Sensors 2017, 17, 1700. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Liang, B.; Chen, J.; Xiong, Y.; Xiong, M. Real-Time Imaging Processing of Squint Spaceborne SAR with High-Resolution Based on Nonuniform PRI Design. Remote Sens. 2022, 14, 3725. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, W.; Huang, P.; Tan, W.; Qi, Y. Azimuth Preprocessing of Squinted Sliding Spotlight Synthetic Aperture Radar Data with Block Varying PRF. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 2206–2212. [Google Scholar]
- Tat Soon, Y.; Ngee Leng, T.; Cheng Bo, Z.; Yi Hui, L. A new subaperture approach to high squint SAR processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 954–968. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Chang, Y.-K.; Lee, S.-H. Optimal Attitude Maneuvering Analyses for Imaging at Squint Staring and Sliding Spotlight Modes of SAR Satellite. Aerospace 2021, 8, 277. [Google Scholar] [CrossRef]
- Lv, Y.; Shang, M.; Zhong, L.; Qiu, X.; Ding, C. A Novel Imaging Scheme of Squint Multichannel SAR: First Result of GF-3 Satellite. Remote Sens. 2022, 14, 3962. [Google Scholar] [CrossRef]
- Dutt, A.; Rokhlin, V. Fast Fourier Transforms for Nonequispaced Data. SIAM J. Sci. Comput. 1993, 14, 1368–1393. [Google Scholar] [CrossRef] [Green Version]
- Sengijpta, S. Fundamentals of Statistical Signal Processing: Estimation Theory. Technometrics 1995, 37, 465–466. [Google Scholar] [CrossRef]
- Chen, S.; Qiu, X.; Shang, M.; Han, B. An Improved Imaging Algorithm for High-Resolution Spotlight SAR with Continuous PRI Variation Based on Modified Sinc Interpolation. Sensors 2019, 19, 389. [Google Scholar] [CrossRef] [Green Version]
- Yih-Chyun, J. Perfect reconstruction of digital spectrum from nonuniformly sampled signals. IEEE Trans. Instrum. Meas. 1997, 46, 649–652. [Google Scholar] [CrossRef]
- Xu, W.; Deng, Y.; Huang, P.; Wang, R. Full-Aperture SAR Data Focusing in the Spaceborne Squinted Sliding-Spotlight Mode. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4596–4607. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Relative platform velocity | 7212 m/s |
| Slant range of the scene center | 750 km |
| Carrier frequency | 5.6 GHz |
| Azimuth antenna length | 6.3 m |
| Number of PRFs | 3 |
| Azimuth beam rotation rate | 2.78°/s |
| Middle squint angle | 25° |
| System PRF | 2462/2511/2562 Hz |
| Pulse bandwidth | 150 MHz |
| Range sampling frequency | 200 MHz |
| Pulse duration | 8 μs |
| Target | Azimuth | Range | ||||
|---|---|---|---|---|---|---|
| Res. (m) | PSLR (dB) | ISLR (dB) | Res. (m) | PSLR (dB) | ISLR (dB) | |
| P1 | 2.87 | −13.27 | −10.19 | 0.94 | −13.25 | −10.10 |
| P2 | 2.86 | −13.25 | −10.18 | 0.94 | −13.25 | −10.11 |
| P3 | 2.76 | −13.26 | −10.18 | 0.94 | −13.28 | −10.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xu, W.; Huang, P.; Tan, W.; Gao, Z.; Qi, Y. Azimuth Full-Aperture Processing of Spaceborne Squint SAR Data with Block Varying PRF. Sensors 2022, 22, 9328. https://doi.org/10.3390/s22239328
Zhang Z, Xu W, Huang P, Tan W, Gao Z, Qi Y. Azimuth Full-Aperture Processing of Spaceborne Squint SAR Data with Block Varying PRF. Sensors. 2022; 22(23):9328. https://doi.org/10.3390/s22239328
Chicago/Turabian StyleZhang, Zhuo, Wei Xu, Pingping Huang, Weixian Tan, Zhiqi Gao, and Yaolong Qi. 2022. "Azimuth Full-Aperture Processing of Spaceborne Squint SAR Data with Block Varying PRF" Sensors 22, no. 23: 9328. https://doi.org/10.3390/s22239328






