LASSO Homotopy-Based Sparse Representation Classification for fNIRS-BCI
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
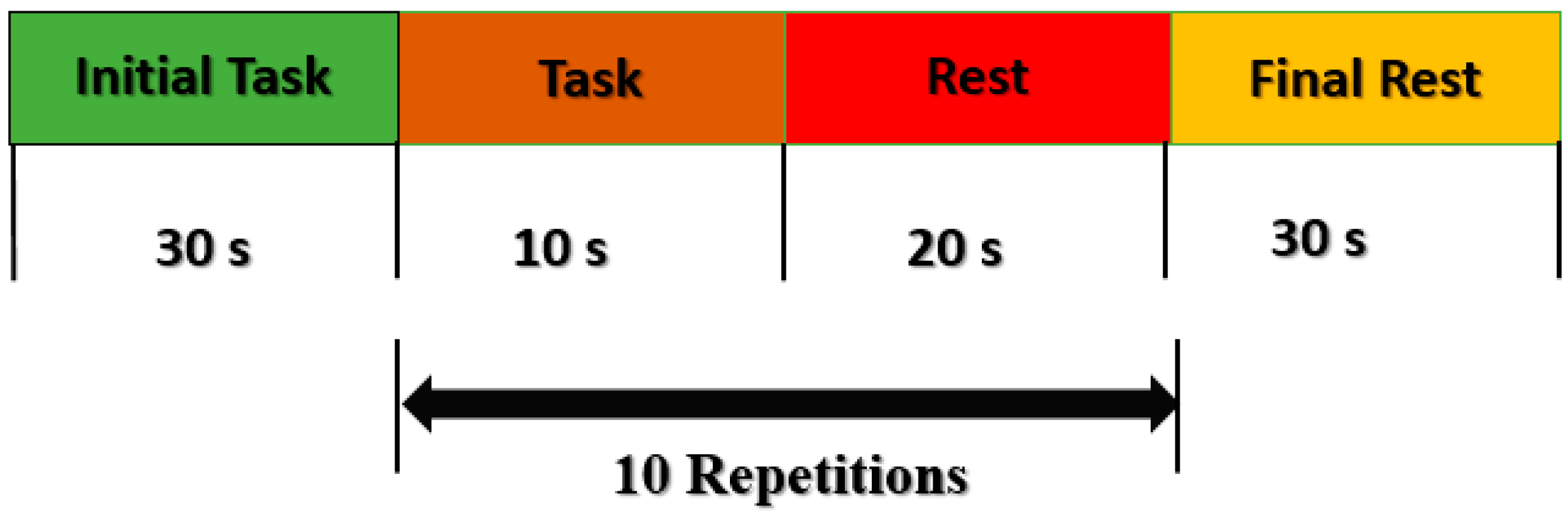
2.2. Experimental Paradigm
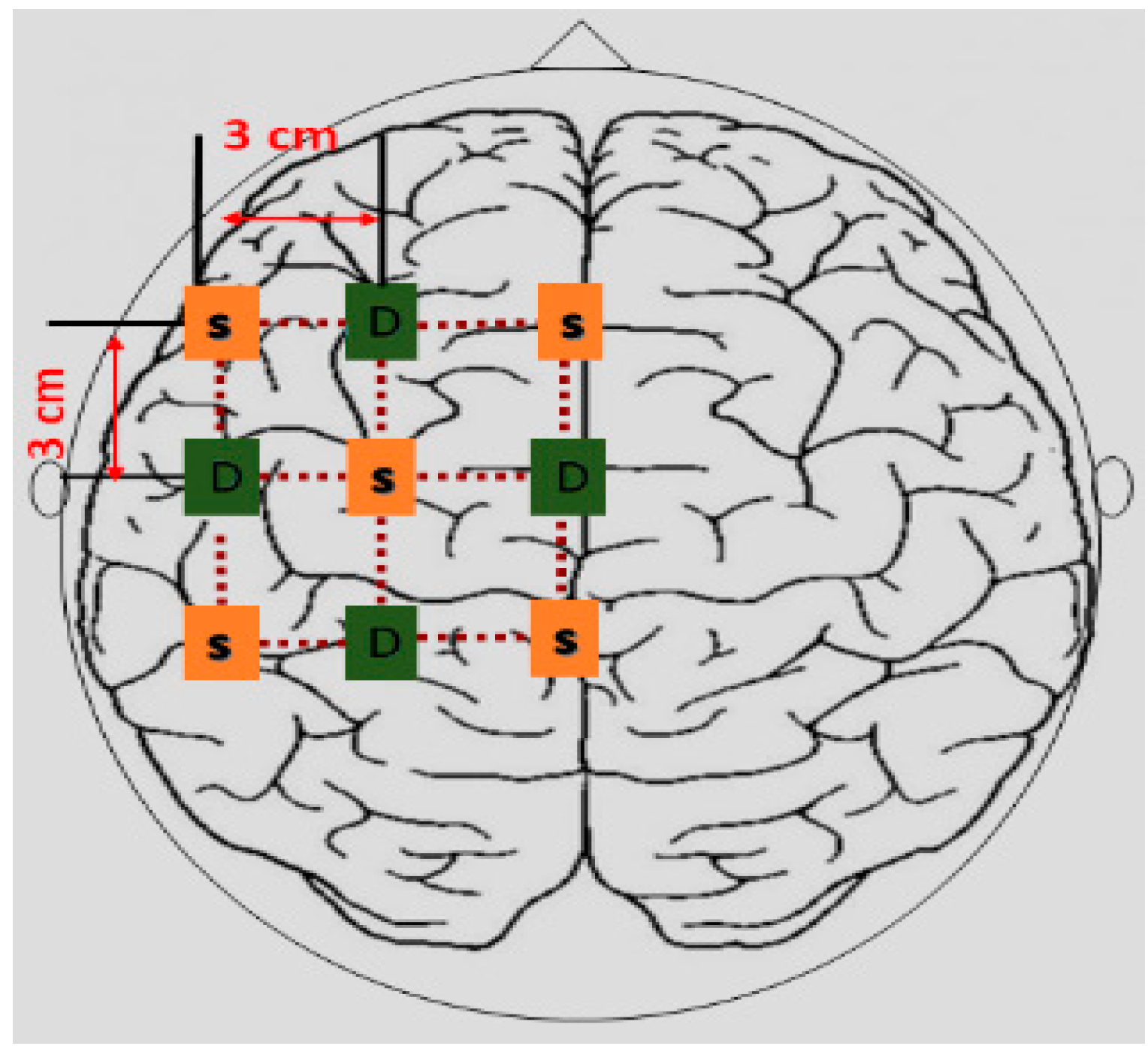
2.3. Experimental Configuration
2.4. Data Acquisition
2.5. Signal Processing
2.6. Feature Extraction
2.7. Channel Selection
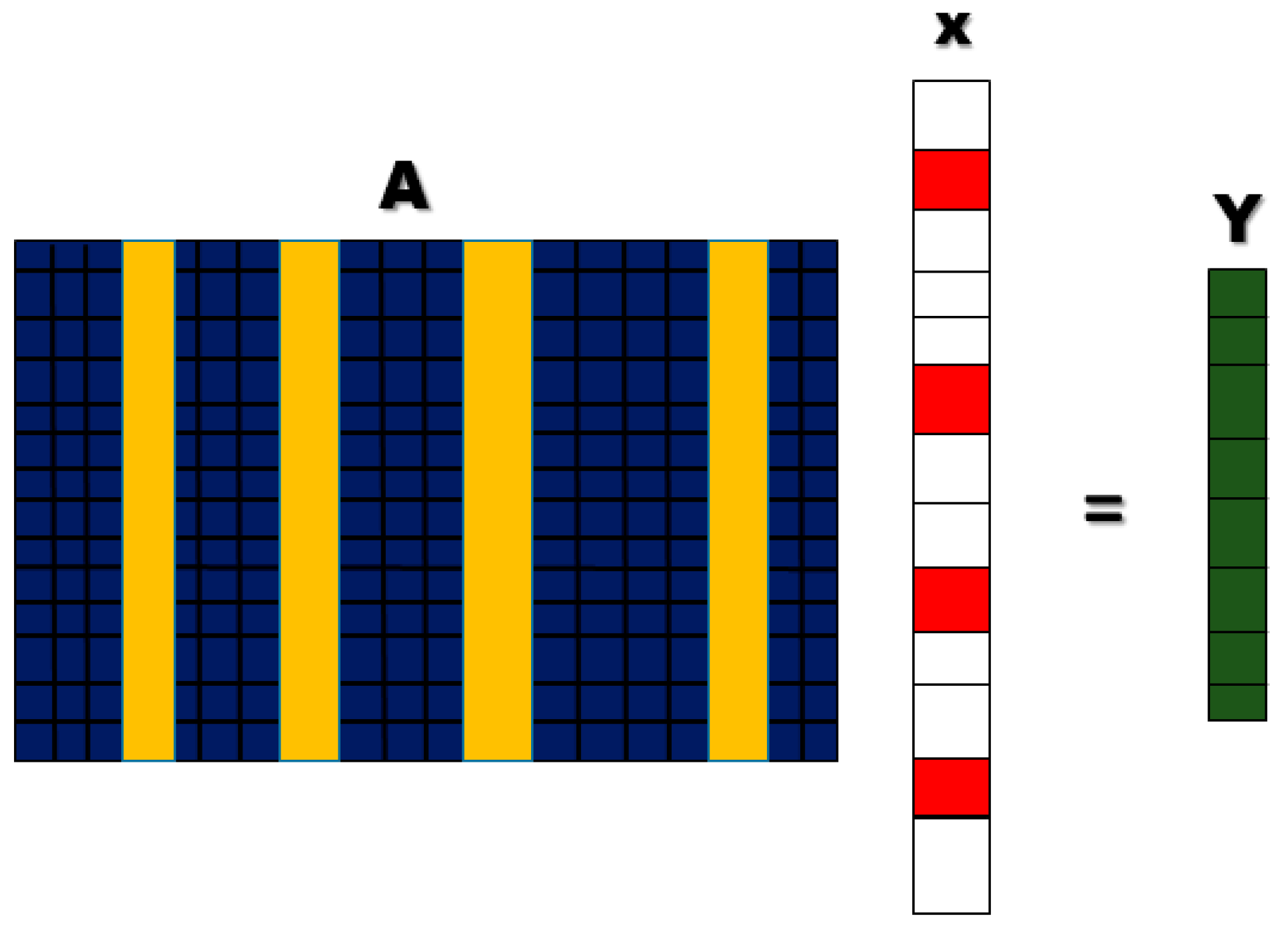
2.7.1. Sparse Representation Classification
2.7.2. LASSO Homotopy
2.8. Classification Algorithms
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Naseer, N.; Hong, K.-S. fNIRS-based brain-computer interfaces: A review. Front. Hum. Neurosci. 2015, 9, 3. [Google Scholar] [CrossRef] [Green Version]
- Hussain, G.; Rasul, A.; Anwar, H.; Sohail, M.U.; Kamran, S.K.S.; Baig, S.M.; Shabbir, A.; Iqbal, J. Epidemiological Data of Neurological Disorders in Pakistan and Neighboring Countries: A Review. Pak. J. Neurol. Sci. 2017, 12, 52–70. [Google Scholar]
- Li, H.; Gong, A.; Zhao, L.; Zhang, W.; Wang, F.; Fu, Y. Decoding of Walking Imagery and Idle State Using Sparse Representation Based on fNIRS. Intell. Neurosci. 2021, 2021, 6614112. [Google Scholar] [CrossRef]
- Shih, J.J.; Krusienski, D.J.; Wolpaw, J. Brain-Computer Interfaces in Medicine. Mayo Clin. Proc. 2012, 87, 268–279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinti, P.; Aichelburg, C.; Gilbert, S.; Hamilton, A.; Hirsch, J.; Burgess, P.; Tachtsidis, I. A Review on the Use of Wearable Functional Near-Infrared Spectroscopy in Naturalistic Environments. Jpn. Psychol. Res. 2018, 60, 347–373. [Google Scholar] [CrossRef] [Green Version]
- Ghaffar, M.S.B.A.; Khan, U.S.; Iqbal, J.; Rashid, N.; Hamza, A.; Qureshi, W.S.; Tiwana, M.I.; Izhar, U. Improving classification performance of four class FNIRS-BCI using Mel Frequency Cepstral Coefficients (MFCC). Infrared Phys. Technol. 2020, 112, 103589. [Google Scholar] [CrossRef]
- Hong, K.-S.; Yaqub, M.A. Application of functional near-infrared spectroscopy in the healthcare industry: A review. J. Innov. Opt. Health Sci. 2019, 12, 91. [Google Scholar] [CrossRef]
- James, L.M.; Enghdal, B.E.; Leuthold, A.C.; Georgopoulos, A.P. Classification of Trauma-Related Outcomes in US Veterans Using Magnetoencephalography (MEG). J. Neurol. Neuromed. 2021, 6, 13–20. [Google Scholar] [CrossRef]
- Thorpe, D.R.; Engdahl, B.E.; Leuthold, A.; Georgopoulos, A.P. Assessing Recovery from Mild Traumatic Brain Injury (Mtbi) using Magnetoencephalography (MEG): An Application of the Synchronous Neural Interactions (SNI) Test. J. Neurol. Neuromed. 2020, 5, 28–34. [Google Scholar] [CrossRef]
- Bokhari, S.; Schneider, R.H.; Salerno, J.W.; Rainforth, M.V.; Gaylord-King, C.; Nidich, S.I. Effects of cardiac rehabilitation with and without meditation on myocardial blood flow using quantitative positron emission tomography: A pilot study. J. Nucl. Cardiol. 2019, 28, 1596–1607. [Google Scholar] [CrossRef]
- Nelles, G.; Jentzen, W.; Jueptner, M.; Müller, S.; Diener, H.C. Arm Training Induced Brain Plasticity in Stroke Studied with Serial Positron Emission Tomography. NeuroImage 2001, 13, 1146–1154. [Google Scholar] [CrossRef] [PubMed]
- Nishida, D.; Mizuno, K.; Yamada, E.; Hanakawa, T.; Liu, M.; Tsuji, T. The neural correlates of gait improvement by rhythmic sound stimulation in adults with Parkinson’s disease–A functional magnetic resonance imaging study. Parkinsonism Relat. Disord. 2021, 84, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Boyne, P.; Doren, S.; Scholl, V.; Staggs, E.; Whitesel, D.; Maloney, T.; Awosika, O.; Kissela, B.; Dunning, K.; Vannest, J. Functional magnetic resonance brain imaging of imagined walking to study locomotor function after stroke. Clin. Neurophysiol. 2020, 132, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Zaidi, H. Single-Photon Emission Computed Tomography: Principles and Applications. In Encyclopedia of Biomedical Engineering; Narayan, R., Ed.; Elsevier: Oxford, UK, 2019; pp. 493–506. [Google Scholar] [CrossRef]
- Dorraji, E.S.; Oteiza, A.; Kuttner, S.; Martin-Armas, M.; Kanapathippillai, P.; Garbarino, S.; Kalda, G.; Scussolini, M.; Piana, M.; Fenton, K.A. Positron emission tomography and single photon emission computed tomography imaging of tertiary lymphoid structures during the development of lupus nephritis. Int. J. Immunopathol. Pharmacol. 2021, 35, e005772. [Google Scholar] [CrossRef]
- Khan, H.; Nazeer, H.; Engell, H.; Naseer, N.; Korostynska, O.; Mirtaheri, P. Prefrontal Cortex Activation Measured during Different Footwear and Ground Conditions Using fNIRS—A Case Study. In Proceedings of the 2021 International Conference on Artificial Intelligence and Mechatronics Systems (AIMS), Delft, The Netherlands, 12–16 July 2021. [Google Scholar]
- Khan, H.; Naseer, N.; Yazidi, A.; Eide, P.K.; Hassan, H.W.; Mirtaheri, P. Analysis of Human Gait Using Hybrid EEG-fNIRS-Based BCI System: A Review. Front. Hum. Neurosci. 2021, 14, 613254. [Google Scholar] [CrossRef]
- Hamid, H.; Naseer, N.; Nazeer, H.; Khan, M.J.; Khan, R.A.; Khan, U.S. Analyzing Classification Performance of fNIRS-BCI for Gait Rehabilitation Using Deep Neural Networks. Sensors 2022, 22, 1932. [Google Scholar] [CrossRef]
- Khan, R.A.; Naseer, N.; Qureshi, N.K.; Noori, F.M.; Nazeer, H.; Khan, M.U. fNIRS-based Neurorobotic Interface for gait rehabilitation. J. Neuroeng. Rehabil. 2018, 15, 7. [Google Scholar] [CrossRef]
- Abdalmalak, A.; Milej, D.; Yip, L.; Khan, A.R.; Diop, M.; Owen, A.M.; Lawrence, K.S. Assessing Time-Resolved fNIRS for Brain-Computer Interface Applications of Mental Communication. Front. Neurosci. 2020, 14, 105. [Google Scholar] [CrossRef] [Green Version]
- Nazeer, H.; Naseer, N.; Mehboob, A.; Khan, M.J.; Khan, R.A.; Khan, U.S.; Ayaz, Y. Enhancing classification performance of fNIRS-BCI by identifying cortically active channels using the z-score method. Sensors 2020, 20, 6995. [Google Scholar] [CrossRef]
- Naseer, N.; Qureshi, N.K.; Noori, F.M.; Hong, K.-S. Analysis of different classification techniques for two-class functional near-infrared spectroscopy-based brain-computer interface. Comput. Intell. Neurosci. 2016, 2016, 5480760. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Yin, H.; Chai, Y.; Li, Y.; Qi, G. A novel multi-modality image fusion method based on image decomposition and sparse representation. Inf. Sci. 2018, 432, 516–529. [Google Scholar] [CrossRef]
- Sreeja, S.; Samanta, D. Distance-based weighted sparse representation to classify motor imagery EEG signals for BCI applications. Multimed. Tools Appl. 2020, 79, 13775–13793. [Google Scholar] [CrossRef]
- Miao, M.; Zhao, F.; Liu, F.; Zeng, H.; Wang, A. Index finger motor imagery EEG pattern recognition in BCI applications using dictionary cleaned sparse representation-based classification for healthy people. Rev. Sci. Instrum. 2017, 88, 094305. [Google Scholar] [CrossRef] [PubMed]
- Miao, M.; Wang, A.; Liu, F. A spatial-frequency-temporal optimized feature sparse representation-based classification method for motor imagery EEG pattern recognition. Med. Biol. Eng. Comput. 2017, 55, 1589–1603. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Lee, S.; Ahn, M.; Cho, H.; Jun, S.C.; Lee, H.-N. Noise robustness analysis of sparse representation based classification method for non-stationary EEG signal classification. Biomed. Signal Process. Control 2015, 21, 8–18. [Google Scholar] [CrossRef]
- Gratton, G.; Brumback, C.R.; Gordon, B.; Pearson, M.A.; Low, K.A.; Fabiani, M. Effects of measurement method, wavelength, and source-detector distance on the fast optical signal. NeuroImage 2006, 32, 1576–1590. [Google Scholar] [CrossRef] [PubMed]
- Delpy, D.T.; Cope, M.; van der Zee, P.; Arridge, S.; Wray, S.; Wyatt, J. Estimation of optical pathlength through tissue from direct time of flight measurement. Phys. Med. Biol. 1988, 33, 1433–1442. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.C.; Tak, S.; Jang, K.E.; Jung, J.; Jang, J. NIRS-SPM: Statistical parametric mapping for near-infrared spectroscopy. NeuroImage 2009, 44, 428–447. [Google Scholar] [CrossRef]
- Noori, F.M.; Naseer, N.; Qureshi, N.K.; Nazeer, H.; Khan, R. Optimal feature selection from fNIRS signals using genetic algorithms for BCI. Neurosci. Lett. 2017, 647, 61–66. [Google Scholar] [CrossRef]
- Santosa, H.; Hong, M.J.; Hong, K.-S. Lateralization of music processing with noises in the auditory cortex: An fNIRS study. Front. Behav. Neurosci. 2014, 8, 418. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.F.; Huang, X.; Ou, K.L.; Lopez-Aparicio, J. Cross Correlation Analysis of Multi-Channel Near Infrared Spectroscopy. Comput. Sci. Inf. Technol. 2016, 6, 23–33. [Google Scholar] [CrossRef]
- Zhang, H.; Patel, V.M. Sparse representation-based open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1690–1696. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Ngom, A. Sparse representation approaches for the classification of high-dimensional biological data. BMC Syst. Biol. 2013, 7, S6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Xuelong, L.; Yang, J.; Li, X.; Zhang, D. A Survey of Sparse Representation: Algorithms and Applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Cleophas, T.J.; Zwinderman, A.H. Statistical Analysis of Clinical Data on a Pocket Calculator; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Qureshi, N.K.; Naseer, N.; Noori, F.M.; Nazeer, H.; Khan, R.; Saleem, S. Enhancing Classification Performance of Functional Near-Infrared Spectroscopy- Brain–Computer Interface Using Adaptive Estimation of General Linear Model Coefficients. Front. Neurorobotics 2017, 11, 33. [Google Scholar] [CrossRef] [PubMed]
- Zafar, A.; Hong, K.-S. Neuronal Activation Detection Using Vector Phase Analysis with Dual Threshold Circles: A Functional Near-Infrared Spectroscopy Study. Int. J. Neural Syst. 2018, 28, 1850031. [Google Scholar] [CrossRef]
- Zafar, A.; Ghafoor, U.; Yaqub, M.; Hong, K.-S. Initial-dip-based classification for fNIRS-BCI. In Neural Imaging and Sensing; SPIE: Bellingham, WA, USA, 2019. [Google Scholar]
- Nazeer, H.; Naseer, N.; Khan, R.A.; Noori, F.M.; Qureshi, N.K.; Khan, U.S.; Khan, M.J. Enhancing classification accuracy of fNIRS-BCI using features acquired from vector-based phase analysis. J. Neural Eng. 2020, 17, 056025. [Google Scholar] [CrossRef]
- Naseer, N.; Noori, F.M.; Qureshi, N.K.; Hong, K.-S. Determining Optimal Feature-Combination for LDA Classification of Functional Near-Infrared Spectroscopy Signals in Brain-Computer Interface Application. Front. Hum. Neurosci. 2016, 10, 237. [Google Scholar] [CrossRef] [Green Version]
- Hong, K.-S.; Santosa, H. Decoding four different sound-categories in the auditory cortex using functional near-infrared spectroscopy. Hear. Res. 2016, 333, 157–166. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Hong, K.-S. Bundled-optode implementation for 3D imaging in functional near-infrared spectroscopy. Biomed. Opt. Express 2016, 7, 3491–3507. [Google Scholar] [CrossRef] [Green Version]
- Petrantonakis, P.C.; Kompatsiaris, I. Single-Trial NIRS Data Classification for Brain–Computer Interfaces Using Graph Signal Processing. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1700–1709. [Google Scholar] [CrossRef] [PubMed]
- Muthukrishnan, R.; Rohini, R. LASSO: A feature selection technique in predictive modeling for machine learning. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016. [Google Scholar]
- Varsehi, H.; Firoozabadi, S.M.P. An EEG channel selection method for motor imagery based brain–computer interface and neurofeedback using Granger causality. Neural Netw. 2020, 133, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Naseer, N.; Hong, K.-S.; Bhutta, M.R.; Khan, M.J. Improving classification accuracy of covert yes/no response decoding using support vector machines: An fNIRS study. In Proceedings of the 2014 International Conference on Robotics and Emerging Allied Technologies in Engineering (iCREATE), Islamabad, Pakistan, 22–24 April 2014. [Google Scholar]



| Subjects | Selected Channels |
|---|---|
| 1 | 1, 2, 3, 4, 7, 8, 9, 10, 11 |
| 2 | 2, 3, 4, 5, 6, 7, 9, 11 |
| 3 | 2, 6, 8, 9, 10, 11 |
| 4 | 8, 9, 12 |
| 5 | 1, 2, 5, 6, 7, 8, 12 |
| 6 | 1, 5, 8, 11, 12 |
| 7 | 2, 4, 5, 6, 8, 9, 11, 12 |
| 8 | 6, 10 |
| 9 | 1, 2, 3, 4, 6, 7, 8, 9 |
| Subjects | LDA | LR | SVM |
|---|---|---|---|
| 1 | 72.6% | 69.1% | 95.7% |
| 2 | 75.7% | 76.7% | 95.9% |
| 3 | 74.6% | 83% | 95.2% |
| 4 | 68% | 67.4% | 85.4% |
| 5 | 71.9% | 72.4% | 91.3% |
| 6 | 68% | 70.4% | 95.2% |
| 7 | 75.9% | 74.6% | 95.4% |
| 8 | 62.6% | 62.2% | 75.9% |
| 9 | 69.8% | 69.8% | 91.3% |
| Subjects | LDA | LR | SVM |
|---|---|---|---|
| 1 | 65.5% | 63.9% | 75.5% |
| 2 | 66.5% | 65.2% | 72.4% |
| 3 | 63.9% | 62.8% | 70.4% |
| 4 | 66.9% | 68.1% | 68.9% |
| 5 | 66.7% | 66.7% | 71.5% |
| 6 | 61.9% | 65.7% | 71.3% |
| 7 | 63.9% | 64.8% | 71.7% |
| 8 | 66.5% | 66.5% | 71.7% |
| 9 | 68.1% | 67.4% | 81.5% |
| Subjects | LDA | LR | SVM |
|---|---|---|---|
| 1 | 65.4% | 65.2% | 78.1% |
| 2 | 66.5% | 69.4% | 78.5% |
| 3 | 64.6% | 63% | 71.9% |
| 4 | 65% | 65.9% | 73% |
| 5 | 66.1% | 65.4% | 74.8% |
| 6 | 61.5% | 65.9% | 73.5% |
| 7 | 62.8% | 64.1% | 72.6% |
| 8 | 66.3% | 68% | 85.2% |
| 9 | 67.6% | 68% | 85.2% |
| LDA | LR | SVM | |
|---|---|---|---|
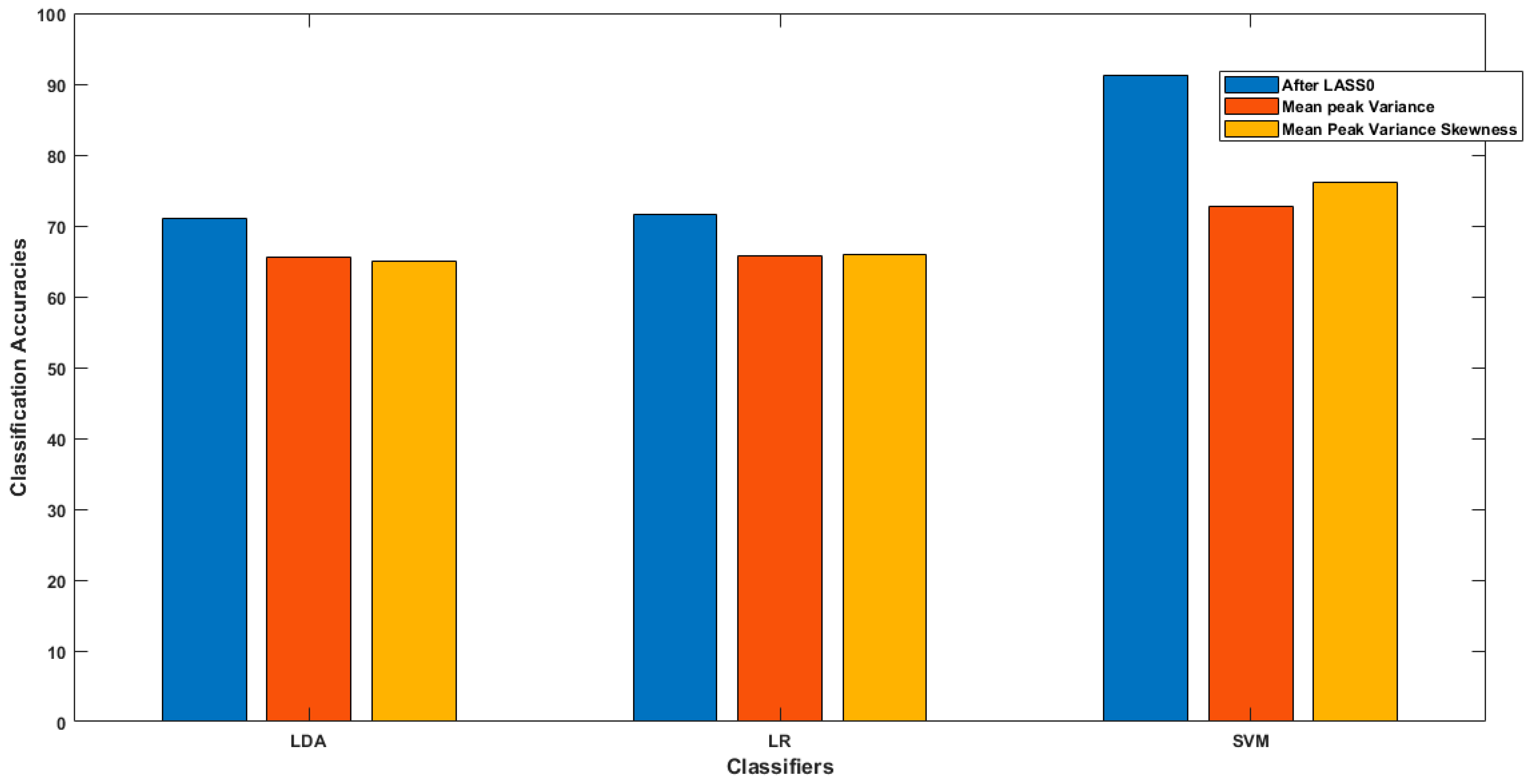
| After LASSO Homotopy | 71.01% | 71.6% | 91.32% |
| Mean, Peak and Variance | 65.54% | 65.67% | 72.7% |
| Mean, Peak, Variance and Skewness | 65.08% | 65.9% | 76.2% |
| Bonferroni Correction Applied (p < 0.0167) | |||
|---|---|---|---|
| SVM | vs. | LDA | 1.0886 × 10−6 |
| LR | 6.8421 × 10−6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulraiz, A.; Naseer, N.; Nazeer, H.; Khan, M.J.; Khan, R.A.; Shahbaz Khan, U. LASSO Homotopy-Based Sparse Representation Classification for fNIRS-BCI. Sensors 2022, 22, 2575. https://doi.org/10.3390/s22072575
Gulraiz A, Naseer N, Nazeer H, Khan MJ, Khan RA, Shahbaz Khan U. LASSO Homotopy-Based Sparse Representation Classification for fNIRS-BCI. Sensors. 2022; 22(7):2575. https://doi.org/10.3390/s22072575
Chicago/Turabian StyleGulraiz, Asma, Noman Naseer, Hammad Nazeer, Muhammad Jawad Khan, Rayyan Azam Khan, and Umar Shahbaz Khan. 2022. "LASSO Homotopy-Based Sparse Representation Classification for fNIRS-BCI" Sensors 22, no. 7: 2575. https://doi.org/10.3390/s22072575
APA StyleGulraiz, A., Naseer, N., Nazeer, H., Khan, M. J., Khan, R. A., & Shahbaz Khan, U. (2022). LASSO Homotopy-Based Sparse Representation Classification for fNIRS-BCI. Sensors, 22(7), 2575. https://doi.org/10.3390/s22072575










