Multi-UAV Content Caching Strategy and Cooperative, Complementary Content Transmission Based on Coalition Formation Game
Abstract
:1. Introduction
- Firstly, a user-clustering method is proposed based on user similarity, which is jointly scaled by distance similarity and content preference similarity among users. Then, a user-clustering-based content caching strategy is proposed to optimize the kinds of content stored in the caching space of each UAV by jointly considering user preference and content popularity.
- Secondly, we model the multi-UAV cooperative, complementary transmission problem as a coalition-formation game and propose a cooperation-order-based coalition-formation-game (CO-CFG) algorithm to maximize the whole network utility, which is defined by jointly considering user satisfaction, transmission energy consumption of UAVs and cooperative, complementary transmission reliability of UAVs.
2. Related Work
3. System Model
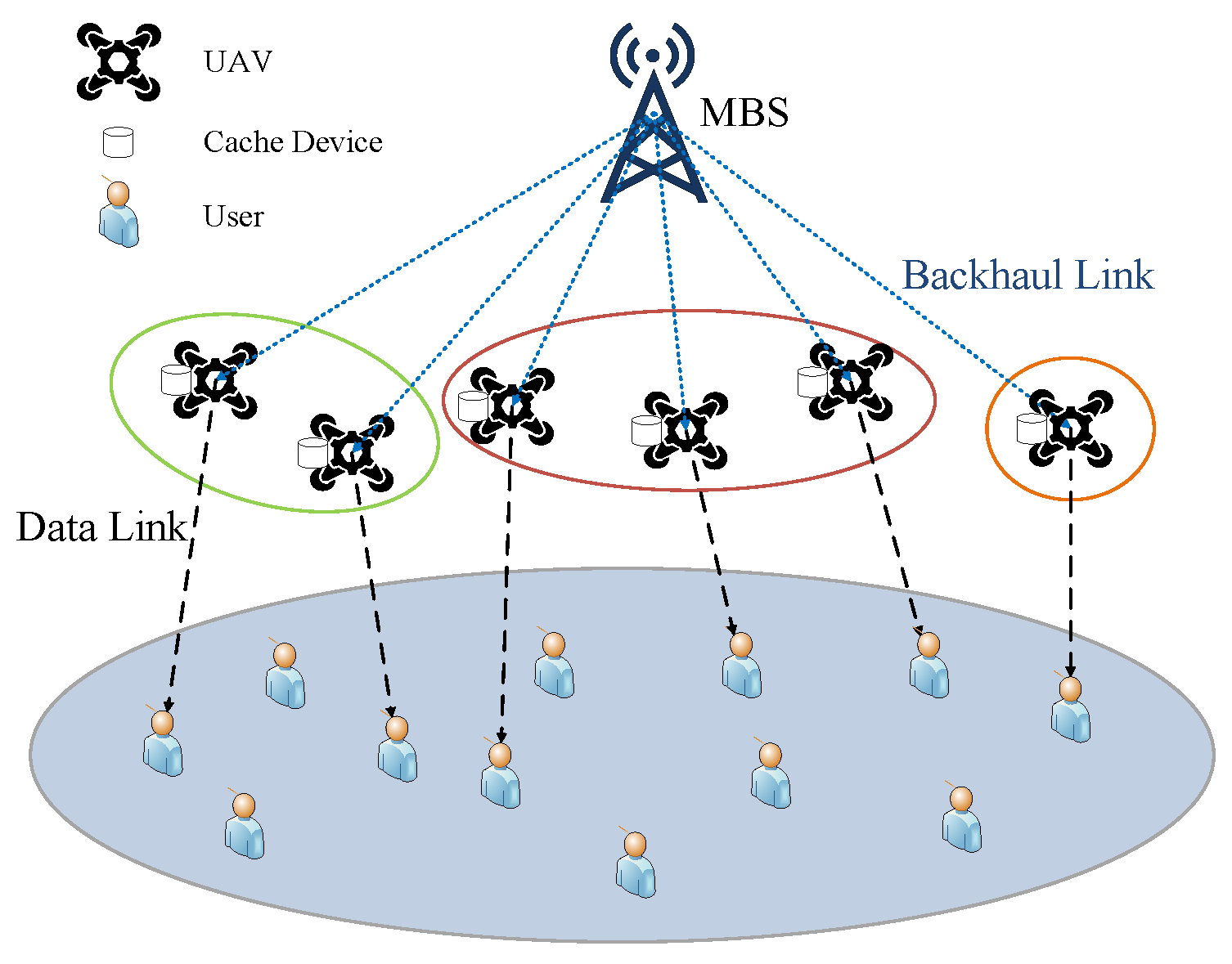
3.1. Network Scenario
3.2. Transmission Model
3.3. Content Model
4. User-Clustering-Based Caching Strategy
4.1. Similarity-Based User Clustering
| Algorithm 1 Similarity-Based User Clustering Algorithm |
|
4.2. User-Clustering-Based Caching Strategy for UAVs
5. Multi-UAV Cooperative, Complementary Transmission Based on Coalition Formation Game
5.1. System Utility
5.1.1. User Satisfaction
5.1.2. Transmission Energy Consumption
5.1.3. Cooperative, Complementary Transmission Reliability of UAVs
5.1.4. System Utility and Problem Formulation
5.2. UAV Coalition Optimization for System Utility Maximization
5.2.1. Coalition Formation Game
5.2.2. CO-CFG Algorithm
| Algorithm 2 CO-CFG Algorithm |
|
6. Simulation Results
6.1. Performance of User-Clustering-Based Caching Strategy
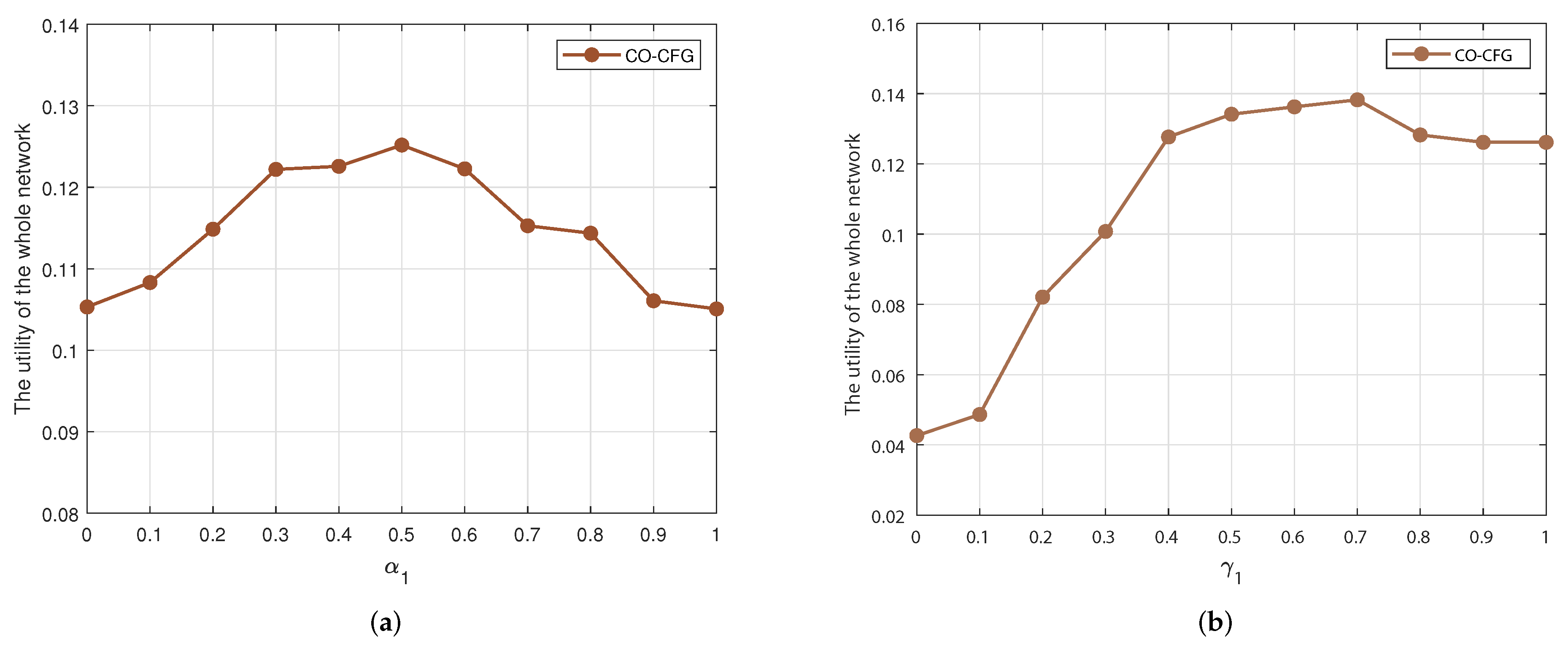
6.2. Performance of Multi-UAV Cooperative, Complementary Transmission
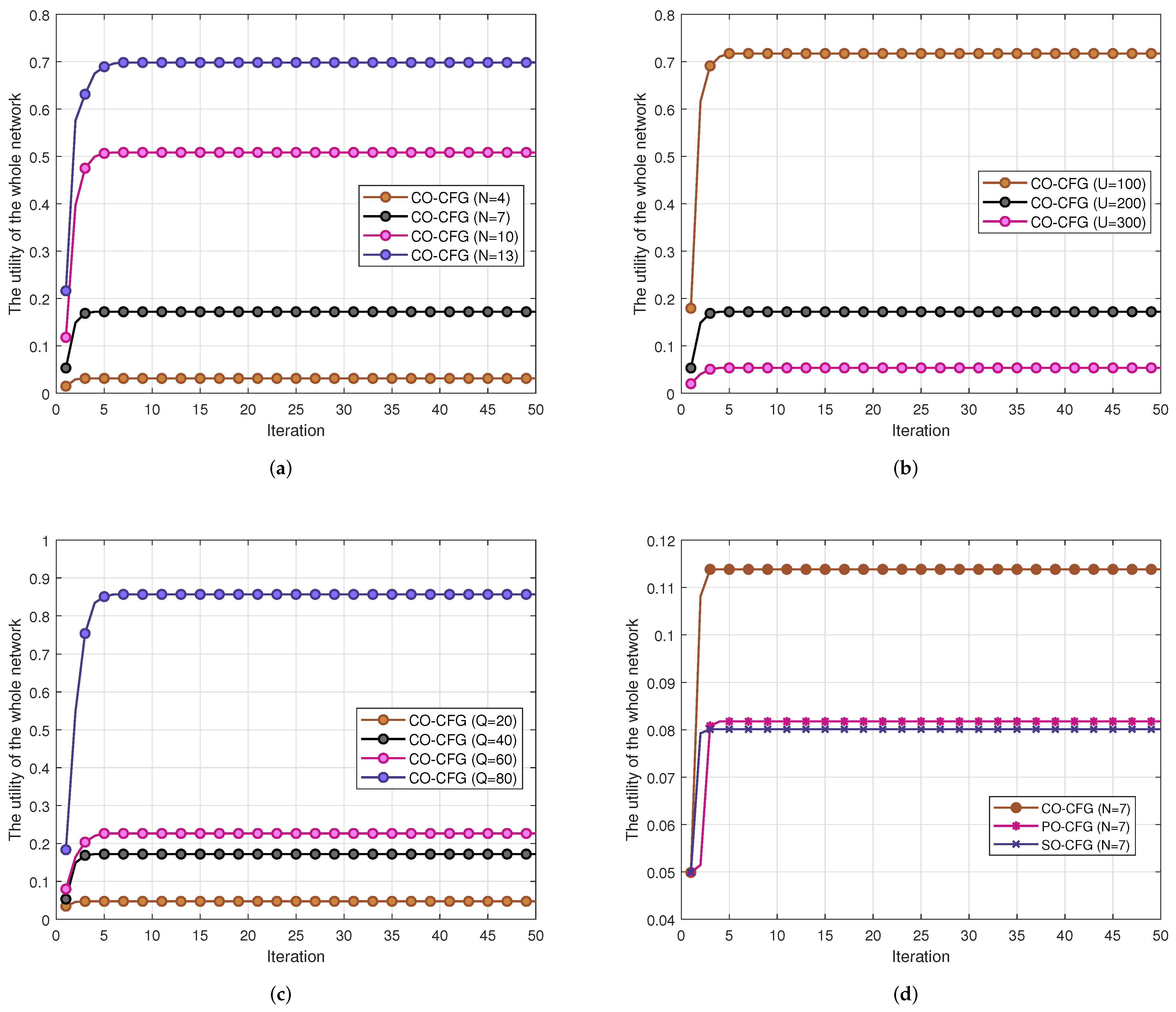
6.3. Convergence Performance
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 4G | 4th Generation Mobile Networks |
| 5G | 5th Generation Mobile Networks |
| BS | Base Station |
| MBS | Macro Base Station |
| SBS | Small Base Station |
| UAV | Unmanned Aerial Vehicle |
| EE | Energy Efficiency |
| D2D | Device-to-Device |
| HetNets | Heterogeneous Networks |
| QoE | Quality of Experience |
| QoS | Quality of Service |
| IoT | Internet of Thing |
| HPPP | Homogeneous Poisson Point Process |
| LoS | Line-of-Sight |
| NLoS | Non-Line-of-Sight |
| SNR | Signal-to-Noise Ratio |
| SC | Spectral Clustering |
| MOS | Mean Opinion Score |
| CFG | Coalition Formation Game |
| CO-CFG | Cooperation-Order-based Coalition Formation Game |
| PO-CFG | Pareto-Order-based Coalition Formation Game |
| SO-CFG | Selfish-Order-based Coalition Formation Game |
| NE | Nash Equilibrium |
| EPG | Exact Potential Game |
Appendix A
Appendix A.1
Appendix A.2
References
- Luong, N.C.; Wang, P.; Niyato, D.; Liang, Y.; Han, Z.; Hou, F. Applications of Economic and Pricing Models for Resource Management in 5G Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3298–3339. [Google Scholar] [CrossRef] [Green Version]
- Teng, Y.; Liu, M.; Yu, F.R.; Leung, V.C.M.; Song, M.; Zhang, Y. Resource Allocation for Ultra-Dense Networks: A Survey, Some Research Issues and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 2134–2168. [Google Scholar] [CrossRef]
- Bastug, E.; Bennis, M.; Debbah, M. Living on the edge: The role of proactive caching in 5G wireless networks. IEEE Commun. Mag. 2014, 52, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Zahed, M.I.A.; Ahmad, I.; Habibi, D.; Phung, Q.V.; Mowla, M.M.; Waqas, M. A Review on Green Caching Strategies for Next Generation Communication Networks. IEEE Access 2020, 8, 212709–212737. [Google Scholar] [CrossRef]
- Li, L.; Zhao, G.; Blum, R.S. A Survey of Caching Techniques in Cellular Networks: Research Issues and Challenges in Content Placement and Delivery Strategies. IEEE Commun. Surv. Tutor. 2018, 20, 1710–1732. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Guo, S.; Xiao, S.; Pan, M.; Zhou, X.; Li, G.Y.; Wu, G.; Li, S. Resource Allocation for Cooperative D2D-Enabled Wireless Caching Networks. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Lee, M.; Molisch, A.F. Caching Policy and Cooperation Distance Design for Base Station-Assisted Wireless D2D Caching Networks: Throughput and Energy Efficiency Optimization and Tradeoff. IEEE Trans. Wirel. Commun. 2018, 17, 7500–7514. [Google Scholar] [CrossRef]
- Li, P.; Gong, S.; Gao, S.; Hu, Y.; Pan, Z.; You, X. Delay-constrained sleeping mechanism for energy saving in cache-aided ultra-dense network. Sci. China Inf. Sci. 2019, 62, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Keshavarzian, I.; Zeinalpour-Yazdi, Z.; Tadaion, A. Energy-Efficient Mobility-Aware Caching Algorithms for Clustered Small Cells in Ultra-Dense Networks. IEEE Trans. Veh. Technol. 2019, 68, 6833–6846. [Google Scholar] [CrossRef]
- Hajri, S.E.; Assaad, M. Energy Efficiency in Cache-Enabled Small Cell Networks With Adaptive User Clustering. IEEE Trans. Wirel. Commun. 2018, 17, 955–968. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Fan, S.; Deng, G.; Tian, H. Local Content Cloud based Cooperative Caching Placement for Edge Caching. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar]
- Jaafar, W.; Ajib, W.; Elbiaze, H. Caching Optimization for D2D-Assisted Heterogeneous Wireless Networks. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar]
- Zhang, T.; Fan, H.; Loo, J.; Liu, D. User Preference Aware Caching Deployment for Device-to-Device Caching Networks. IEEE Syst. J. 2019, 13, 226–237. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Jiang, C.; Gelenbe, E.; Zhang, H.; Ren, Y.; Quek, T.Q.S. Double Auction Mechanism Design for Video Caching in Heterogeneous Ultra-Dense Networks. IEEE Trans. Wirel. Commun. 2019, 18, 1669–1683. [Google Scholar] [CrossRef]
- Routaib, H.; Badidi, E.; Elmachkour, M.; Sabir, E.; ElKoutbi, M. Modeling and evaluating a cloudlet-based architecture for Mobile Cloud Computing. In Proceedings of the 2014 9th International Conference on Intelligent Systems: Theories and Applications (SITA-14), Rabat, Morocco, 7–8 May 2014; pp. 1–7. [Google Scholar]
- Xia, Q.; Ren, W.; Xu, Z.; Wang, X.; Liang, W. When Edge Caching Meets a Budget: Near Optimal Service Delivery in Multi-Tiered Edge Clouds. IEEE Trans. Serv. Comput. 2021. [Google Scholar] [CrossRef]
- Cordero, J.A.; Lou, W. Modeling Dynamic Resource Allocation in the Edge. In Proceedings of the 2019 8th International Conference on Performance Evaluation and Modeling in Wired and Wireless Networks (PEMWN), Paris, France, 26–28 November 2019; pp. 1–6. [Google Scholar]
- Cordero, J.A.; Lou, W. Take your time, get it closer: Content dissemination within mobile pedestrian crowds. Wirel. Netw. 2019, 25, 3385–3403. [Google Scholar] [CrossRef]
- Wu, B.; Chen, T.; Wang, X. A Combinatorial Bandit Approach to UAV-aided Edge Computing. In Proceedings of the 2020 54th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 1–4 November 2020; pp. 304–308. [Google Scholar]
- Chen, M.; Mozaffari, M.; Saad, W.; Yin, C.; Debbah, M.; Hong, C.S. Caching in the Sky: Proactive Deployment of Cache-Enabled Unmanned Aerial Vehicles for Optimized Quality-of-Experience. IEEE J. Sel. Areas. Commun. 2017, 35, 1046–1061. [Google Scholar] [CrossRef]
- Zhao, N.; Cheng, F.; Yu, F.R.; Tang, J.; Chen, Y.; Gui, G.; Sari, H. Caching UAV Assisted Secure Transmission in Hyper-Dense Networks Based on Interference Alignment. IEEE Trans. Commun. 2018, 66, 2281–2294. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Wang, Y.; Liu, Y.; Xu, W.; Nallanathan, A. Cache-Enabling UAV Communications: Network Deployment and Resource Allocation. IEEE Trans. Wirel. Commun. 2020, 19, 7470–7483. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Zhao, N.; Yao, N. A Proactive Joint Strategy on Trajectory and Caching for UAV-Assisted Networks: A Data-Driven Distributionally Robust Approach. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC), Xiamen, China, 28–30 July 2021; pp. 752–757. [Google Scholar]
- Xu, X.; Zeng, Y.; Guan, Y.L.; Zhang, R. Overcoming Endurance Issue: UAV-Enabled Communications With Proactive Caching. IEEE J. Sel. Areas. Commun. 2018, 36, 1231–1244. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Yang, J.; Xu, H.; Song, H.; Zheng, G. Multimedia Data Throughput Maximization in Internet-of-Things System Based on Optimization of Cache-Enabled UAV. IEEE Internet Things. J. 2019, 6, 3525–3532. [Google Scholar] [CrossRef]
- Chen, Y.; Gong, X.; Ou, R.; Duan, L.; Zhang, Q. Crowdcaching: Incentivizing D2D-Enabled Caching via Coalitional Game for IoT. IEEE Internet Things. J. 2020, 7, 5599–5612. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Wu, Q.; Luo, Y.; Xu, Y.; Chen, X.; Anpalagan, A.; Zhang, D. Context Awareness Group Buying in D2D Networks: A Coalition Formation Game-Theoretic Approach. IEEE Trans. Veh. Technol. 2018, 67, 12259–12272. [Google Scholar] [CrossRef]
- Wang, T.; Song, L.; Han, Z.; Jiao, B. Dynamic Popular Content Distribution in Vehicular Networks using Coalition Formation Games. IEEE J. Sel. Areas. Commun. 2013, 31, 538–547. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Wang, W.; Wang, Y.; Zhang, Z. On the Cooperation for Content Caching from a Coalitional Game Perspective. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling air-to-ground pathloss for low altitude platforms in urban environments. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2898–2904. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef] [Green Version]
- Breslau, L.; Cao, P.; Fan, L.; Phillips, G.; Shenker, S. Web caching and zipf-like distributions: Evidence and implications. In Proceedings of the IEEE INFOCOM’99. Conference on Computer Communications, Eighteenth Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 21–25 March 1999; pp. 126–134. [Google Scholar]
- Apt, K.R.; Witzel, A. A generic approach to coalition formation. Int.Game Theory Rev. 2009, 11, 347–367. [Google Scholar] [CrossRef] [Green Version]
- Monderer, D.; Shapley, L.S. Potential games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]




| Symbol | Description |
|---|---|
| N | Number of UAVs |
| U | Number of users |
| F | Quantity of content items |
| Q | Cache capacity of UAV |
| S | Size of each content item |
| B | Bandwidth of downlink data link |
| Bandwidth of backhaul link | |
| Bandwidth of cooperation link | |
| Indicator of whether UAV n caches content f | |
| Indicator of whether user u requests content f | |
| Transmission power of MBS | |
| Transmission power of UAV | |
| H | Flight height of UAV |
| Two-dimensional plane position of MBS, UAV, user | |
| Distance between MBS and UAV, UAV and user, UAV and UAV | |
| pathloss of MBS-to-UAV link, UAV-to-User link, UAV-to-UAV link | |
| SNR of MBS-to-UAV link, UAV-to-User link, UAV-to-UAV link | |
| Data rate of MBS-to-UAV link, UAV-to-User link, UAV-to-UAV link | |
| Delay of MBS-to-UAV link, UAV-to-User link, UAV-to-UAV link |
| Parameter | Value |
|---|---|
| Quantity of content items | 100 |
| UAV height H | 100 m |
| UAV transmission power | 30 dBm |
| MBS transmission power | 43 dBm |
| Variance of the Gaussian noise | −174 dBm/Hz |
| Bandwidth of data link B | 20 MHz |
| Bandwidth of backhaul link | 10 MHz |
| Bandwidth of cooperative link | 10 MHz |
| Size of content S | 10 Mbits |
| Zipf parameter | 0.8 |
| Reliability parameter | |
| Attenuation factors for LoS link | 1.6 dBm |
| Attenuation factors for NLoS link | 23 dBm |
| Carrier frequency f | 5 GHz |
| X | 11.9 |
| Y | 0.13 |
| pathloss exponent | 2 |
| Excessive pathloss coefficient | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhong, X.; Wu, F.; Chen, X.; Zhang, S.; Dong, N. Multi-UAV Content Caching Strategy and Cooperative, Complementary Content Transmission Based on Coalition Formation Game. Sensors 2022, 22, 3123. https://doi.org/10.3390/s22093123
Sun Y, Zhong X, Wu F, Chen X, Zhang S, Dong N. Multi-UAV Content Caching Strategy and Cooperative, Complementary Content Transmission Based on Coalition Formation Game. Sensors. 2022; 22(9):3123. https://doi.org/10.3390/s22093123
Chicago/Turabian StyleSun, Yanzan, Xinlin Zhong, Fan Wu, Xiaojing Chen, Shunqing Zhang, and Nan Dong. 2022. "Multi-UAV Content Caching Strategy and Cooperative, Complementary Content Transmission Based on Coalition Formation Game" Sensors 22, no. 9: 3123. https://doi.org/10.3390/s22093123
APA StyleSun, Y., Zhong, X., Wu, F., Chen, X., Zhang, S., & Dong, N. (2022). Multi-UAV Content Caching Strategy and Cooperative, Complementary Content Transmission Based on Coalition Formation Game. Sensors, 22(9), 3123. https://doi.org/10.3390/s22093123







